A&A 421, 1-8 (2004)
DOI: 10.1051/0004-6361:20034523
S. K. Chakrabarti1,2 - K. Acharyya2 - D. Molteni3
1 - S. N. Bose National Centre for Basic Sciences, Salt Lake, Kolkata 700098, India
2 -
Centre for Space Physics, Chalantika 43, Garia Station Rd., Kolkata, 700084, India
3 -
Dipartimento di Fisica e Tecnologie Relative, Viale delle Scienze, 90128 Palermo, Italy
Received 16 October 2003 / Accepted 16 January 2004
Abstract
We present the results of several numerical simulations of two dimensional
axi-symmetric accretion flows around black holes using Smoothed Particle Hydrodynamics (SPH)
in the presence of cooling effects. We consider both stellar black holes and
super-massive black holes. We observe that due to both radial and vertical
oscillation of shock waves in the accretion flow, the luminosity and average thermal energy
content of the inner disk exhibit very interesting behaviour. When power
density spectra are taken, quasi-periodic variabilities are seen at a few
Hz and also occasionally at hundreds of Hz for stellar black holes.
For super-massive black holes, the time scale of the oscillations
ranges from hours to weeks. The power density spectra have a flat
top behavior with average rms amplitude of a few percent
and a broken power-law behavior. The break frequency is generally found to be
close to the frequency where the shock oscillates.
Key words: methods: numerical - black hole physics - hydrodynamics - instabilities - shock waves
X-rays emitted by galactic black hole candidates are known to exhibit quasi-periodic variations (QPVs). Today, there are almost a dozen confirmed stellar mass black hole candidates for which QPVs are regularly observed, some at normal frequencies (0.1-10 Hz) and some with frequencies of hundreds of Hz. While it is conceptually easier to explain such variations when there is a hard surface, as on a neutron star (e.g., Shaham 1987), in black hole candidates they are difficult to understand as there are no surfaces from which a perturbation could be reflected back so as to produce a sustained oscillation of significant amplitude.
In a very important work, Langer et al. (1981) first suggested that
in the presence of cooling effects standing shocks on a white dwarf surface can
oscillate and in fact the oscillation may also subside when
cooling is increased (Chanmugam et al. 1985). While a black hole does not have a
hard surface like neutron stars or white dwarfs, the centrifugal force in accretion matter
close to a black hole can become strong enough to actually slow down matter and form
centrifugal-pressure-supported axisymmetric standing shocks
(Chakrabarti 1989) depending on specific energy and angular momentum
(this region will be referred to as CENBOL, centrifugal pressure dominated boundary layer).
In the particle dynamics picture, the appearance of a discontinuity can be argued this way: the
centrifugal force
![]() grows more rapidly
(for constant or almost constant specific angular momentum
grows more rapidly
(for constant or almost constant specific angular momentum ![]() )
than the gravitational force
)
than the gravitational force
![]() and they become comparable at a distance of
and they become comparable at a distance of
![]() ,
where M is the mass of the central compact object.
In fluid dynamics, because of the addition of thermal pressure and/or radiation pressure,
such a balance takes place farther out where a shock may develop.
The almost constancy of angular momentum comes into being
primarily because, as has been shown by extensive work done earlier (Chakrabarti 1996a),
the viscosity timescale
,
where M is the mass of the central compact object.
In fluid dynamics, because of the addition of thermal pressure and/or radiation pressure,
such a balance takes place farther out where a shock may develop.
The almost constancy of angular momentum comes into being
primarily because, as has been shown by extensive work done earlier (Chakrabarti 1996a),
the viscosity timescale
![]() is much longer than
the infall time scale
r3/2/(GM)1/2,
is much longer than
the infall time scale
r3/2/(GM)1/2,
![]() being the kinematic viscosity.
It was shown by Molteni et al. (1996, hereafter referred
to as MSC96) and Ryu et al. (1997, hereafter
RCM 1997) that these shocks may also oscillate in the presence of cooling.
These oscillations are explained to be due to a resonance between the dominant
cooling time scale and the infall time scale, and the cooling could be due to
thermal/non-thermal radiative effects (as in MSC96), or to
dynamical cooling due to outflows (as in RCM97) or both. This shock
forms in low-angular-momentum (in the sense mentioned), quasi-spherical
flows which may or may not surround a Keplerian disk located in the equatorial plane. In case the latter disk is present and the soft photons emitted are intercepted, inverse-Comptonized and re-emitted by the post-shock region, as in the two-component advective flow model (Chakrabarti
& Titarchuk 1995; hereafter CT95), then, as the shock oscillates,
the intensity of hard X-rays is also modulated at the same frequency.
being the kinematic viscosity.
It was shown by Molteni et al. (1996, hereafter referred
to as MSC96) and Ryu et al. (1997, hereafter
RCM 1997) that these shocks may also oscillate in the presence of cooling.
These oscillations are explained to be due to a resonance between the dominant
cooling time scale and the infall time scale, and the cooling could be due to
thermal/non-thermal radiative effects (as in MSC96), or to
dynamical cooling due to outflows (as in RCM97) or both. This shock
forms in low-angular-momentum (in the sense mentioned), quasi-spherical
flows which may or may not surround a Keplerian disk located in the equatorial plane. In case the latter disk is present and the soft photons emitted are intercepted, inverse-Comptonized and re-emitted by the post-shock region, as in the two-component advective flow model (Chakrabarti
& Titarchuk 1995; hereafter CT95), then, as the shock oscillates,
the intensity of hard X-rays is also modulated at the same frequency.
If our shock oscillation solution is correct, then a large number of simple predictions could be made: (a) the harder radiation coming from the hot, post-shock region would primarily participate in QPVs while the softer radiation would have less power. This was verified by Chakrabarti & Manickam (2000, hereafter CM00) and Rao et al. (2000). (b) The stronger a shock is, the stronger is the thermally driven outflow rate. Thus, the outflow from the post-shock region depends on the shock strength, i.e., the spectral states (Chakrabarti 1999). This has also been tested by various observations (e.g., Dhawan et al. 2000). (c) In case of outflows, the electron density in the post-shock region is reduced and the Comptonized spectrum should be softened. Chakrabarti et al. (2003) showed that indeed the presence/absence of outflows does change the spectral slope in the hard X-ray region. These observations vindicate that the Comptonized photon, and the major part of the outflows both come out of the post-shock region. Thus, a thorough study of the behavior of CENBOL, especially when it is time dependent, is needed.
In the present paper, we carry out numerical simulation of thick,
inviscid, rotating axisymmetric flows, in the presence of
cooling effects for a large region of the parameter space.
The hot electrons in the CENBOL
reprocess soft photons and generally enhance their
energy before these photons escape. The degree by which the
energy is transferred depends on the so-called
Compton y parameter (Rybicki & Lightman 1979),
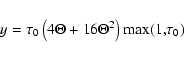 |
(1) |
Unlike MSC96, where symmetry around the equatorial plane was assumed (and thus the simulation was carried out only in one quadrant), we consider both halves above and below the equatorial plane. In this way, allowance is made not only for radial oscillations of the shocks but also for vertical oscillations. Earlier, in a simulation of a non-shock flow it was observed that the outgoing winds could interact with the inflow and the interface might undulate (Molteni et al. 2001). So we expect that shocks should also have vertical oscillations in presence of winds. In the present simulations, we observe that the shocks do oscillate both vertically and horizontally for a range of inflow parameters, and the PDS of the light curve obtained by our numerical simulation does have characteristics similar to the PDS of the observed light curves of the black hole candidates. The PDS of a numerically simulated light curve has a flat top up to a break frequency, and an rms amplitude in the range of a few percent depending on the accretion rate of the flow. Considering that an axisymmetric shock fundamentally separates a flow into a fast moving (lower density) supersonic and a slow moving (higher density) sub-sonic region, it should not be surprising that its oscillation frequency will generally lie at or near the break frequency in the power law. Of course, shocks are not infinitesimally thin. Neither is it true that they exhibit only a single mode of oscillation. Thus broad and often multiple peaks are expected. This is precisely what we see. What is more, since the inner sonic point also separates the flow into two parts, namely, one with the disk-like behavior and the one with free-fall behavior, there is often a weak peak in the PDS at some hundreds of Hz, perhaps corresponding to an oscillation of this inner region. We shall show these as well.
In the next section, we present the basic setup of our numerical simulation. In Sect. 3 we present some results of the simulation for galactic and extra-galactic black holes and analyze them to demonstrate shock oscillations. From the PDS of the "simulated'' light curves, we show that there are sharp peaks at certain frequencies only. The PDS seems to have the familiar flat top shape with a break. In Sect. 4, we discuss possible cause of the behaviour of the shocks. Finally, in Sect. 5 we draw our conclusions.
We are interested in simulating the behavior of an axisymmetric, inviscid flow
in the presence of cooling effects. Unlike an ordinary star, a black
hole is capable of accreting matter even in the absence of viscosity
when the pressure is large enough. However, if the specific angular
momentum is less than the marginally stable value (
3.67 GM1/c for
a Schwarzschild black hole of mass M1), even a cool, non-viscid
gas can enter a black hole without any problem. We chose the
specific angular momentum of the flow ![]() to be lower compared to this value
everywhere. This makes
to be lower compared to this value
everywhere. This makes
![]() ,
the Keplerian value,
everywhere in the flow. We call such a flow a "sub-Keplerian'' flow. The motivation for
studying such a flow stems from the fact that accretion processes
into a black hole are necessarily transonic, and the flow has to be
sub-Keplerian near the horizon. Furthermore, a flow can have a
substantial amount of sub-Keplerian matter itself because of
accretion of winds from the companion. The wind of velocity
,
the Keplerian value,
everywhere in the flow. We call such a flow a "sub-Keplerian'' flow. The motivation for
studying such a flow stems from the fact that accretion processes
into a black hole are necessarily transonic, and the flow has to be
sub-Keplerian near the horizon. Furthermore, a flow can have a
substantial amount of sub-Keplerian matter itself because of
accretion of winds from the companion. The wind of velocity
![]() ,
having "zero'' angular momentum with respect to the
mass-lossing star of mass M2 and radius R2 has an angular momentum of
,
having "zero'' angular momentum with respect to the
mass-lossing star of mass M2 and radius R2 has an angular momentum of
![]() ,
where
,
where
![]() cm is the radius of the accretion disk. For typical
values:
cm is the radius of the accretion disk. For typical
values: ![]()
![]() 1033 gm,
1033 gm,
![]() cm and we get,
in units of 2GM1/c,
cm and we get,
in units of 2GM1/c,
![]() with
with
![]() .
Hence,
our choice of 1.75 which is averaged over the entire
flow (thus could be much smaller than
.
Hence,
our choice of 1.75 which is averaged over the entire
flow (thus could be much smaller than ![]() )
is justified.
Recent observations do indicate the presence of both Keplerian
and sub-Keplerian components (Smith et al. 2002) in half a dozen
black hole components.
)
is justified.
Recent observations do indicate the presence of both Keplerian
and sub-Keplerian components (Smith et al. 2002) in half a dozen
black hole components.
It was shown by Chakrabarti (1989, 1996a) that in the large region
of the parameter space spanned by the specific angular momentum ![]() and energy
and energy ![]() a stable standing shock may form in accretion whenever
the Rankine-Hugoniot conditions are satisfied. Here, the flow first passes through the
outer saddle-type sonic point, then through a standing shock and finally through the
inner saddle-type sonic point. It was subsequently shown by MSC96 and Ryu et al. (1997) that even when the parameters of the
injected flow are outside this region oscillating shocks may form.
In the present paper we use Smoothed Particle Hydrodynamics (SPH) to do the
simulations as in MSC96, but we use both halves of the flow
to inject matter. The code has already been tested for its accuracy against
theoretical solutions already (Chakrabarti & Molteni 1993, MSC96) and we do not repeat this here.
We just want to recall that the "pseudo''-particles have been chosen
to be "toroidal'' in shape and they preserve angular momentum very
accurately (Molteni et al. 1996). In MSC96,
suggestion was made that radial oscillations of the shock may
take place when the infall time in the post-shock region is comparable to the
cooling time scale. Presently, we concentrate on the vast region of the parameter space
where both the radial and vertical oscillations are present.
a stable standing shock may form in accretion whenever
the Rankine-Hugoniot conditions are satisfied. Here, the flow first passes through the
outer saddle-type sonic point, then through a standing shock and finally through the
inner saddle-type sonic point. It was subsequently shown by MSC96 and Ryu et al. (1997) that even when the parameters of the
injected flow are outside this region oscillating shocks may form.
In the present paper we use Smoothed Particle Hydrodynamics (SPH) to do the
simulations as in MSC96, but we use both halves of the flow
to inject matter. The code has already been tested for its accuracy against
theoretical solutions already (Chakrabarti & Molteni 1993, MSC96) and we do not repeat this here.
We just want to recall that the "pseudo''-particles have been chosen
to be "toroidal'' in shape and they preserve angular momentum very
accurately (Molteni et al. 1996). In MSC96,
suggestion was made that radial oscillations of the shock may
take place when the infall time in the post-shock region is comparable to the
cooling time scale. Presently, we concentrate on the vast region of the parameter space
where both the radial and vertical oscillations are present.
Table 1: Inputs and extracted parameters for the model runs.
In the context of galactic black holes one class of QPVs have been observed that are commonly
known as Quasi-Periodic Oscillations or QPOs. Our solutions for QPVs are so generic that
we believe that QPVs should be observed even for super-massive black holes.
Actually there are indications that QPOs in supermassive
black holes may have been observed (Halpern & Marshall 1996). Supermassive
black holes are believed to be fueled by low angular momentum matter generated from
winds of nearby stars. So, a similar consideration
as that for wind accreting galactic black holes will apply. As far as Comptonization
is concerned, we use the following simple procedure: (a) we use an accretion rate
![]() and run the code with bremsstrahlung cooling alone. (b) We get the temperature
of the electrons and the optical depth
and run the code with bremsstrahlung cooling alone. (b) We get the temperature
of the electrons and the optical depth
![]() of the "mean'' size of the CENBOL region
(
of the "mean'' size of the CENBOL region
(![]() in Table 1). To get the corresponding physical parameters (as if the Compton cooling were included to begin with) (c) we assume that the injected soft
photons have energy
in Table 1). To get the corresponding physical parameters (as if the Compton cooling were included to begin with) (c) we assume that the injected soft
photons have energy ![]() 1 kev for the stellar mass black holes and
1 kev for the stellar mass black holes and ![]() 0.01 kev for the
massive black holes and using that (d) we compute the enhancement factor
0.01 kev for the
massive black holes and using that (d) we compute the enhancement factor ![]() from DLC91
for uniform spherical geometry for this injected photon and the electron temperature
(assumed to be lower by a factor of
from DLC91
for uniform spherical geometry for this injected photon and the electron temperature
(assumed to be lower by a factor of
![]() than the proton temperature (e.g., Rees 1984)) obtained
in each run. (e) We reduce the accretion
rate
than the proton temperature (e.g., Rees 1984)) obtained
in each run. (e) We reduce the accretion
rate
![]() by this
by this ![]() to get
to get
![]() and the optical depth by
and the optical depth by
![]() .
For self-consistency, we ensure that
.
For self-consistency, we ensure that
![]() thus obtained is the same as that used while computing
thus obtained is the same as that used while computing ![]() from DLC91. We also
compute the Compton y parameter to check if it has an acceptable value.
This procedure re-formulates the problem of inclusion of the exact cooling
processes into the case where a simplified cooling effect
may be used. Since we are interested in the integrated energy loss due to cooling
and not the spectral properties, this procedure should give reasonable answer.
from DLC91. We also
compute the Compton y parameter to check if it has an acceptable value.
This procedure re-formulates the problem of inclusion of the exact cooling
processes into the case where a simplified cooling effect
may be used. Since we are interested in the integrated energy loss due to cooling
and not the spectral properties, this procedure should give reasonable answer.
Table 1 lists the parameters for the Model runs
we report in this paper. There are basically two groups of
input. In Group A, we consider the black hole to be super-massive (
![]() )
and in Group B, we consider a stellar mass black hole (
)
and in Group B, we consider a stellar mass black hole (
![]() ). Different
runs are characterized by the injected matter density (gm/cc) at the outer boundary
of the numerical grid given in the second column. In all the model runs, we choose
the following parameters: the index
). Different
runs are characterized by the injected matter density (gm/cc) at the outer boundary
of the numerical grid given in the second column. In all the model runs, we choose
the following parameters: the index ![]() in the polytropic relation
in the polytropic relation
![]() (P is the isotropic pressure and
(P is the isotropic pressure and ![]() is the gas density) is 5/3, the outer
boundary
is the gas density) is 5/3, the outer
boundary
![]() ,
the specific angular momentum
,
the specific angular momentum
![]() (in units of 2GM/c),
injected radial velocity
(in units of 2GM/c),
injected radial velocity
![]() ,
the sound velocity a=0.04
and the vertical height h=15. The vertical height at
the outer boundary is so chosen that the flow remains in hydrostatic
equilibrium in the vertical direction at the point of injection
,
the sound velocity a=0.04
and the vertical height h=15. The vertical height at
the outer boundary is so chosen that the flow remains in hydrostatic
equilibrium in the vertical direction at the point of injection
![]() .
We measure all the
distances in units of the Schwarzschild radius of the black hole
.
We measure all the
distances in units of the Schwarzschild radius of the black hole
![]() ,
all the velocities in units of the velocity of
light c and all the masses in units of
,
all the velocities in units of the velocity of
light c and all the masses in units of
![]() ,
the mass of the
black hole. c and G are the velocity of light and the
gravitational constant respectively. Note that the
marginally stable (lowest possible angular momentum with a stable Keplerian
orbit) angular momentum is 1.83 in these units.
In the third column we give the enhancement factor
,
the mass of the
black hole. c and G are the velocity of light and the
gravitational constant respectively. Note that the
marginally stable (lowest possible angular momentum with a stable Keplerian
orbit) angular momentum is 1.83 in these units.
In the third column we give the enhancement factor ![]() that we obtained using DLC91 for our run
and in the fourth column we provide
that we obtained using DLC91 for our run
and in the fourth column we provide
![]() in units of
in units of
![]() ,
the Eddington rate, the effective accretion rate
in the presence of Comptonization. In the fifth column we give the Compton y parameters.
We assume soft injected photon of energy
,
the Eddington rate, the effective accretion rate
in the presence of Comptonization. In the fifth column we give the Compton y parameters.
We assume soft injected photon of energy
![]() keV for galactic black holes, and 0.01 keV
for supermassive black holes in order to calculate
keV for galactic black holes, and 0.01 keV
for supermassive black holes in order to calculate ![]() .
In the sixth column,
we give the average observed location of the shock.
In the seventh column, we give the average number of "pseudo''-particles present in
the disk in each run. In the eight column we present the QPV(QPO) frequency
in Hz as obtained from PDS. In the ninth column, the inverse of the infall timescale
.
In the sixth column,
we give the average observed location of the shock.
In the seventh column, we give the average number of "pseudo''-particles present in
the disk in each run. In the eight column we present the QPV(QPO) frequency
in Hz as obtained from PDS. In the ninth column, the inverse of the infall timescale
![]() corrected for a constant compression ratio R (
corrected for a constant compression ratio R (![]() 4 for a
strong shock) is provided as an indication of the expected oscillation time scale.
In the tenth column, the ratio of the quantities in the eighth and ninth column
is given. In the eleventh column, the rms amplitude in percentage is given,
we shall discuss in the next section. As in MSC96,
we choose the Paczynski-Wiita (1980) pseudo-Newtonian potential
to describe the space-time around the Schwarzschild black hole.
We believe that the result would remain unchanged if a true Schwarzschild
geometry were used, since the transonic properties do not change
very much. However, if a Kerr geometry were used, we expect the locations of the
inner sonic points and shocks to move inward (Chakrabarti 1996b) giving rise to higher QPO frequencies.
4 for a
strong shock) is provided as an indication of the expected oscillation time scale.
In the tenth column, the ratio of the quantities in the eighth and ninth column
is given. In the eleventh column, the rms amplitude in percentage is given,
we shall discuss in the next section. As in MSC96,
we choose the Paczynski-Wiita (1980) pseudo-Newtonian potential
to describe the space-time around the Schwarzschild black hole.
We believe that the result would remain unchanged if a true Schwarzschild
geometry were used, since the transonic properties do not change
very much. However, if a Kerr geometry were used, we expect the locations of the
inner sonic points and shocks to move inward (Chakrabarti 1996b) giving rise to higher QPO frequencies.
One of the important conditions of a standing shock
is that the thermal pressure (P) plus ram pressure (
![]() )
should be
continuous across the shock in the steady state, i.e.,
)
should be
continuous across the shock in the steady state, i.e.,
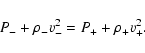 |
(2) |
In Group B Runs, within our parameter range, occasionally there were stronger shocks which oscillated radially, and the interaction between the outflow and the inflow produces vertical oscillations as well. Strong convection and turbulences were seen in the post-shock region which contributed to pushing the shock upstream. As a result, the shock location was not seen to change monotonically with accretion rate. The location is clearly determined by several effects: centrifugal force, thermal pressure, ram pressure, turbulent pressure and the cooling rate. The nature of the dependence has been discussed in earlier work in detail (Chakrabarti 1989; Chakrabarti & Molteni 1995; Molteni et al. 1994; MSC96) and we do not repeat this here. We will just recall that the shock location is independent of the location of the numerical boundary when the fundamental quantities such as specific angular momentum, accretion rate and specific energy at a given point (say, at the inner sonic point) are kept fixed. Cases B.1 and B.2 have very small Compton parameters and negligible Comptonization. Cases B.3 and B.4 are presented for academic purposes, just to indicate the effects of excess cooling. The Compton parameters are very large in these two cases.
For reference, we may add that the light crossing times
of the horizon for the two classes of black hole are
![]() s
and 10-4 s respectively. Since a steady shock (in the Schwarzschild geometry) may form anywhere between
s
and 10-4 s respectively. Since a steady shock (in the Schwarzschild geometry) may form anywhere between
![]() to
to
![]() ,
the QPO time-period, if assumed to be
related to the infall time
,
the QPO time-period, if assumed to be
related to the infall time
![]() ,
may be close
to 105 to 108 s for super-massive black holes, and close to 10-2 s
to 10 s for stellar mass black holes. Since we chose the outer boundary of
the simulation to be at
,
may be close
to 105 to 108 s for super-massive black holes, and close to 10-2 s
to 10 s for stellar mass black holes. Since we chose the outer boundary of
the simulation to be at
![]() ,
the infall time is roughly
,
the infall time is roughly
![]() in units of
in units of
![]() .
In order to trust the results of our simulations,
we ran the code for a duration several hundred times of this timescale (typically,
.
In order to trust the results of our simulations,
we ran the code for a duration several hundred times of this timescale (typically,
![]() or more). For a black hole of
or more). For a black hole of
![]() ,
this time corresponds to only 5-6 s of real time.
,
this time corresponds to only 5-6 s of real time.
First, we show examples of shock formation which exhibit radial and/or
vertical oscillations. Figures 1a-c shows the locations of the SPH particles (dots) along with the velocity vectors (arrows) of every fifth particle for clarity. This case corresponds to
case A.2. The matter distribution is shown at three different times (in units of
![]() )
illustrating the vertical and radial motions of
the shock which oscillates between 11 to 15 Schwarzschild radii, mostly
staying close to
)
illustrating the vertical and radial motions of
the shock which oscillates between 11 to 15 Schwarzschild radii, mostly
staying close to
![]() .
Some matter can be seen bouncing back
from the centrifugal barrier (boundary between the empty region along the vertical axis and the disk/jet
matter) near the axis and forming giant vortices which interact with the
inflow. These vortices push the post-shock region (
.
Some matter can be seen bouncing back
from the centrifugal barrier (boundary between the empty region along the vertical axis and the disk/jet
matter) near the axis and forming giant vortices which interact with the
inflow. These vortices push the post-shock region (
![]() )
alternately into the upper and the lower halves.
)
alternately into the upper and the lower halves.
![\begin{figure}
\par\includegraphics[height=7.1cm,width=8.8cm,clip]{0523fig1.eps}\end{figure}](/articles/aa/full/2004/25/aa0523-03/Timg82.gif) |
Figure 1:
Snapshots of simulations of accretion disks around a
|
| Open with DEXTER | |
In Figs. 2a-d we show the variation of the light curve in runs A.1-A.4 (marked by a-d in the figure). The light curves are the variations of the luminosity of bremsstrahlung radiation (in arbitrary units) for all the matter within r=50 flow as a function of time (in seconds). As the density is increased, the average thermal energy gradually goes down due to the presence of enhanced cooling and thus the luminosity also goes down. The average location of the shock decreases (MSC96, Table 1). The average number of pseudo-particles (Table 1) as well as the variation of the number of these particles also go down. As a result, with the increase in cooling loss, the light curves are found to be less noisy, and the amplitude of fluctuation is found to be lower.
![\begin{figure}
\par\includegraphics[height=8.2cm,width=8.5cm,clip]{0523fig2.eps}\end{figure}](/articles/aa/full/2004/25/aa0523-03/Timg84.gif) |
Figure 2:
a)- d): Total bremsstrahlung luminosity of the accretion flow
(in arbitrary units) as a function of time (in seconds).
The injected densities are a)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=7.9cm,width=7.9cm,clip]{0523fig3.eps}\end{figure}](/articles/aa/full/2004/25/aa0523-03/Timg85.gif) |
Figure 3:
a)- d): Power Density Spectra (PDS) of the four cases shown in Fig. 2.
Quasi Periodic Variation frequencies (denoted by
|
| Open with DEXTER | |
In Figs. 3a-d we show the results of the Fast Fourier Transform of these light curves using FTOOLS provided by NASA, the same software package that is used to
analyze observational results. We find the remarkable result of familiar
power density spectra (PDS) with a QPV near the break frequency.
The QPV frequencies, indicated by the arrows, are presented in Table 1.
We find that, perhaps due to the
presence of both the vertical and radial oscillations, there are
two QPVs; the frequency of the stronger one gradually increases with
the cooling, while that of the weaker one gradually decreases.
The occurrence of QPV frequencies at or near the break frequency of the PDS
can be understood by the following: according
to our solution, QPVs occur due to oscillations of the shock waves that separate
two "phases'' of the flow - the pre-shock flow is supersonic and weakly radiating,
while the post-shock flow is subsonic and strongly radiating. The former
region of the flow produces the "flat-top'' region in the PDS, while the latter region produces
a PDS with a slope ![]() -2. The rms amplitude of the flat top
region up to the break frequency is shown in Table 1. It has generally similar value at around 11.2% except in (d) where it is only around 3.3%. These rms values are similar to the observed results from black hole candidates as well. In Figs. 3a and b, where the cooling is weaker, the QPVs are less prominent and we had to search the locally significant peaks of the PDS for them. As the cooling becomes stronger, the peak becomes stronger.
-2. The rms amplitude of the flat top
region up to the break frequency is shown in Table 1. It has generally similar value at around 11.2% except in (d) where it is only around 3.3%. These rms values are similar to the observed results from black hole candidates as well. In Figs. 3a and b, where the cooling is weaker, the QPVs are less prominent and we had to search the locally significant peaks of the PDS for them. As the cooling becomes stronger, the peak becomes stronger.
In Figs. 4a-d, we present similar results as in Fig. 2 for stellar mass black holes (runs B.1-B.4 of Table 1). Here, too, the disk becomes cooler with increasing density and the light curve changes its character according to whether the shocks are strong or not. In the beginning of the simulation some transient behaviour is seen till the disk settles down within a second in real time. In Fig. 4c, the parameters are such that a strong shock forms and it heats up the disk while for the parameters in Fig. 4d a very weak shock forms. Shock oscillation produces a large amplitude noise in the B.3 case (Fig. 4c). In Figs. 5a-d, the PDS of these four runs are shown. The transient region has been excluded while doing the FFT. As in Figs. 3a-d, here too QPVs are observed. For small black holes QPVs occur at a few Hz and the QPV is located at or near the break frequency. Thus the characteristics are similar to those of QPOs observed from black hole candidates. Radial and vertical oscillations often produce multiple peaks in this case as well. Other details can be seen in Table 1. In Fig. 5c the peak is not very strong, perhaps due to the large amplitude noise that is produced in this case (See, Fig. 4c).
![\begin{figure}
\par\includegraphics[height=8.1cm,width=8.5cm,clip]{0523fig4.eps}\end{figure}](/articles/aa/full/2004/25/aa0523-03/Timg86.gif) |
Figure 4:
a)- d): Total bremsstrahlung luminosity of the accretion flow
(in arbitrary units) as a function of time (in seconds).
The injected densities are a)
|
| Open with DEXTER | |
Occasionally, peaks at a very high frequency could be seen, but these peaks are
found to be transient. If the entire light curve is broken into smaller
pieces, weak peaks at frequencies ![]() 100-300 Hz can be seen, though they
do not persist. One example of this is shown in Fig. 6a where the PDS of the
average thermal energy up to T=36 000 is plotted for the case B.4. In Figs. 6b and c
we show the flow pattern at two times which are separated by only 18 units
(0.0018 s). The shock located at
100-300 Hz can be seen, though they
do not persist. One example of this is shown in Fig. 6a where the PDS of the
average thermal energy up to T=36 000 is plotted for the case B.4. In Figs. 6b and c
we show the flow pattern at two times which are separated by only 18 units
(0.0018 s). The shock located at ![]()
![]() shows two distinctly different
shapes at these two times, bent up and bent down. Oscillation of a density enhancement at
shows two distinctly different
shapes at these two times, bent up and bent down. Oscillation of a density enhancement at ![]()
![]() would have a time period of
would have a time period of ![]()
![]() s, where R, the compression ratio, is
s, where R, the compression ratio, is ![]() 2 for a weak shock. The corresponding frequency is 333 Hz. The weak peak at
2 for a weak shock. The corresponding frequency is 333 Hz. The weak peak at
![]() Hz (Fig. 6a) may be due to this oscillation.
When data for much longer time is analyzed, this weak peak disappears completely.
Hz (Fig. 6a) may be due to this oscillation.
When data for much longer time is analyzed, this weak peak disappears completely.
![\begin{figure}
\par\includegraphics[height=7.8cm,width=8.1cm,clip]{0523fig5.eps}\end{figure}](/articles/aa/full/2004/25/aa0523-03/Timg90.gif) |
Figure 5:
a)- d): Power Density Spectra (PDS) of the four cases shown in Fig. 4.
Quasi Periodic Variation frequencies (denoted by
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=12cm,width=7.3cm,clip]{0523fig6.eps}\end{figure}](/articles/aa/full/2004/25/aa0523-03/Timg91.gif) |
Figure 6:
a)- c): a) Power density spectrum of the average thermal energy for case B.4 with time up to 3.6 s. Snapshots of simulations at closely separated times (marked) are
shown in b) and c). Only the inner 10 Schwarzschild radii are shown.
The dots are particle locations and arrows are
drawn for every fifth particle for clarity. Time (in units of
|
| Open with DEXTER | |
A shock remains steady, or "standing'' if Eq. (2) along with the specific energy and angular momentum flux remain continuous across it. These conditions are known as the Rankine-Hugoniot conditions (Landau & Lifshitz 1959). However, in the presence of an efficient energy extraction mechanism from the disk, whether through thermal/non-thermal radiation or through higher entropy flows along the shocked winds and outflows, the shock should move closer to the black hole as the pressure in the post-shock region (P+) drops. This is what is seen (see, Table 1), except in case B.3 where the turbulence was too strong to push the shock outward.
What about the oscillation time scale? We note that the cooling time
scale
![]() (where
(where ![]() is the
specific energy and a "dot'' indicates its time derivative) competes
with the infall time scale
is the
specific energy and a "dot'' indicates its time derivative) competes
with the infall time scale
![]() .
MSC96 argued that
when these two time scales agree roughly, i.e., roughly when the resonance takes place,
the shocks may start oscillating. The infall time
.
MSC96 argued that
when these two time scales agree roughly, i.e., roughly when the resonance takes place,
the shocks may start oscillating. The infall time ![]() is not easy to compute,
however. CM00 argued that the infall velocity need not be free-fall
velocity
is not easy to compute,
however. CM00 argued that the infall velocity need not be free-fall
velocity
![]() as the post-shock flow is reduced at the shock by at least
a factor of R, the compression ratio. Furthermore, the velocity is
highly modified due to turbulent pressure and angular motion and could be very slowly varying
in between the shock and the inner sonic point (CM00; Chakrabarti et al., in preparation).
A third and perhaps the most important parameter in predicting the time scale
is the rate of outflow from the post-shock region and the extent to which
the total mass of the disk oscillates. These two cooling mechanisms, namely, through radiation loss
and through outflow, are acting in opposite directions - enhanced thermal cooling
reduces the pressure gradient force, thereby reducing the wind rate.
The QPV timescale is expected to be close to
as the post-shock flow is reduced at the shock by at least
a factor of R, the compression ratio. Furthermore, the velocity is
highly modified due to turbulent pressure and angular motion and could be very slowly varying
in between the shock and the inner sonic point (CM00; Chakrabarti et al., in preparation).
A third and perhaps the most important parameter in predicting the time scale
is the rate of outflow from the post-shock region and the extent to which
the total mass of the disk oscillates. These two cooling mechanisms, namely, through radiation loss
and through outflow, are acting in opposite directions - enhanced thermal cooling
reduces the pressure gradient force, thereby reducing the wind rate.
The QPV timescale is expected to be close to
![]() .
In Table 1,
.
In Table 1,
![]() is presented. This ratio seems to be closer to 0.5 (justifying a near resonance condition)
except when the cooling is very strong (runs A.4 and B.4) when the
ratio drastically goes down. In these latter types of runs the shock moves very close to the
black hole and becomes very weak. The QPV could be due to the domination of the
interaction of the winds with the inflow. The two QPV frequencies
often seen could be due to the two types of cooling.
is presented. This ratio seems to be closer to 0.5 (justifying a near resonance condition)
except when the cooling is very strong (runs A.4 and B.4) when the
ratio drastically goes down. In these latter types of runs the shock moves very close to the
black hole and becomes very weak. The QPV could be due to the domination of the
interaction of the winds with the inflow. The two QPV frequencies
often seen could be due to the two types of cooling.
In this paper, we presented the discovery of Quasi-Periodic
Variations of emitted radiation through extensive time-dependent
numerical simulations. In earlier studies, such as in MSC96 and CM00, it was
suggested that shock oscillations might contribute to the observed QPOs.
In the present work, we studied shock oscillations in low-angular-momentum
axisymmetric flows around stellar and super-massive black holes for a range of accretion rates.
Unlike MSC96, we used fully two dimensional inflow (upper and lower halves)
and demonstrated that the shocks participate in vertical and radial oscillations.
Using PDS of light curves obtained from time dependent numerical
simulations of sub-Keplerian flows, we demonstrated that the QPVs
could be the cause of the observed QPOs.
We showed that the computed light curve produces power density spectra with
characteristic QPVs located at or near the break frequency which separates the flat-top
type and power-law type PDSs. For stellar black holes, we see QPVs at
reasonable frequencies (2-20 Hz). Very often high frequency QPVs
(at around 100-300 Hz) could be observed. We demonstrated that
this could be due to oscillation at the very inner edge where the flow becomes supersonic.
For Active Galaxies and Quasars, QPVs at very low frequencies (![]() 10-7-10-6 Hz)
are observed. Their properties are similar to those of QPOs observed in these candidates.
10-7-10-6 Hz)
are observed. Their properties are similar to those of QPOs observed in these candidates.
Based on our simulations we propose that the QPOs observed in black hole candidates are genuinely related to the accretion shock oscillations. Variation of QPO frequencies from time to time in the same object are thus manifestations of the variation of the Keplerian and sub-Keplerian accretion rates. In our work, we assumed a simple Paczynski-Wiita potential to study the shock properties around Schwarzschild black holes. Based on our experience with transonic flows, we are confident that none of the properties would be affected if the simulations were carried out in true Schwarzschild geometry. However, if a rotating black hole is used, the shocks will form much closer to the black hole (Chakrabarti 1996b), resulting in higher QPV frequencies.
Acknowledgements
S.K.C. thanks the support of Indian Space Research Organization for a RESPOND project. Discussions with Prof. A. R. Rao (TIFR) and Mr. A. Nandi (SNBNCBS) are also acknowledged.