A&A 421, 71-81 (2004)
DOI: 10.1051/0004-6361:20041090
D. F. Mota - C. van de Bruck
Astrophysics, University of Oxford, Keble Road, OX1 3RH, UK
Received 23 January 2004 / Accepted 30 March 2004
Abstract
We study the spherical collapse model in dark energy cosmologies, in which
dark energy is modelled as a minimally coupled scalar field. We first
follow the standard assumption that dark energy does not cluster on the
scales of interest. Investigating four different popular potentials in detail,
we show that the predictions of the spherical collapse model depend on the
potential used. We also investigate the dependence on the initial conditions.
Secondly, we investigate in how far perturbations in the quintessence field
affect the predictions of the spherical collapse model. In doing so, we
assume that the field collapses along with the dark matter. Although
the field is still subdominant at the time of virialisation, the predictions
are different from the case of a homogeneous dark energy component.
This will in particular be true if the field is non-minimally coupled.
We conclude that a better understanding of the evolution of dark energy
in the highly non-linear regime is needed in order to make predictions
using the spherical collapse model in models with dark energy.
Key words: cosmology: theory - cosmology: large-scale structure of Universe - cosmology: miscellaneous
The most surprising result of observational cosmology is the discovery that high redshift supernovae are less bright than expected (Perlmutter et al. 1999; Tonry et al. 2003). The interpretation of this finding is that the expansion of the universe accelerates, instead of slowing down. The matter responsible for this accelerated expansion is dubbed "dark energy'' and, according to General Relativity, needs to have negative pressure.
One important goal of cosmology is to obtain information about the nature of dark energy (see e.g., Ratra & Peebles 2002, for a review). The physical origin of dark energy is unknown and its likely that new physics beyond the standard model of particle physics will be needed to explain its properties. Scalar fields are plausible candidates for dark energy (see e.g., Wetterich 1988a,b; Ratra & Peebles 1988; Wetterich 1995) (these scalar fields are called quintessence fields). A distinctive feature of these models is that the properties of dark energy, such as its equation of state, generally vary during the cosmic history.
Cosmological observations probe the properties of dark energy. The anisotropy spectrum of the Cosmic Microwave Background (CMB), the shape of matter power spectrum and the distance-redshift relation are possible sources of information and will help us to distinguish between the different models of dark energy.
The behaviour of small perturbations in a scalar field and its effect on CMB anisotropies and structure formation has been investigated by a number of authors. However, the behaviour of quintessence during the gravitational collapse into the highly non-linear regime is not well understood and currently under investigation (see e.g., Bartelmann et al. 2002; Wetterich 2002; Dolag et al. 2003; Maccio et al. 2003a,b; Mainini et al. 2003a,b; Matarrese et al. 2003; Perrotta et al. 2004; Amendola 2003; Linder & Jenkins 2003; Alcubierre et al. 2002; Guzman & Urena-Lopez 2003, for recent work).
Usually it is assumed that there are no density fluctuations in the quintessence
field on cluster scales and below. The reason for this assumption is that, according to
linear perturbation theory, the mass of the field is very small (the associated
wavelength of the particle is of the order of the Hubble radius) and, hence, it
does not feel overdensities of the size of tenth of Mpc or smaller (Wang & Steinhardt 1998).
Let us assume for instance the particle physics
candidate for dark energy, a scalar field ![]() .
In the linear regime of the small cosmological
perturbations, it
can be shown that, during the matter dominated epoch, perturbations in
the scalar field are described by Hwang & Noh (2001)
.
In the linear regime of the small cosmological
perturbations, it
can be shown that, during the matter dominated epoch, perturbations in
the scalar field are described by Hwang & Noh (2001)
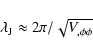 |
(2) |
The assumption of neglecting the effects of matter perturbations on the evolution of dark energy (and its backreaction) at small scales is indeed a good approximation when perturbations in the metric are very small. Notice however, if the field couples explicitly to matter, such as in the coupled quintessence scenario (see e.g., Wetterich 1995; Amendola 2000), the conclusion that the Jeans length is of order the horizon size should no longer hold.
Nevertheless, even if the field is not coupled, one should be careful when extrapolating the small-scale linear-regime results to the highly non-linear regime. Then, locally the flat FRW metric is not a good approximation anymore to describe the geometry of overdense regions. It is natural to think that once a dark matter overdensity decouples from the background expansion and collapses, the field inside the cluster feels the gravitational potential inside the overdensity and its evolution will be different from the background evolution. The backreaction effects in the highly non-linear regime could influence the evolution of perturbations in dark energy considerably, which in turn influence the evolution of the matter perturbation. In Bean & Magueijo (2002) it was suggested that the quintessence field could have an important impact in the highly non-linear regime. Due to these considerations, one may even ask if the quintessence field can be important even on galactic scales? It was speculated by Wetterich (2001, 2002) and by Arbey et al. (2001) that highly non-linear perturbations might indeed be important even on galactic scales. It was found that, at least in principle, the quintessence (or a scalar field) field could be responsible for the observed flat rotation curves in galaxies. In Padmanabhan & Choudhury (2002), Padmanabhan (2002), Bagla et al. 2003 and Causse (2003) more exotic models, based on tachyon fields, have been discussed and it was argued that the equation of state is scale-dependent.
If it turns out that backreaction effects of metric and density perturbations in dark matter could influence perturbations of quintessence on small scales, this could significantly change our understanding of structure formation on galactic and cluster scales in models with quintessence.
One popular model to study the non-linear growth in cold dark matter is the
spherical collapse model (see e.g., Padmanabhan 1995; or Peacock 1999).
The model was used first in the standard cold dark
matter scenario, but later also in the
cold dark matter model with cosmological constant (![]() CDM) by
Lahav et al. (1991). Recently,
the model was also used in quintessential scenarios and dark matter under the
assumption that dark energy does not cluster on scales much smaller than the
horizon (see e.g., Wang & Steinhardt 1998). It was then subsequently used in order to
make predictions for cosmological observations
(see e.g., Weller et al. 2001; Weinberg & Kamionkowski 2003; Battye & Weller 2003).
CDM) by
Lahav et al. (1991). Recently,
the model was also used in quintessential scenarios and dark matter under the
assumption that dark energy does not cluster on scales much smaller than the
horizon (see e.g., Wang & Steinhardt 1998). It was then subsequently used in order to
make predictions for cosmological observations
(see e.g., Weller et al. 2001; Weinberg & Kamionkowski 2003; Battye & Weller 2003).
The aim of this paper is two-fold. Firstly, we model dark energy as a non-minimally
coupled scalar field and consider four different
potentials in order to investigate how the predictions of the spherical
collapse model depend on the potential. In addition, the effect of the initial conditions
are investigated as well. Our second aim is to get a feel about the effects of perturbations
in the quintessence field on the predictions of the spherical collapse model.
In doing so, we investigate two extreme
cases: in the first case we follow the literature and assume that there are no
fluctuations in the quintessence field on the scales of interest. We then assume the
other extreme case and assume that the field inside the overdensity collapses
together with the dark matter![]() .
As we will see, the predictions of the
spherical collapse model will be quite different in this case, although
the field is only slightly non-linear (with density contrasts of order one)
at the time of virialisation, whereas dark matter is in the highly non-linear regime.
Our results imply that the predictions of the spherical collapse model
depend on the assumptions made for the clustering properties of the
quintessence in that model. Thus, a better understanding of the behaviour of the scalar field
in the highly non-linear regime is needed, if the spherical collapse model is
used for predictions involving large scale structures, such as cluster abundances,
weak and strong lensing, etc.
.
As we will see, the predictions of the
spherical collapse model will be quite different in this case, although
the field is only slightly non-linear (with density contrasts of order one)
at the time of virialisation, whereas dark matter is in the highly non-linear regime.
Our results imply that the predictions of the spherical collapse model
depend on the assumptions made for the clustering properties of the
quintessence in that model. Thus, a better understanding of the behaviour of the scalar field
in the highly non-linear regime is needed, if the spherical collapse model is
used for predictions involving large scale structures, such as cluster abundances,
weak and strong lensing, etc.
The paper is organised as follows: in Sect. 2 we describe briefly the spherical collapse model and write down the equations used. We also give an overview of the potentials used. In Sect. 3 we describe our assumptions and give the results of our numerical calculations. A discussion of the results and our conclusions can be found in Sect. 4.
We consider a flat, homogeneous and isotropic background universe with
scale factor a(t). Since we are interested in the matter dominated epoch,
when structure formation starts, we assume that the universe is filled with cold
dark matter of density
![]() and a
dark energy fluid, with energy-density
and a
dark energy fluid, with energy-density
![]() .
The equations that describe our background universe
are (we set
.
The equations that describe our background universe
are (we set
![]() throughout the paper):
throughout the paper):
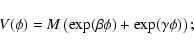 |
(6) |
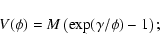 |
(7) |
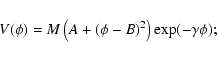 |
(8) |
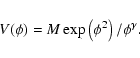 |
(9) |
In order to study the non-linear evolution of the gravitational collapse we make use of the spherical collapse (or infall) model. Here, one considers a spherical overdense region of radius R and models the interior spacetime as a FRW universe. This approach is equivalent to study the effect of perturbations to the Friedmann metric by considering spherically symmetric regions of different spatial curvature in accord with Birkhoff's theorem. Clearly, this model ignores any anisotropic effects of gravitational instability or collapse. However, the model is quite useful to learn about non-linear gravitational collapse and it is widely used as a starting point for (semi-) analytical models of large-scale structure formation.
Consider a spherical perturbation, in the cold dark matter fluid,
with (spatially) constant internal density which, at
an initial time, has an overdense amplitude
![]() and
and
![]() .
The cold dark matter density inside the cluster is then initially
.
The cold dark matter density inside the cluster is then initially
![]() ,
where
,
where ![]() is the initial
radius of the overdensity. The dark energy fluid density inside the overdensity,
is the initial
radius of the overdensity. The dark energy fluid density inside the overdensity,
![]() ,
will initially be considered the same as the
background one
,
will initially be considered the same as the
background one![]() .
At early times the sphere expands along with the background, but with a slightly
different expansion rate. For a
sufficiently large
.
At early times the sphere expands along with the background, but with a slightly
different expansion rate. For a
sufficiently large
![]() gravity prevents the sphere from
expanding for ever: at one point, the overdensity will stop expanding and
start to collapse. Three characteristic phases during the evolution
can then be identified:
gravity prevents the sphere from
expanding for ever: at one point, the overdensity will stop expanding and
start to collapse. Three characteristic phases during the evolution
can then be identified:
Once again, in the case of a scalar field, Eq. (11)
can be written as
We will evolve the spherical overdensity from high redshift until its
virialisation occurs. According to the virial theorem, equilibrium will be
reached when
![]() ;
;
![]() is the total kinetic energy
at virialisation and
is the total kinetic energy
at virialisation and
![]() is the mean-square velocity of the
components of the cluster, and U is the average total potential energy
in the sphere. It is useful to write the condition for virialisation to occur in
terms of the potential energies associated the different components of the
overdensity. The potential energy for a given component "x'' can be calculated from its general form in a spherical region (Landau & Lifshitz 1975):
is the mean-square velocity of the
components of the cluster, and U is the average total potential energy
in the sphere. It is useful to write the condition for virialisation to occur in
terms of the potential energies associated the different components of the
overdensity. The potential energy for a given component "x'' can be calculated from its general form in a spherical region (Landau & Lifshitz 1975):
In addition, we also discuss the linear growth factor
![]() for the four different potentials. The linear density contrast
for the four different potentials. The linear density contrast
![]() obeys
the equation
obeys
the equation
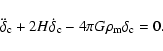 |
(17) |
The behaviour of dark energy during the evolution of a cluster can now be
obtained by numerically evolving the background Eqs. (3)-(5)
and the cluster Eqs. (10)-(12) until the
virialisation condition (16) holds. Additionally to
the four potentials mentioned above, we also have considered three different
types of large scale structure models: the Standard Cold Dark Matter model SCDM, the ![]() CDM model, and a model with dark energy with constant
equation of state
CDM model, and a model with dark energy with constant
equation of state
![]() (QCDM). The SCDM and the
(QCDM). The SCDM and the ![]() CDM
model was used to test our code and we will not give the results for these
models, as they are well known.
CDM
model was used to test our code and we will not give the results for these
models, as they are well known.
In next section we will make two assumptions about the function ![]() .
In one case we assume that the field is homogeneous all over the Universe,
so that the field inside the overdensity evolves just like the background. In the second case we
assume that the field collapses together with the dark matter. We would like
to point out that our assumptions are different from the ones
made in the first version of Lokas & Hoffman (2001), where it was assumed that dark energy
is homogeneous but a Friedmann-like equation was used to study the evolution of R(t).
.
In one case we assume that the field is homogeneous all over the Universe,
so that the field inside the overdensity evolves just like the background. In the second case we
assume that the field collapses together with the dark matter. We would like
to point out that our assumptions are different from the ones
made in the first version of Lokas & Hoffman (2001), where it was assumed that dark energy
is homogeneous but a Friedmann-like equation was used to study the evolution of R(t).
The form of ![]() chosen above is clearly not the
full truth. At least at very late times during the collapse of the
dark matter, especially when the density contrast in dark matter is very large
(
chosen above is clearly not the
full truth. At least at very late times during the collapse of the
dark matter, especially when the density contrast in dark matter is very large
(
![]() ),
the field should no longer feel the background metric,
i.e. expand with the background, but decouple from it. In
this regime, the evolution of dark energy could be different and influence the
details of the collapse.
The detail of this can only be obtained from a fully relativistic calculation,
which is beyond the scope of this paper. However, to get a feel of what
may happen we make now the other extreme assumption that the field follows
the dark matter collapse from the very beginning. That is, we assume that
),
the field should no longer feel the background metric,
i.e. expand with the background, but decouple from it. In
this regime, the evolution of dark energy could be different and influence the
details of the collapse.
The detail of this can only be obtained from a fully relativistic calculation,
which is beyond the scope of this paper. However, to get a feel of what
may happen we make now the other extreme assumption that the field follows
the dark matter collapse from the very beginning. That is, we assume that
![]() .
This is clearly not a realistic assumption either, but the results
we obtain are surprising and interesting in itself.
.
This is clearly not a realistic assumption either, but the results
we obtain are surprising and interesting in itself.
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig1.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg85.gif) |
Figure 1:
Quintessence model
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig2.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg87.gif) |
Figure 2:
Quintessence model
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig3.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg89.gif) |
Figure 3:
Quintessence model
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig4.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg91.gif) |
Figure 4:
Quintessence model
|
| Open with DEXTER | |
In these plots we show for all models the behaviour of the equation of
state inside the cluster and in the background (for the case ![]() ),
the density contrast in matter and field (again for
),
the density contrast in matter and field (again for ![]() ),
the ratio of the radius at turnaround
),
the ratio of the radius at turnaround
![]() and radius at
virialisation RV for both the case
and radius at
virialisation RV for both the case ![]() and an homogeneous scalar field,
the ratio of the energy densities in field and matter, the non-linear
density contrast for both cases and the growth factor for the models
compared to the
and an homogeneous scalar field,
the ratio of the energy densities in field and matter, the non-linear
density contrast for both cases and the growth factor for the models
compared to the ![]() CDM model.
CDM model.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{0129fig5.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg93.gif) |
Figure 5:
Model with constant equation of state w=-0.8.
The upper panel shows the predictions for
|
| Open with DEXTER | |
As it is clear from the upper right
plots, even in the ![]() case (ie. the quintessence field collapses
with together with matter), the field will be subdominant in the virialised
object. This can also be seen from the Figures on the right hand side in
the middle panels in Figs. 1-4: in all cases the ratio
case (ie. the quintessence field collapses
with together with matter), the field will be subdominant in the virialised
object. This can also be seen from the Figures on the right hand side in
the middle panels in Figs. 1-4: in all cases the ratio
![]() is much smaller than
one. Well before turnaround, i.e. while the density contrast in dark matter is smaller
than one, our results agree with what one would obtain from linear perturbation theory.
For
is much smaller than
one. Well before turnaround, i.e. while the density contrast in dark matter is smaller
than one, our results agree with what one would obtain from linear perturbation theory.
For ![]() ,
the perturbations in dark energy remain very small up to this point.
Even after turnaround, our results imply that fluctuations in the dark energy component
remain small, while dark matter enters the highly non-linear regime.
,
the perturbations in dark energy remain very small up to this point.
Even after turnaround, our results imply that fluctuations in the dark energy component
remain small, while dark matter enters the highly non-linear regime.
Concerning the clustering properties of the quintessence field,
it can significantly alter the predictions for the non-linear
density contrast
![]() at virialisation: assuming that the field
is inhomogeneous
at virialisation: assuming that the field
is inhomogeneous ![]() ,
for small virialisation redshifts the predictions
can differ by a factor of four or more. In the same way the predictions
for the ratio
,
for small virialisation redshifts the predictions
can differ by a factor of four or more. In the same way the predictions
for the ratio
![]() strongly depends on how the scalar
field behaves during the highly non-linear regime. The reason for this
is, that the just before the overdensity formally becomes a singularity,
the quintessence field becomes more and more important and changes the
evolution of R(t) during the last stages of the collapse. We remind the
reader that, in the Einstein-de Sitter model
strongly depends on how the scalar
field behaves during the highly non-linear regime. The reason for this
is, that the just before the overdensity formally becomes a singularity,
the quintessence field becomes more and more important and changes the
evolution of R(t) during the last stages of the collapse. We remind the
reader that, in the Einstein-de Sitter model
![]()
![]() At high virialisation redshifts, all models predict
At high virialisation redshifts, all models predict
![]() ,
only at low virialisation redshifts,
significant deviations can be expected due to the fact that the
dark energy becomes more and more important. Note that in the Albrecht-Skordis
model, the field behaves like a cosmological constant in the background (see Fig. 3).
Hence, one would expect that the differences to the
,
only at low virialisation redshifts,
significant deviations can be expected due to the fact that the
dark energy becomes more and more important. Note that in the Albrecht-Skordis
model, the field behaves like a cosmological constant in the background (see Fig. 3).
Hence, one would expect that the differences to the ![]() CDM model are small. This is
indeed the case, because
CDM model are small. This is
indeed the case, because
![]() and, hence,
and, hence,
![]() ,
as
it can be seen from Eq. (18). Thus, in this model, the
fluctuations in the quintessence field remain small and the field is
almost homogeneous.
,
as
it can be seen from Eq. (18). Thus, in this model, the
fluctuations in the quintessence field remain small and the field is
almost homogeneous.
In Fig. 5 we have plotted the case for a dark energy model with constant
equation of state w=-0.8. As it can clearly be seen, the predictions
for
![]() and
and
![]() for the cases of a homogeneous and
an inhomogeneous dark energy component are very small in this case. This
implies, that for models with constant equation of state and as long as the
equation of state doesn't differ too much from w=-1, the fitting formulae
presented in the literature are valid (Wang & Steinhardt 1998; Weinberg & Kamionkowski 2003).
for the cases of a homogeneous and
an inhomogeneous dark energy component are very small in this case. This
implies, that for models with constant equation of state and as long as the
equation of state doesn't differ too much from w=-1, the fitting formulae
presented in the literature are valid (Wang & Steinhardt 1998; Weinberg & Kamionkowski 2003).
The reason for the differences observed is that in the highly non-linear regime
the field will play an important role in determine the collapse time if ![]() .
Although at the time of virialisation the field is only subdominant, it will play an
important role just before collapse.
Thus, backreaction effects could significantly
alter the predictions of the spherical collapse model.
.
Although at the time of virialisation the field is only subdominant, it will play an
important role just before collapse.
Thus, backreaction effects could significantly
alter the predictions of the spherical collapse model.
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig6.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg104.gif) |
Figure 6:
Dependence on the initial conditions for the
double exponential potential (Barreiro et al. 2000) for the case of homogeneous dark energy. The solid and
dashed lines show the results for different initial conditions.
Top left panel:
evolution of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig7.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg105.gif) |
Figure 7:
Dependence on the initial conditions for the
double exponential potential (Barreiro et al. 2000) in the case for an inhomogeneous
dark energy component ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig8.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg106.gif) |
Figure 8:
The predictions for
|
| Open with DEXTER | |
The case for ![]() is shown in Fig. 7. We find that if quintessence
becomes inhomogeneous together with dark matter in the strong non-linear regime,
the predictions of the spherical collapse model depend generically
on the initial conditions of the field.
is shown in Fig. 7. We find that if quintessence
becomes inhomogeneous together with dark matter in the strong non-linear regime,
the predictions of the spherical collapse model depend generically
on the initial conditions of the field.
Different initial conditions lead to different time evolution of the
equation of state and the energy density of quintessence, both in the
background and inside the overdensity (depending on the value
of ![]() ). These two dark energy
properties will affect the dynamics of the overdensity through
Eqs. (10) and (14), hence affecting the predictions for
the non-linear density contrast and the virialisation radius of the
overdensity.
). These two dark energy
properties will affect the dynamics of the overdensity through
Eqs. (10) and (14), hence affecting the predictions for
the non-linear density contrast and the virialisation radius of the
overdensity.
What are the differences in the predictions for the four quintessence models?
In Fig. 8 we plot the predictions for
![]() and
and
![]() for the different potentials with the different
assumptions for
for the different potentials with the different
assumptions for ![]() .
As it can be seen from that figure, the differences can
be quite large if
.
As it can be seen from that figure, the differences can
be quite large if ![]() .
If the field is homogeneous throughout space,
the differences are small. Again, the reason is that the dynamics of the overdensity
(see Eqs. (10) and (14)) strongly depends
on the dark energy properties (Potential,
.
If the field is homogeneous throughout space,
the differences are small. Again, the reason is that the dynamics of the overdensity
(see Eqs. (10) and (14)) strongly depends
on the dark energy properties (Potential, ![]() , etc.).
, etc.).
In Fig. 9 we plot the predictions of the linear growth factor (
![]() ),
normalised today, for the different potentials. As it can be seen, even in the linear
regime there are differences between the four potentials. Such a behaviour was already
noticed in Maccio et al. (2003a).
),
normalised today, for the different potentials. As it can be seen, even in the linear
regime there are differences between the four potentials. Such a behaviour was already
noticed in Maccio et al. (2003a).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0129fig9.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg108.gif) |
Figure 9: The linear growth factor for the different quintessential potentials. It can be seen that the growth factor depends on the potential used. Solid line: Barreiro et al. (2000), dashed-line: Steinhardt et al. (1999), dashed-dotted line: Albrecht & Skordis (2000), dotted-line: Brax & Martin (1999). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.7cm,clip]{0129fig10.eps}
\end{figure}](/articles/aa/full/2004/25/aa0129-04/Timg109.gif) |
Figure 10:
Predictions for
|
| Open with DEXTER | |
In Fig. 10 we show the results for
![]() for all four potentials.
The solid lines are the cases for delayed collapse of dark energy,
whereas the dashed lines correspond to the case of full collapse. As it can be clearly seen,
the predictions for
for all four potentials.
The solid lines are the cases for delayed collapse of dark energy,
whereas the dashed lines correspond to the case of full collapse. As it can be clearly seen,
the predictions for
![]() change. Note, however, that the predictions are still far off
from the the results obtained in the case of a homogeneous scalar field. Of course, the field
is in the linear regime, but it has still an important impact on the predictions of the spherical
collapse model.
change. Note, however, that the predictions are still far off
from the the results obtained in the case of a homogeneous scalar field. Of course, the field
is in the linear regime, but it has still an important impact on the predictions of the spherical
collapse model.
We would like to point out that although the dark matter enters the highly
non-linear regime first, perturbations in dark energy deviate only slightly from linear theory
around virialisation. At the time of virialisation, the energy density of dark energy is always
much smaller than the density of dark matter inside an overdensity. The main effect is that
dark matter perturbations change the evolution of dark energy perturbations.
The physical properties of clusters, such as the
density contrast and virial radius strongly depend on clustering properties
of dark energy (i.e. the parameter ![]() ), the quintessence
potential and the initial conditions for the field fluctuations. The latter is
only important, however, if the field collapses together with the dark matter.
On the other hand, we have found that if the dark energy equation of state is assumed to be
constant, the differences between the homogeneous and inhomogeneous cases are
small, at least if the equation of state w does not differ too much from w=-1.
Thus, for constant equation of state the fitting formulae presented in the literature
(see Wang & Steinhardt 1998; Weinberg & Kamionkowski 2003) do not change drastically even if inhomogeneities in the dark
energy component are taken into account.
), the quintessence
potential and the initial conditions for the field fluctuations. The latter is
only important, however, if the field collapses together with the dark matter.
On the other hand, we have found that if the dark energy equation of state is assumed to be
constant, the differences between the homogeneous and inhomogeneous cases are
small, at least if the equation of state w does not differ too much from w=-1.
Thus, for constant equation of state the fitting formulae presented in the literature
(see Wang & Steinhardt 1998; Weinberg & Kamionkowski 2003) do not change drastically even if inhomogeneities in the dark
energy component are taken into account.
Our results imply, that a better understanding of the behaviour of the
quintessence field in highly non-linear regions is needed before the
predictions of the spherical collapse model can be trusted. The field can
influence the dynamics of the collapse at late times and thus changing
predictions of the turnaround, virialisation and collapse times. In order
to get better predictions, the boundary conditions between the outer and
inner metric have to be understood better. Its likely that the spherical model just gives
qualitative but not quantitative predictions. Nevertheless, an estimate
of the function ![]() is needed, which can only be obtained from a
general relativistic treatment. One way would be to develop a
swiss cheese model in the case of a quintessential universe. This will be discussed
in future work.
is needed, which can only be obtained from a
general relativistic treatment. One way would be to develop a
swiss cheese model in the case of a quintessential universe. This will be discussed
in future work.
Our calculations have also implications for models in which the scalar field couples non-minimally to dark matter. In these models, the scalar field perturbations and the dark matter perturbations are coupled even in the linear regime and backreaction in the highly non-linear regime will certainly be important. A similar conclusion might hold for models based on tachyonic fields.
To summarise, only when the energy flux of scalar field energy density ![]() out of a dark matter overdensity is known, the spherical
collapse model is able to make firm predictions which can be used to
make predictions for weak and strong lensing, the number density of
clusters, etc or even for a help to use N-body simulations in dark energy
models. In the case of a non-minimally coupled dark energy component, the
predictions of the spherical collapse model will certainly be altered.
out of a dark matter overdensity is known, the spherical
collapse model is able to make firm predictions which can be used to
make predictions for weak and strong lensing, the number density of
clusters, etc or even for a help to use N-body simulations in dark energy
models. In the case of a non-minimally coupled dark energy component, the
predictions of the spherical collapse model will certainly be altered.
Acknowledgements
We would like to thank P. G. Ferreira, J. Magueijo, K. Moodley, C. Skordis, J. Silk and D. Tocchini-Valentini, for helpful comments. D.F.M. is supported by Funda cão Ciência e a Tecnologia. C.v.d.B. is supported by PPARC.