A&A 421, 241-254 (2004)
DOI: 10.1051/0004-6361:20041042
J. Setiawan1,5 - L. Pasquini2 - L. da Silva3 - A. P. Hatzes4 - O. von der Lühe5 - L. Girardi6 - J. R. de Medeiros7 - E. Guenther4
1 - Max-Planck-Institut für Astronomie, Koenigstuhl 17, 69117 Heidelberg, Germany
2 -
European Southern Observatory, Karl-Schwarzschild-Str. 3, 85748 Garching bei München, Germany
3 -
Observatório Nacional, R. Gal. José Cristino 77, 20921-400 Sao Cristavao, Rio de Janeiro, Brazil
4 -
Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg, Germany
5 -
Kiepenheuer-Institut für Sonnenphysik, Schoeneckstr. 6, 79104 Freiburg (Brsg), Germany
6 -
Osservatorio Astronomico di Trieste, via Tiepolo 11, 34131 Trieste, Italy
7 -
Departamento de Física, Universidade Federal do Rio Grande do Norte, 59072-970 Natal, Brazil
Received 15 January 2004 / Accepted 14 March 2004
Abstract
We present the results of our radial velocity (RV)
measurements of G and K giants,
concentrating on the presence of multiple systems in our sample. Eighty-three
giants have been observed for 2.5 years
with the fiber-fed echelle spectrograph FEROS at the 1.52 m
ESO telescope in La Silla, Chile.
Seventy-seven stars (93%) of the targets have been analyzed
for RV variability using simultaneous Th-Ar
calibration and a cross-correlation technique.
We estimate the long-term precision of our measurement as
better than 25
![]() .
Projected rotational velocities have been measured for most stars of the sample.
Within our time-base only 21 stars (or 27
.
Projected rotational velocities have been measured for most stars of the sample.
Within our time-base only 21 stars (or 27![]() )
show variability
below 2
)
show variability
below 2![]() ,
while the others show RV variability with
amplitudes up to several
,
while the others show RV variability with
amplitudes up to several
![]() .
The large amplitude (several
.
The large amplitude (several
![]() )
and
shape (high eccentricity)
of the RV variations for 11 of the program stars are consistent with
stellar companions, and possibly brown dwarf companions for two
of the program stars.
In those systems for which a full orbit could be derived,
the companions have minimum masses from
)
and
shape (high eccentricity)
of the RV variations for 11 of the program stars are consistent with
stellar companions, and possibly brown dwarf companions for two
of the program stars.
In those systems for which a full orbit could be derived,
the companions have minimum masses from ![]() 0.6
0.6
![]() down to 0.1
down to 0.1
![]() .
To these multiple systems we add the two candidates of giant planets
already discovered in the sample.
This analysis shows that multiple systems contribute substantially to
the long-term RV variability of giant stars, with about 20
.
To these multiple systems we add the two candidates of giant planets
already discovered in the sample.
This analysis shows that multiple systems contribute substantially to
the long-term RV variability of giant stars, with about 20![]() of the sample being
composed of multiple systems despite screening our sample for known binary
stars.
After removing binaries, the range of RV variability in the whole sample clearly decreases,
but the remaining stars retain a statistical trend of RV variability with luminosity:
luminous cool giants with
of the sample being
composed of multiple systems despite screening our sample for known binary
stars.
After removing binaries, the range of RV variability in the whole sample clearly decreases,
but the remaining stars retain a statistical trend of RV variability with luminosity:
luminous cool giants with
![]() show RV variations
with
show RV variations
with
![]()
![]() ,
while giants with B-V < 1.2 including those in the clump
region exhibit less variability or they are constant within our accuracy.
The same trend is observed with respect to absolute visual magnitudes: brighter stars
show a larger degree of variability and, when plotted in the RV variability vs.
magnitude diagram a trend of increasing RV scatter with luminosity is seen.
The amplitude of RV variability does not increase dramatically, as predicted,
for instance, by simple scaling laws.
At least two luminous and cooler stars of the sample show a correlation between RV and
chromospheric activity and bisector asymmetry, indicating that in these two objects
RV variability is likely induced by the presence of (chromospheric) surface structures.
,
while giants with B-V < 1.2 including those in the clump
region exhibit less variability or they are constant within our accuracy.
The same trend is observed with respect to absolute visual magnitudes: brighter stars
show a larger degree of variability and, when plotted in the RV variability vs.
magnitude diagram a trend of increasing RV scatter with luminosity is seen.
The amplitude of RV variability does not increase dramatically, as predicted,
for instance, by simple scaling laws.
At least two luminous and cooler stars of the sample show a correlation between RV and
chromospheric activity and bisector asymmetry, indicating that in these two objects
RV variability is likely induced by the presence of (chromospheric) surface structures.
Key words: stars: variables: general - stars: binaries: general - stars: late-type - stars: rotation - technique: radial velocities
Precise RV measurements have been the subject of strong
interest in the last years,
thanks mostly to their successful application
to the detection of planetary
companions orbiting solar-type stars
(Mayor & Queloz 1995; Marcy & Butler 1996).
Long-term precision better than 10
![]() is required to detect Jovian planets orbiting a dwarf star
at 5 AU.
Evolved cool stars (hereafter "giants'') show a higher level of RV
variability (see e.g., Walker et al. 1989; Hatzes & Cochran
1993) and for them such a high long-term precision
may not be required, although G-type,
low luminous sub-giants which are not very different
from solar-type stars may exhibit RV variability as low as
a few tens of
is required to detect Jovian planets orbiting a dwarf star
at 5 AU.
Evolved cool stars (hereafter "giants'') show a higher level of RV
variability (see e.g., Walker et al. 1989; Hatzes & Cochran
1993) and for them such a high long-term precision
may not be required, although G-type,
low luminous sub-giants which are not very different
from solar-type stars may exhibit RV variability as low as
a few tens of
![]() ,
as presented in our results
(see Sect. 4.2)
,
as presented in our results
(see Sect. 4.2)
Precise RV measurements have also been applied to the study of stellar pulsations,
e.g. solar-type oscillations, in which a short-term accuracy of better
than 1
![]() is needed to detect p-modes.
Solar-type pulsations have so far been detected on Procyon
(Brown et al. 1991; Barban et al. 1999),
is needed to detect p-modes.
Solar-type pulsations have so far been detected on Procyon
(Brown et al. 1991; Barban et al. 1999),
![]() Hydri (Bedding et al. 2001) and
Hydri (Bedding et al. 2001) and ![]() Cen A
(Bouchy & Carrier 2001).
Until now, the only "solar-like'' oscillations
in a giant star have been detected by Frandsen et al. (2002)
in
Cen A
(Bouchy & Carrier 2001).
Until now, the only "solar-like'' oscillations
in a giant star have been detected by Frandsen et al. (2002)
in ![]() Hya (spectral class G7III). The oscillation period was
P= 2-5.5 h.
Other evidence for p-mode
oscillations in K giants with period of several days have been detected
in Arcturus (Hatzes & Cochran 1994; Merline et al. 1995)
and in
Hya (spectral class G7III). The oscillation period was
P= 2-5.5 h.
Other evidence for p-mode
oscillations in K giants with period of several days have been detected
in Arcturus (Hatzes & Cochran 1994; Merline et al. 1995)
and in ![]() UMa (Buzasi et al. 2000).
UMa (Buzasi et al. 2000).
To achieve high precise RV two techniques are currently in use:
acquiring a simultaneous calibration for the
stellar spectra (Baranne et al. 1996) or
the self absorption-cell technique (Campbell & Walker 1979;
Cochran & Hatzes 1990).
Both techniques are presently able to provide comparable
long-term precision of a few
![]() (Butler et al. 1996; Pepe et al. 2000).
(Butler et al. 1996; Pepe et al. 2000).
G and K giants are cool, evolved stars, which have moved off the main sequence. They span the entire Red Giant Branch (RGB) including the red clump and early-AGB phases. The clump giants are stars which are experiencing the He-core burning phase.
RV variations of K giants with amplitudes between 30-300
![]() and time-scales ranging from a few to hundreds of days
have been
reported by Smith et al. (1987), Walker et al. (1989),
Larson et al. (1993), Hatzes & Cochran (1993, 1996).
The RV variability observed in red giants has been suggested
to result from stellar pulsation, rotational modulation, or low-mass companion.
Before we started to publish the results of this survey
a few sub-stellar companions have been proposed around evolved stars:
the K4IVa sub-giant HD 27442 (Butler et al. 2001),
the K2III giant
and time-scales ranging from a few to hundreds of days
have been
reported by Smith et al. (1987), Walker et al. (1989),
Larson et al. (1993), Hatzes & Cochran (1993, 1996).
The RV variability observed in red giants has been suggested
to result from stellar pulsation, rotational modulation, or low-mass companion.
Before we started to publish the results of this survey
a few sub-stellar companions have been proposed around evolved stars:
the K4IVa sub-giant HD 27442 (Butler et al. 2001),
the K2III giant ![]() Dra (Frink et al. 2002)
and
Dra (Frink et al. 2002)
and ![]() Cephei (Hatzes et al. 2003).
We have enlarged this sample by detecting two giant planet candidates around
HD 47536 (Setiawan et al. 2003b)
and HD 122430 (Setiawan 2003c).
Recently, Sato et al. (2003) reported the first detection of
a planetary companion to a G giant, HD 104985.
The search of extra-solar planets around
giants is quite interesting and complementary to
the surveys carried out on main sequence stars: giants in fact
may cover a range of stellar masses. Stars with masses exceeding 3-4
Cephei (Hatzes et al. 2003).
We have enlarged this sample by detecting two giant planet candidates around
HD 47536 (Setiawan et al. 2003b)
and HD 122430 (Setiawan 2003c).
Recently, Sato et al. (2003) reported the first detection of
a planetary companion to a G giant, HD 104985.
The search of extra-solar planets around
giants is quite interesting and complementary to
the surveys carried out on main sequence stars: giants in fact
may cover a range of stellar masses. Stars with masses exceeding 3-4
![]() cannot be investigated for the presence of
low-mass companions while on the main sequence because they
have fewer stellar absorption lines due to a higher effective temperature.
Furthermore, early-type stars have
broad spectral features due to the more rapid rotation compared to late-type stars.
Both effects severely limit the accuracy of RV measurements.
As an early-type star evolves off the main sequence
its rotation rate slows considerably
(Pasquini et al. 2000; de Medeiros & Mayor 1999)
and the atmosphere cools. The larger number of narrow
absorption lines now makes these objects
suitable objects for precise RV studies.
cannot be investigated for the presence of
low-mass companions while on the main sequence because they
have fewer stellar absorption lines due to a higher effective temperature.
Furthermore, early-type stars have
broad spectral features due to the more rapid rotation compared to late-type stars.
Both effects severely limit the accuracy of RV measurements.
As an early-type star evolves off the main sequence
its rotation rate slows considerably
(Pasquini et al. 2000; de Medeiros & Mayor 1999)
and the atmosphere cools. The larger number of narrow
absorption lines now makes these objects
suitable objects for precise RV studies.
Most of the previous RV results were obtained on relatively smaller samples of giants. We have therefore recognized the need for a RV survey of G and K giants spanning the entire RGB: 1) to determine how the RV variations vary as a star moves along the RGB, and 2) to understand the nature of the long-period variations. If these variations were due to rotational modulation of stellar surface structure, then our survey would provide the ideal targets for stellar interferometers, since many of these objects have angular diameters which are large enough to be resolved by long-baseline interferometry.
Our first work mostly concentrated on the description of the observations and the data reduction techniques and summarized the first results. These showed that some relation was likely to be present between the RV variation amplitudes and the position of the stars in the H-R diagram (Setiawan et al. 2003a, hereafter Paper I). In the present work we will concentrate on the detection of multiple systems. These systems need to be recognized and separated by the rest of the sample stars before the other causes of variability are investigated.
The RV precision achieved with FEROS during commissioning was 23
![]() (Kaufer & Pasquini 1998)
and could be reduced on a short (few months) time-scale to better than 11
(Kaufer & Pasquini 1998)
and could be reduced on a short (few months) time-scale to better than 11
![]() using an improved data reduction method
(Setiawan et al. 2000, and Paper I).
Unfortunately, this precision could not be maintained until the
end of our survey. We detected instrumental instabilities
which affected the simultaneous Th-Ar calibration.
Our precision over 28 months is better than 25
using an improved data reduction method
(Setiawan et al. 2000, and Paper I).
Unfortunately, this precision could not be maintained until the
end of our survey. We detected instrumental instabilities
which affected the simultaneous Th-Ar calibration.
Our precision over 28 months is better than 25
![]() ,
similar to the commissioning accuracy and still appropriate for our scientific goals.
,
similar to the commissioning accuracy and still appropriate for our scientific goals.
The program started with 27 stars in October 1999 and has
been expanded to include 83 G and K stars, mainly giants.
The whole sample covers a large fraction of the upper H-R diagram including the full RGB as well as the "clump'' region (cf. Fig. 1).
The bulk of our sample has been selected on the basis of
HIPPARCOS parallaxes and are not classified as spectroscopic binaries.
A few stars with measured
![]() have been added later
to be used as comparison with our
have been added later
to be used as comparison with our
![]() calibration.
Some of these stars are binaries.
calibration.
Some of these stars are binaries.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=7.4cm,clip]{0081fig1.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg23.gif) |
Figure 1:
H-R diagram of the 83 giant stars in our RV survey
with FEROS. The sample covers the RGB including the "clump''
region. The continuous lines are evolutionary tracks for
solar-metallicity stars of masses comprised between 1.0 and 3.0
|
| Open with DEXTER | |
Being interested in abundances, variability in Ca II H and K core
emission lines and bisector variations,
we required an average signal to noise ratio (S/N) of about
150-200 per pixel in the best exposed part of the spectra.
We found this high S/N is appropriate for
investigating the variations of the deep Ca II K (
![]() Å)
line, the best indicator of chromospheric activity (see e.g. Pasquini et al. 1990).
More details about the observation and the calibration procedure
were presented in Paper I and are only briefly
repeated here.
Å)
line, the best indicator of chromospheric activity (see e.g. Pasquini et al. 1990).
More details about the observation and the calibration procedure
were presented in Paper I and are only briefly
repeated here.
Due to instrumental systematic instabilities we had to apply
RV corrections using the
procedure presented in Paper I.
Figure 2 shows a comparison between the original RV computation method (dashed
open circles) and the
RV obtained after the corrections (dots) for our standard "constant''
star ![]() Cet (HD 10700).
The standard deviation of the corrected
Cet (HD 10700).
The standard deviation of the corrected ![]() Cet radial velocities
is
Cet radial velocities
is
![]()
![]() which we use
as an estimate of our long-term RV (instrumental) precision.
This value is three times worse than reported in Setiawan et al. (2000)
and substantially higher than in Paper I.
We have tried several weighting methods (e.g. by
which we use
as an estimate of our long-term RV (instrumental) precision.
This value is three times worse than reported in Setiawan et al. (2000)
and substantially higher than in Paper I.
We have tried several weighting methods (e.g. by ![]() ,
,
![]() or by flux in the center of order) when combining the RV of each order
to obtain the mean RV of a single spectrum, but these efforts did not
improve the final result.
We cannot exclude that it may be possible to improve our precision,
for instance by using different masks or improving the wavelength calibration.
It is nevertheless worrying that our precision substantially
decreased during the second and third years of observations. We do not have a
clear-cut explanation for this. However, we noticed that over time
the FEROS environment and optical alignment deteriorated
and this could be a cause of the degraded RV performances.
The original specifications for FEROS
were 50
or by flux in the center of order) when combining the RV of each order
to obtain the mean RV of a single spectrum, but these efforts did not
improve the final result.
We cannot exclude that it may be possible to improve our precision,
for instance by using different masks or improving the wavelength calibration.
It is nevertheless worrying that our precision substantially
decreased during the second and third years of observations. We do not have a
clear-cut explanation for this. However, we noticed that over time
the FEROS environment and optical alignment deteriorated
and this could be a cause of the degraded RV performances.
The original specifications for FEROS
were 50
![]() ,
which were at all times fulfilled.
A precision of
,
which were at all times fulfilled.
A precision of ![]() 25
25
![]() is slightly worse than our goal, but
is appropriate for analyzing the long-term variability of the
sample; most of our targets show typical RV variability of
is slightly worse than our goal, but
is appropriate for analyzing the long-term variability of the
sample; most of our targets show typical RV variability of
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.0cm,height=7.4cm,clip]{0081fig2.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg29.gif) |
Figure 2:
RV plot of |
| Open with DEXTER | |
Table 1:
Projected rotational velocity and RV variation of G and K giants/sub-giants. Column (1): identifer, Col. (2): absolute magnitude; Col. (3): color index; Col. (4): visual magnitude; Col. (5): spectral classification (SIMBAD);
Col. (6): CCF width; Col. (7):
![]() from Eq. (2); Col. (8): projected rotational velocity from FEROS and Col. (9) other measurements;
Col. (10): available reference for
from Eq. (2); Col. (8): projected rotational velocity from FEROS and Col. (9) other measurements;
Col. (10): available reference for
![]() ;
Col. (11): rms of RV variation; Col. (12): number of spectra.
;
Col. (11): rms of RV variation; Col. (12): number of spectra.
Since one of the possible sources of
RV variation is stellar surface inhomogeneities (e.g. spots)
it is important to derive rotational velocities for the sample stars which can be
used with measurements (estimates) of the stellar radii to derive upper limits
to the stellar rotational period. These can then be compared to the RV period
derived from a periodogram analysis.
We used the cross-correlation method (see Queloz et al. 1998) to determine
the projected rotational velocity
![]() from the width
from the width
![]() of the stellar CCF.
Melo et al. (2001) determined the calibration value for FEROS
and applied it to compute
of the stellar CCF.
Melo et al. (2001) determined the calibration value for FEROS
and applied it to compute
![]() of giants in the M 67 cluster.
of giants in the M 67 cluster.
By using the cross-correlation technique the rotational velocity can be expressed by the relation
(Benz & Mayor 1984; Queloz et al. 1998):
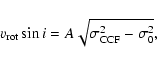 |
(1) |
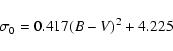 |
(2) |
Nineteen of our targets have published rotational velocities, which are
given in Cols. 9 and 10 of Table 1. The agreement between the FEROS and the previously
published
![]() is excellent, with peak deviations
below 1
is excellent, with peak deviations
below 1
![]() .
For most stars with B-V > 1.2
the derived rotational velocity is negative because
.
For most stars with B-V > 1.2
the derived rotational velocity is negative because
![]() and they are indicated in Table 1 with the value "-''.
Melo et al. (2001) also noticed this effect in their sample,
but they could not find any obvious cause in their calibration.
This indicates that most likely the rotation rates of the coolest stars are
slightly underestimated, and that the estimated error (1
and they are indicated in Table 1 with the value "-''.
Melo et al. (2001) also noticed this effect in their sample,
but they could not find any obvious cause in their calibration.
This indicates that most likely the rotation rates of the coolest stars are
slightly underestimated, and that the estimated error (1
![]() )
should be used as an upper limit for the rotational velocity of these objects.
However it seems clear that none of these stars has significant
rotation rates.
)
should be used as an upper limit for the rotational velocity of these objects.
However it seems clear that none of these stars has significant
rotation rates.
![\begin{figure}
\par\includegraphics[width=6.4cm,height=6.4cm,clip]{0081fig3.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg38.gif) |
Figure 3:
Projected rotational velocity and rotational period. The
- values in Table 1 (undetermined
|
| Open with DEXTER | |
Table 2: Angular diameter, stellar radius and rotational period.
![\begin{figure}
\par\includegraphics[width=6.8cm,height=6.7cm,clip]{0081fig4.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg40.gif) |
Figure 4: Comparison of the stellar radii derived from the photometric determination and the values from the CHARM catalogue. The values are in an excellent agreement. |
| Open with DEXTER | |
In Fig. 3 we plot the
![]() against the color index B-V,
except for those stars with undetermined
against the color index B-V,
except for those stars with undetermined
![]() .
All of our stars are slow rotators, with the highest rotation rate being
less than 7
.
All of our stars are slow rotators, with the highest rotation rate being
less than 7
![]() .
As observed by other authors
(de Medeiros & Mayor 1991), rotation
drops quite abruptly with color among F to early G giants and supergiants:
at about
.
As observed by other authors
(de Medeiros & Mayor 1991), rotation
drops quite abruptly with color among F to early G giants and supergiants:
at about
![]() for subgiants/giants and somewhat redward
for bright giants and supergiants.
for subgiants/giants and somewhat redward
for bright giants and supergiants.
Single giants blueward of this spectral region
present a wide range of rotational velocity, from about a few
![]() to about a hundred times the solar rotation. The large majority of single giants redward
of this spectral type are essentially slow rotators, with
to about a hundred times the solar rotation. The large majority of single giants redward
of this spectral type are essentially slow rotators, with
![]() ranging from about 1 to about 7
ranging from about 1 to about 7
![]() .
Among giant stars with spectral types G-K only those in short-period binary systems
show enhanced rotation that is due to tidal spin-up from the companion.
What we see in Fig. 3 is the expected distribution of the rotational velocity of single G and K
giants at the same color interval, with
.
Among giant stars with spectral types G-K only those in short-period binary systems
show enhanced rotation that is due to tidal spin-up from the companion.
What we see in Fig. 3 is the expected distribution of the rotational velocity of single G and K
giants at the same color interval, with
![]() ranging from 1 to 7
ranging from 1 to 7
![]() .
.
From Fig. 3 we see that only one star with ![]() that has a significant
amount of stellar rotation.
This star, HD 78647, is our coolest and intrinsically brightest star
with an absolute magnitude of
that has a significant
amount of stellar rotation.
This star, HD 78647, is our coolest and intrinsically brightest star
with an absolute magnitude of ![]() -4. This object is
a supergiant which probably also has a larger intrinsic macroturbulent
line broadening (see Gray 1989). Its
color is also far out of the range of application of the Melo et al.
(2001) calibration.
For all these reasons its high rotational velocity should be considered as an upper limit.
-4. This object is
a supergiant which probably also has a larger intrinsic macroturbulent
line broadening (see Gray 1989). Its
color is also far out of the range of application of the Melo et al.
(2001) calibration.
For all these reasons its high rotational velocity should be considered as an upper limit.
As far as radii are concerned, for 22 stars from our sample
interferometric measurements of apparent diameters are
available from the CHARM catalogue (Richichi & Percheron 2002).
Given our sample selection of bright, nearby K giants
this high rate is not surprising.
Indeed, with typical apparent diameters of ![]() 2 mas our
sample provides excellent targets for interferometers.
These values can therefore be used to calculate the projected rotational periods
2 mas our
sample provides excellent targets for interferometers.
These values can therefore be used to calculate the projected rotational periods
![]() .
Furthermore, for the stars with known interferometric angular diameter (Table 2)
we derived the stellar radii and angular diameter by using the relations of
bolometric corrections, effective temperature, and color indexes adopted from
Flower (1996). Figure 4 shows a comparison between our diameter computation and the
measured angular diameters. The linear fit is given by:
.
Furthermore, for the stars with known interferometric angular diameter (Table 2)
we derived the stellar radii and angular diameter by using the relations of
bolometric corrections, effective temperature, and color indexes adopted from
Flower (1996). Figure 4 shows a comparison between our diameter computation and the
measured angular diameters. The linear fit is given by:
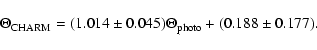 |
(3) |
In fact, the other possible causes of long-term RV variations, such as
surface inhomogeneities or pulsations usually produces significantly lower
RV amplitudes. For example,
for spotted stars with
![]() the RV amplitude due to a 5% starspot filling factor is a few hundred
the RV amplitude due to a 5% starspot filling factor is a few hundred
![]() (see Hatzes 2002).
Stars with much larger spots, or high amplitude pulsations should
produce significant photometric variations which would be evident in the
HIPPARCOS database.
(see Hatzes 2002).
Stars with much larger spots, or high amplitude pulsations should
produce significant photometric variations which would be evident in the
HIPPARCOS database.
We find it useful to analyze our results by
computing the
![]() of the stars, as given in Col. 11 of Table 1.
Out of the full sample of 83 stars, only 77 are analyzed because for the remaining
6 objects less than 4 spectra could be obtained.
Looking at the distribution of all the
of the stars, as given in Col. 11 of Table 1.
Out of the full sample of 83 stars, only 77 are analyzed because for the remaining
6 objects less than 4 spectra could be obtained.
Looking at the distribution of all the
![]() we can immediately see that out of the 77 giants, one star, HD 93257
shows a very low level
of RV variability; with 29
we can immediately see that out of the 77 giants, one star, HD 93257
shows a very low level
of RV variability; with 29
![]() rms indeed it is just slightly above
our "constant'' star
rms indeed it is just slightly above
our "constant'' star ![]() Cet. Other 20 stars show little variability,
with a level of
Cet. Other 20 stars show little variability,
with a level of
![]() below 50
below 50
![]() ,
or 2 times our estimated accuracy.
Of course we cannot exclude the possibility that these
stars are indeed variable, but, unless some clear
periodicity emerges, we can only consider them as constant at the moment.
From the remaining 56 stars, a clear group distinguishes itself from the others:
11 stars have very large variations (more than
800
,
or 2 times our estimated accuracy.
Of course we cannot exclude the possibility that these
stars are indeed variable, but, unless some clear
periodicity emerges, we can only consider them as constant at the moment.
From the remaining 56 stars, a clear group distinguishes itself from the others:
11 stars have very large variations (more than
800
![]() )
and these are the best candidates for
binaries.
)
and these are the best candidates for
binaries.
![\begin{figure}
\par\includegraphics[width=15.4cm,height=9.7cm,clip]{0081fig5.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg46.gif) |
Figure 5: RV measurements of six binary systems: HD 7672, HD 27697, HD 40176, HD 62644, HD 156111 and HD 179799. The orbital parameters of the Kepler model and the mass-functions are given in Table 3. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=7.9cm,height=5.6cm,clip]{0081fig...
...m}
\includegraphics[width=7.9cm,height=5.6cm,clip]{0081fig6b.ps} }\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg47.gif) |
Figure 6: Left: phase folded RV measurements of HD 7672. Right: the same for HD 156111 obtained from FEROS and TLS-Tautenburg. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm,clip]{0081fig7a.ps}\hsp...
...cs[width=7.5cm,height=5.7cm,clip]{0081fig7c.ps}\hspace*{8.5cm}
\par
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg48.gif) |
Figure 7: RV measurements of binary systems HD 21120, HD 22663, HD 176578, HD 187195 and HD 218527. These binaries show much longer period than our total observation span. |
| Open with DEXTER | |
The 45 remaining stars exhibit RV variations which are possibly caused
by pulsations, rotation or low-mass and planetary companions (as for
HD 47536 and HD 122430 with 76 and 79
![]() rms respectively).
For 14 of these 45 objects we have less than 10 measurement
points which is insufficient to classify the nature of their RV variability.
Additionally, two stars are known to belong to
double (visual) systems. They are HD 27256 and HD 224533.
rms respectively).
For 14 of these 45 objects we have less than 10 measurement
points which is insufficient to classify the nature of their RV variability.
Additionally, two stars are known to belong to
double (visual) systems. They are HD 27256 and HD 224533.
With a sample of 77 objects it is possible to apply some statistics to verify our findings. Among giants in open clusters, the incidence of binaries found in spectroscopic surveys with CORAVEL is 26% (Mermilliod et al. 2001). However, this frequency should be considered as a minimum value, which depends on the precision achieved, the time interval and the number of observations. The number of binaries detections is larger when using instrument with better precision (see e.g. Mayor et al. 2001). The RV precision of FEROS is at least ten times better than CORAVEL.
The binary frequency of red giants is lower than that for solar-type stars, which is given, for instance, in Duquennoy et al. (1991). Among red giants, binaries with periods less than 40 days do not exist due to Roche lobe filling, contact phase and mass transfer episodes when the orbital periods are shorter than the critical Roche period at the red giant tip (Mermilliod & Mayor 1992). In particular, clump red giants which have passed through a state of larger radii fulfilled this condition.
Considering the Mermilliod et al. statistics, we could therefore expect that about 20 objects of our sample have stellar companions. Considering, however, that stars already known as binaries were rejected as part of the selection process, we may expect a lower binary rate in our sample, and 11-13 of 77 (14-17%) seem reasonable.
We cannot exclude the possibility that further observations will reveal additional binary candidates, in particular among those that show considerable RV variability, but their number should be limited. If the above statistics can be applied to our sample (and we believe that this should represent an upper limit) we should miss less than 7 additional binaries, and these should likely be very long period systems, whose multiplicity is still hidden in our measurements due to the limited duration of our survey.
When considering the non-binarity bias in our selection criteria, we can also predict that our multiple systems should likely have a high primary to secondary mass ratio, because binary systems composed by stars of similar masses had a higher probability to be discovered in previous studies, since they will tend to show larger RV variations or are double-lined spectroscopic binaries. For the sake of completeness we show all RV curves of the 13 binary candidates so far identified (Figs. 5-7). For 6 stars we had sufficient measurements to compute orbital solutions. These orbital solutions are shown as a line in Figs. 5 and 6. Orbital elements are listed in Table 3.
HD 156111 showed clear short-term RV variability, but we
had too few measurements to be able to derive a period. For these
reasons additional measurements were made using the coude
echelle spectrograph of the Alfred Jensch
2 m telescope of the Thüringer Landessternwarte Tautenburg (TLS).
This was one of the few stars of our target sample
which was accessible from TLS which is located in Germany.
This spectrograph is a grism-crossed dispersed echelle which
provides a wavelength coverage of 4750-7070 Å (using the
so-called VIS grism) at a resolving power,
R (=
![]() ) = 67 000.
An iodine absorption cell placed just before the entrance
slit provides the wavelength reference for precise
(
) = 67 000.
An iodine absorption cell placed just before the entrance
slit provides the wavelength reference for precise
(
![]() )
stellar RV measurements.
At TLS an additional 13 RV measurements were made which enabled us
to determine the period (39.5 days) and to derive an orbit.
The right panel of Fig. 6 shows the phase-folded orbital solution
to the TLS and FEROS RV measurements.
)
stellar RV measurements.
At TLS an additional 13 RV measurements were made which enabled us
to determine the period (39.5 days) and to derive an orbit.
The right panel of Fig. 6 shows the phase-folded orbital solution
to the TLS and FEROS RV measurements.
Figure 8 shows the position of the binaries in the color-magnitude diagram
with the same evolutionary track as in Fig. 1.
For the six binaries with derived orbital elements
we adopted primary masses
![]() ,
depending on the star's position in RGB.
We computed the mass functions f(m) as given in Col. 5 of Table 3.
The resulting companion's masses and the semi-major axes of the orbits
are listed in Cols. 6 and 7 of Table 3.
,
depending on the star's position in RGB.
We computed the mass functions f(m) as given in Col. 5 of Table 3.
The resulting companion's masses and the semi-major axes of the orbits
are listed in Cols. 6 and 7 of Table 3.
HD 7672 (=AY Cet) was not originally in our program, but was added
to increase the number of stars with previously measured
rotational velocities.
Note that the star has a higher rotation rate than the most targets and
our
![]() measurement is in excellent
agreement with the result obtained with the Fourier transformation technique (Gray 1989).
measurement is in excellent
agreement with the result obtained with the Fourier transformation technique (Gray 1989).
Our program provided too few RV measurements to derive an accurate
orbit for HD 7672. Our RV measurements showed clear evidence for a
![]() d period, but the poor phasing did not allow us to determine
the amplitude and eccentricity for the orbit. Fekel & Eitter (1989)
presented RV measurements for this star with lower precision
(
d period, but the poor phasing did not allow us to determine
the amplitude and eccentricity for the orbit. Fekel & Eitter (1989)
presented RV measurements for this star with lower precision
(
![]() km s-1). We have combined these
with our RV measurements to compute a revised orbit.
We found a period of 56.9 days and a circular orbit (e=0.02).
Our RV measurements phased to the orbital period along with
the orbital solution are shown in Fig. 6 (left panel).
km s-1). We have combined these
with our RV measurements to compute a revised orbit.
We found a period of 56.9 days and a circular orbit (e=0.02).
Our RV measurements phased to the orbital period along with
the orbital solution are shown in Fig. 6 (left panel).
We determined a companion mass of 0.25
![]() by
assuming a primary mass of 2.5
by
assuming a primary mass of 2.5
![]() .
The derived semi-major axis is a= 0.4 AU.
We estimated a radius of
.
The derived semi-major axis is a= 0.4 AU.
We estimated a radius of
![]() ,
and
when considering the measured rotational velocity results in
,
and
when considering the measured rotational velocity results in
![]() days, or comparable
to the orbital period, HD 7672 is possibly a tidally locked binary with the same
orbital and rotational period. For binaries with a red giant
primary and P<120 days the circular orbit is due to
tidal interaction between the two components (Mermilliod & Mayor 1992).
days, or comparable
to the orbital period, HD 7672 is possibly a tidally locked binary with the same
orbital and rotational period. For binaries with a red giant
primary and P<120 days the circular orbit is due to
tidal interaction between the two components (Mermilliod & Mayor 1992).
Table 3: Companions of six binaries.
HD 27697 exhibits an orbital period of
![]() days. The
period we found is comparable to the 529.8 day period reported in de Medeiros
et al. (2002a). We obtained an eccentricity e= 0.48. With a
semi-amplitude
days. The
period we found is comparable to the 529.8 day period reported in de Medeiros
et al. (2002a). We obtained an eccentricity e= 0.48. With a
semi-amplitude
![]() and
and
![]() we derived a
minimum mass of
we derived a
minimum mass of
![]()
![]() .
The
semi-major axis of the orbit is 1.76 AU. With a
.
The
semi-major axis of the orbit is 1.76 AU. With a
![]() of 190 days, the orbital period is substantially longer than the rotational one.
of 190 days, the orbital period is substantially longer than the rotational one.
With a period of 1420.6 days and
![]() HD 40176 has a more massive companion than the two giants described
above. We derived a minimum mass of
HD 40176 has a more massive companion than the two giants described
above. We derived a minimum mass of
![]() an eccentricity of e = 0.39 and an orbital semi-major
axis of 3.60 AU.
The systems HD 62644, HD 156111 and HD 179799 each
have companions with high eccentric orbits (
an eccentricity of e = 0.39 and an orbital semi-major
axis of 3.60 AU.
The systems HD 62644, HD 156111 and HD 179799 each
have companions with high eccentric orbits (![]() ).
Their orbital periods are 380.6 days (HD 62644), 39.5 days (HD 156111)
and 856.1 days (HD 179799).
We obtained
).
Their orbital periods are 380.6 days (HD 62644), 39.5 days (HD 156111)
and 856.1 days (HD 179799).
We obtained
![]()
![]() for HD 62644,
0.10
for HD 62644,
0.10
![]() for HD 156111 and 0.30
for HD 156111 and 0.30
![]() for HD 179799. The semi-major axes are 1.2 AU, 0.23 AU and
2.14 AU, respectively.
For HD 156111 which has a stellar radius R= 1.8
for HD 179799. The semi-major axes are 1.2 AU, 0.23 AU and
2.14 AU, respectively.
For HD 156111 which has a stellar radius R= 1.8
![]() and
and
![]()
![]() we compute
we compute
![]() days, which is close to the orbital period.
However, it is not clear if this is a tidal-locked system.
The rotation velocity is rather low for a synchronized system.
days, which is close to the orbital period.
However, it is not clear if this is a tidal-locked system.
The rotation velocity is rather low for a synchronized system.
The systems HD 21120, HD 27256, HD 22663, HD 176578, HD 187195,
HD 218527 and HD 224533 show orbital periods longer
than our total observation timespan, and we
would need more time to derive the RV solution for
these binaries; we consider this goal is outside the
purpose of this project.
![\begin{figure}
\par\includegraphics[width=7.6cm,height=7.4cm,clip]{0081fig8.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg68.gif) |
Figure 8: Color-magnitude diagram of the binaries found. The same evolutionary track as in Fig. 1 has been added. The primary masses can be estimated from the position in this diagram. The dots and triangles represent binaries with and without orbital solutions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm,clip]{0081fig9a.ps}\vspace*{5mm}
\includegraphics[width=8cm,height=6cm,clip]{0081fig9b.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg69.gif) |
Figure 9: RV measurements of HD 27256 and HD 224533. These stars are known as stars in visual double systems. However, the measured RV variations are possibly due to other unseen companions. |
| Open with DEXTER | |
We are very interested in the nature of the companions
around HD 27256 and HD 224533. The reason is that,
although these giants are classified as
stars in visual double systems, we found that the RV variations
observed are not due to the visual secondary component of
the systems. They are instead induced by unseen low-mass,
possibly brown dwarf or very low-mass stellar companions.
HD 27256 and HD 224533 show low RV variability relative to the other
binaries. Their
![]() values are 136
values are 136
![]() and
161
and
161
![]() .
The separation of the two components is 48.56 arcsec for HD 27256 (Torres et al. 1986)
and 0.945 arcsec for HD 224533 (Horch et al. 1999),
with a magnitude difference of respectively, about 8.7 and 5.3 magnitudes.
.
The separation of the two components is 48.56 arcsec for HD 27256 (Torres et al. 1986)
and 0.945 arcsec for HD 224533 (Horch et al. 1999),
with a magnitude difference of respectively, about 8.7 and 5.3 magnitudes.
For HD 27256 which is 50.05 pc far away this implies a separation
between the components of ![]() 2434 AU.
Such a large separation requires a long orbital period.
Under reasonable assumptions on the mass of the two stars
(in the 3
2434 AU.
Such a large separation requires a long orbital period.
Under reasonable assumptions on the mass of the two stars
(in the 3
![]() range for the primary and about 0.5 for the secondary),
the periods required are of the order of 50-100 thousand years,
and the associated
range for the primary and about 0.5 for the secondary),
the periods required are of the order of 50-100 thousand years,
and the associated
![]() .
The maximum linear acceleration of the primary due to this companion
(assuming a circular orbit) would be about
0.004
.
The maximum linear acceleration of the primary due to this companion
(assuming a circular orbit) would be about
0.004
![]() ,
or about 5 orders of magnitude smaller
than the observed accleration. The observed RV variations cannot be due
to the known stellar companion and
we are obliged to look for other interpretations. We suggest
that the RV variability observed on HD 27256 (see Fig. 9 upper panel)
is induced either by another unseen companion or by rotational modulation.
In case of an unseen companion, the low
,
or about 5 orders of magnitude smaller
than the observed accleration. The observed RV variations cannot be due
to the known stellar companion and
we are obliged to look for other interpretations. We suggest
that the RV variability observed on HD 27256 (see Fig. 9 upper panel)
is induced either by another unseen companion or by rotational modulation.
In case of an unseen companion, the low
![]() could imply a sub-stellar object.
This star has also been thoroughly studied for stellar activity, being detected
in the Ca II chromospheric lines (Pasquini et al. 2000),
by EUVE and ROSAT in the soft X-ray.
Its chromospheric activity and rotational velocity are usual
for stars of its mass and temperature, and with a
radius of about 14.5
could imply a sub-stellar object.
This star has also been thoroughly studied for stellar activity, being detected
in the Ca II chromospheric lines (Pasquini et al. 2000),
by EUVE and ROSAT in the soft X-ray.
Its chromospheric activity and rotational velocity are usual
for stars of its mass and temperature, and with a
radius of about 14.5
![]() and a projected rotational velocity in the range of
4.5-6
and a projected rotational velocity in the range of
4.5-6
![]() the expected rotational period is not longer
than 165 days, far shorter than the long period RV variations observed by us.
Therefore rotational modulation does not provide a convincing explanation.
the expected rotational period is not longer
than 165 days, far shorter than the long period RV variations observed by us.
Therefore rotational modulation does not provide a convincing explanation.
In Paper I we discussed HD 224533 based on our 14 months observation data.
There we concluded that the RV variability of this giant
may be caused by an unseen companion rather than the visible component
detected by Horch et al. (1999).
Our new data confirms the previous analysis, and, as can be seen in Fig. 9
(lower panel), we have observed a RV variation of
![]() 600
600
![]() within
within ![]() 800 days.
The mean RV of our measurements for this star is -0.51
800 days.
The mean RV of our measurements for this star is -0.51
![]() .
The
published RV of this star is -0.2
.
The
published RV of this star is -0.2
![]() (Duflot et al. 1995).
The RV value for
(Duflot et al. 1995).
The RV value for ![]() Cet in the same catalogue is of -16.4
Cet in the same catalogue is of -16.4
![]() which differs by about 0.26
which differs by about 0.26
![]() from our mean value. Applying the
from our mean value. Applying the ![]() Cet
offset to HD 224533, the Duflot RV for this star would become -0.46
Cet
offset to HD 224533, the Duflot RV for this star would become -0.46
![]() ,
that is only 50
,
that is only 50
![]() above our mean result.
There is no evidence for this star of velocity amplitude variations
exceeding 1
above our mean result.
There is no evidence for this star of velocity amplitude variations
exceeding 1
![]() .
When considering all of the available RV measurements for this star
the velocity amplitude cannot be much larger than
about 1.0
.
When considering all of the available RV measurements for this star
the velocity amplitude cannot be much larger than
about 1.0
![]() .
If we assume a primary mass m1= 2
.
If we assume a primary mass m1= 2
![]() ,
a
semi-amplitude
,
a
semi-amplitude
![]() ,
a maximal
period of 2000 days (that is about twice of our observation span) and an
eccentricity e= 0.3, we obtain a maximum
,
a maximal
period of 2000 days (that is about twice of our observation span) and an
eccentricity e= 0.3, we obtain a maximum
![]() .
The semi-major axis will be
.
The semi-major axis will be ![]() 4 AU.
The unseen companion around HD 224533 can be a brown dwarf candidate.
4 AU.
The unseen companion around HD 224533 can be a brown dwarf candidate.
In addition to all the binary systems mentioned above we found two stars for which we could produce evidence for planetary companions: HD 47536 (Setiawan et al. 2003b) and HD 122430 (Setiawan 2003c). Not only do these objects show significant periodic variabilities, but, in addition, their RV variabilities are not dependent on stellar activity or bisector variations. Thus, it cannot be ascribed to rotational modulation or pulsations.
![\begin{figure}
\par\includegraphics[width=7.6cm,height=8.0cm,clip]{0081fig10.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg75.gif) |
Figure 10:
Trend of RV variation - given by
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,height=5.8cm,clip]{0081fig11a.ps...
...mm}
\includegraphics[width=7.7cm,height=5.8cm,clip]{0081fig11c.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg76.gif) |
Figure 11:
3 stars from different RGB regions are presented. HD 92588
- located in the lower of RGB - with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,height=7.6cm,clip]{0081fig12.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg77.gif) |
Figure 12: RV variability as a function of the stellar magnitude for the stars of our sample, after eliminating the stars with bona fide stellar companions. The two binaries with possible sub-stellar companions (HD 27256 and HD 224533) are given as dots, whereas stars hosting giant planet candidates HD 47536 and HD 122430 are indicated with filled triangles. Note the increase of spread and of minimum variability with increasing luminosity. |
| Open with DEXTER | |
In Paper I we suggested that the variations in RV observed were broadly
correlated with the position of the star in the H-R diagram.
Is this variation still present in our "cleaned'' sample, that is, after
binaries have been eliminated?
A glance at Fig. 10, in which the size of the dots is proportional to the
RV variations, seems to confirm this trend:
going towards more luminous stars, the circles tend to be bigger.
For the lower part of the RGB, a typical
![]() - with the exception for 3 stars - is
less than 40
- with the exception for 3 stars - is
less than 40
![]() .
In the middle, including the clump region,
.
In the middle, including the clump region,
![]() -60
-60
![]() are measured for the most targets.
In the upper region larger
are measured for the most targets.
In the upper region larger
![]() are detected up to 301
are detected up to 301
![]() .
Figure 11 illustrates examples of RV measurements of giants in the lower
(HD 92588), middle (HD 61935) and upper (HD 81797) regions of the RGB.
The increase of
.
Figure 11 illustrates examples of RV measurements of giants in the lower
(HD 92588), middle (HD 61935) and upper (HD 81797) regions of the RGB.
The increase of
![]() along the RGB is consistent with
the RV survey reported by Mitchell et al. (2001) for a sample of 182 K giants.
along the RGB is consistent with
the RV survey reported by Mitchell et al. (2001) for a sample of 182 K giants.
We found it instructive to plot the RV measured variability as a function of the
absolute stellar magnitude, as done in Fig. 12. In this
figure we have only considered the "single'' stars, plus the two low amplitude binaries,
HD 27256 and HD 224533 (plotted as dots), HD 47536 and HD 122430, the
stars with planetary candidates (plotted as filled triangle).
The lower envelope of the data points suggests that the minimum level of RV variability increases with the stellar luminosity;
that is, no bright giant is constant at the
25
![]() accuracy of our survey.
Also, the degree of variability seems to increase with luminosity, since the
spread of the data increases with magnitude.
Both these results could indicate the dependence of RV variability on some
basic stellar parameter, such as gravity.
The presence of the
two binary systems, however, calls for a cautious interpretation:
they both lie in the upper envelope
distribution and this could suggest that several of the stars in
the upper envelope of the diagram are multiple systems.
The evidences for planetary companions to HD 47536 and HD 122430
(marked with triangles) in the upper envelope of the
distribution, but still in a quite crowded portion of the diagram,
confirm that the presence of planetary companions is also an
attractive explanation for
the upper part of the distribution.
By excluding stars with stellar companions,
the average of all
accuracy of our survey.
Also, the degree of variability seems to increase with luminosity, since the
spread of the data increases with magnitude.
Both these results could indicate the dependence of RV variability on some
basic stellar parameter, such as gravity.
The presence of the
two binary systems, however, calls for a cautious interpretation:
they both lie in the upper envelope
distribution and this could suggest that several of the stars in
the upper envelope of the diagram are multiple systems.
The evidences for planetary companions to HD 47536 and HD 122430
(marked with triangles) in the upper envelope of the
distribution, but still in a quite crowded portion of the diagram,
confirm that the presence of planetary companions is also an
attractive explanation for
the upper part of the distribution.
By excluding stars with stellar companions,
the average of all
![]() is 60
is 60
![]() .
.
We note that two of our targets: HD 78647 and HD 151249 show
![]() and 281
and 281
![]() ,
respectively.
The RV variability of HD 78647 is of long-period
and this star is by far the brightest and coolest of the sample, corresponding
to a late K supergiant.
Our preliminary investigation of their chromospheric activity through the analysis of the
Ca II K emission reveals a measurable variability in these lines, possibly in
phase with the RV measurements, and this would clearly favour the interpretation that their
long-period RV variability is due to rotational modulation rather than due
to sub-stellar companions.
In addition, we observed for HD 78647 a correlation between the RV measurements and the
bisector velocity span (see Queloz et al. 2001), shown in Fig. 13.
,
respectively.
The RV variability of HD 78647 is of long-period
and this star is by far the brightest and coolest of the sample, corresponding
to a late K supergiant.
Our preliminary investigation of their chromospheric activity through the analysis of the
Ca II K emission reveals a measurable variability in these lines, possibly in
phase with the RV measurements, and this would clearly favour the interpretation that their
long-period RV variability is due to rotational modulation rather than due
to sub-stellar companions.
In addition, we observed for HD 78647 a correlation between the RV measurements and the
bisector velocity span (see Queloz et al. 2001), shown in Fig. 13.
![\begin{figure}
\par\includegraphics[width=7.8cm,height=7.4cm,clip]{0081fig13a.ps...
...
\par\includegraphics[width=7.5cm,height=7.4cm,clip]{0081fig13b.ps}
\end{figure}](/articles/aa/full/2004/25/aa0081-04/Timg79.gif) |
Figure 13: The upper panel shows the RV measurements of HD 78647. The lower panel presents the bisector velocity spans vs. the RV measurements. A clear correlation is present; together with variability detected in the Ca II K line, this indicates that the RV variability is induced by rotational modulation. |
| Open with DEXTER | |
More than 70![]() of the sample stars reveal
variability over 50
of the sample stars reveal
variability over 50
![]() and can be considered
bona fide variable. This definitely confirms that
RV variability among G and K giants is ubiquitous.
Based on our sample, we produced evidence that 11 stars
belong to binary/multiple systems.
For 6 of the 11 systems we derived the
minimum masses of the companions
and can be considered
bona fide variable. This definitely confirms that
RV variability among G and K giants is ubiquitous.
Based on our sample, we produced evidence that 11 stars
belong to binary/multiple systems.
For 6 of the 11 systems we derived the
minimum masses of the companions
![]() between 0.1-0.6
between 0.1-0.6
![]() .
We showed that the variabilities observed in 2
additional giants, known as visual binaries, are not induced
by the visual companions, but rather by unseen objects, which
might be in the brown dwarf mass regime.
When considering that our sample was already selected to avoid
known binary stars, the statistics of binary objects is consistent with
surveys among binaries in main sequence stars and binaries with
red giant primary.
The mass distribution shows many low-mass companions,
and this is also in qualitative agreement with our selection bias.
Two stars from our sample, HD 47536 and HD 122430 show evidence of
planetary companions.
The presence of stellar/sub-stellar companions
seems therefore to represent a relevant component in the
RV variability of giant stars.
.
We showed that the variabilities observed in 2
additional giants, known as visual binaries, are not induced
by the visual companions, but rather by unseen objects, which
might be in the brown dwarf mass regime.
When considering that our sample was already selected to avoid
known binary stars, the statistics of binary objects is consistent with
surveys among binaries in main sequence stars and binaries with
red giant primary.
The mass distribution shows many low-mass companions,
and this is also in qualitative agreement with our selection bias.
Two stars from our sample, HD 47536 and HD 122430 show evidence of
planetary companions.
The presence of stellar/sub-stellar companions
seems therefore to represent a relevant component in the
RV variability of giant stars.
Once the known binaries were eliminated from the analysis,
we found that our sample stars exhibit typical RV variability of
![]() .
This average RV is about a factor of 3 greater than the spectrograph precision.
Our results allowed us to establish a relationship between RV variability and
position in the RGB. Stars in the upper region of the RGB
exhibit considerable RV variations with
.
This average RV is about a factor of 3 greater than the spectrograph precision.
Our results allowed us to establish a relationship between RV variability and
position in the RGB. Stars in the upper region of the RGB
exhibit considerable RV variations with
![]() ,
whereas in the other regions
,
whereas in the other regions
![]() .
This result can be seen in more detail by
plotting the RV variability as a function of the
stellar absolute magnitude. In this diagram we can see how the
minimum level of variability increases with the stellar luminosity,
as well as the spread in variability. The presence of the low-mass
binaries in the upper envelope of the distribution may suggest that
low-mass companions can still be discovered.
However, companions cannot explain the whole range of variability
observed, which must be induced by other causes as well.
.
This result can be seen in more detail by
plotting the RV variability as a function of the
stellar absolute magnitude. In this diagram we can see how the
minimum level of variability increases with the stellar luminosity,
as well as the spread in variability. The presence of the low-mass
binaries in the upper envelope of the distribution may suggest that
low-mass companions can still be discovered.
However, companions cannot explain the whole range of variability
observed, which must be induced by other causes as well.
For the two most luminous and coolest stars, our Ca II and bisector analysis
shows that the large RV variability observed (around 300
![]() )
is
likely associated with chromospheric activity, and therefore rotational
modulation is the cause of RV variability.
They deserve further study and they
would be excellent candidates for large interferometers observations.
)
is
likely associated with chromospheric activity, and therefore rotational
modulation is the cause of RV variability.
They deserve further study and they
would be excellent candidates for large interferometers observations.
Finally, the reason for the RV variability for the bulk of the
45 remaining stars is still unknown, and will have to wait for the
ongoing chromospheric and bisector analysis to derive some firm conclusions.
The observed growth of the variability with stellar luminosity is
certainly consistent with the expectation of oscillations,
in that, in general, more luminous stars
will have lower gravities.
Despite the brightness of our sample stars, very few have measured metallicities,
while the knowledge of the star metallicity is necessary to attempt a detailed
analysis of stellar masses, radii and gravities because of the well-known degeneracy affecting mass and metallicity in the colors of RGB stars.
Pending a more accurate
mass determination for each star, which will be attempted after a
detailed chemical analysis of the objects (da Silva et al. 2004, in
preparation) we can say that, with a variability of about
80
![]() at
at
![]() and 40
and 40
![]() at two magnitudes fainter, and assuming the same mass for the objects,
this would lead to a difference in gravity of about a factor of 12
(considering both stars on the RGB);
this would imply only a mild dependence of the
RV variability on gravity, at least in these regimes.
at two magnitudes fainter, and assuming the same mass for the objects,
this would lead to a difference in gravity of about a factor of 12
(considering both stars on the RGB);
this would imply only a mild dependence of the
RV variability on gravity, at least in these regimes.
Concerning the possibility that other mechanisms are responsible for the observed RV, we can only say that at least in two luminous and coolest giants we observed chromospheric variations associated which RV variations, which indicates that rotational modulation may be relevant. The observed dependence is smaller than what is predicted for instance by Kjeldsen & Bedding (1995).
Acknowledgements
We are grateful to A. Torrejon and R. Vega for their assistance during the observation. We thank E. Guenther for observing our target with the TLS-Tautenburg telescope. J. Setiawan thanks the state Baden-Würtemmberg for the grant through the Landesgraduiertenförderungsgesetz. L. da Silva and J. R. de Medeiros thank the CNPq Brazilian Agency for the continuous financial support. G. Caira helped in the analysis of the data, and her work was supported through ESO DGDF. We thank J. Eskdale and M. Pia for a careful reading of the manuscript.