We observed the pre-stellar core L1521F in dust emission at 1.2 mm and in two transitions each of
A&A 420, 957-974 (2004)
DOI: 10.1051/0004-6361:20035915
A. Crapsi1,2 - P. Caselli3 - C. M. Walmsley3 - M. Tafalla4 - C. W. Lee5 - T. L. Bourke6 - P. C. Myers2
1 - Università degli Studi di Firenze Dipartimento di Astronomia e
Scienza dello Spazio, Largo E. Fermi 5, 50125 Firenze, Italy
2 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge,
MA 02138, USA
3 -
INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
4 -
Observatorio Astronómico Nacional (IGN), Alfonso XII, 3, 28014 Madrid, Spain
5 -
Taeduk Radio Astronomy Observatory, Korea Astronomy Observatory, 61-1 Hwaam-dong,
Yusung-gu, Daejon 305-348, Korea
6 -
Harvard-Smithsonian Center for Astrophysics, Submillimeter Array Project, 645 N.
A'ohoku Place, Hilo, HI 96720, USA
Received 19 December 2003 / Accepted 19 March 2004
Abstract
We observed the pre-stellar core L1521F in dust
emission at 1.2 mm and in two transitions each of
![]() ,
,
![]() ,
,
![]() and
and
![]() in order to increase the sample of well studied
centrally concentrated and chemically
evolved starless cores, likely on the verge of star formation, and to
determine the initial conditions for low-mass star formation
in the Taurus Molecular Cloud. The dust observation allows us to infer
the density structure of the core and together with measurements
of CO isotopomers gives us the CO depletion.
in order to increase the sample of well studied
centrally concentrated and chemically
evolved starless cores, likely on the verge of star formation, and to
determine the initial conditions for low-mass star formation
in the Taurus Molecular Cloud. The dust observation allows us to infer
the density structure of the core and together with measurements
of CO isotopomers gives us the CO depletion.
![]() and
and
![]() lines are good tracers of the dust
continuum and thus they give kinematic information on the core nucleus.
We derived in this object a molecular hydrogen number
density n(
lines are good tracers of the dust
continuum and thus they give kinematic information on the core nucleus.
We derived in this object a molecular hydrogen number
density n(![]()
![]()
![]() and a CO depletion factor,
integrated along the line of sight,
and a CO depletion factor,
integrated along the line of sight,
![]() in the
central 20
in the
central 20
![]() ,
similar to the pre-stellar core L1544. However,
the
,
similar to the pre-stellar core L1544. However,
the
![]() column density ratio is
column density ratio is ![]() 0.1, a factor of
about 2 lower than that found in L1544. The observed relation between the
deuterium fractionation and the integrated CO depletion factor across the core
can be reproduced by chemical models if
0.1, a factor of
about 2 lower than that found in L1544. The observed relation between the
deuterium fractionation and the integrated CO depletion factor across the core
can be reproduced by chemical models if
![]() is
slightly (factor of
is
slightly (factor of ![]() 2 in fractional abundance) depleted in the central 3000 AU. The
2 in fractional abundance) depleted in the central 3000 AU. The
![]() and
and
![]() linewidths
in the core center are
linewidths
in the core center are ![]() 0.3
0.3
![]() ,
significantly
larger than in other more quiescent Taurus starless cores but similar
to those observed in the center of L1544.
The kinematical behaviour of L1521F is more complex than
seen in L1544, and a model of
contraction due to ambipolar diffusion is only
marginally consistent with the present data.
Other velocity fields, perhaps produced by accretion
of the surrounding material onto the core and/or unresolved substructure,
are present. Both chemical and kinematical analyses suggest that L1521F is less evolved than L1544, but, in analogy with L1544,
it is approaching the "critical'' state.
,
significantly
larger than in other more quiescent Taurus starless cores but similar
to those observed in the center of L1544.
The kinematical behaviour of L1521F is more complex than
seen in L1544, and a model of
contraction due to ambipolar diffusion is only
marginally consistent with the present data.
Other velocity fields, perhaps produced by accretion
of the surrounding material onto the core and/or unresolved substructure,
are present. Both chemical and kinematical analyses suggest that L1521F is less evolved than L1544, but, in analogy with L1544,
it is approaching the "critical'' state.
Key words: radio lines: ISM - radio continuum: ISM - submillimeter
Clearly trying to extrapolate general trends from a single object is difficult
and a larger number of L1544-like cores (preferably with the same external
environment) should be studied.
Unfortunately there are rather few other objects with similar
properties due to the short timescale of this phase.
According to the Ciolek & Basu (2000) model, for example, (contraction of a disk
driven by ambipolar diffusion) L1544-like properties fit the model structure of a
core at times
![]() years prior to the collapse,
after an evolution of
years prior to the collapse,
after an evolution of
![]() years. Thus in that particular model, L1544 finds itself in the last
few percent of its evolution prior to becoming a protostar.
While this may be a somewhat too literal interpretation of the
model results, it shows that "L1544-type
cores'' should be relatively rare.
years. Thus in that particular model, L1544 finds itself in the last
few percent of its evolution prior to becoming a protostar.
While this may be a somewhat too literal interpretation of the
model results, it shows that "L1544-type
cores'' should be relatively rare.
Further progress requires the definition of what is
a L1544-like core.
One answer is to use current estimates of dust emission
and absorption selecting cores of dust extinction upwards of 50 mag.
Another approach is to say that cores which show signs of
infalling gas (as does L1544, see Williams et al. 1999; Tafalla et al. 1998) are "L1544-twins''. This latter indicator
is complicated by the fact that at the high densities found
in the nuclei of cores similar to L1544, many molecular species and in
particular CO and CS freeze-out onto dust grain surfaces (see Kramer et al. 1999;
Caselli et al. 1999; Bacmann et al. 2002; Bergin et al. 2002; Jørgensen et al. 2002;
Tafalla et al. 2002);
observing such tracers implies observing the low density
surrounding envelope. However, recent studies indicate that species whose
abundance is linked to that of molecular nitrogen such as N2H+ and NH3 (as well as their deuterated
counterparts) do not condense out in the same fashion and hence can be used
as tracers of the dense gas (Bergin & Langer 1997).
The extent to which this is true is
debatable but it is a useful hypothesis and substantiated by the general
similarity of the spatial distributions seen for example in dust
emission and in maps of
![]() (Tafalla et al. 2002, 2004).
(Tafalla et al. 2002, 2004).
Caselli et al. (2002a,b)
have used
![]() and
and
![]() to derive the physical,
chemical and kinematical properties of L1544.
They found that L1544 has a central
to derive the physical,
chemical and kinematical properties of L1544.
They found that L1544 has a central
![]() column density of
column density of
![]() cm-2 and a column density ratio
cm-2 and a column density ratio
![]() of 0.24.
The
of 0.24.
The
![]() linewidths towards the nucleus (the dust emission peak) are
roughly 0.3 km s-1 and decrease as one goes to positions away from the
center. The line of sight velocity measured in
linewidths towards the nucleus (the dust emission peak) are
roughly 0.3 km s-1 and decrease as one goes to positions away from the
center. The line of sight velocity measured in
![]() (1-0) and
(1-0) and
![]() (2-1) shows
a gradient along the minor axis of the elliptical structure seen in 1.3 mm
dust emission but no clear gradient along the major axis.
(2-1) shows
a gradient along the minor axis of the elliptical structure seen in 1.3 mm
dust emission but no clear gradient along the major axis.
In this paper, we will study another core in the Taurus complex,
L1521F (at an assumed distance of 140 parsec) using
the same approach as in our study of L1544.
Repeating the L1544 study carried out by Caselli et al. (2002a,b)
is important because it
allows us to check to what extent L1544 is an exceptional case.
In order to do this we need another source which
has the same general characteristics as L1544.
The source selection was made using some preliminary results we obtained
in a survey carried out at the IRAM-30 m telescope.
L1521F stood out as being the only core in Taurus, besides L1544, with
strong
![]() (2-1)
emission compared to
(2-1)
emission compared to
![]() (1-0).
This suggests enhanced deuterium fractionation implying an advanced
evolutionary state (Caselli et al. 2002b). Previous observations
of this object have been carried out by Mizuno et al. (1994),
Onishi et al. (1996),
Codella et al. (1997), and Lee et al. (1999a).
Onishi et al. (1999) also studied L1521F (which they
call MC 27), and found a high central density, suggesting that this
is the most evolved starless condensation in Taurus. L1521F was also
noted by Lee et al. (1999b) as a strong infall candidate, in their
survey of CS and
(1-0).
This suggests enhanced deuterium fractionation implying an advanced
evolutionary state (Caselli et al. 2002b). Previous observations
of this object have been carried out by Mizuno et al. (1994),
Onishi et al. (1996),
Codella et al. (1997), and Lee et al. (1999a).
Onishi et al. (1999) also studied L1521F (which they
call MC 27), and found a high central density, suggesting that this
is the most evolved starless condensation in Taurus. L1521F was also
noted by Lee et al. (1999b) as a strong infall candidate, in their
survey of CS and
![]() lines in starless cores, although later
mapping of the two tracers has shown extended "red'' asymmetry in the
CS(2-1) profiles (Lee et al. 2001).
lines in starless cores, although later
mapping of the two tracers has shown extended "red'' asymmetry in the
CS(2-1) profiles (Lee et al. 2001).
In Sect. 2 of this paper, we describe our observational procedure. In Sect. 3 we present the observational results deriving the physical characteristics of the source and analysing its chemical and kinematical properties. In Sect. 4 we discuss the observational results and the summary can be found in Sect. 5.
The observations were carried out between April 2002 and January 2003 at the IRAM-30 m in three different runs.
In April 2002,
we observed the core in
![]() (1-0),
(1-0),
![]() (3-2),
(3-2),
![]() (2-1) and
(2-1) and
![]() (3-2). In general, we used the symmetric frequency switch mode
and the facility
autocorrelator; in Table 1, we summarize the main observational
parameters. The frequencies of the
(3-2). In general, we used the symmetric frequency switch mode
and the facility
autocorrelator; in Table 1, we summarize the main observational
parameters. The frequencies of the
![]() (1-0),
(1-0),
![]() (2-1) and
(2-1) and
![]() (3-2) have been updated following the recent determinations of Dore et al. (2004);
the values in the table refer to the
F1 F = 2 3
(3-2) have been updated following the recent determinations of Dore et al. (2004);
the values in the table refer to the
F1 F = 2 3
![]() 1 2, 2 3
1 2, 2 3
![]() 1 2, and 4 5
1 2, and 4 5
![]() 3 4 hyperfine components of
the
3 4 hyperfine components of
the
![]() (1-0),
(1-0),
![]() (2-1) and
(2-1) and
![]() (3-2) transitions, respectively.
For
(3-2) transitions, respectively.
For
![]() (3-2) we used the frequency of the 2 1
(3-2) we used the frequency of the 2 1
![]() 1 0 component
as determined by Caselli et al. (2002a).
In the case of the April 2002
1 0 component
as determined by Caselli et al. (2002a).
In the case of the April 2002
![]() (3-2) observations,
in order to improve the baseline
quality, we used also
the "Wobbler switching'' mode with
a 240
(3-2) observations,
in order to improve the baseline
quality, we used also
the "Wobbler switching'' mode with
a 240
![]() throw.
We reached an rms sensitivity in main-beam brightness units of about 100 mK
in all lines except
throw.
We reached an rms sensitivity in main-beam brightness units of about 100 mK
in all lines except
![]() (3-2) (
(3-2) (![]() 400 mK).
The pointing was checked every 2 h by means of a 3 or 2 mm continuum
scan on nearby quasars and was accurate to within
400 mK).
The pointing was checked every 2 h by means of a 3 or 2 mm continuum
scan on nearby quasars and was accurate to within ![]() 4
4
![]() .
.
In order to refine the maps, originally taken with a 20
![]() spacing, we observed in Nov. 2002 with a 10
spacing, we observed in Nov. 2002 with a 10
![]() grid
(but 5
grid
(but 5
![]() spacing in the inner 20 s).
spacing in the inner 20 s).
Table 1: Telescope settings and parameters.
Between January 2003 and March 2003, we obtained
continuum data at 1.2 mm together with observations of
![]() and
and
![]() (1-0) and (2-1). These data were taken in service mode by the IRAM staff.
(1-0) and (2-1). These data were taken in service mode by the IRAM staff.
The continuum data were obtained using MAMBO II,
the 117-channels bolometer
available at the 30 m.
We mapped the core within an area of
![]() scanning in azimuth
with a 5
scanning in azimuth
with a 5
![]() /s speed and an interval between the subscans of 8
/s speed and an interval between the subscans of 8
![]() .
The atmospheric attenuation was measured to be 0.14 based on tipping curves measured after the map.
The data were calibrated using the sources HL Tau and L1551 for which we assumed fluxes of 0.9 Jy and 1.4 Jy respectively
and the final sensitivity was 5 mJy per 10.5
.
The atmospheric attenuation was measured to be 0.14 based on tipping curves measured after the map.
The data were calibrated using the sources HL Tau and L1551 for which we assumed fluxes of 0.9 Jy and 1.4 Jy respectively
and the final sensitivity was 5 mJy per 10.5
![]() beam. The
calibration error inherent in this comparison is likely to
be at least ten percent due to both atmospheric fluctuations
and calibration errors.
beam. The
calibration error inherent in this comparison is likely to
be at least ten percent due to both atmospheric fluctuations
and calibration errors.
The
![]() data were taken using the on-the-fly technique.
We simultaneously mapped the
data were taken using the on-the-fly technique.
We simultaneously mapped the
![]() (1-0) and
(1-0) and
![]() (2-1) using both
polarizations for each line.
The area covered was
(2-1) using both
polarizations for each line.
The area covered was
![]() and was scanned in the
Right Ascension direction;
the distance between the subscans was 5
and was scanned in the
Right Ascension direction;
the distance between the subscans was 5
![]() as
was the angular separation
between two successive dumps.
We also obtained a 9 points map in
as
was the angular separation
between two successive dumps.
We also obtained a 9 points map in
![]() (1-0) and
(1-0) and
![]() (2-1)
centered
at the dust peak and spaced by 20
(2-1)
centered
at the dust peak and spaced by 20
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f1.ps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg55.gif) |
Figure 1: Dust emission from L1521F. Levels are 30, 55 and 80 mJy/beam. Reference position is RA: 04:28:39.8 DEC: 26:51:35 (J2000). The dashed ellipse best fits the core structure with a 2D Gaussian. The dotted ellipse is the result of a 2D-Gaussian fit to the whole map, including the more extended emission. The black rectangle shows the area mapped in line observations (see Fig. 2). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f2.ps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg56.gif) |
Figure 2:
L1521F integrated intensity maps in the observed molecular transitions. Contour levels are 45, 70, 95% of the relative peak in each map (whose values are: 5.9, 0.74, 1.1, 0.33, 2.5 and 2.3
|
| Open with DEXTER | |
We show the observed map of the 1.2 mm dust continuum in Fig. 1, and
the map of integrated line intensity, obtained
in the observed transitions of
![]() ,
,
![]() ,
and
,
and
![]() ,
in
Fig. 2.
The reference position for these maps is (04:28:39.8, 26:51:35) in
J2000 coordinates.
,
in
Fig. 2.
The reference position for these maps is (04:28:39.8, 26:51:35) in
J2000 coordinates.
The bolometer map was reduced with the IRAM standard
reduction program NIC. From Fig. 1, we see
that the observed emission has a "cometary'' structure in the
sense that the low level contours are well-fitted by an ellipse
with the maximum offset from the center.
We can fit the general
elliptical structure of the core with a
2D-Gaussian centered at offset
(-30
![]() , 20
, 20
![]() )
with full width half-power dimensions of
)
with full width half-power dimensions of
![]() and position angle 25
and position angle 25![]() .
If the more extended emission is not included in the fit,
the 2D-Gaussian is centered on the dust peak position
at (-10
.
If the more extended emission is not included in the fit,
the 2D-Gaussian is centered on the dust peak position
at (-10
![]() , 0
, 0
![]() ), has half-power dimensions of
), has half-power dimensions of
![]() ,
a position angle of 25
,
a position angle of 25![]() and an aspect
ratio equal to 1.6. The peak intensity is 90 mJy/beam.
and an aspect
ratio equal to 1.6. The peak intensity is 90 mJy/beam.
The spectral line data were reduced using
the standard IRAM package CLASS. A summary of line
parameters at the dust peak is given in Table 2
and the corresponding spectra are shown in Fig. 3.
The spectra shown in Fig. 3
(as well as the values in
Table 2) have been derived from data
Gaussian-smoothed to a resolution of 26
![]() in the cases of
in the cases of
![]() and
and
![]() ,
but unsmoothed in the case of
,
but unsmoothed in the case of
![]() .
These are also the effective
resolutions of the
.
These are also the effective
resolutions of the
![]() maps shown in Fig. 2 (the
two
maps shown in Fig. 2 (the
two
![]() maps are smoothed to 16
maps are smoothed to 16
![]() ,
the angular
resolution at the (2-1) frequency).
,
the angular
resolution at the (2-1) frequency).
Table 2:
Line parameters derived from hyperfine structure fitting
at position (-10, 0). The values refer to spatially
averaged spectra (26
![]() beam).
beam).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0915f3.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg66.gif) |
Figure 3:
Spectra of
|
| Open with DEXTER | |
One clear result from Fig. 3
is that in L1521F there is evidence for an "infall signature''
although less marked than in L1544,
where it is attributed to extended infall onto the core
(Williams et al. 1999) or to central infall in a depleted core
nucleus (Caselli et al. 2002a). In fact, we see evidence for
asymmetric profiles, with the blue peak brighter than the
red peak, in
![]() (1-0)
(where we derive an optical depth of order 4
in the main component based on our fit to the hyperfine satellites),
but the two peaks are not clearly separated as in the case of L1544.
(1-0)
(where we derive an optical depth of order 4
in the main component based on our fit to the hyperfine satellites),
but the two peaks are not clearly separated as in the case of L1544.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f4.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg67.gif) |
Figure 4:
Enlargement of the
|
| Open with DEXTER | |
Table 3:
Angular dimensions derived from two dimensionsal
Gauss fits to maps in the 1.2 mm continuum,
![]() ,
and
,
and
![]() emission.
emission.
It is interesting to note that two peaks are
present in the spectrum of
![]() (3-2) line
toward the offset (-10, 10), as shown in Fig. 4.
The hyperfine structure (hfs)
fit to the
(3-2) line
toward the offset (-10, 10), as shown in Fig. 4.
The hyperfine structure (hfs)
fit to the
![]() (3-2) line, assuming the presence of two
velocity components along the line of sight,
gives
(3-2) line, assuming the presence of two
velocity components along the line of sight,
gives
![]()
![]() and
and
![]()
![]() .
The line
widths of the two components are
.
The line
widths of the two components are
![]()
![]() and
and
![]()
![]() ,
marginally (factor
,
marginally (factor ![]() 1.5)
broader than the thermal
1.5)
broader than the thermal
![]() line width at 10 K. Although this
result should be confirmed with higher sensitivity data, the velocities
are consistent with those of the N1 and N2 (
line width at 10 K. Although this
result should be confirmed with higher sensitivity data, the velocities
are consistent with those of the N1 and N2 (
![]() )
clumps observed by
Shinnaga et al. (2004) with interferometric observations. The hfs fit
to the
)
clumps observed by
Shinnaga et al. (2004) with interferometric observations. The hfs fit
to the
![]() (1-0) line,
assuming two velocity components and fixing the velocities
to the values found with the (3-2) line, is consistent with the observed
spectrum (if the two velocities are not fixed, the hfs fitting procedure
applied to the
(1-0) line,
assuming two velocity components and fixing the velocities
to the values found with the (3-2) line, is consistent with the observed
spectrum (if the two velocities are not fixed, the hfs fitting procedure
applied to the
![]() (1-0) spectrum does not converge, probably because
the two components are not well separated).
This suggests that the two clumps observed by Shinnaga et al. (2004)
in
(1-0) spectrum does not converge, probably because
the two components are not well separated).
This suggests that the two clumps observed by Shinnaga et al. (2004)
in
![]() (1-0) are also present in our single dish data, although
the
(1-0) are also present in our single dish data, although
the
![]() (1-0) extended emission partially hides the features arising
from the central region.
(1-0) extended emission partially hides the features arising
from the central region.
Figure 2 shows that L1521F has in common with
several other cores
(see also Tafalla et al. 2002;
Caselli et al. 2002a,b) the property that while the maps of
the nitrogen bearing molecules have a similar
appearance to those observed in dust emission, maps
in rare CO isotopomers such as
![]() show no correlation
with the dust. In fact, the distribution of
show no correlation
with the dust. In fact, the distribution of
![]() (1-0)
and (2-1) is essentially flat over the area we have mapped, suggesting
perhaps that the layer sampled in
(1-0)
and (2-1) is essentially flat over the area we have mapped, suggesting
perhaps that the layer sampled in
![]() is either in the
background or foreground relative to that seen in dust emission.
is either in the
background or foreground relative to that seen in dust emission.
We have been able to make some estimate of the optical depths of
the observed
![]() lines by comparison with our 9-point
lines by comparison with our 9-point
![]() map (20
map (20
![]() spacing centred on (-5, -5)).
From the integrated intensity ratio of
the
spacing centred on (-5, -5)).
From the integrated intensity ratio of
the
![]() and
and
![]() (1-0) lines and assuming
an intrinsic abundance ratio [
(1-0) lines and assuming
an intrinsic abundance ratio [
![]() ]/[
]/[
![]() ]
of 3.65 (from [18O]/[17O] = 3.65, Penzias 1981;
see Kramer et al. 1999 for a discussion of the validity
of these techniques), we can put in general upper limits on
the optical depth of
]
of 3.65 (from [18O]/[17O] = 3.65, Penzias 1981;
see Kramer et al. 1999 for a discussion of the validity
of these techniques), we can put in general upper limits on
the optical depth of
![]() (1-0) of order unity. At the (-5, -5)
and (-25, -5) offsets, there is however
evidence that
(1-0) of order unity. At the (-5, -5)
and (-25, -5) offsets, there is however
evidence that
![]() (1-0) is optically thick and in fact
we derive
(1-0) is optically thick and in fact
we derive
![]() (1-0) optical depths of 1.0 and 1.5 respectively
at these two offsets (errors 50%). In these positions
we used the
(1-0) optical depths of 1.0 and 1.5 respectively
at these two offsets (errors 50%). In these positions
we used the
![]() (1-0) data and, assuming
(1-0) data and, assuming
![]() K (consistent with the observed
K (consistent with the observed
![]() (2-1)/(1-0) line ratio) and [18O]/[17O] = 3.65,
we found an average
(2-1)/(1-0) line ratio) and [18O]/[17O] = 3.65,
we found an average
![]() column density of
column density of ![]()
![]() cm-2 in the central 25
cm-2 in the central 25
![]() .
.
It is also interesting that we find that
![]() (1-0) and
dust emission maps have similar sizes, whereas
(1-0) and
dust emission maps have similar sizes, whereas
![]() maps
are somewhat smaller.
Fitting a 2D Gaussian to
the
maps
are somewhat smaller.
Fitting a 2D Gaussian to
the
![]() and
and
![]() maps in the same fashion as for
the dust emission, we find the parameters given
in Table 3 for the angular sizes of
maps in the same fashion as for
the dust emission, we find the parameters given
in Table 3 for the angular sizes of
![]() and
and
![]() in L1521F. We deduce from these data
a linear size for L1521F seen in
in L1521F. We deduce from these data
a linear size for L1521F seen in
![]() (1-0) of roughly 14 000 AU and dimensions in
(1-0) of roughly 14 000 AU and dimensions in
![]() (2-1) of
(2-1) of
![]() AU. It is interesting to note the smaller sizes
derived in the higher J transitions of both species, suggesting
that they are sampling somewhat higher density gas.
The 1.2 mm dust continuum on the other hand is more
extended suggesting that either an increase in excitation or in
abundances is causing the
AU. It is interesting to note the smaller sizes
derived in the higher J transitions of both species, suggesting
that they are sampling somewhat higher density gas.
The 1.2 mm dust continuum on the other hand is more
extended suggesting that either an increase in excitation or in
abundances is causing the
![]() and
and
![]() (3-2) line emission to increase
in relative strength toward the dust peak. Notable also are
the large aspect ratios (1.6-1.9) observed in
(3-2) line emission to increase
in relative strength toward the dust peak. Notable also are
the large aspect ratios (1.6-1.9) observed in
![]() suggesting
an ellipsoidal or triaxial form for the high density core.
suggesting
an ellipsoidal or triaxial form for the high density core.
We expect the observed continuum emission at mm wavelengths to be optically thin and can relate the 1.2 mm flux
to the ![]() column density under
the approximation of constant dust emissivity and temperature:
column density under
the approximation of constant dust emissivity and temperature:
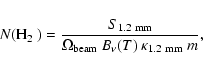
In this fashion, we derive a core mass from the continuum
measurements, within the large ellipse in Fig. 1,
of
![]()
![]() corresponding to an integrated
total flux of
corresponding to an integrated
total flux of
![]() Jy. (The error is dominated by
errors in calibration and baseline removal.) Within the 26
Jy. (The error is dominated by
errors in calibration and baseline removal.) Within the 26
![]() beam, used for our line measurements, the
enclosed mass is 0.7
beam, used for our line measurements, the
enclosed mass is 0.7 ![]() .
It is interesting to note that 5
.
It is interesting to note that 5 ![]() and 0.8
and 0.8 ![]() are the average total mass and 1 Jeans
mass in the Taurus Molcular Cloud complex (Goodwin et al. 2004).
are the average total mass and 1 Jeans
mass in the Taurus Molcular Cloud complex (Goodwin et al. 2004).
For the purpose of comparison with model calculations, we have used the 1.2 mm continuum data to estimate the density distribution under the assumption of spherical symmetry. This inevitably involves a rough approximation since the L1521F core clearly is not spherically symmetric (the aspect ratio in the 1.2 mm continuum emission is 1.6, see Table 3) and would be better approximated with an ellipsoid.
Nevertheless, we have followed the technique adopted by
Tafalla et al. (2002) and fit our data with a model of
the form:
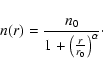
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f5.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg92.gif) |
Figure 5:
Circularly averaged dust emission
fitted with the expression n0/(1+(r/r0) |
| Open with DEXTER | |
The comparison between the dust continuum emission and the
![]() integrated intensity map allows the determination of the
amount of CO freeze-out onto dust grain surfaces, integrated along
the line of sight. This is possible because
the millimeter continuum data furnish
integrated intensity map allows the determination of the
amount of CO freeze-out onto dust grain surfaces, integrated along
the line of sight. This is possible because
the millimeter continuum data furnish
![]() ,
the column density of
molecular hydrogen across the core, assuming optically thin conditions.
The same quantity is obtained from
,
the column density of
molecular hydrogen across the core, assuming optically thin conditions.
The same quantity is obtained from
![]() lines (
lines (
![]() ),
again under the assumption
of optically thin conditions, and adopting the relation between CO and
),
again under the assumption
of optically thin conditions, and adopting the relation between CO and ![]() valid in undepleted conditions ([CO]/[
valid in undepleted conditions ([CO]/[![]()
![]() ,
the "canonical'' CO abundance value; Frerking et al. 1982). From the
,
the "canonical'' CO abundance value; Frerking et al. 1982). From the
![]() /
/
![]() column
density ratio, the integrated CO depletion factor (
column
density ratio, the integrated CO depletion factor (![]() ), or the
ratio between the canonical and the observed CO abundance (
), or the
ratio between the canonical and the observed CO abundance (
![]() /
/
![]() ), is easily derived.
), is easily derived.
In practice, this process requires the division of the 1.2 mm dust continuum
emission (
![]() [mJy/beam
[mJy/beam
![]() [mJy]/
[mJy]/
![]() )
map by the
)
map by the
![]() integrated intensity
(
integrated intensity
(
![]() ) map. The map-division has been carried out using
the IRAM image manipulation software GRAPHIC,
after degrading the continuum map to the angular resolution of the
) map. The map-division has been carried out using
the IRAM image manipulation software GRAPHIC,
after degrading the continuum map to the angular resolution of the
![]() (1-0) observations (22
(1-0) observations (22
![]() )
so that the integrated depletion factor
can be expressed by:
)
so that the integrated depletion factor
can be expressed by:
There are several caveats to the above procedure. One is
that the "canonical abundance'' appears to vary from cloud to
cloud (Lacy et al. 1994;
Alves et al. 1999; Kramer et al. 1999)
and is roughly one third of the diffuse cloud carbon gas
phase abundance (Sofia et al. 1997). Given that CO
is expected to represent essentially all the gas phase carbon in
molecular clouds, this suggests depletion of carbon in some
form (not necessarily as solid CO) even on the outskirts of cores
(we note that the direct study of CO solid state
features in Taurus (Chiar et al. 1995) shows
that solid CO towards 4 field stars in Taurus is less than 40% of the canonical gas phase CO abundance and is
observed for extinctions ![]() greater than 6 mag).
Thus we conclude that in particular cases such as L1521F,
it is quite possible that we are using a value of
greater than 6 mag).
Thus we conclude that in particular cases such as L1521F,
it is quite possible that we are using a value of
![]() which is a factor of order 2 too large or
small thus influencing the values of
which is a factor of order 2 too large or
small thus influencing the values of ![]() which we derive
but not the trends over our map.
which we derive
but not the trends over our map.
Another problem is that the values of ![]() which we
derive are integrated along the line of sight in a situation
where the observed
which we
derive are integrated along the line of sight in a situation
where the observed
![]() emission forms in an outer shell
whereas the dust emission mainly emanates from the dense
core nucleus. As a consequence, we observe
emission forms in an outer shell
whereas the dust emission mainly emanates from the dense
core nucleus. As a consequence, we observe
![]() mainly
from foreground and background gas which (see Fig. 2) has
an essentially flat distribution over the region mapped by
us. One concludes that our values of
mainly
from foreground and background gas which (see Fig. 2) has
an essentially flat distribution over the region mapped by
us. One concludes that our values of ![]() are strict
lower limits to the CO depletion in the core nucleus
from which
dust emission is observed. It is also the case that in
this situation, the form of our map of
are strict
lower limits to the CO depletion in the core nucleus
from which
dust emission is observed. It is also the case that in
this situation, the form of our map of ![]() is essentially
that of the dust emission (as we indeed find, see Eq. (2)).
The local distribution of the CO depletion factor
(which we call
is essentially
that of the dust emission (as we indeed find, see Eq. (2)).
The local distribution of the CO depletion factor
(which we call
![]() ,
see below) may differ greatly
and be much more highly peaked than in our map.
Nevertheless, the
,
see below) may differ greatly
and be much more highly peaked than in our map.
Nevertheless, the ![]() values derived by us are
direct observables and we have therefore used them for the
purpose of correlating with parameters such as the observed
deuterium fractionation. We have also used them for
model comparisons (Sects. 4.1.1 and 4.1.2)
bearing in mind the above discussion.
values derived by us are
direct observables and we have therefore used them for the
purpose of correlating with parameters such as the observed
deuterium fractionation. We have also used them for
model comparisons (Sects. 4.1.1 and 4.1.2)
bearing in mind the above discussion.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f6.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg106.gif) |
Figure 6:
CO depletion factor (full contours)
against dust emission smoothed to a 22
|
| Open with DEXTER | |
In Fig. 6 the ![]() map is shown (thick contour)
overlapped with the smoothed 1.2 mm map (grey scale) and the
map is shown (thick contour)
overlapped with the smoothed 1.2 mm map (grey scale) and the
![]() (2-1) map (dashed contours).
The CO depletion factor increases between 6 at the lowest contour of
the 1.2 mm map (
(2-1) map (dashed contours).
The CO depletion factor increases between 6 at the lowest contour of
the 1.2 mm map (
![]() mJy/22
mJy/22
![]() beam) to 18 at the peak
position (offset [0, 9]), which is 11
beam) to 18 at the peak
position (offset [0, 9]), which is 11
![]() off
the millimeter dust emission peak (offset [-8, +2]), where
off
the millimeter dust emission peak (offset [-8, +2]), where
![]() mJy/22
mJy/22
![]() beam). From Fig. 6 we immediately see
that
beam). From Fig. 6 we immediately see
that ![]() correlates with the
correlates with the
![]() emission (and deuterium
fractionation, see Sect. 3.4) and the 1.2 mm dust flux.
The good correlation between
emission (and deuterium
fractionation, see Sect. 3.4) and the 1.2 mm dust flux.
The good correlation between ![]() and
and
![]() is also evident in Fig. 7,
where
is also evident in Fig. 7,
where ![]() is
plotted as a function of
is
plotted as a function of
![]() (
(![]()
![]() mJy/(22
mJy/(22
![]() beam), with the assumptions on
beam), with the assumptions on
![]() and
and
![]() as described above). Thus, in L1521F, and with
the caveats discussed above,
as described above). Thus, in L1521F, and with
the caveats discussed above, ![]() is linearly dependent on the
is linearly dependent on the ![]() column density (
column density (
![]() );
the best fit to the data in Fig. 7 (dashed curve)
gives:
);
the best fit to the data in Fig. 7 (dashed curve)
gives:
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0915f7.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg119.gif) |
Figure 7:
Integrated CO depletion factor |
| Open with DEXTER | |
The
![]() and
and
![]() column densities have been determined using
the "constant-
column densities have been determined using
the "constant-
![]() '' (CTEX) approximation, which reduces to
simple analytic expressions (see Appendix A in Caselli et al. 2002b),
and the Large Velocity Gradient (LVG) approximation.
Both approaches give reasonable column density estimates as long
as optical depths are small. When, as for example for
'' (CTEX) approximation, which reduces to
simple analytic expressions (see Appendix A in Caselli et al. 2002b),
and the Large Velocity Gradient (LVG) approximation.
Both approaches give reasonable column density estimates as long
as optical depths are small. When, as for example for
![]() (1-0),
the optical depths in the main hyperfine satellites are large, one
is best (independent of method) to use the weakest of the satellites
or alternatively the optical depth inferred from the intensity ratio
of the weakest satellite to the strong main components. The errors in
any case stem from the difficulties in estimating the optical depth
of thick lines compounded with possible non-LTE effects for the
hyperfine satellites (Caselli et al. 1995).
Errors due to the estimate of the
partition function (i.e. the fraction of the species in unobserved
levels) appear to be less. We in general report column
densities for
(1-0),
the optical depths in the main hyperfine satellites are large, one
is best (independent of method) to use the weakest of the satellites
or alternatively the optical depth inferred from the intensity ratio
of the weakest satellite to the strong main components. The errors in
any case stem from the difficulties in estimating the optical depth
of thick lines compounded with possible non-LTE effects for the
hyperfine satellites (Caselli et al. 1995).
Errors due to the estimate of the
partition function (i.e. the fraction of the species in unobserved
levels) appear to be less. We in general report column
densities for
![]() using the CTEX approach based on the
integrated intensity of the weakest satellite of
using the CTEX approach based on the
integrated intensity of the weakest satellite of
![]() (1-0)
and for
(1-0)
and for
![]() assuming optically thin conditions. From comparison
between the different approaches employed by us,
we estimate the column density errors to be
30 percent.
assuming optically thin conditions. From comparison
between the different approaches employed by us,
we estimate the column density errors to be
30 percent.
We have also used LVG estimates to infer the density towards the
peak and edges of our
![]() map. Here, we assume a temperature of 10 K and have used rates from Green (1975) for
collisions of He with
map. Here, we assume a temperature of 10 K and have used rates from Green (1975) for
collisions of He with
![]() .
Based on the values in Table 2
(data smoothed to 26
.
Based on the values in Table 2
(data smoothed to 26
![]() spatial resolution)
for the integrated intensities of
spatial resolution)
for the integrated intensities of
![]() ,
we find
,
we find
![]()
![]() towards the dust peak of L1521F and
towards the dust peak of L1521F and
![]()
![]() 30
30
![]() North (offset [-10, 30]). For
North (offset [-10, 30]). For
![]() (2-1) and (3-2), the corresponding numbers
are
(2-1) and (3-2), the corresponding numbers
are
![]()
![]() and
and
![]()
![]() ,
at the peak and (-10, 30) offset positions, respectively.
These values are similar to the corresponding
values for L1544 consistent with the idea that they have
similar density distributions. The density estimates are
somewhat smaller than estimates based on the dust emission,
probably due to the different (factor of 2.4 lower) spatial
resolution
,
at the peak and (-10, 30) offset positions, respectively.
These values are similar to the corresponding
values for L1544 consistent with the idea that they have
similar density distributions. The density estimates are
somewhat smaller than estimates based on the dust emission,
probably due to the different (factor of 2.4 lower) spatial
resolution![]() ,
and consistent perhaps with the idea that
,
and consistent perhaps with the idea that
![]() is abundant in
a shell outside but close to the dust peak. However, given that
the LVG method
assumes homogeneous conditions, the LVG-derived
densities are averages along the line of sight, thus lower values are
expected when compared to the continuum data analysis, which takes into
account the core density structure.
is abundant in
a shell outside but close to the dust peak. However, given that
the LVG method
assumes homogeneous conditions, the LVG-derived
densities are averages along the line of sight, thus lower values are
expected when compared to the continuum data analysis, which takes into
account the core density structure.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0915f8.ps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg124.gif) |
Figure 8:
[
|
| Open with DEXTER | |
The deuterium fractionation is directly estimated from the
![]() column density ratio (
column density ratio (![]()
![]() ),
and the
),
and the
![]() map in L1521F, assuming CTEX conditions,
is shown in Fig. 8.
map in L1521F, assuming CTEX conditions,
is shown in Fig. 8.
![]() ranges between
ranges between ![]() 0.02 at the core edge to 0.1 in a region about 20
0.02 at the core edge to 0.1 in a region about 20
![]() in size and centered on the dust peak
position. The peak value of
in size and centered on the dust peak
position. The peak value of
![]() is about a factor of 2 smaller than that found in L1544
(Caselli et al. 2002b).
We note that the column density of
is about a factor of 2 smaller than that found in L1544
(Caselli et al. 2002b).
We note that the column density of
![]() is similar in the two cores, and that the factor of 2 of difference in deuterium fractionation
is due to the (factor of 2) larger
is similar in the two cores, and that the factor of 2 of difference in deuterium fractionation
is due to the (factor of 2) larger
![]() column density in L1544.
This suggests that, although the two cores are similar in structure,
L1521F is probably slightly less evolved than L1544 (see
Sect. 4).
column density in L1544.
This suggests that, although the two cores are similar in structure,
L1521F is probably slightly less evolved than L1544 (see
Sect. 4).
Quiescent starless cores mapped in
![]() (1,1) and
(1,1) and
![]() (1-0) lines
typically show a "velocity coherent'' zone of nearly constant line width (
(1-0) lines
typically show a "velocity coherent'' zone of nearly constant line width (![]() )
within the half-maximum contour map, followed by a
)
within the half-maximum contour map, followed by a ![]() rise at larger distances from core center (e.g. Goodman et al.
1998).
There are however exceptions to this general trend, as pointed out
by Caselli et al. (2002c). In particular, L1544 shows a significant
increase of
rise at larger distances from core center (e.g. Goodman et al.
1998).
There are however exceptions to this general trend, as pointed out
by Caselli et al. (2002c). In particular, L1544 shows a significant
increase of
![]() and
and
![]() (but not H13CO+ and DCO+)
line widths toward the center
(factor of 1.5 within
(but not H13CO+ and DCO+)
line widths toward the center
(factor of 1.5 within ![]() 50
50
![]() ;
Caselli et al. 2002a).
This increase has been interpreted as evidence of infall
in the central few thousands AU, where CO and related species
(such as H13CO+ and DCO+) are heavily depleted. Indeed,
the line-width increase is consistent with models of ambipolar diffusion (see
Sect. 4.2).
;
Caselli et al. 2002a).
This increase has been interpreted as evidence of infall
in the central few thousands AU, where CO and related species
(such as H13CO+ and DCO+) are heavily depleted. Indeed,
the line-width increase is consistent with models of ambipolar diffusion (see
Sect. 4.2).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0915f9.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg127.gif) |
Figure 9:
|
| Open with DEXTER | |
The same trend has been observed in L1521F using
![]() and
and
![]() lines, and in Fig. 9 we show the results
obtained in
lines, and in Fig. 9 we show the results
obtained in
![]() (1-0) lines (the linewidth corrected for optical
depth, or the intrinsic linewidth, is plotted).
The figure also shows two
theoretical predictions which will be discussed in Sect. 4.2.
The decrease of the intrinsic line width with impact parameter in L1521F,
although not as steep as in L1544, is clear in Fig. 9, where
the average value of
(1-0) lines (the linewidth corrected for optical
depth, or the intrinsic linewidth, is plotted).
The figure also shows two
theoretical predictions which will be discussed in Sect. 4.2.
The decrease of the intrinsic line width with impact parameter in L1521F,
although not as steep as in L1544, is clear in Fig. 9, where
the average value of ![]() within bins of 15
within bins of 15
![]() (see big
dots) ranges between 0.3
(see big
dots) ranges between 0.3
![]() at the dust peak to 0.25
at the dust peak to 0.25
![]() at
a projected distance of 80
at
a projected distance of 80
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f10.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg128.gif) |
Figure 10:
Isolated component profile along the
|
| Open with DEXTER | |
One might interpret this line
width gradient as being due to increased optical depth towards the dust
peak. This however seems unlikely as illustrated in Fig. 10,
where the profiles of the isolated hyperfine component of the
![]() (1-0) line along the 45
(1-0) line along the 45![]() and -45
and -45![]() axes, passing through
the dust peak position, are shown. If the line is self-absorbed toward
the core center, the hyperfine components with the largest statistical
weight will be broadened compared to the weakest ones, affecting the
hfs fit. However, we performed Gaussian fits to all the hyperfines
components,
finding the same
axes, passing through
the dust peak position, are shown. If the line is self-absorbed toward
the core center, the hyperfine components with the largest statistical
weight will be broadened compared to the weakest ones, affecting the
hfs fit. However, we performed Gaussian fits to all the hyperfines
components,
finding the same ![]() values within the uncertainties. In fact,
a similar trend is
also observed if one plots the linewidth of the
values within the uncertainties. In fact,
a similar trend is
also observed if one plots the linewidth of the
![]() (or weakest) component of the
(or weakest) component of the
![]() (1-0) line
versus the impact parameter. This line, being thin and symmetric
across the core, is not affected by self-absorption.
(1-0) line
versus the impact parameter. This line, being thin and symmetric
across the core, is not affected by self-absorption.
We believe that this is a characteristic of unstable or supercritical (e.g. Mouschovias & Spitzer 1976) cores on the verge of star formation, more briefly called pre-stellar cores, a term which we use to characterize the subset of starless cores undergoing central infall (see also Ward-Thompson et al. 2003).
Assuming that L1521F is in solid body rotation, we determined the
magnitude ![]() and the direction
and the direction ![]() of the corresponding velocity gradient
following the procedure described in Goodman et al. (1993).
The magnitude
of the corresponding velocity gradient
following the procedure described in Goodman et al. (1993).
The magnitude ![]() ranges between 0.4 and 1 km s-1 pc-1
depending on the tracer used, and
large variations are also obtained for the gradient direction
ranges between 0.4 and 1 km s-1 pc-1
depending on the tracer used, and
large variations are also obtained for the gradient direction ![]() (see Table 4, Cols. 2 and 3). There is no tendency for
(see Table 4, Cols. 2 and 3). There is no tendency for ![]() to increase for higher density tracers, as observed in L1544 (Caselli et al. 2002a).
to increase for higher density tracers, as observed in L1544 (Caselli et al. 2002a).
Table 4: Results of velocity gradient fits.
To investigate in more detail the internal motions of L1521F, we
determined "local'' velocity gradients (see Caselli et al. 2002a), where
![]() and
and
![]() have been calculated in adjacent
have been calculated in adjacent ![]() -point grids of the maps. The results are shown
in Figs. 11 and 12 for
-point grids of the maps. The results are shown
in Figs. 11 and 12 for
![]() and
and
![]() maps,
respectively. The arrows across the map indicate the magnitude and the direction
of local gradients, and they are centered on the 9-point grid used to
estimate the corresponding
maps,
respectively. The arrows across the map indicate the magnitude and the direction
of local gradients, and they are centered on the 9-point grid used to
estimate the corresponding
![]() and
and
![]() values. From the figures it is clear that L1521F is not
undergoing solid body
rotation. The velocity structure is quite complex, showing
portions of the core where the gradient direction changes rapidly.
For example, if we concentrate on the
values. From the figures it is clear that L1521F is not
undergoing solid body
rotation. The velocity structure is quite complex, showing
portions of the core where the gradient direction changes rapidly.
For example, if we concentrate on the
![]() (1-0) map (see Fig. 11, top panel),
which has the highest sensitivity, three converging
velocity gradient patterns are clearly
visible: (i) toward South-West in the Northern half, (ii) toward
North-East in the SE quadrant, and (iii) toward North-West in the
SW quadrant of the core. A similar structure is also present in the
other maps (see Fig. 11, bottom panel, and Fig. 12).
(1-0) map (see Fig. 11, top panel),
which has the highest sensitivity, three converging
velocity gradient patterns are clearly
visible: (i) toward South-West in the Northern half, (ii) toward
North-East in the SE quadrant, and (iii) toward North-West in the
SW quadrant of the core. A similar structure is also present in the
other maps (see Fig. 11, bottom panel, and Fig. 12).
Interestingly, the mean of the local-gradient magnitudes (
![]() )
increases going from
)
increases going from
![]() (1-0) to
(1-0) to
![]() (3-2) (see Col. 4 of Table 4), suggesting that internal motions, although complex
(
(3-2) (see Col. 4 of Table 4), suggesting that internal motions, although complex
(
![]() widely varies across the cloud),
tend to become more prominent toward the core center. Moreover,
widely varies across the cloud),
tend to become more prominent toward the core center. Moreover,
![]() gradients appear larger than those derived from
gradients appear larger than those derived from
![]() .
If the observed
velocity structure is at least partially due to inward motions in the core
center, the larger local-gradient magnitudes detected in
.
If the observed
velocity structure is at least partially due to inward motions in the core
center, the larger local-gradient magnitudes detected in
![]() can be
explained by
can be
explained by
![]() being a better tracer of the core central regions, as found
in L1544 (Caselli et al. 2002a,b; see also Sect. 4.1).
However, the magnitude of the local gradients is
generally within a few km s-1 pc-1 (see Table 4), thus
they are produced by small velocity variations (
being a better tracer of the core central regions, as found
in L1544 (Caselli et al. 2002a,b; see also Sect. 4.1).
However, the magnitude of the local gradients is
generally within a few km s-1 pc-1 (see Table 4), thus
they are produced by small velocity variations (
![]()
![]() )
within
)
within ![]() 0.01 pc, the size of the grid where local gradients
have been estimated (see also Sect. 4.2 for discussion).
0.01 pc, the size of the grid where local gradients
have been estimated (see also Sect. 4.2 for discussion).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0915f11a.eps}\par\includegraphics[width=7.5cm,clip]{0915f11b.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg138.gif) |
Figure 11:
Velocity gradient vectors in L1521F derived from the two
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0915f12a.eps}\par\includegraphics[width=7.5cm,clip]{0915f12b.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg139.gif) |
Figure 12:
Same as Fig. 11 for
|
| Open with DEXTER | |
We note that the velocity gradient found with the present
![]() (1-0) observations is significantly smaller than that deduced by Shinnaga et al.
(2004) using interferometric observations, probably because they resolve
out the more extended emission, with smaller or almost opposite (see
Shinnaga et al. 2004)
velocity gradients, compared to the central regions.
(1-0) observations is significantly smaller than that deduced by Shinnaga et al.
(2004) using interferometric observations, probably because they resolve
out the more extended emission, with smaller or almost opposite (see
Shinnaga et al. 2004)
velocity gradients, compared to the central regions.
The previous sections described the results found in our analysis of L1521F.
The density profile, the CO depletion factor, the deuterium fractionation
and the velocity field in the core have been presented. We found several
similarities between L1521F and L1544, including the density structure (with
![]()
![]() at the center),
the amount of integrated
CO depletion (
at the center),
the amount of integrated
CO depletion (
![]() )
toward the dust peak,
and the decrease of line width with increasing distance from the cloud center.
Differences are however present in the amount of deuterium
fractionation (factor of
)
toward the dust peak,
and the decrease of line width with increasing distance from the cloud center.
Differences are however present in the amount of deuterium
fractionation (factor of ![]() 2 less than in L1544) and in the velocity
structure.
In this section we will discuss these findings in view of our knowledge of
the chemical and physical processes in dense cloud cores. The discussion is
thus split in two subsections, one focussing on the chemistry and the other
on the kinematics of L1521F.
2 less than in L1544) and in the velocity
structure.
In this section we will discuss these findings in view of our knowledge of
the chemical and physical processes in dense cloud cores. The discussion is
thus split in two subsections, one focussing on the chemistry and the other
on the kinematics of L1521F.
In cold clouds, the exothermicity of the proton-deuteron exchange reaction
However, the freeze-out of neutral species,
such as CO, O, and ![]() ,
boosts the deuterium fractionation
(e.g. Dalgarno & Lepp 1984). In fact, a decrease in the fractional
abundance of gas phase CO leads to a decrease of the
,
boosts the deuterium fractionation
(e.g. Dalgarno & Lepp 1984). In fact, a decrease in the fractional
abundance of gas phase CO leads to a decrease of the
![]() and
and
![]() destruction rates and to an increase (caused by the higher
destruction rates and to an increase (caused by the higher
![]() abundance) of the
abundance) of the
![]() formation rate
(e.g. Roberts & Millar 2000a; see reaction 3).
An empirical relation between CO depletion and deuterium fractionation in
prestellar cores has been determined by Bacmann et al. (2003)
using doubly deuterated
formaldehyde, whose abundance is also predicted to largely increase with CO freeze-out (Roberts & Millar 2000b; see also Roberts et al.
2003).
formation rate
(e.g. Roberts & Millar 2000a; see reaction 3).
An empirical relation between CO depletion and deuterium fractionation in
prestellar cores has been determined by Bacmann et al. (2003)
using doubly deuterated
formaldehyde, whose abundance is also predicted to largely increase with CO freeze-out (Roberts & Millar 2000b; see also Roberts et al.
2003).
In the previous sections, we found that in L1521F, CO is depleted
(with percentages ranging from 30% at the core edge to 93% at the
center, deduced from the integrated CO depletion factor) and,
similarly to L1544, the deuterium fractionation is large.
The present estimates of
![]() as a
function of distance from the dust peak allow us to study the relation between
deuterium fractionation and CO freeze-out across a dense core for the
first time and test chemical models.
In Fig. 13,
as a
function of distance from the dust peak allow us to study the relation between
deuterium fractionation and CO freeze-out across a dense core for the
first time and test chemical models.
In Fig. 13,
![]() is plotted as a function
of
is plotted as a function
of ![]() for all the positions present in Fig. 8.
We note a clear tendency for the deuterium fractionation to increase
with integrated CO depletion factor.
for all the positions present in Fig. 8.
We note a clear tendency for the deuterium fractionation to increase
with integrated CO depletion factor.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f13.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg147.gif) |
Figure 13:
Deuterium fractionation
(
|
| Open with DEXTER | |
In the following, we will analyse the
observational results with simple chemical models, to better understand
the observed
![]() and
and
![]() trends
shown in Figs. 7 and 13, and the differences between L1521F and L1544. It will be interesting to see whether in L1521F there is
evidence of the so-called "molecular hole'', or the region where
all species heavier than helium are heavily (
trends
shown in Figs. 7 and 13, and the differences between L1521F and L1544. It will be interesting to see whether in L1521F there is
evidence of the so-called "molecular hole'', or the region where
all species heavier than helium are heavily (![]() 98%) depleted from
the gas phase, as deduced in the case of L1544. In fact, the recent detection
of
98%) depleted from
the gas phase, as deduced in the case of L1544. In fact, the recent detection
of
![]() toward the L1544 dust peak is consistent with the
presence of a molecular hole in the central
toward the L1544 dust peak is consistent with the
presence of a molecular hole in the central ![]() 2800 AU (Caselli et al. 2003;
Walmsley et al. 2004). Then, the
2800 AU (Caselli et al. 2003;
Walmsley et al. 2004). Then, the
![]() and
and
![]() emission
maps should show a central hole or emission plateau
of similar size, but this has not been observed perhaps because of the
poor spatial coverage of the central region and the limited
spatial resolution (
emission
maps should show a central hole or emission plateau
of similar size, but this has not been observed perhaps because of the
poor spatial coverage of the central region and the limited
spatial resolution (![]() 2000 AU; Caselli et al. 2002a).
Such a "molecular hole'' was predicted by Caselli et al. (1999)
and Caselli et al. (2002a)
in an attempt to interpret the origin of double peaked
optically thin lines for the case of L1544,
including the thinnest
2000 AU; Caselli et al. 2002a).
Such a "molecular hole'' was predicted by Caselli et al. (1999)
and Caselli et al. (2002a)
in an attempt to interpret the origin of double peaked
optically thin lines for the case of L1544,
including the thinnest
![]() (1-0) hyperfine component.
In the case of L1521F, molecular lines, although asymmetric,
do not clearly show two separated peaks. Thus, if the line asymmetry is
due to the presence of a molecular hole in a contracting core,
the hole should have a smaller size than in the case of L1544. Evidence for
(1-0) hyperfine component.
In the case of L1521F, molecular lines, although asymmetric,
do not clearly show two separated peaks. Thus, if the line asymmetry is
due to the presence of a molecular hole in a contracting core,
the hole should have a smaller size than in the case of L1544. Evidence for
![]() depletion toward core centers has also been claimed in B68
(Bergin et al. 2002) and L1512 (Lee et al. 2003), two starless cores
with central densities
depletion toward core centers has also been claimed in B68
(Bergin et al. 2002) and L1512 (Lee et al. 2003), two starless cores
with central densities ![]() 105
105
![]() and close to hydrostatic
equilibrium, thus in a different chemical and dynamical phase
compared to L1544 and L1521F.
and close to hydrostatic
equilibrium, thus in a different chemical and dynamical phase
compared to L1544 and L1521F.
The four thin curves in Fig. 13 refer to the outputs of a
simple
steady state analytical chemical model including
![]() ,
,
![]() ,
,
![]() ,
HD, CO,
,
HD, CO,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
electrons and negatively charged grains. The recombination
on grain surfaces uses the rates from Draine & Sutin (1987),
assuming that
the grains are bare and that their
abundance by number is given by the MRN (Mathis et al.
1977) distribution
with upper cutoff radius of 0.25
,
electrons and negatively charged grains. The recombination
on grain surfaces uses the rates from Draine & Sutin (1987),
assuming that
the grains are bare and that their
abundance by number is given by the MRN (Mathis et al.
1977) distribution
with upper cutoff radius of 0.25 ![]() m and lower cutoff radius
m and lower cutoff radius
![]() Å (standard case, solid curves), and that all
grains are negatively charged (a more realistic value for the
fraction of negatively charged grains may be
Å (standard case, solid curves), and that all
grains are negatively charged (a more realistic value for the
fraction of negatively charged grains may be ![]() 0.5; see
Flower & Pineau des Forêts 2003). We also
considered a larger
0.5; see
Flower & Pineau des Forêts 2003). We also
considered a larger
![]() (=500 Å, dashed curves) to
roughly take into account the process of grain coagulation in
dense cores (e.g. Ossenkopf & Henning
1994). As expected, larger grains
cause a (slightly) higher deuterium fractionation, given that the number
density of dust grains decreases and so does the recombination rate
on grains of
(=500 Å, dashed curves) to
roughly take into account the process of grain coagulation in
dense cores (e.g. Ossenkopf & Henning
1994). As expected, larger grains
cause a (slightly) higher deuterium fractionation, given that the number
density of dust grains decreases and so does the recombination rate
on grains of
![]() molecular ions (further increasing the grain size does
not significantly change the result, given that dissociative
recombination becomes more important). This simple model also
assumes that the electron fractional abundance x(e) varies with density
as
molecular ions (further increasing the grain size does
not significantly change the result, given that dissociative
recombination becomes more important). This simple model also
assumes that the electron fractional abundance x(e) varies with density
as
![]() (McKee 1989)
(McKee 1989)![]() ,
and that
,
and that
![]() (in the density
range between
(in the density
range between
![]()
![]() and 106
and 106
![]() ),
as found from a linear least square fit to the observed
),
as found from a linear least square fit to the observed ![]() data in
Fig. 6 and the
data in
Fig. 6 and the
![]() data derived in Sect. 3.2
from the 1.2 mm continuum observations.
This allows us to find a
simple relation for the deuterium fractionation as a function
of
data derived in Sect. 3.2
from the 1.2 mm continuum observations.
This allows us to find a
simple relation for the deuterium fractionation as a function
of ![]() in "L1544-like'' cores, if one neglects multiply deuterated
forms of
in "L1544-like'' cores, if one neglects multiply deuterated
forms of
![]() (see below):
(see below):
| |
= | 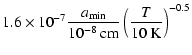 |
|
| (6) |
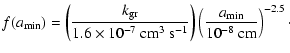 |
(8) |
The value of
![]() typically used in chemical codes is
typically used in chemical codes is
![]() cm3 s-1,
which
we call the "standard rate'' (see e.g. Roberts et al. 2003). However, Gerlich et al. (2002)
have recently measured a lower value for this rate (
cm3 s-1,
which
we call the "standard rate'' (see e.g. Roberts et al. 2003). However, Gerlich et al. (2002)
have recently measured a lower value for this rate (
![]() cm3 s-1, the "GHR rate'') and in Fig. 13 results obtained
with the "standard'' and "GHR'' rate are shown.
The observed data points lie between the two curves,
and the best fit (dotted curve in bottom figure)
is obtained with
cm3 s-1, the "GHR rate'') and in Fig. 13 results obtained
with the "standard'' and "GHR'' rate are shown.
The observed data points lie between the two curves,
and the best fit (dotted curve in bottom figure)
is obtained with
![]() cm3 s-1, which may suggest that a rate slightly (factor or
cm3 s-1, which may suggest that a rate slightly (factor or ![]() 2)
larger than the one recently
measured is probably needed to explain observations.
However, one should note that in the case of L1544 (
2)
larger than the one recently
measured is probably needed to explain observations.
However, one should note that in the case of L1544 (
![]() at
at
![]() ), even the "standard rate'' fails
to reproduce the large deuterium fractionation observed toward the dust peak.
The only way to reach
), even the "standard rate'' fails
to reproduce the large deuterium fractionation observed toward the dust peak.
The only way to reach
![]() with this analytical
model (dash-dotted curve in Fig. 13) is to allow a drop in the
abundance of
with this analytical
model (dash-dotted curve in Fig. 13) is to allow a drop in the
abundance of ![]() in the central
regions where
in the central
regions where
![]() and include in the chemical scheme D2H+(
and include in the chemical scheme D2H+(![]() ), which becomes abundant in heavily (CO,
), which becomes abundant in heavily (CO, ![]() ,
and O)
depleted regions (Roberts et al. 2003; Walmsley et al. 2004).
Therefore, the difference in deuterium fractionation between L1521F and L1544
is likely to be due
to a different evolutionary stage, with L1521F being less
evolved than L1544 (see also Aikawa et al. 2003).
The inclusion of the reaction
,
and O)
depleted regions (Roberts et al. 2003; Walmsley et al. 2004).
Therefore, the difference in deuterium fractionation between L1521F and L1544
is likely to be due
to a different evolutionary stage, with L1521F being less
evolved than L1544 (see also Aikawa et al. 2003).
The inclusion of the reaction
![]() + HD
+ HD
![]() D2H+ +
D2H+ + ![]() (Gerlich et al. 2002) in this model
leads to an increase of the deuterium fractionation by a factor of 2-3.
However, in this simple chemical scheme we did not include the
so-called "back'' reactions due to ortho-
(Gerlich et al. 2002) in this model
leads to an increase of the deuterium fractionation by a factor of 2-3.
However, in this simple chemical scheme we did not include the
so-called "back'' reactions due to ortho-![]() (see Gerlich et al. 2002), which have the effect of reducing the
deuteration degree (see Walmsley et al. 2004); this analysis is beyond
the scope of the present paper.
(see Gerlich et al. 2002), which have the effect of reducing the
deuteration degree (see Walmsley et al. 2004); this analysis is beyond
the scope of the present paper.
The analytic calculation outlined in the previous section has
at least two major defects. One is the assumption of no abundance
variations within the dense core, which should be computed first
in order to estimate molecular abundances as a function of radius and
then determine the column densities via integration along the line of
sight. The second is our neglect of reactions
with species such as O which also act
to limit deuterium fractionation. Here, we present a small toy
model aimed at overcoming these problems, and already described in
Caselli et al. (2002b).
This model follows the (steady-state) chemistry of a spherically
symmetric cloud with a density profile deduced from the 1.2 mm dust continuum
emission (see Sect. 3.2), and constant temperature T= 10 K. Neutral species in the model are ![]() ,
CO,
,
CO, ![]() ,
and
atomic oxygen. We follow depletion of these species onto dust grains and
their desorption due to the cosmic ray impulsive heating of the dust,
following the procedure by Hasegawa & Herbst (1993).
The abundance of molecular ions such as
,
and
atomic oxygen. We follow depletion of these species onto dust grains and
their desorption due to the cosmic ray impulsive heating of the dust,
following the procedure by Hasegawa & Herbst (1993).
The abundance of molecular ions such as
![]() ,
,
![]() and corresponding deuterated isotopomers are given by the
steady state chemical equations using the istantaneous abundances of neutral
species. Analogously, the electron
fraction
and corresponding deuterated isotopomers are given by the
steady state chemical equations using the istantaneous abundances of neutral
species. Analogously, the electron
fraction
![]() can be computed in terms of global estimates for the molecular
and metallic ions and using the same istantaneous abundances of CO,
can be computed in terms of global estimates for the molecular
and metallic ions and using the same istantaneous abundances of CO, ![]() ,
and O in the gas phase. The approach we have adopted is a simplified
version of the reaction scheme of Umebayashi & Nakano (1990),
which includes
molecular ion recombination on grain surfaces using rates from Draine
& Sutin (1987)
(see Caselli et al. 2002b for details).
,
and O in the gas phase. The approach we have adopted is a simplified
version of the reaction scheme of Umebayashi & Nakano (1990),
which includes
molecular ion recombination on grain surfaces using rates from Draine
& Sutin (1987)
(see Caselli et al. 2002b for details).
This model furnishes the abundances of gaseous species as a
function of radius, and the corresponding column densities as
a function of impact parameter are calculated taking into account
the appropriate beam convolution to simulate the observations.
We used the new value of the dissociative recombination rate for
![]() (
(
![]() cm3 s-1
at 10 K) determined by McCall et al. (2003), assumed
cm3 s-1
at 10 K) determined by McCall et al. (2003), assumed
![]() cm3 s-1 (see previous section)
and varied other parameters
(essentially the binding energies on grain surfaces of
cm3 s-1 (see previous section)
and varied other parameters
(essentially the binding energies on grain surfaces of ![]() and O).
The model has been
forced to reproduce within 10% the observed
and O).
The model has been
forced to reproduce within 10% the observed
![]() ,
,
![]() ,
and
,
and
![]() column densities toward the dust peak position
(
column densities toward the dust peak position
(
![]() ,
,
![]() ,
and
,
and
![]() cm-2, respectively), and to
reproduce within a factor of 2 the observed column density profiles in
the above molecules. The best fit binding energies for
cm-2, respectively), and to
reproduce within a factor of 2 the observed column density profiles in
the above molecules. The best fit binding energies for ![]() and O
(800 K and 750 K,
respectively) are quite close
to the values deduced from theoretical calculations and laboratory measurements
(750 K and 800 K, for
and O
(800 K and 750 K,
respectively) are quite close
to the values deduced from theoretical calculations and laboratory measurements
(750 K and 800 K, for ![]() and O, respectively;
see discussion in Hasegawa et al. 1992
and Bergin & Langer 1997).
and O, respectively;
see discussion in Hasegawa et al. 1992
and Bergin & Langer 1997).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0915f14.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg190.gif) |
Figure 14:
Fractional abundances,
|
| Open with DEXTER | |
As illustrated in Fig. 14,
the fractional abundance of
![]() decreases from about
decreases from about
![]() at the edge of the cloud to about
at the edge of the cloud to about
![]() at the
center. The increase of the
at the
center. The increase of the
![]() /
/
![]() abundance ratio
toward the center boosts the formation of
abundance ratio
toward the center boosts the formation of
![]() ,
which presents
an abundance increase of about one order of magnitude from the edge
(where
,
which presents
an abundance increase of about one order of magnitude from the edge
(where
![]() )
to the central 4000 AU
(
)
to the central 4000 AU
(
![]() )
of the core.
Therefore, in the case of L1521F, we do not need to
invoke any "molecular hole'' as in the case of L1544 (see Caselli et al.
2003), although the present data do not allow us to distinguish
between the models with different amounts of
)
of the core.
Therefore, in the case of L1521F, we do not need to
invoke any "molecular hole'' as in the case of L1544 (see Caselli et al.
2003), although the present data do not allow us to distinguish
between the models with different amounts of ![]() freeze out
(and consequent
freeze out
(and consequent
![]() depletion) within few thousands AU.
On the other hand, recent observations of ortho-
depletion) within few thousands AU.
On the other hand, recent observations of ortho-
![]() toward this
object (Caselli, van der Tak, Ceccarelli et al., in preparation)
strongly suggest that the molecular hole in L1521F must be smaller
than in L1544,
given that the line is about two times less intense than in L1544. Indeed,
we predict here an
toward this
object (Caselli, van der Tak, Ceccarelli et al., in preparation)
strongly suggest that the molecular hole in L1521F must be smaller
than in L1544,
given that the line is about two times less intense than in L1544. Indeed,
we predict here an
![]() abundance of 3
abundance of 3![]() 10-10
at radii less than 3000 AU, a factor of about 3 lower than in L1544
(see Caselli et al. 2003).
This is another indication that L1544 is likely to be more evolved,
and more
centrally concentrated, than L1521F. This seems to contradict the
observational evidence that the central densities in the two cores
are quite similar. However, one should keep in mind that the
central density values (and the density structure) in the two cores have been
obtained assuming isothermal conditions. Allowing the temperature to
decrease toward the center, as predicted by models of dense clouds
heated by the external radiation field (e.g. Galli et al. 2002)
one finds that lower values of the central temperature
implies larger central densities (e.g. Evans et al. 2001;
Zucconi et al. 2001).
One possible solution to the L1521F/L1544 puzzle is that L1544 is colder and more centrally concentrated than L1521F and
hence is more depleted in the nucleus. This is
consistent with L1544 being more evolved and closer to the "critical''
state than L1521F.
10-10
at radii less than 3000 AU, a factor of about 3 lower than in L1544
(see Caselli et al. 2003).
This is another indication that L1544 is likely to be more evolved,
and more
centrally concentrated, than L1521F. This seems to contradict the
observational evidence that the central densities in the two cores
are quite similar. However, one should keep in mind that the
central density values (and the density structure) in the two cores have been
obtained assuming isothermal conditions. Allowing the temperature to
decrease toward the center, as predicted by models of dense clouds
heated by the external radiation field (e.g. Galli et al. 2002)
one finds that lower values of the central temperature
implies larger central densities (e.g. Evans et al. 2001;
Zucconi et al. 2001).
One possible solution to the L1521F/L1544 puzzle is that L1544 is colder and more centrally concentrated than L1521F and
hence is more depleted in the nucleus. This is
consistent with L1544 being more evolved and closer to the "critical''
state than L1521F.
We note that the chemical composition shown in
Fig. 14 reproduces
the observed
![]() (see the thick
curve in Fig. 13)
and
(see the thick
curve in Fig. 13)
and
![]() (see the thick curve in Fig. 7)
relations, without any need to change the value of
(see the thick curve in Fig. 7)
relations, without any need to change the value of
![]() (see previous
section). This demonstrates the importance of taking into account core
structure and differential molecular freeze-out in chemical models.
Moreover, note that the depletion factor within the cloud,
(see previous
section). This demonstrates the importance of taking into account core
structure and differential molecular freeze-out in chemical models.
Moreover, note that the depletion factor within the cloud,
![]() ,
is significantly larger
(more than two orders of magnitude) than the integrated
CO depletion factor
,
is significantly larger
(more than two orders of magnitude) than the integrated
CO depletion factor ![]() ,
which is "diluted'' along the line of sight
(compare
,
which is "diluted'' along the line of sight
(compare ![]() in Fig. 14 with
in Fig. 14 with ![]() in
Fig. 7). Finally, the central value of the electron fraction is
in
Fig. 7). Finally, the central value of the electron fraction is ![]()
![]() ,
implying an ambipolar diffusion time scale
(see e.g. Shu et al. 1987) of
,
implying an ambipolar diffusion time scale
(see e.g. Shu et al. 1987) of ![]()
![]() yr, only slightly (factor of
yr, only slightly (factor of ![]() 3) larger than the free-fall time scale,
once again suggesting that the core is close to dynamical collapse
(although not as
close as L1544). As in L1544, the major ion in the core
is H3O+, which is due to the presence of a significant fraction of
gaseous atomic oxygen in the model (see also Aikawa et al. 2001 for
similar results). We should however point out that the more recent
models of Aikawa et al. (2003), where surface chemistry is included,
predict a much lower abundance of O in the gas phase, given that
in this model, an O-atom sticking to a grain
is converted to water, which remains on the surface (assuming desorption
due to the cosmic-ray impulsive heating of dust grains;
see Hasegawa & Herbst 1993). Low ionization potential
elements, essentially S+, Mg+, Fe+, Si+, Na+, generically
called "metals'' (M+ in
Fig. 14), are assumed to freeze out onto dust grains at the
same rate as CO molecules. For this reason, they are negligible carriers
of positive charges within the core, in our model.
3) larger than the free-fall time scale,
once again suggesting that the core is close to dynamical collapse
(although not as
close as L1544). As in L1544, the major ion in the core
is H3O+, which is due to the presence of a significant fraction of
gaseous atomic oxygen in the model (see also Aikawa et al. 2001 for
similar results). We should however point out that the more recent
models of Aikawa et al. (2003), where surface chemistry is included,
predict a much lower abundance of O in the gas phase, given that
in this model, an O-atom sticking to a grain
is converted to water, which remains on the surface (assuming desorption
due to the cosmic-ray impulsive heating of dust grains;
see Hasegawa & Herbst 1993). Low ionization potential
elements, essentially S+, Mg+, Fe+, Si+, Na+, generically
called "metals'' (M+ in
Fig. 14), are assumed to freeze out onto dust grains at the
same rate as CO molecules. For this reason, they are negligible carriers
of positive charges within the core, in our model.
In order to facilitate the comparison between L1521F and L1544, we analyzed the kinematical properties of L1521F using the same models as in Caselli et al. (2002a). In particular, starting from the velocity field predicted by the ambipolar diffusion models of Ciolek & Basu (2000; hereafter CB), we have derived the linewidth gradient and the line profile in a disk-like geometry and compare the results with our observations.
From the analysis of
![]() (1-0) data,
we found that the line width, similarly to L1544,
decreases with distance from the dust peak (see Fig. 9). As seen in
Caselli et al. (2002a), this observational evidence is consistent with the
predictions of the CB model. Here, we applied the
kinematic analysis of L1544 (Caselli et al. 2002a) to the case of L1521F,
assuming that
the cloud has a disk-like shape and is centrally concentrated, with
the center coincident with the 1.2 mm dust continuum map peak.
From the core axial ratio, and following Eq. (1) of CB,
the angle between the vertical axis of the model and the plane of the sky
is found to be 18
(1-0) data,
we found that the line width, similarly to L1544,
decreases with distance from the dust peak (see Fig. 9). As seen in
Caselli et al. (2002a), this observational evidence is consistent with the
predictions of the CB model. Here, we applied the
kinematic analysis of L1544 (Caselli et al. 2002a) to the case of L1521F,
assuming that
the cloud has a disk-like shape and is centrally concentrated, with
the center coincident with the 1.2 mm dust continuum map peak.
From the core axial ratio, and following Eq. (1) of CB,
the angle between the vertical axis of the model and the plane of the sky
is found to be 18![]() .
The disk is contracting via ambipolar diffusion
and the resultant velocity field is used as input in a model which
computes
synthetic profiles of optically thin lines for all lines of sight across
the model disk (for details, see Caselli et al. 2002a). As in the case of L1544, we also assumed that the density profile and the radial velocity
field is given by the CB model at time t = 2.66 Myr (
.
The disk is contracting via ambipolar diffusion
and the resultant velocity field is used as input in a model which
computes
synthetic profiles of optically thin lines for all lines of sight across
the model disk (for details, see Caselli et al. 2002a). As in the case of L1544, we also assumed that the density profile and the radial velocity
field is given by the CB model at time t = 2.66 Myr (![]() t3in CB), which best reproduces the continuum observations of both cores.
Line broadening is both due to thermal motions (
t3in CB), which best reproduces the continuum observations of both cores.
Line broadening is both due to thermal motions (
![]()
![]() at 10 K) and microturbulence described by a turbulent velocity
at 10 K) and microturbulence described by a turbulent velocity
![]() independent of position.
independent of position.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f15.eps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg200.gif) |
Figure 15:
Observed line profiles of the F1 F = 0 1
|
| Open with DEXTER | |
Figure 15 shows the comparison between observed (hystogram) and
synthetic (curves) profiles of the
![]() (1-0) isolated hyperfine component
(
(1-0) isolated hyperfine component
(
![]() 12) along the minor and major axes of the L1521F core.
The (optically thin) weakest component (F1F = 10
12) along the minor and major axes of the L1521F core.
The (optically thin) weakest component (F1F = 10
![]() 11) shows very
similar profiles; so that we decided to present the higher sensitivity
observations of the isolated component. We also considered two different
conditions in the model: (1) the
11) shows very
similar profiles; so that we decided to present the higher sensitivity
observations of the isolated component. We also considered two different
conditions in the model: (1) the
![]() abundance is constant throughout the
core, so that the
abundance is constant throughout the
core, so that the
![]() column density simply follows the dust, and (2) there is a "hole'' (2000 AU in size) in the
column density simply follows the dust, and (2) there is a "hole'' (2000 AU in size) in the
![]() distribution. The difference between the two
synthetic profiles is not significant (only a 4% increase of the linewidth
toward the center, in the presence of the molecular hole, see
Fig. 9), after the convolution with a
Gaussian with
distribution. The difference between the two
synthetic profiles is not significant (only a 4% increase of the linewidth
toward the center, in the presence of the molecular hole, see
Fig. 9), after the convolution with a
Gaussian with
![]()
![]() ,
needed to match the intrinsic
linewidth toward the center
,
needed to match the intrinsic
linewidth toward the center![]() , and thus only one profile
is shown in Fig. 15. Also shown in the Fig. 15
are model profiles for the limiting case of no turbulent or thermal
broadening (filled histograms).
The thing to note is that the agreement with the data is mixed, in the
sense that the predicted velocity gradient along the minor axis is observed
but it is restricted to the
south-west half of the axis. Along the major
axis there is no clear gradient in the north-west half of the axis,
as expected in absence of disk
rotation, but a (0.06
, and thus only one profile
is shown in Fig. 15. Also shown in the Fig. 15
are model profiles for the limiting case of no turbulent or thermal
broadening (filled histograms).
The thing to note is that the agreement with the data is mixed, in the
sense that the predicted velocity gradient along the minor axis is observed
but it is restricted to the
south-west half of the axis. Along the major
axis there is no clear gradient in the north-west half of the axis,
as expected in absence of disk
rotation, but a (0.06
![]() )
blue shift of the line is present toward
south-east.
)
blue shift of the line is present toward
south-east.
The synthetic profiles become narrower as we move away from the central 40
![]() of the disk-like cloud, given that the inward velocity in the
adopted t3 model reaches its maximum (0.12
of the disk-like cloud, given that the inward velocity in the
adopted t3 model reaches its maximum (0.12
![]() )
at radius 0.025 pc
(or 37
)
at radius 0.025 pc
(or 37
![]() )
before rapidly dropping to 0 at the cloud edge (see Fig. 2 of CB). We have analysed this line width variation to check its consistency with
the observed trend shown in Fig. 9. The solid curve in
Fig. 9
is the CB prediction in the case of no central "hole'', whereas the
dashed curve illustrates the effects on the line width of a
molecular "hole'' in the central 2000 AU (i.e. a region where all
heavy elements have condensed onto dust grains).
The line width of model lines has been calculated as the
second moment of the velocity profile and it has been "normalized'' to
the value of the line width observed in the central position by
convolving the purely-kinematic profiles with a Gaussian with
)
before rapidly dropping to 0 at the cloud edge (see Fig. 2 of CB). We have analysed this line width variation to check its consistency with
the observed trend shown in Fig. 9. The solid curve in
Fig. 9
is the CB prediction in the case of no central "hole'', whereas the
dashed curve illustrates the effects on the line width of a
molecular "hole'' in the central 2000 AU (i.e. a region where all
heavy elements have condensed onto dust grains).
The line width of model lines has been calculated as the
second moment of the velocity profile and it has been "normalized'' to
the value of the line width observed in the central position by
convolving the purely-kinematic profiles with a Gaussian with
![]() km s-1, which can be interpreted as the combination of thermal
broadening plus a constant turbulent field across
the cloud. The comparison between the curves and the big dots
(the binned data, see Sect. 3.5) suggests that our data are
consistent with
the CB model. In particular, the correspondence between the solid curve
and the data indicates that the molecular hole is not present in L1521F, in
agreement with the chemical analysis (see previous section). On the other
hand, the steeper
km s-1, which can be interpreted as the combination of thermal
broadening plus a constant turbulent field across
the cloud. The comparison between the curves and the big dots
(the binned data, see Sect. 3.5) suggests that our data are
consistent with
the CB model. In particular, the correspondence between the solid curve
and the data indicates that the molecular hole is not present in L1521F, in
agreement with the chemical analysis (see previous section). On the other
hand, the steeper ![]() -b relation found in L1544 (see Fig. 5 of
Caselli et al. 2002a) suggests that the molecular hole is likely to be
present in that source, again in agreement with the chemical analysis
(see e.g. Caselli et al. 2003).
-b relation found in L1544 (see Fig. 5 of
Caselli et al. 2002a) suggests that the molecular hole is likely to be
present in that source, again in agreement with the chemical analysis
(see e.g. Caselli et al. 2003).
As shown in Sect. 3.6, the kinematics of L1521F is also
characterized by complex motions which may be the result of turbulence
(see e.g. Burkert & Bodenheimer 2000) or
accretion of material onto the core or a combination of both.
Local gradients have been determined in order to quantify these motions,
and we found that the magnitude of local gradient vectors tends to
increase for higher density tracers.
This suggests that turbulence (expected to dissipate more rapidly
in denser environments), is probably not the driving
source of the observed velocity field. Moreover, unresolved substructure may
further complicate the velocity field, as suggested by the
![]() clumps
observed by Shinnaga et al. (2004) (see Fig. 11):
with the exception of their
clump "N4'', the kinematics of the other clumps (N1-N3) is
consistent with the velocity field inferred from our local gradient
maps (see also Sect. 3.1)
and the (marginal, see Fig. 4)
evidence for two velocity components in
clumps
observed by Shinnaga et al. (2004) (see Fig. 11):
with the exception of their
clump "N4'', the kinematics of the other clumps (N1-N3) is
consistent with the velocity field inferred from our local gradient
maps (see also Sect. 3.1)
and the (marginal, see Fig. 4)
evidence for two velocity components in
![]() (3-2),
resembling clumps N1 and N2.
(3-2),
resembling clumps N1 and N2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0915f16.ps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg203.gif) |
Figure 16:
Intensity (thin lines) and velocity (thick lines)
of
|
| Open with DEXTER | |
It is interesting to compare our data with predictions from the
non-magnetic turbulent models of Ballesteros-Paredes et al.
(2003),
who derived velocity profiles for dense cloud cores. As an
example, Fig. 16 shows the velocity cuts observed across L1521F. Within the half maximum contour of
![]() (1-0), the
largest velocity variation observed is
(1-0), the
largest velocity variation observed is ![]() 0.04
0.04
![]() on a scale of 0.027 pc, corresponding
to a velocity gradient of
on a scale of 0.027 pc, corresponding
to a velocity gradient of ![]() 1.5 km s-1 pc-1. On the other hand,
Ballesteros-Paredes et al.
(2003) found that the smallest velocity variation
for their clump 13
at time t1 (see their Fig. 9) is
1.5 km s-1 pc-1. On the other hand,
Ballesteros-Paredes et al.
(2003) found that the smallest velocity variation
for their clump 13
at time t1 (see their Fig. 9) is ![]() 0.3
0.3
![]() within 0.15 pc
or
within 0.15 pc
or ![]() 2 km s-1 pc-1. Thus, current supersonic turbulent models predict
velocity gradients which are somewhat too large.
We also note that the reversal in the velocity gradient direction
observed in L1521F (see bottom panel of Fig. 16)
is not present in the model examples shown in
Ballesteros-Paredes et al. (2003), but it is predicted
by the turbulent models of Burkert & Bodenheimer (2000).
2 km s-1 pc-1. Thus, current supersonic turbulent models predict
velocity gradients which are somewhat too large.
We also note that the reversal in the velocity gradient direction
observed in L1521F (see bottom panel of Fig. 16)
is not present in the model examples shown in
Ballesteros-Paredes et al. (2003), but it is predicted
by the turbulent models of Burkert & Bodenheimer (2000).
In the two starless cores L1498 and L1517B, Tafalla et al. (2004)
found a good correlation between the distribution of CS and the
distribution of the high velocity
![]() (1-0).
The authors argue that the high velocity wing of the
(1-0).
The authors argue that the high velocity wing of the
![]() (1-0) lines
comes from a gas shell that is being accreted by the starless core;
therefore it has not experienced the high density in the core nucleus
and hence its depletion factor is low.
We repeated the same experiment in L1521F producing channel maps
of the core in
(1-0) lines
comes from a gas shell that is being accreted by the starless core;
therefore it has not experienced the high density in the core nucleus
and hence its depletion factor is low.
We repeated the same experiment in L1521F producing channel maps
of the core in
![]() (1-0) but we did not find any strong deviation from
the total intensity distribution.
However, we did find that the
(1-0) but we did not find any strong deviation from
the total intensity distribution.
However, we did find that the
![]() (1-0) velocity pattern across the core
is similar to the
(1-0) velocity pattern across the core
is similar to the
![]() distribution.
In fact, as shown in Fig. 17,
distribution.
In fact, as shown in Fig. 17,
![]() (1-0) presents
red-shifted velocities where CO is bright.
The difference in magnitude of this effect here and in L1517B and L1498 could be due to a brighter core that saturates the emission
from the high velocity wing.
(1-0) presents
red-shifted velocities where CO is bright.
The difference in magnitude of this effect here and in L1517B and L1498 could be due to a brighter core that saturates the emission
from the high velocity wing.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0915f17.ps}
\end{figure}](/articles/aa/full/2004/24/aa0915/Timg204.gif) |
Figure 17:
|
| Open with DEXTER | |
A final thing to note is that Fig. 17, together with Fig. 11 (top figure), suggests the presence of a coherent velocity field resembling low-frequency spatial oscillations of the outer cloud layers around some equilibrium dynamical state as recently proposed by Lada et al. (2003) in the case of the starless core B68. However, L1521F is more massive than B68 and is approaching the critical state for the onset of collapse, so that a situation of near-equilibrium for L1521F may be due to a balance between gravity and a combination of magnetic and thermal forces. If this is the case, the normal modes for L1521F would be more complicated than in the purely thermal case of B68, since the spherical symmetry that is a fair approximation for a thermal-pressure supported cloud such as B68 will no longer be valid for a magnetically supported object (G. E. Ciolek, priv. comm.). In fact, we observe L1521F not to be spherically symmetric (see Table 3).
Finally, in this section we discuss some more speculative
interpretations of the evolutionary state of L1521F. Firstly,
it seems that L1521F
is likely to be in an earlier stage of evolution than L1544,
which is probably colder (![]() 7 K in the central
7 K in the central ![]() 2000 AU, see
e.g. Zucconi et al. 2001) and more centrally concentrated (central
densities
2000 AU, see
e.g. Zucconi et al. 2001) and more centrally concentrated (central
densities ![]() 107
107
![]() ;
e.g. Evans et al. 2001) than L1521F,
and hence more depleted in the nucleus. For example, in the CB model,
this implies that whereas the density profile of L1521F is consistent
with the cloud model at time t3=2.66 Myr, L1544 is closer to t4=2.68 Myr, and thus the estimated age difference is roughly 20 000 yr.
However, these age estimates should be taken with caution given that
the two cores may have had a different formation and contraction history
and that, in general, cores, like stars, can differ in
properties such as size, mass, and temperature regardless of their relative
age.
;
e.g. Evans et al. 2001) than L1521F,
and hence more depleted in the nucleus. For example, in the CB model,
this implies that whereas the density profile of L1521F is consistent
with the cloud model at time t3=2.66 Myr, L1544 is closer to t4=2.68 Myr, and thus the estimated age difference is roughly 20 000 yr.
However, these age estimates should be taken with caution given that
the two cores may have had a different formation and contraction history
and that, in general, cores, like stars, can differ in
properties such as size, mass, and temperature regardless of their relative
age.
An alternative view can be based on the clumpy structure observed
in L1521F (Shinnaga et al. 2004), but not in L1544 (e.g. Williams et al. 1999), using BIMA. If the more complex kinematics in L1521F is
due to the unresolved clumpy substructure, one may speculate that L1521F is close to the formation of a group of low mass
protostars, whereas L1544 is likely to form one or two stellar objects.
Thus, the two cores may show chemical and physical properties
characteristic of the initial conditions of different modes of star
formation in low mass cores. One should also
note that L1521F resides in the middle of the main filament of the
Taurus Cloud, whereas L1544 is at the edges of the complex and hence
the different environments of the two cores may be
responsible for the different kinematics and chemical properties
of apparently similar (in the dust continuum and
![]() emission) dense cores.
emission) dense cores.
We have analysed physical and chemical properties of L1521F, a starless core in the Taurus Molecular Cloud, with characteristics similar to the pre-stellar core L1544. The main similarities and differences between the two cores are listed below:
1. the dust emission distributions
are similar, implying
a fairly closely matched density structure, with central densities
of
![]()
![]() ,
the radius of the "flat'' region
r0 = 20
,
the radius of the "flat'' region
r0 = 20
![]() ,
and similar asymptotic power index
,
and similar asymptotic power index ![]() (see Sect. 3.2 and Tafalla et al. 2002).
In particular, the aspect ratio is quite similar: 1.6 and 1.8 in L1521F
and L1544, respectively.
(see Sect. 3.2 and Tafalla et al. 2002).
In particular, the aspect ratio is quite similar: 1.6 and 1.8 in L1521F
and L1544, respectively.
2. The line width decreases with distance from the cloud
center (![]() 0.3
0.3
![]() )
to 80
)
to 80
![]() away (
away (![]() 0.25
0.25
![]() ;
see Fig. 9), in analogy
with L1544, and consistent with the predictions of ambipolar diffusion
models, although any
gravity-driven contraction in 2-3D is expected to get localized line
broadening. The particular model which best fits the data will be
investigated in the future.
;
see Fig. 9), in analogy
with L1544, and consistent with the predictions of ambipolar diffusion
models, although any
gravity-driven contraction in 2-3D is expected to get localized line
broadening. The particular model which best fits the data will be
investigated in the future.
3. The amount of CO freeze-out (integrated CO depletion factor
![]() )
is also comparable to L1544, as is the column density of
)
is also comparable to L1544, as is the column density of
![]() toward the dust peak (
toward the dust peak (![]()
![]() cm-2).
cm-2).
4. The deuterium fractionation toward the L1521F dust peak (
![]() )
is however
a factor
)
is however
a factor ![]() 2 smaller than in L1544, due to the (factor of 2)
smaller column density of
2 smaller than in L1544, due to the (factor of 2)
smaller column density of
![]() toward L1521F. This can be understood
if L1521F is less chemically evolved than L1544, with a smaller (r < 2000 AU) central molecular hole.
toward L1521F. This can be understood
if L1521F is less chemically evolved than L1544, with a smaller (r < 2000 AU) central molecular hole.
5. Unlike in L1544, the velocity field in L1521F maintains a
complex structure even at the small scales traced by
![]() and
and
![]() (3-2)
(see Figs. 11 and 12). This may be due to
the presence of clumps in the central few thousand AU (as deduced
by the interferometric observations of Shinnaga et al. 2004), but
could also be caused by
normal mode pulsations, as in the case of B68 studied by
Lada et al. (2003). The ambipolar diffusion model with infall of
Ciolek & Basu (2000) has problems in reproducing the whole velocity
field observed across the core. This may be due to the fact that
part of the observed bulk motions result from residual core contraction,
as suggested by Tafalla et al. (2004) in their study of L1517B
and L1498, thus preventing a clear determination of the
velocity field within the core nucleus.
(3-2)
(see Figs. 11 and 12). This may be due to
the presence of clumps in the central few thousand AU (as deduced
by the interferometric observations of Shinnaga et al. 2004), but
could also be caused by
normal mode pulsations, as in the case of B68 studied by
Lada et al. (2003). The ambipolar diffusion model with infall of
Ciolek & Basu (2000) has problems in reproducing the whole velocity
field observed across the core. This may be due to the fact that
part of the observed bulk motions result from residual core contraction,
as suggested by Tafalla et al. (2004) in their study of L1517B
and L1498, thus preventing a clear determination of the
velocity field within the core nucleus.
6. The line profiles in L1521F show asymmetric structure, although the two peaks are not well separated as in L1544. This is consistent with smaller (factor of 1.5) infall velocities in the central few thousand AU of L1521F.
In any case,
the large central density (![]() 106
106
![]() )
and the evidence of
central infall (broader line widths toward the center and central infall
asymmetry in
)
and the evidence of
central infall (broader line widths toward the center and central infall
asymmetry in
![]() (1-0)) indicate that L1521F
is another starless core on the verge of star formation, or a
pre-stellar core.
Although a study of a more complete sample is needed, assuming that L1544 and L1521F are the only two cores in Taurus close to dynamical collapse, and given
that the total number of starless cores in Taurus is 44 (Onishi et al.
2002),
we can argue that this process of contraction towards the "critical''
stage, or the "L1544-phase'', may last about five percent of the core
lifetime.
(1-0)) indicate that L1521F
is another starless core on the verge of star formation, or a
pre-stellar core.
Although a study of a more complete sample is needed, assuming that L1544 and L1521F are the only two cores in Taurus close to dynamical collapse, and given
that the total number of starless cores in Taurus is 44 (Onishi et al.
2002),
we can argue that this process of contraction towards the "critical''
stage, or the "L1544-phase'', may last about five percent of the core
lifetime.
A more detailed analysis of
![]() line profiles will be presented in
a future paper, where the observed chemical abundances will be introduced
in a non spherically symmetric
Monte Carlo radiative transfer code.
This is needed to understand the
nature of the
line profiles will be presented in
a future paper, where the observed chemical abundances will be introduced
in a non spherically symmetric
Monte Carlo radiative transfer code.
This is needed to understand the
nature of the
![]() (1-0) line asymmetry, which may be caused by
self-absorption plus infall, or to infall plus a molecular hole,
or to the relative motion of different clumps, or to a
mixture of the above possibilities.
(1-0) line asymmetry, which may be caused by
self-absorption plus infall, or to infall plus a molecular hole,
or to the relative motion of different clumps, or to a
mixture of the above possibilities.
Acknowledgements
The authors are grateful to the staff of the IRAM 30 m antenna, for their support during observations, and to Richard Crutcher and Daniele Galli for discussion. We also thank the referee, Glenn Ciolek, for clarifying several statements in the paper and Floris van der Tak for a critical reading of the submitted manuscript. P.C. and C.M.W. aknowledge support from the MIUR project "Dust and Molecules in Astrophysical Environments''. C.W.L. acknowledges support from the Basic Research Program (grant KOSEF R01-2003-000-10513-0) of the Korea Science and Engineering Foundation.