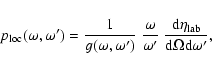G. Malloci1,2,4 - G. Mulas1,4 - P. Benvenuti2,3
1 - INAF - Osservatorio Astronomico di Cagliari - AstroChemistry
Group, Strada n.54, Loc. Poggio dei Pini, 09012 Capoterra (CA), Italy
2 -
Dipartimento di Fisica, Università degli Studi di Cagliari,
S.P. Monserrato-Sestu Km 0.7, 09042 Cagliari, Italy
3 -
INAF, Viale del Parco Mellini 84, 00136 Roma, Italy
4 -
Astrochemical Research in Space Network
http://www.ars-network.org
Received 17 November 2003 / Accepted 23 February 2004
Abstract
We developed a general recipe able to extrapolate the expected
photoluminescence of small particles starting from available laboratory
results obtained on bulk samples. We present numerical results for the
simplest case, namely a spherical, homogeneous dust particle, in the limit of
strongly localised fluorescence. In particular, our theoretical derivation
produces an explicit, analytical, dependence of the photoluminescence
spectrum on the angle between the direction of observation and that of the
incoming exciting light. We expect the present model to be a useful tool that
will allow the study of photoluminescence phenomena of interstellar dust to
move beyond the straight, plain, possibly misleading comparison with
experimental data on bulk samples.
Key words: ISM: dust, extinction - ISM: lines and bands - methods: numerical - radiation mechanisms: general - radiative transfer - scattering
Hence, for meaningful quantitative results, one ought to compare astronomical interstellar PL phenomena, such as the Extended Red Emission (see e.g., Smith & Witt 2002; Duley 2001), with laboratory data taken on samples as similar as possible to interstellar dust. If this is not feasible, one should use a detailed PL model to bridge the gap between experimental bulk properties and small particles, very much in the same way as the extinction properties of dust are usually computed from the knowledge of the complex refractive index of the material they are made of (see e.g., Bohren & Huffman 1998). We present here such a model, in which we represent the emission as stemming from a density of uncorrelated oscillating electric dipoles, whose distribution is a functional of the locally absorbed energy. We expect this representation to be valid as long as the particle being modelled can be described in terms of classical electromagnetic theory (i.e. quantum effects are not taken into consideration at all). The details of our theoretical approach and its limits of applicability are described in Sect. 2. As a quantitative test, we show its specific implementation for a homogeneous, isotropic sphere in Sect. 3, where we present numerical results. For a realistic "proof of concept'' test, we used the optical properties of processed organic refractory residues which are thought to be abundant in the diffuse interstellar medium. Section 5 draws the main conclusions of the present, germinal work, and outlines the directions of its foreseen development. Finally, formal derivation details are reported in Appendix A.
The starting point of our model is the assumption that the photoluminescence (PL) power emitted by a given volume element dV is a functional of the electromagnetic energy absorbed in a neighbourhood around it.
As a first step, we thus need to be able to thoroughly solve the problem
of the scattering and absorption of an electromagnetic wave hitting the dust
particle under consideration.
In particular we need to know the divergence of
the Poynting vector
![]() associated to the Fourier
component of angular frequency
associated to the Fourier
component of angular frequency ![]() of the electromagnetic fields
of the electromagnetic fields
![]() within the particle.
This quantity is commonly referred to as the source function
within the particle.
This quantity is commonly referred to as the source function
![]() in classical electromagnetic
theory (Dusel et al. 1976).
in classical electromagnetic
theory (Dusel et al. 1976).
![]() is the power absorbed by the
unit volume dV at position
is the power absorbed by the
unit volume dV at position ![]() from the Fourier component of the fields of angular
frequency between
from the Fourier component of the fields of angular
frequency between ![]() and
and
![]() .
From the knowledge of
.
From the knowledge of
![]() we can define the photon
absorption rate per unit angular frequency and unit volume as:
we can define the photon
absorption rate per unit angular frequency and unit volume as:
In general, p will vanish for large distances between ![]() and
and ![]() ;
the actual size s of the neighbourhood of
;
the actual size s of the neighbourhood of ![]() which
contributes to PL coming from it will depend on the material. The
specific behaviour of p in
which
contributes to PL coming from it will depend on the material. The
specific behaviour of p in ![]() will thus depend both on the material
and on the shape of the sample in this whole neighbourhood.
If s is small with respect to the size of the sample, and if the sample is
large enough to have "bulk'' optical properties, boundary effects can
be neglected in all but a thin "skin'' close to the surface, and p will only depend on the difference
will thus depend both on the material
and on the shape of the sample in this whole neighbourhood.
If s is small with respect to the size of the sample, and if the sample is
large enough to have "bulk'' optical properties, boundary effects can
be neglected in all but a thin "skin'' close to the surface, and p will only depend on the difference
![]() ;
if the material is furthermore isotropic (which we will assume), p will
only depend on
;
if the material is furthermore isotropic (which we will assume), p will
only depend on
![]() .
We remark that theoretical computations
of the density of states in clusters of atoms yield results
virtually undistinguishable from the bulk for atom numbers as small as a
few hundreds, the specific value depending on the material considered
(see e.g., Jena et al. 1992). This means that the depth of the "skin''
with optical properties significantly different from the bulk will typically
be a few molecular layers, i.e. of the order of a nanometer. Therefore, unless PL is dominated by the surface, it is generally
safe to assume bulk optical properties for particles significantly larger
than
.
We remark that theoretical computations
of the density of states in clusters of atoms yield results
virtually undistinguishable from the bulk for atom numbers as small as a
few hundreds, the specific value depending on the material considered
(see e.g., Jena et al. 1992). This means that the depth of the "skin''
with optical properties significantly different from the bulk will typically
be a few molecular layers, i.e. of the order of a nanometer. Therefore, unless PL is dominated by the surface, it is generally
safe to assume bulk optical properties for particles significantly larger
than ![]() 10 nm.
10 nm.
The integral of p over ![]() and V' will yield the overall efficiency of
PL following the absorption of a photon of a given energy in a
given part of the dust grain. This cannot exceed unity, unless multiple
photons can be emitted upon the absorption of one. In real life situations,
this yield is usually much lower than unity, since even exceedingly efficient
fluorescent materials usually show efficiencies of the order of
and V' will yield the overall efficiency of
PL following the absorption of a photon of a given energy in a
given part of the dust grain. This cannot exceed unity, unless multiple
photons can be emitted upon the absorption of one. In real life situations,
this yield is usually much lower than unity, since even exceedingly efficient
fluorescent materials usually show efficiencies of the order of ![]() 20% at
most. The detailed variation of p on the distance
20% at
most. The detailed variation of p on the distance
![]() will depend on the properties of the material, but it becomes very simple in
the following two extreme cases:
will depend on the properties of the material, but it becomes very simple in
the following two extreme cases:
We emphasise that we cite the two cases above merely as possible examples of the practical applicability of our approach, which is by no means limited to them. The present approach would not fail even if one or both of the cited examples should fail to fulfil the requirements for its applicability, which are indeed clearly and quantitatively stated. It would be proven to be inapplicable only if an example should be found which indeed fulfils the stated limits of applicability and shows a behaviour in contrast with our calculations. We will here restrict ourselves to these two limiting cases.
The simplest case is that of "pseudo-thermal''
PL. In this case,
![]() does not depend on
does not depend on
![]() at all, but only on
at all, but only on ![]() ,
,
![]() and on the material and
geometry of the sample. Multiplying p by
and on the material and
geometry of the sample. Multiplying p by
![]() as defined in Eq. (1) and integrating over all
as defined in Eq. (1) and integrating over all ![]() and over the volume
and over the volume
![]() of the
particle yields the rate
of the
particle yields the rate
![]() of emission of PL photons per unit emitting volume
of emission of PL photons per unit emitting volume
![]() and unit frequency
interval
and unit frequency
interval
![]() ,
produced by absorption over the whole particle at all
frequencies:
,
produced by absorption over the whole particle at all
frequencies:
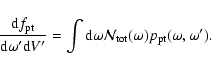 |
(3) |
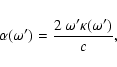
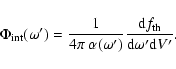 |
(5) |
![\begin{displaymath}\Phi_{\rm int}(\omega') = \frac{\left\{\Re~\left[m_1(\omega')\right]\right\}^2~B(\omega')}
{\hslash \omega^\prime},
\end{displaymath}](/articles/aa/full/2004/24/aa0703/img51.gif)
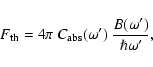 |
(6) |
![\begin{displaymath}F_{\rm th} = 4 \pi ~C_{\rm abs}(\omega')~{\Phi_{\rm int}(\omega')
\over \left\{\Re~\left[m_1(\omega')\right]\right\}^2},
\end{displaymath}](/articles/aa/full/2004/24/aa0703/img55.gif)
Equation (8) is of limited practical use, since
![]() itself
can have, in principle, a nontrivial dependence on particle size and shape,
which can only be obtained by direct measurements on appropriately sized and
shaped samples. It is elegant in that it does show explicitly that
size and shape effects can be quite relevant in this limiting case of
pseudo-thermal PL and thus measures on bulk laboratory samples are bound
to be useless for direct comparison with astronomical PL stemming from
small particles.
itself
can have, in principle, a nontrivial dependence on particle size and shape,
which can only be obtained by direct measurements on appropriately sized and
shaped samples. It is elegant in that it does show explicitly that
size and shape effects can be quite relevant in this limiting case of
pseudo-thermal PL and thus measures on bulk laboratory samples are bound
to be useless for direct comparison with astronomical PL stemming from
small particles.
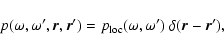 |
(9) |
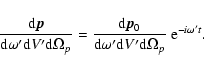 |
(11) |
Such a representation will be obviously appropriate if PL is indeed due to electric dipole permitted transitions, while a different representation, such as a density of (possibly higher order) electric or magnetic oscillating multipoles, would be more appropriate for a different transition. We remark, however, that in the case of absorption an adequate description can usually be obtained just in terms of the complex refractive index which, for non-magnetic materials, is determined only by the electric polarisability. There is no reason a priori why such a simplified representation should not be just as adequate to describe PL in the same material; however, in any case, using a more detailed representation would pose no significant conceptual problems, but merely complicate the practical calculations involved.
A single electric dipole
![]() ,
oscillating
with frequency
,
oscillating
with frequency
![]() inside the grain, radiates a power given by:
inside the grain, radiates a power given by:
In the particularly simple case in which the dipole distribution is isotropic,
the integral over
![]() amounts to a simple multiplication by
amounts to a simple multiplication by ![]() ,
hence
from Eqs. (14) and (15) we obtain the relation:
,
hence
from Eqs. (14) and (15) we obtain the relation:
We now need to determine the electromagnetic fields leaving the dust
grain, given an oscillating dipole moment located at a specified position
inside it. This problem is completely analogous to that of
calculating absorption and scattering by a dust particle, given its optical
properties and an incoming plane wave. The transmitted fields outside
the particle are expressed as (![]() ,
,
![]() ), while the internal
fields (
), while the internal
fields (![]() ,
,
![]() )
are decomposed into the sum:
)
are decomposed into the sum:
We are ultimately interested in the total power irradiated by the particle
into a unit solid angle about a given direction. To obtain it, we first
evaluate the instantaneous Poynting vector ![]() from the outgoing fields (
from the outgoing fields (![]() ,
,
![]() ), under the far-field approximation; then a time
average and a sum over all possible orientations of the dipole are
performed. This is the power
), under the far-field approximation; then a time
average and a sum over all possible orientations of the dipole are
performed. This is the power
![]() emitted per unit solid angle around a given direction,
after the radiation emitted by the volume element
emitted per unit solid angle around a given direction,
after the radiation emitted by the volume element
![]() escapes
the particle. As derived in detail in Appendix A,
if the dipole distribution is isotropic the above quantity turns out to
be given by
escapes
the particle. As derived in detail in Appendix A,
if the dipole distribution is isotropic the above quantity turns out to
be given by
In light scattering theory the extinction properties of small particles are
usually expressed in terms of the extinction cross-section
![]() ,
which is the sum of the absorption cross-section
,
which is the sum of the absorption cross-section
![]() and the
scattering cross-section
and the
scattering cross-section
![]() (Bohren & Huffman 1998). To follow this
convention and to clearly separate the dependence of
(Bohren & Huffman 1998). To follow this
convention and to clearly separate the dependence of
![]() on the position inside the particle, we express the source function
on the position inside the particle, we express the source function
![]() in Eq. (1) as the
irradiance
in Eq. (1) as the
irradiance![]()
![]() ,
times
,
times
![]() :
:
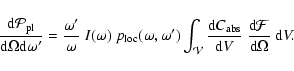 |
(23) |
The above Eq. (27), derived for monochromatic incident
light and a specific dust particle shape and size, can be
straightforwardly generalised for a distribution n(a) of particles and
non-monochromatic incident light. In this case one simply gets
To provide a simple, practical "proof of concept'' implementation of our model, while still able to yield some useful physical insight in the study of PL from interstellar dust grains, we consider a spherical, homogeneous particle illuminated by an unpolarised, parallel light beam. This enables us to make use of the standard Lorenz-Mie theory to describe the absorption and to derive analytical results for the resulting PL. This simple case can also be easily adapted to model a realistic laboratory configuration, hence providing the foundation for both the first and the second steps outlined in the previous section.
To exploit the symmetry of the problem we expand all of the fields as series
of vector spherical harmonics (VSHs), which can be shown to be orthogonal and
complete for transverse waves (see e.g., Bohren & Huffman 1998). As usual, the
expansion coefficients can be derived by imposing the continuity of tangential
components of the fields at the boundary surface between the particle and the
surrounding medium, and using the orthogonality properties of the VSHs.
All of the relevant formulae obtained for this case are presented in
Appendix A. We refer the reader interested in the details of
the full analytical derivation to Malloci (2003). We expressed the angular
dependence of both
![]() and
and
![]() into Eq. (33) with the help of the generalised
spherical functions (GSFs) Pm,nl (Hovenier & Van der Mee 1983).
As expected from the symmetry of the problem, we obtain
into Eq. (33) with the help of the generalised
spherical functions (GSFs) Pm,nl (Hovenier & Van der Mee 1983).
As expected from the symmetry of the problem, we obtain
In turn, according to the first step outlined in the previous section, we can
express
![]() in terms of the experimentally measured
PL yield
in terms of the experimentally measured
PL yield
![]() :
:
We can now combine Eqs. (29) and (30) to obtain
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0703f3.eps}
\end{figure}](/articles/aa/full/2004/24/aa0703/Timg126.gif) |
Figure 3:
The function
|
![\begin{figure}
\par\begin{tabular}{cc}
\begin{tabular}[t]{c}
\includegraphics[wi...
...bular}&
\includegraphics[width=10cm,clip]{0703f4b.eps}\end{tabular}\end{figure}](/articles/aa/full/2004/24/aa0703/Timg127.gif) |
Figure 4:
Sample or1: incident wavelength 0.411 |
In the practical implementation we presented here, we made the simplifying
approximation to only consider primary PL, i.e. the
emission of photons following the absorption of one photon from the incoming
external field. We solved the well known problem of the absorption of light
from an incident unpolarised wave and expressed the source function
as proportional to the divergence of the resulting Poynting vector
inside the particle. However,
![]() should also include
a contribution from self-absorbed photons, as computed from the
divergence of the Poynting vector stemming from the PL itself.
This contribution to
should also include
a contribution from self-absorbed photons, as computed from the
divergence of the Poynting vector stemming from the PL itself.
This contribution to
![]() gives rise to
secondary PL, i.e. the emission of a photon following the
self-absorption of a previous PL photon.
This does not formally affect the derivation above at all, except for one
point: one should consider the contribution of self-absorbed photons to the
source function, which is obtained from the divergence of the Poynting vector
associated to the internal field (
gives rise to
secondary PL, i.e. the emission of a photon following the
self-absorption of a previous PL photon.
This does not formally affect the derivation above at all, except for one
point: one should consider the contribution of self-absorbed photons to the
source function, which is obtained from the divergence of the Poynting vector
associated to the internal field (![]() ,
,
![]() ), of
Eq. (17). As a consequence of this inclusion, PL at
any given wavelength will be related to the PL and optical properties
of the material at all smaller wavelengths, making practical calculations much
more difficult. A perturbative approach is always possible, in which one
considers, as a first approximation, just the contribution to the source
function from the incident exciting field, computes the resulting
PL and the resulting contribution of self-absorption to the source
function, and repeats the calculations in a self-consistent way until the
desired accuracy is reached. However, each subsequent correction will be of
the order of the PL yield times the previous one; therefore, for any
reasonable PL yield, the zero order approximation to completely
neglect secondary PL will already be a good one, and any corrections
beyond the first order will be extremely small.
), of
Eq. (17). As a consequence of this inclusion, PL at
any given wavelength will be related to the PL and optical properties
of the material at all smaller wavelengths, making practical calculations much
more difficult. A perturbative approach is always possible, in which one
considers, as a first approximation, just the contribution to the source
function from the incident exciting field, computes the resulting
PL and the resulting contribution of self-absorption to the source
function, and repeats the calculations in a self-consistent way until the
desired accuracy is reached. However, each subsequent correction will be of
the order of the PL yield times the previous one; therefore, for any
reasonable PL yield, the zero order approximation to completely
neglect secondary PL will already be a good one, and any corrections
beyond the first order will be extremely small.
From a qualitative point of view, the effect of secondary PL is obviously in the direction of increasing the yield, this increase being necessarily in the form of lower energy photons, moving the peak of the spectrum slightly to the red.
We present here the numerical results of the application of our local PL model to the specific case of a spherical, homogeneous dust particle, considering only primary PL. We used the optical properties of processed organic refractory residues, in a form as expected in the diffuse interstellar medium, as given by Jenniskens (1993). In particular, we used the optical constants corresponding to two different organic refractory residues subjected to energetic processing, here labelled or1 and or2, the latter being the more heavily processed one. The outer medium was assumed to be the vacuum.
![\begin{figure}
\begin{tabular}{ccc}
\begin{tabular}[p]{c}
\includegraphics[width...
...ular}&&
\includegraphics[width=10cm,clip]{0703f9b.eps}\end{tabular}\end{figure}](/articles/aa/full/2004/24/aa0703/Timg133.gif) |
Figure 9:
Sample or1: incident wavelength 0.411 |
Figures 4 through 11 display a sample of the results,
relative to excitation with different monochromatic exciting wavelengths,
namely 220 nm, 411 nm and 514 nm; the sphere radius is taken to be in the
range 50-2050 nm and two sets of complex refractive indices were considered,
corresponding to
organic refractory residues obtained by UV irradiation of laboratory analogues
of interstellar ices at different doses of absorbed energy. While we sampled a
much larger grid of the parameter space, these results suffice to clearly
demonstrate the main effects of self-absorption on the expected PL,
and the impact on them of each parameter.
They are illustrated with reference to the geometric configuration depicted in
Fig. 1. The direction of propagation of the incident light defines the
z axis, the forward direction. The angle expressing the position of
the detector in the laboratory setup assumed (see Fig. 2) is taken
to be
![]() .
Each figure shows at the left the distribution of the
absorbed energy inside the sphere, expressed in terms of the absorption cross
section per unit volume, evaluated through Eq. (A.1), normalised to
the total
.
Each figure shows at the left the distribution of the
absorbed energy inside the sphere, expressed in terms of the absorption cross
section per unit volume, evaluated through Eq. (A.1), normalised to
the total
![]() ,
computed using Eq. (A.2). The contour plots
show the distribution of the locally absorbed energy in a plane containing the
z-axis (cf. Fig. 1). Given the symmetry of the problem, if the
exciting light is unpolarised the absorption pattern is the same in any such
plane.
,
computed using Eq. (A.2). The contour plots
show the distribution of the locally absorbed energy in a plane containing the
z-axis (cf. Fig. 1). Given the symmetry of the problem, if the
exciting light is unpolarised the absorption pattern is the same in any such
plane.
The box at the right represents the form factor
![]() ,
as
a function of the angle
,
as
a function of the angle ![]() between the incident beam and the direction of
observation and of the emission wavelength
between the incident beam and the direction of
observation and of the emission wavelength
![]() .
Therefore, these
three-dimensional plots offer an explicit visual representation of the impact
of particle size effects in modulating the spectral distribution of the
PL observed in laboratory experiments. The form factor
.
Therefore, these
three-dimensional plots offer an explicit visual representation of the impact
of particle size effects in modulating the spectral distribution of the
PL observed in laboratory experiments. The form factor
![]() is expressed in gigabarns (1 Gb = 10-15 cm2).
is expressed in gigabarns (1 Gb = 10-15 cm2).
The distribution of the locally absorbed energy inside a particle is well
known to be a complicated function of the position (Dusel et al. 1976; Kerker 1973).
Our contour plots of the absorbed energy distribution correspond to increasing
particle radii. As expected, featureless absorption is observed for very small
size parameters (defined as
![]() ), while for
increasing a, the absorption shows an increasingly
structured pattern. For the optical properties of the sample or1
considered in this work there are cases in which the absorption is larger on
the side opposite to the illuminated one. At large size parameters absorption
is increasingly concentrated on the side where the particle is irradiated, as
expected when approaching the geometrical optics limit.
), while for
increasing a, the absorption shows an increasingly
structured pattern. For the optical properties of the sample or1
considered in this work there are cases in which the absorption is larger on
the side opposite to the illuminated one. At large size parameters absorption
is increasingly concentrated on the side where the particle is irradiated, as
expected when approaching the geometrical optics limit.
This richly structured
absorption pattern governs the behaviour of
![]() ,
which
turns out to strongly depend on the emitted wavelength
,
which
turns out to strongly depend on the emitted wavelength
![]() and on the angle
and on the angle ![]() .
This vindicates our initial Ansatz that geometry effects are able
to considerably modify the spectral distribution of the PL observed
in laboratory experiments. In particular, the
.
This vindicates our initial Ansatz that geometry effects are able
to considerably modify the spectral distribution of the PL observed
in laboratory experiments. In particular, the
![]() dependence is conspicuous
for any particle sizes: in the Rayleigh limit (
dependence is conspicuous
for any particle sizes: in the Rayleigh limit (
![]() and size parameters of about 0.8 and 0.6 for
and size parameters of about 0.8 and 0.6 for
![]() nm and 514 nm,
respectively)
nm and 514 nm,
respectively)
![]() changes by a factor of about 2-3 for
changes by a factor of about 2-3 for
![]() between
between ![]() m and
m and ![]() m, becoming even more marked for larger
particles all the way up to the geometrical optics limit at 2.05
m, becoming even more marked for larger
particles all the way up to the geometrical optics limit at 2.05 ![]() m
(with size parameters of about 31.3 for
m
(with size parameters of about 31.3 for
![]() nm and 25.1 for
nm and 25.1 for
![]() nm).
nm).
As to the angular dependence, the results show an increasing variation for growing size parameters; the astrophysical implications are discussed in a subsequent paper (Mulas et al. 2004).
When the incident wavelength is comparable to the particle dimensions,
![]() displays an oscillatory behaviour,
which tends to be damped in the geometrical optics limit. This is not
unexpected, as it is very similar to what one observes for extinction (see
for example Fig. 4.6 on page 105 of Bohren & Huffman (1998), which shows an interference
structure showing a series of alternating broad maxima and minima, with
weaker and weaker oscillations around the expected asymptotic value for
increasingly large size parameters).
displays an oscillatory behaviour,
which tends to be damped in the geometrical optics limit. This is not
unexpected, as it is very similar to what one observes for extinction (see
for example Fig. 4.6 on page 105 of Bohren & Huffman (1998), which shows an interference
structure showing a series of alternating broad maxima and minima, with
weaker and weaker oscillations around the expected asymptotic value for
increasingly large size parameters).
It should be noted that the positions of peaks and valleys, for a chosen
material, depend on particle size and on exciting wavelength; therefore, the
small scale interference structure is likely to be washed out if one observes
a broad distribution of particle radii and/or if their PL is
excited by non-monochromatic light with a broad spectrum. In the most generic
case of non-monochromatic light and a distribution n(a) of particle sizes
we may rewrite Eq. (28) as
| |
= | 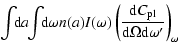 |
(34) |
| = | 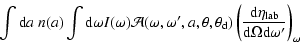 |
||
| = | 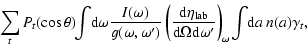 |
Indeed, in Mulas et al. (2004) we consider two standard dust particle size distributions of the kind first proposed by Mathis et al. (1977), in order to infer the impact of the present model on the actual astrophysical problem of the Extended Red Emission.
In this case,
![]() will retain only the overall large scale
features of
will retain only the overall large scale
features of
![]() ,
while smoothing out the smaller
oscillatory interference details (see Mulas et al. 2004). The overall
behaviour will be governed by and large by the complex refractive index
of the material.
,
while smoothing out the smaller
oscillatory interference details (see Mulas et al. 2004). The overall
behaviour will be governed by and large by the complex refractive index
of the material.
In spite of the extreme simplifications in its present numerical application, this model unambiguously demonstrates that self-absorption and geometric effects must be taken into account when comparing laboratory PL data taken on macroscopic samples with the observed PL from small particles, since they can have a rather important effect. Some perhaps misleading conclusions drawn from a direct comparison neglecting these effects may have to be regarded in a new light. In this respect, we present a more thorough analysis of the implications of this model for the specific case of the Extended Red Emission in a second paper (Mulas et al. 2004). We expect to soon obtain new laboratory measurements of the optical and PL properties of various IPHAC samples in collaboration with the research group of Laboratory Astrophysics at the Catania Astrophysical Observatory, to use them along with the present model for a meaningful, quantitative comparison with available ERE observations.
To reconcile the observed under-solar abundances of heavy elements and the observed extinction, the present, state-of-the-art interstellar dust models represent dust particles as complex aggregates (core-mantle and/or fluffy, porous grains), very different from our oversimplified homogeneous spheres. This makes it clear that the present application of our physical model of PL must be but a first step towards more realistic interstellar dust grain PL models. The first, and easiest unrealistic assumption which needs to be relaxed is homogeneity, in order to assess the impact of a multi-layer core-mantle structure on the outgoing PL while retaining spherical symmetry. To drop the latter is a more ambitious project, which will need a more sophisticated, and computationally expensive, approach, such as the T-matrix method, recently used to study the extinction of fluffy and porous dust grains (Saja et al. 2001; Iatì et al. 2001, 2003). This method is a natural match to our model, the major obstacle to its implementation being the need of much larger computing power resources to first find the coefficients of the expansions in VSHs and then numerically integrate the PL over the contributing volume of the particle.
On a parallel track, we want to extend our model to compute physical quantities related to other Stokes parameters besides I (as defined, e.g., in Bohren & Huffman 1998, Sect. 2.11.1), to be able to study any polarisation effects stemming from the inhomogeneous distribution of absorption and resulting PL within the dust grain.
Acknowledgements
G. Malloci acknowledges the financial support by INAF - Osservatorio Astronomico di Cagliari. The authors are thankful to Prof. C. V. M. Van der Mee for his help with generalised spherical functions theory, and Dr. C. Cecchi-Pestellini and Prof. F. Borghese for their suggestions and useful discussions.
This appendix provides the basic concepts of the theoretical background
of this work as well as the derivation of the main relations used in
the application of our model of PL by small particles.
We will discuss separately the two mechanisms of excitation and subsequent
emission. The distribution of the absorbed energy inside the particle is
presented in Sect. (A.1), while the treatment of the PL emission is given in Sect. (A.2). Section (A.3) provides the derivation of
![]() for the case implemented in the
present work. We followed the same units and notations adopted in Bohren &
Huffman's book (1998), henceforth B&H. Details of the reductions
to obtain the formulae here presented are given in Malloci (2003).
for the case implemented in the
present work. We followed the same units and notations adopted in Bohren &
Huffman's book (1998), henceforth B&H. Details of the reductions
to obtain the formulae here presented are given in Malloci (2003).
We consider a spherical, isotropic and homogeneous dust particle of
radius a. As depicted in Fig. 1, we choose the centre of the
particle as the origin of a rectangular coordinate system (x, y, z). We are
interested in the distribution of the absorbed energy inside the particle under
the hypothesis of incident natural light. Unpolarised light is described as the
incoherent superposition of the two mutually orthogonal plane waves at
frequency ![]() ,
both of which are expanded in an infinite sum of vector
spherical harmonics (henceforth VSHs). This expansion also dictates the form
of the scattered and internal fields (B&H).
,
both of which are expanded in an infinite sum of vector
spherical harmonics (henceforth VSHs). This expansion also dictates the form
of the scattered and internal fields (B&H).
Assuming the magnetic permeability of the particle to be the same as that of
the surrounding medium, the resulting expression for the contribution of the
volume element ![]() to
to
![]() is given by:
is given by:
Equation (A.1) is independent of the azimuthal angle ![]() ,
as
expected on physical grounds for unpolarised incident light. The integration
over the volume
,
as
expected on physical grounds for unpolarised incident light. The integration
over the volume
![]() of the sphere leads to an expression of
of the sphere leads to an expression of
![]() in terms of cn and dn:
in terms of cn and dn:
We consider a dipole moment localised at position ![]() inside the sphere
and oscillating at frequency
inside the sphere
and oscillating at frequency
![]() :
:
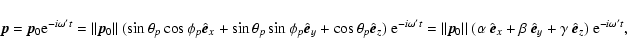
After a lengthy, although straightforward, procedure, the expansion of
![]() and
and
![]() in VSHs results in:
in VSHs results in:
The expansion above, along with the orthogonality of the VSHs,
the boundary conditions and the far field asymptotic behaviour expected,
set the form of the complete solution, i.e. the expansion of both the
scattered field (
![]() )
and the outgoing field (
)
and the outgoing field (
![]() ). On physical grounds, the finiteness of the fields at
the origin requires only the well behaved spherical Bessel functions
of the first kind
jn(k1 r) to be present in the
expansion inside the sphere, whereas the spherical Bessel functions of
the second kind
yn(k1 r), which diverge for r=0, do not occur.
The asymptotic behaviour of the
spherical Hankel functions (B&H) leads to the choice
of
hn(1)(k r) = jn(k r) + i yn(k r) in the region outside the sphere,
since the electromagnetic field leaving the particle must be an
outgoing wave. Thus, appending as usual the superscript (1) which specifies
that jn is the function containing the radial dependence in the VSHs:
). On physical grounds, the finiteness of the fields at
the origin requires only the well behaved spherical Bessel functions
of the first kind
jn(k1 r) to be present in the
expansion inside the sphere, whereas the spherical Bessel functions of
the second kind
yn(k1 r), which diverge for r=0, do not occur.
The asymptotic behaviour of the
spherical Hankel functions (B&H) leads to the choice
of
hn(1)(k r) = jn(k r) + i yn(k r) in the region outside the sphere,
since the electromagnetic field leaving the particle must be an
outgoing wave. Thus, appending as usual the superscript (1) which specifies
that jn is the function containing the radial dependence in the VSHs:
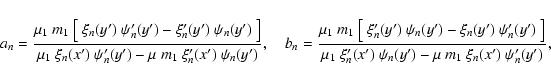
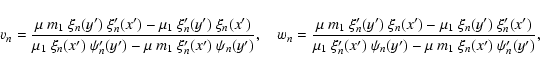
We are eventually interested in the total power irradiated by the
particle at very large distances from it, into a small solid angle about
a given direction. In the far-field region the radial components Er and Hr of the external fields become negligible with respect to the
angular ones, which are related by:
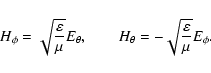
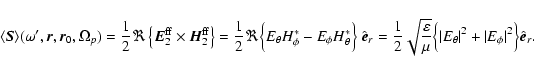
So far we have been considering a single,
discrete dipole, oscillating at a given frequency. We can move
to a continuous distribution of dipoles with the obvious substitutions
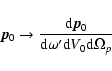 |
(A.15) |
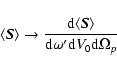 |
(A.16) |
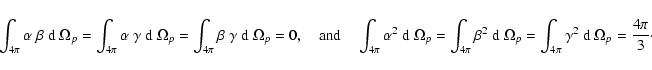
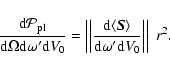
With the help of Eq. (A.12) defining
![]() ,
we obtain, after some manipulation, Eq. (18)
of Sect. 2.2:
,
we obtain, after some manipulation, Eq. (18)
of Sect. 2.2:
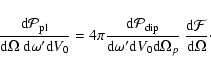
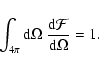
We thus obtained all of the ingredients occurring in Eq. (25)
in the specific case of a homogeneous, isotropic sphere. The angular
integrations can be evaluated analytically expanding the angular functions
contained in
![]() and
and
![]() as linear
combinations of generalised spherical functions (GSFs) Pm,nl (Hovenier & Van der Mee 1983),
which yields
as linear
combinations of generalised spherical functions (GSFs) Pm,nl (Hovenier & Van der Mee 1983),
which yields
| |
= | ![$\displaystyle \frac{(2 r + 1)}{{\vert\rho_0\vert}^2}\bigg\{
\Re\Big[f_n f_m^*(c...
...\prime d_m^*{\psi_m^\prime}^*)\Big]
\left(A_{r,n}^m\right)^2[1 + (-1)^{m+n+r} ]$](/articles/aa/full/2004/24/aa0703/img219.gif) |
|
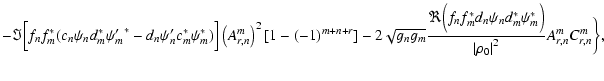 |
|||
| = | ![$\displaystyle \frac{(2 s + 1)}{{\vert\rho_0^\prime\vert}^2}\bigg\{
\Re\Big[f_{p...
...\prime a_q^*{\psi_q^\prime}^*)\Big]
\left(A_{s,p}^q\right)^2[1 + (-1)^{q+p+s} ]$](/articles/aa/full/2004/24/aa0703/img222.gif) |
||
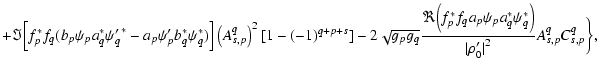 |
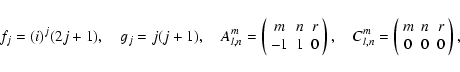
Substituting Eqs. (A.19) and (A.20) in
Eq. (25), the angular integration can be evaluated making use of
the properties of the GSFs yielding, after a hearty amount of algebra which
we spare the reader:
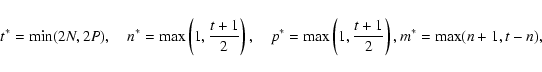
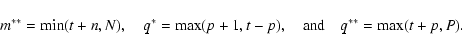
We need to practically evaluate Eq. (26), to obtain
![]() from laboratory measurements of the PL yield of
a bulk sample in a specific experimental setup. We consider the experimental
configuration of Fig. 2, in which a bulk sample is illuminated
by a collimated laser beam of frequency
from laboratory measurements of the PL yield of
a bulk sample in a specific experimental setup. We consider the experimental
configuration of Fig. 2, in which a bulk sample is illuminated
by a collimated laser beam of frequency ![]() travelling in the positive z direction, and the PL emission at frequency
travelling in the positive z direction, and the PL emission at frequency
![]() is observed at
angle
is observed at
angle
![]() with respect to the exciting radiation. We may rewrite
Eq. (26) multiplying both the numerator and the denominator
by the irradiance
with respect to the exciting radiation. We may rewrite
Eq. (26) multiplying both the numerator and the denominator
by the irradiance ![]() of the incident beam and the total power
of the incident beam and the total power
![]() absorbed by the sample, to obtain:
absorbed by the sample, to obtain:
To be able to derive
![]() from the experimental
measurement of
from the experimental
measurement of
![]() we must now
evaluate the fraction
we must now
evaluate the fraction
In a typical experimental configuration, the collimating optics will have a
diameter of the order of 2 cm, a focal length of the order of 15 cm, and will
illuminate a spot of less than 10 ![]() m on the surface of the sample, when
focused. The parallel laser beam before focusing has a diameter of the order of 2 mm. This beam penetrates into the sample for a depth of the order of a few
times
m on the surface of the sample, when
focused. The parallel laser beam before focusing has a diameter of the order of 2 mm. This beam penetrates into the sample for a depth of the order of a few
times
![]() ,
,
![]() being the absorption coefficient at incident
wavelength, which translates into less than 10
being the absorption coefficient at incident
wavelength, which translates into less than 10 ![]() m for the organic refractory
residues considered for the examples in this work.
m for the organic refractory
residues considered for the examples in this work.
Given its small aperture, the relatively large focal length and the short
path it travels inside the sample, the collimated laser beam can be
considered as a portion of a parallel beam, confined into a cylinder: the
diameter of the beam will change by less than one part in 104 due to its
divergence before being completely absorbed.
Hence, we represent this experimental configuration as
a plane parallel slab in which a cylinder of diameter ![]() 10
10 ![]() m is
illuminated by a normally incident portion of plane wave, which is
exponentially attenuated as it travels inwards, so that only about 10
m is
illuminated by a normally incident portion of plane wave, which is
exponentially attenuated as it travels inwards, so that only about 10 ![]() m
of its length need to be considered. In the local PL limit, only this same
cylinder will produce luminescence photons.
It is clear that as long as only such a
small portion of the sample is participating in the PL, we
can consider this portion to be a part of a sphere, provided it
is large enough for the curvature of the surface to be negligible over lengths
of the order of the absorption length. In this geometry, the illuminated
part of the sample (imagined as a sphere centred in the origin of the
reference system and illuminated by a parallel beam along the z-axis)
can be approximated by a small portion of a narrow right circular cone of
aperture
m
of its length need to be considered. In the local PL limit, only this same
cylinder will produce luminescence photons.
It is clear that as long as only such a
small portion of the sample is participating in the PL, we
can consider this portion to be a part of a sphere, provided it
is large enough for the curvature of the surface to be negligible over lengths
of the order of the absorption length. In this geometry, the illuminated
part of the sample (imagined as a sphere centred in the origin of the
reference system and illuminated by a parallel beam along the z-axis)
can be approximated by a small portion of a narrow right circular cone of
aperture
![]() centred around the beam axis and having its vertex in the
centre of the sphere. This frustum of cone, for sphere radius much larger than
the cylinder section, becomes undistinguishable from the actually illuminated
cylinder we are considering. If the circular spot illuminated on the sample
surface has area
centred around the beam axis and having its vertex in the
centre of the sphere. This frustum of cone, for sphere radius much larger than
the cylinder section, becomes undistinguishable from the actually illuminated
cylinder we are considering. If the circular spot illuminated on the sample
surface has area ![]() ,
the aperture
,
the aperture
![]() of the frustum of cone will be
given by the relation
of the frustum of cone will be
given by the relation
![]() .
We remark that, for the
sizes, wavelengths and optical properties we are considering, a sphere of
radius of the order of 1 mm is already quite large enough. Since the outgoing
light is collected at distances of the order of
.
We remark that, for the
sizes, wavelengths and optical properties we are considering, a sphere of
radius of the order of 1 mm is already quite large enough. Since the outgoing
light is collected at distances of the order of ![]() 15 cm, we can still quite
safely consider it to be in the far field limit. The power absorbed by a
unit volume within the illuminated cylinder (or frustum of cone, defined
by
15 cm, we can still quite
safely consider it to be in the far field limit. The power absorbed by a
unit volume within the illuminated cylinder (or frustum of cone, defined
by
![]() ), can be thus written as
), can be thus written as
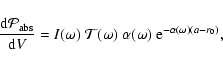 |
(A.25) |
The integral at the denominator of the right hand side of Eq. (A.24)
can thus be written as
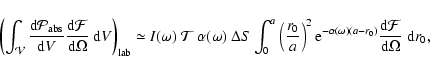 |
(A.26) |
The total power absorbed by the sample is
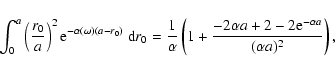
With the help of the previous equations, we can write
Substituting Eqs. (A.24) and (31) into
Eq. (A.23) yields the desired expression for
![]() in terms of measurable and calculable quantities:
in terms of measurable and calculable quantities: