A&A 420, 937-944 (2004)
DOI: 10.1051/0004-6361:20035700

An evolutionary model for pulsar-driven supernova remnants

A hydrodynamical model

E. van der Swaluw1,2 - T. P. Downes3 - R. Keegan3


1 - Dublin Institute for Advanced Studies, 5 Merrion Square, Dublin 2, Ireland
2 - FOM-Institute for Plasma Physics Rijnhuizen, PO Box 1207, 3430 BE Nieuwegein, The Netherlands
3 - School of Mathematical Sciences, Dublin City University, Glasnevin, Dublin 9, Ireland

Received 17 November 2003 / Accepted 8 March 2004

Abstract
We present a model of a pulsar wind nebula evolving inside its associated supernova remnant. The model uses a hydrodynamics code to simulate the evolution of this system when the pulsar has a high velocity. The simulation distinguishes four different stages of pulsar wind nebula evolution: the supersonic expansion stage, the reverse shock interaction stage, the subsonic expansion stage and ultimately the bow shock stage. The simulation bears out that, due to the high velocity of the pulsar, the position of the pulsar is off-centered with respect to its pulsar wind nebula, after the passage of the reverse shock. Subsequently the pulsar wind nebula expands subsonically until the event of the bow shock formation, when the motion of the pulsar becomes supersonic. The bow shock formation event occurs at roughly half the crossing time, when the pulsar is positioned at 0.677 times the radius of the supernova remnant blastwave, in complete agreement with analytical predictions. The crossing time is defined by the age of the supernova remnant when the pulsar overtakes the blastwave bounding the supernova remnant.

The results of the model are applied to three supernova remnants: N157B, G327.1-1.1 and W44. We argue that the head of the pulsar wind nebula, containing the active pulsar, inside the first two systems is not bounded by a bow shock. However, in the case of W44 we argue for a scenario in which the pulsar wind nebula is bounded by a bow shock, due to the supersonic motion of the pulsar.

Key words: pulsars: general - stars: supernova remnants - shocks waves - hydrodynamics

1 Introduction

A supernova remnant (SNR) is the relic of a supernova explosion, which injects an energy of ${\sim} 10^{51}$ erg into the surrounding medium. The dynamics of a young SNR expanding into the interstellar medium (ISM) is determined by two shocks: a forward shock which propagates into the ISM and is being decelerated by sweeping up material from the ISM, and a reverse shock which results from the high pressure behind the forward shock and propagates back into the freely expanding ejecta of the SNR (McKee 1974; McKee & Truelove 1995).

A young SNR becomes dynamically more interesting in those cases where the collapse of the progenitor star preceding the supernova explosion yields a pulsar: a rapidly rotating neutron star. In those cases the dynamics of the central region of the SNR is dominated by the continuous injection of energetic particles by a relativistic pulsar wind driven by the spin-down energy of the pulsar. The pulsar wind is terminated by a strong MHD shock (Rees & Gunn 1974), and drives a pulsar wind nebula (PWN) in the interior of the young SNR. The dynamics of the PWN is coupled to the evolution of the SNR, because the total energy release over the pulsar's lifetime is small ( ${\sim} 10^{49}{-}10^{50}$ erg) compared with the total mechanical energy of the SNR ( ${\sim} 10^{51}$ erg).

Several authors (Reynolds & Chevalier 1984; van der Swaluw et al. 2001; Blondin et al. 2001; Bucciantini et al. 2003) have considered the evolution of a centered PWN inside an evolving SNR. In these systems, the initial stage of the PWN is the supersonic expansion stage: the pulsar wind bubble is bounded by a strong PWN shock propagating through the freely expanding ejecta of the SNR. A transition to the reverse shock interaction stage takes place when the reverse shock collides with the PWN shock, and subsequently crushes the pulsar wind bubble (van der Swaluw et al. 2001; Blondin et al. 2001). This reverse shock interaction stage is characterised by an unsteady expansion of the pulsar wind bubble (van der Swaluw et al. 2001), due to the reverberations from the violent collision between the reverse shock and the PWN shock. The expansion of the PWN proceeds subsonically when these reverberations have vanished. The expansion is subsonic because the surroundings of the PWN have been reheated by the passage of the reverse shock: the PWN shock, bounding the swept-up shocked ejecta around the hot pulsar wind bubble, has disappeared.

In this paper we discuss the evolution of PWNe inside SNRs, for pulsars with a constant kick velocity: initially the PWN starts its expansion at the center of the SNR, however the pulsar motion will move the pulsar wind cavity along as it moves through the SNR interior. We present results from hydrodynamical simulations for such a system, which distinguishes all three evolutionary stages mentioned above, i.e. the supersonic expansion stage, the reverse shock interaction stage and the subsonic expansion stage. However at the end of the simulation an additional stage can be distinguished, when the head of the PWN, containing the active pulsar, deforms into a bow shock due to the supersonic motion of the pulsar.

The supersonic expansion stage in the simulation shows a PWN which is off-centered with respect to the twofold shock structure of the SNR, due to the kick velocity of the pulsar. Therefore the timescale on which the reverse shock collides with the complete shock surface bounding the PWN can be a significant fraction of the total lifetime of the PWN when the reverse shock interaction stage starts. We use a semi-analytical approach to estimate the timescale of the collision process, which is shown to scale roughly with the pulsar velocity. The results from the simulation are in almost complete agreement with these semi-analytical calculations. Due to the high velocity of the pulsar, its position inside the PWN is strongly off-centered after the passage of the reverse shock. Ultimately, at the end of the simulation, when the pulsar is approaching the shell of its SNR, the head of the PWN, containing the active pulsar, is deformed into a bow shock at a time and position, in complete agreement with analytical predictions made by van der Swaluw et al. (1998).

We determine the evolutionary stage of the PWNe inside the SNRs N157B, G327.1-1.1, and W44, using our model. For the first two systems, we argue that the position of the pulsar at the head of its PWN is a result of the passage of the reverse shock and the high velocity of the pulsar: the heads of these PWNe are not bounded by a bow shock. Therefore these PWNe are either in the reverse shock interaction stage or the subsonic expansion stage. The PWN inside the SNR W44 however, is shown to be a good candidate for having a bow shock nebula around its pulsar.

2 The evolution of a PWN inside a SNR

2.1 The interaction between the reverse shock and the PWN shock

The initial stage of PWN evolution is characterised by a hot pulsar wind bubble, bounded by a strong PWN shock, propagating through the freely expanding ejecta of the SNR. A transition to the subsonic expansion stage occurs via the reverse shock interaction stage. This interaction stage starts when the reverse shock collides with the PWN shock. In the case of a centered pulsar ( $V_{\rm psr}=0$), the reverse shock collides with the PWN shock surface instantaneously, due to the spherical symmetry of the SNR and the PWN. However, when the pulsar has a kick velocity, there will be an associated timescale on which the reverse shock collides with the complete surface of the PWN shock. This is the first stage of the reverse shock interaction stage. Next, the pulsar wind bubble oscillates back and forward due to the presence of reverberations from the passage of the reverse shock (van der Swaluw et al. 2001). The reverse shock interaction stage ends when these reverberations have vanished and the pulsar wind bubble proceeds its expansion subsonically. In this section we use a semi-analytical approach to derive a timescale on which the reverse shock collides with the complete surface of the PWN shock.

McKee & Truelove (1995) give analytical approximations for the trajectories of the forward shock and the reverse shock of a SNR in the case of a uniform ambient medium. Their equations for the trajectories of both shocks are normalised to a timescale $t_{\rm ST}$, which marks the age of the remnant when it has swept up roughly 1.61 the ejected mass $M_{\rm ej}$. Their equations describe the expansion of an isolated SNR in the free expansion stage and the Sedov-Taylor stage. The trajectory of the forward shock converges to the Sedov-Taylor solution when the SNR age $t \gg t_{\rm ST}$. Internal (radiative) cooling is not included in their model, therefore the pressure-driven snowplow stage is not described (see however Blondin et al. 1998).

The reverse shock hits the center of the SNR at approximately 5 times the transition time $t_{\rm ST}$, putting an upper limit on the age $t_{\rm col}$, when the reverse shock has collided with the complete shock surface bounding the PWN:

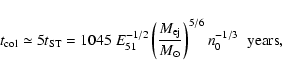\begin{displaymath}t_{\rm col}\simeq 5t_{\rm ST} = 1 045\; E^{-1/2}_{51} \left({M_{\rm ej}\over M_\odot}\right)^{5/6}n_0^{-1/3}\;\;{\rm years} , \end{displaymath} (1)

here E51 is the total mechanical energy of the SNR in units of 1051 erg and n0 is the ambient hydrogen number density assuming an interstellar composition of 10 H: 1 He. The above timescale is very close to the one given by Reynolds & Chevalier (1984).

An equation for the radius of the PWN shock, when it is interacting with the freely expanding ejecta of its SNR was given by van der Swaluw et al. (2001), where a constant pulsar wind luminosity $L_{\rm pw}=L_0$ was taken:

 \begin{displaymath} R_{\rm pwn}(t)\simeq 0.889\left({L_0t\over E_0}\right)^{1/5}V_0t\propto t^{6/5}, \end{displaymath} (2)

here E0 is the total mechanical energy of the SNR and V0 is defined as:

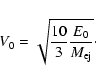\begin{displaymath}V_0 = \sqrt{{10\over 3}{E_0\over M_{\rm ej}}} \cdot \end{displaymath} (3)

We have taken the case for which the adiabatic heat ratio of the pulsar wind material $\gamma_{\rm pwn}=5/3$.


  \begin{figure} \par {\includegraphics[width=7.8cm,clip]{0700fig1.eps} } \end{figure} Figure 1: Radii of the forward and the reverse shocks of a SNR with an explosion energy of E0=1051 erg and a total ejected mass of $M_{\rm ej}=3~ M_\odot$. The dashed lines indicate the position of the front ( $R^{\rm f}_{\rm pwn}$) and the back ( $R^{\rm b}_{\rm pwn}$) of the PWN shock. The luminosity of the pulsar wind is constant, L0=1038 erg/s and the velocity of the pulsar $V_{\rm psr} = 1000$ km s-1. The timescale on which the reverse shock collides with the complete shock surface of the PWN equals $\Delta t_{\rm col}\simeq 1050$ years. This timescale is of the same order as the age of the PWN, $t\simeq 1200$ years, on which the reverse shock interaction stage starts.
Open with DEXTER

We will use the equations for the trajectories of the forward and the reverse shock of the SNR from Truelove & McKee (1995) and the above equation for the radius of the PWN shock to calculate the collision time $t_{\rm col}$, i.e. when the reverse shock collides with the PWN shock. We make a distinction between the front of the PWN shock $R^{\rm f}_{\rm pwn}=R_{\rm pwn}+V_{\rm psr}t$, and the back of the PWN shock $R^{\rm b}_{\rm pwn}=R_{\rm pwn}-V_{\rm psr}t$, which enables us to calculate $\Delta t_{\rm col}$, the timescale on which the reverse shock collides with the complete shock surface bounding the PWN. This approach neglects the change in the PWN expansion due to the displacement of the pulsar inside the freely expanding ejecta. Figure 1 shows an example of this approach, where the position of the four different shocks are plotted as a function of time. The parameters have been taken similarly to the parameters which we will use in the simulation. The figure shows that the timescale on which the reverse shock collides with the complete PWN shock surface equals $\Delta t_{\rm col}\simeq 1050$ years. Figure 2 shows $\Delta t_{\rm col}$ as a function of the pulsar velocity, where one observes that this timescale correlates almost linearly with the pulsar velocity. We conclude that the collision timescale  $\Delta t_{\rm col}$ of PWNe containing a high velocity pulsar can be a significant fraction of the timescale associated with the supersonic expansion stage.


  \begin{figure} \par {\includegraphics[width=8.3cm,clip]{0700fig2.ps} } \end{figure} Figure 2: The timescale $\Delta t_{\rm col}$ on which the reverse shock collides with the complete shock surface bounding the PWN, as a function of the pulsar velocity. Apart from the velocity, the same parameters have been taken as in Fig. 1.
Open with DEXTER

2.2 The formation of the PWN bow shock

After the passage of the reverse shock the PWN consists of two distinct parts: The age of the remnant when the pulsar overtakes the shell of its remnant was given by van der Swaluw et al. (2003):

 \begin{displaymath} t_{\rm cr}\simeq 1.4 \times 10^4 \; E_{51}^{1/3} V_{\rm 1000}^{-5/3}n_0^{-1/3}\; {\rm years} . \end{displaymath} (4)

$V_{\rm 1000}$ denotes the velocity of the pulsar in units of 1000 km s-1. This timescale was calculated in the limit of a Sedov-Taylor SNR, i.e. it is assumed that the pulsar will break through the shell of the remnant, when radiative losses of the SNR are neglible.

We follow van der Swaluw et al. (1998) by calculating the Mach number ${\cal M}_{\rm psr}$ of the pulsar as it propagates through the SNR interior, using the Sedov-Taylor solution (Sedov 1959). Figure 3 shows the Mach number ${\cal M}_{\rm psr}$ as a function of the age of the remnant t, normalised to the crossing time $t_{\rm cr}$. Alternatively Fig. 4 shows the Mach number ${\cal M}_{\rm psr}$ as a function of the position of the pulsar $R_{\rm psr}$, normalised to the position of the SNR blastwave $R_{\rm snr}$.


  \begin{figure} \par {\includegraphics[width=7.5cm,clip]{0700fig3.ps} } \end{figure} Figure 3: The Mach number of the pulsar ${\cal M}_{\rm psr}$, as a function of the SNR age t scaled to the crossing time $t_{\rm cr}$ of the pulsar. The event of bow shock formation ( ${\cal M}_{\rm psr}=1$) occurs at $t=0.5t_{\rm cr}$.
Open with DEXTER

The figures show that the PWN head, containing the active pulsar, is deformed into a bow shock (i.e. when ${\cal M}_{\rm psr}=1$) at half the crossing time when the pulsar is positioned at a radius of 0.677 times the radius of the SNR blastwave. The Mach number will slowly increase after the formation of the bow shock, due to the decrease of the sound speed, as the PWN is approaching the shell of the remnant. When the pulsar breaks through the shell, the Mach number of the pulsar equals ${\cal M}_{\rm psr}={7\over\sqrt{5}}\simeq 3.13$ (van der Swaluw et al. 2003).

A lower limit for the pulsar velocity can be derived, such that the bow shock formation occurs while the SNR is in the Sedov-Taylor stage. We follow van der Swaluw et al. (2003), who already give a lower limit for the pulsar velocity in order for the pulsar to cross the SNR shell in its Sedov-Taylor stage. They use the transition time calculated by Blondin et al. (1998) as the age of the SNR when the transition from the Sedov-Taylor stage to the pressure-driven snowplow stage occurs:

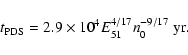\begin{displaymath}t_{\rm PDS} = 2.9 \times 10^4 E_{51}^{4/17}n_0^{-9/17} \; {\rm yr}. \end{displaymath} (5)

Our results show that the bow shock creation occurs at half the crossing time, therefore the requirement $0.5t_{\rm cr}\le t_{\rm PDS}$ yields a lower limit for the pulsar velocity to let the bow shock formation event occur when the SNR is in its Sedov-Taylor stage:

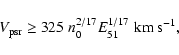\begin{displaymath}V_{\rm psr} \ge 325\; n_0^{2/17} E_{51}^{1/17} \; {\rm km~s^{-1}} , \end{displaymath} (6)

which is a reasonable fraction of the pulsar velocities observed by Hansen & Phinney (1997).


  \begin{figure} \par {\includegraphics[width=7.5cm,clip]{0700fig4.ps} } \end{figure} Figure 4: The Mach number of the pulsar ${\cal M}_{\rm psr}$ as a function of the ratio of the pulsar position $R_{\rm psr}$ and the SNR blastwave $R_{\rm snr}$. The bow shock formation of the SNR. The event of the bow shock formation ( ${\cal M}_{\rm psr}=1$) occurs at $R_{\rm psr}/R_{\rm snr}\simeq 0.677$.
Open with DEXTER

3 Numerical simulations

3.1 Simulation method

We use a second order, properly upwinded hydrodynamics code (described in Downes & Ray 1999) to simulate the dynamics of the interaction between a pulsar wind and a supernova remnant when the pulsar has a high velocity. The hydrodynamics equations are intergrated in cylindrical symmetry, and the boundary conditions are taken as gradient zero everywhere except on the r=0 boundary, where they are set to reflecting.

In these simulations, shocks reach the edge of the grid, and hence some inaccuracy will be introduced by the assumption of gradient zero boundary conditions. We can get a feel for the importance of this inaccuracy by considering the shape of the blastwave close to the boundaries (see Figs. 7 and 8). There will be a deformation of the shock near these boundaries if the boundary conditions are causing a significant error in the results. It can be seen that there is little, if any, such deformation. Therefore we conclude that gradient zero boundary conditions are sufficiently accurate for these simulations.


  \begin{figure} \par\includegraphics[width=11.5cm,clip]{aa0700f5.eps}\end{figure} Figure 5: Logarithmic gray-scale plot of the density distribution at an age $t_{\rm snr} = 1000$ years.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=11.5cm,clip]{aa0700f6.eps}\end{figure} Figure 6: Logarithmic gray-scale plot of the density distribution at an age $t_{\rm snr} = 1 800$ years.
Open with DEXTER

3.2 Initialising the system

The simulations are performed in the rest frame of the pulsar. The pulsar velocity equals $V_{\rm psr} = 1000$ km s-1. An expanding SNR is created by initialising a sphere of radius 0.25 pc, or 21 grid cells, with a high thermal energy and density such that the total energy contained in the sphere is E0=1051 erg, while the ejecta mass is $M_{\rm ej}=3~ M_\odot$. Note that this material also has a velocity of 1000 km s-1 in the negative z direction. Initially, the ambient density and pressure are uniform with a uniform velocity of 1000 km s-1 in the negative z direction. The ambient density is $\rho_0=10^{-24}$ g/cm-3 (corresponding with $n_0\simeq 0.427$), and the pressure is chosen such that the ambient temperature is $T = 1\times 10^5$ K. We use a uniform grid on which the resolution has been taken as $\Delta r =\Delta z = 3.6\times10^{16}$ cm.

A realistic pulsar wind is highly relativistic with an adiabatic heat ratio $\gamma =4/3$. The (shocked) stellar ejecta and ISM material on the other hand are non-relativistic, with $\gamma = 5/3$. The hydrodynamics code we use does not include relativistic hydrodynamics, so we make the approximation of using a value of the adiabatic index $\gamma = 5/3$. Recently Bucciantini et al. (2003) have performed a simulation, using a relativistic hydrodynamics code, for a centered pulsar wind nebula inside a supernova remnant. The same simulation was performed earlier by van der Swaluw et al. (2001) using a non-relativistic hydrodynamics code (with a value for the adiabatic heat ratio $\gamma = 5/3$). The two simulations show a qualitatively similar and quantitatively almost similar behaviour. This confirms the validity of the approximation we make in this paper.

The pulsar wind luminosity has been approximated using a constant value, in order to resolve the pulsar wind termination shock throughout the whole simulation. The results of the simulation will not change qualitatively, because the total energy injected by the pulsar during its stay in the SNR interior $E_{\rm pw}={L_{\rm pw} t_{\rm cr}}\ll E_0$. Therefore this approximation still ensures that the evolution of the PWN is largely determined by the evolution of the whole supernova remnant.


  \begin{figure} \par\includegraphics[width=12cm,clip]{aa0700f7.eps}\end{figure} Figure 7: Logarithmic gray-scale plot of the density distribution at an age $t_{\rm snr} = 3 000$ years.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{aa0700f8.eps}\end{figure} Figure 8: Logarithmic gray-scale plot of the density distribution at an age $t_{\rm snr} = 11~400$ years.
Open with DEXTER

The source of the pulsar wind is modeled as a small sphere of radius 0.175 pc (15 grid cells) into which thermal energy is deposited at a rate of $L_{\rm pw}=10^{38}$ erg/s. Mass is also deposited into this region at a rate chosen such that the pulsar wind terminal velocity is $v_{\infty}=30~000$ km s-1.

3.3 The reverse shock interaction stage

The initial stage of the PWN evolution is the supersonic expansion stage. Figure 5 shows the density profile of the PWN/SNR system during this stage. One can clearly distinguish the four different shocks of the system: the pulsar wind termination shock, the PWN shock, the reverse shock and the forward shock. One clearly observes the off-centered position of the PWN with respect to the twofold shock structure of the SNR, caused by the motion of the pulsar. Furthermore the pulsar wind cavity is roughly spherically symmetric. This results from the high sound speed inside the pulsar wind bubble, which smooths out pressure perturbations rapidly, yielding an almost uniform pressure distribution in the PWN.

Figure 6 shows the density profile of the PWN/SNR system, when the front of the PWN shock has already collided with the reverse shock. At this stage the pulsar position starts to get off-centered with respect to the PWN structure. This is caused by the reverse shock interaction, which raises the presssure inside the disturbed parts of the bubble, which results in pulsar wind material flowing towards the back of the PWN. Furthermore the increase in the pressure inside the front part of the pulsar wind bubble pushes the forward termination shock backwards (towards the pulsar) as well. On the other hand, the downstream pressure at the backward termination shock has not been influenced by the reverse shock interaction yet. Therefore the pulsar wind cavity structure is no longer spherically symmetric, as can be seen in Fig. 6. The total time on which the reverse shock collides with the complete shock structure bounding the pulsar wind bubble equals $\Delta t_{\rm col}\simeq 1200$ years in the simulation, after which the age of the SNR equals $t \simeq 2400$ years. These timescales are in almost complete agreement with the analysis performed in Sect. 2.1 of this paper, which validates the approach made in that section to derive the collision timescale $\Delta t_{\rm col}$.

Figure 7 shows the PWN/SNR system shortly after the passage of the reverse shock. The pulsar is positioned at the head of the PWN, due to the passage of the reverse shock and the high velocity of the pulsar. The PWN structure consists of roughly two parts, a relic PWN and the head of the PWN, as was described in Sect. 2.2 of this paper. After the passage of the reverse shock, the reverse shock interaction stage is continued by the reflected and transmitted shock waves, which propagate through both the pulsar wind bubble and the surrounding ejecta of the SNR. This stage was described in detail by van der Swaluw et al. (2001) for a spherically symmetric PWN/SNR system. We observe a qualitatively similar process, in which the pulsar wind bubble is oscillating. The dynamics are more complicated compared with the simulations of van der Swaluw et al. (2001), due to the asymmetry of the PWN/SNR system caused by the motion of the pulsar. During this stage of the reverse shock interaction, the PWN is oscillating between expansion and compression and the simulations reveal Rayleigh-Taylor and Kelvin-Helmholtz instabilities. These instabilities lead to the mixing of ejecta and pulsar wind material, as was also observed in the simulations performed by Blondin et al. (2001). Therefore at the end of the reverse shock interaction stage, the relic PWN consists of a mixture of pulsar wind material and ejecta. In our simulation the relic PWN will move off the grid, before the bow shock formation occurs around the head of the PWN.

3.4 The formation of the bow shock

At the end of the simulation, as the pulsar approaches the shell of the SNR, the head of the PWN, containing the active pulsar, deforms into a bow shock, due to the supersonic motion of the pulsar. The simulation shows that the bow shock formation event occurs at roughly $t\simeq 0.5 t_{\rm cr}$, when the position of the pulsar $R_{\rm psr}$ with respect to the radius of the blastwave $R_{\rm snr}$equals $R_{\rm psr}/R_{\rm snr}\simeq 0.677$. This clearly demonstrates the validity of the analytical approximation made in Sect. 2.2 of this paper. Figure 8 shows the density profile of the PWN/SNR system after the bow shock formation. The curvature of the SNR shock is small compared with the bow shock structure, which validates the assumptions made by van der Swaluw et al. (2003) to model the break-through event.

4 Observations

After the passage of the reverse shock, the PWN consists of a relic PWN and the head of the PWN, containing the active pulsar. Figures 7 and 8 show the density profiles of the PWN/SNR before and after the formation of the bow shock. For both cases the pulsar is located inside the head of the PWN. The synchrotron maps from PWNe will therefore show a similar morphology, which makes it hard to determine the presence of a bow shock based on the observed PWN/SNR morphology. However, we have demonstrated that the following criteria can be used to determine the presence of a bow shock around the head of the PWN:

We will apply the above two criteria to three SNRs: N157B, G327.1-1.1 and W44. We will argue that the head of the PWNe inside the first two SNRs are not bounded by a bow shock, and therefore these PWNe are in either the reverse shock interaction stage or the subsonic expansion stage. The PWN inside SNR W44 is shown to be the best candidate of a PWN in the bow shock stage.

4.1 The pulsar wind nebula inside N157B

N157B is a young SNR dominated by plerionic emission from the PWN inside this remnant. The age of the remnant is approximated to be 5000 yrs (Wang & Gotthelf 1998) and contains a 16 ms pulsar (Marshall et al. 1998). The velocity of the pulsar is high ( $V_{\rm psr}\simeq 1000$ km s-1), if one assumes that the pulsar was born at the central region of the bright radio emission (Lazendic et al. 2000).

Wang & Gotthelf (1998) argue for a bow shock interpretation of the PWN in N157B: the supersonic motion of the pulsar has deformed the PWN around the pulsar into a bow shock. In this scenario the SNR N157B is a young variant of the SNR CTB80, which is thought to have a PWN bow shock located close to the shell of the remnant (see e.g. Strom 1987; Kulkarni et al. 1988; Migliazzo et al. 2002). It is remarkable though, that the spindown luminosity of the pulsar inside N157B ( $L_0\simeq 4.8\times 10^{38}$ erg/s) is so much higher compared with the spindown luminosity from the pulsar inside CTB80 ( $L_0\simeq 4.0\times 10^{36}$ erg/s). If there is a bow shock around the PWN inside N157B, this implies that an upper limit for the age of the SNR, when the pulsar crosses the shell, is approximately 10 000 years (using the current age of 5000 years and the criterion that bow shock creation occurs at half the crossing time). This is again a remarkable contrast with the current age of CTB80 of 100 000 years, which is close to the crossing time of this SNR. Furthermore from Fig. 2 of Wang et al. (2001) it seems as if the position of the pulsar is more or less centered in the SNR. This is in contrast with what one would expect from the analysis performed in Sect. 2.2 of this paper, which predicts $R_{\rm psr}/R_{\rm snr} \ge 0.677$.

We propose a scenario for SNR N157B in which the contradictions mentioned above disappear. Following the results from Sects. 2 and 3, we suggest that the central bright parts of the radio and X-ray emission inside N157B correspond with the relic PWN, being blown in the initial stage of the PWN, when it was expanding supersonically. The PWN inside N157B has just collided with the reverse shock; this collision and the high velocity of the pulsar has off-centered the pulsar with respect to the PWN structure as was discussed in the Sects. 2 and 3.3 of this paper. Therefore the head of the PWN is not bounded by a bow shock: the PWN is in the aftermath of the reverse shock interaction stage or in the beginning of the subsonic expansion stage.

4.2 The pulsar wind nebula inside G327.1-1.1

Another example of a young SNR, containing a PWN with the position of the pulsar off-centered with respect to its PWN is G327.1-1.1. No pulsar has been detected inside this remnant so far. Sun et al. (1999) presented a radio contour map using MOST data overlaid with X-ray data from ROSAT. The X-ray emission is centered around a finger of radio emission sticking out of a central radio bright region, indicating the presence of a pulsar wind. Following Sun et al. (1999) the SNR can be modelled in X-rays by the following set of parameters: E51=0.23, n0=0.10, $V_{\rm psr}=600$ km s-1 and an age of $t=1.1\times 10^4$. Using Eq. (4) to calculate $t_{\rm cr}$ we get a value of $4.3\times 10^4$ years. The age of the system therefore is less than half the crossing time, implying the absence of a bow shock. Furthermore the displacement of the PWN finger (i.e. the head of the PWN), containing the pulsar, does not satisfy the other criterion for the presence of a bow shock, i.e. $R_{\rm psr}/R_{\rm snr} \ge 0.677$. This criterion is less restrictive, since one might introduce an angle between the pulsar velocity and the observer such that the ratio $R_{\rm psr}/R_{\rm snr} \ge 0.677$. Notice however that this will not influence the age of the remnant!

Therefore we propose a scenario for G327.1-1.1 in which there is no bow shock around the head of the PWN: the pulsar has been positioned at the head of the PWN due to the high velocity pulsar and the passage of the reverse shock. The central bright part of the remnant corresponds with the relic PWN. The finger of the PWN corresponds with the head of the PWN, which contains the active pulsar. Because of the larger value of the ratio $R_{\rm psr}/R_{\rm snr}$ and the larger age with respect to the PWN inside SNR N157B we favour the scenario where the PWN is in its subsonic expansion stage.

4.3 The pulsar wind nebula inside W44

The SNR W44 is an older remnant than the previous two SNRs discussed. Furthermore only a small fraction of the radio emission from this remnant is characterised by plerionic emission (Frail et al. 1996). Taking the characteristic age of the pulsar, 20 000 years (Wolszcan et al. 1991), as the age of this remnant yields an upper limit of $t_{\rm cr}\simeq 40~000$ years for the crossing time of this remnant. This age is much closer to the age of the SNR CTB80. The displacement of the pulsar position only marginally violates the condition for bow shock formation, i.e. $R_{\rm psr}/R_{\rm snr} \ge 0.677$. We therefore conclude that the PWN observed in the SNR W44 corresponds with the head of the PWN, which has been deformed into a bow shock.

5 Conclusions

We have considered the case of a PWN interacting with a SNR, for which the associated pulsar is moving at a high velocity through the interior of its SNR. The model we discussed made use of a hydrodynamics code. One could distinguish four different stages in the simulation: the supersonic expansion stage, the reverse shock interaction stage, the subsonic expansion stage and the bow shock stage. Below we summarise the most important results from our model:

From our model it follows that a SNR containing a pulsar at the head of its PWN does not imply the presence of a bow shock, bounding the head feature of the PWN. We discussed three SNRs and interpreted their morphology, using the results from our model. For the SNRs N157B and G327.1-1.1 we argued that they contain PWNe that do not have a bow shock. The PWN inside the SNR W44 seems to be a good candidate for having a bow shock around the head of its PWN.

Acknowledgements
This work was part-funded by the CosmoGrid project, funded under the Programme for Research in Third Level Institutions (PRTLI) administered by the Irish Higher Education Authority under the National Development Plan and with partial support from the European Regional Development Fund.

References


Copyright ESO 2004