A&A 420, 1009-1023 (2004)
DOI: 10.1051/0004-6361:20034546
D. Stamatellos 1 - A. P. Whitworth 1 - P. André 2 - D. Ward-Thompson 1
1 - Department of Physics & Astronomy, Cardiff University,
PO Box 913, 5 The Parade, Cardiff CF24 3YB, Wales, UK
2 -
CEA, DSM, DAPNIA, Service d' Astrophysique, C.E. Saclay,
91191 Gif-sur-Yvette Cedex, France
Received 21 October 2003 / Accepted 8 March 2004
Abstract
We present 2D Monte Carlo radiative transfer simulations of
prestellar cores. We consider two types of asymmetry: disk-like asymmetry, in which the core is denser towards the
equatorial plane than towards the poles; and axial asymmetry,
in which the core is denser towards the south pole than the north
pole. In both cases the degree of asymmetry is characterized by
the ratio e between the maximum optical depth from the centre
of the core to its surface and the minimum optical depth from the
centre of the core to its surface. We limit our treatment here
to mild asymmetries with e = 1.5 and 2.5 . We consider both
cores which are exposed directly to the interstellar radiation
field and cores which are embedded inside molecular clouds.
The SED of a core is essentially independent
of the viewing angle, as long as the core is optically thin. However,
the isophotal maps depend strongly on the viewing angle. Maps at
wavelengths longer than the peak of the SED (e.g. 850 ![]() m)
essentially trace the column-density. This is because at long
wavelengths the emissivity is only weakly dependent on temperature,
and the range of temperature in a core is small (typically
m)
essentially trace the column-density. This is because at long
wavelengths the emissivity is only weakly dependent on temperature,
and the range of temperature in a core is small (typically
![]() ). Thus, for instance, cores with
disk-like asymmetry appear elongated when mapped at 850
). Thus, for instance, cores with
disk-like asymmetry appear elongated when mapped at 850
![]() m from close to the equatorial plane. However, at
wavelengths near the peak of the SED (e.g. 200
m from close to the equatorial plane. However, at
wavelengths near the peak of the SED (e.g. 200 ![]() m), the
emissivity is more strongly dependent on the temperature, and
therefore, at particular viewing angles, there are
characteristic features which reflect a more complicated
convolution of the density and temperature fields within
the core.
m), the
emissivity is more strongly dependent on the temperature, and
therefore, at particular viewing angles, there are
characteristic features which reflect a more complicated
convolution of the density and temperature fields within
the core.
These characteristic features are on scales 1/5 to
1/3 of the overall core size, and so high resolution observations are
needed to observe them. They are also weaker if the core is embedded in a
molecular cloud (because the range of temperature within the core
is then smaller), and so high sensitivity is needed to detect them.
Herschel, to be launched in 2007, will in principle provide
the necessary resolution and sensitivity at 170 to 250 ![]() m.
m.
Key words: stars: formation - ISM: clouds - ISM: structure - methods: numerical - radiative transfer
Prestellar cores are condensations in molecular clouds that are
either on the verge of collapse or already collapsing (e.g. Myers
& Benson 1983; Ward-Thompson et al. 2002). They represent
the initial stage of star formation and their study is important
because theoretical models of protostellar collapse suggest that the
outcome is very sensitive to
the initial conditions. Prestellar cores have been observed both in
isolation and in protoclusters. Isolated prestellar cores (e.g.
L1544, L43 and L63; Ward-Thompson et al. 1999) have extents
![]()
![]() AU and masses
AU and masses
![]() (see also André et al. 2000). On the other hand, prestellar cores in protoclusters
(e.g. in
(see also André et al. 2000). On the other hand, prestellar cores in protoclusters
(e.g. in ![]() Oph and NGC 2068/2071) are generally smaller, with
extents
Oph and NGC 2068/2071) are generally smaller, with
extents ![]()
![]() AU and masses
AU and masses ![]()
![]() (Motte et al. 1998, 2001).
(Motte et al. 1998, 2001).
Many authors have modelled prestellar cores with Bonnor-Ebert (BE) spheres, i.e. equilibrium isothermal spheres in which self-gravity is balanced by gas pressure (Ebert 1955; Bonnor 1956). For example, Barnard 68 has been modelled in this way by Alves et al. (2001).
However, it is evident from 850 ![]() m continuum maps of
prestellar cores, which essentially trace the column-density
through a core, that prestellar cores are not usually
spherically symmetric (e.g. Motte et al. 1998; Ward-Thompson
et al. 1999; Kirk et al. 2004). Indeed, statistical analyses
of the projected shapes of a large sample of cores (Jijina
et al. 1999) suggest that prestellar cores do not
even have spheroidal symmetry and are better represented by
triaxial ellipsoids (Jones et al. 2001; Goodwin et al. 2002).
m continuum maps of
prestellar cores, which essentially trace the column-density
through a core, that prestellar cores are not usually
spherically symmetric (e.g. Motte et al. 1998; Ward-Thompson
et al. 1999; Kirk et al. 2004). Indeed, statistical analyses
of the projected shapes of a large sample of cores (Jijina
et al. 1999) suggest that prestellar cores do not
even have spheroidal symmetry and are better represented by
triaxial ellipsoids (Jones et al. 2001; Goodwin et al. 2002).
This is not surprising, given the highly turbulent nature of star-forming molecular clouds, and the short time-scale on which star formation occurs (e.g. Elmegreen 2000). Normally, prestellar cores are formed - and then either collapse or disperse - so rapidly that they do not have time to relax towards equilibrium structures. Even in more quiescent environments where cores can evolve quasi-statically, the combination of magnetic and rotational stresses is likely to produce significant departures from spherical symmetry.
For instance, SPH simulations of isothermal, turbulent, molecular clouds by Ballesteros-Paredes et al. (2004) show (a) that most of the cores that form are transient and non-spherical; and (b) that, despite this fact, the column density can, more often than not, be adequately fitted with the Bonnor-Ebert profile, although the parameters of the fit depend on the observer's viewing angle. Likewise, the FD simulations of magnetic, isothermal, turbulent, molecular clouds reported by Gammie et al. (2003) produce transient, triaxial cores.
Similarly, evolutionary models of individual prestellar cores predict the formation of flattened (oblate spheroidal) structures, either due to rotation (e.g. Matsumoto et al. 1997), or due to flattening along the lines of a bipolar magnetic field (e.g. Ciolek & Mouschovias 1994). Other models invoke a toroidal magnetic field to create prolate equilibrium cores (e.g. Fiege & Pudritz 2000). Triaxial structures can be generated with a suitable combination of rotation and magnetic field.
It is therefore important to investigate, by means of radiative transfer modelling, how the intrinsic asymmetries inherent in the formation and evolution of a core might translate into observable asymmetries on continuum maps of cores. Previous continuum radiative transfer modelling of prestellar cores has examined non-embedded BE spheres (Evans et al. 2001; Young et al. 2003) and embedded BE spheres (Stamatellos & Whitworth 2003a), using 1D (spherically-symmetric) codes. Zucconi et al. (2001) have used an approximate, semi-analytic method to model non-embedded, magnetically flattened prestellar cores, in 2D. We have recently developed a Monte Carlo code for modelling continuum radiative transfer in arbitrary geometry, and with arbitrary accuracy. Preliminary results have been presented in Stamatellos & Whitworth (2003b,c).
In this paper we develop continuum radiative transfer
models of non-spherical cores. Since these models are
intended to be exploratory, rather than definitive, we consider
here only 2D models (i.e. we impose azimuthal symmetry so that
in spherical polar co-ordinates
![]() there is no
dependence on
there is no
dependence on ![]() ).
).
Since star formation is a chaotic process, it is not sensible to appeal to numerical simulations for the detailed density field in a prestellar core. From both observations (e.g. Kirk et al. 2004) and simulations (e.g. Goodwin et al. 2004), it is clear that each core has a unique distribution of gas in its outer envelope, and a unique radiation field incident on its boundary. Even if existing simulations are a good representation of the real dynamics of star formation, they are not presently able to reproduce particular sources, and therefore they can only be compared realistically with observations in a statistical sense.
We will be presenting SEDs and isophotal maps for prestellar cores formed in SPH simulations of star formation in turbulent molecular clouds in a subsequent paper (Stamatellos et al., in preparation). However, for interpreting observations of individual cores, it is more appropriate to generate SEDs and isophotal maps using simply parametrized models which capture generically the different features we might hope to detect.
In this regard, we have been guided by the
observations, which indicate that prestellar cores have
approximately uniform density in their central regions, and
the density then falls off in the envelope. If the density
in the envelope is fitted with a power law,
![]() ,
then
,
then
![]() .
Here
.
Here
![]() is characteristic of more extended prestellar
cores in dispersed star formation regions (e.g. L1544,
L63 and L43), whereas
is characteristic of more extended prestellar
cores in dispersed star formation regions (e.g. L1544,
L63 and L43), whereas
![]() is characteristic of more
compact cores in protoclusters (e.g.
is characteristic of more
compact cores in protoclusters (e.g. ![]() Oph and NGC 2068/2071).
Oph and NGC 2068/2071).
These features are conveniently represented by a Plummer-like
density profile (Plummer 1915),
![\begin{displaymath}n(r) = n_0~\frac{1}{ \left[ 1 + \left( \frac{r}{r_0}
\right)^2 \right]^{\eta/2} },
\end{displaymath}](/articles/aa/full/2004/24/aa0546/img39.gif) |
(1) |
The Plummer-like density profile is ad hoc, but given the transient, non-hydrostatic nature of prestellar cores, and the coarseness of the observational constraints, this is unavoidable. It has the advantage of being simple, with only three free parameters. Uniquely amongst analytic models, it predicts lifetimes, accretion rates, collapse velocity fields, SEDs and isophotal maps which agree well with observation (Whitworth & Ward-Thompson 2001; Young et al. 2003). It also reproduces approximately the BE density profile, and the density profiles predicted by the ambipolar diffusion models of Ciolek & Mouschovias (1994) and Ciolek & Basu (2000). Tafalla et al. (2004) use a similar density profile to model the starless cores L1498 and L1517B in Taurus-Auriga.
Furthermore, the Plummer-like profile
can be modified easily to include azimuthally
symmetric departures from spherical symmetry. We treat two
types of asymmetry. In the first type (disk-like asymmetry),
we construct flattened cores, using density profiles of the form
![\begin{displaymath}n(r,\theta) = n_0~\frac{1 + A \left( \frac{r}{r_0} \right)^2 ...
...+ \left( \frac{r}{r_0} \right)^2
\right]^{(\eta+2)/2} } \cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0546/img40.gif) |
(2) |
In the second type (axial asymmetry), we construct cores which
are denser towards the south pole (
![]() )
than the north pole (
)
than the north pole (
![]() ), using density
profiles of the form
), using density
profiles of the form
![\begin{displaymath}n(r,\theta) = n_0~\frac{1 + A \left( \frac{r}{r_0} \right)^2 ...
...+ \left(
\frac{r}{r_0} \right)^2 \right]^{(\eta+2)/2} } \cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0546/img42.gif) |
(3) |
In all models the core has a spherical boundary at radius
![]() .
.
For the purpose of this paper, and in order
to isolate a manageable parameter space, we fix
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
These are
typical values for isolated cores. We can then explore the
effect of varying A and p, or equivalently e and p.
.
These are
typical values for isolated cores. We can then explore the
effect of varying A and p, or equivalently e and p.
In Sect. 2, we outline the basic principles underlying our Monte Carlo radiative transfer code. In Sect. 3, we present results obtained for cores having disk-like asymmetry; we treat both non-embedded cores and cores embedded in molecular clouds. In Sect. 4, we present results for cores having axial asymmetry. In Sect. 5, we summarize our results.
![\begin{figure}
{\includegraphics[width=7.3cm,clip]{0546fig58.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg48.gif) |
Figure 1:
L-packet injection into the core: the packet is injected
from a random point ( |
| Open with DEXTER | |
Our method (Stamatellos & Whitworth 2003a) is similar to that developed by Wolf et al. (1999) and Bjorkman & Wood (2001), and is based on the fundamental principle of Monte Carlo methods, according to which we can sample a physical quantity from a probability distribution using random numbers. We represent the radiation field of a source (star or background radiation) by a large number of monochromatic luminosity packets (L-packets). These L-packets are injected into the system and interact stochastically with it. If an L-packet is absorbed its energy is added to the local cell and raises the local temperature. To ensure radiative equilibrium the L-packet is re-emitted immediately with a new frequency chosen from the difference between the local cell emissivity before and after the absorption of the packet (Bjorkman & Wood 2001). This method conserves energy exactly, accounts for the diffuse radiation field, and its 3-dimensional nature makes it attractive for application to a variety of systems. The code ( PHAETHON) has been thoroughly tested using the thermodynamic equilibrium test (Stamatellos & Whitworth 2003a), and also against the benchmark calculations defined by Ivezic et al. (1997) and by Bjorkman & Wood (2001).
Table 1: Model parameters for cores with disk-like asymmetry.
![\begin{figure}
\par {
\includegraphics[angle=-90,width=5.75cm,clip]{0546fig1.ps}...
...,clip]{0546fig4.ps} }
\vspace{-3cm}\hspace{1cm}{d}\vspace{+3cm}
\par\end{figure}](/articles/aa/full/2004/24/aa0546/Timg55.gif) |
Figure 2:
Density distribution on the x=0 plane a) for a flattened
asymmetric core with equatorial-to-polar optical depth ratio e=1.5
and p=4 (model 1.1), b) for a more flattened asymmetric core, with
e=2.5 and p=4 (model 1.2), c) for a core with e=1.5 and p=1
(model 1.3), and d) for a more flattened core, with e=2.5 and p=1
(model 1.4). We plot iso-density contours every
|
| Open with DEXTER | |
![\begin{figure}
{
\includegraphics[angle=-90,width=5.7cm]{0546fig5.ps} }
\vspace{...
....7cm,clip]{0546fig8.ps} }
\vspace{-3cm}\hspace{1cm}{d}\vspace{+3cm}
\end{figure}](/articles/aa/full/2004/24/aa0546/Timg56.gif) |
Figure 3: Temperature distribution on the x=0 plane, for the models presented in Fig. 2. We plot iso-temperature contours from 8 to 18 K, every 2 K. |
| Open with DEXTER | |
The code used here is adapted for the study of cores having azimuthal symmetry. The core itself is divided into a number of cells by spherical and conical surfaces. The spherical surfaces are evenly spaced in radius, and there are typically 50-100 of them. The conical surfaces are evenly spaced in polar angle, and there are typically 10-20 of them. Hence the core is divided into 500-2000 cells. The specific number of cells used is chosen so that the density and temperature differences between adjacent cells are small.
The L-packets are injected from the outside of the core with injection
point and injection direction chosen to mimic an isotropic radiation
field incident on the core (see Fig. 1). We first
generate the L-packet injection point on the surface of the core using
random numbers
![]() ,
,
| r | = | (4) | |
| = | (5) | ||
| = | (6) |
| |
= | (7) | |
| = | (8) |
We further assume that the radiation field incident on the core is the Black (1994) interstellar radiation field (hereafter BISRF), which consists of radiation from giant stars and dwarfs, thermal emission from dust grains, mid-infrared emission from transiently heated small grains, and the cosmic background radiation. This is a good approximation to the radiation field in the solar neighbourhood but it is not always a good choice when studying prestellar cores, since in many cases the immediate core environment plays an important role in determining the radiation field incident on the core. In this work, we simulate the effect of the immediate core environment by embedding the core in a molecular cloud which modulates the radiation field incident on the core. Another option is to estimate the effective radiation field incident on an embedded core by observing it directly (André et al. 2003).
The dust composition (and therefore the dust opacity) in prestellar cores
is uncertain, but in such cold and dense conditions, dust particles are
expected to coagulate and accrete ice. As in our previous study of
prestellar cores (see Stamatellos & Whitworth 2003a), we use the
Ossenkopf & Henning (1994) opacities for a standard MRN interstellar
grain mixture (53% silicate and 47% graphite) that has coagulated and
accreted thin ice mantles over a period of 105 yr at a density of
![]() .
.
The density profile in model cores with disk-like asymmetry is
given by
![\begin{displaymath}n(r,\theta) = 10^6~{\rm cm}^{-3}\;~\frac{1 + A \left( \frac{r...
... +
\left( \frac{r}{2000~{\rm AU}} \right)^2 \right]^2 } \cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0546/img69.gif) |
(9) |
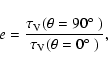 |
(10) |
In non-embedded cores, the dust temperature drops from around 17 K
at the edge of the core to 7 K at the centre of the core, as previous
studies have already indicated (Zucconi et al. 2001; Evans et al. 2001;
Stamatellos & Whitworth 2003a). We also find that the dust temperature
inside cores with disk-like asymmetry is ![]() dependent (see
Fig. 3), similar to the results of Zucconi et al.
(2001). As expected, the equator of the core is colder than the poles.
The difference in temperature between two points having the same distance
r from the centre of the core but with different polar angles
dependent (see
Fig. 3), similar to the results of Zucconi et al.
(2001). As expected, the equator of the core is colder than the poles.
The difference in temperature between two points having the same distance
r from the centre of the core but with different polar angles ![]() ,
is larger for the more asymmetric cores (i.e. those with larger e
and/or p; Fig. 3). For example, at half
the radius of the core (104 AU) the temperature difference
between the point at
,
is larger for the more asymmetric cores (i.e. those with larger e
and/or p; Fig. 3). For example, at half
the radius of the core (104 AU) the temperature difference
between the point at
![]() (core pole) and the point at
(core pole) and the point at
![]() (core equator), is 5-6 K for the p=4 models
(Figs. 3a,b) but only
(core equator), is 5-6 K for the p=4 models
(Figs. 3a,b) but only ![]() 2 K
for the p=1 models (Figs. 3c,d).
This temperature difference will affect the appearance of the core at
wavelengths shorter than or near the core peak emission, where the Planck
function is strongly (exponentially) dependent on the temperature.
2 K
for the p=1 models (Figs. 3c,d).
This temperature difference will affect the appearance of the core at
wavelengths shorter than or near the core peak emission, where the Planck
function is strongly (exponentially) dependent on the temperature.
![\begin{figure}
\par {\includegraphics[width=6.5cm,clip]{0546fig9.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg72.gif) |
Figure 4: SED for the core models in Figs. 2 and 3; model 1.1 (e=1.5, p=4; short-dashed line), model 1.2 (e=2.5, p=4; solid line), model 1.3 (e=1.5, p=1; dash-dot line) and model 1.4 (e=2.5, p=1; long-dashed line). The SED of each core is independent of the observer's viewing angle. The dotted line on the graph corresponds to the incident/background SED. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=6.5cm,clip]{0546fig10.ps} }
\end{figure}](/articles/aa/full/2004/24/aa0546/Timg75.gif) |
Figure 5:
A perpendicular cut through the centre of the core images
presented in Fig. 7 for model 1.2 at 200
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=5.8cm,clip]{0546fig11.ps} ...
...mm}
{\includegraphics[angle=-90,width=5.8cm,clip]{0546fig14.ps} }
\end{figure}](/articles/aa/full/2004/24/aa0546/Timg76.gif) |
Figure 6:
Isophotal maps at 200
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=5.8cm,clip]{0546fig15.ps} ...
...\par {\includegraphics[angle=-90,width=5.8cm,clip]{0546fig18.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg77.gif) |
Figure 7: Same as Fig. 6, but for a more flattened core, with equatorial-to-polar optical depth ratio e=2.5 and p=4 (model 1.2). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=5.9cm,clip]{0546fig19.ps} ...
...par {\includegraphics[angle=-90,width=5.9cm,clip]{0546fig22.ps} }
\end{figure}](/articles/aa/full/2004/24/aa0546/Timg78.gif) |
Figure 8: Same as Fig. 6, but for a core with equatorial-to-polar optical depth ratio e=1.5 and p=1 (model 1.3). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=6.cm,clip]{0546fig23.ps} }...
...{2mm}
{\includegraphics[angle=-90,width=6.cm,clip]{0546fig26.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg79.gif) |
Figure 9: Same as Fig. 6, but for a core with equatorial-to-polar optical depth ratio e=2.5 and p=1 (model 1.4). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=6.1cm,clip]{0546fig27.ps} ...
...3mm}
{\includegraphics[angle=-90,width=6.1cm,clip]{0546fig30.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg80.gif) |
Figure 10:
Isophotal maps at 850
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=6.1cm,clip]{0546fig31.ps} ...
...\par {\includegraphics[angle=-90,width=6.1cm,clip]{0546fig34.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg81.gif) |
Figure 11: Same as Fig. 10, but for a more flattened core, with equatorial-to-polar optical depth ratio e=2.5 and p=4 (model 1.2). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=6.1cm,clip]{0546fig35.ps} ...
...2mm}
{\includegraphics[angle=-90,width=6.1cm,clip]{0546fig38.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg82.gif) |
Figure 12: Same as Fig. 10, but for a core with equatorial-to-polar optical depth ratio e=1.5 and p=1 (model 1.3). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=6.1cm,clip]{0546fig39.ps} ...
...2mm}
{\includegraphics[angle=-90,width=6.1cm,clip]{0546fig42.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg83.gif) |
Figure 13: Same as Fig. 10, but for a core with equatorial-to-polar optical depth ratio e=2.5 and p=1 (model 1.4). |
| Open with DEXTER | |
The SED (Fig. 4) of a specific core, for the
model parameters we examine, is the same at any viewing angle, because
the core is optically thin to the radiation it emits (FIR and longer
wavelengths). Thus, it is not possible to distinguish between flattened
and spherical cores, using SED observations, unless the core is
extremely flattened, so that it is optically thick on the equator at
FIR and longer wavelengths. Using the Ossenkopf & Henning (1994)
opacities, the minimum optical depth through the model core at
![]() is
is
![]() ,
so we would need to treat much larger
values of e (
,
so we would need to treat much larger
values of e (![]() 25) in order for the SED to be
significantly dependent on viewing angle.
25) in order for the SED to be
significantly dependent on viewing angle.
In contrast, the isophotal maps of a core do depend on the observer's
viewing angle. Additionally, they depend on the wavelength of observation.
Our code calculates images at any wavelength, and therefore provides a
useful tool for direct comparison with observations, e.g. at mid-infrared
(ISO/ISOCAM), far-infrared (ISO/ISOPHOT) and submm/mm (SCUBA, IRAM)
wavelengths. We distinguish two wavelength regions on which we focus:
(i) wavelengths near the peak of the core emission (150-250
![]() ;
we choose 200
;
we choose 200
![]() as a representative wavelength), and (ii)
wavelengths much longer than the peak (submm amd mm region; we choose
850
as a representative wavelength), and (ii)
wavelengths much longer than the peak (submm amd mm region; we choose
850
![]() as a representative wavelength). In each of the above
regions the isophotal maps have similar general characteristics.
as a representative wavelength). In each of the above
regions the isophotal maps have similar general characteristics.
At 200
![]() the core appearance depends both on its temperature and its
column density in the observer's direction. It is seen in
Figs. 6-9, that cores with disk-like
asymmetry appear spherical when viewed pole-on and flattened when viewed edge-on.
The outer parts of a core can be more or less luminous than the central
parts, depending on the core temperature and the observer's viewing
angle. For example, at close to pole-on viewing angles the outer parts
of the core are more luminous than the inner parts of the core (limb
brightening; e.g. Figs. 6-9,
the core appearance depends both on its temperature and its
column density in the observer's direction. It is seen in
Figs. 6-9, that cores with disk-like
asymmetry appear spherical when viewed pole-on and flattened when viewed edge-on.
The outer parts of a core can be more or less luminous than the central
parts, depending on the core temperature and the observer's viewing
angle. For example, at close to pole-on viewing angles the outer parts
of the core are more luminous than the inner parts of the core (limb
brightening; e.g. Figs. 6-9,
![]()
![]() ). This happens because the temperature is higher in the
outer parts and this more than compensates for the lower column density
(since at wavelengths near the peak of the core emission and shorter,
the Planck intensity
). This happens because the temperature is higher in the
outer parts and this more than compensates for the lower column density
(since at wavelengths near the peak of the core emission and shorter,
the Planck intensity ![]() depends on temperature as
depends on temperature as
![]() ,
,
![]() ). At other viewing angles the
appearance of the core is determined by a combination of temperature and
column density effects (Figs. 6-9,
). At other viewing angles the
appearance of the core is determined by a combination of temperature and
column density effects (Figs. 6-9,
![]()
![]() ,
60
,
60![]() ,
90
,
90![]() ). This interplay between core temperature
and column density along the line of sight results in characteristic
features on the images of the cores. Such features include (i) the two
intensity minima at almost symmetric positions relative to the centre of
the core, on the images at 30
). This interplay between core temperature
and column density along the line of sight results in characteristic
features on the images of the cores. Such features include (i) the two
intensity minima at almost symmetric positions relative to the centre of
the core, on the images at 30![]() (Figs. 7-9), and (ii) the two
intensity maxima, again at symmetric positions relative to the centre
of the core, on the images at 90
(Figs. 7-9), and (ii) the two
intensity maxima, again at symmetric positions relative to the centre
of the core, on the images at 90![]() (Figs. 6 and 7). (It is also
worth mentioning that although the characteristic features appear in
symmetric positions relative to both axes of density-symmetry, we
should expect deviations from symmetry to arise if the radiation field
incident on the core is not isotropic.)
(Figs. 6 and 7). (It is also
worth mentioning that although the characteristic features appear in
symmetric positions relative to both axes of density-symmetry, we
should expect deviations from symmetry to arise if the radiation field
incident on the core is not isotropic.)
We conclude that isophotal maps at 200
![]() contain detailed
information, and sensitive, high resolution observations at
200
contain detailed
information, and sensitive, high resolution observations at
200
![]() ,
could be helpful in constraining the core density
and temperature structure and the orientation of the core with
respect to the observer. In Fig. 5, we present
a perpendicular cut through the centre of the core images shown in
Fig. 7. We also plot the beam size of the
ISOPHOT C-200 camera (90
,
could be helpful in constraining the core density
and temperature structure and the orientation of the core with
respect to the observer. In Fig. 5, we present
a perpendicular cut through the centre of the core images shown in
Fig. 7. We also plot the beam size of the
ISOPHOT C-200 camera (90
![]() ,
or 9000 AU for a core at 100 pc)
and the beam size of the upcoming (2007) Herschel (13
,
or 9000 AU for a core at 100 pc)
and the beam size of the upcoming (2007) Herschel (13
![]() or 1300 AU for the
or 1300 AU for the
![]() band of PACS; 17
band of PACS; 17
![]() or 1700 AU
for the
or 1700 AU
for the
![]() band of SPIRE). ISOPHOT's resolution is probably
not good enough to detect the features mentioned above. Indeed, a
search in the Kirk et al. (2004) sample of ISO/ISOPHOT observations
(also see Ward-Thompson et al. 2002) does not reveal any cores with
such distinctive features. However, Herschel should, in
principle, be able to detect such features in the future.
band of SPIRE). ISOPHOT's resolution is probably
not good enough to detect the features mentioned above. Indeed, a
search in the Kirk et al. (2004) sample of ISO/ISOPHOT observations
(also see Ward-Thompson et al. 2002) does not reveal any cores with
such distinctive features. However, Herschel should, in
principle, be able to detect such features in the future.
In the second wavelength region (submm and mm wavelengths) the core
emission is mainly regulated by the column density (e.g. at 850
![]() ,
Figs. 10-13). Thus, the
intensity is larger at the centre, where the column density is larger.
For the same reason the core appears flattened when the observer looks
at it from any direction other than pole-on. It is also evident that the
peak intensity of the core is much larger when the core is viewed edge-on.
Therefore, flattened cores are more prominent when viewed edge-on. This
introduces a possible observational selection effect which should be
taken into account when studying the shape statistics of prestellar
cores. Low-mass flattened cores are more likely to be detected if they
are edge-on, than if they are face-on. This is true for optically thin
mm and submm continuum observations, and also for optically thin molecular
line observations. For example, when comparing the projected shapes of
condensations from hydrodynamic simulations with the observed shapes
using solely optically thin continuum or optically thin molecular line
observations, one should expect a lower number of observed near-spherical
cores than indicated by the simulations. This may be the reason for the
small excess of high axis ratio cores in the simulations by Gammie et al.
(2003) (see their Fig. 9).
,
Figs. 10-13). Thus, the
intensity is larger at the centre, where the column density is larger.
For the same reason the core appears flattened when the observer looks
at it from any direction other than pole-on. It is also evident that the
peak intensity of the core is much larger when the core is viewed edge-on.
Therefore, flattened cores are more prominent when viewed edge-on. This
introduces a possible observational selection effect which should be
taken into account when studying the shape statistics of prestellar
cores. Low-mass flattened cores are more likely to be detected if they
are edge-on, than if they are face-on. This is true for optically thin
mm and submm continuum observations, and also for optically thin molecular
line observations. For example, when comparing the projected shapes of
condensations from hydrodynamic simulations with the observed shapes
using solely optically thin continuum or optically thin molecular line
observations, one should expect a lower number of observed near-spherical
cores than indicated by the simulations. This may be the reason for the
small excess of high axis ratio cores in the simulations by Gammie et al.
(2003) (see their Fig. 9).
In the previous section, we studied cores that are directly exposed to
the interstellar radiation field (as approximated by the BISRF). However,
cores are generally embedded in molecular clouds, with visual optical
depths ranging from 2-10 (e.g. in Taurus) up to 40 (e.g. in ![]() Ophiuchi). The ambient cloud absorbs the energetic UV and optical
photons and re-emits them in the FIR and submm (because the ambient cloud
is generally cold,
Ophiuchi). The ambient cloud absorbs the energetic UV and optical
photons and re-emits them in the FIR and submm (because the ambient cloud
is generally cold,
![]() K). Therefore, the radiation
incident on a core that is embedded in a cloud is reduced in the UV and
optical, and enhanced in the FIR and submm (Mathis et al. 1983). Previous
radiative transfer calculations of spherical cores embedded at the centre
of an ambient cloud (Stamatellos & Whitworth 2003a), have shown that
embedded cores are colder (T<12 K) and that the temperature gradients
inside these cores are smaller than in non-embedded cores. André et al.
(2003) also found that the temperatures inside embedded cores are lower
than in non-embedded cores (assuming that they are heated by the same
ISRF), using a different approach, in which they estimated the effective
radiation field incident on an embedded core from observations.
K). Therefore, the radiation
incident on a core that is embedded in a cloud is reduced in the UV and
optical, and enhanced in the FIR and submm (Mathis et al. 1983). Previous
radiative transfer calculations of spherical cores embedded at the centre
of an ambient cloud (Stamatellos & Whitworth 2003a), have shown that
embedded cores are colder (T<12 K) and that the temperature gradients
inside these cores are smaller than in non-embedded cores. André et al.
(2003) also found that the temperatures inside embedded cores are lower
than in non-embedded cores (assuming that they are heated by the same
ISRF), using a different approach, in which they estimated the effective
radiation field incident on an embedded core from observations.
![\begin{figure}
\par {
\includegraphics[width=6.3cm,clip]{0546fig43.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg96.gif) |
Figure 14:
The effect of the parent cloud on cores. Temperature profiles
of a non-embedded core (model 1.2; dashed lines), and of a core at the
centre of an ambient cloud with visual extinction
|
| Open with DEXTER | |
Here, we examine the more general case of embedded flattened cores. We
model a core with the same set of parameters as model 1.2 (p=4, e=2.5)
but embedded in a uniform density ambient cloud with different visual
extinctions ![]() (
(
![]() ). The ambient
cloud is illuminated by the BISRF. In Fig. 14,
we present the temperature profiles at
). The ambient
cloud is illuminated by the BISRF. In Fig. 14,
we present the temperature profiles at
![]() (core pole;
upper curves) and
(core pole;
upper curves) and
![]() (core equator; lower curves), (i)
for a non-embedded core (dashed lines; model 1.2), (ii) for the same
core embedded at the centre of an ambient cloud with
(core equator; lower curves), (i)
for a non-embedded core (dashed lines; model 1.2), (ii) for the same
core embedded at the centre of an ambient cloud with
![]() (dotted lines), and (iii) for the same core embedded at the centre of
an ambient cloud with
(dotted lines), and (iii) for the same core embedded at the centre of
an ambient cloud with
![]() (full lines).
(full lines).
![\begin{figure}
\par {\includegraphics[width=6cm,angle=-90]{0546fig44.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg99.gif) |
Figure 15:
Temperature distribution on the x=0 plane, for the same model presented in Figs. 2b and 3b
(e=2.5, p=4, model 1.2), but embedded in the centre of an ambient
molecular cloud with visual extinction
|
| Open with DEXTER | |
![\begin{figure}
\par {
\includegraphics[width=6.5cm,clip]{0546fig45.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg100.gif) |
Figure 16:
Same as Fig. 5, i.e. model 1.2, but for a
core embedded in a uniform molecular ambient cloud with visual extinction
|
| Open with DEXTER | |
Relative to an non-embedded core, a core embedded in an ambient cloud
with
![]() is colder and has lower temperature gradient (cf.
Figs. 3b and 15). The isophotal maps are similar to those of the
non-embedded core (Figs. 7 and 11), but the characteristic features
are less pronounced. This is because the temperature gradient inside
the core is smaller when the core is embedded (see
Fig. 14). For example, at half the radius of
the core (r = 104 AU) the temperature difference between the
point at
is colder and has lower temperature gradient (cf.
Figs. 3b and 15). The isophotal maps are similar to those of the
non-embedded core (Figs. 7 and 11), but the characteristic features
are less pronounced. This is because the temperature gradient inside
the core is smaller when the core is embedded (see
Fig. 14). For example, at half the radius of
the core (r = 104 AU) the temperature difference between the
point at
![]() and the point at
and the point at
![]() ,
is 5-6 K
for the non-embedded core, but only
,
is 5-6 K
for the non-embedded core, but only ![]() 1.5 K for the same core
embedded in an
1.5 K for the same core
embedded in an
![]() ambient cloud. In Fig. 16
we present a perpendicular cut through the centre of the embedded core
image at viewing angle 30
ambient cloud. In Fig. 16
we present a perpendicular cut through the centre of the embedded core
image at viewing angle 30![]() .
It is evident that the features are
quite weak, but they have the same size as in the non-embedded core
(Fig. 5), and they may be detectable with Herschel, given an estimated rms sensitivity better than
.
It is evident that the features are
quite weak, but they have the same size as in the non-embedded core
(Fig. 5), and they may be detectable with Herschel, given an estimated rms sensitivity better than ![]() 1-3 MJy sr-1 at 170-250
1-3 MJy sr-1 at 170-250
![]() for clouds outside the Galactic
plane (dependent on cirrus confusion).
for clouds outside the Galactic
plane (dependent on cirrus confusion).
![\begin{figure}
\par {\includegraphics[width=6.5cm,clip]{0546fig46.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg101.gif) |
Figure 17:
Same as Fig. 5, i.e. model 1.2, but for a
core embedded in a uniform molecular ambient cloud with visual extinction
|
| Open with DEXTER | |
For a core embedded in an ambient cloud with
![]() ,
the
temperature differences between different parts of the core are even
smaller (
,
the
temperature differences between different parts of the core are even
smaller (![]() 1 K at r = 104 AU, see
Fig. 14), but characteristic features persist
(e.g. two symmetric intensity minima at 60
1 K at r = 104 AU, see
Fig. 14), but characteristic features persist
(e.g. two symmetric intensity minima at 60![]() and 90
and 90![]() ,
see
Fig. 17).
,
see
Fig. 17).
Thus, continuum observations near the peak of the core emission, can
be used to obtain information about the core density and temperature
structure and orientation, even if the core is very embedded
(
![]() ).
).
We now examine the effect that a UV-enhanced ISRF has
on the temperature profiles and isophotal maps of deeply embedded cores.
We consider an ISRF that consists of the BISRF, plus an additional
component of diluted blackbody radiation from stars with
![]() K
or
K
or
![]() K, that illuminates isotropically the ambient molecular
cloud in which the core resides. We use a dilution parameter
K, that illuminates isotropically the ambient molecular
cloud in which the core resides. We use a dilution parameter
![]() ,
so that the total additional luminosity
illuminating the ambient cloud is
,
so that the total additional luminosity
illuminating the ambient cloud is
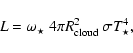 |
(11) |
![\begin{figure}
\par {
\includegraphics[width=6.3cm,clip]{0546fig47.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg109.gif) |
Figure 18:
The effect of an UV-enhanced ISRF on embedded cores. Temperature
profiles of a core with the same set of parameters as model 1.2 (p=4,
e=2.5), embedded in a uniform density ambient cloud with visual extinction
|
| Open with DEXTER | |
![\begin{figure}
\par {
\includegraphics[angle=-90,width=7cm,clip]{0546fig48.ps} }
\end{figure}](/articles/aa/full/2004/24/aa0546/Timg110.gif) |
Figure 19:
Density distribution on the x=0 plane for a core with
axial asymmetry, south-to-north pole optical depth ratio e=2.5
and p=4 (model 2.2). We plot iso-density contours every
|
| Open with DEXTER | |
![\begin{figure}
\par {
\includegraphics[angle=-90,width=7cm,clip]{0546fig49.ps} }
\end{figure}](/articles/aa/full/2004/24/aa0546/Timg111.gif) |
Figure 20: Temperature distribution on the x=0 plane, for the model presented in Fig. 19 (e=2.5, p=4, model 2.2). We plot iso-temperature contours from 8 to 18 K, every 2 K. The denser, southern parts of the core are colder. |
| Open with DEXTER | |
Table 2: Model parameters for cores with axial asymmetry.
![\begin{figure}
\par {\includegraphics[angle=-90,width=6.1cm,clip]{0546fig50.ps} ...
...4mm}
{\includegraphics[angle=-90,width=6.1cm,clip]{0546fig53.ps} }\end{figure}](/articles/aa/full/2004/24/aa0546/Timg112.gif) |
Figure 21:
Isophotal maps at 200
|
| Open with DEXTER | |
![\begin{figure}
{\includegraphics[angle=-90,width=6.1cm,clip]{0546fig54.ps} }\vsp...
...{3mm}
{\includegraphics[angle=-90,width=6.1cm,clip]{0546fig57.ps} }
\end{figure}](/articles/aa/full/2004/24/aa0546/Timg113.gif) |
Figure 22:
Isophotal maps at 850
|
| Open with DEXTER | |
In Fig. 18, we present the temperature profiles
at
![]() (core pole; upper curves) and
(core pole; upper curves) and
![]() (core
equator; lower curves) for a core with the same set of parameters as model 1.2 (p=4, e=2.5), embedded in a uniform density ambient cloud with visual
extinction
(core
equator; lower curves) for a core with the same set of parameters as model 1.2 (p=4, e=2.5), embedded in a uniform density ambient cloud with visual
extinction
![]() ,
illuminated by different ISRFs. The bottom pair
of curves corresponds to illumination by the standard BISRF, and the upper
two pairs of curves to illumination enhanced by a diluted blackbody with
,
illuminated by different ISRFs. The bottom pair
of curves corresponds to illumination by the standard BISRF, and the upper
two pairs of curves to illumination enhanced by a diluted blackbody with
![]() K and
K and
![]() K. The core is hotter when the ambient
cloud is illuminated by a more energetic UV field, by 1-2 K for the models
we examine. The temperature differences between different parts of the core
seem also to increase, but only by a small amount (<0.5 K). This means that
the characteristic features on the isophotal maps at wavelengths near the peak
of the core emission are not significantly changed.
K. The core is hotter when the ambient
cloud is illuminated by a more energetic UV field, by 1-2 K for the models
we examine. The temperature differences between different parts of the core
seem also to increase, but only by a small amount (<0.5 K). This means that
the characteristic features on the isophotal maps at wavelengths near the peak
of the core emission are not significantly changed.
For an even more energetic illuminating radiation field the enhancement would
be larger. For example, the external UV radiation field incident on ![]() Ophiuchi is estimated to be
Ophiuchi is estimated to be ![]() 10-100 times stronger than the BISRF,
due to the presence of a nearby B2V star (Liseau et al. 1999). In this
circumstance, we would expect cores to be hotter and the temperature
differences may then be sufficiently large (
10-100 times stronger than the BISRF,
due to the presence of a nearby B2V star (Liseau et al. 1999). In this
circumstance, we would expect cores to be hotter and the temperature
differences may then be sufficiently large (![]() 2 K) to produce detectable
features on isophotal maps at 200
2 K) to produce detectable
features on isophotal maps at 200
![]() .
However, if the illuminating
radiation field is very much stonger than the BISRF, it is likely to involve
significant contributions from a few discrete luminous stars in the immediate vicinity. It will therefore be markedly anisotropic and this will produce
additional asymmetries in the isophotal maps, making their analysis more
difficult.
.
However, if the illuminating
radiation field is very much stonger than the BISRF, it is likely to involve
significant contributions from a few discrete luminous stars in the immediate vicinity. It will therefore be markedly anisotropic and this will produce
additional asymmetries in the isophotal maps, making their analysis more
difficult.
Thus, continuum observations near the peak of the core emission may reveal
features characteristic of the core structure even if the core is more
deeply embedded (
![]() ), provided that the radiation field incident
on the core is sufficiently intense, and provided the effect of discrete
local sources can be treated.
), provided that the radiation field incident
on the core is sufficiently intense, and provided the effect of discrete
local sources can be treated.
The density profile in model cores with axial asymmetry is given by
![\begin{displaymath}n(r,\theta) = 10^6~{\rm cm}^{-3}\;~\frac{1 + A \left( \frac{r...
... +
\left( \frac{r}{2000~{\rm AU}} \right)^2 \right]^2 } \cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0546/img69.gif) |
(12) |
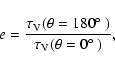 |
(13) |
In Fig. 19, we present the core density profile on the
x=0 plane for model 2.2 (p=4, e=2.5), and in Fig. 20
the corresponding temperature profile. The temperature drops from ![]() 18 K
at the edge of the core to
18 K
at the edge of the core to ![]() 7 K at the centre of the core, and the
denser "southern'' parts of the core are colder. The difference between
regions of the core with the same r but different
7 K at the centre of the core, and the
denser "southern'' parts of the core are colder. The difference between
regions of the core with the same r but different ![]() is larger for
the p=4 models than for the p=1 models, and also larger for the more
asymmetric models (e=2.5) than for the less asymmetric models (e=1.5).
For example, at half the radius of the core (104 AU) the
temperature difference between the point at
is larger for
the p=4 models than for the p=1 models, and also larger for the more
asymmetric models (e=2.5) than for the less asymmetric models (e=1.5).
For example, at half the radius of the core (104 AU) the
temperature difference between the point at
![]() (core north
pole) and the point at
(core north
pole) and the point at
![]() (core south pole) is
(core south pole) is ![]() 7 K for
the p=4, e=2.5 model,
7 K for
the p=4, e=2.5 model, ![]() 5 K for the p=4, e=1.5 model,
5 K for the p=4, e=1.5 model, ![]() 4 K
for the p=1, e=2.5 model and
4 K
for the p=1, e=2.5 model and ![]() 3 K for the p=1, e=1.5 model.
3 K for the p=1, e=1.5 model.
As in the case of cores with disk-like asymmetry, these temperature
differences result in
characteristic features on isophotal maps at wavelengths near the peak of
the core emission. In Fig. 21, we present
200
![]() images at different viewing angles. The core appears
spherically symmetric when viewed pole-on, but the effects of axial
asymmetry start to show when we look at the core from other viewing
angles (e.g.
images at different viewing angles. The core appears
spherically symmetric when viewed pole-on, but the effects of axial
asymmetry start to show when we look at the core from other viewing
angles (e.g.
![]() ,
,
![]() and
and
![]() ). Comparing with the
images at 200
). Comparing with the
images at 200
![]() for cores with disk-like asymmetry
(Figs. 6-9), we see that for cores
with axial asymmetry there is only one axis of symmetry. Thus, the symmetry of the
characteristic features is indicative of the underlying core density structure.
These features contain information about the core density, temperature
and orientation with respect to the observer, and therefore observations
near the peak of the core emission are important. The resolution of
ISO/ISOPHOT was not high enough to detect such features.
for cores with disk-like asymmetry
(Figs. 6-9), we see that for cores
with axial asymmetry there is only one axis of symmetry. Thus, the symmetry of the
characteristic features is indicative of the underlying core density structure.
These features contain information about the core density, temperature
and orientation with respect to the observer, and therefore observations
near the peak of the core emission are important. The resolution of
ISO/ISOPHOT was not high enough to detect such features.
The 850
![]() images (Fig. 22) map the column
density of the core along the line of sight. We point out the similarities
between the maps in Fig. 22, and SCUBA observations
of L1521F, L1544, L1582A, L1517B, L63 and B133 (Kirk et al. 2004). Further
modelling for each specific core is required to make more detailed comparisons.
images (Fig. 22) map the column
density of the core along the line of sight. We point out the similarities
between the maps in Fig. 22, and SCUBA observations
of L1521F, L1544, L1582A, L1517B, L63 and B133 (Kirk et al. 2004). Further
modelling for each specific core is required to make more detailed comparisons.
As in the case of cores with disk-like asymmetry, the SEDs of cores with axial asymmetry are independent of the observer's viewing angle, because they are optically thin at long wavelengths.
We have performed accurate two dimensional continuum radiative transfer calculations for non-spherical prestellar cores. We argue that such non-spherical models are needed because observed cores are clearly not spherically symmetric, and are not expected to be spherically symmetric. Our models illustrate the characteristic features on isophotal maps which can help to constrain the intrinsic density and temperature fields within observed non-spherical cores. They demonstrate the importance of observing cores at wavelengths around the peak of the SED and with high resolution.
Our main results are:
We are now extending our study by treating the effect of an anisotropic illuminating radiation field. We are also studying the triaxial molecular cores that result from 3-dimensional hydrodynamic simulations.
Acknowledgements
We gratefully acknowledge support from the EC Research Training Network "The Formation and Evolution of Young Stellar Clusters'' (HPRN-CT-2000-00155).