| (1) | |||
| (2) | |||
| (3) |
A&A 420, 1123-1127 (2004)
DOI: 10.1051/0004-6361:20034278
M. Selwa1 - R. Skartlien2 - K. Murawski1
1 - Institute of Physics, UMCS, ul. Radziszewskiego 10, 20-031 Lublin, Poland
2 -
Norwegian Defence Research Establishment (FFI), Postboks 25, 2027 Kjeller, Norway
Received 5 September 2003 / Accepted 4 March 2004
Abstract
In turbulent acoustic media such as the solar
envelope, both wave sources and the propagation characteristics
(background density, refractive index, dissipation, etc.) are
stochastic quantities. By means of numerical simulation of the
Euler equations, we study two cases in a homogeneous stochastic
medium in which the background density fluctuations and wave
sources are 1) correlated and 2) uncorrelated. We find that in the
uncorrelated case, the coherent (or mean) acoustic field is zero,
leaving only an incoherent field. In the correlated case, the
coherent field is nonzero, yielding both coherent and incoherent
fields. We question the use of mean-field dispersion relations to
determine frequency shifts in p-mode and f-mode spectra, since the
coherent field can be non-existent or weak relative to the
incoherent field. We demonstrate the importance of accounting for
a stochastic wave source by showing that the two cases give very
different frequency shifts.
Key words: waves - Sun: interior - Sun: oscillations - convection - turbulence
Motivated by the origin of solar p-modes (e.g., Gough 1994), we discuss generation and propagation of sound waves in a stochastic medium. Simple models acquire much attention as they allow for separation and quantification of effects on the waves from various stochastic quantities in the medium. Indeed, analytical and numerical studies of sound waves in a space-dependent random mass density field reveals that the waves are accelerated and attenuated (Nocera et al. 2001). On the other hand, a time-dependent random mass density field accelerates and amplifies the sound waves (Murawski et al. 2001).
The above mentioned studies treat sound waves in a random medium without discussing the effect of a random wave source. Random wave generation was discussed recently by Skartlien (2002), who used linear theory to show that the existence of the coherent field (or mean field) requires a correlation between the source and the random background fluctuations. Furthermore, it was shown that the power spectrum can be understood as cross power between multiply scattered wave components, and in terms of correlation functions of the random background fluctuations and of the wave source.
The main purpose of this paper is to verify by numerical simulation that the coherent field exists only when there is a correlation between the source and the background fluctuations. We assume 1d geometry for the purpose of clear demonstration, but the essential results are valid in 2d and 3d as well. The paper is organized as follows. Section 2 presents the numerical model. Section 3 describes ensemble averaging and the coherent field. Section 4 contains results of the numerical simulations. Conclusions are found in Sect. 5.
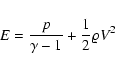 |
(4) |
The source terms
![]() and SV represent mass and momentum sources, respectively.
We note that these sources are merely phenomenological, and that mass,
momentum and energy is not conserved due to these sources.
The term
and SV represent mass and momentum sources, respectively.
We note that these sources are merely phenomenological, and that mass,
momentum and energy is not conserved due to these sources.
The term ![]() has the meaning of a temporal derivative
of a random mass density and SV generates a wave field. These terms are described
below for the case of a static equilibrium.
has the meaning of a temporal derivative
of a random mass density and SV generates a wave field. These terms are described
below for the case of a static equilibrium.
The equilibrium state which is set initially at t=0 is defined with a varying background density,
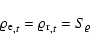 |
(6) |
The random part of the background mass density,
![]() ,
is
chosen to be statistically homogeneous (i.e., the statistical
properties are independent of the coordinates in space and time),
with Gaussian
power spectrum
,
is
chosen to be statistically homogeneous (i.e., the statistical
properties are independent of the coordinates in space and time),
with Gaussian
power spectrum
Linear theory shows that a coherent field exists only when
the source in the wave equation correlates to the coefficients in the wave equation
(Skartlien 2002). We linearize the mass, momentum and energy equations and
obtain to leading order the perturbed wave equation
| L0[V]+L1[V]=S, | (8) | ||
![\begin{displaymath}S=\left[S_{V}(1+\varepsilon)\right]_{,t}-(\gamma-1)\left[(1+\varepsilon)VS_V\right]_{,x}.
\end{displaymath}](/articles/aa/full/2004/24/aa0278/img29.gif) |
(9) |
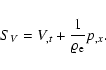 |
(10) |
For the correlated case, we use a spatially localized source which is proportional to the density fluctuations,
| (12) |
| (14) |
There are at least two ways of observing independent realizations of the wave field such that ensemble averaging can be performed. 1) One can observe one single field of view within N time windows that are separated by more than one correlation time. The medium needs to be statistically stationary in time, but not necessarily statistically homogeneous in space. 2) One can observe N different fields of view (with sufficient spatial separation) within the same time window. The medium needs to be statistically homogeneous in space, but not necessarily statistically stationary in time. One can also imagine a combination of 1) and 2).
After having observed N realizations of the wave field, we perform ensemble averaging,
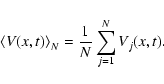 |
(15) |
In order to evaluate the global convergence, we calculate
the mean energy of the ensemble averaged field,
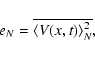 |
(16) |
![\begin{displaymath}E[e_N]=\overline{\langle V\rangle_\infty^2} +
\frac{\overline{E[(\delta V)^2]}}{N}\cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0278/img52.gif) |
(17) |
![\begin{displaymath}e_N({\rm uncorrelated})={\cal O}({\overline{E[(\delta
V)^2]}})/N
\end{displaymath}](/articles/aa/full/2004/24/aa0278/img53.gif) |
(18) |
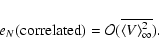 |
(19) |
Our intention here is to verify numerically the non-existence (existence) of
the coherent field when the density fluctuations
![]() are uncorrelated (correlated) to the source SV, and to
compare the frequency shifts of the line profiles in the ensemble
averaged power spectra. The standard deviation of the relative
density fluctuation
are uncorrelated (correlated) to the source SV, and to
compare the frequency shifts of the line profiles in the ensemble
averaged power spectra. The standard deviation of the relative
density fluctuation
![]() is chosen as
is chosen as
![]() ,
corresponding to the weak scattering regime. The amplitude of the
source is set such that we remain in the linear regime where
,
corresponding to the weak scattering regime. The amplitude of the
source is set such that we remain in the linear regime where
![]() .
.
To perform numerical simulations, we have adapted the code CLAWPACK (LeVeque 2002), a packet of Fortran routines for solving hyperbolic equations (e.g., Murawski 2002). We use a homogeneous grid in space x and time t, and periodic boundaries in xfor simple adaption to spectral analysis via the Fast Fourier Transform.
Figure 1 shows the mean energy of the ensemble
averaged field,
![]() ,
in both
correlated and uncorrelated cases. When the density fluctuations
are correlated to the source, the mean energy converges to the mean energy of the coherent field,
,
in both
correlated and uncorrelated cases. When the density fluctuations
are correlated to the source, the mean energy converges to the mean energy of the coherent field,
![]() .
When the density fluctuations
are not correlated to the source, the mean energy converges
to zero (
.
When the density fluctuations
are not correlated to the source, the mean energy converges
to zero (
![]() )
because
the coherent field is zero.
We note that in the
uncorrelated case, the field is purely incoherent, while in the
correlated case, it has both coherent and incoherent
contributions.
)
because
the coherent field is zero.
We note that in the
uncorrelated case, the field is purely incoherent, while in the
correlated case, it has both coherent and incoherent
contributions.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0278fig1.eps}\end{figure}](/articles/aa/full/2004/24/aa0278/Timg60.gif) |
Figure 1: Convergence of the mean energy of the ensemble averaged fields. The mean energy converges to the mean energy of the coherent field in the correlated case (dashed line). For the uncorrelated case, the mean energy converges to zero because the coherent field is zero in this case (full line). The mean energy is proportional to 1/N in the uncorrelated case, and results in a slope of -1 in the given log-log plot (thick line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0278fig2.eps}\vspace*{2mm}
\includegraphics[width=8.8cm,clip]{0278fig3.eps}\end{figure}](/articles/aa/full/2004/24/aa0278/Timg61.gif) |
Figure 2:
Ensemble averaged power spectra for the correlated case as function of frequency |
| Open with DEXTER | |
Figure 2 shows ensemble averaged power spectra
of the velocity field as function of frequency ![]() in the
correlated case (with the wavenumber k as parameter). The power
maxima in the frequency spectra are close to the frequencies dictated
by the unperturbed dispersion relation
in the
correlated case (with the wavenumber k as parameter). The power
maxima in the frequency spectra are close to the frequencies dictated
by the unperturbed dispersion relation
![]() .
Thus,
we get only one power maximum for each wavenumber, and most of the
energy is concentrated around these frequencies.
Previous studies on similar problems show that stochastic
perturbations in the medium can lead to shifts in frequency for
the power maxima, or for the line profile as a whole (e.g.,
Murawski et al. 2001 (undriven free waves) or Skartlien 2002
(stochastically driven waves, uncorrelated medium and source)).
.
Thus,
we get only one power maximum for each wavenumber, and most of the
energy is concentrated around these frequencies.
Previous studies on similar problems show that stochastic
perturbations in the medium can lead to shifts in frequency for
the power maxima, or for the line profile as a whole (e.g.,
Murawski et al. 2001 (undriven free waves) or Skartlien 2002
(stochastically driven waves, uncorrelated medium and source)).
Figure 3 shows (for both cases) the relative
frequency shifts
![]() of the line profiles for
different k. We see that a correlation between the source and
the density fluctuations is also manifested in the frequency
shifts. The shifts are mostly positive in the uncorrelated case
(squares). In the correlated case, the shifts are much smaller and
mostly negative (crosses). These differences demonstrate the
importance of accounting for a stochastic wave source when
attempting to explain p-mode and f-mode spectra.
of the line profiles for
different k. We see that a correlation between the source and
the density fluctuations is also manifested in the frequency
shifts. The shifts are mostly positive in the uncorrelated case
(squares). In the correlated case, the shifts are much smaller and
mostly negative (crosses). These differences demonstrate the
importance of accounting for a stochastic wave source when
attempting to explain p-mode and f-mode spectra.
We note that the expectation value of the power spectrum
![]() can be split in coherent and incoherent parts,
can be split in coherent and incoherent parts,
![\begin{displaymath}E[P]=\left\langle \tilde{V} \tilde{V}^* \right\rangle_\infty ...
...gle
\delta \tilde{V} \delta \tilde{V}^* \right\rangle_\infty,
\end{displaymath}](/articles/aa/full/2004/24/aa0278/img64.gif) |
(20) |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{0278fig4.eps}\end{figure}](/articles/aa/full/2004/24/aa0278/Timg68.gif) |
Figure 3: Relative frequency shifts for the correlated case (crosses) and for the uncorrelated case (squares). The frequency shifts are mostly positive in the uncorrelated case. In the correlated case, the shifts are much smaller and mostly negative. |
| Open with DEXTER | |
We have studied stochastic sound waves in a one-dimensional random medium by numerical solution of the Euler equations. We considered two cases in which the background density and wave source were either correlated or uncorrelated. The coherent field is non-zero in the correlated case, yielding both coherent and incoherent fields. In the uncorrelated case, there is only an incoherent field.
The physical content of this result is that there must be a correlation between the perturbed wave operator and the wave source, for the coherent field to exist. The perturbed wave operator corresponds to fluctuations in the propagation characteristics of the waves, and in our case it was the background density fluctuations which provided these fluctuations. It is also important to note the diagnostic potential; we can in principle determine from observations whether or not there is a correlation between the wave source and the physical quantity which provides the fluctuating propagation characteristics.
Much attention has been given to frequency shifts in the solar p-mode and f-mode spectra in the past, motivated by the desire to understand the solar interior. An important question is therefore: do we make significant errors in predicted frequency shifts using deterministic helioseismic modelling? To answer this question we need good stochastic models. The usual approach in stochastic modelling so far is to use mean-field dispersion relations to arrive at solar eigenfrequencies. Is this a valid approach? The mean-field dispersion relation governs the coherent field only, and one can therefore only calculate eigenfrequencies for the coherent field. There are two strong reasons for questioning the use of mean-field dispersion relations: 1) the coherent field can simply be non-existent, as we have demonstrated for the uncorrelated case, and 2) the coherent field might only contribute with a small amount of power to the power spectrum.
We demonstrated that the frequency shifts in the power spectrum depend on the correlation between the stochastic source and the background fluctuations. An explanation of this will be attempted in a forthcoming paper by using linear theory to calculate the expectation value of the power spectrum without going through dispersion relations (Skartlien 2002). Much work still needs to be done in this direction, and simple homogeneous models are going to give us more valuable insight. We encourage researchers in the field of helioseismology to determine the magnitude of the errors made in both deterministic modelling and in stochastic modelling using mean-field dispersion relations.
Acknowledgements
M.S.'s and K.M.'s works were financially supported by the State Committee for Scientific Research in Poland, KBN grant no. 2 PO3D 016 25. R.S. thanks the co-authors and Tore Smestad.