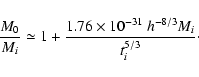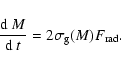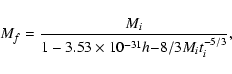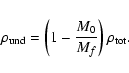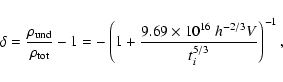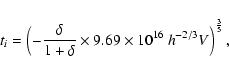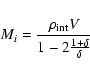A&A 420, 847-851 (2004)
DOI: 10.1051/0004-6361:20041166
Cosmological black holes as seeds of voids in the galaxy distribution
S. Capozziello1,4 - M. Funaro2 - C. Stornaiolo3,4
1 - Dipartimento di Fisica "E.R. Caianiello'',
Università di Salerno, via S. Allende, 84081 Baronissi
(Salerno), Italy
2 -
Dipartimento di Matematica e Informatica,
Università di Salerno, via Ponte Don Melillo, 84084 Fisciano
(Salerno), Italy
3 - Dipartimento di Scienze Fisiche,
Università di Napoli, Complesso Universitario di Monte S.
Angelo, via Cinthia, Edificio N - 80126 Napoli, Italy
4 -
Istituto Nazionale di Fisica Nucleare, Sezione di Napoli,
Complesso Universitario di Monte S. Angelo, via Cinthia, Edificio
G, 80126 Napoli, Italy
Receveid 5 February 2004 / Accepted 11 March 2004
Abstract
Deep surveys indicate a bubbly structure on cosmological large
scales which should be the result of evolution of primordial
density perturbations. Several models have been proposed to
explain the origin and dynamics of such features but, till now, no
exhaustive and fully consistent theory has been found. We discuss
a model where cosmological black holes, deriving from primordial
perturbations, are the seeds for large-scale-structure voids. We
give details of the dynamics and accretion of the system
voids-cosmological black holes from the epoch
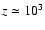 till
now, finding that a void of 40 h-1 Mpc diameter and
under-density of -0.9 fits the observations without conflicting
with the homogeneity and isotropy of the cosmic microwave
background radiation.
till
now, finding that a void of 40 h-1 Mpc diameter and
under-density of -0.9 fits the observations without conflicting
with the homogeneity and isotropy of the cosmic microwave
background radiation.
Key words: cosmology: large scale structure of Universe - cosmology: dark matter - black hole physics
The existence of voids has been evident after the discovery by
Kirshner et al. 1981 of a large void with a diameter of 60 Mpc in Böotes. Systematic surveys have shown the existence of
many regions with similar characteristics. Computer analysis of
galaxy distribution gives evidence that voids occupy about 50% of
the volume of the universe (e.g., see El-Ad & Piran 1997) or,
according to a more recent paper (Hoyle & Vogeley 2002), about 40% of
the volume of the universe.
Today, there is a general agreement on the issue that voids are
not just empty regions of space, but that they are regions with a
very low density of luminous matter.
As observed by Peebles (2001), the velocity dispersion of
galaxies indicates that most matter must be inside the voids, not
only if the density parameter (for the matter component)
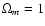 but also for
but also for
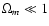 .
In any case, recent
observations (de Bernardis et al. 2000; Perlmutter et al. 1999;
Schimdt et al. 1998) indicate that the total value of the density
parameter is
.
In any case, recent
observations (de Bernardis et al. 2000; Perlmutter et al. 1999;
Schimdt et al. 1998) indicate that the total value of the density
parameter is
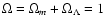 where
where
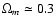 and
and
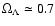 .
Here
.
Here
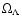 is the contribution due to the whole content of
unclustered matter which can be the cosmological constant, some
kind of scalar field (Caldwell et al. 1998; de Ritis et al. 2000;
Rubano & Barrow 2001; Capozziello 2002) or, in general, "dark
energy''.
is the contribution due to the whole content of
unclustered matter which can be the cosmological constant, some
kind of scalar field (Caldwell et al. 1998; de Ritis et al. 2000;
Rubano & Barrow 2001; Capozziello 2002) or, in general, "dark
energy''.
It is worthwhile to stress that the visual inspection of the
galaxy distribution suggests nothing other than the absence of
large amounts of luminous matter in wide regions. Furthermore, it
is not clear whether the voids are spherical regions approximately
empty or under-dense regions with arbitrary shapes. Several
definitions of voids have been proposed, but a general agreement
on their real nature has not been reached yet (Schmidt et al. 2001).
The Swiss-Cheese cosmological model, initially proposed by
Einstein & Straus (1945, 1946), appears suitable for the
description of the cosmological voids. In a recent paper
(Stornaiolo 2002), it was proposed to approach the formation of
the cosmological voids in the framework of this model. It was
shown that voids are the consequence of the collapse of extremely
large wavelength perturbations into low-density black holes and of
the comoving expansion of matter surrounding the collapsed
perturbations.
As a result, it was claimed that in the center of each void there
is a black hole whose mass M compensates the mass which the void
would have if it were completely filled with matter having a
cosmological density.
In Stornaiolo (2002) the voids are empty regions of the universe which
grow in a comoving frame with the cosmological expansion. In that
paper, the presence of cosmic background radiation was neglected.
In this paper, we analyze the physical mechanism capable of
explaining the structure of voids in the presence of baryonic
matter and cosmic background radiation (CBR) with central black
holes acting as seeds. The layout of the paper is the following:
in Sect. 2, we will present the cosmological black hole (CBH) model
in the framework of the Friedmann-Lemaître-Robertson-Walker
(FLRW) cosmology. Section 3 is devoted to the discussion of the
effects of interaction between the CBR and a CBH. A mechanism for
the formation of an under-dense regime void is analyzed in Sect. 4,
while the comparison with observations, which makes it possible to
determine the initial time of voids formation and the mass
function of CBHs, is studied in Sect. 5. The discussion of the
results and the conclusions are given in Sect. 6.
The cosmological model proposed in Stornaiolo (2002) is an
Einstein-Straus universe which is embedded in an FLRW metric. A
central spherical black hole with mass
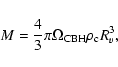 |
(1) |
is present in all the voids.
In Eq. (1), the parameter
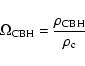 |
(2) |
represents the fraction of density due to all these black holes
with respect to the total density of the universe;
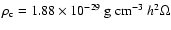 is
the present-day critical density of the universe.
is
the present-day critical density of the universe.
All the voids are assumed to be spherical.
A black hole forms when a body of mass M collapses entirely
within a sphere of radius
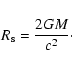 |
(3) |
This statement is equivalent to say that its density satisfies the
relation,
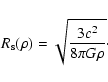 |
(4) |
Conversely, Eq. (4) defines for any density a
corresponding Schwarzschild radius. In other words, any space-like
sphere of matter, with uniform density 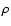 and radius equal to
and radius equal to
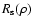 ,
is a black hole.
,
is a black hole.
From Eqs. (1) and (3), we determine the mass
M and the corresponding Schwarzschild radius and consequently,
from Eq. (4) the mass density of the central black
hole. For example, a black hole in the center of a 50 h-1 Mpc
diameter void would have a mass
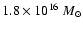 corresponding to a Schwarzschild radius 1.7 kpc and a density of
corresponding to a Schwarzschild radius 1.7 kpc and a density of
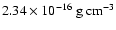 .
.
The above value of the density is the one reached by the
collapsing matter when it crossed the Schwarzschild radius. It
suggests that the process of formation of a CBH started with large
wavelength perturbations at cosmological densities of the order of
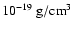 i.e. for
i.e. for
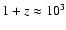 .
According to the inflationary scenario, we only need to suppose
that the inflation occurred during a time long enough to provide
such perturbations
.
According to the inflationary scenario, we only need to suppose
that the inflation occurred during a time long enough to provide
such perturbations![[*]](/icons/foot_motif.gif) .
.
Note that, since the Einstein-Straus model assumes spherical
symmetry, the perturbation does not experience the cosmic
expansion during its collapse.
For this reason, we can assume that the total mass of the
perturbation
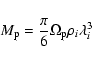 |
(5) |
remains constant during the whole process.
The Schwarzschild radius of the spherical perturbation is equal to
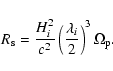 |
(6) |
We can distinguish two cases:
- 1.
- the case in
which the relation
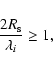 |
(7) |
is satisfied. The perturbation is in the linear regime and,
according to the evolution equations of a universe with perfect
fluid equation of state, it is frozen when
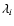 is larger
than the Hubble radius (Mukhanov et al. 1992). After crossing the
Hubble horizon, it collapses and becomes a black hole when
is larger
than the Hubble radius (Mukhanov et al. 1992). After crossing the
Hubble horizon, it collapses and becomes a black hole when
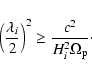 |
(8) |
- 2.
- The case where
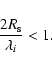 |
(9) |
Here the perturbation evolves as shown in Stornaiolo
(2002). During the contraction, it becomes unavoidably a
black hole if the final density is very low and the internal
pressure and temperature cannot increase to values large enough to
prevent the collapse. This is true also when the perturbation
enters a non-linear regime. In addition, any possible centrifugal
barrier can be reduced to values smaller than the Schwarzschild
radius (Loeb 1993) by the interaction of collapsing matter with
the cosmic background radiation. According to the Einstein-Straus
model, after the formation of the black hole the matter around it
expands in a comoving way leading to the formation of an empty
region between it and the rest of the universe. As the central
black hole cannot be seen, the whole region appears as a void to
an external observer.
A CBH can be detected through its lensing properties, since it
behaves like a Schwarzschild gravitational lens. According to our
hypothesis, a CBH sits in the center of a void and the Einstein
angle is (Schneider et al. 1992)
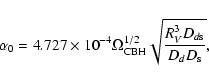 |
(10) |
where RV is the radius of the void, 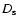 is the distance
of the source from the observer,
is the distance
of the source from the observer,
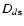 is the distance of the
source from the CBH, and Dd is the distance of the CBH from
the observer; all these quantities are expressed in Mpc. For a 50
Mpc void, with the center placed at a distance of 80 Mpc from the
Sun and with a source at the opposite edge of the void, we expect
a deflection angle
is the distance of the
source from the CBH, and Dd is the distance of the CBH from
the observer; all these quantities are expressed in Mpc. For a 50
Mpc void, with the center placed at a distance of 80 Mpc from the
Sun and with a source at the opposite edge of the void, we expect
a deflection angle
On the other hand, Zeldovich &
Sazhin (1987) point out that generally static structures can raise
the temperature of the cosmic background radiation by an amount
proportional to the Hubble parameter and the gravitational time
delay. Considering the Swiss-Cheese model case, they find a
temperature fluctuation
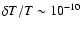 for a giant
galaxy (
for a giant
galaxy (
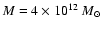 ). Since this result is
proportional to the mass, it follows that it corresponds to a
fluctuation of temperature
). Since this result is
proportional to the mass, it follows that it corresponds to a
fluctuation of temperature
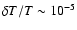 for a large
CBH with mass
for a large
CBH with mass
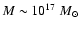 ,
which does not contradict
the recent Boomerang and WMAP measurements (de Bernardis et al. 2000;
Tegmark et al. 2003).
,
which does not contradict
the recent Boomerang and WMAP measurements (de Bernardis et al. 2000;
Tegmark et al. 2003).
An interesting feature of voids with central CBH is derived
starting from a Swiss-Cheese model based on an Einstein- de Sitter
cosmology. To this aim, let us consider the energy balance in
Newtonian terms for a galaxy with mass m sitting on the edge of
a void i.e. at a distance
r=rea(t) where re is a
covariant radius. We have
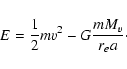 |
(11) |
As the void is expanding in a comoving frame, we can impose
v=Hrea(t). The mass Mv inside the void is
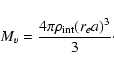 |
(12) |
By Eq. (11), one obtains
![\begin{displaymath}
E=\frac{m(r_{e}a)^{2}}{2}\left[H^{2} -\frac{8\pi
G\rho_{\rm int}}{3}\right]
\end{displaymath}](/articles/aa/full/2004/24/aa0205/img35.gif) |
(13) |
and then
![\begin{displaymath}
E=\frac{m(r_{e}a)^{2}}{2}\left[ \frac{8\pi
G}{3}(\rho_{\rm tot}-\rho_{\rm int})\right].
\end{displaymath}](/articles/aa/full/2004/24/aa0205/img36.gif) |
(14) |
From this relation, we see that, E=0 if
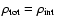 ,
i.e. the expansion velocity of a galaxy on the edge of a void coincides
with the escape velocity
,
i.e. the expansion velocity of a galaxy on the edge of a void coincides
with the escape velocity![[*]](/icons/foot_motif.gif) . On the other
hand, a galaxy on the edge of a void is gravitationally bound to
a CBH, if
. On the other
hand, a galaxy on the edge of a void is gravitationally bound to
a CBH, if
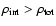 .
In this paper, we shall
adopt as definition of edge of a void the spherical
region where the galaxies have energy E=0.
.
In this paper, we shall
adopt as definition of edge of a void the spherical
region where the galaxies have energy E=0.
These considerations can be immediately extended to the case in
which the spatial curvature is different from zero (i.e. to
Friedmann models different from the considered Einstein-de Sitter
one). This simply implies that
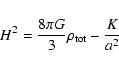 |
(15) |
and Eq. (13) becomes
![\begin{displaymath}\
E=\frac{m(r_{e}a)^{2}}{2}\left[ \frac{8\pi
G}{3}(\rho_{\rm tot}-\rho_{\rm int})-\frac{K}{a^{2}}\right]\cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0205/img42.gif) |
(16) |
In this case, the value of E depends also on K/a2.
3 Interaction between CBR and CBH
So far we have considered the Einstein-Straus Swiss-cheese model
in a universe filled only with matter. In this section, we shall
show how the interaction with the CBR will lead to accretion by a
CBH. Since the pressure of radiation is different from zero, the
radiation itself may cross the edge of the voids regardless of the
Einstein-Straus junction conditions (Einstein & Straus 1945, 1946). As
we consider this physical process during the matter epoch, we can
neglect the contribution of radiation to the black hole formation.
A CBH absorbs energy from the CBR according to the law
(Custodio & Horvath 2002)
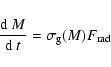 |
(17) |
where
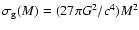 is the
gravitational cross section of CBH and
is the
gravitational cross section of CBH and
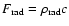 is
the radiation flux of CBR.
is
the radiation flux of CBR.
In a matter dominated universe, (dust), the evolution of radiation
density is given by
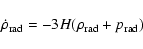 |
(18) |
where
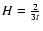 and the equation of state
is
and the equation of state
is
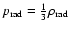 .
.
Immediately, we get
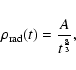 |
(19) |
where the constant A has the dimensions
![$[{\rm g}~{\rm cm}^{-3}~{\rm s}^{8/3}]$](/articles/aa/full/2004/24/aa0205/img50.gif) .
At the present
epoch, assuming
.
At the present
epoch, assuming
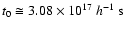 (this value is consistent with WMAP observations (Tegmark et al. 2003) for
(this value is consistent with WMAP observations (Tegmark et al. 2003) for
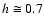 )
and
)
and
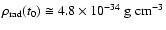 ,
we obtain
,
we obtain
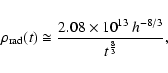 |
(20) |
disregarding the physical dimensions.
Equation (17) becomes
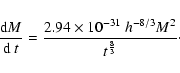 |
(21) |
Integrating from an initial epoch ti to the present epoch, we
have that the ratio between the present mass M0 and the initial
mass Mi is
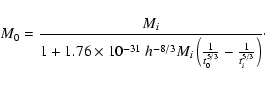 |
(22) |
If
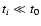 ,
we can approximate the formula for the mass
accretion to
,
we can approximate the formula for the mass
accretion to
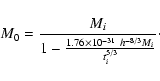 |
(23) |
The growth of mass of a CBH is then
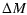 |
= |
M0-Mi |
|
| |
= |
![$\displaystyle M_{i}\left[\frac{1.76\times
10^{-31}~h^{-8/3}M_{i}\left(\frac{1}{...
...-8/3}M_{i}\left(\frac{1}{t_{0}^{5/3}}-\frac{1}{t_{i}^{5/3}}\right)}\right]\cdot$](/articles/aa/full/2004/24/aa0205/img60.gif) |
(24) |
For
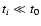 ,
we have
,
we have
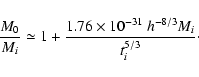 |
(25) |
Therefore, it is evident that the BH accretion is proportional to
its initial mass.
Voids are under-dense regions of space depleted of galaxies with
respect to the external background. We can estimate the amount of
such an under-density in the framework of our CBH-void model.
Taking into account the accretion process in the void, we cannot
neglect the fact that, as the void increases in volume, a certain
amount of galaxies enters in the void contributing to the total
mass inside the void. This implies that the accretion of mass
inside the void, given by Eq. (17), has to be
corrected to
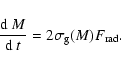 |
(26) |
The factor 2 can be justified in the following way.
If we consider any mass increment in Eq. (11), it is easy
to observe that the mass of galaxies entering the void is equal to
the mass increment of the black hole, if one takes into account
the conservation equation for
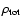 .
In a first
approximation, one can double the righthand side of
Eq. (17). To be rigorous, one should consider a delay
effect, since gravity does not propagate instantaneously. Due to
this, it would be correct to deal with this problem within the
standard of the General Relativity. However, it is possible to
show that the delay effect can be neglected, at least in first
approximation.
.
In a first
approximation, one can double the righthand side of
Eq. (17). To be rigorous, one should consider a delay
effect, since gravity does not propagate instantaneously. Due to
this, it would be correct to deal with this problem within the
standard of the General Relativity. However, it is possible to
show that the delay effect can be neglected, at least in first
approximation.
To find the density of galaxies
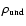 which enter
expanding voids, one has to subtract the accreted mass of the CBH,
obtained from Eq. (23), from the total final accretion
mass, given by Eq. (26), (in the approximation
which enter
expanding voids, one has to subtract the accreted mass of the CBH,
obtained from Eq. (23), from the total final accretion
mass, given by Eq. (26), (in the approximation
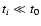 )
)
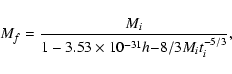 |
(27) |
and divide the result by the volume of the void taken as
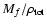 .
.
Finally, we find that
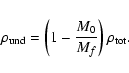 |
(28) |
The under-density is given by the contrast of the density of
galaxies in the void with the total density
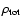 ,
i.e.
,
i.e.
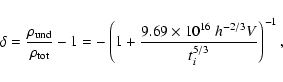 |
(29) |
where V is the volume of the void expressed in
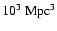 and ti is the initial time expressed
in seconds. From this last equation, we obtain the formula for the
initial time ti, which is
and ti is the initial time expressed
in seconds. From this last equation, we obtain the formula for the
initial time ti, which is
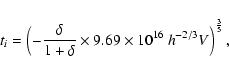 |
(30) |
where 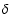 and V can be retrieved from the respective values
found in the catalogs (El-Ad & Piran 1997). On the other hand, we
can also determine the initial masses of the CBHs just after their
formation. This can be expressed by the formula
and V can be retrieved from the respective values
found in the catalogs (El-Ad & Piran 1997). On the other hand, we
can also determine the initial masses of the CBHs just after their
formation. This can be expressed by the formula
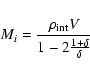 |
(31) |
where
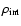 is the internal density of the void.
is the internal density of the void.
Using the data of the volume and the under-density of voids given
in the catalog of El-Ad & Piran (1997) which deduced their data
from SSRS2 (da Costa et al. 1988, 1994) and IRAS (Fisher et al. 1995)
observations, we found the following initial times and
corresponding initial and final masses according to formulas
(30, 31, 27).
Table 1:
Evolution of the properties
of the voids and black holes features derived from our model using
the data in El-Ad & Piran (1997).
The dynamics deduced from our model is consistent with the
observations and seems to confirm the gravitational origin of
voids. In this approach, the role of dark matter has to be revised
since most of the mass (about one half) of the structure is
concentred in the central CBH. In this picture, it is only the
density contrast between voids and background which drives the
dynamics. CBHs are just the remnant of primordial collapsed
perturbations while voids, or precisely the edges of voids, are
the result of perturbations of which the wavelength follows the
cosmic expansion. The whole system, also if expanding and
interacting with CBR, remains in equilibrium.
In this paper, we have developed a model where cosmological black
holes are seeds for large scale structure voids. Such systems are
a result of the evolution of primordial perturbations and become
stable structures from
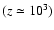 up to now. They enlarge
to diameters of about 40 h-1 Mpc and the under-density of voids
is of the order -0.9 with respect to the background. The whole
structure is a sort of honeycomb where most galaxies (i.e.
luminous matter) are located on the edge of the voids while most
dynamical mass is sited in the central black hole. The edge is
defined by a natural equilibrium condition for the energy due to
the balance of the gravitational pull of the central black hole
and the cosmic expansion. The cosmic background radiation
contributes to the accretion of the black hole but its
homogeneity and isotropy are not affected, in agreement with the
data. The picture which emerges agrees with optical and IRAS
observations (El-Ad & Piran 1997) giving a
up to now. They enlarge
to diameters of about 40 h-1 Mpc and the under-density of voids
is of the order -0.9 with respect to the background. The whole
structure is a sort of honeycomb where most galaxies (i.e.
luminous matter) are located on the edge of the voids while most
dynamical mass is sited in the central black hole. The edge is
defined by a natural equilibrium condition for the energy due to
the balance of the gravitational pull of the central black hole
and the cosmic expansion. The cosmic background radiation
contributes to the accretion of the black hole but its
homogeneity and isotropy are not affected, in agreement with the
data. The picture which emerges agrees with optical and IRAS
observations (El-Ad & Piran 1997) giving a 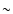
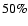 of the
volume filled by voids with the above characteristics. The
presence of central black holes seems to confirm the gravitational
origin of the voids and stabilizes the system against cosmic
expansion preventing its evaporation.
of the
volume filled by voids with the above characteristics. The
presence of central black holes seems to confirm the gravitational
origin of the voids and stabilizes the system against cosmic
expansion preventing its evaporation.
It is interesting to note that the order of magnitude observed for
the masses of CBH concides with that of the Great Attractor
(Fairall 1997). It is very tempting to identify the Great
Attractor as a CBH and to use the model described in this paper to
explain the large scale motions observed for the galaxies
surrounding it.
However, the main problem with observations of cosmic velocity
fields (Faber et al. 1994) is that the voids are, in general, the
opposite to the Great Attractor, and large scale structure around
the voids does not show velocity fields converging toward the
voids, but toward the visible clusters and superclusters around
the voids. This apparent shortcoming, in the framework of our
model (see also Stornaiolo 2002), can be overcome by the Birkoff
theorem which states that the stationary solutions are also static
if the spherical symmetry is restored. So, a fraction of galaxies
is attracted by clusters and superclusters "outside" the void
while another fraction shows no dynamics since it has been already
attracted "inside" the void. This fact could be interpreted as an
early selection due to a competitive mechanism between CBHs and
external matter contained in clusters and superclusters.
However, if the Swiss-Cheese model were always valid such a
selection would never have been achieved; instead, in a more
realistic situation, the model holds only approximately so then we
have to expect galaxies inside and outside the void due to the
deviations from sphericity and to the perturbations of the CBH
mass.
Furthermore, as observed in Davis & Peebles (1983) and Peebles
(2001), the small relative velocity dispersion shows that, if
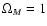 ,
then most of the mass has to be contained in the
voids. The same authors conjecture that this must be true even
when
,
then most of the mass has to be contained in the
voids. The same authors conjecture that this must be true even
when
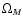 is smaller than 1 as predicted by several CDM simulations.
is smaller than 1 as predicted by several CDM simulations.
- Caldwell,
R. R., Dave, R., & Steinhardt, P. J. 1998, Phys. Rev. Lett.,
80, 1582 [NASA ADS] [CrossRef] (In the text)
-
Capozziello, S. 2002, Int. J. Mod. Phys. D, 11, 483 [NASA ADS] [MathSciNet] (In the text)
- Custodio, P. S.,
& Horvath, J. E. 2002, GRG, 34, 1895 (In the text)
- da Costa, L. N.,
Pellegrini, P. S., Sargent, W. L. W., et al. 1988, ApJ, 327,
544 [NASA ADS] [CrossRef] (In the text)
- da Costa, L. N.,
Geller, M. S., Pellegrini, P. S., et al. 1994, ApJ, 424, L1 [NASA ADS] [CrossRef]
- Davis, M., & Peebles,
P. J. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef] (In the text)
- de Bernardis, P.,
Ade, P. A. R., Bock, J. J., et al. 2000, Nature, 404, 955 [NASA ADS] [CrossRef] (In the text)
- de Ritis,
R., Marino, A. A., Rubano, C., & Scudellaro, P. 2000, Phys.
Rev. D, 62, 043506 [NASA ADS] [CrossRef] (In the text)
- Einstein, A.,
& Straus, E. G. 1945, Rev. Mod. Phys., 17, 120 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Einstein, A.,
& Straus, E. G. 1946, Rev. Mod. Phys., 18, 148 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- El-Ad, H.,
& Piran, T. 1997, ApJ, 491, 421 [NASA ADS] [CrossRef] (In the text)
- Faber, S. M, Courteau,
S., Dekel, A., et al. 1994, J. Roy. Astron. Soc. Can., 88(2)
(In the text)
- Fairall, A. 1997,
Large-scale structure in the Universe (Wiley-Praxis)
(In the text)
- Fisher, K. B., Huchra, J.
P., Strausss, M. A., et al. 1995, ApJS, 100, 69 [NASA ADS] [CrossRef] (In the text)
- Hoyle, F., & Vogeley,
M. S. 2002, ApJ, 566, 641 [NASA ADS] [CrossRef] (In the text)
- Kirshner R. P., Oemler,
A., Schechter, P. L., & Shectman, S. A. 1981, ApJ, 248,
L57 [NASA ADS] [CrossRef] (In the text)
- Loeb, A. 1993, ApJ, 403,
542 [NASA ADS] [CrossRef] (In the text)
- Mukhanov, V. F.,
Feldman, H. A., & Brandenberger, R. H. 1992, Phys. Rept., 215,
203 [NASA ADS] [MathSciNet] (In the text)
- Oppenheimer, J. R., &
Snyder, H. 1939, Phys. Rev., 57, 455 [NASA ADS]
- Peebles, P. J. E.
2001, ApJ, 557, 495 [NASA ADS] [CrossRef] (In the text)
- Perlmutter,
S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] (In the text)
- Rubano,
C., & Barrow, J. D. 2001, Phys. Rev. D, 64, 127301 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Schimdt, B.
P., Suntzeff, N. B., Phillips, M. M., et al. 1998, ApJ, 507,
46 [NASA ADS] [CrossRef] (In the text)
- Schmidt, J., Ryden, B. S.,
& Mellott, A. 2001, ApJ, 546, 609 [NASA ADS] [CrossRef] (In the text)
- Schneider, P., Ehlers, J.,
& Falco, E. E. 1992, Gravitational Lenses (Berlin:
Springer-Verlag)
(In the text)
- Stornaiolo, C. 2002,
GRG, 34, 2089 [MathSciNet] (In the text)
- Tegmark, M., Strauss, M.,
Blanton, M., et al., Cosmological parameters from SDSS and WMAP,
PRD, in press [arXiv:astro-ph/0310723]
(In the text)
- Zeldovich, Ya. B., &
Sazhin, M. V. 1987, Sov. Astron. Lett., 13, 145 [NASA ADS] (In the text)
Copyright ESO 2004
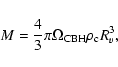
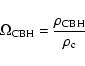
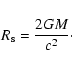
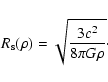
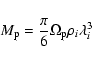
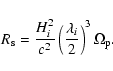
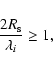
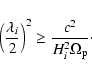
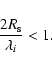
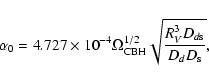
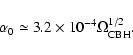
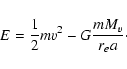
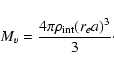
![\begin{displaymath}
E=\frac{m(r_{e}a)^{2}}{2}\left[H^{2} -\frac{8\pi
G\rho_{\rm int}}{3}\right]
\end{displaymath}](/articles/aa/full/2004/24/aa0205/img35.gif)
![\begin{displaymath}
E=\frac{m(r_{e}a)^{2}}{2}\left[ \frac{8\pi
G}{3}(\rho_{\rm tot}-\rho_{\rm int})\right].
\end{displaymath}](/articles/aa/full/2004/24/aa0205/img36.gif)
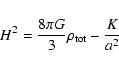
![\begin{displaymath}\
E=\frac{m(r_{e}a)^{2}}{2}\left[ \frac{8\pi
G}{3}(\rho_{\rm tot}-\rho_{\rm int})-\frac{K}{a^{2}}\right]\cdot
\end{displaymath}](/articles/aa/full/2004/24/aa0205/img42.gif)
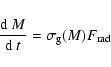
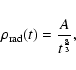
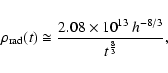
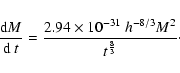
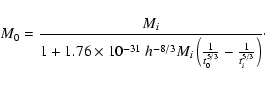
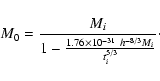
![$\displaystyle M_{i}\left[\frac{1.76\times
10^{-31}~h^{-8/3}M_{i}\left(\frac{1}{...
...-8/3}M_{i}\left(\frac{1}{t_{0}^{5/3}}-\frac{1}{t_{i}^{5/3}}\right)}\right]\cdot$](/articles/aa/full/2004/24/aa0205/img60.gif)