A&A 420, 881-888 (2004)
DOI: 10.1051/0004-6361:20034035
On the contribution of microlensing to X-ray variability of
high-redshifted QSOs
A. F. Zakharov
1,2,3,4 - L. C. Popovic5,6,7 -
P. Jovanovic5,7
1 - National Astronomical Observatories, Chinese Academy of Sciences,
100012 Beijing, China
2 - Institute of Theoretical and
Experimental Physics,
25 B.Cheremushkinskaya st., Moscow 117259, Russia
3 -
Astro Space
Centre of Lebedev Physics Institute, Moscow, Russia
4 - Isaac Newton
Institute of Chile,
Moscow Branch, Russia
5 - Astronomical Observatory, Volgina 7, 11160 Beograd, Serbia
6 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16,
14482 Potsdam, Germany
7 - Isaac Newton Institute of Chile,
Yugoslavia Branch, Yugoslavia
Received 2 July 2003 / Accepted 10 March 2004
Abstract
We consider a contribution of microlensing to the X-ray
variability of high-redshifted QSOs. Such an effect could be
caused by stellar mass objects (SMO) located in a bulge or/and in
a halo of this quasar as well as at cosmological distances
between an observer and a quasar. Here, we not consider
microlensing caused by deflectors in our Galaxy since it is
well-known from recent MACHO, EROS and OGLE observations that the
corresponding optical depth for the Galactic halo and the Galactic
bulge is lower than 10-6. Cosmologically distributed
gravitational microlenses could be localized in galaxies (or even
in bulge or halo of gravitational macrolenses) or could be
distributed in a uniform way. We have analyzed both cases of such
distributions. As a result of our analysis, we obtained that the
optical depth for microlensing caused by stellar mass objects is
usually small for quasar bulge and quasar halo gravitational
microlens distributions (
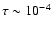 ). On the other hand,
the optical depth for gravitational microlensing caused by
cosmologically distributed deflectors could be significant and
could reach
10-2 - 0.1 at
). On the other hand,
the optical depth for gravitational microlensing caused by
cosmologically distributed deflectors could be significant and
could reach
10-2 - 0.1 at 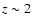 .
This means that
cosmologically distributed deflectors may contribute
significantlly to the X-ray variability of high-redshifted QSOs
(z>2). Considering that the upper limit of the optical depth
(
.
This means that
cosmologically distributed deflectors may contribute
significantlly to the X-ray variability of high-redshifted QSOs
(z>2). Considering that the upper limit of the optical depth
(
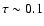 )
corresponds to the case where dark matter forms
cosmologically distributed deflectors, observations of the X-ray
variations of unlensed QSOs can be used for the estimation of the
dark matter fraction of microlenses.
)
corresponds to the case where dark matter forms
cosmologically distributed deflectors, observations of the X-ray
variations of unlensed QSOs can be used for the estimation of the
dark matter fraction of microlenses.
Key words: accretion, accretion disks - gravitational lensing - galaxies: quasars: general
The X-ray radiation of Active Galactic Nuclei (AGNs), in the
continuum as well as in
spectral lines, has rapid and irregular variability
(see e.g. Manners et al. 2002; Marshall et al. 1981; Weaver et al. 2001; Turner et al. 1999; Lawrence & Papadakis 1993; Green et al. 1993; Barr & Mushotzky 1986, etc.).
X-ray flux variability has long been known to be a common property of
active galactic nuclei (AGNs), e.g., Ariel 5 and HEAO 1 first
revealed long-term (days to years) variability in AGNs and
by uninterrupted observations of EXOSAT rapid (thousands of
seconds) variability was also established as common in these
sources (see, for example reviews by Mushotzky et al. 1993; Ulrich et al. 1993, and
references therein). X-ray flux variations are observed on
timescales from 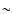 1000 s to years, and amplitude variations of
up to an order of magnitude are observed in the
1000 s to years, and amplitude variations of
up to an order of magnitude are observed in the 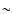 0.1-10 keV band. It was first suggested by Barr & Mushotzky (1986)
that the flux variation of an AGN is inversely
proportional to its luminosity.
Lawrence & Papadakis (1993) and Green et al. (1993) confirmed the
variability-luminosity relationship, finding that the variability
amplitude (
0.1-10 keV band. It was first suggested by Barr & Mushotzky (1986)
that the flux variation of an AGN is inversely
proportional to its luminosity.
Lawrence & Papadakis (1993) and Green et al. (1993) confirmed the
variability-luminosity relationship, finding that the variability
amplitude (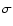 )
varies with luminosity as
)
varies with luminosity as
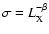 with
with
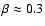 .
Recently, Manners et al. (2002)
analyzed the variability of a sample of 156 radio-quiet quasars
taken from the ROSAT archive, considering the trends in variability of the
amplitude with luminosity and with redshift. They found that there
were evidences for a growth in AGN X-ray variability amplitude
towards high redshift (z) in the sense that AGNs of the same
X-ray luminosity were more variable at z>2. They explained the
.
Recently, Manners et al. (2002)
analyzed the variability of a sample of 156 radio-quiet quasars
taken from the ROSAT archive, considering the trends in variability of the
amplitude with luminosity and with redshift. They found that there
were evidences for a growth in AGN X-ray variability amplitude
towards high redshift (z) in the sense that AGNs of the same
X-ray luminosity were more variable at z>2. They explained the
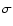 vs. z trend assuming that the high-redshifted
AGNs accreted at a larger fraction of the Eddington limit than
the low-redshifted ones.
vs. z trend assuming that the high-redshifted
AGNs accreted at a larger fraction of the Eddington limit than
the low-redshifted ones.
On the other hand, the contribution of microlensing to AGN variability was considered in many papers (see e.g.
Hawkins 2002; Zakharov 1997a; Hawkins 1993; Wambsganss 2001b,a, and references
therein). Moreover, recently X-ray microlensing of AGN has been
considered (Chartas et al. 2002a; Takahashi et al. 2001; Popovic et al. 2003,2001a; Dai et al. 2003). Taking into
account that the X-rays of AGNs are generated in the innermost and
very compact region of an accretiondisc, the X-ray radiation in
the continuum as well as in a line can be strongly affected by
microlensing (Popovic et al. 2003)![[*]](/icons/foot_motif.gif) .
.
Recent
observations of three lensed QSOs seem to support this idea
(Chartas et al. 2002a; Oshima et al. 2002; Dai et al. 2003). Popovic et al. (2003) showed that
objects in a foreground galaxy with very small masses can cause
strong changes in the X-ray line profile. This fact may
indicate that the observational probability of X-ray variation
due to microlensing events is higher than in
the UV and optical radiation of AGNs. This is connected with
the fact that typical sizes of X-ray emission regions are much
smaller than typical sizes of those producing optical and UV bands.
Typical optical and UV emission region sizes could be
comparable or even larger than Einstein radii of microlenses and
therefore microlenses magnify only a small part of the region emitting in
the optical or UV band (see e.g. Abajas et al. 2002; Popovic et al. 2001b, for UV and
optical spectral
line
region). This is reason that it could be a
very tiny effect from an observer point of view.
The aim of this paper is to discuss the contribution of
microlensing to the relation 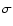 vs. z for X-ray radiation
considering
the recent results given by Manners et al. (2002) and Popovic et al. (2003). In
the next section we will consider the optical depth.
vs. z for X-ray radiation
considering
the recent results given by Manners et al. (2002) and Popovic et al. (2003). In
the next section we will consider the optical depth.
The optical depth 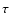 (the chance of seeing a microlens (ML))
is the probability that at any instant of time a source is covered
by the Einstein ring of a deflector. Here we will consider
deflectors from the host bulge and halo as well as at
cosmological distances between observer and source. We will
not consider microlensing caused by Galactic microlenses
since it is well-known from recent MACHO, EROS and OGLE
observations that the corresponding optical depth for Galactic halo
and Galactic bulge is lower than 10-6. Therefore, by analogy, one
could expect that the optical depth for microlensing due to
objects in the halo or/and bulge of a quasar is small (similar to
the optical depth for microlensing in the Galaxy). However, it would be
appropriate to present some more accurate estimates for optical depths for
microlensing by bulge/halo objects
assuming reasonable values for density distribution
of QSO bulges/halos. This is because, as we mentioned above,
the X-ray emission regions are much smaller than UV/optical ones, and
even small mass deflectors
from a QSO bulge/halo can produce significant magnification in the X-ray
radiation (Popovic et al. 2003),
while it will
not happen in the UV/optical band.
(the chance of seeing a microlens (ML))
is the probability that at any instant of time a source is covered
by the Einstein ring of a deflector. Here we will consider
deflectors from the host bulge and halo as well as at
cosmological distances between observer and source. We will
not consider microlensing caused by Galactic microlenses
since it is well-known from recent MACHO, EROS and OGLE
observations that the corresponding optical depth for Galactic halo
and Galactic bulge is lower than 10-6. Therefore, by analogy, one
could expect that the optical depth for microlensing due to
objects in the halo or/and bulge of a quasar is small (similar to
the optical depth for microlensing in the Galaxy). However, it would be
appropriate to present some more accurate estimates for optical depths for
microlensing by bulge/halo objects
assuming reasonable values for density distribution
of QSO bulges/halos. This is because, as we mentioned above,
the X-ray emission regions are much smaller than UV/optical ones, and
even small mass deflectors
from a QSO bulge/halo can produce significant magnification in the X-ray
radiation (Popovic et al. 2003),
while it will
not happen in the UV/optical band.
In this section we consider gravitational microlensing caused by stellar
mass objects in the bulge of an observed quasar. Of
course, to calculate an optical depth we have to know the radial
mass density distribution in the QSO bulge. In this case the optical
depth could be evaluated by the integral
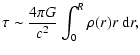 |
|
|
(1) |
where R is the bulge radius. For qualitative discussions of the
optical depth range we make the assumption of
constant mass density (see also
Popovic et al. 2003). Evaluating this integral, we obtain
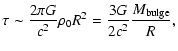 |
|
|
(2) |
where
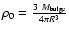 is the average
density of the bulge. It is clear that the maximal optical depth
corresponds to the most compact galactic bulge for a fixed bulge
mass.
For an estimate of the bulge mass use can be made of scaling from the
black hole mass; McLure & Dunlop (2002) give
is the average
density of the bulge. It is clear that the maximal optical depth
corresponds to the most compact galactic bulge for a fixed bulge
mass.
For an estimate of the bulge mass use can be made of scaling from the
black hole mass; McLure & Dunlop (2002) give
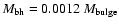 ,
and
Shields et al. (2003)
,
and
Shields et al. (2003)
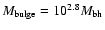 .
However, for Seyfert 1 galaxies ratios of
the central black hole mass and the bulge mass could be about
.
However, for Seyfert 1 galaxies ratios of
the central black hole mass and the bulge mass could be about
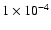 (Bian & Zhao 2003).
We can derive an upper limit from the estimate by
Czerny et al. (2001) that for
AGN
(Bian & Zhao 2003).
We can derive an upper limit from the estimate by
Czerny et al. (2001) that for
AGN
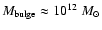 (with
(with
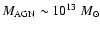 ,
Shields et al. 2002).
Schade et al. (2000) found typical values for the radii of AGN bulges
in the range 1-10 kpc. So, using the lower limit for the AGN
bulge radius and the total mass estimation
,
Shields et al. 2002).
Schade et al. (2000) found typical values for the radii of AGN bulges
in the range 1-10 kpc. So, using the lower limit for the AGN
bulge radius and the total mass estimation
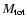 ,
we obtain an
upper limit of the optical depth for microlensing by bulge stellar
mass objects of
,
we obtain an
upper limit of the optical depth for microlensing by bulge stellar
mass objects of
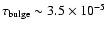 .
This
upper limit is about the value evaluated earlier (Popovic et al. 2003)
and the contribution to the total optical depth for microlensing
is small. Microlensing would thus be detectable only in a small
fraction of quasars.
.
This
upper limit is about the value evaluated earlier (Popovic et al. 2003)
and the contribution to the total optical depth for microlensing
is small. Microlensing would thus be detectable only in a small
fraction of quasars.
Here we assume a mass density distribution described
by a singular isothermal sphere model, namely
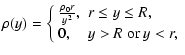 |
|
|
(3) |
where r is the inner and R is the outer radius of halo, and
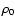 is the mass density at the inner radius r,
is the mass density at the inner radius r,
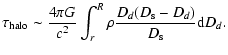 |
|
|
(4) |
Evaluating this integral, we obtain
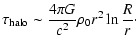 |
|
|
(5) |
The halo mass can be expressed as
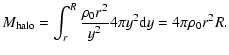 |
|
|
(6) |
Thus,
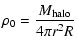 |
|
|
(7) |
and
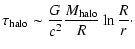 |
|
|
(8) |
Typical halo masses are in the range
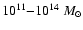 range (Ferrarese 2002; Bullock et al. 2001) and typical halo radii are R are
range (Ferrarese 2002; Bullock et al. 2001) and typical halo radii are R are
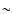 few
few
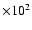 kpc (Ferrarese 2002; Klypin et al. 2002),
and typical inner radii
kpc (Ferrarese 2002; Klypin et al. 2002),
and typical inner radii 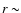 a few
a few 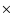 10 kpc
(Ferrarese 2002), we can estimate the optical depth using
these values. Assuming that
10 kpc
(Ferrarese 2002), we can estimate the optical depth using
these values. Assuming that
 ,
,
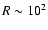 kpc and
kpc and 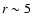 kpc we obtain
kpc we obtain
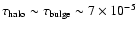 .
.
Let us calculate the optical depth for Navarro-Frenk-White
(NFW) halo profiles of mass density distributions. A
two-parameter form for halo profiles was proposed by
Navarro et al. (1995,1997,1996)
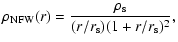 |
|
|
(9) |
where 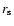 is a characteristic inner radius and
is a characteristic inner radius and
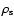 is the
corresponding inner density,
is the
corresponding inner density,
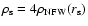 and
and
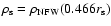 (Bullock et al. 2001), where
(Bullock et al. 2001), where
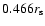 is the approximate solution of the equation
is the approximate solution of the equation
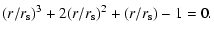 |
|
|
(10) |
Navarro et al. (1995,1997,1996) showed that these halo profiles provide
a good fit over a large range of masses and for several cosmological
scenarios (including a flat cosmological model with
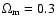 and
and
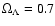 ). Bullock et al. (2001) confirmed the success of
this model at z=0, but mentioned that the NFW model significantly
over-predicts the concentration of halos at early times z >
1 and suggested some modifications of the NFW model. However,
we will use the standard NFW model.
). Bullock et al. (2001) confirmed the success of
this model at z=0, but mentioned that the NFW model significantly
over-predicts the concentration of halos at early times z >
1 and suggested some modifications of the NFW model. However,
we will use the standard NFW model.
One can calculate the halo mass
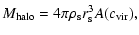 |
|
|
(11) |
where
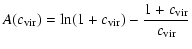 |
|
|
(12) |
and
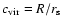 .
Using Eq. (4) and the NFW halo
profile, one obtains
.
Using Eq. (4) and the NFW halo
profile, one obtains
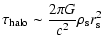 |
|
|
(13) |
and substituting
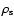 from Eq. (11)
from Eq. (11)
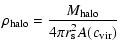 |
|
|
(14) |
we obtain
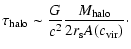 |
|
|
(15) |
Since typical
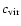 values are in the range 5-30,
values are in the range 5-30,
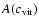 varies in the range 1-3, and
varies in the range 1-3, and
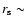 a
few
a
few 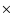 10 kpc (Ferrarese 2002). Assuming
10 kpc (Ferrarese 2002). Assuming
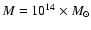 ,
,
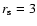 kpc,
kpc,
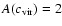 ,
we obtained
,
we obtained
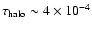 .
Therefore, the optical depth
estimates by Popovic et al. (2003) are realistic if we consider
objects inside the halo and/or
bulge. We recall that they found the optical depth to be in the range
10-4 - 10-3.
.
Therefore, the optical depth
estimates by Popovic et al. (2003) are realistic if we consider
objects inside the halo and/or
bulge. We recall that they found the optical depth to be in the range
10-4 - 10-3.
To estimate the optical depth we will use the point size source
approximation for an emitting region of X-ray radiation. This means
that the size of emitting region is smaller than this
Einstein-Chwolson radius. This approximation is used commonly to
investigate microlensing in optical and UV bands. The typical
Einstein-Chwolson radius of a lens can be expressed in
the following way (Wambsganss 2001a)
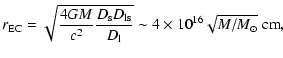 |
|
|
(16) |
where "typical" lens and source redshift of
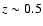 and
and 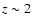 were chosen, M is the lens mass,
were chosen, M is the lens mass, 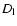 ,
,
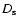 and
and
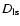 are angular diameter distances between observer and lens,
observer and source, lens and source respectively. A typical
quasar size is parameterized in units of 1015 cm (Wambsganss 2001a).
Since the point size source approximation for an emitting region
is reasonable for optical and for UV bands, and as it is generally adopted
that X-ray radiation is formed in the inner parts of accretion
disks we can use this an approximation for X-ray sources.
However, let us make some estimates. The relevant length scale
for microlensing in the source plane for this sample
are angular diameter distances between observer and lens,
observer and source, lens and source respectively. A typical
quasar size is parameterized in units of 1015 cm (Wambsganss 2001a).
Since the point size source approximation for an emitting region
is reasonable for optical and for UV bands, and as it is generally adopted
that X-ray radiation is formed in the inner parts of accretion
disks we can use this an approximation for X-ray sources.
However, let us make some estimates. The relevant length scale
for microlensing in the source plane for this sample
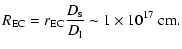 |
|
|
(17) |
Even if we consider a supermassive black hole in the center of the
quasar
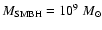 ,
then its Schwarzschild
radius is
,
then its Schwarzschild
radius is
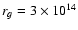 cm and assuming that the emission
region for the X-ray radiation is located near the black hole
cm and assuming that the emission
region for the X-ray radiation is located near the black hole
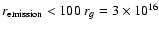 cm, we obtain that
cm, we obtain that
 ,
therefore the point size source
approximation can be adopted for the X-ray emitting
region
,
therefore the point size source
approximation can be adopted for the X-ray emitting
region![[*]](/icons/foot_motif.gif) . Note that sometimes this
approximation cannot be used
when the microlens lies in the bulge or halo of a quasar (see
previous subsections), because then the
Einstein-Chwolson radius would be about several astronomical units, since
we have
. Note that sometimes this
approximation cannot be used
when the microlens lies in the bulge or halo of a quasar (see
previous subsections), because then the
Einstein-Chwolson radius would be about several astronomical units, since
we have
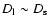 ,
,
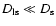 from Eqs. (16) and (17),
from Eqs. (16) and (17),
and
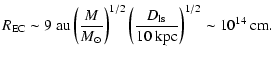 |
|
|
(18) |
In this case one has to take into account the size of the X-ray emission
region.
To evaluate the optical depth, we assume a source
located at
redshift
z.
The expression for optical depth has been taken from
Fukugita & Turner (1991); Turner et al. (1984); Wang et al. (1996)
![$\displaystyle \tau^p_{\rm L}= \frac{3}{2}\frac{\Omega_{\rm L}}{\lambda(z)}
\int...
...w)^3[\lambda(z)-\lambda(w)]\lambda(w)}
{\sqrt{\Omega_0(1+w)^3+\Omega_\Lambda}},$](/articles/aa/full/2004/24/aa0035/img83.gif) |
|
|
(19) |
where
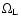 is the matter fraction in compact lenses,
is the matter fraction in compact lenses,
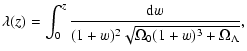 |
|
|
(20) |
is the affine distance (in units of
cH-10).
We will use some realistic cosmological parameters to evaluate the
integral (19). According to the cosmological SN
(Supernova) Ia data
and cosmic microwave background (CMB) anisotropy one can take
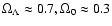 (Perlmutter et al. 1999; Peebles 2002; Balbi 2001; Bond et al. 2001; Lahav 2002). Recent CMB anisotropy
observations by the WMAP satellite team have confirmed important
aspects of the current standard cosmological model, the
WMAP team determined
(Perlmutter et al. 1999; Peebles 2002; Balbi 2001; Bond et al. 2001; Lahav 2002). Recent CMB anisotropy
observations by the WMAP satellite team have confirmed important
aspects of the current standard cosmological model, the
WMAP team determined
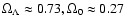 (Spergel et al. 2003; Bennett et al. 2003) for the "best" fit of
cosmological parameters (see also Bridle et al. 2003 for
discussion). Therefore we will assume
(Spergel et al. 2003; Bennett et al. 2003) for the "best" fit of
cosmological parameters (see also Bridle et al. 2003 for
discussion). Therefore we will assume
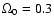 and
and
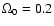 as realistic cases. If we assume that
microlensing is caused by stars we have to take into account
cosmological constraints on baryon density. Big Bang
Nucleosynthesis (BBN) calculations together with observational
data about the abundance of 2D give the following constraints on
the cosmic baryon density (O'Meara et al. 2001; Burles et al. 2001; Turner 2002)
as realistic cases. If we assume that
microlensing is caused by stars we have to take into account
cosmological constraints on baryon density. Big Bang
Nucleosynthesis (BBN) calculations together with observational
data about the abundance of 2D give the following constraints on
the cosmic baryon density (O'Meara et al. 2001; Burles et al. 2001; Turner 2002)
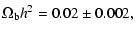 |
|
|
(21) |
taking into account the Hubble constant estimation
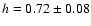 (Freedman et al. 2001). However,
Tammann & Reindl (2002b); Parodi et al. (2000); Tammann & Reindl (2002a) give lower limits for
(Freedman et al. 2001). However,
Tammann & Reindl (2002b); Parodi et al. (2000); Tammann & Reindl (2002a) give lower limits for
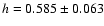 .
Therefore, using for example the estimate by
Freedman et al. (2001) one could obtain for the cosmic baryon density
(Turner 2002)
.
Therefore, using for example the estimate by
Freedman et al. (2001) one could obtain for the cosmic baryon density
(Turner 2002)
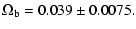 |
|
|
(22) |
Using CMB anisotropy data of
the BOOMERANG and MAXIMA-1 experiments Stompor et al. (2001) found that
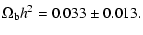 |
|
|
(23) |
An analysis of recent WMAP data on CMB anisotropy gives as the
best fit (Spergel et al. 2003)
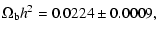 |
|
|
(24) |
which is very close to the BBN constraints, but with much
smaller error bars.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{0035f1a.eps}\vspace*{3mm}
...
...1b.eps}\vspace*{3mm}
\includegraphics[width=7.2cm,clip]{0035f1c.eps}\end{figure}](/articles/aa/full/2004/24/aa0035/Timg94.gif) |
Figure 1:
The calculated optical depth as a function of redshift
fordifferent value
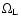 and
and 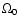 . . |
| Open with DEXTER |
Therefore, the cases with
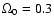 and
and
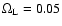 (
(
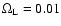 )
can be adopted as realistic (the top
panel in Fig. 1, here we assume that almost all baryon
matter and a small fraction of non-baryon matter
can form microlenses (
)
can be adopted as realistic (the top
panel in Fig. 1, here we assume that almost all baryon
matter and a small fraction of non-baryon matter
can form microlenses (
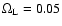 ), or, alternatively, that about
25% of
baryon matter forms such microlenses (
), or, alternatively, that about
25% of
baryon matter forms such microlenses (
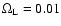 )).
However, for both cases and for distant objects (
)).
However, for both cases and for distant objects (
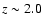 )
the optical depth could reach
)
the optical depth could reach
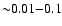 (see Table 1
and Fig. 1). If about
30% of non-baryonic dark matter forms objects with stellar
masses,
(see Table 1
and Fig. 1). If about
30% of non-baryonic dark matter forms objects with stellar
masses,
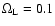 can be adopted, and
then
can be adopted, and
then
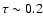 at
at 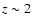 .
The optical depths for realistic values of
.
The optical depths for realistic values of
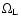 as
a function of redshift are presented in Table 1.
The middle and bottom
panels of Fig. 1 show the optical depth as a funciton of
redshift for chosen cosmological parameters (densities).
as
a function of redshift are presented in Table 1.
The middle and bottom
panels of Fig. 1 show the optical depth as a funciton of
redshift for chosen cosmological parameters (densities).
Recently, Wyithe & Turner (2002a) considered probability distributions for
the cases when lensing objects are concentrated in galaxies. The
authors found that about 1% of high-redshift sources (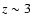 )
are microlensed by stars at any time. The microlensing rate
by stars in elliptical/S0 galaxies is 10 times higher than in
spiral galaxies. Multiple imaged sources dominate the stellar
microlensing statistics. However, if CDM halos are composed of
compact objects, Wyithe & Turner (2002a) concluded that the microlensing rate
should be about 0.1, i.e.
)
are microlensed by stars at any time. The microlensing rate
by stars in elliptical/S0 galaxies is 10 times higher than in
spiral galaxies. Multiple imaged sources dominate the stellar
microlensing statistics. However, if CDM halos are composed of
compact objects, Wyithe & Turner (2002a) concluded that the microlensing rate
should be about 0.1, i.e. 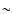 1 high-redshift source out of 10 is
microlensed at any time.
1 high-redshift source out of 10 is
microlensed at any time.
Table 1:
The calculated optical depth as a function of redshift
fordifferent values of
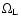 and
and
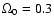 .
.
Wyithe & Turner (2002b) calculated variability rates for a hypothetical
survey. Let us recall their results. For a limiting quasar
magnitude mB=21 the authors found that the probability that a
quasar could show a variability larger than mB=0.5 due to microlensing
by stars is about
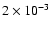 (the
cosmological density of stars is assumed to be equal to
(the
cosmological density of stars is assumed to be equal to
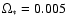 ). 90% of these events are in multiple-imaged
systems. Therefore, microlenses in gravitational lenses forming
multiple-imaged quasars dominate in these statistics.
Assuming that a dark halo (truncated so that the total mass density
equals the critical density) is also composed of compact
objects, the fraction of quasar images which exhibit
microlensing variability larger than mB=0.5 rises to
). 90% of these events are in multiple-imaged
systems. Therefore, microlenses in gravitational lenses forming
multiple-imaged quasars dominate in these statistics.
Assuming that a dark halo (truncated so that the total mass density
equals the critical density) is also composed of compact
objects, the fraction of quasar images which exhibit
microlensing variability larger than mB=0.5 rises to 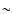 10%.
Thus, Wyithe & Turner (2002b) pointed out that the comparison of lensed
and un-lensed quasars will provide a powerful test for dark compact
objects in the halo.
10%.
Thus, Wyithe & Turner (2002b) pointed out that the comparison of lensed
and un-lensed quasars will provide a powerful test for dark compact
objects in the halo.
Just after the discovery of the first multiple-imaged quasar
QSO 0957+561 A,B by Walsh et al. (1979) the idea of microlensing by low
mass stars in a heavy halo was suggested by Gott (1981). First
evidence of quasar microlensing was found by Irwin et al. (1989). Now
there is a number of known gravitational lens systems
(Claeskens & Surdej 2002; Browne et al. 2003) and some of them show evidence
for microlensing (Wambsganss 2001a).
In this subsection we consider the optical depth for gravitational
microlensing in multiple-imaged quasars. There is many approaches
to calculate probability for this case. See for
example, the papers by Deguchi & Watson (1987); Seitz & Schneider (1994); Neindorf (2003); Seitz et al. (1994).
Here we will present some rough estimates for such a phenomenon, using
calculations by Wang et al. (1996); Turner (1990) for a flat universe
with 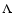 -term. According to Turner (1990)
-term. According to Turner (1990)
![$\displaystyle \tau_{\rm GL}= \frac{F}{30} \left[\int_1^y \frac{{\rm d}w}{(\Omega_0
w^3-\Omega_0+1)^{1/2}}\right]^3,$](/articles/aa/full/2004/24/aa0035/img106.gif) |
|
|
(25) |
where
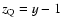 (
(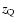 is the quasar redshift) and
is the quasar redshift) and
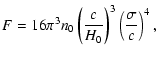 |
|
|
(26) |
F characterizes the gravitational lens effectiveness, 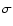 is the one-dimensional velocity dispersion and n0 is the co-moving
space density. According to Turner et al. (1984); Turner (1990) the
effectiveness F can be chosen to be F=0.15. As was shown by
Turner (1990), for the most popular cosmological model
is the one-dimensional velocity dispersion and n0 is the co-moving
space density. According to Turner et al. (1984); Turner (1990) the
effectiveness F can be chosen to be F=0.15. As was shown by
Turner (1990), for the most popular cosmological model
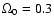 and a distant quasar
and a distant quasar
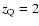 the optical depth
could be about 0.01. In Fig. 2 the optical depth
as a function of cosmological redshift
is given. As one can see from Fig. 2, the optical depth has similar trend
as in the case of cosmologically distributed objects.
the optical depth
could be about 0.01. In Fig. 2 the optical depth
as a function of cosmological redshift
is given. As one can see from Fig. 2, the optical depth has similar trend
as in the case of cosmologically distributed objects.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{0035f2.eps}\end{figure}](/articles/aa/full/2004/24/aa0035/Timg111.gif) |
Figure 2:
The calculated optical depth for gravitational
macrolensing
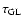 as a function of redshift for the most
realistic cosmological matter density
as a function of redshift for the most
realistic cosmological matter density
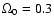 . . |
| Open with DEXTER |
If we try to find the microlensing phenomenon in multiply imaged
quasars, we should recall that Wyithe & Turner (2002b) showed that
if we restrict ourselves to quasars for which the sum of the
macro-images is brighter than mB=21, one image in three
multiply imaged quasars should vary by more than 0.5 mag during 10
years of monitoring. This means that roughly speaking the probability of
microlensing for multiple imaged quasars is about 0.3.
More than 10 years ago Hawkins (1993) (see also Hawkins 2002,1996)
put
forward the idea that nearly all quasars are being microlensed.
Recently, Hawkins (2002) considered three basic models to
explain AGN variability: the disc instability model proposed by
Rees (1984),
the starburst model developed by Aretxaga & Terlevich (1994)
as an alternative, and finally the idea
that the observed variations are not intrinsic to the AGN, but a
result of gravitational microlensing by stellar mass objects along
the line of sight (Hawkins 1993). Suggesting that different mechanisms
dominate in different luminosity regimes Hawkins (2002) divided AGN
into two categories, quasars with MB < -23 and Seyfert galaxies
with MB > -23.
To distinguish different models of variability Hawkins (2002) used
quantitative predictions for the statistics of AGN variability
based on structure functions of Kawaguchi et al. (1998). Hawkins (2002) analyzed
about 1500 quasars in the central 19 deg2 of ESO/SERC Field 287 up
to magnitude BJ=22, and 610 have been confirmed
with
redshifts. The structure function was calculated for a sample of 401
quasars from the survey of Hawkins (1996). For
comparison he considered the results of monitoring Seyfert galaxy
NGC 5548 and a sample of 45 Seyfert galaxie from the survey of
Hawkins (1996). He calculated structure function slopes of two
classes of AGN and found that the slope is
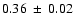 for
Seyfert galaxies and
for
Seyfert galaxies and
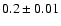 for quasars. Since the model
prescriptions give structure function slopes of
for quasars. Since the model
prescriptions give structure function slopes of
 for the starburst model,
for the starburst model,
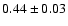 for the disc instability
model and
for the disc instability
model and
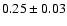 for microlensing,
the observational results favor the disc
instability model for Seyfert galaxies, and the microlensing model
for quasars. The starburst and disc
instability models are ruled out for quasars, while the microlensing model
is
in good agreement with the observations. As was shown by
Hawkins (1996) the cosmological density of microlenses should be
comparable with the critical density or at least with
for microlensing,
the observational results favor the disc
instability model for Seyfert galaxies, and the microlensing model
for quasars. The starburst and disc
instability models are ruled out for quasars, while the microlensing model
is
in good agreement with the observations. As was shown by
Hawkins (1996) the cosmological density of microlenses should be
comparable with the critical density or at least with
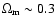 .
However, the analysis of the
structural function only cannot confirm or rule out the hypothesis
of microlensing origin of quasar variability, but it is an additional
argument in favor of the microlensing model.
.
However, the analysis of the
structural function only cannot confirm or rule out the hypothesis
of microlensing origin of quasar variability, but it is an additional
argument in favor of the microlensing model.
As was mentioned earlier by Popovic et al. (2003) the probability of
microlensing by stars or other compact objects in halos and bulges of
quasars is very low (about
10-4 - 10-3). However, for
cosmologically distributed microlenses it could reach
10-2 - 0.1 at
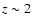 .
The
upper limit
.
The
upper limit
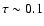 corresponds to the case where
compact dark matter forms cosmologically distributed microlenses.
As one can see from Fig. 1, in this case the optical
depth for the considered value of
corresponds to the case where
compact dark matter forms cosmologically distributed microlenses.
As one can see from Fig. 1, in this case the optical
depth for the considered value of 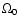 is around 0.1 for
z > 2. This indicates that such a phenomenon could be observed
frequently, but only for
distant sources (
is around 0.1 for
z > 2. This indicates that such a phenomenon could be observed
frequently, but only for
distant sources (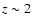 ). Moreover, it is in good agreement with
the trend in the variability amplitude with redshift found by
Manners et al. (2002), where
AGNs of the same X-ray luminosity are more variable at z>2.
). Moreover, it is in good agreement with
the trend in the variability amplitude with redshift found by
Manners et al. (2002), where
AGNs of the same X-ray luminosity are more variable at z>2.
To investigate distortions of spectral line shapes due to
microlensing (Popovic et al. 2003) the most promising candidates are
multiply imaged quasars, since the corresponding probability could
be about 0.3 (for magnification of one image
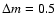 during 10 years). However,
these cases the simple point-like microlens model may not be very good
approximation (Wambsganss 2001b,a) and one should use a numerical
approach, such as the MICROLENS ray tracing program, developed by
Wambsganss (Wyithe & Turner 2002b), or some analytical approach
for magnification near caustic curves like folds
(Fluke & Webster 1999; Schneider et al. 1992) or near singular caustic points like
cusps (Mao 1992; Zakharov 1997b,1999,1995; Schneider & Weiss 1992)
as was realized by Yonehara (2001).
during 10 years). However,
these cases the simple point-like microlens model may not be very good
approximation (Wambsganss 2001b,a) and one should use a numerical
approach, such as the MICROLENS ray tracing program, developed by
Wambsganss (Wyithe & Turner 2002b), or some analytical approach
for magnification near caustic curves like folds
(Fluke & Webster 1999; Schneider et al. 1992) or near singular caustic points like
cusps (Mao 1992; Zakharov 1997b,1999,1995; Schneider & Weiss 1992)
as was realized by Yonehara (2001).
If we believe in the observational arguments of Hawkins (2002) that the
variability of a significant fraction of distant quasars is caused by
microlensing, the analysis of the properties of X-ray line shapes
due to microlensing (Popovic et al. 2003) is a powerful tool to
confirm or rule out Hawkins' (2002) conclusions.
Table 2:
The calculated optical depths (
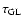 and
and
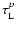 for 3 gravitational lensed objects). The used parameters
are:
for 3 gravitational lensed objects). The used parameters
are:
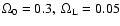 ,
F=0.15.
,
F=0.15.
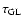 is the
optical depth for macrolensing for quasars located at the same
redshifts as the gravitational lensed objects.
is the
optical depth for macrolensing for quasars located at the same
redshifts as the gravitational lensed objects.
As it was mentioned, the probability that the shape of the Fe K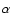 line is distorted (or amplified) is highest in gravitationally lensed
systems.
Actually, this phenomenon was
discovered by Chartas et al. (2002a,2004,2002b); Oshima et al. (2002); Dai et al. (2003) who found
evidence for such an effect for QSO H1413+117 (the Cloverleaf,
z=2.56), QSO 2237+0305 (the Einstein Cross, z=1.695), MG J0414+0534 (z=2.64) and possibly for BAL QSO 08279+5255 (z=3.91). Let us consider quasars located at the same redshifts as
the gravitational lensed objects. The probabilities that these
quasars are gravitationally microlensed by objects in a foreground
galaxy (
line is distorted (or amplified) is highest in gravitationally lensed
systems.
Actually, this phenomenon was
discovered by Chartas et al. (2002a,2004,2002b); Oshima et al. (2002); Dai et al. (2003) who found
evidence for such an effect for QSO H1413+117 (the Cloverleaf,
z=2.56), QSO 2237+0305 (the Einstein Cross, z=1.695), MG J0414+0534 (z=2.64) and possibly for BAL QSO 08279+5255 (z=3.91). Let us consider quasars located at the same redshifts as
the gravitational lensed objects. The probabilities that these
quasars are gravitationally microlensed by objects in a foreground
galaxy (
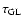 )
and by cosmologically distributed objects
(
)
and by cosmologically distributed objects
(
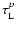 )
are given in Table 2 (if we have no a priori information about gravitational macrolensing for the
quasars). One
can see from Table 2
that the optical depth for
microlensing by cosmologically distributed microlenses are one
order higher than for microlensing by objects in a foreground
galaxy. So the observed microlensing in the X-ray Fe K
)
are given in Table 2 (if we have no a priori information about gravitational macrolensing for the
quasars). One
can see from Table 2
that the optical depth for
microlensing by cosmologically distributed microlenses are one
order higher than for microlensing by objects in a foreground
galaxy. So the observed microlensing in the X-ray Fe K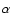 line from these objects should be caused by cosmologically
distributed objects rather than by the objects from a lensed
galaxy. For example, in the case of the redshift corresponding to
the famous Einstein Cross
QSO 2237+0305 where the optical depth is smaller than for other
two redshifts.
One could say that it is
natural that the discovery of X-ray microlensing was made for this
quasar, since the Einstein Cross QSO 2237+0305 is the
most "popular" object to search for microlensing, because the
first cosmological microlensing phenomenon was found by
Irwin et al. (1989) in this object and several groups have been
monitoring the quasar QSO 2237+0305 to find evidence for
microlensing. Microlensing has been suggested for the quasar
MG J0414+0534 (Angonin-Willaime et al. 1999) and for the quasar QSO H1413+117
(Ostensen et al. 1997; Chae et al. 2001; Remy et al. 1996; Turnshek et al. 1997). Therefore,
in future may be a chance to find X-ray microlensing for other
gravitationally lensed systems that have signatures of
microlensing in the optical and radio bands. Moreover, considering the
sizes of the sources of
X-ray radiation, the variability in the X-ray range during microlensing
event
should be more prominent than in the optical and UV.
Consequently, gravitational microlensing in the X-ray band
is a powerful tool for
dark matter investigations, as the upper limit of optical
depth (
line from these objects should be caused by cosmologically
distributed objects rather than by the objects from a lensed
galaxy. For example, in the case of the redshift corresponding to
the famous Einstein Cross
QSO 2237+0305 where the optical depth is smaller than for other
two redshifts.
One could say that it is
natural that the discovery of X-ray microlensing was made for this
quasar, since the Einstein Cross QSO 2237+0305 is the
most "popular" object to search for microlensing, because the
first cosmological microlensing phenomenon was found by
Irwin et al. (1989) in this object and several groups have been
monitoring the quasar QSO 2237+0305 to find evidence for
microlensing. Microlensing has been suggested for the quasar
MG J0414+0534 (Angonin-Willaime et al. 1999) and for the quasar QSO H1413+117
(Ostensen et al. 1997; Chae et al. 2001; Remy et al. 1996; Turnshek et al. 1997). Therefore,
in future may be a chance to find X-ray microlensing for other
gravitationally lensed systems that have signatures of
microlensing in the optical and radio bands. Moreover, considering the
sizes of the sources of
X-ray radiation, the variability in the X-ray range during microlensing
event
should be more prominent than in the optical and UV.
Consequently, gravitational microlensing in the X-ray band
is a powerful tool for
dark matter investigations, as the upper limit of optical
depth (
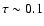 )
corresponds to the case where dark matter forms
cosmologically distributed deflectors. On the other hand, one can see from
Table 2 that, if we have no a priori information
about gravitational lensing of distant quasars, the expected
variabilities in the X-ray band due to microlensing tend to
be the same for the lensed and unlensed QSOs at the same
redshift. This means that cosmologically distributed deflectors play the
main
role in microlensing of high redshifted QSOs. The comparison of X-ray
variation in lensed and unlensed QSOs at the same redshift can provide a
powerful test for the cosmologically distribution of the dark compact
objects.
The observed rate of
microlensing can be used for estimates of the cosmological density of
microlenses (see, for example, Sect. 2.3), but durations of
microlensing events could be used to estimate microlens masses
(Wambsganss 2001b,a).
)
corresponds to the case where dark matter forms
cosmologically distributed deflectors. On the other hand, one can see from
Table 2 that, if we have no a priori information
about gravitational lensing of distant quasars, the expected
variabilities in the X-ray band due to microlensing tend to
be the same for the lensed and unlensed QSOs at the same
redshift. This means that cosmologically distributed deflectors play the
main
role in microlensing of high redshifted QSOs. The comparison of X-ray
variation in lensed and unlensed QSOs at the same redshift can provide a
powerful test for the cosmologically distribution of the dark compact
objects.
The observed rate of
microlensing can be used for estimates of the cosmological density of
microlenses (see, for example, Sect. 2.3), but durations of
microlensing events could be used to estimate microlens masses
(Wambsganss 2001b,a).
For a discussion of the contribution of microlensing to the X-ray
variability of high-redshift QSOs we calculated optical depth
considering the density of deflectors in the halo and bulge of
the host galaxy as well as for a cosmological distribution of
microdeflectors.
From our calculations we can conclude:
-
- i)
- The optical depth in the bulge and halo of host galaxy is
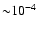 .
This is in good agreement with previous estimates by
Popovic et al. (2003).
Microlensing by deflectors from the host galaxy halo and
bulge makes a minor contribution to the X-ray
variability of QSOs.
.
This is in good agreement with previous estimates by
Popovic et al. (2003).
Microlensing by deflectors from the host galaxy halo and
bulge makes a minor contribution to the X-ray
variability of QSOs.
- ii)
- The optical depth for cosmologically distributed deflectors could
be
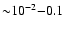 at
at 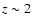 and might contribute significantly
to the
X-ray variability of high-redshift QSOs. The value
and might contribute significantly
to the
X-ray variability of high-redshift QSOs. The value
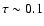 corresponds to the
case where compact dark matter forms cosmologically distributed
microlenses.
corresponds to the
case where compact dark matter forms cosmologically distributed
microlenses.
- iii)
- The optical depth for cosmologically distributed deflectors (
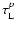 )
is higher for z>2 and increases slowly beyond z=2.
This indicates that the contribution of microlensing on the
X-ray variability of QSOs with redshift z>2 may be significant,
and also that this contribution could be nearly constant for
high-redshift QSOs. This is in good agreement with the fact that
AGNs of the same X-ray luminosity are more variable at z>2(Manners et al. 2002).
)
is higher for z>2 and increases slowly beyond z=2.
This indicates that the contribution of microlensing on the
X-ray variability of QSOs with redshift z>2 may be significant,
and also that this contribution could be nearly constant for
high-redshift QSOs. This is in good agreement with the fact that
AGNs of the same X-ray luminosity are more variable at z>2(Manners et al. 2002).
- iv)
- Observations of X-ray variations of unlensed QSOs can be used
for estimations of matter fraction of microlenses.
The rate of
microlensing can be used for estimates of the cosmological density of
microlenses, and consequently (see Sect. 2.3) the fraction of dark
matter microlenses, but the durations of microlensing events could be used
for gravitational microlens mass estimations.
Acknowledgements
This work was supported by the National Natural Science Foundation
of China (No.:10233050) (A.F.Z.), the Ministry of Science,
Technologies and Development of Serbia through the project
"Astrophysical Spectroscopy of Extragalactic Objects" (L.C.P. &
P.J.) and the Alexander von Humboldt Foundation through the program for
foreign scholars (L.C.P.).
A.F.Z. is grateful to E. F. Zakharova for the kindness and support
necessary to complete this work. A.F.Z. would like to thank the
National Astronomical Observatories of the Chinese Academy of
Sciences for their hospitality and prof. J. Wang and Dr.
Z. Ma for very
useful discussions.
The authors are grateful to an anonymous referee for very useful
remarks.
- Abajas, C., Mediavilla,
E. G., Muñoz, J. A., Popovic, L. C., & Oscoz, A. 2002,
ApJ, 576, 640 [NASA ADS] [CrossRef]
- Angonin-Willaime,
M.-C., Vanderriest, C., Courbin, F., et al. 1999, A&A,
347, 434 [NASA ADS] (In the text)
- Aretxaga, I., &
Terlevich, R. 1994, MNRAS, 269, 462 [NASA ADS] (In the text)
- Balbi, A. 2001, in
Cosmology and particle physics, ed. R. Durrer et al., AIP
Conf. Proc., 555, 107
- Barr, P., &
Mushotzky, R. F. 1986, Nature, 320, 421 [NASA ADS]
- Bennett, C. L., Halpern,
M., Hinshaw, G., et al. 2003, ApJ, accepted
[arXiv:astro-ph/0302207]
- Bian, W.-H., &
Zhao, Y.-H. 2003, Chin. J. Astron. Astrophys., 3, 119 [NASA ADS] (In the text)
- Bond, J. R., Pogosyan,
D., Prunet, S., et al. 2001, in Cosmology and particle
physics, ed. R. Durrer et al., AIP Conf. Proc., 555, 263
- Bridle, S. L.,
Lahav, O., Ostriker, J. P., & Steinhardt, P. J. 2003, Science,
299, 1532 [NASA ADS] [CrossRef] (In the text)
- Browne, I. W. A.,
Wilkinson, P. N., Jackson, N. J. F., et al. 2003, MNRAS, 341,
13 [NASA ADS] [CrossRef]
- Bullock, J. S.,
Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [NASA ADS] [CrossRef]
- Burles, S.,
Nollett, K., & Turner, M. S. 2001, ApJ, 552, L1 [NASA ADS] [CrossRef]
- Chae, K.-H., Turnshek,
D. A., Schulte-Ladbeck, R. E., et al. 2001, ApJ, 568, 509 [NASA ADS]
- Chartas, G., Agol,
E., Eracleous, M., et al. 2002a, ApJ, 568, 509 [NASA ADS] [CrossRef]
- Chartas, G., Brandt, W.
N., Gallagher, S. M., & Garmire, G. P. 2002b, ApJ, 579,
169 [NASA ADS] [CrossRef]
- Chartas, G., Eracleous,
M., Agol, E., & Gallagher, S. C. 2004, ApJ, accepted
[arXiv:astro-ph/0401240]
- Claeskens, J.
F., & Surdej, J. 2002, A&ARv, 10, 263 [NASA ADS]
- Czerny, B.,
Nikolajuk, M., Piasecki, M., & Kuraszkiewicz, J. 2001, MNRAS,
325, 865 [NASA ADS] [CrossRef] (In the text)
- Dai, X., Chartas, G.,
Agol, E., Bautz, M. W., & Garmire, G. P. 2003, ApJ, 589,
100 [NASA ADS] [CrossRef]
- Deguchi, S.,
& Watson, W. D. 1987, Phys. Rev. Lett., 59, 2814 [NASA ADS] [CrossRef]
- Ferrarese, L.
2002, ApJ, 578, 90 [NASA ADS] [CrossRef]
- Fluke, C. J., &
Webster, R. L. 1999, MNRAS, 302, 68 [NASA ADS] [CrossRef]
- Freedman, W.
L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553,
47 [NASA ADS] (In the text)
- Fukugita, M., &
Turner, E. L. 1991, MNRAS, 253, 99 [NASA ADS]
- Irwin, M. J.,
Webster, R. L., Hewett, P. C., et al. 1989, AJ, 98, 1989 [NASA ADS] [CrossRef] (In the text)
- Hawkins, M. R. S. 1993,
Nature, 366, 242 [NASA ADS] [CrossRef]
- Hawkins, M. R. S. 1996,
MNRAS, 278, 787 [NASA ADS]
- Hawkins, M. R. S. 2002,
MNRAS, 329, 76 [NASA ADS] [CrossRef]
- Gott, J. R. 1981, ApJ,
243, 140 [NASA ADS] [CrossRef] (In the text)
- Green, A. R., McHardy, I.
M., & Lehto, H. J. 1993, MNRAS, 265, 664 [NASA ADS]
- Kawaguchi, T.,
Mineshige, S., Umemura, M., & Turner, E. L. 1998, ApJ, 504,
671 [NASA ADS] [CrossRef] (In the text)
- Klypin, A. A.,
Zhao, H., & Somerville, R. S. 2002, ApJ, 573, 597 [NASA ADS]
- Lahav, O. 2002
[arXiv:astro-ph/0208297]
- Lawrence, A., &
Papadakis, I. 1993, ApJ, 414, 85 [NASA ADS] [CrossRef]
- Manners, J., Almaini, O.,
& Lawrence, A. 2002, MNRAS, 330, 390 [NASA ADS] [CrossRef]
- Marshall, N., Warwick, R.
S., & Pounds, K. A. 1981, MNRAS, 194, 987 [NASA ADS]
- Mao, S. 1992, ApJ, 389,
63 [NASA ADS]
- McLure, R. J.,
& Dunlop, J. S. 2002, MNRAS, 331, 795 [NASA ADS] [CrossRef] (In the text)
- Mushotzky, R. F., Done,
C., & Pounds, K. A. 1993, ARA&A, 31, 717 [NASA ADS]
- Navarro, J. F., Frenk, C.
S., & White, S. D. M. 1995, MNRAS, 275, 56 [NASA ADS]
- Navarro, J. F., Frenk, C.
S., & White, S. D. M. 1996, MNRAS, 462, 563 [NASA ADS]
- Navarro, J. F., Frenk, C.
S., & White, S. D. M. 1997, MNRAS, 490, 493 [NASA ADS]
- Neindorf, B.
2003, A&A, 404, 83 [EDP Sciences] [NASA ADS] [CrossRef]
- O'Meara, J. M.,
Tytler, D., Kirkman, D., et al. 2001, ApJ, 552, 718 [NASA ADS] [CrossRef]
- Oshima, T., Mitsuda, K.,
Fujimoto, R., et al. 2001, ApJ, 563, L103 [NASA ADS] [CrossRef]
- Ostensen, R.,
Remy, M., Lindblad, P. O., et al. 1997, A&AS, 126,
393 [NASA ADS]
- Parodi, B. R.,
Saha, A., Sandage, A., & Tammann, G. A. 2000, ApJ, 540,
634 [NASA ADS] [CrossRef]
- Peebles, P. J. E.
2002 [arXiv:astro-ph/0208037]
- Perlmutter, S., Aldering,
G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef]
- Popovic, L. C.,
Mediavilla, E. G., Muñoz, J., Dimitrijevic, M. S., &
Jovanovic, P. 2001a, Serb. Aston. J., 164, 73 [NASA ADS] (Also, presented on
GLITP Workshop on Gravitational Lens Monitoring, 4-6 June
2001, La Laguna, Tenerife, Spain)
- Popovic, L. C.,
Mediavilla, E. G., & Muñoz, J. 2001b, A&A, 378,
295 [EDP Sciences] [NASA ADS] [CrossRef]
- Popovic, L. C.,
Mediavilla, E. G., Jovanovic, P., & Muñoz, J. A. 2003,
A&A, 398, 975 [EDP Sciences] [NASA ADS] [CrossRef]
- Rees, M. 1984,
ARA&A, 22, 471 [NASA ADS] (In the text)
- Remy, M., Gosset, E.,
Hutsemekers, D., et al. 1996, in Astrophysical applications of
gravitational lensing: Proc. of the 173rd IAU Symp., ed. C. S.
Kochanek, & J. N. Hewitt (Dordrecht: Kluwer Academic
Publishers), 261
- Schade, D. J.,
Boyle, B. J., & Letawsky, M. 2000, MNRAS, 194, 987 [NASA ADS] (In the text)
- Schneider,
P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses
(Berlin: Springer)
- Schneider,
P., & Weiss, A. 1992, A&A, 260, 1 [NASA ADS] [MathSciNet]
- Seitz, C., &
Schneider, P. 1994, A&A, 288, 1 [NASA ADS]
- Seitz, C.,
Wambsganss, J., & Schneider, P. 1994, A&A, 335, 379 [NASA ADS]
- Spergel, D. N., Verde,
L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef]
- Shields, G. A.,
Gebhard, K., Salviander, S., et al. 2003, ApJ, 583, 124 [NASA ADS] [CrossRef] (In the text)
- Stompor, R.,
Abroe, M., Ade, P., et al. 2001, ApJ, 561, L7 [NASA ADS] [CrossRef] (In the text)
- Takahashi, R., Yonehara,
A., & Mineshige, S. 2001, PASJ, 53, 387 [NASA ADS]
- Tammann, G. A.,
& Reindl, B. 2002a, Ap&SS, 280, 165 [NASA ADS]
- Tammann, G. A.,
& Reindl, B. 2002b [arXiv:astro-ph/0208176]
- Turner, E. L. 1990,
ApJ, 365, L43 [NASA ADS] [CrossRef]
- Turner, E. L., Ostriker,
J. P., & Gott, J. R. 1984, ApJ, 284, 1 [NASA ADS]
- Turner, M. S. 2002,
ApJ, 576, L101 [NASA ADS] [CrossRef]
- Turner, T. J., George, I.
M., Nandra, K., & Turcan, D. 1999, ApJ, 524, 667 [NASA ADS] [CrossRef]
- Turnshek, D.
A., Lupie, O. L., Rao, S. M., et al. 1997, ApJ, 485, 100 [NASA ADS] [CrossRef]
- Ulrich, M.-H.,
Maraschi, L., & Megan, C. M. 1997, ARA&A, 35, 445 [NASA ADS]
- Walsh, D., Carswell,
R. F., & Weymann, R. J. 1979, Nature, 279, 381 [NASA ADS] (In the text)
- Wambsganss, J. 2001a,
in Microlensing 2000: A new Era of Microlensing Astrophysics, ed.
J. W. Menzies, & P. D. Sackett, ASP Conf. Ser., 239, 351
- Wambsganss, J. 2001b,
PASA, 18, 207 [NASA ADS]
- Wang, Y., Stebbins, A.,
& Turner, E. L. 1996, Phys. Rev. Lett., 77, 2875 [NASA ADS] [CrossRef]
- Weaver, K. A., Gelbord,
J., & Yaqoob, T. 2001, ApJ, 550, 261 [NASA ADS] [CrossRef]
- Wyithe, J. S. B.,
& Turner, E. L. 2002a, ApJ, 567, 18 [NASA ADS] [CrossRef] (In the text)
- Wyithe, J. S. B.,
& Turner, E. L. 2002b, ApJ, 575, 650 [NASA ADS] [CrossRef] (In the text)
- Yonehara, A.
2001, PASA, 18, 211 [NASA ADS] (In the text)
- Zakharov, A. F.
1995, A&A, 293, 1 [NASA ADS]
- Zakharov, A. F. 1997a,
Gravitational lenses and microlensing (Moscow: Janus-K)
- Zakharov, A. F.
1997b, Ap&SS, 252, 369 [NASA ADS]
- Zakharov, A. F.
1999, in Recent Developments in Theoretical and Experimental
General Relativity, Gravitation, and Relativistic Field Theories,
ed. Ts. Piran, & R. Ruffini (Singapore: World Scientific
Publishers), 1500
- Zakharov, A. F.,
Kardashev, N. S., Lukash, V. N., & Repin, S. V. 2003, MNRAS,
342, 1325 [NASA ADS] [CrossRef]
- Zakharov, A. F.,
& Repin, S. V. 2002a, Astron. Rep., 46, 360 [NASA ADS] [CrossRef]
- Zakharov, A.
F., & Repin, S. V. 2002b, in Proc. of the Eleven Workshop on
General Relativity and Gravitation in Japan, ed. J. Koga, T.
Nakamura, K. Maeda, & K. Tomita (Tokyo: Waseda University),
68
-
Zakharov, A. F., & Repin, S. V. 2002c, in Proc. of the
Workshop, XEUS - studying the evolution of the hot Universe,
ed. G. Hasinger, Th. Boller, & A.N. Parmar, MPE Report, 281,
339
- Zakharov,
A. F., & Repin, S. V. 2003a, in Ad. Space Res., accepted
- Zakharov,
A. F., & Repin, S. V. 2003b, A&A, 406, 7 [EDP Sciences] [NASA ADS] [CrossRef]
- Zakharov,
A. F., & Repin, S. V. 2003c, in Proc. of the 214th IAU Symp.,
High Energy Processes and Phenomena in Astrophysics, ed. X. D. Li,
V. Trimble, & Z. R. Wang, 214, 97
Copyright ESO 2004
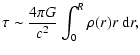
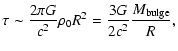
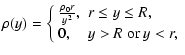
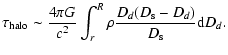
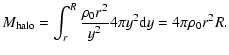
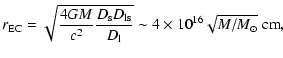
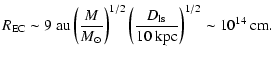
![$\displaystyle \tau^p_{\rm L}= \frac{3}{2}\frac{\Omega_{\rm L}}{\lambda(z)}
\int...
...w)^3[\lambda(z)-\lambda(w)]\lambda(w)}
{\sqrt{\Omega_0(1+w)^3+\Omega_\Lambda}},$](/articles/aa/full/2004/24/aa0035/img83.gif)
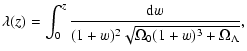
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{0035f1a.eps}\vspace*{3mm}
...
...1b.eps}\vspace*{3mm}
\includegraphics[width=7.2cm,clip]{0035f1c.eps}\end{figure}](/articles/aa/full/2004/24/aa0035/Timg94.gif)
![$\displaystyle \tau_{\rm GL}= \frac{F}{30} \left[\int_1^y \frac{{\rm d}w}{(\Omega_0
w^3-\Omega_0+1)^{1/2}}\right]^3,$](/articles/aa/full/2004/24/aa0035/img106.gif)
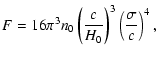
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{0035f2.eps}\end{figure}](/articles/aa/full/2004/24/aa0035/Timg111.gif)