A&A 420, 595-604 (2004)
DOI: 10.1051/0004-6361:20040115
M. Afsar1 - P. A. Heckert2 - C. Ibanoglu1
1 - Ege University, Science Faculty, Department of Astronomy and Space Sciences, Bornava, Izmir 35100, Turkey
2 -
Western Carolina University, Department of Chemistry and Physics, Cullowhee, NC 28723, USA
Received 27 August 2003 / Accepted 16 February 2004
Abstract
We report new photometry of CG Cyg from 1998-2002.
We also analyze published photometry collected since 1965. An O-C analysis
reveals evidence of a third body in the system having a 51 year orbital
period. After removing the effects of the third body, we note a remaining 22.5 year cyclic variation in the O-C curve that is similar to the period of the
luminosity variations. Modeling the spot activity for 28 V band light curves
obtained between 1965 and 2002 confirms the presence of two active longitude
belts (ALBs) at approximately
![]() and
and
![]() .
Most of the spots occur at mid
latitudes with a few at low latitudes. We note no spots at latitudes greater
than
.
Most of the spots occur at mid
latitudes with a few at low latitudes. We note no spots at latitudes greater
than
![]() .
.
Key words: stars: activity - stars: binaries: eclipsing - stars: individual: CG Cyg - stars: starspots
The eclipsing binary CG Cygni (BD
![]() 4217, HIP 103505, V= 9
4217, HIP 103505, V= 9
![]() 7, Sp. G9+K3,
P= 0
7, Sp. G9+K3,
P= 0
![]() 63) is a well-known RS CVn-type star. Among the
most peculiar of the short-period chromospherically active binary
stars, it is No. 177 in the catalog of Chromospherically Active
Binary Stars (Strassmeier et al. 1993). Since its
eclipsing nature was discovered by Williams (1922), many
light curves have been obtained by various authors (Yü
1923; Milone et al. 1979; Jassur 1980;
Sowell et al. 1987; Naftilan et al. 1987;
Bedford et al. 1987; Dapergolas et al.
1988, 1989a,b, 1994; Zeilik et al.
1989,1991; Kjurkchieva et al. 2003). These
workers have shown that the light curve of CG Cyg changes over
short and long time intervals. Naftilan et al. (1987) found that
the mean light level outside eclipse increased between 1964 and 1976, after which the brightening of the mean light level halted.
Sowell et al. (1987) confirmed this result, noting that the mean
light level outside eclipse increased by 15% rather uniformly
between 1964 and 1977. A third minimum at phase 0.36 detected by
Bedford et al. (1987) was attributed to the
circumstellar material located in the orbital plane. Such
depressions in the light curve have been observed recently by
Kjurkchieva et al. (2003) at phases 0.17 and 0.78.
63) is a well-known RS CVn-type star. Among the
most peculiar of the short-period chromospherically active binary
stars, it is No. 177 in the catalog of Chromospherically Active
Binary Stars (Strassmeier et al. 1993). Since its
eclipsing nature was discovered by Williams (1922), many
light curves have been obtained by various authors (Yü
1923; Milone et al. 1979; Jassur 1980;
Sowell et al. 1987; Naftilan et al. 1987;
Bedford et al. 1987; Dapergolas et al.
1988, 1989a,b, 1994; Zeilik et al.
1989,1991; Kjurkchieva et al. 2003). These
workers have shown that the light curve of CG Cyg changes over
short and long time intervals. Naftilan et al. (1987) found that
the mean light level outside eclipse increased between 1964 and 1976, after which the brightening of the mean light level halted.
Sowell et al. (1987) confirmed this result, noting that the mean
light level outside eclipse increased by 15% rather uniformly
between 1964 and 1977. A third minimum at phase 0.36 detected by
Bedford et al. (1987) was attributed to the
circumstellar material located in the orbital plane. Such
depressions in the light curve have been observed recently by
Kjurkchieva et al. (2003) at phases 0.17 and 0.78.
The orbital period changes of CG Cyg have been the subject of various papers since Milone
& Ziebarth (1974) reported a possible change in the
period. The studies on the orbital period changes can be divided
into three categories: parabolic fits, multiple linear fits, and a
third body in the system. Initial studies assumed that O-C values
can be fit with a parabola (cf. Milone et al. 1979;
Naftilan et al. 1987). Then, Hall (1991)
represented the O-C values with four straight-line segments, i.e.
a decrease and a subsequent increase and so on, in the orbital
period. He suggested that the mean brightness of the system
outside eclipse and the period vary with the same cycle length by
about 50 years. Finally, Albayrak et al. (1999) took
into account the possibility of a light-time effect caused by a
third body in the system. They fit a model with a third-body orbit
of period 46.54 yr, an eccentricity of 0.12 and an orbit of the
third that is coplanar with the eclipsing pair's orbit. They
estimated a mass about 0.12
![]() for the third body.
for the third body.
Naftilan & Milone (1979) detected a third emission
component in the middle of the
![]() K line.
This weak emission, which was best seen on the higher quality
plates taken near quadrature, moves not with either star but
rather at the systemic velocity. They explain this feature as
material concentrated in the L1 point or in a shell
surrounding both stars. Popper (1994) and Lazaro &
Arevalo (1997) published spectroscopic observations of CG Cyg, but found no evidence for the existence of a third component
in the spectra. However, Lazaro & Arevalo found an H
K line.
This weak emission, which was best seen on the higher quality
plates taken near quadrature, moves not with either star but
rather at the systemic velocity. They explain this feature as
material concentrated in the L1 point or in a shell
surrounding both stars. Popper (1994) and Lazaro &
Arevalo (1997) published spectroscopic observations of CG Cyg, but found no evidence for the existence of a third component
in the spectra. However, Lazaro & Arevalo found an H![]() excess from both components. In addition, they noted that the
variations in H
excess from both components. In addition, they noted that the
variations in H![]() do not seem to be related to the presence
of photometric spots. The most recent spectroscopic observations
in the spectral region around the H
do not seem to be related to the presence
of photometric spots. The most recent spectroscopic observations
in the spectral region around the H![]() line of CG Cyg were
made by Kjurkchieva et al. (2003). They clearly
revealed a third absorption line between the spectral profiles of
the components both in the H
line of CG Cyg were
made by Kjurkchieva et al. (2003). They clearly
revealed a third absorption line between the spectral profiles of
the components both in the H![]() and
and
![]() 6678 lines.
The depth of this line changed with the phase the cycle and was
comparable to the depths of lines of the component stars. They
suggest that this third component originated from cool matter
around the center-of-mass of the binary.
6678 lines.
The depth of this line changed with the phase the cycle and was
comparable to the depths of lines of the component stars. They
suggest that this third component originated from cool matter
around the center-of-mass of the binary.
The more recent observers and analyzers of the photometry and spectroscopy of CG Cyg have been interested in studying the light curve variations, the spectral line behaviors and the interconnection between them. These studies led to evaluations of starspot parameters and their variations with time, as well as physical parameters of the component stars. The aim of this study is to analyze all the photoelectric times of minima, including new ones obtained by the present authors, and also to analyze all the available light curves to reveal the spot parameters.
Johnson BV observations of CG Cygni were obtained on the nights of 23, 24 June and 1, 2 July 2000 and 14, 15, 17, 28 July and 6 August 2001 by an SSP5-type photometer mounted on the 0.5 m
telescope of the Ege University Observatory (EUO, Izmir (Turkey)). The integration
time for each band was 10 s. All observations were made in the
normal manner, and followed well-known reduction
procedures. We obtained differential magnitudes, in the sense of
variable minus comparison, and then corrected for atmospheric
extinction for each band using the observed magnitudes of the
comparison star. We used BD
![]() 4216 as a comparison
star. The data were phased using the ephemeris:
4216 as a comparison
star. The data were phased using the ephemeris:
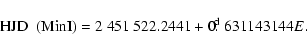 |
(1) |
We also obtained new Johnson Cousins BVRI photometry of CG Cyg
from the Mount Laguna Observatory in 1998 to 2002.
For these observations we used the 0.61 m telescope equipped with
a Hamamatsu R943-02 tube operated at -1450 V and
thermoelectrically cooled to -15![]() C. The same comparison
star was used. Using standards from Landolt (1983) we
transformed the magnitudes to the standard system and found
average calibrated magnitudes for this comparison star of B= 9.71,
V= 8.96, R= 8.46, I= 7.97, which agree with the values for B and Vreported by Milone (1979). Each reported data point in
our light curves represents the average of two 20 s
integrations. The light curves are shown in Fig. 2.
C. The same comparison
star was used. Using standards from Landolt (1983) we
transformed the magnitudes to the standard system and found
average calibrated magnitudes for this comparison star of B= 9.71,
V= 8.96, R= 8.46, I= 7.97, which agree with the values for B and Vreported by Milone (1979). Each reported data point in
our light curves represents the average of two 20 s
integrations. The light curves are shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4753_fig1.ps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg13.gif) |
Figure 1: The 2001 V-band light curve of CG Cyg (Ege University Observatory). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.95cm,clip]{4753_fig2a.eps}\vspace*{1...
...}\vspace*{1cm}
\includegraphics[width=4.95cm,clip]{4753_fig2e.eps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg14.gif) |
Figure 2: The 1998-2002 BVRI light curves of CG Cyg (Mount Laguna Observatory). |
| Open with DEXTER | |
From the observations bf obtained between 1999-2002, 25 epochs of minimum light, including 15 primary and 10 secondary eclipse timings, were determined by the Kwee-van Woerden (1956) algorithm using the least squares fit of the data. The new timings of the minimum light together with those published by other authors are listed in the table which is accessible in electronic form from the Strasbourg Astronomical Data Center (CDS).
A possible orbital period change of CG Cyg was first reported
by Milone & Ziebarth (1974). Since the secondary
minimum changes are in the same sense as the primary minimum
they used both to improve the light elements. They determined two
sets of ephemerides for pre-1967 and post-1967, and noted a
decrease in the orbital period after 1967. Milone et al.
(1979) applied a parabolic fit to the available O-C data
obtained between 1965 and 1977. They concluded that the orbital
period of the system appears to have lengthened and to be
continuously changing since the late 1960s. Naftilan et al.
(1987) confirmed this finding and suggested a period
change of 4.15 ![]()
![]() .
.
Hall (1991) updated the O-C curve and suggested that the
mean brightness outside eclipse and the orbital period vary with
the same cycle length of about 50 yr, on the basis of multiple
linear fits. This may arise from the magnetic activity of the G9 primary component and it was the first test case for confirmation
of Applegate's (1992) prediction. Applegate
(1992) proposed that the orbital period changes in RS CVn type binaries are a consequence of magnetic activity in one or
both of the component stars. He proposed not only a mechanism
that explains period changes, but also suggested a possible
connection with the variations of the luminosity of the system.
According to his theory, angular momentum exchanges are
accompanied by a variation of the total kinetic energy of the
star. This energy is supplied by the stellar luminosity. This idea
was re-examined and improved by Lanza et al. (1998) and
by Lanza & Rodono (1999), who included the effects of
a magnetic field on the internal mass distributions of the active
star. This model has been applied to 46 close binary systems and
evidence was found that orbital period modulation is related to
magnetic activity. Sowell et al. (2001) also
investigated the period changes for CG Cyg and presented an O-C variation which is similar to Hall's (1991). The large
orbital period change observed in this binary was attributed to
the chromospheric activity in one or both components of the
system. Albayrak et al. (1999) studied long-term period
variation of six RS CVn type binaries, including CG Cyg. They
suggested that the most probable cause of the sinusoidal O-C variation was the light-time effect due to an invisible component,
dynamically bound to the eclipsing pair. Their analysis of 155 O-C residuals yielded a period of 46.54 yr for the orbital revolution
of the eclipsing pair around the center-of-mass of the triple
system. A mass of about 0.12
![]() was estimated for the
third component assuming the third-body orbit is coplanar with
that of the eclipsing pair.
was estimated for the
third component assuming the third-body orbit is coplanar with
that of the eclipsing pair.
We have obtained 25 timings and combined them with all published
epochs of both mid-primary and mid-secondary eclipses as in the
table accessible in electronic form. The behavior of the
deviation of each timing from the mean orbital period
depends strictly on the mean period used at the calculation. Figure 3 shows the O-C(I), which is the difference in the values of
the primary and secondary minima from the ephemeris given by (Yü 1923),
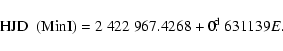 |
(2) |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4753_fig3.ps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg19.gif) |
Figure 3: The O-C(I) curve for CG Cyg based on the linear ephemeris of Yü (1923). The solid line indicates the computed light-time effect. The first four points are photographic times. |
| Open with DEXTER | |
The additional time delay of any observed eclipse due to orbiting around a third body can be represented by (Mayer 1990),
![\begin{displaymath}%
\Delta{T} =\frac{A}{\sqrt{1-e^{2}\cos^{2}\omega}}
\left[\f...
...-e^{2}}{1+e\cos\omega}{\sin(\nu+\omega)+e\sin\omega}
\right]
\end{displaymath}](/articles/aa/full/2004/23/aah4753/img20.gif) |
(3) |
| (4) |
We found the semi-amplitude of the O-C curve to be 0
![]() 0058 due to the third-body orbit,
while it was estimated by Albayrak et al. (1999) as
0.0082 days. We derived the semi-amplitude of the radial velocity
of the eclipsing pair's center of gravity as 0.8 km s-1. Using
the projected semi-major axis of 1.064 AU and a period of 50.73 yr, the mass function for the third star was calculated as
4.68
0058 due to the third-body orbit,
while it was estimated by Albayrak et al. (1999) as
0.0082 days. We derived the semi-amplitude of the radial velocity
of the eclipsing pair's center of gravity as 0.8 km s-1. Using
the projected semi-major axis of 1.064 AU and a period of 50.73 yr, the mass function for the third star was calculated as
4.68 ![]()
![]() .
Since the masses of the
components of the eclipsing pair were derived recently by
Kjurkchieva et al. (2003) as 0.97 and 0.80 solar masses and
the eclipsing pair orbiting around the common center of mass with
a period of 50.73 yr, the mass of the third star may be obtained
from the mass function. The estimated mass of the third-body
depends on the inclination of the long-period orbit. We compute
the mass of the third star as 0.12, 0.14, 0.25 for inclinations of 90
.
Since the masses of the
components of the eclipsing pair were derived recently by
Kjurkchieva et al. (2003) as 0.97 and 0.80 solar masses and
the eclipsing pair orbiting around the common center of mass with
a period of 50.73 yr, the mass of the third star may be obtained
from the mass function. The estimated mass of the third-body
depends on the inclination of the long-period orbit. We compute
the mass of the third star as 0.12, 0.14, 0.25 for inclinations of 90![]() ,
60
,
60![]() and 30
and 30![]() ,
respectively. If we
assume that the mass of the third component is 0.9
,
respectively. If we
assume that the mass of the third component is 0.9
![]() ,
the
inclination of the third-body orbit should be about 10
,
the
inclination of the third-body orbit should be about 10![]() .
Then, the projected semi-major axis (
.
Then, the projected semi-major axis (![]() )
of the
third-body around the eclipsing pair is 19 AU.
)
of the
third-body around the eclipsing pair is 19 AU.
Table 1: Parameters of the third-body orbit.
Using the parameters of the third body orbit, the times for each mid-eclipse have been computed and subtracted from the O-C(I) values
and the new O-C(II) values were obtained. On this remaining
O-C(II) curve (Fig. 4), a cyclic change is still seen. The
semi-amplitude of this variation is about (200 ![]() 35) s. with a
cycle length about (22.5
35) s. with a
cycle length about (22.5 ![]() 0.7) yr. This small amplitude,
shorter period change in the orbital period of the eclipsing pair
may be attributed to the magnetic activity, because brightness
variation of the system has a similar cycle length (see next
section). The time differences between observed and calculated by
light-time orbit and sine-like change have also been plotted in Fig. 5.
0.7) yr. This small amplitude,
shorter period change in the orbital period of the eclipsing pair
may be attributed to the magnetic activity, because brightness
variation of the system has a similar cycle length (see next
section). The time differences between observed and calculated by
light-time orbit and sine-like change have also been plotted in Fig. 5.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4753_fig4.ps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg30.gif) |
Figure 4: An O-C comparison between eclipse timings and the third-body ephemeris and the remaining cyclic changes. |
| Open with DEXTER | |
Many complete light curves of CG Cyg have been obtained and
published by various authors since 1921. In general, two
comparison stars were used in the photometric observations. Most
of the observers used BD
![]() 4216 as a comparison while
the others preferred either Yü's (a) (GSC 02696-02622) or (b)
(GSC 02696-02207) stars as the comparison. To reduce all
the light curves to a common base we determined the brightness
differences between the primary comparison star, BD
4216 as a comparison while
the others preferred either Yü's (a) (GSC 02696-02622) or (b)
(GSC 02696-02207) stars as the comparison. To reduce all
the light curves to a common base we determined the brightness
differences between the primary comparison star, BD
![]() 4216 and the others. We observed these stars near the
meridian on the same night and derived the magnitude difference in
B and V bands, BD
4216 and the others. We observed these stars near the
meridian on the same night and derived the magnitude difference in
B and V bands, BD
![]() 4216 minus Yü's stars, as
4216 minus Yü's stars, as
![]() -1
-1
![]() 083
083 ![]() 0
0
![]() 018 and
018 and
![]() -1
-1
![]() 480
480 ![]() 0
0
![]() 019 for (a) and
019 for (a) and
![]() -1
-1
![]() 341
341 ![]() 0
0
![]() 019 and
019 and
![]() -1
-1
![]() 610
610 ![]() 0
0
![]() 011 for (b)
respectively. The magnitude differences between Yü's (b) and
Yü's (a) stars are 0
011 for (b)
respectively. The magnitude differences between Yü's (b) and
Yü's (a) stars are 0
![]() 258 and 0
258 and 0
![]() 130 in
B and V bands. These differences were also derived by Jassur
(1980) as 0
130 in
B and V bands. These differences were also derived by Jassur
(1980) as 0
![]() 279 and 0
279 and 0
![]() 114 for
the corresponding bandpasses. Standard magnitudes for
BD +34
114 for
the corresponding bandpasses. Standard magnitudes for
BD +34![]() 4216 were given by Milone et al. (1979)
as V = 8
4216 were given by Milone et al. (1979)
as V = 8
![]() 969, B = 9
969, B = 9
![]() 713. Using the differences we reduced all the light curves to the standard system.
713. Using the differences we reduced all the light curves to the standard system.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4753_fig5.ps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg33.gif) |
Figure 5: Light-time values and sine-like variation due to another cause (attributed to the magnetic activity) and the computed O-C values. The residuals of O-C values from the computed curve are shown in the bottom panel. |
| Open with DEXTER | |
After transforming all the available differential observations into the standard system, the magnitudes were read from the each light curve at four phases 0.0, 0.25, 0.5, 0.75. These data, presented in Table 2, are plotted in Fig. 6 and cover the time interval between 1965 and 2002. The data gathered between 1992 and 2002 show that the mean B-V color of the system outside eclipse gets redder by about 0.03 mag when the brightness dims. The brightness and color appear to change in the same direction as previously predicted by Hall (1991). As the O-C residuals are decreasing the brightness dims and the B-V color gets redder.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4753_fig6.ps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg34.gif) |
Figure 6: Standard V magnitudes for CG Cyg. a) At phase 0.0, b) 0.25, c) 0.5 and d) 0.75, respectively. |
| Open with DEXTER | |
The variations of the mean brightness at mid-primary eclipse show an almost cyclic change in both the B and V bandpasses. The amplitude of the variation is about 0.15 mag in B and 0.13 mag in the V band. While the mean brightness was the smallest around 1967 for these four phases it reached the maximum around 1978. The brightness began to decrease until 1986 then increased again. Both the two maxima and the two minima, have different values. The pattern of the variations is suggestive of either the existence of an approximately 20-year period with a changing amplitude or two kinds of variations with different amplitudes having a 40-year period.
In Figs. 6b and 6d we show the variation of the brightness at the first and second maxima. The amplitude of the variation of the brightness at first maximum is about 0.17 mag in B and 0.14 mag in V band. The brightness seems to change with a period of about 21 years. The amplitude in the color variation is less than 0.03 mag. The variation of the mean brightness at second quadrature seems to be smaller than that of first maximum. Figure 7 shows the variation of the mean brightness level at maxima, i.e. (MaxI + MaxII)/2, at different epochs. This figure also shows that the variation in mean brightness at quadratures is almost cyclic but not exactly periodic, because the time intervals between consecutive minima and maxima are not equal. The data obtained over 37 years indicate that the mean brightness of the system has reached, at least, two local maxima and two minima. Despite the large fluctuations in magnitudes the average period seems to be about 18 yr. It should also be noted that the magnitude difference between the maxima, in the sense of MaxI - MaxII, varies with almost the same period.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4753_fig7.ps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg35.gif) |
Figure 7: Variation of the mean brightness level at maxima, i.e. (MaxI + MaxII)/2. |
| Open with DEXTER | |
In addition to these long term brightness variations, previous observers have noted short term fluctuations
relative to the orbital period. These fluctuations were initially attributed
to the variability of the comparison star, which was Yü's star
(a). Zeilik et al. (1991) and Beckert et al.
(1989,1991) used Yü's (a) star as the comparison.
However, Heckert & Zeilik (1991) observed this star
continuously for about 1.5 h and found a variation of only about
0.04 mag in its brightness which was not enough to explain the
light fluctuations in CG Cyg. In addition, Dapergolas et al.
(1991) observed such fluctuations using BD
![]() 4216 as the comparison star. Other observations show
that these fluctuations in CG Cyg do not occur at all epochs.
Hence, Zeilik et al. (1994) concluded that the observed
light fluctuations do not originate in the comparison star used,
but that the rapid, small amplitude fluctuations are intrinsic to the system.
4216 as the comparison star. Other observations show
that these fluctuations in CG Cyg do not occur at all epochs.
Hence, Zeilik et al. (1994) concluded that the observed
light fluctuations do not originate in the comparison star used,
but that the rapid, small amplitude fluctuations are intrinsic to the system.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4753_fig8.ps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg36.gif) |
Figure 8: The 1992 V-light curve and the computed curve by using the WD code. |
| Open with DEXTER | |
Zeilik et al. (1994) collected all the available photometric data
from 1922 to 1991 and analysed for the orbital parameters of the
system, as well as the starspot parameters. They found that the
spots on CG Cyg tend to be located at two active longitude belts
(ALB) at about
![]() and
and
![]() ,
i.e. at quadrature
longitudes. Photometric data obtained after 1991 have been
analyzed by Heckert (1994,1996,1998),
Dapergolas et al. (2000) and Kjurkchieva (2003).
They found similar results in that the wave-like distortions on
the light curves could be represented by two cool spots on the
primary component. In addition to wave-like distortion on the
light curves, Bedford et al. (1987), Zeilik et al.
(1994) and Kjurkchieva (2003) detected some
depression on the light curves at different orbital phases.
,
i.e. at quadrature
longitudes. Photometric data obtained after 1991 have been
analyzed by Heckert (1994,1996,1998),
Dapergolas et al. (2000) and Kjurkchieva (2003).
They found similar results in that the wave-like distortions on
the light curves could be represented by two cool spots on the
primary component. In addition to wave-like distortion on the
light curves, Bedford et al. (1987), Zeilik et al.
(1994) and Kjurkchieva (2003) detected some
depression on the light curves at different orbital phases.
We collected photometric data for as many complete light curves as possible from the literature beginning in 1965. A total of 28 light curves obtained between 1965 and 2002, listed in Table 3, were analyzed by the Information Limit Optimization Technique (ILOT) described by Budding & Zeilik (1987) and Banks (1989). The main assumptions made during the analysis by the ILOT are: (1) the activity originates in the hotter star (late G), (2) maculation effects are separable from proximity and eclipse effects, and (3) a cool, circular spot model may represent the parameters of the spotted regions, i.e. longitude, latitude, radius and temperature relative to the photosphere. The reliability of these key parameters of the stellar magnetic activity, of course, depends on the photometric accuracies. Due to the small light contribution of the secondary star, which amounts to 0.34 in the V bandpass, the hotter primary star should be responsible for the magnetic activity. Therefore we assumed that the primary component should be heavily spotted.
The steps of our analysis are the same as those used by Zeilik et al. (1994): (1) optimize a model eclipsing binary curve to the observations; (2) calculate the residuals by subtracting data points from the model to define the maculation wave; (3) optimize a model for the maculation wave to calculate the starspot parameters.
Table 4: 1992 V-light curve solutions.
First, we solved the 1992 V-light curve of CG Cyg to obtain the input parameters. This light curve, which is complete, has a small amplitude
wave-like distortion located just after secondary eclipse. The
one-spot solution with the standard package of the Wilson-Devinney
code (Wilson & Devinney 1971; Wilson 1993)
gives the parameters listed in Table 4. The final fit is compared
with the observations in Fig. 8. The second step was to produce
the distortion curve using ILOT. The difference between the
observed curve and the synthetic curve computed using the
parameters given in Table 4 was revealed for 28 V-band light
curves obtained between 1965 and 2002. The shape of the distortion
curve depends on the number of spots, locations and sizes on the
star's surface. The distortion curves could be reproduced by two
cool spots on the primary star except for 1965, 1967, 1991 and 1992
for which one spot was used. In Table 5 the longitude,
latitude and radius of the spot(s) are listed in degrees for each
light curve. The longitude is defined so that ![]() is at
the nominal center of primary eclipse and increases with
increasing phase. The latitude is defined with
is at
the nominal center of primary eclipse and increases with
increasing phase. The latitude is defined with ![]() at the equator.
at the equator.
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{4753_fig9a.eps}\hspace*{3m...
...} \includegraphics[width=5.7cm,clip]{4753_fig9e.eps}\hspace*{3cm}}
\end{figure}](/articles/aa/full/2004/23/aah4753/Timg39.gif) |
Figure 9: Mercator maps of the surface of the hotter primary. |
| Open with DEXTER | |
Many of the V light curves that we model here have been previously modeled (Zeilik et al. 1994; Heckert 1994, 1996, 1998) using the same ILOT method. Our new results are generally close to but not exactly the same as the previous results. One source of the small differences in modeling results may be slightly different initial input solutions. The input parameters, derived from the 1992 light curve used in this work differ by a small amount from the parameters used in the previous work. Previous workers obtained the orbital input parameters individually for each year. The 1972, 1975, 1979, 1980, 1981, 1983, 1984, 1987, 1989, and 1995 light curves were previously modeled with just one spot. In this work, we model each of these light curves with two spots. Fitting an additional spot will have an effect on the fit parameters of the existing spot, however the spot parameters usually agree to within the errors. The 1967, 1991, 1994, and 1998 light curves are modeled with the same number of spots as the previous work and tend to agree to within the errors. With the exception of the 1967 and the 1984 light curves, the new results have lower chi square values than the previous results.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4753_fig10.eps} \end{figure}](/articles/aa/full/2004/23/aah4753/Timg40.gif) |
Figure 10: The changes of the spot longitudes vs. time. |
| Open with DEXTER | |
We plot the starspot parameters on the Mercator maps of the surface of the hotter primary in Fig. 9. These are the two-dimensional maps of determinate starspot solutions for
1965-2002 for V band only. The size of each circle shows the
relative area of spotted regions, labeled by year of observation.
It is clearly seen that there is an indication of two active
regions on the primary star, which are located in two longitude
zones centered around the quadrature points as reported by
Zeilik et al. (1994). One is located near
![]() and the other near
and the other near
![]() (Fig. 10); both are at latitudes
between
(Fig. 10); both are at latitudes
between ![]() and
and
![]() .
These appear to be the ALBs
proposed by Eaton & Hall (1970) and Uchida & Sakurai
(1983, 1985) for RS CVn systems. Such ALBs are
found on the Sun and often appear as two regions, tens of degrees
wide, separated by roughly 180 degrees (Sawyer 1968). As
seen in Fig. 10, the spot longitudes show a tendency to migrate
in opposite directions. When the longitude in one ALB increases,
the other decreases. Some data sets have large observational
scatter (for instance, 1965, 1972, 1984) therefore spot parameters
for such sets are not reliable. On the other hand some light
curves (i.e. 1967, 1969, 1977, 1983, 1984, 1998) have too large
gaps to find a reliable starspot solution. If we do not take
into account starspot parameters found from these incomplete
and/or less accurate observational data CG Cyg has, in general,
two ALBs. While the longitude of spots in the first ALB is
decreasing the longitude of spots in the other ALB is increasing.
.
These appear to be the ALBs
proposed by Eaton & Hall (1970) and Uchida & Sakurai
(1983, 1985) for RS CVn systems. Such ALBs are
found on the Sun and often appear as two regions, tens of degrees
wide, separated by roughly 180 degrees (Sawyer 1968). As
seen in Fig. 10, the spot longitudes show a tendency to migrate
in opposite directions. When the longitude in one ALB increases,
the other decreases. Some data sets have large observational
scatter (for instance, 1965, 1972, 1984) therefore spot parameters
for such sets are not reliable. On the other hand some light
curves (i.e. 1967, 1969, 1977, 1983, 1984, 1998) have too large
gaps to find a reliable starspot solution. If we do not take
into account starspot parameters found from these incomplete
and/or less accurate observational data CG Cyg has, in general,
two ALBs. While the longitude of spots in the first ALB is
decreasing the longitude of spots in the other ALB is increasing.
For more than a century it has been known that long-term variations occur in the surface activity of our star, the Sun. The dominant one is the well-known 11-year cycle. Chromospherically active late-type stars also display solar-type activity phenomena but to a much stronger degree than the Sun itself. The outstanding photometric indicator of chromospherically-active close binaries is the light variability with an amplitude of about a tenth of a magnitude in phase with the rotation of the active component(s). On the other hand, the photometric signature of a magnetic cycle may be long-term changes in the mean brightness of these systems. Long-term magnetic cycles have been determined to date for only limited number of systems. The length of magnetic cycles for RS CVn type active systems range from about ten years to about a century. Hall (1991) proposed that cyclic changes in mean brightness were common among known chromospherically active stars. The amplitudes of the changes in mean brightness range from about 0.1 to 0.5 mag, whereas the luminosity change of the Sun is about 0.001 mag in phase with its 11-year cycle. The enhanced magnetic activity in CG Cyg and similar systems enhances these luminosity variations as well as the spot activity, suggesting that these luminosity variations are also magnetic in nature.
CG Cyg consists of two late-type stars. The G9 primary has an active chromosphere as proven by spectroscopic and photometric studies. However,
the latest spectroscopic study made by Kjurkchieva et al. (2003) revealed that the emission cores of the H![]() line of both components vary
with the orbital phase indicating that both components have inhomogeneous active chromospheres. In addition they have noted that the H
line of both components vary
with the orbital phase indicating that both components have inhomogeneous active chromospheres. In addition they have noted that the H![]() emmision
line of the secondary star showed a flare-like event. The amplitude of the light variations due to spots on the components is at most 0.089 mag.
Since the light contribution of the primary exceeds 0.6 of the total light of the system, it should be more active than its companion. As is suggested by all previous studies, our light curve analysis indicates two active regions on the more massive primary star.
emmision
line of the secondary star showed a flare-like event. The amplitude of the light variations due to spots on the components is at most 0.089 mag.
Since the light contribution of the primary exceeds 0.6 of the total light of the system, it should be more active than its companion. As is suggested by all previous studies, our light curve analysis indicates two active regions on the more massive primary star.
The brightness variation at four special orbital phases has been studied as well as the total brightness of the system at the maxima. Although the lengths of the time intervals are not the same, the average cycle of the mean brightness is about 20 yr. The photometric data obtained over the period of 37 years indicate that at least two definite maxima and minima have been obtained. The largest amplitude of the variation in the mean brightness is about 0.17 mag in B and 0.14 mag in V band.
In addition to the light curve analysis and examination of the mean brightness changes we also studied the orbital period changes. The up-to-date
O-C deviations resemble the light-time effect, orbiting around a third body. Therefore we analyzed all available O-C data under the hypothesis
of a light-time effect. This analysis yields that the eclipsing pair revolves around the common center of gravity with a tertiary body with
a period of about 51 years. The eccentricity of this orbit is about 0.56, and
![]() 1.06 AU. We estimate the mass of the tertiary
component as 0.12
1.06 AU. We estimate the mass of the tertiary
component as 0.12
![]() for the orbital inclination of the eclipsing pair's orbit. Using the parameters given in Table 2 the times for each
mid-eclipse have been computed from the observed ones. The resultant O-C values indicate a cyclic change as shown in Fig. 4. The semi-amplitude
of these variations is about 200 s with a cycle length about 22.5 yr. This change in the orbital period of the system has been attributed
to the magnetic activity in one or both components of CG Cyg. By comparing Figs. 4 and 7 we conclude that the O-C curve minimum coincides
with the maximum total brightness and vice versa; both have similar period of about 20 years.
for the orbital inclination of the eclipsing pair's orbit. Using the parameters given in Table 2 the times for each
mid-eclipse have been computed from the observed ones. The resultant O-C values indicate a cyclic change as shown in Fig. 4. The semi-amplitude
of these variations is about 200 s with a cycle length about 22.5 yr. This change in the orbital period of the system has been attributed
to the magnetic activity in one or both components of CG Cyg. By comparing Figs. 4 and 7 we conclude that the O-C curve minimum coincides
with the maximum total brightness and vice versa; both have similar period of about 20 years.
Acknowledgements
M. Afsar would like to thank Turkish Scientific and Research Council for their invaluable supports during her Master of Science and Ph.D. studies. P. Heckert thanks Ron Angione and Paul Etzel for scheduling generous amounts of telescope time at Mount Laguna Observatory. Also support from the American Astronomical Society Small Grants Program is acknowledged.