A&A 420, 475-489 (2004)
DOI: 10.1051/0004-6361:20040117

What drives the Balmer extinction sequence in spiral galaxies?

Clues from the Sloan Digital Sky Survey

G. Stasinska1 - A. Mateus Jr.2 - L. Sodré Jr.2 - R. Szczerba3


1 - LUTH, Observatoire de Meudon, 5 place Jules Janssen, 92195 Meudon Cedex, France
2 - Departamento de Astronomia, Instituto de Astronomia, Geofísica e Ciências Atmosféricas da USP, Rua do Matão 1226, 05508-090, São Paulo, Brazil
3 - N. Copernicus Astronomical Center, Rabianska 8, 87-100 Torun, Poland

Received 31 March 2003 / Accepted 3 March 2004

Abstract
Using spectra of normal emission line galaxies from the First Data Release of the Sloan Digital Sky Survey (SDSS) we have investigated the relations between the extinction $C({\rm H}\beta )$ as derived from the H$\alpha $/H$\beta $ emission line ratio and various global parameters of the galaxies. Our main findings are that: 1) $C({\rm H}\beta )$ is linked with the galaxy spectral type and colour, decreasing from early- to late-type spirals; 2) $C({\rm H}\beta )$ increases with increasing metallicity; 3) $C({\rm H}\beta )$ is larger in galaxies with an older stellar population; 4) $C({\rm H}\beta )$ is larger for more luminous galaxies; 5) The extinction of the stellar light is correlated with both the extinction of the nebular light and the intrinsic galaxy colours. We propose phenomenological interpretations of our empirical results. We have also cross-correlated our sample of SDSS galaxies with the IRAS data base. Due to the lower redshift limit of our sample and to the detection limit of IRAS, such a procedure selected only luminous infrared galaxies. We found that correlations that were shown by other authors to occur between optical and infrared properties of galaxies disappear when restricted the sample to luminous infrared galaxies. We also found that the optical properties of the luminous infrared galaxies in our SDSS sample are very similar to those of our entire sample of SDSS galaxies. This may be explained by the IRAS luminosity of the galaxies originating in the regions that formed massive stars less than 1 Myr ago, while the opacity of galaxies as derived from the H$\alpha $/H$\beta $ emission line ratio is due to diffuse dust. We show some implications of our empirical results for the determination of global star formation rates and total stellar masses in normal galaxies.

Key words: galaxies: spiral - galaxies: abundances - galaxies: evolution - galaxies: ISM - galaxies: stellar content - ISM: dust, extinction

1 Introduction

Accounting for the presence of dust is paramount for our understanding of the constitution and evolution of galaxies. Indeed, dust modifies the light we receive from galaxies by both dimming it and modifying its colour. The determination of the bolometric luminosity of galaxies, the description of their stellar populations using galaxy colours, the estimates of the star formation rates using observed fluxes in either the emission lines or ultraviolet continua, all depend on a correction for the effects of dust. Dust in itself is also an important constituent of galaxies, not so much by its mass but by the effects it has on the thermal balance of the interstellar medium and on the formation of H2 molecules, which has important consequences for the efficiency of star formation (e.g. Omukai 2000; Hirashita & Ferrara 2002).

Yet, the question of dust opacity of galaxies is still a subject of strong debate. Earlier, the presence of dust in galaxies was essentially inferred from its impact on the observed distribution of stellar light. The spectacular extinction in the edge-on Sombrero galaxy was attributed to dust located in its plane. The mottled aspect of the arms in face-on spiral galaxies was attributed to higher extinction in zones of star formation. Such observations developed the view that dust is a common constituent of spiral galaxies. In lenticular galaxies, dust lanes have been noticed (Sandage 1961). Studies using various techniques have led to the conclusion that the average extinction decreases following the sequence late-type spirals - early-type spirals - lenticulars and ellipticals (see review by Calzetti 2001). Inclination tests measure the dependence of galaxy disk surface brightness on inclination (e.g. Valentijn 1994 and references therein). This method is statistical by nature and strongly depends on sample selection, as discussed by Valentijn. Another method is to consider multiwavelength data of galaxies and solve simultaneously for the intrinsic colours of the stellar populations and for the reddening. The results of this method strongly rely on the adopted dust distribution models, as emphasized by Witt et al. (1992), Bianchi et al. (1996), and Witt & Gordon (2000). Infrared data from the IRAS survey provide detection of dust through its emission in the infrared. However, the interpretation of the infrared dust emission in terms of dust content is not straightforward (see e.g. Sauvage & Thuan 1994; Dale & Helou 2002). A different approach is to study the transparency of galaxies with respect to background light (see Keel & White 2001 and references therein for methods using one nearby background galaxy, and González et al. 1998 for methods using distant galaxies as background sources). Unfortunately, this method suffers from extremely low statistics.

Another extinction indicator that can be used in galaxies presenting emission lines is the observed Balmer decrement. As is known, the intrinsic intensity ratios of hydrogen recombination lines in ionized nebulae have a negligible dependence on the emission conditions (Osterbrock 1989) so that the observed values are a consequence of the dust extinction being different at the relevant wavelengths. This has for example been used in the influential work by Calzetti et al. (1994) to determine an empirical extinction law for starburst galaxies. However, few studies have used this method to investigate the relation between extinction and overall galaxy type (e.g. Hubble type). To do this, one needs spectra of galaxies spanning the entire range of Hubble types. The atlas of Kennicutt (1992) provided such a data base for a limited sample of galaxies. Among these galaxies, 15 were considered by Sodré & Stasinska (1999, hereinafter SS99) to be normal emission line galaxies, and these authors showed that the extinction at H$\beta $  as measured by the H$\alpha $/H$\beta $ ratio (in the remaining of the paper we will call it the Balmer extinction) decreases steadily from early-type to late-type spirals. Later, using the Nearby Field Galaxy Survey (NFGS) of Jansen et al. (2000a,b), which provided adequate data for about 100 galaxies, Stasinska & Sodré (2001, hereinafter SS01) showed that redder galaxies have a larger Balmer extinction. The Sloan Digital Sky Survey (SDSS), which aims to obtaining spectra of 106 galaxies in the nearby Universe, provides a wonderful opportunity to study this question in more detail.

The present paper makes use of the observations from the First Data Release (DR1; Abazajian et al. 2003, see also Stoughton et al. 2002) of the SDSS to study the relation between the Balmer extinction and other global properties of the galaxies. Section 2 explains the selection of the observational sample and quantities used in the analysis. Section 3 presents the relation between Balmer extinction and other galaxy parameters. Section 4 presents an interpretation of our results. In Sect. 5 we cross-correlate the galaxies of our sample with galaxies detected by IRAS, looking for additional clues to the origin of the observed extinction. Section 6 summarizes the main conclusions of this work and outlines some prospects.

2 The observational sample

2.1 Measurements of emission line parameters

The equivalent widths of H$\alpha $and H$\beta $, EW(H$\alpha $) and EW(H$\beta $) respectively, measured by the SDSS team and available in the survey database, do not account for underlying absorption, which may be significant for objects with faint emission lines. Consequently, we have developed a code for measuring simultaneously the emission and absorption features of these Balmer lines (see Mateus & Sodré 2004 for additional details). For H$\beta $the code fits two Gaussian functions, one in emission and the other in absorption, allowing for different centroids and widths for these features. For H$\alpha $ we fit, additionally, two other Gaussian functions to the emission lines of [N  II]$\lambda $6548 and [N  II]$\lambda $6584. The continuum is estimated through a robust linear adjustment considering two wavelength regions on the sides of the lines. In Fig. 1 we show examples of the fits obtained for H$\beta $ (top panels) and H$\alpha $ (bottom panels) for two spectra with a signal-to-noise ratio in the g-band of 5.9 and 12.4, respectively from left to right of the figure. Note that these are among the worst cases in the sample selected for this study (see Sect. 2.2). This procedure allowed us to determine, for each spectrum, the fluxes and equivalent widths resulting from the absorption and emission features of H$\alpha $ and H$\beta $, as well as their errors and a signal-to-noise ratio (S/N) for each fit.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3793.f1}\end{figure} Figure 1: Examples of two fits using our code to measure the equivalent widths and fluxes of H$\beta $ ( top panels) and H$\alpha $ ( bottom panels). The left and right figures are for spectra with signal-to-noise ratio in g-band of 5.9 and 12.4, respectively. We also show the equivalent widths (EW) in Å and signal-to-noise ratio ( S/N) of the measured emission lines.
Open with DEXTER

We have made many simulations to verify the reliability of these fits and the presence of any bias in the results. We simulated absorption plus emission lines, with realistic noise, and compared the input line parameters with the outcome of our fitting software. The initial parameters (essentially the equivalent widths of the components in emission and absorption of H$\alpha $ and H$\beta $ lines) used in these simulations were based on the results of the spectrophotometric model of Barbaro & Poggianti (1997), for different spectral types. For each out of 5 types, we simulated 1000 spectral regions at H$\alpha $ and H$\beta $ lines, varying the amplitude of the noise, as well as the linear spectral dispersion (0.5, 1.0 and 2.0 Å). Then, we applied our code to compare the equivalent widths of the H$\alpha $ and H$\beta $ features. In Fig. 2 we show a typical result obtained from our simulations, where the initial equivalent widths of H$\alpha $ and H$\beta $ (input parameters) are compared with their respective values measured by our code. We concluded that for S/N high enough (larger than $\sim$10) the results recovered by our software are, within the errors, consistent with the input values and do not depend on the dispersion we used.

In this study we use our own measurements of the equivalent widths of the hydrogen emission lines, and the measurements available in the SDSS database for the remaining lines.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3793.f2}\end{figure} Figure 2: Results of the simulations for a spectral dispersion of 1.0 Å and typical noise. The input equivalent widths are based on the results of the spectrophotometric model of Barbaro & Poggianti (1997) for different spectral types: Sa, Sb, Sc, Sd and "Extreme'' case with constantly increasing star formation rates. These equivalent widths are compared with the values recovered by our code. The large squares are the mean values of the output equivalent widths, with the error bars showing their dispersion.
Open with DEXTER

2.2 The selection procedure

The spectroscopic data analyzed in this work were extracted from the SDSS main galaxy sample available on the First Data Release (Abazajian et al. 2003). This flux-limited sample consists of galaxies with r-band Petrosian magnitudes $r \le 17.77$ and r-band Petrosian half-light surface brightnesses $\mu_{50} \le 24.5$ mag arcsec-2, comprising a total of 113 199 galaxies. We first selected all galaxies with spectra obtained by the survey and with a redshift confidence $\ge $0.7. This selection resulted in a first sample with 110 913 galaxies. Following the conclusions of Zaritsky et al. (1995), we have used a redshift limit of $z \ge 0.05$ to minimize the effects of the aperture bias in our sample, since we are interested in the global spectral properties of the galaxies. We have also rejected galaxies with an average spectroscopic signal-to-noise ratio smaller than 5 in the photometric g passband. These criteria result in a selection of 89 174 spectra of galaxies.


  \begin{figure} \par\includegraphics[width=4.9cm,clip]{ms3793.f3}\end{figure} Figure 3: Emission line diagnostic diagram to separate normal galaxies from galaxies hosting an AGN. The points represent the 10 822galaxies from the SDSS that have been selected according to the criteria described in Sect. 2.1. Solid line: the curve of Heckman & Kauffmann (2003); all the galaxies below that curve (9840 objects) constitute our sample of normal galaxies. Dot-dashed line: the theoretical curve of Kewley et al. (2001) above which galaxies are dominated by an AGN; dashed line: empirical lower bound of normal galaxies (see Sect. 2.2).
Open with DEXTER

For these objects, we have applied our code to measure the fluxes and equivalent widths of the emission Balmer lines, obtaining 40 672 spectra with these parameters measured with ${\it S/N}> 1$. Following the previous discussion on the H$\alpha $ and H$\beta $ measurements, we consider only galaxies with high S/N for their emission lines, equal to or larger than 10, and measured EW(H$\alpha $) and EW(H$\beta $) larger than 1 Å. For galaxies with strong emission in the Balmer lines (where the absorption equivalent width is much smaller than the emission equivalent width), our emission equivalent widths are very similar to those in the SDSS database. With these criteria, the sample comprises 11 066 spectra. In the case of duplicate spectra, we removed the ones with lower S/N in the g band. The resulting sample contains 10 854 objects.


  \begin{figure} \par\includegraphics[width=12cm,clip]{ms3793.f4}\end{figure} Figure 4: Histograms of general properties of our sample of normal galaxies.
Open with DEXTER

We then excluded from the sample the galaxies whose spectra are contaminated by non-stellar activity. For this, we used the [O  III] $\lambda $5007/H$\beta $ vs. [N  II] $\lambda $6584/H$\alpha $ diagram introduced by Baldwin et al. (1981) and Veilleux & Osterbrock (1987). The resulting diagram for our sample is shown in Fig. 3, where we only plot the objects with measured fluxes for all emission lines (10 822 objects). The dot-dashed line is a limit defined by Kewley et al. (2001), above which an active galactic nucleus (AGN) dominates the emission-line spectrum. The solid curve shows the empirical limit proposed by Heckman & Kauffmann (2003), below which star formation dominates the emission-line spectrum. Galaxies below this curve will be referred to as normal galaxies. The dashed line delimits the narrow strip where normal galaxies are found in this diagram. Note that this strip has roughly the same location as the sequence drawn by individual giant H  II regions in galaxies (Mc Call et al. 1985; van Zee et al. 1998). Thus, in our selection we can distinguish 9840 normal galaxies and 982 AGNs. In the following, our sample will contain only these 9840 normal emission line galaxies, to avoid any interference of active nuclei in our interpretation of the data.

2.3 Overall properties of our sample of normal galaxies

With 9840 objects, we have over 80 times more galaxies at our disposal than in the SS01 study based on the NFGS sample (Jansen et al. 2000a,b), and over 600 times more than in the SS99 study based on the Kennicutt (1992) atlas. Note also that at the spectral resolution of the SDSS, which is about 3 Å, it is much easier to separate emission from absorption at H$\beta $ and H$\alpha $ than in the NFGS (spectral resolution 6 Å) and in the Kennicutt (1992) atlas (spectral resolution 12-25 Å). Therefore we are able to explore with confidence galaxies with quite weak H$\beta $ emission.

  \begin{figure} \par\includegraphics[width=12cm,clip]{ms3793.f5}\end{figure} Figure 5: Some global properties of the galaxies of our sample as a function of their "spectral type''. The top number on the right is the total number of data points (including a few individual points that may lie outside the panel frame). Below are: the value of Kendall's $\tau _{\rm K}$, then the associated probability and finally the Spearman rank correlation coefficient $r_{\rm S}$ (see Sect. 2.3).
Open with DEXTER

The global characteristics of the selected sample are shown in Fig. 4. Panel a shows the histogram of the galaxy spectral classification parameter eClass as provided by the SDSS for DR1. This spectral classification parameter is based on a principal component analysis method (Connolly et al. 1995; Connolly & Szalay 1999). Note that the spectral classification of galaxies by Connolly et al. (1995) is slightly different from the one used in SS99 who removed from the analysis the wavelength regions containing emission lines. We will nevertheless refer to the parameter eClass as to a "galaxy spectral type''. Note that eClass is strongly correlated with the galaxy colour (u-i). The values of eClass, range from about -0.2to 0.6 from early- to late-type in our sample of galaxies. Panel b shows the distribution of redshifts z. Some SDSS spectra have residual sky lines that may affect our H$\alpha $and H$\beta $ measurements. Despite the mask array contained in each spectrum file that can be used to remove any inconvenient features, like bright sky lines, we have chosen an alternative way by excluding all objects in which the bright sky lines at 5578.5 Å and 7246.0 Å fall on the H$\alpha $ and H$\beta $ line regions, which explains the bizarre aspect of the redshift distribution of this sample. Panel c shows the distribution of galaxy absolute magnitudes in the SDSS photometric r band, M(r). This magnitude is utilized because K-corrections are modest, the radiation is produced mainly by the older stars that dominate the stellar mass, and uncertainties in Galactic reddening make little difference to the inferred galaxy magnitude (Strauss et al. 2002). To compute M(r) from the observed rmagnitude given by the SDSS, we assumed a standard cosmology with $\Omega_{M}$ = 0.3, $\Omega_{\lambda}$ = 0.7, and H0 = 75 km s-1 Mpc-1 and applied a K-correction (computed with kcorrect v1_11; Blanton et al. 2003).

Because of our restrictions on the quality of the spectra, we miss the less luminous galaxies of the SDSS (compare e.g. the histogram of the M(r) values in Blanton et al. 2001). Finally, panel d shows the distribution of the galaxy surface brightness, SB (in mag arcsec-2), defined within the radius containing 50% of the Petrosian flux for each band, petroR50. Note that for this study, we do not work with a complete volume- or magnitude- limited sample, so that the distribution of galaxies among the various classes does not correspond to the true distribution in the local universe. Also, note that, because of the conditions imposed on the quality of the spectra, the redshifts in our sample do not exceed a value of 0.25.

Some of the overall characteristics of galaxies are in fact correlated. For example, galaxies of earlier spectral types tend to be more luminous, as shown in panel a of Fig. 5 which plots M(r)vs. eClass. The top number on the right corresponds to the total number of data points (including a few individual points that may lie outside the panel frame). Next, are given the results of non parametrical tests: from top to bottom, the value of Kendall's $\tau _{\rm K}$, the associated probability (a large value of this probability indicates no correlation) and the Spearman rank correlation coefficient $r_{\rm S}$(see Press et al. 1992). Thus, we see that indeed M(r) is correlated with eClass. On the other hand, the galaxy surface brightness $S\!B$ is virtually independent of eClass (panel b).

3 Balmer extinction of normal galaxies

3.1 Definition of the diagnostic plots

The value of the Balmer extinction is derived from the observed ratio of H$\alpha $ and H$\beta $ line intensities using the relation

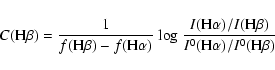\begin{displaymath}C({\rm H}\beta) = \frac{1}{f({\rm H}\beta)-f({\rm H}\alpha)} ... ...a)/I({\rm H}\beta)} {I^{0}({\rm H}\alpha)/I^{0}({\rm H}\beta)} \end{displaymath} (1)

where ${I^{0}({\rm H}\alpha)/I^{0}({\rm H}\beta)}$is the intrinsic intensity ratio of these two lines and $f({\rm H}\beta)-f({\rm H}\alpha)$ is equal to 0.335. The value of ${I^{0}({\rm H}\alpha)/I^{0}({\rm H}\beta)}$ is essentially insensitive to the physical conditions of the gas, being 3.03 at a temperature of 5000 K, 2.86 at 10 000 K, and 2.74 at 20 000 K (Osterbrock 1989). Thus, there is a practically linear relation between $C({\rm H}\beta )$ and log ( $I({\rm H}\alpha)/I({\rm H}\beta)$) (in the following simply noted log (H$\alpha $/H$\beta $)).


  \begin{figure} \par\includegraphics[width=16.3cm,clip]{ms3793.f6}\end{figure} Figure 6: The relation between log (H$\alpha $/H$\beta $) and various properties of the galaxies. The meaning of the numbers in the upper right is the same as in Fig. 5. The thick curve represents the median value of log (H$\alpha $/H$\beta $). The thin curves delimit the zone containing 80% of the data points (see Sect. 3.1).
Open with DEXTER

In Fig. 6, we plot the value of log (H$\alpha $/H$\beta $) as a function of various parameters characterizing the galaxies. In all the panels, the presentation is the same. The meaning of the numbers reported on the upper right is the same as in Fig. 5. The thick curve represents the median value of log (H$\alpha $/H$\beta $) and the thin curves represent the 10 and 90 percentiles, meaning that 10% of the data points are respectively above or below these curves (the data are binned according to the abscissa in bins with equal numbers of points). Such a representation, associated with the relevant statistics, is believed to give a fair idea of the behaviour of our sample in the different planes. Panel a concerns the galaxy spectral type eClass, panel b the colour (u-i) as obtained from the SDSS data base. Panel c the discontinuity at 4000 Å, D(4000), defined by the ratio of the flux from 4050 to 4250 Å to the flux from 3750 to 3950 Å. Thus, panels a-c relate H$\alpha $/H$\beta $ to quantities linked to the stellar continuum. Panels d-f  involve respectively the absolute magnitude M(r), the surface brightness $S\!B$defined above and the concentration index $C\!I$defined as the ratio of petroR50 to petroR90 retrieved from the SDSS data base. Panel g concerns the total radius R of the galaxy in kpc, computed from the petroR90 radius. Thus, one can consider that panels d-g are linked to the masses and mass distributions of the galaxies. Panel h concerns the inclination parameter b/a derived from the SDSS data base. The fact that the SDSS contains such a large number of galaxies allows us to infer conclusions from the variation of observed properties with galaxy inclination, which was not the case in our previous studies (SS99, SS01). Panel i concerns  $L({\rm H}\beta )_{\rm corr}$, the total luminosity of the galaxy in H$\beta $ (in solar luminosities) after correction for extinction using the value of  $C({\rm H}\beta )$. Panel j concerns the equivalent width of H$\alpha $. Panels i and j are thus related to the importance of H  II regions in the global galaxy spectra. Finally, panels k and l concern the metallicity of the galaxies. Among the various metallicity indicators, we have chosen two which are complementary. The first one, [N  II] $\lambda $6584/H$\alpha $ (panel k) has been proposed rather recently as a metallicity indicator in giant H  II regions (van Zee et al. 1998; Denicoló et al. 2002). Its advantages are that it increases monotonically with metallicity and is independent of reddening, since the two lines it involves have similar wavelengths. The other one, [O  III] $\lambda $5007/[N  II] $\lambda $6584 (panel l) was first proposed by Alloin et al. (1979). This indicator also varies monotonically with metallicity (it is smaller at large metallicities) which, in a study of the present kind, makes it safer to use than the traditional ([O  II] $\lambda $3727+[O  III] $\lambda $5007)/H$\beta $ indicator first proposed by Pagel et al. (1979) and still widely in use. The [O  III] $\lambda $5007/[N  II] $\lambda $6584 indicator has one advantage over the [N  II] $\lambda $6584/H$\alpha $ one: its larger dynamical range in galaxies. Unfortunately this indicator is affected by reddening. With the SDSS data, we are able to correct line intensities for reddening using the H$\alpha $/H$\beta $ ratio, and we use the reddening-corrected values in our study, assuming that the intrinsic value of H$\alpha $/H$\beta $ is 2.9. When using the [O  III] $\lambda $5007/[N  II] $\lambda $6584 or [N  II] $\lambda $6584/H$\alpha $ line ratios, we rejected the objects where the measured equivalent width in any of these lines is smaller than 1 Å, to avoid spurious values of the ratios linked to large uncertainties in the measurements of line fluxes.

3.2 Systematics of Balmer extinction in galaxies

Among the investigated relations between the Balmer extinction and various parameters of the galaxies, the most outstanding correlation is the one between H$\alpha $/H$\beta $ and the galaxy spectral types eClass, for which $r_{\rm S} = -0.665$, followed by the one with galaxy colour (u-i) for which $r_{\rm S}$ = 0.630. We find that early-type and redder galaxies suffer higher Balmer extinction. Of course, without any modelling, one could be tempted to say that early-type galaxies are redder not intrinsically, but because they suffer larger reddening. Such an extreme explanation would of course be unreasonable, since there are many arguments showing that early-type galaxies are indeed composed of older stellar populations (e.g. Sommer-Larsen 1996; Fioc & Rocca-Volmerange 1997). There are, however, indicators of the characteristics of the stellar population that do not depend on reddening, like for example the discontinuity at 4000 Å, D(4000). This discontinuity is larger for older and for more metal-rich stellar populations. This is due to higher Balmer opacity for lower stellar effective temperatures dominating the spectra in the first hypothesis, and higher metal opacity in the second case. It has been argued on empirical grounds (Dressler & Shectman 1987) that D(4000) is rather sensitive to star formation, but others (e.g. Poggianti & Barbaro 1997) point out that metallicity is important. The correlation we observe with D(4000) ($r_{\rm S}$ = 0.501) indicates that the Balmer extinction is higher for galaxies with older and/or more metal-rich stellar populations. That the correlation is slightly worse than in panels a and b probably reflects the fact that D(4000) is not sensitive to reddening.

We also see a strong correlation with M(r) ( $r_{\rm S} = -0.451$) expressing that the Balmer extinction is higher for more luminous (thus likely more massive) galaxies. Correlation with other parameters linked with galaxy stellar mass and concentration are present but are less important ( $r_{\rm S} = -0.298$ for $S\!B$, $r_{\rm S} = -0.182$ for $C\!I$ and $r_{\rm S}$ = 0.182 for R).

Surprisingly, there is no correlation with b/a ( $r_{\rm S} = -0.091$), while one would expect the extinction to be larger for more inclined galaxies. One interpretation might be that most of the Balmer extinction comes from dusty blobs which are more or less uniformly distributed in the galaxy, so that the extinction of the integrated flux does not depend on inclination. However, such an interpretation is not compatible with the fact the near-infrared colours of spiral galaxies depend on inclination (Masters et al. 2003). We will come back to this point later.

There is a weak anticorrelation with EW(H$\alpha $) ( $r_{\rm S} = -0.194$). EW(H$\alpha $) is a star formation history indicator (Kennicutt 1998) and the observed anticorrelation suggests that the Balmer extinction is higher in galaxies with a larger proportion of old stellar populations. On the other hand, the correlation with the total H$\beta $ luminosity ($r_{\rm S}$ = 0.607) suggests that the Balmer extinction is larger for galaxies with a larger total amount of young stars.

Finally, correlations with the metallicity indicators are fairly important (panels k and l): $r_{\rm S} = 0.418$ for [N  II] $\lambda $6584/H$\alpha $ and $r_{\rm S} = -0.449$ for [O  III] $\lambda $5007/[N  II] $\lambda $6584, suggesting that metallicity and Balmer extinction are strongly correlated.

3.3 Is the metallicity of galaxies the only driver of Balmer extinction?

It is known that many properties of galaxies are correlated in the Hubble sequence of galaxies (Roberts & Haynes 1994). Early-type galaxies tend to be more massive, composed of older stellar populations and more metal-rich (see e.g. Zaritsky et al. 1994; Kennicutt 1998; Fioc & Rocca-Volmerange 1997). Could it be that the main parameter responsible for the trends mentioned above between $C({\rm H}\beta )$ and other galaxy parameters is simply metallicity?

Let us assume for simplicity that $C({\rm H}\beta )$ can be written as:

\begin{displaymath}C({\rm H}\beta) = f(Z) g(X), \end{displaymath} (2)

where f(Z) is a function of metallicity and g(X) is a function of other parameters.

We know that [N  II] $\lambda $6584/H$\alpha $ and [O  III] $\lambda $5007/ [N  II] $\lambda $6584 are metallicity indicators and that they vary monotonically with metallicity. The problem is that we do not know the exact relation between the value of these ratios and the average metallicity of the interstellar medium in the galaxy. It is not possible to directly use the calibrations proposed for giant H  II regions (which in themselves are already a matter of debate, see Pilyugin 2003) because, as mentioned by SS01, spectra of galaxies are affected by metallicity gradients and by the contribution of diffuse ionized regions to the spectrum. This can be illustrated as follows. In the sample of spiral galaxies studied by Zaritsky et al. (1994) the average metallicities vary from 12 + log (O/H) = 8.3 to 9.3 when the galaxy absolute B magnitudes MB range from -17 to -21. The slope of the relation between log O/H and MB in their Fig. 10 is roughly -0.25 (but there is substantial dispersion). If we would apply the calibration of Van Zee et al. (1998) (12 + log (O/H) = 1.02 log ([N  II] $\lambda $6584/H$\alpha $) + 9.35), the corresponding [N  II] $\lambda $6584/H$\alpha $ values would range between -1.04 and -0.06and the slope between log [N  II] $\lambda $6584/H$\alpha $ and MB would again roughly be -0.25. Figure 7 shows the relation between log ([N  II] $\lambda $6584/H$\alpha $) and MB in our sample (the value of MBhas been estimated using the transformations between the SDSS photometric system and the standard UBV system following Smith et al. 2002). Most of the observed values of log ([N  II] $\lambda $6584/H$\alpha $) are between -0.7 and -0.3 even for the galaxies with the lowest luminosities in our sample. This is likely due to the fact that in spectra of galaxies both the radial metallicity gradients and the contribution of emission from the diffuse ionized medium would tend to enhance the [N  II] $\lambda $6584/H$\alpha $ ratio.


  \begin{figure} \par\includegraphics[width=5cm,clip]{ms3793.f7}\end{figure} Figure 7: The relation between the metallicity indicator [N  II] $\lambda $6584/H$\alpha $ and the absolute magnitude $M_{\rm B}$ in the galaxies of our sample. Same layout as for the panels in Fig. 6.
Open with DEXTER

What we can do, however, is study the function $C({\rm H}\beta )$/([N  II] $\lambda $6584/H$\alpha $)awhere a is determined empirically so as to remove any dependence of this function on [N  II] $\lambda $6584/H$\alpha $, implying that $C({\rm H}\beta )$/([N  II] $\lambda $6584/H$\alpha $)a is independent of metallicity. We find that a is approximately equal to 0.9 in our sample. While this procedure is very schematic and relies on assumptions, the fact that we find $C({\rm H}\beta )$/([N  II] $\lambda $6584/H$\alpha $)0.9 to be independent of the other metallicity indicator, [O  III] $\lambda $5007/[N  II] $\lambda $6584, gives us confidence in our approach. (Note that the value of a depends on the definition of our sample and should not be used for other samples without caution). Figure 8 shows the same plots as Fig. 6, with log (H$\alpha $/H$\beta $) now replaced by $C({\rm H}\beta )$/([N  II] $\lambda $6584/H$\alpha $)0.9. We see that $C({\rm H}\beta )$/([N  II] $\lambda $6584/H$\alpha $)0.9 (which can be assimilated to g(X) in Eq. (2)) is strongly correlated with the galaxy spectral type eClass ( $r_{\rm S} = -0.436$) and colour (u-i) ($r_{\rm S}$ = 0.394) and also with D(4000) ( $r_{\rm S}=0.340$) although less tightly than  $C({\rm H}\beta )$. The strongest correlation in this figure is with $L({\rm H}\beta )_{\rm corr}$ ($r_{\rm S}$ = 0.512). However, we show in Fig. 9, that $L({\rm H}\beta )_{\rm corr}$ is very strongly correlated with M(r) ( $r_{\rm S} = -0.691$) so that we conclude that an important driver of the Balmer extinction is actually the total galaxy luminosity (or mass). On the other hand, D(4000) is not correlated with M(r) as seen in Fig. 9, so the observed correlation between $C({\rm H}\beta )$/([N  II] $\lambda $6584/H$\alpha $)0.9 and D(4000) implies that the presence of old stars is in itself also a driver of the Balmer extinction.

We also note in Fig. 8 (panel h) that $C({\rm H}\beta )$/ ([N  II] $\lambda $6584/H$\alpha $)0.9 is linked with galaxy inclination ( $r_{\rm S} = -0.200$). One explanation that can account for this as well as for the absence of correlation between H$\alpha $/H$\beta $ and b/a is that H  II regions are rather close to the galactic plane of galaxies (which is in better agreement with the observed height scale of H  II regions in nearby galaxies), and that the increased path length of the attenuating dust in inclined galaxies is roughly compensated by abundance gradients: when a galaxy is inclined, the innermost regions, that are more metal-rich and therefore most likely dust-rich, are more obscured than the outermost H  II regions, which suffer less extinction at optical wavelengths. The compensating effect of the metallicity gradients at near-infrared wavelengths is far less important due to smaller optical depths at these wavelengths, which explains why Masters et al. (2003) do find a correlation between near-infrared colours and inclination. We have tested by simple toy models that such an explanation can be viable.


  \begin{figure} \par\includegraphics[width=16.6cm,clip]{ms3793.f8}\end{figure} Figure 8: Same diagrams as in Fig. 6 except that the ordinate is $C({\rm H}\beta )$/([N  II] $\lambda $6584/H$\alpha $)0.9 instead of log (H$\alpha $/H$\beta $) (see Sect. 3.3).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=10.4cm,clip]{ms3793.f9}\end{figure} Figure 9: $L({\rm H}\beta )_{\rm corr}$ versus M(r) ( left) and D(4000)vesus M(r). Same layout as Fig. 5.
Open with DEXTER

4 Discussion

We have thus found (confirming the results of SS99 and SS01) that the Balmer extinction of galaxies decreases steadily from early- to late-type spirals (whether classified according to their spectral type or according to their colour). We have also shown that there is a direct dependence of Balmer extinction on metallicity, and also on the age of the stellar populations and on the total galaxy luminosity. This last statement is consistent with the finding of Wang & Heckman (1996), based on relations using far-ultraviolet and far-infrared fluxes, that "the optical depth of normal galactic disks increases with galaxy luminosity''. On the other hand, the dependence we find on galaxy type seems to contradict the general opinion summarized by Calzetti (2001) and the recent result by Kauffmann et al. (2003) who conclude that "galaxies with the youngest stellar populations are the most attenuated by dust''. While previous studies were sometimes based on small samples, the result of Kauffmann et al. (2003) comes from a model fitting of the continua of 105 galaxies from the SDSS. It should be noted that what they measure with this elaborate procedure is the attenuation of the stellar light. Our work concerns the extinction of nebular light and the determination of the Balmer extinction is straightforward. The interpretation in terms of global opacity of galaxies is however not simple: with H$\alpha $/H$\beta $ we measure some sort of average opacity of the zones dimming the light from H  II regions (excluding the most opaque ones). Still, it is striking to see how well $C({\rm H}\beta )$ correlates with the galaxy spectral type. In this section, we present a possible phenomenological interpretation of our results, and show that our findings can actually be reconciled with the results of Kauffmann et al. (2003).

4.1 A phenomenological interpretation of the observed Balmer extinction trends in our sample

Let us write $C({\rm H}\beta )$as the following product:

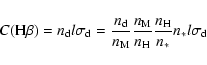\begin{displaymath}C({\rm H}\beta) = n_{\rm d} l \sigma_{\rm d} = \frac{n_{\rm d... ... M}}{n_{\rm H}} \frac{n_{\rm H}}{n_{*}} n_{*} l \sigma_{\rm d} \end{displaymath} (3)

where $n_{\rm d}$ is average number of dust particles per unit volume in a galaxy, $n_{\rm M}$ is average number of metallic atoms (in any form) per unit volume, $n_{\rm H}$ is the average number of hydrogen particles per unit volume, n* is the average number of stars per unit volume, l is the geometrical thickness of the region responsible for the optical extinction, and $\sigma_{\rm d}$ is the typical extinction cross section of dust grains.

The common view that the opacity should increase from early- to late-types is comforted by such arguments that "galaxies with young stars contain more gas and hence more dust than galaxies with old stellar populations'' (Kauffmann et al. 2003). On the other hand, early-type galaxies are more metal-rich and on average more massive than late-type galaxies, so it is not necessarily surprising that the extinction is actually larger for late-type galaxies. In Sect. 3.2 we have given arguments to say that the Balmer extinction is also determined by the mean age of the stellar population. This could indicate that in late-type galaxies $n_{\rm d}/n_{\rm M}$ is larger than in early-type ones. Such a view seems indeed to be supported by recent models for the evolution of dust in galaxies (Hirashita 1999) which take into account the processes of formation and destruction of dust (note however that there are presently many assumptions and uncertainties in such models, see e.g. Dwek 1998 or Edmunds 2001). In these models, condensation in cool stellar winds from low-mass stars is an important source of dust production.

We note that 75% of the galaxies of our sample have a measured $C({\rm H}\beta )$between 0.3 and 0.9, as seen from the histogram shown in Fig. 10. On the other hand, judging from the metallicities derived for galaxies of luminosities similar to those of our sample (Zaritsky et al. 1994; Charlot et al. 2002), the metallicity range in our sample is likely higher than just a factor of three. This suggests that factors other than metallicity act to reduce the observed range in $C({\rm H}\beta )$. Obviously, $n_{\rm H}/n_{*}$ is a good candidate, since it decreases from late- to early-type galaxies (Roberts & Haynes 1994).

On the other hand n* l, which can be assimilated to the stellar surface density, decreases from early- to late-types.

The last factor in Eq. (3) is $\sigma_{\rm d}$, and one might expect some systematic effects if the grain size distribution depends on the processes for grain growth or destruction that could have different relative importances in galaxies of different types.

In conclusion, dust extinction in galaxies involves many factors, and our finding that $C({\rm H}\beta )$ increases from late- to early-types can easily be accounted for, at least qualitatively, within our present-day understanding of galaxies and their constituents.

4.2 The extinction of stellar light versus the extinction of nebular light

As emphasized above, what we measure with $C({\rm H}\beta )$ is actually the reddening of the nebular light (called Cl in SS01). On the other hand, what is determined by Kauffmann et al. (2003) is the reddening of the stellar light (called Cc in SS01). We now examine the relation between these two quantities in our sample of galaxies.


  \begin{figure} \par\includegraphics[width=4.8cm,clip]{ms3793.f10}\end{figure} Figure 10: Histogram of the values of the Balmer extinction at H$\beta $, $C(\mbox{H$\beta$ })$ in our sample of galaxies.
Open with DEXTER

It had already been noted by SS99 and SS01, on much smaller samples of galaxies, that EW(H$\alpha $) and EW(H$\beta $) correlate extremely well (see also Kennicutt 1992). This implies that the difference between the extinction of the stellar continuum and that of the nebular emission is strongly linked to the colours of the galaxies, being larger for redder galaxies (see Eq. (5) in SS01). In Fig. 11 we show the values of EW(H$\beta $) as a function of EW(H$\alpha $) in our sample of galaxies. The correlation is extremely strong, with $\tau_{\rm K} = 0.782$ and $r_{\rm S} = 0.931$. Assuming that the relation between these emission line equivalent widths is EW(H$\beta $) = $A \times EW$(H$\alpha $) (the same model as adopted in SS01), an ordinary least square bisector linear fitting (Isobe et al. 1990) gives $A = 0.185 \pm 0.001$. Considering only objects for which EW(H$\alpha $) > 20 Å the result is the same, $A = 0.185 \pm 0.001$. These results may be compared with $A = 0.194 \pm 0.011$ and $A = 0.245 \pm 0.007$, presented in SS99 and SS01, respectively. Our value A is consistent with that obtained by SS99 but not with that obtained by SS01. The cause of this discrepancy is not clear; it might be due to differences in the spectral resolution, because the spectral resolution of the SDSS spectra is almost half that of the NFGS spectra (Jansen et al. 2000a,b) used by SS01.
  \begin{figure} \par\includegraphics[width=4.9cm,clip]{ms3793.f11}\end{figure} Figure 11: The relation between EW(H$\beta $)and EW(H$\alpha $) in our sample of galaxies. The layout of the figure is the same as for Fig. 5.
Open with DEXTER

From Eq. (5) in SS01 and the value of A, we derive that

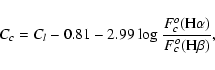\begin{displaymath}C_{c} = C_{l} - 0.81 - 2.99 ~ {\rm log}~ \frac {F_{c}^{o} ({\rm H}\alpha)}{F_{c}^{o}({\rm H}\beta)}, \end{displaymath} (4)

where Fco(H$\alpha $) and Fco(H$\beta $) are the intrinsic (i.e. not affected by extinction) stellar fluxes in the continuum adjacent to H$\alpha $ and H$\beta $ respectively. We can use the dust-free spectrophotometric models of Barbaro & Poggianti (1997) to relate the value of Fco(H$\alpha $)/Fco(H$\beta $) to the values of D(4000) and EW(H$\alpha $). Using panel j of our Fig. 6 we can relate EW(H$\alpha $) to log (H$\alpha $/H$\beta $) (by taking the median value of H$\alpha $/H$\beta $ for a given EW(H$\alpha $)) and therefore to Cl. With the help of Eq. (4) we thus find that Ccgoes from about 0.02 for D(4000) = 1.7 to about 0.2 for D(4000) = 1.3. This goes in the same direction as the results of Kauffmann et al. (2003) who find that the median value of Az, which is approximately equal to our Cc, roughly goes from 0.2 at D(4000) = 1.7 to 0.6 at D(4000) = 1.3. That the numbers are not exactly the same as the ones found by our analysis is not necessarily a worry given the dispersion in the observational points (both here and in the work of Kauffman et al. 2003) and given that the definition of the derived extinction is not exactly the same.

As for Cl, it can be evaluated using Fig. 6c and Eq. (1). We find $C_{l} \simeq 0.8$ for D(4000) = 1.7 and $C_{l} \simeq 0.3$ for D(4000) = 1.3. We note that Cc is smaller than Cl at both extremes of the spectral type range, which can be interpreted as due to the fact that dust is more concentrated (and thus more opaque to radiation) in molecular clouds associated with H  II regions than in the diffuse interstellar medium. One may wonder why Cc increases from early- to late-type spirals while Cl decreases. The answer to this may be related to the fact that the stellar light from early-type galaxies is dominated by the bulge and to a specific distribution of dust resulting from dynamical effects. Advanced 3D-modelling of the star, dust and gas distribution in galaxies would be needed to test any interpretation of our empirical result.

5 The relation between C(H$\beta $) and infrared luminosity in our sample

Another indicator of the presence of dust in galaxies is their far-infrared radiation attributed to the emission from dust grains heated by stellar radiation (e.g. Inoue 2002). Kewley et al. ( 2002), using 81 galaxies with relevant data from the NFGS sample, noted the existence of a very strong correlation between the far-infrared luminosity $L(\rm FIR)$ and the H$\alpha $ luminosity (corrected for reddening using the observed H$\alpha $/H$\beta $ ratio). They find a Spearman rank correlation coefficient of $r_{\rm S} = 0.98$. They do not plot the relation between H$\alpha $/H$\beta $ and  $L(\rm FIR)$, but this plot is shown by Wang & Heckman (1996) for about 30 galaxies from the Kennicutt (1992) atlas with relevant data, and they find a correlation to within better than a 0.1% level of confidence (the correlation coefficient from a standard linear regression is 0.63).


  \begin{figure} \par\includegraphics[width=10.4cm,clip]{ms3793.f12}\end{figure} Figure 12: Galaxies from our sample detected by IRAS (see Sect. 5). Plots of log (H$\alpha $/H$\beta $) vs. log $L(\rm FIR)$(panel a)) and log $L(\mbox{H$\beta$ })$ (corrected for Balmer extinction) vs. log $L(\rm FIR)$ (panel b)).
Open with DEXTER

It was tempting to produce such diagrams for our sample of galaxies using the IRAS data base. We have searched the IRAS Faint Source Catalogue (Moshir et al. 1989) and the IRAS Point Source Catalogue (IPAC 1986) for far-infrared counterparts of galaxies from our sample. Since the IRAS beam size at 60 $\mu$m is 1 $\hbox{$.\mkern-4mu^\prime$ }$5 and the IRAS uncertainty in position is about 30 $\hbox{$^{\prime\prime}$ }$, we used a conservative circular window of 1 $\hbox{$^\prime$ }$radius around the SDSS positions of our sample galaxies to search for far-infrared sources. Note that we also constituted a subsample of IRAS galaxies using a search window of 30 $\hbox{$^{\prime\prime}$ }$ instead of 1 $\hbox{$^\prime$ }$; this subsample is twice smaller but the conclusions drawn below are not altered. Since an estimate of the total infrared luminosity requires IRAS fluxes at both 60 $\mu$m and 100 $\mu$m (f60 and f100, respectively), we kept only those galaxies with available fluxes in both bands and IRAS quality flags greater than 1. About 80 galaxies were common to both the IRAS Point Source Catalogue and the IRAS Faint Source Catalogue. For those objects, we retained the flux values given by the Faint Source Catalogue, which have greater quality.

This search resulted in 189 galaxies. We have computed $L(\rm FIR)$ using the formula from Thuan & Sauvage (1992):

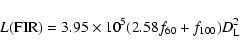\begin{displaymath}L({\rm FIR}) = 3.95\times10^{5}(2.58 f_{60} + f_{100} ) D_{\rm L}^{2} \end{displaymath} (5)

where $L(\rm FIR)$ is in solar units, f60 and f100 are in Jy and $D_{\rm L}$ is the cosmological luminosity distance of the galaxy in Mpc. In most cases, $L(\rm FIR)$ $ > 2 \times 10^{10}$ $L_{\odot}$. Note that this lower limit actually corresponds to the high luminosity tail of the luminosities of spiral galaxies detected by IRAS (Thuan & Sauvage 1992). This stems from the fact that our samples contains only galaxies at redshifts larger than 0.05, and at such distances only luminous infrared galaxies can be detected.


  \begin{figure} \par\includegraphics[width=16.6cm,clip]{ms3793.f13}\end{figure} Figure 13: Same diagrams as in Fig. 6, with the galaxies detected by IRAS represented with large circles.
Open with DEXTER

Figure 12 plots the values of log (H$\alpha $/H$\beta $) (panel a) and log  $L({\rm H}\beta )_{\rm corr}$ (panel b) versus log  $L(\rm FIR)$. We do not see any correlation between log (H$\alpha $/H$\beta $) and $L(\rm FIR)$ (the probability associated to the Kendal statistics is as large as 0.2). A correlation between $L({\rm H}\beta )_{\rm corr}$ and $L(\rm FIR)$ is present in our sample, but much weaker than found by Kewley et al. (2002). It thus turns out that correlations between optical and infrared properties become much less conspicuous or even disappear when restricting the sample to luminous infrared galaxies[*]. Note that in the samples of Wang & Heckman (1996) and Kewley et al. (2002) galaxies with $ L({\rm FIR}) > 2 \times 10^{10}$ L$_{\odot}$ are only a handful and do not show a clear correlation either.

It is also interesting to see how our luminous infrared galaxies compare with our entire sample of galaxies. For this, we show in Fig. 13 the same diagrams as in Fig. 6, with the luminous infrared galaxies now indicated by large circles. We see that in all the diagrams the galaxies detected by IRAS are found in the entire domain covered by the SDSS galaxies except the regions corresponding to the least luminous galaxies (which cannot be detected by IRAS at the redshits of our SDSS sample). The distributions of the luminous infra-red galaxies is very similar to that of our entire set of SDSS galaxies, except that is is slightly skewed towards the highest values of H$\alpha $/H$\beta $.

The comparison of our SDSS sample with IRAS data raises two questions. Why were only 2% of our sample of SDSS galaxies detected by IRAS? Why are those IRAS detected galaxies found at any value of H$\alpha $/H$\beta $? Concerning the first question, we have already noted that, because of the limit imposed on the redshift in our SDSS sample, only luminous infrared galaxies can be identified as IRAS sources. An IRAS source is characterized by the presence of warm dust (50-200 K), which lies relatively close to the stars. Such a situation is encountered in zones where star formation has occured very recently, and which have not yet been swept out by stellar winds. In a galaxy, the H  II regions that emit the observed H Balmer lines have ages between 1 and 10 Myr, but the H  II regions that will emit most efficiently in the IRAS bands are younger than that. This explains, at least qualitatively, why only a small proportion of the galaxies from our SDSS sample have been detected by IRAS. These are the ones that happen to have a larger number of zones of very recent star formation. Such galaxies are more likely found among more massive galaxies at a given spectral type, but may be found at any galaxy spectral type. Since the IRAS emission probes these extremely young star forming regions, there is no reason why it should show any correlation with the global optical properties of the galaxies, which answers the second question.

6 Summary, implications and prospects

We have used the observations from the First Data Release of the SDSS to examine a sample of normal galaxies (as opposed to galaxies with an active nucleus) and to investigate how the Balmer extinction $C({\rm H}\beta )$ (i.e. the extinction at the wavelength of  H$\beta $ derived from the H$\alpha $/H$\beta $ emission line ratios) relates with other global properties of the galaxies. Our selection criteria to build up the sample resulted in a data set of 9840 galaxies with adequate data. All these galaxies are at redhifts larger than 0.05 to avoid strong aperture effects.

Our main findings are the following:

1.
$C({\rm H}\beta )$ is linked with the galaxy spectral type and colour, decreasing from early- to late-type spirals;
2.
$C({\rm H}\beta )$ increases with increasing metallicity;
3.
$C({\rm H}\beta )$ is, probably, also affected by the age of the stellar population, being larger in the case of older stellar populations;
4.
$C({\rm H}\beta )$ depends on galaxy masses;
5.
The extinction of the stellar light is correlated with both the extinction of the nebular light and the intrinsic galaxy colours, resulting in a trend with galaxy colour that may be opposite to the trend of $C({\rm H}\beta )$.
The present work thus confirms the conclusions of our previous studies (Sodré & Stasinska 1999; Stasinska & Sodré 2001), which were based on much smaller samples and used data with lower spectral resolution (Kewley et al. 2002, using the same sample as SS01, also found that early-types in that sample are more heavily reddened than late-types).

Compared to our previous studies, the large number of galaxies in the SDSS sample allows us to investigate issues related to the inclination of galaxies.

The fact that $C({\rm H}\beta )$correlates so well with other properties of galaxies is remarkable, given that the extinction, especially in late-types, is known to be not uniform across the face of galaxies (e.g. Beckman et al. 1996).

We have cross-correlated our sample of SDSS galaxies with the IRAS data base in order to investigate any relationship between $C({\rm H}\beta )$ and total infrared luminosity of the galaxies. Due to the lower redshift limit imposed to our sample and to the detection limit of IRAS, such a procedure selected only luminous infrared galaxies. We found that correlations that were shown by other authors to exist between optical and infrared properties of galaxies disappear when restricting to luminous infrared galaxies. We also found that the optical properties of the luminous infrared galaxies in our SDSS sample are very similar to those of our entire sample of SDSS galaxies.

We have proposed a phenomenological interpretation of our findings. We suggest that the main driver of the Balmer extinction of galaxies is their mass, combined with their metallicity and presence of old stellar populations. The infrared luminosity of the galaxies as determined by IRAS, which is attributed to radiation from hot stars reprocessed by dust grains, samples the regions with the most recent episodes of star formation, and is not connected with the Balmer extinction. Obviously, detailed modelling of the spectral light from galaxies taking into account the effects of dust and using a complete code such as GRASIL (Silva et al. 1998, see also http://web.pd.astro.it/granato/grasil/grasil.html) is needed for a deeper understanding of the empirical relations we have found. This is not an easy task, however, since as noted by Witt at al. (1992) and Witt & Gordon (2000), equal amounts of dust in different configurations may produce very different reddening and attenuation effects. In any case, future models of the integrated light from galaxies including the effects of dust should also aim at reproducing the correlations we have shown.

An important outcome of our study is to open the way for an improved correction for extinction in the determination of such parameters as the global star formation rate in galaxies or their total stellar masses. For normal galaxies, the global star formation rate can be obtained from the total H$\alpha $ luminosity corrected for extinction using the extinction derived from the H$\alpha $/H$\beta $ emission line ratio (keeping in mind the reservations expressed e.g. by Hirashita et al. 2003). If observations do not allow one to determine the Balmer extinction, one can make use of e.g. the observed galaxy colour or the D(4000) parameter to obtain an estimate of statistical value since we have shown that all these quantities are correlated. On the contrary, the total stellar mass can be estimated from the observed stellar fluxes of the galaxy after correcting for stellar extinction. This should be done with a proper model fitting of the observed continuum as in Kauffmann et al. (2003). However, the strong correlation that we have found empirically between stellar extinction, Balmer extinction and galaxy colours can provide a basis for a statistical method to determine the total masses of galaxies. These aspects will be developed in future work and should be important especially for the study of galaxies at intermediate and high redshifts.

Acknowledgements

This work has benefited from grants from the PICS franco-brésilien, from the jumelage France-Pologne and from the Observatoire de Paris. A.M. and L.S. acknowledge support from FAPESP and CNPq; L.S. is also grateful to CCINT/USP. The Instituto de Astronomia, Geofísica e Ciências Atmosféricas da USP has provided hospitality to G.S. and the Observatoire de Paris to L.S. and R.S. All the authors wish to thank the team of the Sloan Digital Sky Survey (SDSS) for their dedication to a project which has made the present work possible. The Sloan Digital Sky Survey is a joint project of The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, the Johns Hopkins University, the Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Princeton University, the United States Naval Observatory, and the University of Washington. Funding for the project has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. Thanks are also due to the referee whose comments led to a substantial clarification of the paper.

References


Copyright ESO 2004