A&A 420, 783-788 (2004)
DOI: 10.1051/0004-6361:20035793

Radiative rates for transitions in Fe XVII[*]

K. M. Aggarwal - F. P. Keenan - R. Kisielius[*]

Department of Pure and Applied Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland, UK

Received 3 December 2003 / Accepted 8 March 2004

Abstract
Energies of the lowest 157 levels belonging to the (1s2) 2s22p6, 2s22p53${\ell}$, 2s22p54${\ell}$, 2s22p55${\ell}$, 2s2p63${\ell}$, 2s2p64${\ell}$ and 2s2p65${\ell}$ configurations of Fe XVII have been calculated using the GRASP code of Dyall et al. (1989). Additionally, radiative rates, oscillator strengths, and line strengths are calculated for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transitions among these levels. Comparisons are made with the results already available in the literature, and the accuracy of the data is assessed. Our energy levels are expected to be accurate to better than 1%, whereas results for other parameters are probably accurate to better than 20%.

Key words: atomic data - atomic processes

1 Introduction

Iron is an abundant element, particularly in solar and fusion plasmas, and its emission lines are observed in almost all ionization stages. Emission lines of Ne-like Fe XVII are of special interest, because these have been observed in a variety of plasmas including astrophysical, laser produced, magnetically confined, Z-pinch and EBIT (see, Laming et al. 2000; Bhatia & Doschek 2003; Beiersdorfer et al. 2003 for references). To interpret the vast amount of observational data, atomic parameters such as energy levels, radiative rates, and collision strengths are required. Since there is a paucity of experimental data for these parameters, theoretical results are of vital importance. Therefore, in this work we report our results for energy levels and radiative rates for transitions among the lowest 157 levels of the (1s2) 2s22p6, 2s22p53${\ell}$, 2s22p54${\ell}$, 2s22p55${\ell}$, 2s2p63${\ell}$, 2s2p64${\ell}$ and 2s2p65${\ell}$ configurations of Fe XVII.

Realising the importance of Fe XVII, a number of workers in the past have performed a variety of calculations to compute atomic parameters, particularly energy levels, radiative rates, oscillator strengths, and electron impact excitation collision strengths. The most notable among the available data are the recent calculations of Aggarwal et al. (2003a), Bhatia & Doschek (2003) and Chen et al. (2003). Aggarwal et al. have computed energy levels and radiative rates for transitions among 89 fine-structure levels of the 2s22p6, 2s22p53${\ell}$, 2s22p54${\ell}$, 2s2p63${\ell}$, and 2s2p64${\ell}$ configurations. Their calculations are fully relativistic, as they have adopted the GRASP (General purpose Relativistic Atomic Structure Program) code of Dyall et al. (1989) for the generation of wavefunctions, and the Dirac Atomic R-matrix Code (DARC) of Norrington & Grant (2004) for the computation of collision strengths ($\Omega$). However, their results for $\Omega$ are confined to the lowest 55 levels, and are available only at energies above thresholds. Therefore, these results are of limited use because resonances in thresholds region have not been resolved. The closed-channel (Feshbach) resonances are known to contribute significantly to the calculations of effective collision strengths ($\Upsilon$) or excitation rate coefficients. Therefore, any results of $\Upsilon$ derived from the $\Omega$ values of Aggarwal et al. may be seriously underestimated, even at the high temperatures ( $T_{\rm e} \le$ 107 K) at which data are required for modelling spectral lines of Fe XVII. Bhatia & Doschek adopted a semi-relativistic approach for the computation of their results. They employed the SuperStructure (SS) code of Eissner et al. (1974) for the computation of wavefunctions, and the Distorted-Wave (DW) program of Eissner (1998) for calculating $\Omega$. One-body relativistic operators were included through term coupling coefficients. This semi-relativistic approach does not significantly affect the accuracy of $\Omega$ values, as has been shown by a good agreement between the DARC and DW results for a majority of transitions - see Aggarwal et al. for details and comparisons. Furthermore, Bhatia & Doschek included a larger number of levels (73) in their calculations of $\Omega$, and also extended the energy range from the 300 Ryd of Aggarwal et al. to 425 Ryd. However, they too ignored resonances in the thresholds region, and hence their results are again of limited practical use. On the other hand, Chen et al. have not only included all the 89 levels among the configurations listed above, but have also resolved resonances in thresholds region. They have adopted the SS code for the calculations of wavefunctions, and results for $\Omega$ have been obtained from the R-matrix code of Berrington et al. (1995). Furthermore, their calculations include one-body relativistic operators in the Breit-Pauli approximation. Therefore, the energy levels and radiative rates of Aggarwal et al., and excitation rates of Chen et al. should be the most reliable available to date for transitions among the 89 fine-structure levels noted above.

The motivation for the present work comes from the fact that even the most exhaustive results of Chen et al. (2003) available to date are unable to fully resolve the discrepancy between theory and measurements. Of particular recent interest (beside others) are the six resonance lines of Fe XVII, namely 3C (2p6 1S0-2p53d 1P$^\circ_1$: 1-17), 3D (2p6 1S0-2p53d 3D$^\circ_1$: 1-23), 3E (2p6 1S0-2p53d 3P$^\circ_1$: 1-27), 3F (2p6 1S0-2p53s 3P$^\circ_1$: 1-5), 3G (2p6 1S0-2p53s 1P$^\circ_1$: 1-3), and 3H (2p6 1S0-2p53s 3P$^\circ_2$: 1-2), at respective wavelengths of 15.015 $\AA$, 15.262 $\AA$, 15.450 $\AA$, 16.778 $\AA$, 17.053 $\AA$, and 17.098 $\AA$ - see Table 1 below for level indices. These prominent strong lines have been observed in the X-ray spectra of the solar and other stellar coronae, active galactic nuclei, X-ray binaries, and supernovae from the Chandra and XMM Newton satellites - see Chen et al. for references. Furthermore, line intensity ratios have also been measured on EBIT (electron beam ion trap) machines at the Lawrence Livermore National Laboratory (LLNL: Beiersdorfer et al. 2003 and references therein), and at the National Institute of Standards and Technology (NIST: Laming et al. 2000). There is satisfactory agreement between theory and experiment for the ratio R1 (3C/3D), but the discrepancy is $\sim$15% for R2 (3E/3C) - see Table 4 of Chen et al. Similarly, the discrepancy is even greater for the ratio R3 (3F/3C), particularly at temperatures below 4 $\times$ 106 K, at which Fe XVII has its maximum fractional abundance in ionization equilibrium. Some of the discrepancies between theory and astrophysical observations can perhaps be resolved by the consideration of multi-ion model in stead of the widely used single ion model, as discussed and demonstrated by Doron & Behar (2002). However, there are still serious differences between the LLNL and NIST measurements, while Beiersdorfer et al. (2003) have questioned the accuracy of the atomic data of Chen et al. (2003), suggesting that the contribution of resonances may have been overestimated. Additionally, Beiersdorfer et al. do not observe any appreciable variation in line ratios with energy, whereas Chen et al. do show a significant variation, as expected. To resolve the laboratory measurements, new experiments are planned at NIST (Laming 2003), and we have a fresh look at the theoretical atomic data. This is for several reasons as explained below.

Firstly, in our opinion the most reliable results available to date for effective collision strengths (or excitation rates) are those of Chen et al. (2003), because: (i) they have explicitly resolved the resonances in thresholds region, (ii) have included configuration interaction(CI) and relativistic effects, (iii) have included a large number of levels (89), besides adopting the widely used R-matrix method, (iv) have ensured the convergence of $\Omega$ with the partial wave expansion, and (v) have taken into account the high energy behaviour of $\Omega$ while computing results for $\Upsilon$. Therefore, we do not see any apparent deficiency in their work. However, the past experience of similar work on other ions of iron has shown that different calculations of comparable complexity and employing the same R-matrix method (but in different approximations) often produce strikingly different sets of results. Examples of serious differences are results for Fe XI (Aggarwal & Keenan 2003a,b), Fe XV (Aggarwal et al. 2000, 2001, 2003b), and Fe XXI (Aggarwal & Keenan 2001). Therefore, in the absence of any other results being available for Fe XVII with comparable accuracy, a fresh calculation with an independent approach may be useful in confirming the accuracy of the available atomic data.

Secondly, all the resonance lines of Fe XVII, including the prominent ones, exhibit numerous resonances throughout the thresholds region - see Figs. 7-13 of Chen et al. (2003), and hence make a significant contribution to the values of $\Upsilon$. Since most of the line ratios either measured in the laboratory, or observed in the solar and astrophysical plasmas, are at high energies/temperatures ($\sim$0.8-1.2 keV, 106-107 K), resonances towards the higher end of the thresholds region may make an appreciable contribution. Therefore, we find that there is scope for improvement in the calculations of Chen et al., because all 50 levels of the 2s22p55${\ell}$ configurations lie below the energy levels of the 2s2p64p configuration, and the 18 levels of the 2s2p65${\ell}$ configurations are just above the levels of the 2s2p64f configuration - see Table 1. All the 68 levels of the 2s22p55${\ell}$ and 2s2p65${\ell}$ configurations lie in the $\sim$80-91 Ryd energy range, and interact closely with the levels of the 2s2p64${\ell}$ configurations. Therefore, the resonances arising from the missing 68 levels may make an appreciable contribution. Since calculations for $\Omega$ are still in progress the contribution of such resonances cannot be estimated at present. Nevertheless, inclusion of these additional 68 levels in a calculation will be helpful in spectral modelling, because cascading effect from higher levels is important (Chen et al. 2003; Beiersdorfer et al. 2003).

Finally, inclusion of CI with the 2s22p55${\ell}$ and 2s2p65${\ell}$ configurations will be helpful in determining the convergence of the expansion of the wavefunction. Therefore, for all the above reasons we are performing a larger calculation with the aim of providing a consistent set of results for energy levels, radiative rates, collision strengths, and effective collision strengths for all transitions among 157 levels of Fe XVII. However, in this paper we are reporting our results for the first two parameters only, because the calculations for $\Omega$ are computationally intensive, and hence will take a significant time to complete.

2 Energy levels

The (1s2) 2s22p6, 2s22p53${\ell}$, 2s22p54${\ell}$, 2s22p55${\ell}$, 2s2p63${\ell}$, 2s2p64${\ell}$, and 2s2p65${\ell}$ configurations of Fe XVII give rise to 157 fine-structure levels, listed in Table 1. To generate the wavefunctions, we have used the fully relativistic GRASP code of Dyall et al. (1989) with the option of extended average level (EAL), in which a weighted (proportional to 2j + 1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate accuracy. Also, as in calculations by other workers, we have included CI among the above basic 25 configurations.

Table 1: Target levels of Fe XVII and their threshold energies (in Ryd).

In Table 1 we list our energies for the 157 fine-structure levels of Fe XVII. Also included in the table are the experimentally compiled energies of NIST (http://www.physics.nist.gov/PhysRefData), and energies of 89 levels reported in our previous work (Aggarwal et al. 2003a) using the same GRASP code. Other available experimental and theoretical results have already been compared and discussed in our previous work, and are therefore not included in Table 1. Experimental energies for all levels are not available, but the agreement is better than 1% for the common levels. Furthermore, the level orderings are the same in both theoretical and experimental results, which is highly satisfying. Similarly, apart from the additional 68 levels included in the present work, the agreement with the previous results is better than 1%. In fact, the discrepancy is less than 0.02 Ryd, except for level 114 (2s2p64s 3S1) for which the present results are higher by 0.034 Ryd, amounting to less than 0.05%. Therefore, we may state with confidence that the energy levels listed in Table 1 are accurate to better than 1%.

While computing our energy levels (and radiative rates), we also explored the impact of including larger CI. Configurations such as 2p63$\ell^2$, 2p64$\ell^2$, 2p65$\ell^2$, 2p63${\ell}$4${\ell}$, and 2p63${\ell}$5${\ell}$ do not have any appreciable effect either on energy levels or radiative rates, because levels arising from the above configurations lie in the 118-175 Ryd energy range, well above that of the 157 levels in Table 1, i.e. below 91 Ryd. Similarly, levels of the 2s2p53$\ell^2$, 2s2p54$\ell^2$ etc. configurations have energies above 118 Ryd, and have no noticeable effect on the energies of the lower levels. Therefore, inclusion of these higher levels in a calculation may affect the calculations of $\Omega$ (and particularly of $\Upsilon$ at very high temperatures), but is non-contributory to the determination of energy levels and radiative rates among the lower levels. To conclude, inclusion of 68 levels of the 2s22p55${\ell}$ and 2s2p65${\ell}$ configurations will be beneficial for the subsequent computation of $\Upsilon$, whereas the higher levels are too distant to make any significant contribution.

3 Radiative rates

The absorption oscillator strength (fij) and radiative rate Aji (in s-1) for a transition $i \to j$ are related by the following expression:

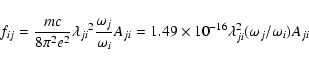\begin{displaymath}% f_{ij} = \frac{mc}{8{\pi}^2{e^2}}{\lambda_{ji}}^2 \frac{{\o... ...1.49 \times 10^{-16} \lambda^2_{ji} (\omega_j/\omega_i) A_{ji} \end{displaymath} (1)

where m and e are the electron mass and charge, respectively, c is the velocity of light, $\lambda_{ji}$ is the transition energy/wavelength in $\AA$, and $\omega_i$ and $\omega_j$ are the statistical weights of the lower i and upper j levels, respectively. Similarly, the oscillator strength fij (dimensionless) and the line strength S (in atomic unit, 1 au = 6.460 $\times$ 10-36 cm2 esu2) are related by the following standard equations:

for the electric dipole (E1) transitions:

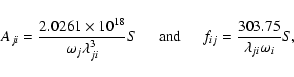\begin{displaymath}% A_{ji} = \frac{2.0261\times{10^{18}}}{{{\omega}_j}\lambda^3... ...pace*{0.5 cm} f_{ij} = \frac{303.75}{\lambda_{ji}\omega_i} S, \end{displaymath} (2)

for the magnetic dipole (M1) transitions:

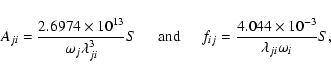\begin{displaymath}% A_{ji} = \frac{2.6974\times{10^{13}}}{{{\omega}_j}\lambda^3... ... f_{ij} = \frac{4.044\times{10^{-3}}}{\lambda_{ji}\omega_i} S, \end{displaymath} (3)

for the electric quadrupole (E2) transitions:

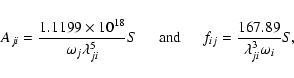\begin{displaymath}% A_{ji} = \frac{1.1199\times{10^{18}}}{{{\omega}_j}\lambda^5... ...ce*{0.5 cm} f_{ij} = \frac{167.89}{\lambda^3_{ji}\omega_i} S, \end{displaymath} (4)

and
for the magnetic quadrupole (M2) transitions:

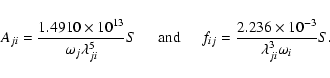\begin{displaymath}% A_{ji} = \frac{1.4910\times{10^{13}}}{{{\omega}_j}\lambda^5... ...{ij} = \frac{2.236\times{10^{-3}}}{\lambda^3_{ji}\omega_i} S. \end{displaymath} (5)

In Tables 2-5 we present transition energies ($\Delta$Eij in $\AA$), radiative rates (Aji in s-1), oscillator strengths (fij, dimensionless), and line strengths (S in au), in length form only, for all 3401 electric dipole (E1), 3334 magnetic dipole (M1), 4439 electric quadrupole (E2), and 4503 magnetic quadrupole (M2) transitions, respectively, among the 157 levels of Fe XVII. The indices used to represent the lower and upper levels of a transition have already been defined in Table 1. Also, in calculating the above parameters we have used the Breit and QED corrected theoretical energies/wavelengths as listed in Table 1. It may be noted that E1 (allowed and intercombination) transitions are the most important for applications, but data for other transitions are also required for modelling calculations, and that is why we have presented here a complete set of results for all types of transitions.

The most complete and accurate set of A-values available in the literature to compare with are our earlier results (Aggarwal et al. 2003a) for E1 transitions among the 89 levels up to the n = 4 configurations. Results of earlier workers, limited to a lesser number of transitions, have already been compared and discussed in our previous work, and therefore here we focus on the comparison between our present and earlier results alone. As seen in Table 1, the lowest 75 levels are common between the two calculations. A comparison made between our earlier and present results for transitions among these 75 levels, shows an agreement of better than 20% for all strong transitions with $f \ge$ 0.01, and the only exception is the 47-71 (2s22p54p 3P2-2s22p54d 1P$^\circ_1$) intercombination transition, for which the present results are lower by 30%. This highly satisfactory agreement between the two sets of results confirms that A-values have converged within the n = 5 configurations, and the results presented in Tables 2-5 are accurate to better than 20% for a majority of strong transitions. However, for weaker transitions the results may be comparatively less accurate.

In a recent paper, Nahar et al. (2003) have reported radiative rates for a large number of transitions. They included 490 levels for the calculations of E1 transitions, but only 89 for other types of transitions. For the E1 transitions they adopted the R-matrix code of Berrington et al. (1995), and included one-body relativistic operators in a Breit-Pauli approximation. This method generates results for a large number of transitions with comparatively less effort than required in a standard atomic structure code such as GRASP, but the accuracy achieved is generally not high mainly because of the exclusion of two-body relativistic operators. The level orderings of their R-matrix calculations are also slightly different than those of NIST or obtained from GRASP - see, for example, levels 9-13 in Table 7 of Nahar et al. The inadequacy of this method to produce accurate results for radiative rates has already been commented on by Nahar et al. (and see their Table 6 for comparisons with other results), and has recently been discussed in detail by Hibbert (2003). For the remaining E2, M1 and M2 transitions, Nahar et al. have adopted the GRASP program as by us, and hence the results are expected to be similar. However, as stated earlier they have included only 89 levels in their calculations, whereas 157 levels are included in the present work. Furthermore, for the E2 transitions a factor of 2/3 is associated in the relationship between A and S. Nahar et al. have absorbed it in the calculations of S, whereas we have kept it in the multiplying coefficient in Eq. (4), which is in agreement with others, such as NIST (http://physics.nist.gov/Pubs/AtSpec/node17.html). As a result of this, our listed values of S for E2 transitions are higher by 50% than those reported by Nahar et al., whereas the A-values are comparable. To conclude, for the included 157 levels of Fe XVII, the present work reports a consistent set of radiative rates for all types of transitions, and the accuracy achieved is higher than available to date.

4 Conclusions

In this work, energy levels, radiative rates, oscillator strengths, and line strengths for transitions among the lowest 157 fine-structure levels of Fe XVII are computed using the fully relativistic GRASP code of Dyall et al. (1989), and results are reported for electric and magnetic dipole and quadrupole transitions. Energy levels agree in magnitude and orderings with the listings of NIST, and are assessed to be accurate to better than 1%. However, the accuracy of other parameters for a majority of strong transitions is better than 20%. Our calculations for other required atomic parameters ($\Omega$ and $\Upsilon$) are still in progress, and will take a considerably long time to complete. We hope with the availability of those results (along with the present ones) some of the discrepancies between theory and observations will be resolved.

Acknowledgements
This work has been financed by the Engineering and Physical Sciences and Particle Physics and Astronomy Research Councils of the United Kingdom. We thank Dr. Martin Laming, Dr. John Gillaspy and Dr. Eric Silver for highlighting the discrepancies in experimental and theoretical line ratios, suggesting the problem to us, and for taking keen interest in the progress of the work. F.P.K. is grateful to AWE Aldermaston for the award of a William Penny Fellowship.

References


Copyright ESO 2004