A&A 420, 763-768 (2004)
DOI: 10.1051/0004-6361:20035719

Atomic data from the iron project

LV. Electron impact excitation of Ni II[*]

M. A. Bautista

Centro de Física, Instituto Venezolano de Investigaciones Científicas (IVIC), PO Box 21827, Caracas 1020A, Venezuela

Received 20 November 2003 / Accepted 26 February 2004

Abstract
We study the effects of using a $\bar{4\rm d}$ pseudo-orbital on the collision strengths for electron impact excitations of forbidden transitions in Ni II computed in the close coupling approximation. It is found that the resonance structures of the collision strengths are quite sensitive to the way the pseudo-orbital is created. Further, the close coupling expansion with a single $\bar{\rm 4d}$ orbital does not converge, resulting in a poor representation of (N+1)-electrons auto-ionizing states. Much greater expansions are needed to properly represent resonance structures in electron impact excitation calculations, resulting in variations of up to factors of two, with respect to previous computations, in the Maxwellian averaged excitation rate coefficients.

Key words: atomic data - line: formation - ISM: abundances - atomic processes - ISM: HII regions

1 Introduction

Collision strengths for low ionization stages of iron peak elements are of great importance for these ions are commonly observed in the spectra of astronomical and laboratory plasmas. The open 3d-shell of these systems yields many low-lying strongly coupled levels that are responsible for rich optical and infrared spectra. But this complexity also makes accurate calculations difficult and computationally very intensive. Currently available atomic data for these species, particularly for Ni II, are often questioned by researchers when those data are used to derive Ni abundances in gaseous nebulae and supernova remnants, where they find abnormally high abundances of this element. Such apparent overabundance can reach up to orders of magnitude and the problem is known as the nickel-to-iron problem (e.g. Bautista et al. 1996, and references therein).

The most extensive calculation of collision strengths for Ni II reported so far is the close coupling (CC) calculation of Watts et al. (1996) for 27 LSterms of the configurations $\rm 3d^9$, $\rm 3d^84s$, and $\rm 3d^84p$. Here, Watts et al. found that it was important to include a $\bar{\rm 4d}$ non-physical pseudo-orbital in the CI expansion of the Ni+ target to improve on its computed eigenvalues, just like in previous calculations for Fe II (Zhang & Pradhan 1995; Nussbaumer & Storey 1980; Pradhan & Berrington 1993) and Ni II (Bautista & Pradhan 1996; Nussbaumer & Storey 1982). Further, Watts et al. showed that an important consequence of this $\bar{\rm 4d}$ orbital in the target representation is that the associated $\rm 3d^74p\bar {4d}$ coupling in the (N+1)-electron Hamiltonian lowers the energy of $\rm 3d^8(^3F)4p^2$ auto-ionizing states and changes the resonance structures of the collision strengths. The most notable of these resonances is a large feature right on the excitation threshold of the $\rm 3d^84s (^4F) {-} 3d^84s (^2F)$ transition. Similar resonances and overall changes of the resonance structures arise in other forbidden transitions, e.g. $\rm 3d^9 (^2D) {-} 3d^84s (^2F)$ and $\rm 3d^84s(^4P) {-} 3d^84s(^2P)$. Such resonances make important contributions to the effective collision strengths and could have consequences for the derived Ni+ abundances from observed spectra.

Although Watts et al. did not provide fine structure collision strengths for spectroscopic applications, it was apparent that effective collision strengths for many transitions should be significantly greater than those of Bautista & Pradhan (1996) and Nussbaumer & Storey (1982) due to the dominance of extensive resonance structures. The much smaller CC calculation of Bautista & Pradhan (1996) did not include the (N+1) configurations considered by Watts et al. and the distorted wave calculation of Nussbaumer & Storey (1982) neglected resonances altogether.

In this work we present several CC calculations that aim to study in detail the effects of pseudo-orbitals on the collision strengths for Ni II. It is found that the resonance structure of the collision strengths is quite sensitive to the way the $\bar{\rm 4d}$orbital is created. Then we study the convergence of the CC expansion as more pseudo-orbitals are included and a new very large calculation is performed, which provides improved effective collision strengths. This work is carried out under the auspices of the IRON Project, an international collaboration devoted to the computation of atomic data for the iron group elements (Hummer et al. 1993). A complete list of papers can be found at http://www.am.qub.uk/projects/iron/paper/

2 Theoretical methods

Quantum-mechanical representations of atomic systems with a partially filled $\rm 3d$ shell, often require the use of $\bar{\rm 4d}$ pseudo-orbitals. This is because in simultaneous representations of  $3{\rm d}^{N+1}$ and $3{\rm d}^Nnl$ configurations the (N+1)th electron, when added to the $3{\rm d}^N$ sub-shell, may have a radial distribution different from that of all other $\rm 3d$'s. A model that would describe such radial correlations in detail would be that in which each electron had its own radial function, but this is difficult to treat computationally except in very simple cases (Froese 1966). Another option (Botch et al. 1981) is to model the $3{\rm d}^{N+1}$configurations as $3{\rm d}^N3{\rm d}'$, i.e. N equivalent electrons and one non-equivalent, non-orthogonal orbital $\rm 3d'$. In a CI scheme of orthogonal orbitals, $3{\rm d}' = a_1 3{\rm d} + a_2 \bar {4{\rm d}}$, where $\bar{\rm 4d}$ is the orthogonal projection of $\rm 3d'$ on $\rm 3d$. Thus,

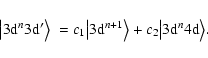\begin{displaymath}\big\vert 3{\rm d}^n3{\rm d}'\big> ~= c_1 \big\vert 3{\rm d}^{n+1}\big> + c_2 \big\vert 3{\rm d}^n4{\rm d}\big>. \end{displaymath} (1)

This simple method was designed for improving term energy separations, yet it does not guarantee convergence of the CC expansion used to calculate collisional excitation rates.

In the CC approximation (Burke & Seaton 1971) the wavefunctions for states of an N-electron target and a colliding electron with total angular momentum and parity $J\pi$ are expanded in terms of the target eigenfunction

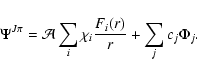\begin{displaymath}\Psi^{J\pi}={\cal A}\sum_i \chi_i{F_i(r)\over r}+\sum_jc_j\Phi_j . \end{displaymath} (2)

The functions $\chi_i$ are vector-coupled products of the target eigenfunctions and the angular part of the incident-electron functions, Fi(r) are the radial part of the latter and $\mathcal{A}$ is an antisymmetrization operator. The functions $\Phi_j$ are bound-type functions of the total system constructed with target orbitals; they are introduced to compensate for orthogonality conditions imposed on the Fi(r) and to improve short-range correlations. The target states included in the first sum of Eq. (2) are coupled, in a form equivalent to CI in the atomic structure context.

In the CC approximation, resonances in collisional excitation cross sections arise naturally when the incident electron energies are close to those of autoionizing levels above the ground state of the (N+1)-system, resulting in a coupling between "closed'' and "open'' channels, i.e. between free and bound wavefunctions. Furthermore, the accuracy in position and shape of resonances depends on a good representation of both short- and long-range correlations, thus one needs a CC expansion that accurately represents the system's radial wavefunction throughout the interaction region.

In the present work we have computed collision strengths for transitions among levels of the Ni II configurations $\rm 3d^9,$ $\rm 3d^84s$, $\rm 3d^84p$, and $\rm 3d^74s^2$. These collisions strengths were calculated from six different CC expansions that vary in the construction of the $\bar{\rm 4d}$ pseudo-orbital and in the inclusion of additional orbitals. In all cases, single-electron orbitals and CI target state eigenfunctions were generated with the atomic structure code AUTOSTRUCTURE, an extension by Badnell (1997,1986) of the program SUPERSTRUCTURE (Eissner et al. 1974). This method employs a statistical Thomas-Fermi-Dirac model potential $V(\lambda_{nl})$ (Nussbaumer & Storey 1978; Eissner & Nussbaumer 1969) with scaling parameter $\lambda_{nl}$determined variationally for each orbital. The target expansions used are:

It is important to point out that in target expansions E2 and E3  $\lambda_{\bar{\rm 4d}}$ were arbitrarily chosen as to investigate their effect on the collision strengths.


  \begin{figure} \par\includegraphics[angle=-90,width=15.3cm,clip]{0719fig1.eps}\end{figure} Figure 1: Collision strengths for the $\rm 3d^9 (^2D) {-} 3d^84s (^2F)$ transition as obtained from various target expansions of the Ni II system.
Open with DEXTER

Table 1: Sample of energy levels (in Ryd), scaling parameters for pseudo-orbitals in the Thomas-Fermi-Dirac potential, and mean orbital radii (in AU) for various expansions for the Ni II target ion. Calculated energies are compared with experimental values from NIST (2000).

Table 1 compares computed energy levels from the various Ni II expansions with experimental energies in NIST (2000). For conciseness, the table only shows the lowest 10 states from the physical configurations of interest and the first state found for each configuration that includes pseudo-orbitals. The table also shows the scaling parameters and mean radii of the pseudo-states in each expansion. The energies from models E1-E3 reveal that the representation of the $\rm 3d^9$ and $\rm 3d^84s$configurations is quite sensitive to the $\bar{\rm 4d}$ pseudo-orbital, and even the relative order of the ground and first two excited states changes with $\lambda_{\bar{\rm 4d}}$. Of these models E1 offers a reasonably good representation of the low lying states, but the energies of the $\rm 3d^84p$ levels are up to 10% lower than experiment and this model uses a $\rm 3d^8\bar{\rm 4d}$ configuration that departs the most from a physical one. In the E4 representation the ${\bar{\rm 4f}}$ improved correlation in the odd parity configuration increases the energy separation of the odd and even configurations, thus improving the overall agreement with experiment. Model E5 offers the best representation of the low lying states and the $\bar{\rm 5d}$ orbital makes the $\rm 3d^8 4d $ configuration less diffuse and in closer agreement with a physical one. Yet, in this model the $\rm 3d^8\bar{\rm 5d}$ states appear very far from the experimental values. The largest expansion E6 reproduces reasonably well low and high spectroscopic configurations and also yields good eigenenergies for the correlation configurations. Another important difference between the various target representation is the size of the interaction region for the collision process, which is indicated by the mean radius of the last orbital in each case. These radii go from 3.19 AU in model E1 to 10.36 AU in model E6.

3 Scattering calculations

The scattering calculations were carried out using the R-matrix method as implemented in the RMATRX package of codes (Berrington et al. 1995). The computations were done in LS-coupling and included 32 states coming from the target configurations $\rm 3d^9,$ $\rm 3d^84s$, $\rm 3d^84p$, and $\rm 3d^74s^2$. For the partial waves expansion of the collision strengths we included all values of total orbital angular momentum L between 0 and 12, sufficient to ensure convergence for the forbidden and allowed transitions within the energy range of interest. We included 30 continuum orbitals per angular momentum and all possible (N+1)-electron configurations that resulted by adding the extra electron to each target configuration. In all calculations we corrected the energies of the spectroscopic target states to experimental values during the diagonalization of the hamiltonian matrix and computation of the reactance K-matrix and scattering S-matrix. Thus, the changes in the positions of the (N+1) daughter resonances described below are only due to correlation effects.


  \begin{figure} \par\includegraphics[angle=-90,width=15cm,clip]{0719fig2.eps}\end{figure} Figure 2: Collision strengths for the $\rm 3d^84s (^4F) {-} 3d^84s (^2F)$ transition as obtained from various target expansions of the Ni II system.
Open with DEXTER

Figures 1 and 2 plot the collision strengths for the transitions $\rm 3d^9 (^2D) {-} 3d^84s (^2F)$ and $\rm 3d^84s (^4F) {-} 3d^84s (^2F)$ respectively, which are the same transitions presented by Watts et al. (1996). The various panels in each figure are the results of calculations with the different expansions E1-6. Striking differences are found between the results of different expansions. The collision strengths from expansion E1 are similar to those of Watts et al. (1996), yet small variations in the scaling parameter of the $\bar{\rm 4d}$ pseudo-orbital cause significant shifts of whole resonance structures, as seen in the results of E2 and E3. This pronounced susceptibility of the results on the $\bar{\rm 4d}$ orbital suggests the CC expansion may have not converged. Expansion E4 and E5 that include additional ${\bar{\rm 4f}}$ and $\bar{\rm 5d}$ pseudo-orbitals respectively yield significant changes in the structure of resonances between 0.15 and 0.4 Ryd, while the near threshold region remains similar to that of Watts et al. The additional correlations of expansion E6 produce severe changes throughout the whole resonance region. In the $\rm 3d^9 (^2D) {-} 3d^84s (^2F)$ transition the new correlations break up the broad resonances at threshold and around 0.25 Ryd causing a complete change in the appearance of the collision strength. In the $\rm 3d^84s (^4F) {-} 3d^84s (^2F)$ transition the additional correlations in E6 move the large resonance previously at threshold to below it, and lead to additional changes in the structure between 0.1 and 0.4 Ryd.

Table 2: Effective collision strengths for Ni II at 10 000 K for transitions from the ground and first excited states.

The various target expansions lead to changes in the resonance structures of the collision strengths for most transitions, and this has substantial effects on the Maxwellian averaged effective collision strengths, defined as:

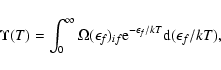\begin{displaymath}\Upsilon(T) = \int_0^\infty \Omega(\epsilon_f)_{if}{\rm e}^{-\epsilon_f/kT}{\rm d}(\epsilon_f/kT), \end{displaymath} (3)

where $\Omega_{if}$ is the collision strength for the transition i to f, and $\epsilon_f$ is the energy of the outgoing electron. Table 2 presents the effective collisions strengths at 10 000 K from the different calculations together with the results of Watts et al. Here we can see large differences, up to factors of two, between results from different target expansions. For example, the effective collision strength for the transition $2\to 3$ (shown in Fig. 2) is seen to increase by more than $20\%$ between expansion E1 and E5, but then drops to half this value with expansion E6.

4 Fine structure collision strengths

We adopt the largest target model E6 as the one that yields the CC expansion closest to convergence, thus it is expected to give the most reliable collision strengths. R-matrix calculations were carried out in LS coupling and followed by the intermediate-coupling frame transformation (ICFT) method of Griffin et al. (1998) to produce fine structure level-to-level excitation cross sections. The LS calculation was done in two parts that included low and high partial waves. The first part of the calculation included full exchange for partial waves from 78 $SL\pi$ total symmetries with angular momentum L=0-12, total multiplicity (2S+1)=1,3, and 5, and parities even and odd. This, was followed by a calculation without exchange for partial waves up to L=25. Additional "top-up'' was computed for dipole allowed transitions using the Burgess (1974) method. The collision strengths were computed at 10 000 energy points from 0 to 11 Ryd, with most of the points in the near threshold region so as to properly resolve resonances.

Effective collision strengths were derived for 11 different temperatures between 1000 and 30 000 K for 2926 transitions among the lowest 77 levels of the Ni II ion. The entire dataset is available in electronic form at the CDS or by request to the author.

5 Conclusions

The present calculations show that the use of a single $\bar{\rm 4d}$ pseudo-orbital in the target expansion of Ni II does not provide convergence of the CC expansion of the electron-ion scattering process. This is because this single orbital is insufficient to properly account for short- and long-range correlations simultaneously, thus resulting in a poor representation of quasi-bound autoionizing states. As additional pseudo-orbitals are included in the CC expansion the complex resonance structures of the collision strengths change and the prominent resonances found very near the threshold shift around this, which causes the averaged effective collision strengths to vary significantly.

One important consideration to make when using pseudo-orbitals in the CC expansion is that these could introduce unphysical resonances in the collision strengths. Firstly, when using large CC expansions that include pseudo-orbitals it becomes difficult in practice to keep complete consistency between the parent configurations in the first summation of Eq. (1) and the (N+1)-electron correlation configurations in the summation of this expansion. Such inconsistency could lead to pseudo-resonances. Fortunately, there seems to be no large pseudo-resonances in the collision strengths from present calculations, where various sets of CC expansion are used, or they could be readily detected by comparisons between the various datasets.

A very large CC expansion was adopted as the best representation of the Ni II system and it was then used to compute fine structure level-to-level effective collision strengths.

An investigation similar to the one presented here is now being carried out for the astrophysically important Fe II ion. Also, we are studying the effects of these large target representations in CC computations of bound energy levels and photoionization cross sections of Ni I and Fe I

References


Copyright ESO 2004