A&A 420, 547-552 (2004)
DOI: 10.1051/0004-6361:20034117
Experimental study of gas phase titanium and aluminum oxide clusters
K. Demyk1,2 - D. van Heijnsbergen1 - G. von Helden1 - G. Meijer1,3,4
1 - FOM-Institute for Plasmaphysics Rijnhuizen, Edisonbaan 14,
3439MN Nieuwegein, The Netherlands
2 -
Present address: PhLAM, Université des Sciences
et Technologies
de Lille, 59655 Villeneuve d'Ascq Cedex, France
3 -
Dept. of Molecular and Laser Physics, University of Nijmegen,
Toermooiveld 1, 6525 Nijmegen, The Netherlands
4 -
Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg
4-6, 14195 Berlin, Germany
Received 24 July 2003 / Accepted 23 February 2004
Abstract
We present an experimental study of the vibrational
properties of gas phase titanium oxide and aluminum oxide
clusters. The titanium and aluminum oxide clusters have a
stoichiometry of (Ti2O3)x-(TiO2)y (with (x, y) from
(2, 4) to (11, 29)) and AlO-(Al2O3)n (5 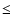 n
n 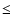 70). The
vibrational properties of the clusters are obtained using infrared
resonance enhanced multi-photon ionization (IR-REMPI)
spectroscopy. Titanium oxide clusters have a strong vibrational band
at
70). The
vibrational properties of the clusters are obtained using infrared
resonance enhanced multi-photon ionization (IR-REMPI)
spectroscopy. Titanium oxide clusters have a strong vibrational band
at 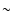 13.5
13.5  m, suggesting that their structure is close to the
rutile bulk phase of TiO2. Aluminum oxide clusters seem to have a
structure comparable to the bulk
m, suggesting that their structure is close to the
rutile bulk phase of TiO2. Aluminum oxide clusters seem to have a
structure comparable to the bulk 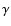 -Al2O3; their IR-REMPI
spectra exhibit a vibrational band at
-Al2O3; their IR-REMPI
spectra exhibit a vibrational band at 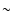 11
11  m and another
band at
m and another
band at 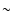 15
15  m which appears in the spectra of clusters
containing more than 7-8 Al atoms and becomes more intense as the
cluster size increases. As hot neutral clusters are observed to
evaporate more easily electrons than neutral fragments, one can
conclude that they are very stable and thus very good nucleation seeds
for dust growth.
m which appears in the spectra of clusters
containing more than 7-8 Al atoms and becomes more intense as the
cluster size increases. As hot neutral clusters are observed to
evaporate more easily electrons than neutral fragments, one can
conclude that they are very stable and thus very good nucleation seeds
for dust growth.
Key words: methods: laboratory - ISM: dust, extinction
The presence of large organic molecules and/or very small particles
(nanometric in size) in many and diverse astrophysical environments
such as reflection and planetary nebulae, in the Interstellar Medium
(ISM) or in galaxies is now well established thanks to space-born
observations. For example, IRAS observations of an excess of emission
at 25 and 60  m in the ISM have revealed the presence of very
small grains (VSG) heated by the absorption of
single UV photons (Désert et al. 1990). The exact
composition of these grains is not yet known. The existence of various
populations of nanograins has recently been proposed to explain
various spectroscopic observations. The Extended Red Emission (ERE)
observed in stars, planetary nebulae and in the ISM is proposed to be
due to a population of nanograins of silicon (Ledoux et al. 2001; Witt et al. 1998) or nanograins of
carbonaceous matter (Duley 2001). Nanodiamonds and
titanium carbide nanoparticles have been proposed to be the carrier
of the 21
m in the ISM have revealed the presence of very
small grains (VSG) heated by the absorption of
single UV photons (Désert et al. 1990). The exact
composition of these grains is not yet known. The existence of various
populations of nanograins has recently been proposed to explain
various spectroscopic observations. The Extended Red Emission (ERE)
observed in stars, planetary nebulae and in the ISM is proposed to be
due to a population of nanograins of silicon (Ledoux et al. 2001; Witt et al. 1998) or nanograins of
carbonaceous matter (Duley 2001). Nanodiamonds and
titanium carbide nanoparticles have been proposed to be the carrier
of the 21  m emission band observed in planetary nebulae (Hill et al. 1998; von Helden et al. 2000a).
m emission band observed in planetary nebulae (Hill et al. 1998; von Helden et al. 2000a).
Nanoparticles, containing few tens of atoms, are also produced around
evolved stars. These grains are thought to play a crucial role in the
dust formation process by constituting the nucleation seed on which
bigger grains - such as silicate and carbonaceous grains - will grow
(e.g. Gail & Sedlmayr 1999; Kozasa & Sogawa
1997). Depending on the types of star, i.e. on the composition
of their atmosphere, models of the dust formation process show that
several nucleation seeds can be produced such as Al2O3, TiO2,
TiC and/or ZrC clusters (Jeong et al. 1999; Ferrarotti
& Gail 2002).
Important efforts are made in the laboratory to study the physical
properties of these "exotic" and poorly known species under conditions
which approach those in the interstellar medium (see, for example,
Spectrochimica Acta A 2001). Among these properties,
vibrational frequencies are particularly important since these allow us
to compare the experimental data to the astronomical observations.
In this paper we present an experimental study of the vibrational
properties of gas-phase clusters relevant to the formation of
interstellar dust: titanium and aluminum oxide clusters. The
vibrational properties of the clusters are obtained using IR Resonance
Enhanced Multi-Photon Ionization (IR-REMPI) spectroscopy (von Helden
et al. 2003). In this technique, neutral clusters are
irradiated with intense tunable IR radiation. When the IR radiation is
resonant with an IR allowed vibrational mode of the cluster, multiple
absorption of photons can occur, resulting in a dramatic increase in
the internal energy of the cluster. These heated clusters may then
dissociate or emit an electron via thermo-ionic electron emission. The
latter only occurs for strongly bound clusters having a relatively low
ionization potential.
Infrared spectra of individual clusters are obtained by recording mass
spectra and monitoring the intensity of the mass peak of the cluster
of interest as a function of the IR wavelength. This technique has
been successfully applied to a wide range of species such as
fullerenes (von Helden et al. 1997), metal carbides (van Heijnsbergen et al. 1999; von Helden et al.
2000a) and oxides (von Helden et al. 2000b;
van Heijnsbergen et al. 2002, 2003).
This paper is organized as follow. The experimental setup and
procedure are described in Sect. 2. The results are presented in
Sect. 3. Discussion of the results and the astrophysical implications
are presented in Sects. 4 and 5, respectively.
The experimental set-up, described in detail in von Helden et al.
(2003), is only briefly outlined here. The clusters
are produced by pulsed Nd:Yag laser vaporization at 532 nm of rotating
metal rods (Ti or Al). The produced plasma is quenched in a mixture of 5-10% of O2 in Ar in which the clusters form. The pulsed beam
expands into vacuum. After passage through a skimmer the charged
clusters are deflected out of the beam by static electric fields. Then
the neutral clusters enter the interaction region with the ionization
laser, situated between the plates of a time-of-flight (TOF) mass
spectrometer. Different ionization sources can be used such as excimer
lasers (ArF or KrF) or an infrared tunable laser. The IR light source
used in the experiments is the Free Electron Laser for Infrared
eXperiments (FELIX) in Nieuwegein, The Netherlands (Knippels et al. 1995). It is tunable from 40-2000 cm-1. In resonance
with a vibrational transition of the cluster, the IR light can induce
the excitation and ionization of this cluster. These ionized clusters are
detected by TOF mass spectrometry. By varying the IR laser wavelength,
IR-REMPI spectra are obtained.
![\begin{figure}
\par\includegraphics[height=6.8cm,width=8.8cm,clip]{0117fig1.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg6.gif) |
Figure 1:
Mass distribution of titanium oxide
cluster cations produced via IR-REMPI. The mass distribution has been
spectrally integrated over the 9-24  m wavelength range. m wavelength range. |
| Open with DEXTER |
Starting from a titanium rod and a pulsed flow of about 5-10% of
oxygen mixed with argon, titanium oxide clusters are produced by the
method described in the previous section. The mass distribution of the
clusters produced via IR-REMPI is obtained for different wavelengths
of FELIX. The mass distribution spectrally integrated over the 9-24  m wavelength range is shown in Fig. 1.
m wavelength range is shown in Fig. 1.
The mass spectrum is composed of groups of 3 mass peaks (see inset
Fig. 1). The groups are equally spaced by 80 amu
corresponding to a TiO2 group. Within a group, the peaks are spaced
by 16 amu and the different peaks correspond to titanium oxide
clusters having different oxygen content. Titanium has 5 naturally
occurring isotopes. Consequently, the isotopic distribution of large
titanium oxide clusters is very broad and their mass peaks overlap,
causing the underlying continuum in the mass spectrum. Because the
average titanium mass is three times the oxygen mass, it is difficult
to unambiguously assign cluster stoichiometries to the mass peaks. In
bulk TiO2, oxygen deficient structures are frequently observed and
attributed to Ti2O3 sites. Furthermore, oxygen deficient
clusters can be expected to have comparatively low IP's, being thus
easier to detect in the IR-REMPI experiment. When looking at the low
mass part of the cluster distribution, many possible combinations of Ti and O atoms can be excluded as assignments for mass peaks based on
chemical arguments. A consistent assignment of the mass peaks starting
from small clusters and following the observed progressions is that
the clusters have a composition (Ti2O3)x-(TiO2)y with
(x, y) from (2, 4) to (11, 29) (see von Helden et al. 2003 for further details). No dependence of the mass distribution on the incident IR beam intensity has been
observed. This indicates that fragmentation processes are negligible and that the observed cluster ions are particularly stable against dissociation.
The wavelength of FELIX is tuned from 5 to 30  m with 0.1
m with 0.1  m
steps and a mass spectrum of the ionized clusters is recorded at each
wavelength position. Plotting the intensity of a certain mass peak as
a function of wavelength gives then its IR-REMPI spectrum. Spectra of
different clusters are presented in Fig. 2 in the 9-24
m
steps and a mass spectrum of the ionized clusters is recorded at each
wavelength position. Plotting the intensity of a certain mass peak as
a function of wavelength gives then its IR-REMPI spectrum. Spectra of
different clusters are presented in Fig. 2 in the 9-24  m range. In the 5-9
m range. In the 5-9  m and 24-30
m and 24-30  m wavelength ranges
(not shown), no ion signal is observed. A Gaussian fit of the IR spectra shows that, as the size of the cluster increases, the position
of the peak slightly shifts from
m wavelength ranges
(not shown), no ion signal is observed. A Gaussian fit of the IR spectra shows that, as the size of the cluster increases, the position
of the peak slightly shifts from 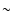 13.8 to
13.8 to 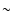 13.5
13.5  m
whereas the full width at half maximum (FWHM) of the peak increases
from
m
whereas the full width at half maximum (FWHM) of the peak increases
from 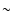 1.5 to 3.8
1.5 to 3.8  m. The spectra are thus similar for all
cluster sizes and stoichiometries, suggesting that the structure of
the clusters does not change dramatically as the clusters grow.
m. The spectra are thus similar for all
cluster sizes and stoichiometries, suggesting that the structure of
the clusters does not change dramatically as the clusters grow.
![\begin{figure}
\par\includegraphics[height=13.6cm,width=7.7cm,clip]{0117fig2.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg7.gif) |
Figure 2:
IR-REMPI spectra of three titanium oxide
clusters of different sizes and stoichiometries (histogram-like
curve). The spectra have been shifted for clarity. From bottom to top
the mass of the cluster is: m = 688, 1152, 1920 amu, with assignment:
(Ti2O3)2-(TiO2O)5,
(Ti2O3)3-(TiO2O)9,
(Ti2O3)5-(TiO2O)15. The linear curves overlaying the
experimental spectra represent Gaussian fits of the spectra. For
comparison with the bulk phase, the bottom curve shows the extinction
efficiency of rutile modeled from the optical constants for spherical
grains in the Rayleigh limit (see Sect. 4.1). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=6.45cm,width=8.8cm,clip]{0117fig3.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg8.gif) |
Figure 3:
Mass distribution of aluminum oxide
cluster cations produced via IR-REMPI. The mass distribution has been
spectrally integrated over the FELIX wavelength range of 9-18  m. m. |
| Open with DEXTER |
Aluminum oxide clusters are produced by ablating an aluminum rod in a 5-10% O2 in argon mixture. Neutral clusters interact with FELIX
and mass as well as IR-REMPI spectra are taken using the same
methods as in the case of titanium oxide. A mass spectrum averaged
over the wavelength range from 9  m to 18
m to 18  m is
shown in Fig. 3. Different to the case of titanium, the
mass of aluminum is not an integer multiple of the mass of oxygen and an
unambiguous assignment of the mass peaks is possible. The clusters
have the stoichiometry AlO-(Al2O3)n with 5
m is
shown in Fig. 3. Different to the case of titanium, the
mass of aluminum is not an integer multiple of the mass of oxygen and an
unambiguous assignment of the mass peaks is possible. The clusters
have the stoichiometry AlO-(Al2O3)n with 5 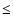 n
n 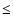 70, close to that of bulk aluminum oxide. As in the case of titanium
oxide clusters, the mass distribution of the aluminum oxides does not
depend significantly on the intensity of the ionizing IR beam.
70, close to that of bulk aluminum oxide. As in the case of titanium
oxide clusters, the mass distribution of the aluminum oxides does not
depend significantly on the intensity of the ionizing IR beam.
IR-REMPI spectra of aluminum oxide clusters are obtained by tuning the
wavelength of FELIX in the 9-18  m range with 0.1
m range with 0.1  m steps. As
can be seen in Fig. 4, the resulting infrared spectra of
different clusters do depend on cluster size. The spectra of small
clusters, with n
m steps. As
can be seen in Fig. 4, the resulting infrared spectra of
different clusters do depend on cluster size. The spectra of small
clusters, with n 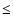 8-9, show a prominent feature at
8-9, show a prominent feature at 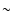 11
11  m. As the cluster size increases, a band at
m. As the cluster size increases, a band at 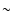 15
15  m
appears in the IR spectra and its relative intensity with respect to
the 11
m
appears in the IR spectra and its relative intensity with respect to
the 11  m feature increases. In the IR spectra of the largest
clusters produced in the present experiments, the two peaks have about
the same intensity.
m feature increases. In the IR spectra of the largest
clusters produced in the present experiments, the two peaks have about
the same intensity.
![\begin{figure}
\par\includegraphics[height=14.7cm,width=8.25cm,clip]{0117fig4.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg10.gif) |
Figure 4:
IR-REMPI spectra of aluminum oxide
clusters of different sizes. All spectra have been normalized to unity
and shifted for clarity. The extinction efficiency of bulk
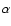 -Al2O3 spherical grains, modeled from the optical
constant (upper trace) and the position of the infrared bands of
ultra thin films of -Al2O3 spherical grains, modeled from the optical
constant (upper trace) and the position of the infrared bands of
ultra thin films of 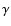 -Al2O3 are shown for comparison (see
Sect. 4.2). -Al2O3 are shown for comparison (see
Sect. 4.2). |
| Open with DEXTER |
4.1 Titanium oxide clusters
To our knowledge, no experimental vibrational data on gas-phase
titanium oxide clusters are available yet. However, electronic and
structural properties of neutral titanium oxide molecules
(Ti1-6O1-12) have been investigated using density functional
methods (Jeong et al. 2000). Depending on the stoichiometry
and size of the molecules, Jeong et al. found IR transitions at 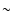 900-1000 cm-1 (10-11
900-1000 cm-1 (10-11  m) and/or at
m) and/or at 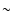 600-800 cm-1(12.5-16
600-800 cm-1(12.5-16  m). Results from these calculations show that, as the
size of the molecules increases, the transition at
m). Results from these calculations show that, as the
size of the molecules increases, the transition at 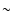 1050 cm-1 weakens; its intensity is less than 10% of the intensity
of the 600-800 cm-1 bands for (TiO2)n clusters with n
1050 cm-1 weakens; its intensity is less than 10% of the intensity
of the 600-800 cm-1 bands for (TiO2)n clusters with n 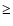 5.
5.
Bulk titanium oxide can have different stoichiometries: TiO, TiO2,
Ti2O3 and Ti3O5. The most common, titanium dioxide, has
three polymorphes: brookite and anatase which convert at high
temperature into the third and most widespread type of titanium
dioxide: rutile. The infrared spectra of rutile and anatase
submicronic grains (40-50 nm), measured by Koike & Shibai
(1998), reflect the different structures of these two
materials. The rutile spectrum shows a broad and strong band at 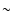 13-16
13-16  m and two weak bands around 25 and 29
m and two weak bands around 25 and 29  m. The spectrum of anatase shows two strong and broad bands around 17 and 29
m. The spectrum of anatase shows two strong and broad bands around 17 and 29  m.
m.
Independently of their size and stoichiometry, the titanium oxide
clusters have a vibrational transition at 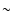 13.5
13.5  m. Although
the clusters studied here are larger than those studied by Jeong et al. (2000), the position of the IR transition is in
reasonable agreement with calculations on their largest
molecules. More surprisingly, it is also in good agreement with the
band position in the spectrum of bulk rutile grains (Koike & Shibai
1998). This is also illustrated in Fig. 2 which
shows the comparison between the spectrum of the titanium oxide
clusters and the modeled spectrum of the bulk rutile TiO2 phase. The spectrum is modeled from the optical constants (Ribarsky 1985) using Mie Theory (Bohren & Huffman 1983) for
spherical grains in the Rayleigh limit (i.e. small with respect to the
wavelength). The peak position of the observed vibrational band in the
cluster spectrum is close to the one of rutile (13.5
m. Although
the clusters studied here are larger than those studied by Jeong et al. (2000), the position of the IR transition is in
reasonable agreement with calculations on their largest
molecules. More surprisingly, it is also in good agreement with the
band position in the spectrum of bulk rutile grains (Koike & Shibai
1998). This is also illustrated in Fig. 2 which
shows the comparison between the spectrum of the titanium oxide
clusters and the modeled spectrum of the bulk rutile TiO2 phase. The spectrum is modeled from the optical constants (Ribarsky 1985) using Mie Theory (Bohren & Huffman 1983) for
spherical grains in the Rayleigh limit (i.e. small with respect to the
wavelength). The peak position of the observed vibrational band in the
cluster spectrum is close to the one of rutile (13.5  m).
m).
The agreement between the spectra of gas-phase clusters and rutile is
not complete and two differences remain: the absence of the long
wavelength bands (22.9 and 27.4  m) observed in the rutile
spectrum and the width of the 13.5
m) observed in the rutile
spectrum and the width of the 13.5  m band. The absence of the
long wavelength bands in the cluster spectra could be due to
experimental effects. For the IR-REMPI process to occur, a large
amount of energy needs to be absorbed by the cluster. This means that
when the wavelength gets longer, more and more photons need to be
absorbed to reach the same internal energy. A combination of
lower transitions strengths, anharmonicities and reduced laser fluence
might thus makes it more difficult to observe transitions at longer
wavelengths. The width of the peak is influenced by several
factors. First, the spectrum is not a single photon absorption
spectrum and the width of a multiphoton spectrum is influenced by the
photon absorption dynamics (von Helden 2003).
Additionally, the symmetry of the cluster will affect the width of the
transition such, that for lower symmetry species, resonances will
split and the result will be a peak that could consist of several
unresolved resonances. Further, we cannot exclude an inhomogeneous
broadening caused by the presence of several structural isomers that
all have slightly shifted peak positions.
m band. The absence of the
long wavelength bands in the cluster spectra could be due to
experimental effects. For the IR-REMPI process to occur, a large
amount of energy needs to be absorbed by the cluster. This means that
when the wavelength gets longer, more and more photons need to be
absorbed to reach the same internal energy. A combination of
lower transitions strengths, anharmonicities and reduced laser fluence
might thus makes it more difficult to observe transitions at longer
wavelengths. The width of the peak is influenced by several
factors. First, the spectrum is not a single photon absorption
spectrum and the width of a multiphoton spectrum is influenced by the
photon absorption dynamics (von Helden 2003).
Additionally, the symmetry of the cluster will affect the width of the
transition such, that for lower symmetry species, resonances will
split and the result will be a peak that could consist of several
unresolved resonances. Further, we cannot exclude an inhomogeneous
broadening caused by the presence of several structural isomers that
all have slightly shifted peak positions.
4.2 Aluminum oxide clusters
The infrared spectra of the aluminum oxide clusters change as the
cluster size increases (Fig. 4). For very small clusters
(n 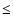 8-9) only one band is observed at 11
8-9) only one band is observed at 11  m. A band at 15
m. A band at 15  m appears in the spectrum of bigger clusters and becomes more
prominent as the cluster size increases. Figure 4 shows the
spectra of four Al2O3 clusters together with the modeled
spectrum of crystalline bulk
m appears in the spectrum of bigger clusters and becomes more
prominent as the cluster size increases. Figure 4 shows the
spectra of four Al2O3 clusters together with the modeled
spectrum of crystalline bulk 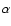 -Al2O3. As for the
simulation of the absorption efficiency of titanium oxide, the
spectrum of
-Al2O3. As for the
simulation of the absorption efficiency of titanium oxide, the
spectrum of 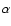 -aluminum oxide is modeled using Mie theory for
spherical grains in the Rayleigh limit. The optical constants of
-aluminum oxide is modeled using Mie theory for
spherical grains in the Rayleigh limit. The optical constants of
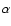 -aluminum oxide were taken from Gervais (1991). Bulk
-aluminum oxide were taken from Gervais (1991). Bulk 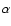 -Al2O3 shows a strong band at 13
-Al2O3 shows a strong band at 13  m and a weak band
at 20.7
m and a weak band
at 20.7  m. Clearly the spectra do not match.
m. Clearly the spectra do not match.
However, the comparison with IRAS and HREELS spectra of
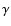 -Al2O3 ultra-thin films (Frank et al. 2001)
is better. The spectrum shows a strong band at 11.5
-Al2O3 ultra-thin films (Frank et al. 2001)
is better. The spectrum shows a strong band at 11.5  m and two
weak bands at 16 and 16.5
m and two
weak bands at 16 and 16.5  m (Fig. 4). These latter
bands are probably not resolved in the IR-REMPI spectra in which only
one band is observed at
m (Fig. 4). These latter
bands are probably not resolved in the IR-REMPI spectra in which only
one band is observed at 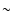 15
15  m. Other very weak bands at
wavelengths greater than 20
m. Other very weak bands at
wavelengths greater than 20  m are observed in the spectra of thin
films but are not present in the IR-REMPI spectra.
m are observed in the spectra of thin
films but are not present in the IR-REMPI spectra.
From these comparisons we conclude that the Al2O3 clusters have
a structure close to the 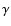 -Al2O3 bulk structure. This was
also observed for nanometer-sized Al2O3 clusters (5 nm) produced
from an
-Al2O3 bulk structure. This was
also observed for nanometer-sized Al2O3 clusters (5 nm) produced
from an 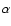 alumina sputter target (Ying et al. 1993). However, it is not clear if this is the case for
bigger cluster (n
alumina sputter target (Ying et al. 1993). However, it is not clear if this is the case for
bigger cluster (n 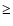 56-70). Depending on the experimental
conditions, such clusters can also be produced. For these very large
clusters, it is observed that the 11.5 and 16
56-70). Depending on the experimental
conditions, such clusters can also be produced. For these very large
clusters, it is observed that the 11.5 and 16  m bands evolve into
a very broad asymmetric band in the 10-20
m bands evolve into
a very broad asymmetric band in the 10-20  m region. This band
compares well with the modeled spectrum of spherical grains of
amorphous Al2O3 (van Heijnsbergen et al. 2003).
The fact that the structure of the Al2O3 clusters tends towards
the structure of bulk
m region. This band
compares well with the modeled spectrum of spherical grains of
amorphous Al2O3 (van Heijnsbergen et al. 2003).
The fact that the structure of the Al2O3 clusters tends towards
the structure of bulk 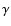 -Al2O3 and/or of amorphous
Al2O3, is compatible with the study of Gutiérrez & Johansson
(2002) who found that the structure of amorphous alumina
presents close similarity with the surface structure of
-Al2O3 and/or of amorphous
Al2O3, is compatible with the study of Gutiérrez & Johansson
(2002) who found that the structure of amorphous alumina
presents close similarity with the surface structure of 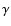 alumina.
alumina.
The formation of dust in the envelopes around late-type stars has
been extensively studied (e.g. Gail & Sedlmayr 1999; Kozasa
& Sogawa 1997). It is thought that this is a two step
process. In that scheme small solid particles are first formed by
clustering of molecular gas-phase species. These first condensates
constitute nucleation seeds for the formation of bigger grains which
grow by accreting molecules from the gas phase onto these seeds. The
formation of different metal oxide clusters around evolved stars
depends on the composition of the molecular gas phase of the
circumstellar shell. For example oxide clusters such as TiO2 and Al2O3 are the most expected ones to form around oxygen-rich AGB stars (Jeong et al. 1999). Very small Al2O3 grains
(10-20 Å) are also expected to be formed in the ejecta of type II
supernovae (Kozasa et al. 1991; Todini & Ferrara
2001). Around S stars which are transition objects between
O-rich and C-rich stars at the top of the Asymptotic Giant Branch,
both oxide and carbide clusters could nucleate such as TiO2, TiC,
ZrC (Ferrarotti & Gail 2002). The latter two are also
expected to form around carbon-rich stars.
The formation of these species around AGB or red giants stars is
supported by the discovery of presolar inclusions in meteorites
(Nittler et al. 1997). Indeed presolar grains such as TiC,
nanodiamonds, Al2O3, have been observed in meteorites. A
presolar titanium oxide grain has also been tentatively identified
(Nittler & Alexander 1999).
Some of these oxides or carbides, if they condense from the gas phase
at higher temperature than the other dust species, may constitute the
nucleation seeds for the dust formation. This seems to be the case for
titanium dioxide and aluminum oxide and thus, titanium and aluminum
oxide clusters appear to be good candidates for dust nucleation seeds
in oxygen-rich stars.
The detection method used in the experiments is based on the
thermo-ionic emission properties of the clusters. When heated, the
clusters preferentially emit an electron instead of evaporating atoms
or small molecules. This unique property is only observed for very
strongly bound species like fullerenes and some pure metal, metal
oxide, metal nitride and metal carbide systems. As thermo-ionic
electron emission is observed for titanium and aluminum oxide
clusters, those species must be very stable and resilient to
dissociation. This has important consequences for the dust formation
process in circumstellar shells and makes aluminum and titanium oxide
clusters very good candidates for the dust nucleation process. In
addition, the fact that the clusters undergo thermo-ionic emission
rather than dissociation when heated has consequences for the growth
efficiency. In a normal growth reaction where two particles A and B
react to form the transient AB*, the binding energy has to be
either carried away by a third collision partner or the transient AB* has to cool itself by radiation to form a stable AB molecule. As the density around stars and in the ISM is too low for
collisions with a third body to occur, radiative association is
usually the only mechanism for growth. Since emission at IR radiation
is a slow process, most of the transiently formed AB* molecules
will dissociate back to reactants. When the transient AB* can now
emit an electron instead, it can form the stable ion AB+. This ion
can then recapture an electron to form AB* again, which then has
another chance to radiatively cool itself or the electron will leave
again. In any case, the complex will not dissociate back to reactants A + B. In general, thermo-ionic electron emission might greatly
enhance growth rates of small particles and should be included in the
modeling of dust growth for those species.
Clearly, the excitation mechanism influences the obtained spectra,
which can therefore be different from the linear absorption
spectra. Anharmonicities will broaden lines and tend to shift them to
the red. In that sense, the spectra measured here are expected to be
comparable to emission spectra of warm species. A detailed discussion
of the excitation mechanism and the relevance of multiphoton spectra
to astronomical observations can be found elsewhere (Oomens et al. 2003)
Direct observation of the spectroscopic signatures of the dust
nucleation seeds would be the most favorable in the ideal situation in
which the dust formation process has just begun and other components
of the dust such as silicates are not yet formed. In that case, even
if the abundance of these seeds is low, it should be possible to
observe their emission. However, this is generally not the case and
the nucleation seeds are usually deeply embedded into larger
grains. In that case, the silicate emission dominates. Some stars
surrounded by dust shells dominated by oxide dust rather than by
silicates have recently been found (Posch et al. 2002). Their spectra present a very broad emission feature at 10-22  m that Posch et al. reproduce with a mixture of
amorphous Al2O3 and Mg0.1Fe0.9O grains to account for
maxima at
m that Posch et al. reproduce with a mixture of
amorphous Al2O3 and Mg0.1Fe0.9O grains to account for
maxima at 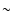 11
11  m and 19.5
m and 19.5  m, respectively. These types
of star may represent very good objects to look for the spectroscopic
signatures of nucleation seeds such as aluminum and titanium
oxides. Apparently, titanium oxide is not needed to get a reasonable
fit of the spectra. However, regarding the broadness of the observed
band, the fit is not unequivocal and the presence of titanium oxide
cannot be excluded.
m, respectively. These types
of star may represent very good objects to look for the spectroscopic
signatures of nucleation seeds such as aluminum and titanium
oxides. Apparently, titanium oxide is not needed to get a reasonable
fit of the spectra. However, regarding the broadness of the observed
band, the fit is not unequivocal and the presence of titanium oxide
cannot be excluded.
We have presented an experimental study of gas-phase aluminum and
titanium oxide clusters. The vibrational properties of the titanium
oxide clusters, (Ti2O3)x-(TiO2)y, are very similar for
all cluster sizes and stoichiometries. Their IR-REMPI spectra show a
vibrational transition at 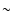 13.5
13.5  m, very close to the
frequencies observed for the corresponding oxide bulk phase, rutile
(TiO2). The vibrational properties of the aluminum oxide clusters,
AlO-(Al2O3)n, change with the cluster size. The IR-REMPI
spectra of small clusters (n
m, very close to the
frequencies observed for the corresponding oxide bulk phase, rutile
(TiO2). The vibrational properties of the aluminum oxide clusters,
AlO-(Al2O3)n, change with the cluster size. The IR-REMPI
spectra of small clusters (n 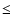 7-8) exhibit a band at
7-8) exhibit a band at 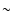 11
11  m. As the size of the clusters increases, a band at
m. As the size of the clusters increases, a band at 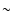 15
15  m appears and its intensity increases. Comparison with IR spectra
of
m appears and its intensity increases. Comparison with IR spectra
of 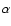 -and
-and 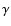 -Al2O3 shows that the structure of the
clusters is clearly different from
-Al2O3 shows that the structure of the
clusters is clearly different from 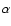 -Al2O3 and points
toward a
-Al2O3 and points
toward a 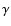 -Al2O3 type structure. The large width of the
vibrational transitions observed in the IR-REMPI spectra could be due
to size effects inducing a certain degree of distortion or disorder in
the arrangement of the atoms.
-Al2O3 type structure. The large width of the
vibrational transitions observed in the IR-REMPI spectra could be due
to size effects inducing a certain degree of distortion or disorder in
the arrangement of the atoms.
The ability of titanium and aluminum oxide clusters to undergo
thermo-ionic emission illustrates their high stability. They thus
constitute very good potential nucleation seeds on which the dust can
grow. However, direct observation of such very small clusters will be
difficult as they should rapidly be embedded into bigger
grains. Furthermore, as the spectra of clusters containing more than
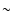 7-8 metal atoms are identical for all clusters and are in
addition close to the spectrum of the corresponding bulk species, it
would be difficult to determine the size of the clusters and to
distinguish between clusters and big, submicronic grains.
7-8 metal atoms are identical for all clusters and are in
addition close to the spectrum of the corresponding bulk species, it
would be difficult to determine the size of the clusters and to
distinguish between clusters and big, submicronic grains.
Acknowledgements
This work is part of the research program of the "Stichting voor
Fundamenteel Onderzoek der Materie'' (FOM), which is supported
financially by the "Nederlandse organisatie voor Wetenschappelijk
Onderzoek'' (NWO). Financial support from the EU IHP Research Training
Network (Delayed Ionisation and Competing Cooling Mechanisms in Atomic
Clusters) and from the ESA (external fellowship) is gratefully
acknowledged.
- Bohren, C. F.,
& Huffman, D. R. 1983, in Absorption and Scattering of Light by
Small Particles (New York: John Wiley)
(In the text)
- Desert, F. X.,
Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] (In the text)
- Duley, W. W.
2001, ApJ, 553, 575 [NASA ADS] [CrossRef] (In the text)
- Ferrarotti, A.,
& Gail, H. P. 2002, A&A, 382, 256 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Frank, M.,
Wolter, K., Magg, N., et al. 2001, Surf. Sci., 492, 270 [NASA ADS] [CrossRef] (In the text)
- Gail, H. P., &
Sedlmayr, E. 1998, Chemistry and Physics of Molecules and Grains in
Space. Faraday Discussions (London: The Faraday Division of the
Royal Society of Chemistry), 109, 303 [NASA ADS]
- Gail, H. P., &
Sedlmayr, E. 1999, A&A, 347, 549 [NASA ADS] (In the text)
- Gervais, F. 1991, in
Handbook of Optical Constants II, ed. E. Palik (Acad. Press.),
761
(In the text)
- Gutiérrez, G.,
& Johansson, B. 2002, Phys. Rev. B, 65, 104202 [NASA ADS] [CrossRef] (In the text)
- van Heijnsbergen, D.,
von Helden, G., Duncan, M. A., et al. 1999, Phys. Rev. Lett., 83,
4983 [NASA ADS] [CrossRef] (In the text)
- van Heijnsbergen,
D., von Helden, G., Meijer, G., et al. 2002, J. Chem. Phys., 116,
2400 [NASA ADS] [CrossRef] (In the text)
- van
Heijnsbergen, D., Demyk, K., Duncan, M. A., et al. 2003, Phys.
Chem. Chem. Phys., 5, 2515 [NASA ADS] [CrossRef] (In the text)
- von Helden, G.,
Holleman, I., Knippels, G. M. H., et al. 1997, Phys. Rev. Lett.,
5234, 79 [NASA ADS] (In the text)
- von Helden, G.,
Tielens, A. G. G. M., van Heijnsbergen, D., et al. 2000a, Science,
288, 313 [NASA ADS] [CrossRef] (In the text)
- von Helden, G.,
Kirilyuk, A., van Heijnsbergen, D., et al. 2000b, Chem. Phys., 262,
31 [NASA ADS] [CrossRef] (In the text)
- von
Helden, G., van Heijnsbergen, D., & Meijer, G. 2003, J. Phys.
Chem. A, 107, 1671 [NASA ADS] [CrossRef] (In the text)
- Hill, H. G. M., Jones,
A. P., & d'Hendecourt, L. 1998, A&A, 336, L41 [NASA ADS] (In the text)
- Jeong, K. S.,
Winters, J. M., & Sedlmayr, E. 1999, in Asymptotic Giant Branch
Stars, ed. T. Lebertre, A. Lèbre, & C. Waelkens, IAU
Symp., 191, 233
(In the text)
- Jeong, K. S., Chang,
Ch., Sedlmayr, E., et al. 2000, J. Phys. B, 33, 3417 [NASA ADS] (In the text)
- Knippels, G. M. H., Mols, R.
F. X. A. M., van der Meer, A. F. G., et al. 1995, Phys. Rev. Lett.,
75, 1755 [NASA ADS] [CrossRef] (In the text)
- Koike, C., &
Shibai, H. 1998, ISAP Report, # 671
(In the text)
- Kozasa, T., Hasegawa,
H., & Nomoto, K. 1991, A&A, 249, 474 [NASA ADS] (In the text)
- Kozasa, T., & Sogawa,
H. 1997, Ap&SS, 251, 165 [NASA ADS] (In the text)
- Ledoux, G.,
Guillois, O., Huisken, F., et al. 2001, A&A, 377, 707 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Nittler, L. R.,
Alexander, C. M. O. D., Gao, X., et al. 1997, ApJ, 483, 475 [NASA ADS] [CrossRef] (In the text)
- Nittler, L. R.,
& Alexander, C. M. O. D. 1999, in Lunar and Planetary Science
XXX, abstract No. 204
(In the text)
- Oomens, J. ,
Tielens, A. G. G. M., Sartakov, B. G., von Helden, G., &
Meijer, G. 2003, ApJ, 591, 968 [NASA ADS] [CrossRef] (In the text)
- Posch, Th.,
Kerschbaum, F., Mutschke, H., et al. 2002, A&A, 393, L7 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ribarsky, M. W. 1985, in
Handbook of Optical Constants of Solids, 795
(In the text)
-
Spectrochimica Acta A 2001, Special issue on astrophysics and
astrochemistry 57, Issue 4
(In the text)
- Todini, P., &
Ferrara, A. 2001, MNRAS, 325, 726 [NASA ADS] [CrossRef] (In the text)
- Witt, A. N., Gordon, K.
D., & Furton, D. G. 1998, ApJ, 501, L111 [NASA ADS] [CrossRef] (In the text)
- Ying, J. Y., Benziger,
J. B., & Gleiter, H. 1993, Phys. Rev. B, 48, 1830 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[height=6.8cm,width=8.8cm,clip]{0117fig1.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg6.gif)
![\begin{figure}
\par\includegraphics[height=13.6cm,width=7.7cm,clip]{0117fig2.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg7.gif)
![\begin{figure}
\par\includegraphics[height=6.45cm,width=8.8cm,clip]{0117fig3.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg8.gif)
![\begin{figure}
\par\includegraphics[height=14.7cm,width=8.25cm,clip]{0117fig4.ps}\end{figure}](/articles/aa/full/2004/23/aa0117/Timg10.gif)