A&A 420, 1-16 (2004)
DOI: 10.1051/0004-6361:20035741

The structure and radiation spectra of illuminated accretion disks in AGN

II. Flare/spot model of X-ray variability

B. Czerny1 - A. Rózanska 1 - M. Dovciak2,3 - V. Karas2,3 - A.-M. Dumont4


1 - Copernicus Astronomical Center, Bartycka 18, 00-716 Warsaw, Poland
2- Astronomical Institute, Academy of Sciences of the Czech Republic, Prague, Czech Republic
3 - Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
4 - Observatoire de Paris-Meudon, DAEC, Meudon, France

Received 25 November 2003 / Accepted 10 February 2004

Abstract
We discuss a model of the X-ray variability of active galactic nuclei (AGN). We consider multiple spots that originate on the surface of an accretion disk following intense irradiation by coronal flares. The spots move with the disk around the central black hole and eventually decay while new spots continuously emerge. We construct time sequences of the spectra of the spotted disk and compute the corresponding energy-dependent fractional variability amplitude. We explore the dependence on the disk inclination and other model parameters. AGN seen at higher inclination with respect to the observer, such as Seyfert 2 galaxies, are expected to have a fractional variability amplitude of the direct emission that is by a factor of a few higher than objects seen face on, such as Seyfert 1s.

Key words: radiative transfer - accretion, accretion disks - atomic processes - galaxies: active - X-rays: galaxies - radiation mechanisms: thermal

1 Introduction

Broad band spectra of active galactic nuclei show the presence of several components. The two principle contributions are: (i) the Big Blue Bump extending from the optical/UV band to (sometimes) the soft X-ray band, and (ii) the hard X-ray power law. The Big Blue Bump emission is conventionally interpreted as originating from an accretion disk (Czerny & Elvis 1987; Koratkar & Blaes 1999; however, see e.g. Collin et al. 2002 for discussion of problems encountered in this scheme). On the other hand, the nature and geometry of the region responsible for the hard X-ray emission is still under discussion. Several models have been proposed, the most popular being a hot extended corona overlaying a relatively cold disk (e.g. Czerny & Elvis 1987; Haardt & Maraschi 1991; Rózanska & Czerny 2000; Liu et al. 2002; Merloni 2003), an inner hot flow (e.g. Ichimaru 1977; Narayan & Yi 1994; Narayan et al. 2002), the lamp-post model (where a point-like X-ray source is located at a specified height above the disk, e.g. Henri & Pelletier 1991; Malzac et al. 1998), and the model of multiple hot flares produced via magnetic field reconnections (Galeev et al. 1979 and later papers). The field was reviewed, for example, by Leighly (1999), Collin (2001), Poutanen (1998) and Done et al. (2002) (in the context of X-ray binaries). Notice that these scenarios are not completely disparate and there may be a certain overlap between them. In all models the primary source of X-rays is strongly variable.

Indeed, AGN are variable in the X-ray band (e.g. Lawrence et al. 1987; Taylor et al. 2003) but the origin of the variability cannot be examined directly because the relevant central regions still remain unresolved by direct imaging. However, studies of the X-ray spectral variability offer a direct insight into the structure of accretion flows onto a central black hole, which is assumed to power AGN and determine their spectra.

In the flare model, sudden dissipation occurs in very localized regions above the disk surface (coronal loops, in analogy with the solar corona). In this case the local irradiation flux can be orders of magnitude higher then the steady level of the disk flux itself, but the irradiation does not last very long and only a small fraction of the disk surface is irradiated at any moment.

Such an arrangement of X-ray emitting region was suggested for the first time by Galeev et al. (1979) and was developed in many papers (e.g. Abramowicz et al. 1991; Haardt et al. 1994; van Oss et al. 1993; Poutanen & Fabian 1999; Zycki 2002). The development of a flare leads to a burst of "primary emission'' as well as to the formation of a hot spot underlying the flare where roughly half of the X-ray flux is reprocessed by the disk. Irradiation of the disk surface in hydrostatic equilibrium leads to the formation of a strongly stratified medium - a hot fully ionized skin covering a cooler, more neutral zone - and so the X-ray spectrum resulting from reprocessing should contain signatures that are characteristic of multi-temperature gas (Nayakshin et al. 2000; Ballantyne et al. 2001; Rózanska et al. 2002). The irradiating flux is locally very large, considerably exceeding the stationary energy flux that is dissipated inside the disk (e.g. Nayakshin 2000; Ballantyne et al. 2001). The resulting ionized skin is relatively optically thick (Collin et al. 2003).

The flare/spot model is a possible (although not unique) explanation of narrow emission features, which have been reported in $\sim$5-6 keV X-ray spectra of several AGNs and interpreted in terms of localized iron-line emission (Turner et al. 2002, 2004; Guainazzi 2003; Yaqoob et al. 2003; Dovciak et al. 2004).

In the present paper we test the flare/spot model by analyzing its predictions for the fractional variability amplitude in the X-ray band. We model the local spot/flare spectrum as a sum of flare (primary) emission of a power law shape and a spot (reflected) emission. The spot emission is determined by using the coupled TITAN/NOAR codes (Dumont et al. 2000) to solve the radiative transfer and the code of Rózanska et al. (1999) to calculate the hydrostatic equilibrium. We assume a random distribution of spots and flares across the disk and we account for their motion during the time-integrated observation. We consider both non-rotating (Schwarzschild) and rapidly rotating (Kerr) black holes, and we apply general relativity corrections using the KY code of Dovciak et al. (2003).

In our approach, a sequence of solutions is specified by fixing statistical properties that the flare/spot distribution is required to obey. Given a particular solution, the corresponding energy-dependent fractional variability amplitude $F_{\rm {}var}$ is calculated. The model is described in Sect. 2. Results are given in Sect. 3. The relevance of the model to explain the spectrum and variability of a typical Seyfert 1 galaxy is discussed in Sect. 4.

   
2 The model

   
2.1 Intrinsic spectrum of the spot

We model the X-ray spectrum from an irradiated accretion disk around a massive black hole, assuming a power law profile of the flare primary emission and computing the radiation spectrum from a hot spot underlying the compact flare. The spot emission travels directly to the observer without any further secondary Comptonization within the flare (we neglect the size of the flare itself) and we adopt a plane parallel symmetry for local computations.

Reprocessing of the incident flux is computed with the code TITAN (Dumont et al. 2000). The radiative transfer is solved both for the continuum and for lines, because the escape probability approach does not give reliable results for the lines (Dumont et al. 2003). The Comptonization is taken into account by coupling with the Monte Carlo code NOAR (also Dumont et al. 2000).

The vertical structure of the underlying disk is calculated with the code of Rózanska et al. (1999). As our principal model, we consider an irradiated disk in hydrostatic equilibrium, which requires iterations between the disk structure and the radiation transfer computations. These iterations are carried out as described by Rózanska et al. (2002). The computations of equilibrium are extremely time-consuming because of coupling between the equations of radiation transfer for the lines and for continuum. Therefore, in the present paper we performed computations at a certain representative radius in the disk ( $R=18 ~R_{\rm g}$ in terms of gravitational radii, $R_{\rm g}~{\equiv}~GM/c^2$) with the aim of obtaining a typical reflection spectrum, $F_{\rm loc}(E)$. Local reflection spectra at other radii were obtained with the help of scaling.

   
2.2 Assumptions about the flare-spot connection

We intend to represent a typical observation of an AGN, and therefore we choose as model parameters preferentially those properties that are as close as possible to observations. We define a very simple model (in fact, too simple to explain the origin of power spectra themselves). The model takes into account the basic observational properties, such as mean luminosity and luminosity dispersion. This approach is complementary to the papers devoted to the development of an isolated flare (e.g. Böttcher et al. 2003).

The fundamental parameters of the model are the mass of the black hole, M, and the mean X-ray luminosity, $L_{\rm {}X}$. This X-ray luminosity is assumed to originate from  $n_{\rm {}mean}$ flares per second, on average. The actual number of flares fluctuates at any given moment around this mean value according to a Poisson's distribution. Flares are assumed to co-rotate with the underlying disk.

A fraction of the radiation from each flare reaches the observer as the direct component. A part of flare photons is reprocessed by the disk surface, producing the reflection component.

In the model, a flare occurs at height h above the disc, it irradiates the disk surface and creates a hot spot. Irradiation is greatest and is strictly perpendicular just below the flare (in the centre of the spot where it first appears). Away from the centre, the irradiation slowly decreases over distance up to $R_{\rm {}X} \approx h$ from the central point (with the inclination angle of the incident X-rays increasing) and it drops fast further out. We start by simplifying our analysis and assuming that the irradiation does not show any gradient across the spot radius up to  $R_{\rm {}X}$. Then it drops sharply to zero. Linked with the spatial dependence of illumination across the spot surface there should be also a corresponding change in the incident angle. However, this incident angle is about 60$^{\circ}$ at most of the spot surface so we assume illumination to be isotropic. In this way, we consider the reprocessed radiation as coming from uniformly radiating circular spots. Given the incident radiation flux of a single flare, $F_{\rm {}inc}$, and the spot spectrum $F_{\rm loc}(E)$, the reflection is calculated through simple scaling,

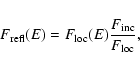\begin{displaymath}F_{\rm {}refl}(E) = F_{\rm {}loc}(E) {F_{\rm {}inc} \over F_{\rm {}loc}}, \end{displaymath} (1)

where $F_{\rm {}loc}$ is the radiation flux assumed in TITAN/NOAR computations. This approach neglects aberration and light bending in the local irradiation event, which is roughly correct if the flare height is small in comparison to the radius in the disk. In this manner, we can connect the flare luminosity, $L_{\rm {}i}$, the incident radiation flux and the size of the spot:

 \begin{displaymath}L_{\rm {}i} = F_{\rm {}inc}\pi R_{\rm {}X}^2\cdot \end{displaymath} (2)

We further assume that all flares occur at the same height above the disk surface, h. This simplification is additionally supported by the fact that the disk thickness does not depend on radius in a standard, radiation pressure-dominated Shakura-Sunyaev model. Therefore, all spots are chosen of the same size ( $R_{\rm {}X}$). Finally, we assume that flares are generated above the disk according to a uniform random distribution between the inner radius, $R_{\rm {}in}$, and outer radius, $R_{\rm {}out}$. Gravitational energy available in the disk depends on radius, and so we cannot expect all flares to be identical. In the present paper we adopt  $L_{\rm {}i}$ as a function of flare location, $R_{\rm {}i}$, in the form

 \begin{displaymath}L_{\rm {}i}(R_{\rm {}i})\propto \left({R_{\rm {}i}} \over {R_{\rm {}in}}\right)^{-\beta_{\rm {}rad}}\cdot \end{displaymath} (3)

This formula implies that the incident radiation flux scales with distance of the flare from the centre as a power law. We denote the corresponding power-law index  $\beta_{\rm {}rad}$and we normalize the flux amplitude to F0 at the inner rim. Therefore,

 \begin{displaymath}F_{\rm {}inc} = F_0 \left({R_{\rm {}i}} \over {R_{\rm {}in}}\right)^{-\beta_{\rm {}rad}}\cdot \end{displaymath} (4)

Spots are instantaneously created by the flare occurrence, and hence one can think of them as being attached to flares and orbiting with them at the local Keplerian speed around the central body. We assume that the duration of all flares is the same and equal to  $t_{\rm {}life}$, and we determine the average spectrum as seen by the observer after integration over the period $T_{\rm {}obs}$.

The nine input parameters of the model, M, $n_{\rm {}mean}$, $R_{\rm {}in}$, $R_{\rm {}out}$, $R_{\rm {}X}$, F0, $\beta_{\rm {}rad}$, $t_{\rm {}life}$, and $T_{\rm {}obs}$ fully define the flare distribution, including the total mean luminosity of the source, $L_{\rm {}X}$. In practice it may be more convenient to use $L_{\rm {}X}$ as a free parameter instead of, for example, $R_{\rm {}X}$.

Prediction of the observed spectrum involves two additional parameters which are inherent to any model involving an accretion disk around a rotating black hole: inclination angle of the observer, i, and dimension-less angular momentum of the black hole, a. These parameters span the range $0\hbox{$^\circ$ }\leq{i}\leq90\hbox{$^\circ$ }$ ( $i=0\hbox{$^\circ$ }$the disk axis, while $i=90\hbox{$^\circ$ }$ is the disk plane), and $0\leq{a}\leq1$ (a=0 refers to a non-rotating black hole, while a=1 corresponds to a Kerr black hole with maximum rotation).

   
2.3 Properties of the flare distribution

In the previous section we introduced several assumptions about the flare/spot connection. In the present section we use these assumptions to determine analytical relations describing secondary properties of the flare distribution. Such formulae are very useful for rough estimates and for discussion of properties of real sources. Since we assume that the spot radius is small in comparison to the overall size of the disk, general relativity corrections also are assumed to be negligible for the spot local properties[*].

We first derive the mean luminosity, $L_{\rm {}X}$. Uniform distribution of flares over the disk surface means that probability of a flare occuring at a given radial and azimuthal position, ( $R_{\rm {}i},\phi_{\rm {}i}$), is equal to

 \begin{displaymath}p(R_{\rm {}i},\phi_{\rm {}i})~{\equiv}~ p(R_{\rm {}i})~p(\phi... ...R_{\rm {}out}^2-R_{\rm {}in}^2}~{\times}~ {1 \over 2 \pi}\cdot \end{displaymath} (5)

One can associate the average total luminosity of a source with an exemplary distribution of flares,

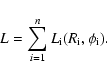\begin{displaymath}L = \sum_{i=1}^{n} L_{\rm {}i}(R_{\rm {}i},\phi_{\rm {}i}). \end{displaymath} (6)

The mean (expected) value of this quantity is determined as the integral over the probability distributions,
 
                                  $\displaystyle L_{\rm {}X}$ = $\displaystyle \sum_{n=1}^{\infty} P(n;n_{\rm {}mean})$  
    $\displaystyle \times \int_{\rm {}R_{\rm {}in}}^{R_{\rm {}out}}...\int_{\rm {}R_{\rm {}in}}^{R_{\rm {}out}} \int_{0}^{2 \pi}...\int_{0}^{2 \pi} p(R_1)...p(R_n)$ (7)
    $\displaystyle \times~ p(\phi_1)...p(\phi_n) ~{\rm {}d}R_1...~{\rm {}d}R_n ~{\rm... ...hi_1...~{\rm {}d}\phi_n \sum_{i=1}^{n} L_{\rm {}i}(R_{\rm {}i},\phi_{\rm {}i}),$  

where $P(n;n_{\rm {}mean})$ denotes the Poisson distribution around $n_{\rm {}mean}$. The multiple integrals can be performed easily because there is no dependence of the integrand on  $\phi_{\rm {}i}$. All integrals over $R_{\rm {}i}$ are identical (there are n of them) and can be performed independently of each other. Summation over the Poisson distribution gives

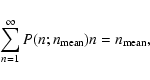\begin{displaymath}\sum_{n=1}^{\infty} P(n;n_{\rm {}mean})n = n_{\rm {}mean}, \end{displaymath} (8)

and the expression for the mean luminosity reduces to a single integral over the adopted radial distribution of luminosity,

 \begin{displaymath}L_{\rm {}X} = n_{\rm {}mean} \int_{\rm {}R_{\rm {}in}}^{R_{\rm {}out}} p(R_{\rm {}i})L_{\rm {}i} ~{\rm {}d}R_{\rm {}i}. \end{displaymath} (9)

This integral can be calculated analytically. Taking into account Eqs. (2)-(5) and denoting $\zeta~{\equiv}~R_{\rm {}in}/R_{\rm {}out}$, we obtain

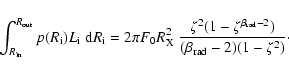\begin{displaymath}\int_{R_{\rm {}in}}^{R_{\rm {}out}} p(R_{\rm {}i})L_{\rm {}i}... ...}rad} - 2}) \over (\beta_{\rm {}rad} - 2)(1 - \zeta^2)}\cdot \end{displaymath} (10)

Using this formula, we can express the spot radius as a function of  $L_{\rm {}X}$ and the other parameters involved:

 \begin{displaymath}R_{\rm {}X} = \left[{L_{\rm {}X} \over n_{\rm {}mean} 2 \pi F... ...er \zeta^2 (1-\zeta^{\beta_{\rm {}rad}-2})}\right]^{1/2}\cdot \end{displaymath} (11)

At any given moment, the mean covering factor of the disk surface with spots is

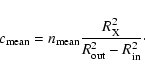\begin{displaymath}c_{\rm {}mean} = n_{\rm {}mean}{R_{\rm {}X}^2 \over R_{\rm {}out}^2 - R_{\rm {}in}^2}\cdot \end{displaymath} (12)

The disk surface is completely covered with reprocessing spots if $c_{\rm {}mean}$ is close to (or greater than) unity.

The mean number of flares during an observation of duration  $T_{\rm {}obs}$ is given by

 \begin{displaymath}N_{\rm {}mean} = n_{\rm {}mean}\left({T_{\rm {}obs} \over t_{\rm {}life}} + 1 \right). \end{displaymath} (13)

Obviously, if the observation is much shorter than the flare duration then $N_{\rm {}mean}$ is determined just by the mean number of flares. On the other hand, $N_{\rm {}mean}$ linearly increases with time at the opposite limit of a very long observation.

Since some of the flares existing during the observation were born before the beginning of the observation or they will disappear after the end of observation, the mean observing time of any single flare is clearly shorter than the flare duration time. We therefore introduce the effective life-time, $t_{\rm {}life}^{\rm {}eff}$, which is a combination of the two timescales:

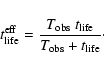\begin{displaymath}t_{\rm {}life}^{\rm {}eff} = {T_{\rm {}obs} ~t_{\rm {}life}\over T_{\rm {}obs} + t_{\rm {}life}}\cdot \end{displaymath} (14)

The model specifies only the mean number of flares, but in each specific observation we expect various numbers of flare events to occur. They are scattered across the disk and we model this distribution by drawing the number of flares from a Poisson distribution around  $N_{\rm {}mean}$. To this aim we assume all flares last for $t_{\rm {}life}^{\rm {}eff}$.

Therefore, each simulated observation will show clear dispersion of the total luminosity around the assumed mean value, $L_{\rm {}X}$. We can calculate this dispersion analytically, deriving the mean number of flares during observation $N_{\rm {}mean}$ from Eq. (13). Luminosity of a single flare is specified by Eq. (2) and combined with Eqs. (4) and (11), assuming random fluctuations around the mean value of flare number, as well as random variations in the distribution of flares and spots over the disk surface.

The time-integrated luminosity is given by

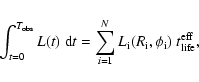\begin{displaymath}\int_{t=0}^{T_{\rm {}obs}} L(t) ~{\rm {}d}t = \sum_{i=1}^{N}... ...m {}i}(R_{\rm {}i},\phi_{\rm {}i})~t_{\rm {}life}^{\rm {}eff}, \end{displaymath} (15)

where N is a random number drawn from the Poisson distribution around $N_{\rm {}mean}$, and $R_{\rm {}i}$ and $\phi_{\rm {}i}$ are random numbers that can be derived from the probability distribution (5).

The mean (expected) value of this quantity is defined in the same way as in Eq. (8). This expression simplifies to

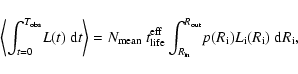\begin{displaymath}\left<\int_{t=0}^{T_{\rm {}obs}} \!L(t) ~{\rm {}d}t \right>... ...(R_{\rm {}i}) L_{\rm {}i}(R_{\rm {}i}) ~{\rm {}d}R_{\rm {}i}, \end{displaymath} (16)

because $t_{\rm {}life}^{\rm {}eff}$ is constant, in accordance with the assumptions. It is also evident that

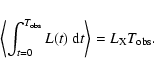\begin{displaymath}\left< \int_{t=0}^{T_{\rm {}obs}} L(t) ~{\rm {}d}t \right > = L_{\rm {}X} T_{\rm {}obs}. \end{displaymath} (17)

Variance $\sigma^2$ of this quantity is defined analogously,
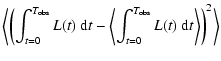                                       $\displaystyle \sigma^2$ = $\displaystyle \left < \left(\int_{t=0}^{T_{\rm {}obs}} L(t) ~{\rm {}d}t - \left< \int_{t=0}^{T_{\rm {}obs}} L(t) ~{\rm {}d}t \right> \right)^2 \right>$  
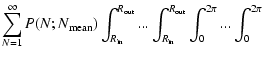  = $\displaystyle \sum_{N=1}^{\infty} P(N;N_{\rm {}mean}) \int_{R_{\rm {}in}}^{R_{\... ...ut}}... \int_{R_{\rm {}in}}^{R_{\rm {}out}} \int_{0}^{2 \pi}...\int_{0}^{2 \pi}$  
    $\displaystyle \times \left[ \sum_{i=1}^{N} t_{\rm {}life}^{\rm {}eff} L_{\rm {}... ...{\rm {}i},\phi_{\rm {}i}) - L_{\rm {}X} T_{\rm {}obs} \right]^2 p(R_1)...p(R_N)$  
    $\displaystyle \times~ p(\phi_1)...p(\phi_N) ~{\rm {}d}R_1...~{\rm {}d}R_N ~{\rm {}d}\phi_1...~{\rm {}d}\phi_N.$ (18)

This integration can be carried out in a similar way as in Eq. (8), taking into account the relation

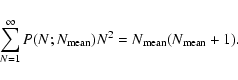\begin{displaymath}\sum_{N=1}^{\infty} P(N;N_{\rm {}mean}) N^2 = N_{\rm {}mean} (N_{\rm {}mean} + 1). \end{displaymath} (19)

The factor N2 on the left side of this equation comes from the number of mixed terms which arise from the expression in square parenthesis. When the square of the first sum in the square parenthesis is computed, the number of mixed terms is equal to N(N-1)/2. Therefore, the entire expression reduces to a single integral:

 \begin{displaymath}\sigma^2 =(t_{\rm {}life}^{\rm {}eff})^2 N_{\rm {}mean} \int_... ...m {}out}} p(R_{\rm {}i}) L_{\rm {}i}^2 ~{\rm {}d}R_{\rm {}i}. \end{displaymath} (20)

It is more convenient to use the normalized variance, i.e. the fractional variability amplitude $F_{\rm {}var}$ (see e.g. Vaughan et al. 2003)

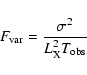\begin{displaymath}F_{\rm {}var} = {\sigma^2 \over L_{\rm {}X}^2 T_{\rm {}obs} } \end{displaymath} (21)

which can be expressed as

\begin{displaymath}F_{\rm {}var}^2 = {1 \over N_{\rm {}mean}}\; {\int_{R_{\rm {}... ...}} p(R_{\rm {}i}) L_{\rm {}i} ~{\rm {}d}R_{\rm {}i} \right]^2} \end{displaymath} (22)

using Eqs. (9) and (20). In our case this expression is equal

 \begin{displaymath}F_{\rm {}var} ^2 = {(\beta_{\rm {}rad}-2)^2(1 -\zeta^{2 \beta... ...1-\zeta^{\beta_{\rm {}rad}-2})^2}{1 \over N_{\rm {}mean}}\cdot \end{displaymath} (23)

The formula is more complex than the simple $1/N_{\rm mean}$ dependence because different spots give different contributions to the total luminosity (parameter $\beta_{\rm {}rad}$ describes the flux energy distribution). It reduces to the familiar case $F_{\rm {}var} ^2 = 1/N_{\rm {}mean}$ if all flares have the same luminosity (i.e. $\beta_{\rm {}rad} = 0$). However, it shows strongly enhanced variability if flare luminosity scales with the flare radius proportionally to the dissipative disk flux (i.e. $\beta _{\rm {}rad}=3$) since in this case the formula gives approximately

 \begin{displaymath}F_{\rm {}var} ^2 \approx {1 \over 8} \left({R_{\rm out} \over R_{\rm in}}\right)^2 {1 \over N_{\rm {}mean}} \end{displaymath} (24)

for $R_{\rm out}\gg R_{\rm in}$.

We stress that Eq. (23) for the normalized variance does not include relativistic corrections. It can be applied to the case of a non-rotating Schwarzschild black hole with acceptable accuracy, but it turns out to be quite inaccurate for a maximally rotating Kerr solution.

Naturally, spots should only be generated between the adopted inner radius of the disk, $R_{\rm {}in}+R_{\rm {}X}$, and the outer radius, $R_{\rm {}out}-R_{\rm {}X}$. To model a source with a prescribed luminosity, non-zero spot size has to be taken into account. A correction factor is obtained numerically through iterations. The spot radius  $R_{\rm {}X}$ is constrained to be much smaller than $R_{\rm {}out}$, and also it must be smaller than $R_{\rm {}in}$.

2.4 Generating an exemplary flare/spot distribution

A specific distribution of spots can be generated from the adopted parameters of the model in four steps:
(i)
choice of the black-hole mass, mean source luminosity, duration of observation and mean properties of the flare distribution, i.e. input model parameters M, $L_{\rm {}X}$, $T_{\rm {}obs}$, $n_{\rm {}mean}$, $R_{\rm {}in}$, $R_{\rm {}out}$, F0, $\beta_{\rm {}rad}$, and $t_{\rm {}life}$;
(ii)
a starting guess of the spot radius $R_{\rm {}X}$ from Eq. (11) and subsequent iterations of the radius, which allows one to reproduce the required luminosity from the flare distribution between $R_{\rm {}in}+R_{\rm {}X}$ and $R_{\rm {}out}-R_{\rm {}X}$;
(iii)
generation of the specific number of flares and corresponding spots, N, assuming a Poisson distribution with the mean $N_{\rm {}mean}$;
(iv)
generation of the position of each spot from the uniform random distribution over the disk surface, again within the range ${\langle}R_{\rm {}in}+R_{\rm {}X},R_{\rm {}out}-R_{\rm {}X}{\rangle}$.
The last operation means that the azimuthal angle $\phi_{\rm {}i}$ of a flare is determined as

\begin{displaymath}\phi_{\rm {}i} = ~{\tt {}rnd}~ \times 2 \pi, \end{displaymath} (25)

and the radius $R_{\rm {}i}$ is
$\displaystyle R_{\rm {}i} = \big[(R_{\rm {}in}+R_{\rm {}X})^2$$\displaystyle + {\tt {}rnd}~ \times~\big[(R_{\rm {}out}-R_{\rm {}X})^2 - (R_{\rm {}in}+R_{\rm {}X})^2\big]\big]^{1/2},$     (26)

where " ${\tt {}rnd}$'' is a random number between 0 and 1.

An example of the generated spot distribution is shown in Fig. 1. Each spot is localized at the disk surface at the moment of its generation. Spots occurring closer to the black hole are brighter than those which happen to be born farther out, because we assumed the power law scaling with $\beta_{\rm {}rad}>0$ in Eq. (4).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{0741fig1a.eps}\hspace*{4mm} \includegraphics[width=8.8cm,clip]{0741fig1b.eps} \end{figure} Figure 1: Illustration of the spot distribution created by flares that illuminate the underlying disk. The plane of the disk is shown, as viewed from the top, along the symmetry axis; (x,y) coordinates are scaled with the black hole gravitational radius, $R_{\rm {}g}$. Left: a snapshot of an instantaneous spot distribution. Right: effective covering of the disk surface by radiating belts in a time-integrated observation. Different realizations of the spot distribution have been explored in the paper (see Table 2).
Open with DEXTER

2.5 Time-integrated properties of spots

Spots are in Keplerian motion around the center. During the whole observation each spot moves along the $\phi$-direction, completing the distance

 \begin{displaymath}\Delta \phi(r) = \Omega_K(r) ~t_{\rm {}life}^{\rm {}eff}. \end{displaymath} (27)

Therefore, the integrated emission comes effectively from elongated belts rather than circular spots. The width of these belts is determined by radius of the flare and the length of the arc which it has circumscribed, $r~\Delta\phi(r)$.

The belts are relevant for observational properties inferred from the model, because actual observations have, indeed, some finite (and non-negligible) duration, $T_{\rm {}obs}$. If the integration time is long enough, some spots may complete one whole revolution, or even more full orbits, and so the length of the belt can be much longer than the circumference of a circle at the corresponding radius. This is particularly relevant for spots in the innermost part of the disk where motion is fast. The right panel of Fig. 1 shows an example of the resulting coverage of the disk surface by radiation belts.

Computation of the time integrated spectrum is therefore performed as the integration of the local intrinsic emissivity of the belts. The locally emitted flux must be renormalized to take into account that the emission now originates from the belt instead of a spot. Also, belt size is a function of radius  $R_{\rm {}i}$. We find

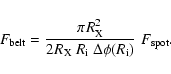\begin{displaymath}F_{\rm {}belt} = {\pi R_{\rm {}X}^2 \over 2 R_{\rm {}X}~R_{\rm {}i}~\Delta\phi(R_{\rm {}i})} \;F_{\rm {}spot}. \end{displaymath} (28)

The spectral shape of the local spectrum is assumed to be the same for all spots (see Sect. 2.1), and the reflected spectrum is supplemented with the primary emission in the proportion determined by the radiation transfer computations (Sect. 2.1). The local emissivity is assumed to be isotropic for both the primary flare emission and for the spot/reflected emission. Finally, observed time-integrated spectrum is subject to relativistic corrections.

   
2.6 Computations of general relativity effects

To include general relativity effects in the Kerr spacetime, we have developed a new computational routine which combines the advantages of different approaches used in the past (Laor 1991; Karas et al. 1992; Martocchia et al. 2000). A redesign was desirable to achieve sufficient resolution in both energy and time for the signal arising in multiple spots spread over the whole range of radii. The routine, KY, is flexible enough to allow easy modification of local emissivity profiles and it can be used as a rapid stand-alone code as well as linked to the standard XSPEC package (Arnaud 1996) for X-ray spectral analysis. In this paper we linked KY with the above-described computations of intrinsic emissivity of the spotted disk.

The routine employs pre-stored data tables to look up and interpolate four relevant quantities. These are (i) the energy shift of photons, (ii) relative delay of their arrival time, (iii) magnification of radiation (lensing effect) in the Kerr metric, and (iv) the local emission angle (to account for directional anisotropy of the emission)[*]. Given the local (intrinsic) emissivity in the disk plane, the predicted (observed) spectrum can be integrated. To achieve higher accuracy than it was possible with previous routines, the resolution in energy and time can be controlled and the grid covering the disk plane can be adjusted. Light rays are integrated in Kerr ingoing coordinates, so that the frame-dragging effect is tracked even very close to a fast rotating black hole (Misner et al. 1973). The equation of geodesic deviation is integrated separately to ensure precise determination of the flux magnification due to lensing near caustics.

In general, the disk emissivity is characterized by radiation energy  $F_{\rm em}$ and the related photon flux produced in the equatorial plane as function of emission energy  $E_{\rm em}$,

 \begin{displaymath}F_{\rm em}({E}_{\rm em};r_{\rm em},\theta_{\rm em})= F(r_{\rm em})\varphi_1({E}_{\rm em})\varphi_2(\mu), \end{displaymath} (29)

where $F(r_{\rm {}em})$ is total radiation flux emitted at the disk surface, $\varphi_1({E}_{\rm {}em})$ is the emissivity profile in frequency, $\varphi_2(\mu)$ is the limb-darkening law ($\mu$ denotes the cosine angle between a ray and the direction normal to the disk in the local co-rotating frame). To evaluate the terms in Eq. (29), one can employ analytic formulae or tabular data (both forms are used in this paper). In the case of a variable source in Eq. (29), the time-delay between light rays is taken into account at the point of their interception in a detector. Ray-tracing was performed in the Kerr geometry with the redshift function g being given by
 
                                      g = $\displaystyle \frac{\hat{p}_\alpha\hat{\eta}^\alpha}{p_\alpha\eta^\alpha}$  
  = $\displaystyle g^{tt}\hat{\eta}_t +g^{t\phi}\left(\hat{\eta}_\phi-\xi\hat{\eta}_t\right) -g^{\phi\phi}\xi\hat{\eta}_\phi +g^{rr}\hat{\eta}_r\hat{p}_r/p_t,$ (30)

and

 \begin{displaymath} \mu=-\frac{p_{\alpha}n^{\alpha}} {p_{\alpha}\eta^{\alpha}} \cdot \end{displaymath} (31)

Here, $p^\alpha$ and $\eta^\alpha$ denote, respectively, the four-momenta of the photon and of the emitting material in the disk, and analogously $\hat{p}^\alpha$ and $\hat{\eta}^\alpha$ that of the photon and of the observer at $r\rightarrow\infty$; $n^{\alpha}$ denotes a unit space-like vector perpendicular to the disk surface. For further details, see Dovciak et al. (2003).

As mentioned above, the influence of relativistic corrections on the local spectrum can be parameterized by the angular momentum of the black hole, a, and the inclination angle of an observer, i. On the other hand, by scaling lengths with  $R_{\rm {}g}$ and time intervals with ${R_{\rm {}g}}/c$, one conveniently ensures that graphs of predicted spectra do not explicitly show dependence on the black hole mass.

Relativistic effects, particularly in the case approaching a maximally rotating Kerr solution, significantly affect the shape of the radiation spectrum (especially at large inclination angle). Also the magnitude of the observed luminosity as well as the observed variance turn out to be more sensitive to inclination if relativistic effects are taken into account.

2.7 Fractional variability amplitude


  \begin{figure} \par\includegraphics[width=7cm,clip]{0741fig2a.eps}\hspace*{5mm} \includegraphics[width=7cm,clip]{0741fig2b.eps} \end{figure} Figure 2: Local reflection spectrum of an individual hot spot, which arises due to irradiation of the disk surface by a flare. Left: broad energy range is shown (log-log scale) with the intrinsic spectral resolution $E/\delta {E}=30$. The dotted line shows the incident spectrum. Right: an expanded part of the same spectrum around the iron line energy (linear scale). Here, a higher intrinsic spectral resolution was adopted, $E/\delta {E}=100$. In both panels, common parameters are $M=10^8 ~M_{\odot}$, $\dot{m}=0.001$, $R=18 ~R_{\rm g}$, $F_{\rm {}X}=10^{15}$ erg s-1 cm-2, $\Gamma =1.9$ (see Sect. 3.1 for details).
Open with DEXTER

We computed several radiation spectra representing different realizations of the same mean spot distribution. In this way we simulated independent time-integrated observations of a given source. We generate each distribution independently which means that we assume the lapse of time among simulated observations to be larger than the life-time of flares.

Fractional variability amplitude was then calculated in the standard way (see e.g. Edelson et al. 2002), as the energy-dependent variance of radiation flux normalized by the mean flux at a given energy. The variance was determined numerically, including relativistic corrections, from a finite number of realizations, K. Then the relative error of the normalized dispersion $\sigma$ was estimated as

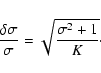\begin{displaymath}{\delta \sigma \over \sigma } = \sqrt{\sigma^2 + 1 \over K}\cdot \end{displaymath} (32)

This dispersion error is purely due to intrinsic statistical properties and does not contain any additional finite count rate term usually present in the observational data. This specific formula is appropriate for our simulation because we draw the number of flares from a Poisson distribution. Models aimed at reproducing the entire power spectrum of AGN require a more sophisticated approach.

   
3 Results

   
3.1 Locally emitted spectrum

Radiative transfer computations were performed for flare parameters similar to those used by Ballantyne et al. (2001). We adopt the black hole mass of $10^8 ~M_{\odot}$. The irradiating X-ray flux, $F_{\rm {}X}=10^{15}$ erg cm-2 s-1, extends from 1 eV to 100 keV in the form of a power law (photon index $\Gamma =1.9$). Iterations between the vertical disk structure (in hydrostatic equilibrium) and radiative transfer are performed untill convergence is achieved (Rózanska et al. 2002). We choose the dimensionless accretion rate of $\dot{m}=10^{-3}$, ($\dot{m}$ is scaled to the Eddington rate, $2.2 \times 10^{18} M/M_{\odot}$ g s-1), and radius $r=18 ~R_{\rm g}$ as typical values where local computations are carried out.

Hence, the ratio of the X-ray incident flux to the disk flux due to the internal dissipation for an assumed incident flux and accretion rate is equal to 144. The disk thickness is determined self-consistently by proceeding from the disk surface down to the equatorial plane and adopting the diffusion approximation deeply below the disk atmosphere (for Thomson optical depth $\ga$4). The intrinsic spectrum of a spot (i.e. the reflection component) is shown in Fig. 2. Notice that the disk surface is highly ionized, and so the reflection is efficient also at low energies.

Emission line properties from the local spectrum
A number of soft X-ray emission lines are visible in the spectrum, despite the adopted very strong irradiation. Since the soft X-ray emission lines have started to be seen in recent high-quality XMM and Chandra data for AGN (Kaastra et al. 2002; Rózanska et al. 2004), we list in Table 1 the equivalent widths of the strongest lines. The equivalent widths are determined with respect both to the reflected continuum and to the total continuum, i.e. primary plus reflected.

Sulphur and silicate lines are the strongest. Several other lines from highly ionized species, such as oxygen and carbon, are also clearly visible.

Table 1: Equivalent widths of the most intensive emission lines from the local spot model (this paper), measured (i) with respect to the reflected continuum, $EW_{\rm {}refl}$, and (ii) to the sum of the incident plus reflected continuum, $EW_{\rm {}total}$. Only lines with EWs higher than 1 eV are listed.

An expanded region of the iron line (in linear scale) is shown in the right panel of Fig. 2. The iron line is strong and multi-component. This emission is mostly due to helium-like and hydrogen-like ions. The two-component structure is clearly visible, although the $\sim$6.7 keV component slightly dominates. Narrow-line components are accompanied by a broad shoulder due to Comptonization in the disk surface layers. The iron edge is quite deep, as is usual in the case of a highly ionized medium, and complex, as we actually see two separate edges due to Fe XXV and Fe XXVI, at 8.83 and 9.28 keV correspondingly. These features are also considerably smeared by Compton scattering.

3.2 General relativity effects in predicted spectra

   
Relativistically smeared reflection from a disk uniformly covered with spots
Thanks to its featureless power-law character, relativistic effects do not change the spectral shape of primary continuum emission. However, spectral lines are still subject to the well-known relativistic smearing (e.g. Fabian et al. 1989; Laor 1991). It is interesting to see if the smearing of a realisticspectrum is distinguishable from the case of separate monochromatic lines which may be superimposed on the broad-band continuum. To examine the effect of the smearing we consider in this section the disk surface, which is covered uniformly by a spot-like emission. The local emissivity is given by the reflection component, as specified in Sect. 3.1. The emissivity is assumed to decrease with radius ( $\beta _{\rm {}rad}=3$).
  \begin{figure} \par\includegraphics[width=7cm,clip]{0741fig3.eps} \end{figure} Figure 3: The reflection spectrum from the spotted disk. The local intrinsic emissivity decreases ( $\beta _{\rm {}rad}=3$) as radius increases up to $R_{\rm{}out}=50 ~R_{\rm{}g}$. The case of a Schwarzschild black hole, a=0, and moderate inclination, $i=30{\hbox {$^\circ $ }}$(panel a)), can be compared with the case a=0, $i=60{\hbox {$^\circ $ }}$ (panel b)), rapidly rotating case a=0.998, $i=30{\hbox {$^\circ $ }}$ (panel c)), and a=0.998, $i=60{\hbox {$^\circ $ }}$. Dotted lines show the case of a relativistically smeared monochromatic line at 6.4 keV superimposed on a flat continuum.
Open with DEXTER

There is a clear distinction between the relativistic smearing of a monochromatic line and the shape of the relativistically smeared realistic reflection component. From Fig. 3 we see that the sharp blue edge, which is characteristic for a monochromatic line, is replaced by a much smoother feature. This is due to the presence of a double-peaked and Compton-broadened iron line in the realistic spectrum, as well as due to the contribution of the complex and Compton-smeared iron edge.

Weak emission lines of other elements are also noticeable in smeared spectra. Therefore it is not surprising that traces of these relativistically broadened emission lines are noticeable in the observational data (e.g. Rózanska et al. 2004 for Ton S180; Kaastra et al. 2002 for NGC 5548). Soft X-ray lines as strong as those claimed to be detected in the data by Branduardi-Raymond (2001) and Mason et al. (2003) are not expected within the framework of our model.

This result clearly supports the argument (Zycki et al. 1997; see also Bao et al. 1998; Young et al. 1998; Martocchia et al. 2000; Gondoin et al. 2002; Ballantyne et al. 2003) that proper interpretation of the observational data requires consideration of the relativistic broadening of the entire reflected component, i.e. the reflected continuum together with the iron line, instead of treating the two components separately.

Dependence of the luminosity on the inclination angle
The importance of the relativistic effects for variability models was discussed in several papers (e.g. Abramowicz & Bao 1994; Xiong et al. 2000). Its complexity is mostly due to the effect of light bending and Doppler boosting. Relativistic effects play a crucial role in the observed time-dependent behaviour, particularly for the maximally rotating Kerr case. Therefore, in this section we start by considering all effects in this extreme case.
  \begin{figure} \par\includegraphics[width=6.7cm,clip]{0741fig4.eps} \end{figure} Figure 4: The dependence of the luminosity of the uniformly radiating disk belts on the inclination angle for the maximally rotating Kerr black hole a=0.998. Power law spectrum and no radial dependence of the intensity were assumed.
Open with DEXTER

The radiation originating in the innermost part of the disk shows significantly different dependence on the inclination angle than the emission of the outer parts. We illustrate this by assuming, as a special example, that the disk surface is radiating uniformly in the local frame co-rotating with the disk. No separate spots and no radial dependence of luminosity are present. We consider two examples of such spectra: (A) the local emission is a pure power law with an energy index $\alpha = 0.9$; (B) the local emission is a pure reflection component as described in Sect. 3.1. In both cases, we consider the emission coming from three detached regions: (1) an inner ring, $r<7~R_{\rm {}g}$, (2) an intermediate ring, $7~R_{\rm {}g}<r<20~R_{\rm {}g}$, and (3) an outer ring, $20~R_{\rm {}g}<r<50~ R_{\rm {}g}$. We assume no limb darkening (locally isotropic emission).

In Fig. 4 we consider a strictly power-law emissivity profile and we show the corresponding behaviour of radiation flux at 6 keV on the inclination angle. We notice that the emission from the outer ring roughly follows a purely geometrical effect (trivial in the flat space), i.e. the decrease proportional to $\cos~i$, where i is the inclination angle of observation. However, the emission from the innermost part is more complicated: moving the observer from the disk axis towards its plane (i.e. i increasing), the observed flux first brightens, peaks at some intermediate inclination, and finally it decreases when the disk is inclined very strongly. This behaviour is due to competition between the relativistic boosting and reduction of the projected radiating area. The plot does not depend on the energy at which the monochromatic luminosity is measured, because the shape of the observed spectrum does not depend on inclination in the absence of spectral features.

In the case of the reflection component the results are practically identical outside the region of the intense iron line. On the other hand, there is a more complex behaviour within the line range, as can be seen from Fig. 3.

The assumption of radius-independent emissivity (between  $R_{\rm {}in}$and $R_{\rm {}out}$) and zero emission beyond the outer edge is rather artificial. Therefore we also show the results for the disk whose radial emissivity normalization decays with the radius as ${\propto}r^{-3}$( $r\leq50~ R_{\rm {}g}$). In Fig. 5 observed luminosity is plotted as a function of inclination. We see that the dependence is now even stronger than for the emission from the inner ring in Fig. 4, because with the adopted steep emissivity law most of the radiation is generated below $6~R_{\rm {}g}$. A decline in luminosity is observed only at very large inclination, i.e. close to the disk equatorial plane ( $i>85{\hbox{$^\circ$ }}$, probably unrealistic for real objects). Additionally, at such inclinations very close to 90$^{\circ}$multiple images appear (Zakharov & Repin 2003).

  \begin{figure} \par\includegraphics[width=6.6cm,clip]{0741fig5.eps} \end{figure} Figure 5: The dependence of the luminosity of uniformly radiating disk on the inclination angle with isotropic local emission, limb brightening ( $I(\mu )\propto 5-4\mu $), and limb darkening ( $I(\mu )\propto 1+2.06\mu $). The radial emissivity law $\propto $r-3 was assumed together with a power-law spectral shape.
Open with DEXTER

Table 2: Exemplary flare distribution properties for the black hole/disk system seen at a moderate inclination, $i=30{\hbox {$^\circ $ }}$. Parameters above the double line are assumed while the parameters below the double line are calculated as described in Sect. 2.2.

This dependency on inclination angle is only seemingly in contradiction with several other examples of such a trend published in the literature (see e.g. Gierlinski et al. 2001; Ebisawa et al. 2001; Bhattacharyya et al. 2001). There are three reasons why our results are different.

First, the emissivity law is usually assumed to be less concentrated towards the center. When the emission from the multi-black-body Keplerian disk around a low mass object is calculated (as in all papers mentioned above) the emissivity goes down to zero at the marginally stable orbit due to the assumed boundary conditions. This is in accordance with the standard thin disk model. However, dissipation in the hot corona does not need to follow this law. Also the presence of the large-scale magnetic field may eventually lead to more dissipation close to the marginally stable orbit (or even below it) than predicted in models based on zero-torque condition (see Afshordi & Paczynski 2003 for the discussion). Models of the broad iron line actually indicate a high concentration of the generated radiation flux towards the center (e.g. Wilms et al. 2001; Martocchia et al. 2002).

Second, many computations have assumed some kind of limb darkening. For illustration we include in Fig. 5 the same limb-darkening profile as adopted by Laor (1991), $I \propto 1 + 2.06 \mu $. We see that in this case, under the assumed radial emissivity law, the flux still rises with the inclination but more slowly. The angle-dependent computations of the Compton reflection component show this effect clearly. The increase of emissivity with inclination strongly depends on the ionization state of the reflecting material. For the incident angle of  $60{\hbox{$^\circ$ }}$ of the incoming beam the ratio of local intensity at  $90{\hbox{$^\circ$ }}$ to that at  $0{\hbox{$^\circ$ }}$ at $\sim$6 keV is equal to 9 (for a weakly ionized medium) and 5 (for a strongly ionized medium; cf. Zycki & Czerny 1994; George & Fabian 1991; Martocchia et al. 2000). Therefore, in Fig. 5 we show an example of the flux dependence with limb brightening $I(\mu )\propto 5-4\mu $ roughly representing realistic reflection by the strongly ionized medium. In this case the flux rises almost by 50% with the change of inclination angle from  $0{\hbox{$^\circ$ }}$ to  $30{\hbox{$^\circ$ }}$. However, in the total spectrum the primary emission dominates over the reflected component. The angular distribution of this emission is not known so in further considerations we assume isotropic emission.

The dependence of the observed radiation on the inclination angle has two important consequences. First, we recognize the tendency of the spectral shape on the inclination angle, as already illustrated in Fig. 3. Second, at low inclination angles the emission from the innermost part of the disk is under-represented in comparison with the emission from the outer parts, while at higher inclinations the opposite tendency appears. Since in the model outlined in our paper most of the variability is due to rare but luminous flares from the inner region, we find strong dependence of the variability properties on the inclination angle. We will discuss this in more detail in Sect. 3.3.

3.3 Fractional variability amplitude

Parameters of the flare distribution

The model depends on a number of parameters but most of them are well constrained by observations, and hence the actual freedom is not so large.

The mean number of flares at any moment, $n_{\rm {}mean}$, cannot be less than $\sim$10 because observed lightcurves do not show strong dips even on short timescales. Neither it can be very large, because in that case the variability amplitude would be far too small. To quantify variability, we use a standard rms as its measure. The typical normalized rms of AGN is known to be of order of 0.3 (see e.g. Abrassart & Czerny 2000; Uttley et al. 2002; Markowitz et al. 2003). The parameter $\beta_{\rm {}rad}$ is expected to be $\sim$3 on the basis of theoretical arguments as well as successful fits of some iron $\mbox{K}{\alpha}$ profiles in such sources, including MCG-6-15-30 (e.g. Iwasawa et al. 1996; Sulentic et al. 1998; Nandra et al. 1997; Guainazzi et al. 1999), although more complex distributions were also advocated (see Merloni & Fabian 2003 and references therein).

In Table 2 we give several combinations of parameters that we considered together with the properties of the chosen flare distribution. In most cases, we fix the mass of a black hole at a representative value $10^8 ~M_{\odot}$, for which the local computations of the disc structure and radiation reprocessing were performed. The inclination angle of  $30{\hbox{$^\circ$ }}$ was taken as a representative value (the view of the nucleus is frequently obscured at high inclinations by the presence of a molecular or dusty torus, so the average inclination in type 1 objects must be significantly lower than $60{\hbox{$^\circ$ }}$). The opening angle of the dusty torus is statistically constrained by the ratio of type 2 to type 1 objects. It was estimated to be most probably between 2 and 4 (see Krolik 1999; Veron-Cetty & Veron 2000). Therefore, the torus opening angle is of the order of $\sim$ $40{\hbox{$^\circ$ }}$, a typical type 1 object is seen at $\sim$ $30{\hbox{$^\circ$ }}$, and a typical type 2 object at $\sim$ $ 70{\hbox{$^\circ$ }}$.

Dependence of $F_{\rm {}var}$ on energy


  \begin{figure} \par\includegraphics[width=7.4cm,clip]{0741fig6.eps} \end{figure} Figure 6: Two random realizations of the same spot distribution (thin lines) and the original local emission (thick line histogram) for model A; the ratio of the two random realizations are shown below. The local input spectrum is the sum of the primary (flare) emission and the reflected (spot) component, without any limb-darkening.
Open with DEXTER

An example of the X-ray spectra from two random realizations of model A is shown in Fig. 6. The intrinsic spectrum of spots/flares was assumed to be a combination of the intrinsic flare emission and reflected/reprocessed spot emission. The observed spectral features are now weaker than the example in Fig. 2 where only the spot emission was taken into account. The two spectra of statistically identical distributions of spots differ in normalization, but otherwise their form is very similar. Variations are slightly enhanced at the energy where the strong iron line occurs. The tails of the line vary more significantly because this emission comes from the several most luminous spots at the innermost part of the disk, and so random variations in the position of those few spots are relatively frequent and important.

  \begin{figure} \par\includegraphics[width=7.2cm,clip]{0741fig7.eps} \end{figure} Figure 7: Fractional variability amplitude calculated as a function of energy. The model A ( $i=30^{\circ }$; upper panel), the model D ( $i=30^{\circ }$; middle panel), and the model D at high observed inclination ( $i=70^{\circ }$; bottom panel). Duration of a single observation 105 s, number of exposures 300.
Open with DEXTER

This effect is best seen in plots where the energy-dependent fractional variability amplitude is calculated from many random realizations. Such a plot (for model A) is shown in Fig. 7.

In the case of a Schwarzschild black hole, variations are almost independent of energy. There is only marginal enhancement of variability in the red wing of the iron line, around 5 keV. There is also a small dip in the plot at $\sim$7 keV. However, the overall energy dependence is not strong, and so the value of the dispersion at 1 keV is representative for the entire spectrum (Table 2).

The energy dependence of $F_{\rm {}var}$ is stronger in the case of emission from the disk surrounding a fast-rotating Kerr black hole. We show the corresponding plot for model D in the lower panel of Fig. 7. Here we adopted a higher value of the mean number of clouds, because otherwise the obtained variance would be unrealistically high in the context of AGN. We see in this case strong variations in the region of the red wing of the iron line, around 5 keV, and again a small dip in the plot at $\sim$7 keV. Still, the overall variability is well characterized by the dispersion at 1 keV, as given in Table 2.

The fractional variability amplitude in this case must be calculated with the relativistic corrections. The effect depends also on the inclination angle. An example for the model D but computed this time at a much higher inclination angle of  $ 70{\hbox{$^\circ$ }}$ is also shown in Fig. 7. At such a high inclination, line wings are still broader than at  $30{\hbox{$^\circ$ }}$, influencing the entire energy range between 4 and 8 keV.

   
Dependence of $F_{\rm {}var}$ on the inclination angle
We noticed in Fig. 7 the strong dependence of the overall variance on inclination angle, which occurs in the case of a rapidly rotating Kerr solution. In order to examine this trend in more detail, we plot in Fig. 8 the variance measured at 1 keV as a function of the inclination angle.

There is a noticeable difference between the variability level of the source observed at $i=0\hbox{$^\circ$ }$ versus the case of $i=30{\hbox {$^\circ $ }}$ (the value typically expected for broad-line galaxies on the basis of an AGN unification scheme). The fractional variability amplitude is enhanced by 47%. Further increase, by a factor of 3.1-4.6 in the variability level, is expected for objects observed at $i\sim60$- $77{\hbox{$^\circ$ }}$. Such inclinations are typical of Seyfert 2 galaxies. In these objects, in the soft X-ray band, we do not see the direct emission from the nucleus. Instead, in some of them the direct emission is visible in hard X-rays (Done et al. 2003), which allows us to test our prediction regarding the expected level of variability.

  \begin{figure} \par\includegraphics[width=7cm,clip]{0741fig8.eps} \end{figure} Figure 8: The dependence of the normalized dispersion measured at 1 keV on the inclination angle of observation for model A (upper panel, continuous line), model J (upper panel, dashed line) and model L (lower panel, middle curve). Two other curves in the lower panel show the result of increasing the mean number of flares to 3000 and decreasing the mean number of flares to 300. Number of exposures was 100.
Open with DEXTER

Several authors have recognized the importance of general relativity effects for the observed dependence of the variability properties on the inclination. Abramowicz & Bao (1994) noticed the flattening of the power spectrum slope with an increase of the inclination angle. Their approximate results were in general confirmed by Xiong et al. (2000) for a Schwarzschild geometry. Karas (1997) discussed Fourier-phase analysis of the spotted disk model.

The quantitative effect of the inclination depends on details of the assumed variability model. We show this dependence for model J, which is characterized by steeper emissivity ( $\beta_{\rm {}rad}=4$) than adopted in other cases. We see that the rise of the fractional variability amplitude with inclination is faster than for $\beta _{\rm {}rad}=3$ because more radiation comes from the innermost region where the relativistic effects are important.

The importance of the limb brightening
As mentioned in Sect. 3.2, limb brightening is expected for spot emission. We found, however, that it has no strong effect on the overall dependence of the fractional variability on the inclination angle (the increase of the variance with inclination angle is still present, although it is slightly reduced). Limb-brightening of the primary emission (in the form adopted in Fig. 5) results in further flattening of the plots. For the model P, the ratio of the variance at  $60{\hbox{$^\circ$ }}$ to the variance at  $1{\hbox{$^\circ$ }}$ is 3.1 while for the same model with limb brightening of the spot emission the ratio is 2.6, and for the limb brightening of both the flare and spot emission it is 2.2.

The accuracy of the analytical formula for $F_{\rm {}var}$

The value of the fractional variability amplitude given by Eq. (23) is independent of both the energy and inclination angle. In Table 2 we give these analytical values as $F_{\rm {}var}^{\rm {}a}$. We also calculate semi-analytical values $F_{\rm {}var}^{\rm {}b}$ taking into account the finite size of the spot but neglecting relativistic corrections; a new radius is calculated iteratively and inserted into Eq. (23) with $\zeta = (R_{\rm {}in} + R_{\rm {}X})/(R_{\rm {}out} - R_{\rm {}X})$.

We see that the analytical formula for $F_{\rm {}var}^{\rm {}a}$ gives a rather good approximation of the exact value in the model K, which involves the Schwarzschild solution and relatively small size of spots (less than $1~R_{\rm g}$). For other Schwarzschild models with larger sizes of the spots, the simplest approximation is no longer satisfactory, but $F_{\rm {}var}^{\rm {}b}$ still provides a reasonable approximation. Relativistic effects are important but the formulae neglecting them can be used for qualitative estimates.

For Kerr models, the analytical value given by Eq. (23) over-predicts the variability level at low inclination angle by a factor up to 3, but it represents roughly the correct values at large inclination angles. In this case, analytical estimates give large errors, and so accurate numerical energy-dependent and inclination-dependent results with general relativity effects are needed.

Trends with assumed model parameters
We see that a short duration of the flare (below a few $\times10^4$ s) leads to too small normalized dispersion in X-ray lightcurves for a typical long observation lasting about 1 day. It does not mean that short-lasting flares are ruled out, but such flares clearly cannot be responsible for variability timescales of days or more.

Increasing the assumed radius of the disk also increases the variance because, in our model, larger $R_{\rm {}out}$ translates into a smaller number of flares generated in the innermost part of the disk where flares are the most energetic. This is clearly related to our assumption of the uniform covering of the disk and the power-law radial decay of flare luminosity, as given by $\beta_{\rm {}rad}$. Equivalently, we can modify the dispersion by changing the slope $\beta_{\rm {}rad}$: a lower value (model F) reduces variations, while a higher value increases it (model J).

3.4 Special case of MCG-6-30-15

This nearby ( z = 0.007749; cf. NASA/IPAC Extragalactic Database) NLS1 galaxy is one of the best studied objects in the X-ray band. It is well-known for its extremely broad, relativistically smeared iron line (Tanaka et al. 1995; Fabian et al. 1995; Iwasawa et al. 1996; Fabian & Vaughan 2003 and the references therein). The slope of the power law component in this source (photon index $\Gamma=1.87\pm0.01$; Wilms et al. 2001) is not significantly different from the value $\Gamma =1.9$ adopted in our radiation transfer computations.

The energy-dependent fractional variability amplitude was studied for this source by Matsumoto et al. (2003) on the basis of ASCA data. They showed that the overall 2-10 keV amplitude of $\sim$18-20% is enhanced in the region of the red wing of the iron line (modeled as a broad feature around 5.4 keV) up to 40% (but with a large error), and somewhat less at its blue wing (around 6.4 keV). A detailed analysis was performed by Markowitz et al. (2003) on the basis of several RXTE observations. They found that the overall variability decreases with energy, going from $\sim$20% at 4 keV down to $\sim$13-14% above 10 keV. There is also a slight relative enhancement at $\sim$5 keV and at $\sim$8 keV, and a dip at $\sim$6.5 keV. A similar trend was noticed by Fabian et al. (2002) in their long XMM observations, but in this case the variability level was found to be slightly higher. We model the observed fractional variability assuming parameters appropriate for this source.

The mass of the black hole is rather small on the basis of X-ray power spectrum analysis: $\log M=6.0$ follows from the normalization method (Czerny et al. 2001), while $\log M=5.7$ has been derived from the high-frequency break model (Uttley et al. 2002). However, in view of the uncertainties, a mass as large as $\log M=5.9$ is still compatible. No results have been obtained from reverberation studies for this source. The mass was estimated to be $\log M=7.0$ (Czerny et al. 2001) using the disk method. Reynolds (2000) also argues for this higher value on the basis of the bulge-black hole mass relation (Magorrian et al. 1998). We thus adopt $M=10^7~ M_{\odot}$ in our computations.

X-ray luminosity varies significantly, but taking the typical 2-10 keV flux to be $\sim$ $ 4 \times 10^{-11}$ erg s-1 cm-2 (Weaver et al. 2001) we can estimate the total X-ray flux (1 eV-100 keV) to be of the order of $5~ \times~ 10^{43}$ erg s-1(assuming the Hubble constant H0=70 km s-1 Mpc-1).

The bolometric luminosity of this source can be estimated either from the 2-10 keV luminosity, taking into account the bolometric correction of 27 (Padovani & Rafanelli 1988), or directly from the broad-band data corrected for extinction. The first method gives $1.6 \times 10^{44}$ erg s-1 while the second one gives $9.1 \times 10^{43}$ erg s-1 (Niko\lajuk, in preparation). This means that for the adopted mass of the black hole the source radiates at $\sim$10% of the Eddington luminosity.

We considered three values of the mean number of flares: 300, 1000, and 3000. The corresponding models are denoted L, P and Q in Table 2. We choose the duration of the observations to be 103 s, the typical duration of continuous observation in the data, but the result does not depend strongly on this value. The adopted life-time of flares, 105 s, is chosen to reproduce the knee in the power spectrum of this source, as determined by Uttley et al. (2002). Therefore, we model the day-to-day variability (and the result does not apply to longer timescales).

Comparison of the observed $F_{\rm {}var}$ in short (day-to-day) timescales (see Fig. 5 of Markowitz et al. 2003) with theoretical level of variability indicates that the most appropriate mean number of flares is between 300 and 1000.

There is evident similarity in the energy dependence of $F_{\rm {}var}$ between observed data and the theoretical diagram: variability in the region of the iron line red wing ($\sim$5 keV) is enhanced, and a dip occurs at about 7 keV. However, the dependence on energy is generally much weaker in the model than in the data. Also, the model does not show the observed strong rise of the  $F_{\rm {}var}$ towards low energies.

This presence of strong variation at $\sim$3-4 keV in the data and the lack of such variations in the model may indicate that this energy band is still affected by varying conditions in the warm absorber (Inoue & Matsumoto 2003).

   
4 Discussion

The flare/spot model is an attractive explanation of the X-ray spectra and variability of AGN. In this scenario X-ray emission is generated both in hot magnetic loops above an accretion disks and in the bright spots created under the loops by strong irradiation. In the present paper we tested this model by analyzing the predicted fractional variability amplitude, $F_{\rm {}var}$.

We derived simple analytical formulae which allow us to estimate the level of variability from the assumed mean number of flares, flare duration, integration time of a single observation, the ratio of inner to outer disk radius and the radial dependence of the flare luminosity. This energy-independent and inclination-independent formula roughly applies to the case of a non-rotating black hole and small size of the spots. The formula is based on an assumption of a uniformly covered disk surface but it can be readily generalized to another kind of distribution.

Larger spots and/or a fast rotating black hole, with an inner disk radius close to the marginally stable orbit require a numerical approach, and we show the dependence of the resulting  $F_{\rm {}var}$ both on energy and inclination angle.

This leads to a firm prediction of our model which can be used to test the basic scenario. The model shows that if the disk extends close enough to the black hole, the general relativity effects lead to significant enhancement of the variability at large inclination angles of observation. Therefore, Seyfert 2 galaxies, if intrinsically identical to Seyfert 1 objects but viewed at a larger angle, should exhibit statistically higher  $F_{\rm {}var}$when measured at the same energy. A factor of 3 difference between Seyfert 2 and Seyfert 1 galaxies is expected for a Kerr black hole and a factor of 1.4 for a Schwarzschild black hole.

The observational evidence for a trend in this direction is scarce at present, but it may be used to support or reject our view more firmly in the future. However, some values can be given already. The mean variability level of Seyfert 1 objects is $\sim$18% on the short timescales of 1 day in the sample of Markowitz et al. (2003). The Seyfert 2 galaxy NGC 4945 is seen through the torus and it displays variability at the level of $\sim$40% in the hard X-ray band. Another example, NGC 7582 (Mihara et al. 2000), has revealed the normalized variability amplitude in the hard X-ray band to be about $\sim$30%. Studies of more Seyfert 2 objects are clearly needed.

The overall intra-day variability level of Seyfert galaxies is well explained by the flare model if the mean number of flares is of the order of 30-100 for an assumed non-rotating black hole, or 300-1000 for a fast rotating black hole. The number of flares required is much larger than the usual expectation of $\sim$10 flares. Such a small number of flares is predicted when an assumption is made that all flares have the same luminosity. In our more realistic model we allow for the flare luminosity to depend on the occurrence radius. When we assume that the flare luminosity scales with radius as $\propto $r-3, most of the source X-ray luminosity comes from a few flares generated in the innermost part of the disk which enhances the variability. This trend is clearly seen from our analytical expression (23) for the normalized variance, which, for $\beta _{\rm {}rad}=3$, and $R_{\rm out}\gg R_{\rm in}$, reduces to Eq. (24). Therefore, the total number of flares, $N_{\rm {}mean}$ can still be quite high for a source with moderate variance.

The energy dependence of $F_{\rm {}var}$ is generally weaker in the model than in the data. Observed variations show trends with energy in 1-10 keV band. For example, in Markowitz et al. (2003) Akn 564 varies at the level of 18-22%, IC 4329A at the level of 11-14% and MCG-6-30-15 of 14-21%, depending on the considered energy. In our models the trends with energy in  $F_{\rm {}var}$ never exceed 2%.

This discrepancy possibly can be solved by relaxing several simplifications:

It is to be seen whether elimination of these assumptions would lead to better agreement of the predicted energy dependence of  $F_{\rm {}var}$ with the data. The explanation of both apparently lower observed variability in the iron line region as well as the enhancement of the variability towards low energies seen in Fig. 5 of Markowitz et al. (2003) seems to be particularly difficult.

We have considered a few special cases.

A change of the life-time of a flare from radius-independent to scaled with a Keplerian timescale, without a change of other parameters, resulted in a fractional variability amplitude even less dependent on the energy than previously. This is caused by the fact that in the case of such a scaling relatively more energy is dissipated in the outer region, so the most relativistically broadened and variable inner region contributes less to the total lightcurve. The overall normalization of the  $F_{\rm {}var}$ depends on the proportionality constant between the life times and the Keplerian timescale (with other parameters fixed).

If we assume that the overall radial dependence of the dissipation should not be modified, we can consider two representative examples.

In the first case we assume that the life-time of a flare scales with the Keplerian timescale but the probability of a flare appearing at a given radius scales inversely with the local Keplerian timescale. We have therefore fewer long-living flares in the outer region and more short-living flares in the inner region, with the scaling of a single flare luminosity with radius unchanged. In this case again the fractional variability amplitude is less dependent on the energy than in our basic model. Having more flares localized in the inner region leads to reduction in the fluctuations in the relativistically smeared red wing.

In the second case we again assume that the life-time of a flare scales with the Keplerian timescale, we still adopt the uniform distribution of the flares across the disk surface but this time we assume that flare luminosity decreases with radius even more strongly ( $\beta_{\rm rad} = 4.5$ instead of the usually adopted $\beta _{\rm {}rad}=3$) to compensate for an increase of the flare life-time. Such a solution leads to slightly enhanced dependence of the fractional variability amplitude on the energy but the effect is not strong.

Complex dependence of the spectral shape of the reflected component on the disk radius may introduce significant modification to the predicted energy dependence. A clear suggestion of what is needed can be obtained from the recent analysis of MCG-6-30-15 by Vaughan & Fabian (2003). A constant component with complex energy dependence is apparently needed to formally model the fractional variability amplitude in this source (see their Figs. 11 and 16, top panel). This component may perhaps be understood as a reflection component (above $\sim$1 keV) and a contribution from emission/scattering by some extended medium (below $\sim$1 keV). However, it is not clear whether there is any possibility finding a parameter range that would satisfy the two "opposing'' trends seen in these data: we need strong reflection from the distant disk region to reproduce the constant component but we need strong reflection from the innermost region to explain the strongly relativistically broadened iron line profile also seen in these data. Attempts by Zycki & Rózanska (2001) and Ballantyne et al. (2003) were not successful.

Flares are not the only possibility to explain the X-ray emission of AGN. Other scenarios include the lamp-post (standing shock) model (e.g. Henri & Pelletier 1991; Malzac et al. 1998), model of gradual or rapid disk evaporation and its replacement by the hot flow (e.g. Narayan & Yi 1994; Liu et al. 2002), possibly with an outflow (e.g. Blandford & Begelman 1999), and the cloud model (e.g. Collin et al. 1996; Karas et al. 2000). Further work, taking into account variability issues, is needed to determine whether the flare/spot model is the most satisfactory.

Acknowledgements

We thank Piotr Zycki for very helpful discussions and we are grateful to Sergei Nayakshin, the referee, for comments which helped to improve the manuscript. Part of this work was supported by grant 2P03D00322 of the Polish State Committee for Scientific Research and by Jumelage/CNRS No. 16 "Astronomie France/Pologne''. V.K. and M.D. acknowledge support from grants GAUK 188/2001 and GACR 205/03/0902 and M.D. acknowledges support from the grant GACR 202/02/0735 in the Czech Republic.

References


Copyright ESO 2004