A&A 420, 115-123 (2004)
DOI: 10.1051/0004-6361:20034165

The magnetic field along the jets of NGC 4258

as deduced from high frequency radio observations

M. Krause - A. Löhr

Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany

Received 6 August 2003 / Accepted 31 January 2004

Abstract
We present 2 $.\!\!^{\prime\prime}$4 resolution, high sensitivity radio continuum observations of the nearby spiral galaxy NGC 4258 in total intensity and linear polarization obtained with the Very Large Array at $\lambda$3.6 cm (8.44 GHz).
The radio emission along the northern jet and the center of the galaxy is polarized and allows investigation of the magnetic field. Assuming energy-equipartition between the magnetic field and the relativistic particles and distinguishing between (1) a relativistic electron-proton jet and (2) a relativistic electron-positron jet, we obtain average magnetic field strengths of about (1) 310 $\mu$G and (2) 90 $\mu$G. The rotation measure is determined to range from -400 to -800 rad/m²in the northern jet. Correcting the observed E-vectors of polarized intensity for Faraday rotation, the magnetic field along the jet turns out to be orientated mainly along the jet axis. An observed tilt with respect to the jet axis may indicate also a toroidal magnetic field component or a slightly helical magnetic field around the northern jet.

Key words: galaxies: spiral - galaxies: indvidual: NGC 4258 - radio continuum: galaxies - polarization - galaxies: magnetic field - galaxies: jets

1 Introduction

The nearby galaxy NGC 4258 (M 106) is a bright SAB(s)bc spiral (de Vaucouleurs et al. 1976) at a distance of 7.2 Mpc (Herrnstein et al. 1999). It seems to possess a small bright nucleus with a highly excited emission line spectrum (Burbidge et al. 1963) and has been classified as a weakly active Seyfert 2-type galaxy.

Most striking are the two so-called "anomalous arms'', which are not visible in the optical and were first detected in H$\alpha$ by Courtès & Cruvellier (1961) in the inner region of the galaxy. Van der Kruit et al. (1972) detected these anomalous arms in the radio range where they extend out to the optical periphery. Spectral index studies indicate that their radio emission is of non-thermal origin (de Bruyn 1977; van Albada 1978).

The anomalous arms of NGC 4258 have been extensively discussed in terms of ejection of matter from the nucleus. The detection of a water-maser (Claussen et al. 1984; Henkel et al. 1984) and an accretion disk around a supermassive central object (Miyoshi et al. 1995; Herrnstein et al. 1998), and the fact that inner anomalous arms are orientated parallel to the rotation axis of the accretion disk and can be traced even on subparsec scale (Herrnstein et al. 1997) indicate that the anomalous arms indeed are jets. Whereas in the inner regions the anomalous arms clearly reveal their jet character, many of the features at a greater distance from the nucleus (e.g. their bifurcation) remain unexplained.

The three-dimensional geometry of the galaxy and its jets has been discussed for a long time (cf. e.g. van Albada & van der Hulst 1982; Hummel et al. 1989). The detection of an accretion disk revealed directly for the first time that the central part of the galaxy has a significant tilt with respect to the galactic disk: the accretion disk itself has an inclination angle of $83\hbox{$^\circ$ }$and a position angle (PA) of $86\hbox{$^\circ$ }$ (Miyoshi et al. 1995), i.e. it is oriented nearly east-west. The PA of the galactic disk, however, is $150\hbox{$^\circ$ }$, which is nearly north-south, and its inclination is $72\hbox{$^\circ$ }$ (van Albada 1980). Thus, the plane of the galactic disk and the plane of the accretion disk have a significant angle to each other. As the jets emerge perpendicular to the accretion disk, they have to pass the galactic disk at a rather small angle. Due to the projection of the whole system with respect to the Earth, the inner jet direction is almost parallel to the major axis of the galactic disk.

To further investigate the jet geometry and especially the magnetic field along the jets we obtained data with the Very Large Array (VLA) at $\lambda$3.6 cm and compared these with already published but reprocessed VLA data by Hummel et al. (1989) at $\lambda$6.2 cm (4.86 GHz) and $\lambda$20 cm (1.49 GHz) and with observations at $\lambda$2.8 cm (10.55 GHz) made with the Effelsberg 100-m telescope.

The observations and data reduction procedures are described in Sect. 2. In Sect. 3 we present the results and examine the measurements of the linearly polarized emission in terms of Faraday rotation, magnetic field strength and direction. The discussion of the results and the summary follow in Sects. 4 and 5, respectively.

  
2 Data acquisition and reduction

2.1 Observations with the VLA

We observed the radio continuum emission from NGC 4258 with the Very Large Array (VLA) in its C-configuration at 8.44 GHz ($\lambda$3.6 cm) in March 1996 for 14 h in total and linearly polarized intensity. The observations were done with two independent IFs, each with a bandwidth of 50 MHz and separated by 50 MHz. The two IFs were combined afterwards. The resulting observational parameters are given in Table 1. For a detailed description of the VLA see Thompson et al. (1980) and Napier et al. (1983).

Table 1: Observational parameters of the VLA measurements. The rms noise values are given for total intensity (I) and polarized intensity ($I_{\rm P}$). Further explanations are given in the text below.

The data reduction was performed using the Astronomical Image Processing System (AIPS) of the NRAO.

The flux density scale was calibrated by observing 3C 138 and 3C 286 and is based on the Baars et al. (1977) scale. We assumed flux densities of 2.52 Jy for 3C 138 and 5.21 Jy for 3C 286. We used an angle of $-12\hbox{$^\circ$ }$ for the polarized emission of 3C 138 and $-33\hbox{$^\circ$ }$ for that of 3C 286. The phase calibrator 1216+487, whose position is known with an accuracy of ${\leq} 0\hbox{$.\!\!^{\prime\prime}$ }1$, was also used to correct for the instrumental polarization.

The edited and calibrated visibility data were cleaned interactively, self-calibrated and Fourier transformed to obtain maps of the Stokes parameters I, U and Q. We produced uniformely weighted maps (with ROBUST = 0) to obtain the best resolution and sensitivity compromise with a HPBW of $2\hbox{$.\!\!^{\prime\prime}$ }2 \times 2\hbox{$.\!\!^{\prime\prime}$ }4$. Maps even more sensitive to weak extended structures and the polarized emission were made with natural weights (ROBUST = 4) at the expense of a slightly lower HPBW of $2\hbox{$.\!\!^{\prime\prime}$ }9 \times 3\hbox{$.\!\!^{\prime\prime}$ }3$. We used the zero flux correction provided by AIPS as a first-order correction for the missing large-scale flux. The U- and Q-maps were combined to obtain maps of the linearly polarized intensity $I_{\rm P}$ (corrected for the positive zero level offset) and the position angles of the polarized emission (the E-vectors). Values of the respective noise levels are summarized in Table 1, the full resolution map is shown in Figs. 1 and 2.

	Figure 1: The 8.44 GHz high resolution ( HPBW =  $2\hbox{$.\!\!^{\prime\prime}$ }2~ \times~ 2\hbox{$.\!\!^{\prime\prime}$ }4$) map of total intensity as obtained with the VLA C-configuration. The rms noise is $8~\mu$Jy/b.a.
Open with DEXTER

For a comparison we used and reproduced already published VLA data by Hummel et al. (1989) at 4.86 GHz ($\lambda$6.2 cm) and 1.49 GHz ($\lambda$20 cm). The observational parameters at $\lambda$6.2 cm are listed in Table 1. The entire reduction was done in the same way as described above. The full resolution maps obtained at $\lambda$6.2 cm and $\lambda$20 cm have HBPWs of  $14\hbox{$^{\prime\prime}$ }$; the $\lambda$6.2 cm map is shown in Fig. 3. For a comparison we also smoothed the naturally weighted maps at $\lambda$3.6 cm to $14\hbox{$^{\prime\prime}$ }$ HPBW by folding with Gaussian beams in two steps with the AIPS task CONVL. Noise level values of the $\lambda$6.2 cm and the smoothed $\lambda$3.6 cm maps are also included in Table 1. The data at $\lambda$20 cm were of little use for the comparison because the polarized intensity was only detected at large distances from the center.

Figure 2: The 8.44 GHz high resolution ( HPBW =  $2\hbox{$.\!\!^{\prime\prime}$ }2~ \times~ 2\hbox{$.\!\!^{\prime\prime}$ }4$) map in total intensity as obtained with the VLA C-configuration superimposed on the H$\alpha$ map of the galaxy observed at the Hoher List Observatory of the University of Bonn (by courtesy of N. Neininger). The normal spiral arms are marked as SP$_{\rm N}$and SP$_{\rm S}$, the anomalous arms as AN$_{\rm N}$ and AN$_{\rm S}$.

Open with DEXTER

2.2 Observations with the Effelsberg 100-m telescope

NGC 4258 was observed with the Effelsberg 100-m telescope at 10.55 GHz ($\lambda$2.8 cm) in July 1995. The multi-beam receiver has 4 horns and 16 channels. Each horn is equipped with two total-power amplifiers and an IF polarimeter. The bandwidth is 300 MHz, the system noise temperature about 50 K and the resolution is $69\hbox{$^{\prime\prime}$ }$ HPBW.

For pointing and focusing we observed regularly the sources 3C 48 and 3C 286. The calibration was done with 3C 286 according to the flux values of Baars et al. (1977). The observing procedure is essentially the same as described by Klein & Emerson (1981). We obtained 28 coverages of NGC 4258 which led, after restoration (Emerson et al. 1979) and combination (Emerson & Gräve 1988), to an rms noise in the final maps of $900~\mu$Jy/b.a. in total power and $300~\mu$Jy/b.a. in linear polarization.

3 Results

3.1 Total intensity

Figure 1 shows the full resolution map of NGC 4258 in total intensity at 8.44 GHz as obtained with the VLA in its C-configuration. The HPBW is $2\hbox{$.\!\!^{\prime\prime}$ }2~ \times~ 2\hbox{$.\!\!^{\prime\prime}$ }4$ and the inner region of the galaxy is well resolved. The S-shaped feature of the anomalous arms is clearly visible (marked as AN$_{\rm S}$ and AN$_{\rm N}$ in Fig. 2) with the southern jet being fainter than the northern one. The jet direction in the central part is approximately north to south, whereas it changes to about east-west orientation in the outer parts. The northern arm bifurcates at least two times (as first detected by van Albada & van der Hulst 1982).

Maximum radiation is emitted from the galactic center. The normal spiral arms of the disk are also visible to the north and south (marked as SP$_{\rm N}$ and SP$_{\rm S}$ in Fig. 2). Along them, three very bright regions can be observed at $\rm\delta_{50}=47\hbox{$^\circ$ }32\hbox{$^\prime$ }10\hbox{$^{\prime\prime}$ }\ (\rm {SP}_{\rm S})$, $\rm\delta_{50}=47\hbox{$^\circ$ }35\hbox{$^\prime$ }45\hbox{$^{\prime\prime}$ }\ (\rm {SP}_{\rm N}1)$ and $\rm\delta_{50}=47\hbox{$^\circ$ }37\hbox{$^\prime$ }20\hbox{$^{\prime\prime}$ }\ (\rm {SP}_{\rm N}2)$, where the intensity is $200~\mu$Jy/b.a. ( $\rm {SP}_{\rm S}$), $500~\mu$Jy/b.a. (SP$_{\rm N}$1) and $200~\mu$Jy/b.a. (SP$_{\rm N}$2).

We observe a ridge of high intensity of $100~\mu$Jy/b.a. along the northern jet. The southern jet shows a maximum brightness of $100~\mu$Jy/b.a. at large distance from the center. Between the center and this region the southern jet is very weak. The northern region of high brightness ($80~\mu$Jy/b.a.) at $\alpha_{50}=12\hbox{$.\!\!^{\rm h}$ }16\hbox{$.\!\!^{\rm m}$ }28.9$and $\delta_{50}=47\hbox{$^\circ$ }35\hbox{$^\prime$ }43\hbox{$^{\prime\prime}$ }$ (marked as "A'' in Fig. 6) has been interpreted as a radio hot spot of the northern jet by Cecil et al. (2000). The same source has been classified as a supernova remnant candidate by Hyman et al. (2001), noted as source 7 therein.

The corresponding hot spot in the southern jet (marked as "B'' in Fig. 6) has been reported to be located $24\hbox{$^{\prime\prime}$ }$ south of the nucleus at $\alpha_{50}=12\hbox{$.\!\!^{\rm h}$ }16\hbox{$.\!\!^{\rm m}$ }29.6$ and $\delta_{50}=47\hbox{$^\circ$ }34\hbox{$^\prime$ } 30\hbox{$^{\prime\prime}$ }$ (Cecil et al. 2000). In this region we also detected a local maximum in brightness of $50~\mu$Jy/b.a. which coincides with the change of the jet direction as indicated by the solid line in Fig. 6.

The total flux of the central source was measured by fitting a two-dimensional Gaussian to the central emission in the map with highest resolution (Fig. 1). It is derived to be $2.45\pm 0.09$ mJy.

In Fig. 2 the contour plot of the total intensity is superimposed on an H$\alpha$ map of the galaxy (observed at the Hoher List Observatory of the University of Bonn, (courtesy of N. Neininger)). In H$\alpha$the central region as well as the normal spiral arms to the north and south show the highest intensity. The superposition assigns clearly which part of the radio emission belongs to the spiral arms and which belongs to the jets. The clumps of strong emission along the spiral arms mentioned above are well correlated with the regions of highest intensity in H$\alpha$. They are most probably star-forming regions as they emit unpolarized thermal radiation, whereas the radio emission along the anomalous arm is polarized and of nonthermal origin (cf. e.g. Hummel et al. 1989; Hyman et al. 2001).

	Figure 3: The 4.86 GHz map in total intensity with HPBW = 14 $^{\prime \prime }$. The rms noise is $60~\mu$Jy/b.a. The length of the E-vectors is proportional to the linearly polarized intensity.
Open with DEXTER

	Figure 4: The 8.44 GHz map of the total intensity at HPBW = 14 $^{\prime \prime }$. The rms noise is $70~\mu$Jy/b.a. The length of the E-vectors is proportional to the linearly polarized intensity.
Open with DEXTER

Figure 3 shows the observations of NGC 4258 at 4.86 GHz ($\lambda$6.2 cm) as observed with the VLA in its C-configuration. The contours give the total intensity, the length of the E-vectors is proportional to the linearly polarized intensity. The rms noise values are given in Table 1 and the HPBW is 14 $^{\prime \prime }$. To compare the $\lambda$3.6 cm map with the $\lambda$6.2 cm map we smoothed the $\lambda$3.6 cm to the resolution of $14\hbox{$^{\prime\prime}$ }$HPBW. This map is shown in Fig. 4. The shape of the total intensity is very similar at both wavelengths.

The observations at $\lambda$2.8 cm made with the Effelsberg 100-m telescope are presented in Fig. 5. The HPBW is 69 $^{\prime \prime }$, hence the distribution is much smoother and the bifurcation in the western arm is barely resolved. The normal spiral arms, notably the southern one, are indicated.

3.2 Jet geometry

To investigate the jet geometry and in particular the outflow direction from the nucleus, Fig. 6 shows the central region in detail up to $60\hbox{$^{\prime\prime}$ }$ away from the nucleus. The location of the circumnuclear accretion disk and the observed direction of the ejected matter are indicated. From our observations we determined the position angle of the jet in the central region to be $\rm PA=-3\hbox{$^\circ$ }\pm 1\hbox{$^\circ$ }$. This is in full agreement with the value given by Cecil et al. (2000) from their radio observations and along the projected spin axis of the accretion disk as determined by Miyoshi et al. (1995).

At larger distances from the nucleus the jets change their direction from a north-south orientation to northwestern to southeastern as visible on larger scales (cf. also Fig. 1). This change is not smooth but can be described by symmetric kinks on both sides at a projected distance of $24\hbox{$^{\prime\prime}$ }$ from the galactic center to $\rm PA= -43\hbox{$^\circ$ }\pm 1\hbox{$^\circ$ }$.

	Figure 5: The 10.55 GHz map of NGC4258 in total intensity (contours) with HPBW $~=69\hbox{$^{\prime\prime}$ }$. The rms noise is $900~\mu$Jy/b.a. The length of the E-vectors is proportional to the linearly polarized intensity.
Open with DEXTER

As described by Martin et al. (1989) both anomalous arms bifurcate as seen in H$\alpha$. The projected nuclear distance of the bifurcation is, however, non-symmetric: the southern jet splits at about $84\hbox{$^{\prime\prime}$ }$ and the northern jet at about $62\hbox{$^{\prime\prime}$ }$from the nucleus, both to $\rm PA= 71\hbox{$^\circ$ }$. The northern jet reveals two more bifurcations, at $104\hbox{$^{\prime\prime}$ }$ and at about $125\hbox{$^{\prime\prime}$ }$(marginally detected) projected distances from the nucleus.

	Figure 6: The 8.44 GHz high resolution ( HPBW =  $2\hbox{$.\!\!^{\prime\prime}$ }2 \times 2\hbox{$.\!\!^{\prime\prime}$ }4$) map detail of the central region in total intensity. The rms noise is $8~\mu$Jy/b.a. The location of the circumnuclear accretion disk and the observed geometry of the jets (solid lines) as well as the supposed hot spots A and B are indicated.
Open with DEXTER

3.3 Polarized intensity

In addition to the total intensity we obtained the linearly polarized intensity at a resolution of $2\hbox{$.\!\!^{\prime\prime}$ }9 \times 3\hbox{$.\!\!^{\prime\prime}$ }3$ HPBW. This is the first time that extended linear polarization has been detected in NGC 4258 with arcsec resolution. In Fig. 7 the E-vectors of the linearly polarized emission are superimposed on the total intensity maps at 8.44 GHz. The length of the vectors is proportional to the polarized intensity.

As can be seen, polarized intensity has been detected exclusively along the jets. The highest polarized emission occurs at the center and along the northern jet, there mainly to the northwest of the bifurcation. The map shown in Fig. 7 will be used later to calculate the magnetic field strength (Sect. 3.6).

The degree of linear polarization (polarized intensity/total intensity) along the jets is high and lies in the range between 35% and 65%. In the center the degree of linear polarization is below 2% and may be partly instrumental. A high degree of polarization of about 55% was detected at the presumed hot spot A, whereas no polarization was detected at the position of source B. This will be discussed further in Sect. 4.

In the smoothed map (Fig. 4) the highest polarized emission was detected along the jets and is particularly strong along the northern jet. The polarization percentage varies between 20% and 45% there. These values are lower than those of the higher resolution map (Fig. 7) which indicates that the polarized intensity is patchy and no longer resolved at $14\hbox{$^{\prime\prime}$ }$ HPBW. The smoothed map also reveals several small regions of low percentage polarization (20%) in the southern jet.

A comparison of the $\lambda$3.6 cm map (Fig. 4) to the $\lambda$6.2 cm map (Fig. 3) shows very different orientation of the E-vectors in both maps, indicating strong Faraday rotation.

	Figure 7: The 8.44 GHz map of the total intensity with HPBW = $2\hbox{$.\!\!^{\prime\prime}$ }9 \times 3\hbox{$.\!\!^{\prime\prime}$ }3$. The rms noise is $8~\mu$Jy/b.a. The length of the E-vectors is proportional to the linearly polarized intensity.
Open with DEXTER

3.4 Faraday rotation measure and depolarization

The observed electric vectors are rotated by Faraday effects. The amount of the Faraday rotation can be determined by calculating the rotation measure RM between different wavelengths. Correction of the observed electric vectors according to these RMs and rotation by $90\hbox{$^\circ$ }$ leads to the intrinsic direction of the magnetic field in the sky plane. The RM value itself depends on the strength of the magnetic field component parallel to the line of sight, its sign indicates the direction of this parallel field component.

Although also we had $\lambda$20 cm data, we could not use them for the calculation because at this wavelength and resolution polarized intensity was only detected at large distances from the center. At $\lambda$3.6 cm and $\lambda$6.2 cm the polarized intensity was detected closer to the nucleus and along the jets. Thus the polarized regions detected do not coincide with those at $\lambda$20 cm.

We determined the RM between $\lambda$3.6 cm and $\lambda$6.2 cm. The calculated RM varies between 400 and $\rm 800~rad/m^2$. The $n\pi$ ambiguity (i.e. the RM value that corresponds to a Faraday rotation of $n 180\hbox{$^\circ$ }$ and hence is undistinguishable by observations at only two wavelengths) between these two wavelengths is as high as $\rm 1216~rad/m^2$ for n=1. A substraction of one $180\hbox{$^\circ$ }$rotation (n=-1) from these values leads to RM between -800 and $\rm -400~rad/m^2$ which is in absolute value not distinguishable from the values above. Futhermore, a rotation of the observed vectors at $\lambda$3.6 cm by e.g. $\rm -400~rad/m^2$ or $\rm 816~rad/m^2$(which corresponds to the $\pi$ ambiguity) leads to an angle difference of  $88\hbox{$^\circ$ }$, hence about perpendicular to each other.

We tried to solve the RM ambiguity using the $\lambda$2.8 cm observations. Therefore we smoothed the $\lambda$3.6 cm map (Fig 4) out to 69 $^{\prime \prime }$ HPBW, the angular resolution of the $\lambda$2.8 cm map (Fig. 5), and determined the RM between these two wavelengths. The $n\pi$ ambiguity between these wavelengths is as large as about $\rm 7200~rad/m^2$. The vectors between $\lambda$2.8 cm and $\lambda$3.6 cm rotate clockwise by about 40- $80\hbox{$^\circ$ }$ which correspond to negative RM between about -1500 and $\rm -3000~rad/m^2$. We conclude that the vectors rotate further clockwise towards the E-vectors observed at $\lambda$6.2 cm. This corresponds to negative RM values. Hence we consider the values for n=1 between $\lambda$3.6 cm and $\lambda$6.2 cm as more probable. The corresponding RM ranges from -800 to $\rm -400~rad/m^2$ and is presented graphically in Fig. 8.

	Figure 8: The rotation measure RM between $\lambda$3.6 cm and $\lambda$6.2 cm ( HPBW = 14 $^{\prime \prime }$).
Open with DEXTER

As the galactic foreground rotation measure is negligible towards the direction of this galaxy (Krause et al. 1984) we conclude that the observed RM is excusively associated with NGC 4258.

To verify the consisitency of the derived values we estimate the depolarization DP between $\lambda$3.6 cm and $\lambda$6.2 cm using

$$DP=\frac{\textrm{polarization percentage}_{\rm\lambda 6.2~cm}}{\textrm{polarization percentage}_{\rm\lambda 3.6~cm}}\cdot$$

From our observations we derive $DP \approx 0.3$ in the northern jet. A uniform magnetic field in the jet leads to differential Faraday depolarization (Burn 1966; Sokoloff et al. 1998)

$$DP = \left\vert \frac{\sin\left(2 RM \lambda^2\right)}{2 RM \lambda^2} \right\vert \cdot$$

Using this formula we obtain |RM| of 600-650 rad/m² for $DP \approx 0.3$, which is in perfect agreement with the values calculated above for the RM from the rotation of the observed E-vectors in that area. The rotation of the electric vectors between $\lambda$3.6 cm and $\lambda$6.2 cm that belongs to |RM| of 600 rad/m² is already more than $90\hbox{$^\circ$ }$. If the Faraday rotation (and depolarization) takes place inside the emitting region we have to conclude that the Faraday depth of the jet at $\lambda$6.2 cm is smaller than the jet itself, hence we do not see the full jet in linear polarization as part of its linearly polarized emission cancels with that from other parts to form unpolarized emission.

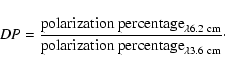
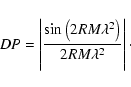
However, the observed RM may also be due to a layer of higher thermal density but fewer relativistic particles around the jet that does not contribute to the polarized emission as proposed by Bicknell et al. (1990). This layer would act as a foreground screen and rotate the observed vectors without depolarizing the emission.

The observed depolarization of the emission can also be explained by beam depolarization and Faraday dispersion (Burn 1966; Sokoloff et al. 1998) which is expected to occur in the emitting region, especially in the case of a toroidal magnetic field (see Sect. 3.5) that is not resolved by the beam size.

With the observed large values for the RM we expect strong depolarization at $\lambda$20 cm in all scenarios mentioned above. This can explain the lack of linearly polarized emission in the inner part of NGC 4258 as observed by Hummel et al. (1989).

3.5 Magnetic field direction

To obtain the direction of the intrinsic magnetic field, we corrected the E-vectors (Fig. 4) for Faraday rotation with the help of the RM (Fig. 8). The resulting magnetic field is shown in Fig. 9 superimposed on the smoothed $\lambda$3.6 cm map. The vectors generally follow the jet direction, also along the main bifurcation of the northern jet. They are, however, somewhat tilted with respect to the jet direction, especially in the outermost part of the northern bifurcation of the northern jet and along the southern part of this bifurcation. We infer that the magnetic field is mainly poloidal along the jet axis with a (weaker) toroidal component especially in the outer part of the northern bifurcation and along the southern bifurcation. This can be a superposition of a poloidal and (weaker) toroidal magnetic field in different layers around the jet axis or is consistent with a slightly helical magnetic field around the jet axis.

	Figure 9: The 8.44 GHz map of the total intensity ( HPBW = 14 $^{\prime \prime }$) as shown in Fig. 4. The rms noise is $70~\mu$Jy/b.a. The B-vectors show the magnetic field direction with their length proportional to the polarized intensity.
Open with DEXTER

3.6 Magnetic field strength

To calculate the magnetic field strength we used the polarized data at ${\it HPBW}\approx 3\hbox{$^{\prime\prime}$ }$ (Fig. 7). As the polarized emission is not homogeneously distributed but varies strongly along the jets, we only calculate the magnetic field in the regions of strongest polarized emission, which are: region I northeast of the bifurcartion, region II northwest of the bifurcation and region III just south of the bifurcation.

For the nonthermal spectral index along the jets we used the latest value derived by Hyman et al. (2001) which is $\alpha_{n}=-0.65\pm0.10$. This value is in good agreement with the average spectral index in jets of $\alpha_{n}=-0.7\pm 0.1$ and also with the previously derived spectral index between $\lambda$6.2 cm and $\lambda$20 cm by Hummel et al. (1989) of $\alpha_{n}=-0.6\pm0.1$.

The jet is assumed to be cylindrical. For the line of sight Lthrough the jets we assume L=50 pc as we do not resolve the jet width with our linear resolution of 90 pc. Based on our previous results in Sect. 3.5 we assume a magnetic field mainly along the jet axis. As the inclination of the jet we considered values between $5\hbox{$^\circ$ }$ and $45\hbox{$^\circ$ }$ (as argued in Sect. 4).

We calculate the magnetic field strengths assuming energy equipartition between the magnetic field and the relativistic particles. The calculations consider two different models concerning the composition of the ejected jet-matter in active galactic nuclei:

1.

The jets contain relativistic electrons and protons similar to the cosmic rays observed near the Earth. According to Ginzburg & Syrovatskij (1964) the electron energy density in the relevant energy interval is then 1% of that of the proton energy density and thus negligible. The K-factor used in this case is 100 (Krause et al. 1984; Beck 1991).

2.

The plasma jets contain relativistic electrons and positrons indistinguishable by observation. Then the total energy density is given by both sorts of particles. The K-factor used in this case is 1.

Table 2 shows the magnetic field strengths in the three regions along the northern jet for an electron-proton jet and Table 3 shows the results for an electron-positron jet.

Table 2: Magnetic field strengths for an electron-proton jet. Region I is south of the northern bifurcation, II is the southern part of the N bifurcation; III is the northern part of the N bifurcation.

Table 3: Magnetic field strengths for an electron-positron jet. Regions I, II, and III are chosen as in Table 2.

4 Discussion

The large-scale radio and H$\alpha$ features of NGC 4258 could only be interpreted as jets (Falcke & Biermann 1999; Yuan et al. 2002) after the accretion disk around a super-massive central object had been discovered from observations of water-maser emission (Claussen et al. 1984; Henkel et al. 1984). Previously they were called "anomalous arms'' and explained in terms of ejected matter that interacts strongly with the disk gas and hence is compressed (van der Kruit et al. 1972) or as jet-like outflows (Sanders et al. 1982).

The detection of a water-maser implies a thin, rotating Keplerian disk and is strong evidence for a black hole in the center of NGC 4258 (Miyoshi et al. 1995). Jets require enormous amounts of energy and it is generally assumed that they are produced by accretion disks which rotate around black holes and eject matter along their rotation axis.

The jets in NGC 4258 are, however, extraordinary jets, as they are not strongly collimated but show a diffuse structure and even bifurcation. They are also strongly bent.

The three-dimensional geometry of this galaxy is somewhat unusual in that the accretion and galactic disk are almost perpendicular to each other (cf. Sect. 1). If the jets emerge almost perpendicular to the nuclear disk, they have to pass the galactic disk and seem to interact with it at least in the inner 4 kpc (cf. Krause et al. 1990).

Our data are the first that are sensitive enough to detect the magnetic field in the northern jet regions also in the inner $2\hbox{$^\prime$ }$ from the galactic center. We determined the rotation measure and corrected the polarization angles for Faraday rotation. The derived intrinsic magnetic field orientation is mainly along the jet direction.

As the determined RMs are negative, the uniform magnetic field component along the jet axis points away from us, hence it is directed towards the nucleus in the northern jet. The few RM values that are found in the southern jet are also negative and may indicate that the magnetic field there is directed away from the nucleus.

The magnetic field in the northern jet however is also somewhat tilted towards the jet direction, especially in the outermost part of the northern bifurcation and along the southern part of the bifurcation. This can indicate an additional (weaker) toroidal component that is either located in different layers around the jet axis or may be due to a partly helical magnetic field around the jet axis. This is found to be typical of extragalactic jets (Begelmann et al. 1984).

The longitudinal field (along the jet axis) can either be in the inner part of the jet near the jet axis, in the so-called beam, with a toroidal field further away from the jet axis (e.g. Roland & Hermsen 1995) or be part of a helical magnetic field (e.g. Lesch et al. 1989) that may be amplified by dynamo action such as the screw dynamo (Shukurov & Sokoloff 1993).

As $RM = 0.81 \int n_{\rm e} B_\parallel {\rm d}l$ (the sign of RM is determined by the direction of $B_\parallel$), the observed high RM values require a uniform magnetic field component $B_\parallel$parallel to the line of sight with uniform direction. It has been argued from the geometry of the accretion disk (see Sect. 1) that the inner jet orientation is almost parallel to the major axis of the galactic disk of NGC 4258. A magnetic field along the jet that is parallel to the major axis of the disk would not contribute to a field component parallel to the line of sight, and hence not cause Faraday rotation. However, even an angle of the jet to the line of sight of only $5\hbox{$^\circ$ }$ yields $B_\parallel = 0.1~B_{\rm long}$, where $B_{\rm long}$ is the field component along the jet axis. Additionally, we observe several kinks in the northern jet as described in Sect. 3.2. The first appeared at  $24\hbox{$^{\prime\prime}$ }$ projected distance from the nucleus where the jet changes direction by as much as $40\hbox{$^\circ$ }$ in the plane of the sky. We consider it highly improbable that this change of direction happens only in the plane of the sky. It will take place at an arbitrary angle to the line of sight.

Let us assume that we have a kink of equal strength along the line of sight. With the uniform magnetic field strength of about $250~\mu$G we estimate $B_\parallel$ of about $160~\mu$G in the case of an electron-proton jet. We calculate the thermal electron density $n_{\rm e}$ using

$$RM=0.81 n_{\rm e} B_{\parallel} L.$$

With RM=650 rad/m², $B_{\parallel} =160~\mu$G, and L=50 pc we derive $n_{\rm e} = 0.1~{\rm cm}^{-1}$. This value is about three times higher than usual values for the intersteller medium. A higher value is reasonable as both jets are visible in H$\alpha$.

If the jet consists of relativistic particles (electron-positron jet), the expected rotation measure in the jet is RM=0 and the Faraday rotation is produced in a cocoon around the jet (e.g. Bicknell et al. 1990) with a correspondingly smaller line of sight, hence an even higher thermal electron density and/or magnetic field strength there. In this case the expected depolarization is smaller (as described in Sect. 3.4.) but still compatible with our observations.

Previous investigations on the magnetic field were only able to determine the magnetic field orientation in the outermost parts of the jets (outside $r\simeq 2\hbox{$^\prime$ }$) (cf. Krause et al. 1984; Hummel et al. 1989). The magnetic field there was also derived to be along the jets.

Concerning the hot spots detected by Cecil et al. (2000), we can confirm that we also detected high emission at both locations. Hot spots are usually detected when the relativistic jet matter hits intergalactic gas and undergoes strong interaction. The observed electric vector at $\lambda$3.6 cm fits, however, into the general pattern of the northern jet. As we have no high-resolution polarization information at $\lambda$6.2 cm we cannot determine the RM and the intrinsic magnetic field direction at the presumed hot spot A.

On the other hand, the observed high degree of linear polarization of about 55% as averaged over the whole source makes it rather improbable that source A is a supernova remnant as has been proposed by Hyman et al. (2001).

5 Conclusions

We present interferometer data obtained with the VLA in its C-configuration at $\lambda$3.6 cm (8.4399 GHz) in total power and linear polarization. For comparison and to obtain quantities like rotation measure and depolarization we also reprocessed VLA data at $\lambda$6.2 cm (4.8851 GHz) and $\lambda$20 cm (1.4899 GHz) that were previously published by Hummel et al. (1989) and observations at $\lambda$2.8 cm (10.55 GHz) made with the Effelsberg 100-m telescope.

The high resolution maps ( $2\hbox{$.\!\!^{\prime\prime}$ }4$ HPBW) at $\lambda$3.6 cm as obtained with the C-configuration of the VLA are able for the first time to resolve the jets in the central region of the galaxy. Detailed inspection shows that they emerge from the galactic center along the projected spin axis of the accretion disk as determined by Miyoshi et al. (1995). At a distance $24\hbox{$^{\prime\prime}$ }$ away from the center they change direction towards the previously seen northwest to southeast and bifurcate at $62\hbox{$^{\prime\prime}$ }$ from the nucleus in the northern jet and at $85\hbox{$^{\prime\prime}$ }$ in the southern jet. The multiple splitting of the northern jet is clearly visible at this resolution.

The polarized emission was detected exclusively along the jets and allowed the calculation of the magnetic field strength in the inner region of the northern jet. Energy equipartition considerations lead to magnetic field strengths of $310\pm 15~\mu$G assuming a relativistic electron-proton jet and $90\pm 5~\mu$G assuming an electron-positron jet. The rotation measure could be determined between $\lambda$3.6 cm and $\lambda$6.2 cm, at a linear resolution of $14\hbox{$^{\prime\prime}$ }$ HPBW. It is derived to be -400 to -800 rad/m² in the northern jet. Correcting the observed E-vectors of polarized emission for Faraday rotation, the magnetic field is mainly along the jet axis in the central region and tends to become somewhat tilted with respect to the jet direction in the outer part of the northern jet. This may be consistent with a slightly helical magnetic field around the northern jet or may indicate a superposition of a longitudinal magnetic field near the jet axis and a toroidal magnetic field away from the axis.

Acknowledgements

We thank N. Neininger for providing the H$\alpha$ image and M. Ehle for helping us with the Effelsberg observations. We acknowledge fruitful discussions with H. Falcke and A. Shukurov and are grateful for helpful comments by R. Perley.

References

• van Albada, G. D. 1978, A&A, 90, 123 [NASA ADS] (In the text)
• van Albada, G. D. 1980, A&A, 90, 123 [NASA ADS] (In the text)
• van Albada, G. D., & van der Hulst, J. M. 1982, A&A, 115, 263 [NASA ADS] (In the text)
• Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] (In the text)
• Beck, R. 1991, A&A, 251, 15 [NASA ADS] (In the text)
• Begelmann, M. C., Blandford, R. D., & Rees, M. J. 1984, Rev. Mod. Phys., 56, 255 [NASA ADS] [CrossRef] (In the text)
• Bicknell, G. V., Cameron, R. A., & Gingold, R. A. 1990, ApJ, 357, 373 [NASA ADS] [CrossRef] (In the text)
• de Bruyn, A. G. 1977, A&A, 58, 22 [NASA ADS] (In the text)
• Burbidge, E. M., Burbidge, G. R., & Prendergast, K. H. 1963, ApJ, 138, 375 [NASA ADS] [CrossRef] (In the text)
• Burn, B. J. 1966, MNRAS, 133, 76 [NASA ADS] (In the text)
• Cecil, G., Wilson, A. S., & Tully, R. B. 1995, ApJ, 390, 365 [NASA ADS]
• Cecil, G., Greenhill, L. J., DePree, C. G., et al. 2000, ApJ, 536, 675 [NASA ADS] [CrossRef] (In the text)
• Claussen, M. J., Heiligman, G. M., & Lo, K. Y 1984, Nature, 310, 298 [NASA ADS] (In the text)
• Courtès, G., & Cruvellier, P. 1961, Compt. Rend. Acad. Sci. Paris, 253, 218 [NASA ADS] (In the text)
• Emerson, D. T., Klein, U., & Haslam, C. G. T. 1979, A&A, 76, 92 [NASA ADS] (In the text)
• Emerson, D. T., & Gräve, R. 1988, A&A, 190, 353 [NASA ADS] (In the text)
• Falcke, H., & Biermann, P. L. 1999, A&A, 342, 49 [NASA ADS] (In the text)
• Ginzburg, V. L., & Syrovatskij, S. I. 1964, The Origin of Cosmic Rays (Oxford: Pergamon Press) (In the text)
• Haslam, C. G. T. 1974, A&AS, 15, 333 [NASA ADS]
• Henkel, C., Güsten, R., Downes, D., et al. 1984, A&A, 141, L1 [NASA ADS] (In the text)
• Herrnstein, J. R., Moran, J. M., Greenhill, L. J., et al. 1997, ApJ, 475, L17 [NASA ADS] [CrossRef] (In the text)
• Herrnstein, J. M., Greenhill, J. R., Moran, L. J., et al. 1998, ApJ, 497, L69 [NASA ADS] [CrossRef] (In the text)
• Herrnstein, J. M., Moran, L. J., Greenhill, J. R., et al. 1999, Nature, 400, 539 [NASA ADS] [CrossRef] (In the text)
• Horellou, C., Beck, R., Berkhuijsen, E. M., Krause, M., & Lesch, H. 1992, A&A, 265, 417 [NASA ADS]
• Hummel, E., Krause, M., & Lesch, H. 1989, A&A, 211, 266 [NASA ADS] (In the text)
• Hyman, S. D., Calle, D., Weiler, K. W., et al. 2001, ApJ, 551, 702 [NASA ADS] [CrossRef] (In the text)
• Klein, U., & Emerson, D. T. 1981, A&A, 94, 29 [NASA ADS] (In the text)
• Klein, U., Urbanik, M., Beck, R., & Wielebinski, R. 1983, A&A, 108, 176 [NASA ADS]
• Krause, M., Beck, R., & Klein, U. 1984, A&A, 138, 385 [NASA ADS] (In the text)
• Krause, M., Cox, P., Garcia-Barreto, J. A., & Downes D. 1990, A&A, 233, L1 [NASA ADS] (In the text)
• van der Kruit, P. C., Oort, J. H., & Mathewson, D. S. 1972, A&A, 21, 169 [NASA ADS] (In the text)
• Lesch, H., Appl, S., & Camenzind, M. 1989, A&A, 225, 341 [NASA ADS] (In the text)
• Martin, P., Roy, J.-R., Noreau, L., & Lo, K. Y. 1989, ApJ, 345, 707 [NASA ADS] [CrossRef] (In the text)
• Miyoshi, M., Moran, J., Herrnstein, J. R., et al. 1995, Nature, 373, 127 [NASA ADS] [CrossRef] (In the text)
• Napier, P. J., Thompson, A. R., & Ekers, R. D. 1983, Proc. IEEE, 71, 1295 [NASA ADS] (In the text)
• Pacholczyk, A. G. 1970, Radio Astrophysics (San Francisco: Freeman)
• Roland, J., & Hermsen, W. 1995, A&A, 297, L9 [NASA ADS] (In the text)
• Sanders, R. 1982, in Extragalactic Radio Sources, ed. D. S. Heeschen, & C. M. Wade (Dordrecht: Reidel), IAU Symp., 97, 145 (In the text)
• Shukurov, A., & Sokoloff, D. D. 1993, in The Cosmic Dynamo, ed. F. Krause, K.-H. Rädler, & G. Rüdiger (Dordrecht: Kluwer), IAU Symp., 157, 367 (In the text)
• Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] (In the text)
• Thompson, A. R., Clark, B. G., Wade, C. M., & Napier, P. J. 1980, ApJS, 44, 151 [NASA ADS] [CrossRef] (In the text)
• de Vaucouleurs, G., de Vaucouleurs, A., & Corwin, H. G. 1976, Second Reference Catalogue of Bright Galaxies (Austin: University of Texas Press) (In the text)
• Yuan, F., Markoff, S., Falcke, H., & Biermann, L. P. 2002, A&A, 391, 139 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)