A&A 419, 439-447 (2004)
DOI: 10.1051/0004-6361:20035587

Measuring dark matter flows in merging clusters of galaxies

J. A. Rubiño-Martín - C. Hernández-Monteagudo - T. A. Enßlin

Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str.1, Postfach 1317, 85741 Garching, Germany

Received 28 October 2003 / Accepted 11 February 2004

Abstract
The Rees-Sciama effect produced in mergers of galaxy clusters is discussed, and an analytical approximation to compute this effect from numerical simulations is given. Using this approximation and a novel model describing the physics of the merger, we characterize the spatial properties and symmetries of the Rees-Sciama signal. Based on these properties, we propose a method to extract the physical parameters of the merger, which relies on the computation of the quadrupole moment of the observed brightness distribution on the sky. The relationships between the quadrupole coefficients and the physical parameters of the merger (physical separation, projection angle on the sky and angular momentum) are discussed. Finally, we propose a method to co-add coherently the RS signals from a sample of cluster mergers, to achieve a statistical detection of the effect for those cases where individual signals are masked by the kinetic SZ effect, the primordial CMB components, and by observational noise.

Key words: galaxies: intergalactic medium - galaxies: clusters: general - galaxies: interactions - gravitational lensing - cosmology: cosmic microwave background

  
1 Introduction

The integrated Sachs-Wolfe (ISW; Hu & Sugiyama 1994; Sachs & Wolfe 1967) effect produces CMB temperature fluctuations due to the accumulation of red- or blue-shift of photons travelling in time dependent gravitational potentials. Several recent studies (Fosalba & Gaztañaga 2003; Boughn & Crittenden 2004; Nolta et al. 2003) have claimed evidence for its detection in the WMAP data (Bennett et al. 2003). The non-linear contribution to the ISW effect, in which the density contrast producing the gravitational potential is in its non-linear regime, is usually called the Rees-Sciama (RS; Rees & Sciama 1968; Seljak 1996) effect.

Here we discuss the RS effect in the extremely non-linear regime of present day galaxy cluster mergers. The regime of moving single galaxy clusters was already examined by Birkinshaw & Gull (1983), Aghanim et al. (1998), Molnar & Birkinshaw (2003,2000), and Cooray (2002). However, galaxy clusters reach the largest velocities, and therefore the strongest RS signal, during mergers in which two or more clusters are invoked. Due to the slow centre-of-mass velocity of the merging system, the RS signals of the merging subclusters can partly cancel or increase each other, depending on the merger geometry and the location of the line-of-sight (LOS).

Furthermore, the spectral signature of the RS effect is a temperature change of the measured CMB photons, and therefore indistinguishable form the kinematic Sunyaev-Zeldovich (kSZ; Sunyaev & Zeldovich 1972,1980) effect spectrally. However, both effects have distinct morphologies, which in principle allow to discriminate them.

The focus of this work is to examine methods to extract the RS signature from merging pairs of galaxy clusters. The layout of the paper is as follows. In Sect. 2 we provide an approximation to compute the RS effect either from theoretical cluster models or numerical simulations. In addition, a brief description of the kSZ and the thermal Sunyaev-Zeldovich (tSZ) effects is also given, emphasizing their phenomenological differences with the RS effect. In Sect. 3 we present and use an analytic model of a merger of two galaxy clusters to characterize the typical morphologies of these effects (RS, kSZ and tSZ). Based on its spatial properties, we present in Sect. 4 a method to extract both the RS signal and the physical parameters describing the system from a given merger. A method to stack the signal from a sample of mergers is also proposed. Conclusions are presented in Sect. 5.

2 Formalism

2.1 Rees Sciama effect

The CMB temperature change in a LOS direction  $\vec{\hat{n}}$ caused by the RS effect can be written as (Cooray 2002)

 \begin{displaymath}% \delta T_{\rm RS}(\vec{\hat{n}}) = - \frac{2}{c^3} ~ \int {\rm d}r~ \dot{\Phi}(\vec{\hat{n}}~r, r/c)~T(\vec{\hat{n}}) , \end{displaymath} (1)

where $\dot{\Phi}(\vec{r},t)$ is the time derivative of the gravitational potential and r/c the look-back time along the LOS.

In the following, we are dealing with well separated structures, galaxy clusters, which do not change significantly during the time of a photon passage. Thus, we explicitly neglect the intrinsic variation of the cluster potential while the photon is passing through it. This allows an approximative treatment.

In Newtonian approximation, the gravitational potential depends on the total mass density  $\varrho(\vec{r},t)$ via

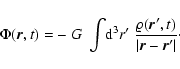\begin{displaymath}% {\Phi}(\vec{r},t) = -~G~ \int\! {\rm d}^3 r' ~ \frac{\varrho(\vec{r}',t)}{\vert\vec{r}-\vec{r}'\vert}\cdot \end{displaymath} (2)

The time derivative of the gravitational potential therefore follows the change of the matter density, leading to

 \begin{displaymath}% \dot{\Phi}(\vec{r},t) = -~G~\int\! {\rm d}^3r' ~ \varrho(\v... ...c{\cdot} \frac{\vec{r}-\vec{r}'}{\vert\vec{r}-\vec{r}'\vert^3} \end{displaymath} (3)

by using the continuity equation $\dot{\varrho} +\vec{\nabla} (\vec{v}~{\varrho}) = 0$, then the Gauss' theorem, and neglecting boundary terms in the integration. Here, $\vec{v}$ is the mean velocity of matter, which is the density weighted mean of all matter species' velocities $\vec{v} = \sum_i ~\vec{v}_{i} ~\varrho_{i}/\varrho$, where the i runs over all species like dark matter, gas, and galaxies, and $\varrho = \sum_i ~\varrho_{i}$.

By inserting Eq. (3) into Eq. (1) we approximate all LOS to be parallel to the z-direction, we ignore the explicit dependency of $\varrho$ and v on time, and integrate out the LOS integral, yielding

 \begin{displaymath}% \frac{\delta T_{\rm RS}}{T} (\vec{r_\perp}) = -\frac{4~G}{c... ...p- \vec{r}_\perp'}{\vert\vec{r}_\perp- \vec{r}_\perp'\vert^2}, \end{displaymath} (4)

where vectors are split into a LOS-parallel and perpendicular part according to $\vec{r}= (\vec{r}_\perp, z)$, and where the Z-axis is taken pointing towards the observer. This approximative description of the RS effect ignores small corrections due to non-parallel LOSs, gravitational lensing, the actual change of the matter distribution during the photon passage, and the finite velocity of gravitational interaction.

Nevertheless, its accuracy is sufficient to study the general difficulties in RS signal extraction from merging clusters of galaxies. Its simplicity allows easy inclusion into any code which calculates the kSZ effect from numerical simulations.

One can introduce the LOS projected momentum

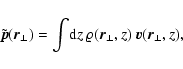\begin{displaymath}% \tilde{\vec{p}}(\vec{r}_\perp) = \int\! {\rm d}z ~ \varrho(\vec{r}_\perp,z)~ \vec{v}(\vec{r}_\perp, z), \end{displaymath} (5)

in order to write

 \begin{displaymath}% \frac{\delta T_{\rm RS}}{T} (\vec{r_\perp}) = -\frac{4~G}{c... ...vec{r}_\perp'}{\vert\vec{r}_\perp- \vec{r}_\perp'\vert^2}\cdot \end{displaymath} (6)

From this, one easily sees that the RS effect measures the convergence of the projected perpendicular momentum.

2.2 Moving cluster of galaxies effect

Equation (6) can also be reproduced using a different approach. The moving cluster of galaxies (MCG) effect (Birkinshaw & Gull 1983) was originally derived as a gravitational lensing effect. However, and as it was pointed out by Molnar & Birkinshaw (2000), this effect can be seen as a special type of RS effect, which is not caused by intrinsic variations of the gravitational field, but due to the movement of the cluster with respect to the rest frame of the CMB. Given that we have used exactly this assumption when deriving Eq. (4), then our expression is completely explained as a gravitational lensing effect.

Following Birkinshaw & Gull (1983) and Molnar & Birkinshaw (2000), the MCG effect for a cluster moving with velocity $\vec{v}$, for small values of the lensing deflection angle, can be written as

 \begin{displaymath}% \frac{\delta T_{{\rm MCG}}}{T}(\hat{n}) = - \frac{v}{c} \sin \alpha ~ \vec{\hat{u}}_{v \perp} \cdot \vec{\delta}(\hat{n}), \end{displaymath} (7)

where $\alpha$ is the angle between the cluster's peculiar velocity vector and its angular position vector, $\vec{\hat{u}}_{v \perp}$ is an unit vector parallel to the projection of the velocity in the lens plane ( $\vec{v}_\perp= v \sin \alpha ~ \vec{\hat{u}}_{v \perp}$), and $\vec{\delta}(\hat{n})$ is the vector describing the deflection angle. If we now use the equation for a geometrically-thin lens from Schneider et al. (1992),

 \begin{displaymath}% \vec{\delta} (\vec{r_\perp}) = \frac{4~G}{c^2}~ \int {\rm d... ...p- \vec{r}_\perp'}{\vert\vec{r}_\perp- \vec{r}_\perp'\vert^2}, \end{displaymath} (8)

where $\Sigma$ is the surface mass density, and we insert it in Eq. (7), we recover Eq. (6) in its limit of a constant velocity field. Since the MCG effect is linear, one can build a superposition of differently moving matter distributions, and therefore fully recover the more general Eq. (6). It should be noted that Eq. (8) requires that the gravitational fields should be weak (which is true for clusters of galaxies), and that the matter distribution of the lens must be nearly stationary (i.e. $v/c \ll 1$).

2.3 Kinematic SZ effect

Since the kSZ effect has the same spectral signature as the RS effect, it is crucial to include the latter into the considerations. Using similar planar and time-independent approximations the kSZ effect reads

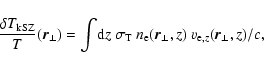\begin{displaymath}% \frac{\delta T_{\rm kSZ}}{T} (\vec{r}_\perp) = \int\! {\rm ... ... n_{\rm e}(\vec{r}_\perp,z)~ v_{{\rm e},z}(\vec{r}_\perp,z)/c, \end{displaymath} (9)

where $n_{\rm e}$, and $\vec{v}_{\rm e}$ are the electron density and velocity, respectively.

Since the electron and dark matter velocity fields are not too different, and the baryonic matter density follows roughly the dark matter density ( $\varrho_{\rm gas}(\vec{r}) \approx f_{\rm b}~ \varrho(\vec{r})$, with $f_{\rm b}$ the cosmic baryon mass fraction), one can state that

 \begin{displaymath}% \frac{\delta T_{\rm kSZ}}{T} (\vec{r}_\perp) \approx \frac... ..._{\rm T}~f_{\rm b}}{m~c} ~ \tilde{\vec{p}}_{z}(\vec{r}_\perp), \end{displaymath} (10)

where $m= m_{\rm p} ~(1+\frac{1}{4} ~X_{\rm He})/(1+\frac{1}{2} ~X_{\rm He})$ is the gas mass per electron, $X_{\rm He}=0.24$ the primordial He gas mass fraction, and $m_{\rm p}$ the proton mass.

Comparing Eq. (6) with Eq. (10) one recognises properties which hopefully allow to separate the RS signal from the kSZ effect:

1.
The RS effect is only sensitive to perpendicular momentum, whereas the kSZ effect traces only parallel momentum. Thus, in a cluster merger which happens mainly within the sky plane the RS effect is enhanced relatively to the kSZ effect.
2.
The kSZ effect is restricted to LOSs with baryonic matter along it, whereas the RS effect reaches further out due to its gravitational origin. This can be used to enhance the relative signal strength.
3.
The RS has a more complex morphology compared to the kSZ since for a single moving mass, the RS has a dipole, whereas the kSZ a monopole morphology. For a pair of merging clusters with opposite momenta of the same strength this leads to a mostly quadrupole morphology of the RS effect and a dipole morphology of the kSZ effect.

2.4 Thermal SZ effect

Because of its different spectral characteristic the tSZ effect can be separated from the the kSZ and RS effects. However, it has to be considered simultaneously not only because of possible residuals from incomplete removing of the tSZ effect from measurements, but also since the tSZ effect helps to localise the gas distribution and therefore to identify the regions which are expected to contain the strongest kSZ contamination. The usual tSZ y-parameter is given by

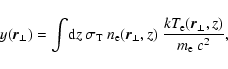\begin{displaymath}% y(\vec{r}_\perp) = \int\! {\rm d}z ~ \sigma_{\rm T}~ n_{\rm... ...erp,z)~ \frac{ kT_{{\rm e}}(\vec{r}_\perp,z)}{m_{\rm e}~c^2}, \end{displaymath} (11)

where $T_{\rm e}$ stands for the electron temperature, and measures the LOS thermal gas energy content.

3 Model

3.1 Justification of approximations

To be able to study the strength of the signal we construct a simplified model of a binary cluster merger. We grossly simplify the complicated gravitational and hydrodynamical process in order to have an analytic model. Nevertheless this model should provide us with maps of the RS, kSZ, and tSZ effects, which are sufficiently realistic for the purpose to study RS signatures by describing the typical strength and morphology of the effects.

We build the merger model out of two cluster models, labelled with the numbers 1 and 2, and each described by a NFW dark matter profile (Navarro et al. 1997) filled by isothermal hydrostatic gas. The two clusters approach each other. Each cluster velocity $\vec{v}_i$ ( $i\in\{1,2\}$) is calculated to be the velocity of a free-falling object in the gravitational potential of the other cluster. The total momentum of the merging system is assumed to be negligible.

Deformation of the clusters due to mutual tidal forces are ignored for simplicity, so that the dark matter and the gas of each cluster are streaming with the same velocity. Furthermore, hydrodynamical interactions of the gases of the two clusters are ignored, the gases are treated as non-interacting fluids. This coarse approximation is justified in so far that the kSZ and the RS effects both are only sensitive to momentum, and only in projection, but not to the thermodynamical state of the gas. The ignorance of shock waves exchanging the momentum of the gases therefore does not strongly change the signal strength, only its exact spatial morphology.

In contrast to that, the tSZ effect is very sensitive to the thermodynamical state of the gas and has therefore to be treated with a little bit more care. Again we do not try to model the exact spatial structure but try to get a good estimate of the signal strength. For that, we have to estimate the amount of shocked gas produced by the merger. We do this by measuring for each volume element the excess kinetic energy of the gas of the two superposed clusters with respect to the volume's bulk kinetic energy and assuming this to be dissipated. The total thermal energy density of a volume element is therefore approximated to be

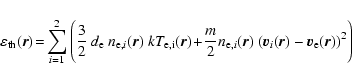\begin{displaymath}% \varepsilon_{\rm th}(\vec{r}) \!=\! \sum_{i=1}^2 \Bigg( \... ...c{r}) ~(\vec{v}_i(\vec{r})-\vec{v}_{\rm e}(\vec{r}))^2 \Bigg) \end{displaymath} (12)

where $d_{\rm e} = 2~(1+\frac{3}{8} ~X_{\rm He})/(1+\frac{1}{2} ~X_{\rm He})$ is the number of particles per electron, $T_{{\rm e},i}(\vec{r})$ ( $i\in\{1,2\}$) is the temperature of the gas in each cluster, and $\vec{v}_{\rm e}= \sum_{i\in\{1,2\}} ~\vec{v}_i ~n_{{\rm e},i} /\sum_i ~n_{{\rm e},i}$ is the local mean gas velocity. From this, the electron pressure entering the tSZ effect estimate is easily obtained:
                      $\displaystyle % (n_{\rm e}~kT_{\rm e}) (\vec{r})$ = $\displaystyle n_{{\rm e},1}(\vec{r})~kT_{\rm e,1}(\vec{r}) + n_{{\rm e},2}(\vec{r})~kT_{\rm e,2}(\vec{r})$  
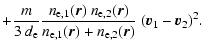    $\displaystyle + \frac{m}{3~d_{\rm e}} \frac{n_{{\rm e},1}(\vec{r})~n_{{\rm e},2... ...})}{n_{{\rm e},1}(\vec{r}) + n_{{\rm e},2}(\vec{r})} ~ (\vec{v}_1-\vec{v}_2)^2.$ (13)

3.2 Simulations of the effect

In this subsection, we present the equations outlined in the previous one for the simulation of a merger of two galaxy clusters, with a null total linear momentum. We assume a NFW dark matter profile for each cluster,

 \begin{displaymath}% \varrho_{{\rm DM}} (r) = \frac{\varrho_0}{(r/r_{\rm s})(1+r/r_{\rm s})^2}\cdot \end{displaymath} (14)

The gas is considered isothermal, and distributed in hydrostatic equilibrium, so we have (Makino et al. 1998)

 \begin{displaymath}% \varrho_{\rm g}(r) = \varrho_{{\rm g}0} {\rm e}^{-b} \Bigg( 1 + \frac{r}{r_{\rm s}} \Bigg)^{b r_{\rm s} /r} \end{displaymath} (15)

where b is a constant for each halo, given by:

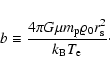\begin{displaymath}% b \equiv \frac{4\pi G \mu m_{\rm p} \varrho_0 r_{\rm s}^2}{k_{\rm B} T_{\rm e}}\cdot \end{displaymath} (16)

The value for $\varrho_{{\rm g}0}$ is determined using the following expression for the gas mass fraction

 \begin{displaymath}% \frac{M_{{\rm gas}}(r_v)}{M_{{\rm tot}}(r_v)} = \Upsilon \frac{\Omega_b}{\Omega_m}, \end{displaymath} (17)

where the masses are evaluated at the virial radius (rv). We use here the values $\Omega_b=0.044$ and $\Omega_m=0.27$ (Bennett et al. 2003), and we adopt $\Upsilon = 0.8$ (Makino et al. 1998). It should be noted that when deriving Eq. (15), and when computing the total mass for Eq. (17), we have neglected the gas contribution to the total density.


  \begin{figure} \par\includegraphics[width=4.9cm,clip]{587fig1a.eps}\hspace*{5mm}... ...1b.eps}\hspace*{5mm} \includegraphics[width=5cm,clip]{587fig1c.eps} \end{figure} Figure 1: RS ( left image), kSZ ( central image) and the sum of both effects ( right image), for a pair of merging clusters with masses $10^{15}~M_\odot$ (left cluster) and $5\times 10^{14}~M_\odot$ (right cluster), with zero angular momentum, when observed with projection angle  $80\hbox {$^\circ $ }$, and a physical separation of 1 Mpc. Contour lines in all plots correspond to (-64, -16, -4, -1, 1, 4, 16, 64) times the maximum of the map (dotted-lines for negative regions and solid lines for positive ones).
Open with DEXTER

For the computation of the RS effect, we use the 2-D projection of the NFW profile (Eq. (14)), which is given by

\begin{eqnarray*}&&\!\!\!\!\!\! \Sigma_{{\rm NFW}}(r_\perp) = \int_{-\infty}^{+\... ... \varrho_0, & \qquad r_\perp = r_{\rm s}. \\ \end{array}\right. \end{eqnarray*}


A simulation of two merging clusters is then characterised by the set of parameters ${\vec{\hat{\theta}}}$ = $\{ M_1,M_2,d,\hat{\i},\vec{J}\}$, which correspond to the masses of the two clusters, the true physical separation, the projection angle of sky ( $\hat{\i}=90\hbox{$^\circ$ }$ is a face-on merger), and the angular momentum of the system. Once these parameters are given, we can derive the remaining quantities describing the system. For definiteness, we use the following scaling relations. Both clusters are taken to be isothermal, with electron temperatures given by (Eke et al. 1996; Atrio-Barandela & Mücket 1999)

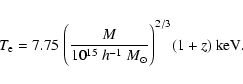
\begin{eqnarray*}T_{\rm e} = 7.75 ~ \Bigg( \frac{M}{10^{15}~{h}^{-1}~M_\odot} \Bigg)^{2/3} (1+z) ~ {\rm keV}. \end{eqnarray*}


Virial radii are derived as (Molnar & Birkinshaw 2000)

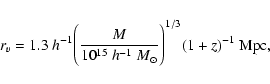
\begin{eqnarray*}r_v = 1.3~h^{-1} \Bigg( \frac{M}{10^{15}~h^{-1}~M_\odot} \Bigg)^{1/3} (1+z)^{-1} ~{\rm Mpc}, \end{eqnarray*}


and the $r_{\rm s}$ parameter is computed as $r_{\rm c} = 0.22 r_{\rm s}$ (Makino et al. 1998). We have used a constant ratio $r_v/r_{\rm c}=10$(self-similar core evolution, Kaiser (1986)). The electron density is derived as $n_{\rm e}(r) = \varrho_{\rm g}(r)(1+X)/(2 m_{\rm p})$, where we fix the hydrogen abundance X to the primordial value (X=0.76).

Velocities are estimated following the formalism described in Sarazin (2002), although we modified it to use the gravitational energy associated to the NFW matter distribution described by Eq. (14), because it is more realistic and better behaved at r=0. For this latter profile, the gravitational potential is found to be

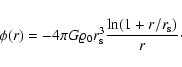\begin{displaymath}% \phi(r) = -4\pi G \varrho_0 r_{\rm s}^3 \frac{\ln(1 + r/r_{\rm s})}{r}\cdot \end{displaymath} (18)

When estimating from here the gravitational energy associated to the two clusters, we follow Sarazin (2002) and use the approximation $E_{{\rm grav}} \approx 1/2 (\phi_1 M_2 + \phi_2 M_1)$, where $\phi_i$ is the gravitational potential of cluster i at the position of the centre of the other cluster. From this we calculate the relative velocity as

\begin{displaymath}% v^2 \approx \frac{2}{m} \Bigg[ E_{{\rm grav}}(d_0) - E_{{\rm grav}}(d) \Bigg] \Bigg[ 1 - \frac{b^2}{d_0^2} \Bigg]^{-1}, \end{displaymath} (19)

where d is the 3-dimensional separation of the clusters, d0 is the initial distance from which clusters fall together (see Eq. (10) in Sarazin 2002), $m \equiv M_1 M_2 /(M_1+M_2)$ is the reduced mass of the system, and b is the impact parameter of the merger. From here, the individual cluster velocities are calculated as v1 = M2/(M1+M2)v and v2 = -M1/(M1+M2)v, so that the total momentum is zero and that v1 - v2 = v.


  \begin{figure} \par\includegraphics[width=5cm,clip]{587fig2a.eps}\hspace*{5mm} \... ....eps}\hspace*{5mm} \includegraphics[width=5.2cm,clip]{587fig2c.eps} \end{figure} Figure 2: Same as Fig. 1, but considering angular momentum, and with a larger projection angle. Here, $\hat{\i}= 60\hbox{$^\circ$ }$, and the velocity vector is defined by the spherical angles $(60\hbox {$^\circ $ },60\hbox {$^\circ $ })$. Contours have the same meaning as in Fig. 1.
Open with DEXTER

3.3 Spatial properties/symmetries

In this subsection, we use our toy model for two merging clusters to present two examples illustrating the spatial properties and symmetries of the effect. For definiteness, we choose the coordinate system with the Z-plane as the sky plane, with positive values pointing towards the observer. If we define $\alpha_{{\rm CM}}$ as the angle between the direction joining the two centres of mass of the clusters (from M1 to M2) and the X-axis, then we choose $\alpha_{{\rm CM}}=0$ (i.e. clusters on the X-axis, and M1 on the left of the image). This coordinate system will be used throughout the paper, unless otherwise stated.

We first show in Fig. 1 the result for a merger with ${\vec{\hat{\theta}}}$ = $\{ 10^{15}~M_\odot, 5\times 10^{14}~M_\odot, 1~{\rm Mpc}, 80\hbox{$^\circ$ }, \vec{0}\}$. This is a very optimistic case (in terms of the RS signal strength compared to the kSZ effect), where the merger is practically face-on.

As pointed out in Sect. 2.3, the spatial pattern of the RS effect for a merging of two clusters shows a peculiar quadrupole structure. This quadrupole structure carries information about the velocity field of the clusters, and can exhibit, for example, if both clusters are in a pre- or post- merger state.

This fact is used in the next section to extract the RS signal in a map where kSZ is also present, given that the kSZ has a dipole spatial structure. On the other hand, it can also be seen in the figure that the RS effect has a much more extended pattern than the kSZ, because of its gravitational nature.

As a second example, in Fig. 2 we consider a more pessimistic case in which the velocity forms an angle of  $60\hbox{$^\circ$ }$ with the line of sight. We incorporate also angular momentum. In this case, ${\vec{\hat{\theta}}}$ = $\{ 10^{15}~M_\odot,~ 5\times 10^{14}~M_\odot,~ 1~{\rm Mpc},~ 60\hbox{$^\circ$ },~ \vec{J}\}$. Here a non-zero angular momentum is implicitly defined by assigning a velocity direction to the cluster M1 different from the direction joining the two cluster centres. The direction of $\vec{v}_1$ is specified by the spherical polar angles $(\theta_v,\phi_v) = (60\hbox{$^\circ$ },60\hbox{$^\circ$ })$, where $\theta_v$ is the usual polar angle from the Z axis, and $\phi _v$ the usual azimuthal angle measured from the X-axis. In the case presented in Fig. 2, the RS effect is practically hidden by the kSZ, although it can be marginally seen at large distances.

4 Signal extraction

Once we have illustrated the morphology of the RS effect, we will study how to extract the RS information from observations of merging clusters.

4.1 RS signature detection

The peculiar structure of the RS effect in merging clusters can be quantified studying the dipole and quadrupole moments of the observed intensity map. It is worth remarking that the quadrupole moment of the surface brightness is also used as a tool to extract the shear signal when studying weak lensing-induced distortion of faint background galaxies (Kaiser et al. 1995).

We propose the following recipe to proceed with future experiments aiming to measure this effect:

1.
Using a catalogue of cluster mergers, one identifies those clusters with a suitable projection angle (close to face-on mergers);
2.
Observations of the merger in frequencies far from the tSZ cross-over frequency (217 GHz, or 1.38 mm), or in X-rays, will show the spatial distribution of the gas. One of these images can be used to find the "centre of light'' point, to which we refer the dipole and quadrupole moments[*]. In what follows, we will place the origin of our coordinate system at this point;
3.
Observations at 217 GHz (or performing a spectral component separation using observations at several frequencies) will provide us with a map where only kSZ and RS effects (as well as the CMB fluctuations) are present. In this map, we proceed to extract the RS component by computing the dipole ($\vec{d}$) and quadrupole ($\vec{Q}$) moments.
We will adopt here the following definitions for the multipole moments of a given 2-dimensional map, $M(\vec{x})$, with respect to the coordinate origin:

\begin{displaymath}% \vec{d}[M] = \int \frac{\vec{x}}{\vert\vec{x}\vert} M(\vec{x}) {\rm d}^2 x \end{displaymath} (20)


 \begin{displaymath}% Q_{ij}[M] = \int \frac{2 x_i x_j - \vert\vec{x}\vert^2 \delta_{ij}}{\vert\vec{x}\vert^2} M(\vec{x}) {\rm d}^2 x. \end{displaymath} (21)

Weighting in this way, we assure that we give equal weights to equal areas. Thus, this is a robust approach in the sense that it should tolerate some level of noise (CMB or instrumental).

For a 2D image, the $\vec{Q}$-matrix only has 2 independent elements because it is symmetric, and tr($\vec{Q}$) = 0. Thus, the matrix is specified by quoting Qxx and Qxy. However, the quadrupole matrix can be rotated to its principal axis, so that a single number characterises the matrix (one of the eigenvalues), plus an angle specifying the orientation of the principal axis. It is easy to show that the two eigenvalues for $\vec{Q}$ are $\pm \sqrt{Q_{xx}^2 + Q_{xy}^2}$, which suggests to introduce the total, coordinate independent quadrupole moment as $ Q = \sqrt{Q_{xx}^2 + Q_{xy}^2}$.

We will now illustrate how to extract information about the physical parameters describing the merger from the suggested recipe. For definiteness, we will assume here that we have two observational maps available, one of the Compton y-parameter ( $y(\vec{x})$), and another map of the brightness distribution on the sky at $\nu=217~{\rm GHz}$ ( $B_{217}(\vec{x})$). We will denote as ${\vec{Q}^{{\rm tSZ}}} \equiv \vec{Q}[y(\vec{x})]$ the quadrupole moment associated to the y-parameter map, and $\vec{Q}^{T} \equiv \vec{Q}[B_{217}(\vec{x})]$, the one associated to the thermal temperature fluctuation map ( $\vec{Q}^{T} = \vec{Q}^{{\rm RS}}+ \vec{Q}^{{\rm kSZ}} + \vec{Q}^{{\rm CMB}}$). We will start by considering the case of zero angular momentum, and neglecting the CMB contribution. These other cases will be discussed in the following two subsections.


  \begin{figure} \par\includegraphics[width=7.15cm,clip]{587fig3.eps} \end{figure} Figure 3: Dependence of the measured quadrupole (Qxx) on the projection angle $\hat{\i}$. These curves have been derived for the case of $M_1 = 10^{15}~M_\odot$ (left cluster), M2 = 5 $\times $ $10^{14}~M_\odot$ (right cluster), separation of 1 Mpc, $\phi _v = 0\hbox {$^\circ $ }$ and the clusters placed along the X-axis (so Q=|Qxx|) and we use $\hat{\i}= \theta_v$ (i.e. zero angular momentum). We performed the computation of the quadrupole in the whole image (quoted as "all''), and masking the region that in the y-parameter map has a signal above the 10% of the peak intensity (quoted as "outer''). We can see that when doing this, the quadrupole signal is dominated by the RS component. The flux is given in mJy, at the cross-over frequency of the tSZ effect ( $\nu=217~{\rm GHz}$). The merging system is assumed to be at $300~{\rm Mpc}$.
Open with DEXTER

In Fig. 3 we show the dependence of the observed quadrupole with the projection angle. The coordinate system has been placed at the "center-of-light'' of the y-parameter map, and the maps have been rotated so the cluster centres in the tSZ map lie along the X-axis (so we only quote Qxx because Qxy=0). Given that the weighting-factor in Eq. (21) is dimensionless, then  $\vec{Q}^{T}$ has units of flux, so in order to quote these values in mJy, we have assumed that the merging system is located at an angular distance of 300 Mpc. The map-size used for the computation of the quadrupole was 10.24 Mpc. This size has been used throughout the paper[*]. For illustration purposes, the signal coming from the RS and the kSZ components has been computed separately, although the observable is the sum of the two quantities. Given that the RS signal has a more extended pattern than the kSZ, we have used a mask based on the tSZ map in order to enhance the signal from the RS effect. In this example, this mask was obtained by tapering all pixels with a temperature in the y-parameter map larger than 10% of the peak temperature. We can see that when using this taper, the quadrupole becomes totally dominated by the RS contribution.

For illustration purposes, we also present in Fig. 4 the same plot but for the dipole modulus ( $d = \vert\vec{d}\vert = \sqrt{d_x^2 + d_y^2}$). We can see that this dipole signal is dominated by the kSZ contribution, and even when we mask 90% of the tSZ emission (note that the dipole signal from kSZ is also reduced by approximately the same factor) the signals from kSZ and RS are comparable, but in this latter case only for high values of the projection angle ( $\hat{\i}\ge 60\hbox{$^\circ$ }$). For (close to) face-on mergers, the kSZ contribution goes down because of the geometrical projection of the velocity ( $v_z \propto \cos \hat{\i}$) while the RS component is non zero ( $v_\perp \propto \sin \hat{\i}$). Therefore, as expected, we conclude that the quadrupole moment is better suited for the extraction of the RS signal, while the dipole moment is more suitable for the kSZ (or tSZ) component (note that when considering only the inner part of the map, where 90% of the tSZ emission comes from, then the dipole is totally dominated by the kSZ component).


  \begin{figure} \par\includegraphics[width=7.1cm,clip]{587fig4.eps} \end{figure} Figure 4: Dependence of the measured dipole modulus ( $d=\sqrt {d_x^2+d_y^2}$) with the projection angle $\hat{\i}$. We consider exactly the same case and notation as in Fig. 3, but here we also show the dipole signal from the region where the 90% of the tSZ emission comes from (quoted as "inner''), as well as the complementary "outer'' region.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.3cm,clip]{587fig5.eps} \end{figure} Figure 5: Dependence of the measured quadrupole (Qxx) on the separation between clusters. We consider the case $M_1 = 10^{15}~M_\odot$, M2 = 5 $\times $ $10^{14}~M_\odot$, $\phi _v = 0\hbox {$^\circ $ }$ (so Qyy=0) and we use $\hat{\i}= \theta_v=80\hbox{$^\circ$ }$ (zero angular momentum). Notation and units are the same as in Fig. 3. Separations are measured from the most massive to the less massive cluster, so in this picture a positive separation represents a pre-merger state, where the two clusters are approaching each other, while a negative separation represents a post-merger state.
Open with DEXTER

In Fig. 5 we show the dependence of Qxx on the physical separation, keeping fixed the other parameters. Here the separations are measured from M1 (the most massive cluster, i.e. the one with larger tSZ signal) to M2, and the velocity for M1 is taken to be pointing towards the positive direction of X axis. Within this picture, a positive separation (i.e. cluster M1 on the left) represents a pre-merger state, where the two clusters are approaching each other, while a negative separation (i.e. cluster M1 on the right) represents a post-merger state. Thus, we see that the sign of the quadrupole components carries information about the merger kinematics. We also stress here that tapering the central region of the map makes the quadrupole dominated by the RS signal. Finally, it is worth remarking that depending on the particular configuration of the merging system, the RS signal adds-up coherently or cancels in the computation of the quadrupole (or dipole), so we find that the outer region has a larger quadrupole-flux than the total map for some physical separations.

4.2 Characterising the angular momentum

The quadrupole pattern of the RS effect associated to merging clusters can also be used to learn about the angular momentum of the system, at least in the plane of the sky: it is clear from Figs. 1, 2 that the direction of cluster velocities conditions the nature of the quadrupole pattern imprinted by the RS effect.

This is the motivation of the following approach, which is entirely based in the computation of the moments of the kSZ, tSZ and RS components, and hence is well defined for any morphology of the system:

Taking as the origin of our coordinate frame the centre of tSZ-light of the system, the first angle should be related to the angle of the direction joining the centres of mass of each cluster ( $\alpha_{{\rm CM}}$). Indeed, we find that $\alpha_{\vec{Q}^{{\rm tSZ}}} \simeq \alpha_{{\rm CM}}$. In a similar way, the angle $\alpha_{\vec{Q}^{T}}$ is related to the direction of the individual velocities of the clusters via $\alpha_{\vec{Q}^{T}} \simeq \phi_{v}/2$. Thus, we can use the two observables given in Eqs. (22) and (23) to directly estimate the two physical angles  $\alpha_{{\rm CM}}$ and $\phi _v$.


  \begin{figure} \par\includegraphics[width=7.35cm,clip]{587fig6.eps}\end{figure} Figure 6: Recovery of $\phi _{v} - \alpha _{{\rm CM}}$ from $2 \alpha_{\vec{Q}^{T}} - \alpha_{\vec{Q}^{{\rm tSZ}}} $. Thick solid line excludes that area containing 90% of the tSZ emission, whereas thin solid line considers the entire map. The dotted line gives the expected scaling $2 \alpha_{\vec{Q}^{T}} - \alpha_{\vec{Q}^{{\rm tSZ}}} = \phi_v - \alpha_{{\rm CM}}$. A projection angle of $\hat{\i}= 60\hbox{$^\circ$ }$ was used in the calculation.
Open with DEXTER

This is illustrated in Fig. 6, where we use the cluster parameters { $M_1 = 10^{15}~M_\odot$, M2=5 $\times $ $10^{14}~M_\odot$, $\hat{\i}=\theta_v=60\hbox{$^\circ$ }$, $d=1~{\rm Mpc}$}, and we vary the azimuthal angle $\phi _v$ from 0 to $2\pi$ radians. The quadrupole induced by the kSZ component perturbs our estimate of $\phi _v$ from  $2 \alpha_{\vec{Q}^{T}}$ as it is shown in the figure. Note that the value of $\phi _v$ at which we have the maximum departure from the real value is not constant, but depends on the relative amplitude ratio of the kSZ and RS quadrupoles, i.e. depends on the other physical parameters of the merger. Finally, we again obtain better results for the case in which we mask out the area where 90% of the tSZ emission comes from, even for cases with low values of the projection angle.

With respect to the amplitude of the angular momentum, one can see that it is closely related to the cross component of the $\vec{Q}^{{\rm RS}}$tensor, provided the X-axis of our coordinate system is located along the axis joining the cluster centres, and its centre is the system centre of mass. In this reference frame, a merger with $\vec{J}=0$shows no $Q^{{\rm RS}}_{xy}$ component. Indeed, for the case of two point-like clusters, it can be shown that $Q^{{\rm RS}}_{xy} = J_z\; f(x_1,x_2)$, with x1,x2 the coordinates of the cluster centres, and Jz the projected component of the angular momentum along the Z-axis (see Appendix). Therefore, one can make use of the transformations of the components of the quadrupole under a rotation of the coordinate system by an angle $\alpha$,

 
    $\displaystyle {\tilde Q}_{xx} = \cos (2\alpha) \; Q_{xx} - \sin (2\alpha) \; Q_{xy}$  
    $\displaystyle {\tilde Q}_{xy} = \sin (2\alpha) \; Q_{xx} + \cos (2\alpha) \; Q_{xy},$ (24)

in order to relate Jz with the observable quantities (QTxx,QTxy) computed in an arbitrarily oriented reference frame. Using the observable $\alpha_{\vec{Q}^{{\rm tSZ}}}$ to estimate the orientation of the axis joining the cluster mass centres ( $\alpha_{{\rm CM}}$), then the quadrupole components in the reference system aligned with the mass centre axis can be computed from Eq. (24) using $\alpha=\alpha_{\vec{Q}^{{\rm tSZ}}}$. As we have seen above, for high values of the projection angle $\hat{\i}$, we have that ${\tilde Q}^{T}_{xy} \approx {\tilde Q}^{{\rm RS}}_{xy}$, and the latter is proportional to the magnitude of Jz. In Fig. 7 we illustrate this dependence of ${\tilde Q}^{{\rm RS}}_{xy}$versus the Z-projection of the angular momentum, for the same physical parameters as in Fig. 6.


  \begin{figure} \par\includegraphics[width=7.45cm,clip]{587fig7.eps}\end{figure} Figure 7: Dependence of |QTxy | with the absolute value of the projected component of the angular momentum, |Jz|. We use the same physical parameters of the previous figure, and computed for each value of $\phi _v$ the projected Z-component of the angular momentum (note that, for $\phi _v = 0\hbox {$^\circ $ }$ and $\phi _v=180\hbox {$^\circ $ }$, $\vec{J}=0$). Under the symmetry of our system (clusters along the X-axis), the kSZ residual affects mostly the QTxx values, leaving the crossed term  QTxy practically unaltered.
Open with DEXTER

4.3 Stacking of clusters

The RS effect produces only a small temperature fluctuation making it very hard to be measured at individual clusters. It is therefore worth to develop ideas on how to co-add the signals from a large sample of clusters leading to a statistical RS effect detection.

The simplest approach could be to co-add the quadrupole strength Q, which is always positive. However, there are two problems with this. First, the intrinsic CMB temperature fluctuations contribute also to Q, although their contribution can relatively accurately be estimated by measuring at non-cluster positions. Second, the kSZ effect imprints some quadrupole structure, which can not be completely masked away. Estimates of its strength are not possible from the observational data alone and therefore would rely on numerical simulations of galaxy cluster mergers in a cosmological setting.

We therefore propose a different approach to stack the signal from several clusters. First, the cluster should be rotated in a way that its major axis (of the tSZ effect or X-ray image) is aligned with the X-axis. Then, the quadrupole tensor of the temperature fluctuations $\vec{Q}^{T} = \vec{Q}^{{\rm CMB}} + \vec{Q}^{{\rm RS}} + \vec{Q}^{{\rm kSZ}}$ is calculated in this coordinate system and its components are co-added for all the clusters in the sample. We expect that for a sufficiently large number of clusters all contributions to $\vec{Q}^{T}$ cancel out due to symmetry properties except the ones from the RS effect.

The components of $\vec{Q}^{{\rm CMB}}$ have both signs with equal probability, since the CMB fluctuations are not correlated with the foreground cluster and the signs of quadrupole components are not rotational invariant (they reverse after a $90^\circ$ rotation). For the same reason, we expect that the lensing-induced cluster signal in the CMB (Seljak & Zaldarriaga 2000) will also cancel out, because the quadrupole moment is a linear function of the temperature fluctuations, for which we expect both signs with equal probability.

Also the components of $\vec{Q}^{{\rm kSZ}}$ have both signs with equal probability: mirroring a cluster through the X-Y plane going through its centre of mass reverses the sign of the kSZ map, and due to linearity also the sign of all $\vec{Q}^{{\rm kSZ}}$ components. Since a cluster and its mirrored counterpart are equally likely in the cluster sample, their contributions to the co-added quadrupole cancel each other statistically.

The components of $\vec{Q}^{{\rm RS}}$ have both signs with different probabilities. Since galaxy clusters are growing, one should find more clusters with converging velocity fields than with diverging ones. Diverging velocity fields should be present shortly after core passage of the dark matter clumps of two merging clusters. However, dynamical effects due to gravitational interactions (violent relaxation) should convert rapidly the organised bulk motion of the dark matter particles into an undirectional motion. This reduces the statistical contribution of diverging matter flows to the co-added $\vec{Q}^{T}$ compare to the contribution of the converging matter flows of early stage mergers.

For this reason, only a contribution from the RS effect due to the growing large-scale structure should survive statistically. However, there is one possible contamination to the described measurement scheme: any residual tSZ contamination to the temperature fluctuations is expected to be co-aligned with the major axis, and therefore to add coherently to $\vec{Q}^{T}$, unless they appear with both signs with equal probability. This point could be achieved by taking relativistic corrections to the tSZ effect into account.

Therefore, further theoretical investigations are required before this stacking method can be fully established. This issue will be addressed in a follow-up paper.

5 Conclusions

In this paper we have presented a formalism that can be easily incorporated to N-body simulation codes in order to predict the Rees-Sciama effect in merging systems of clusters of galaxies. For the typical range of velocities in those systems ($v/c \ll 1$), the obtained expression (Eq. (4)) can also be seen as a gravitational lensing effect produced by a moving lens.

Using simple modelling for the cluster merger, we have illustrated the morphology and symmetries of this effect, and we have developed a method to extract the signal, which should be applicable to realistic maps. This method is based on the computation of the (weighted) dipole and quadrupole moments of the brightness distribution. In particular, it has been shown how the quadrupole moment is related to the kinematic properties of the merger, so we can extract information about the dynamical state of the system: pre-merger or post-merger, and the magnitude of the angular momentum.

Since we expect that in the near future the observation of a single cluster merger will be extremely difficult, given the weak signal strength, we have proposed a simple method of stacking the signal from a large number of clusters in order to extract their RS signature statistically. The procedure is straight-forward: for a sample of clusters (e.g. a complete, or a merging cluster sample) a coordinate system is attached to the center of light (X-ray or tSZ map) so that the X-axis is aligned with the major elongation of the gas. Then the quadrupole moments of the CMB temperature fluctuations (outside the gas region, defined by the tSZ effect) are calculated for each cluster. Finally the individual quadrupole moment components are co-added for the sample. Intrinsic CMB fluctuations and kSZ effect residuals should cancel out statistically, leaving only a signature of the RS effect. A detailed investigation of this stacking method will be carried out in a follow-up paper.

Acknowledgements
We acknowledge useful comments by S. D. M. White and M. Bartelmann. J.A.R.M. and C.H.M. acknowledge the financial support provided through the European Community's Human Potential Programme under contract HPRN-CT-2002-00124, CMBNET. We thank an anonymous referee for useful comments.

Appendix A: Relationship between the quadrupole moment and the angular momentum

In this section, we prove that for two point-like clusters, $Q^{{\rm RS}}_{xy}$ is directly proportional to the component of the angular momentum projected along the line of sight, provided the coordinate origin is located at the mass centre of the system and the X-axis is aligned to the axis joining the clusters. Thus, the z=0 plane is the image plane.

Let us assume that the coordinates of clusters are given by ${\vec x}_i\equiv (x_i,0)$, for i=1,2. Their linear momenta will be labelled as ${\vec P}_i \equiv M_i {\vec v}_i$, i=1,2 and we set the total momentum of the system to zero, so ${\vec P}_1=-{\vec P}_2$. Also note that from the choice of the coordinate system, then ${\vec x}_1$ and  ${\vec x}_2$ are related. The xy component of the RS-induced quadrupole is then given by:

 \begin{displaymath}% Q^{{\rm RS}}_{xy}= \frac{-4G}{c^3}\int {\rm d}^2 x\; \int {... ...\vec{\cdot} \frac{{\vec x}-{\vec x'}}{({\vec x}-{\vec x'})^2}, \end{displaymath} (A.1)

with ${\tilde{\vec p}}_\perp({\vec x'})$ the projection on the z=0 plane of the LOS projected momentum density, given in Eq. (4). For our two point masses, we can take ${\tilde{\vec p}}_\perp ({\vec x'}) = {\vec P}_1 \delta_{\rm D} ({\vec x'}- {\vec x}_1) + {\vec P}_2 \delta_{\rm D} ({\vec x'}- {\vec x}_2) $, $\delta_{\rm D}$ denoting Dirac delta. It yields

 \begin{displaymath}% Q^{{\rm RS}}_{xy}= \frac{-8G}{c^3}\int {\rm d}^2 x \;\frac{... ...ec x}-{\vec x}_2}{\vert{\vec x}-{\vec x}_2\vert^2}\right]\cdot \end{displaymath} (A.2)

The scalar product in this equation can be decomposed in two terms:
 
                                  $\displaystyle % Q^{{\rm RS}}_{xy}$ = $\displaystyle \frac{-8G}{c^3}\int {\rm d}^2 x \; \frac{x y}{{\vec x}^2}\biggl\{ P_{1,x} \biggl( \frac{x-x_1}{(x-x_1)^2+y^2} - \frac{x-x_2}{(x-x_2)^2+y^2} \biggr)$  
    $\displaystyle + P_{1,y} \biggl( \frac{y}{(x-x_1)^2+y^2}\;- \frac{y}{(x-x_2)^2+y^2} \biggr) \biggr\}\cdot$ (A.3)

The term proportional to P1,x vanishes when integrating over y, because the integrand is an odd function on y. The remaining term can easily be rewritten as:
 
                               $\displaystyle % Q^{{\rm RS}}_{xy}$ = $\displaystyle J_z \; \frac{8G}{c^3}\int {\rm d}^2 x \;\frac{x\;y^2}{{\vec x}^2}$  
    $\displaystyle \times \biggl\{ \frac{(x_1-x+x_2-x)}{\left[(x-x_1)^2+y^2\right] \left[ (x-x_2)^2+y^2\right]} \biggr\},$ (A.4)

with $J_z \equiv -P_{1,y} (x_2 - x_1)$ the LOS projected component of the angular momentum. Therefore,

 \begin{displaymath}% Q^{{\rm RS}}_{xy}= J_z\; f(x_1,x_2), \end{displaymath} (A.5)

with f(x1,x2) a function depending exclusively on the geometry of the system.

References


Copyright ESO 2004