A&A 419, 335-343 (2004)
DOI: 10.1051/0004-6361:20040070
Wind accretion in binary stars
I. Mass accretion ratio
T. Nagae1 - K. Oka1 - T. Matsuda1 -
H. Fujiwara2 -
I. Hachisu3 -
H. M. J. Boffin4,5
1 - Department of Earth and Planetary Sciences, Kobe University,
Rokko-dai 1-1, Nada-ku, Kobe 657-8501, Japan
2 -
IBM Japan Ltd., Yamato-shi, Kanagawa 242-8502, Japan
3 -
Department of Earth Science and Astronomy, College of Arts
and Sciences, University of Tokyo, Komaba 3-8-1, Meguro-ku,
Tokyo 153-8902, Japan
4 -
Royal Observatory of Belgium, Av. Circulaire 3,
1180 Brussels, Belgium
5 -
European Southern Observatory,
Karl-Schwarzschild-Str. 2, 85738 Garching, Germany
Received 12 April 2002 / Accepted 16 February 2004
Abstract
Three-dimensional hydrodynamic calculations are performed in order to
investigate mass transfer in a close binary system, in which one
component undergoes mass loss through a wind.
The mass ratio is assumed to be unity. The radius of the
mass-losing star is taken to be about a quarter of the separation between
the two stars. Calculations are performed for gases with a ratio of
specific heats
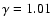 and 5/3. Mass loss is assumed to be
thermally driven so that the other parameter is the sound speed of the
gas on the mass-losing star.
and 5/3. Mass loss is assumed to be
thermally driven so that the other parameter is the sound speed of the
gas on the mass-losing star.
Here, we focus our attention on two features: flow patterns and mass
accretion ratio, which we define as the ratio of the mass accretion
rate onto the companion,
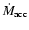 ,
to the mass loss rate
from the mass-losing primary star,
,
to the mass loss rate
from the mass-losing primary star,
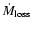 .
We characterize
the flow by the mean normal velocity of the wind on the critical Roche surface
of the mass-losing star,
.
We characterize
the flow by the mean normal velocity of the wind on the critical Roche surface
of the mass-losing star, 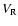 .
When
.
When
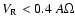 ,
where A and
,
where A and 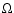 are the separation between the two stars and the
angular orbital frequency of the binary, respectively, we obtain
Roche-lobe over-flow (RLOF), while for
are the separation between the two stars and the
angular orbital frequency of the binary, respectively, we obtain
Roche-lobe over-flow (RLOF), while for
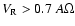 we observe
wind accretion.
We find very complex flow patterns in between these
two extreme cases. We derive an empirical formula of the mass accretion
ratio as
we observe
wind accretion.
We find very complex flow patterns in between these
two extreme cases. We derive an empirical formula of the mass accretion
ratio as
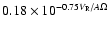 in the low velocity regime
and
in the low velocity regime
and
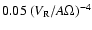 in the high velocity regime.
in the high velocity regime.
Key words: accretion, accretion disks - hydrodynamics - stars: binaries: general
Wind accretion plays an essential role especially in the evolution of
detached binary systems such as symbiotic stars, precursor of
peculiar red giants, 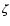 Auriga stars and massive X-ray binaries.
In the majority of symbiotic stars, the system contains a hot component -
believed to be a mass-gaining white dwarf - and a cool component, the
mass-losing red giant (e.g., Miko
Auriga stars and massive X-ray binaries.
In the majority of symbiotic stars, the system contains a hot component -
believed to be a mass-gaining white dwarf - and a cool component, the
mass-losing red giant (e.g., Miko ajewska 1997 for a review).
Recent studies indicate that many of the red giant
components in symbiotic stars do not fill their Roche lobe, i.e.,
ajewska 1997 for a review).
Recent studies indicate that many of the red giant
components in symbiotic stars do not fill their Roche lobe, i.e.,
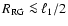 ,
where
,
where
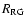 is the radius of
the red giant component and
is the radius of
the red giant component and 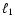 is the distance of the inner
Lagrangian point from the centre of the red giant
(e.g., Mürset & Schmid 1999).
This possibly discloses that symbiotic stars are - with probably
only the exception of T CrB (e.g., Anupama & Miko
is the distance of the inner
Lagrangian point from the centre of the red giant
(e.g., Mürset & Schmid 1999).
This possibly discloses that symbiotic stars are - with probably
only the exception of T CrB (e.g., Anupama & Miko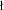 ajewska
1999) - well detached binary systems.
Thus, mass transfer in symbiotic stars seems to be driven by wind, and
wind mass loss is therefore a key ingredient for triggering symbiotic
activity on a white dwarf companion.
On the other hand, the mass accretion rates expected in the Bondi-Hoyle
picture (Bondi & Hoyle 1944) for such detached
binary systems are usually much lower than those required to maintain
the symbiotic activity of the systems.
For example, Nussbaumer (1991) pointed out that in most symbiotic
stars the typical rates of wind mass loss red giant are in the range
ajewska
1999) - well detached binary systems.
Thus, mass transfer in symbiotic stars seems to be driven by wind, and
wind mass loss is therefore a key ingredient for triggering symbiotic
activity on a white dwarf companion.
On the other hand, the mass accretion rates expected in the Bondi-Hoyle
picture (Bondi & Hoyle 1944) for such detached
binary systems are usually much lower than those required to maintain
the symbiotic activity of the systems.
For example, Nussbaumer (1991) pointed out that in most symbiotic
stars the typical rates of wind mass loss red giant are in the range
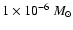 yr-1
to
yr-1
to
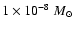 yr-1 and that
the expected accretion efficiency of wind capture is probably
no better than one percent. Hence, the accretion rates
associated with most symbiotic white dwarfs are probably
in the range of
yr-1 and that
the expected accretion efficiency of wind capture is probably
no better than one percent. Hence, the accretion rates
associated with most symbiotic white dwarfs are probably
in the range of
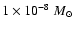 yr-1 to
yr-1 to
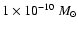 yr-1, which are too low to
power the typical luminosities of symbiotics (
yr-1, which are too low to
power the typical luminosities of symbiotics (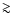
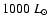 )
unless they are all in a late phase of hydrogen shell-flash (novae)
on a white dwarf (e.g., Sion & Ready 1992;
Sion & Starrfield 1994).
It will nevertheless be shown in the
present paper that the mass accretion rate is smaller than
that expected by a simple Bondi-Hoyle picture.
)
unless they are all in a late phase of hydrogen shell-flash (novae)
on a white dwarf (e.g., Sion & Ready 1992;
Sion & Starrfield 1994).
It will nevertheless be shown in the
present paper that the mass accretion rate is smaller than
that expected by a simple Bondi-Hoyle picture.
It has recently been suggested that some of the mass-accreting
white dwarfs in symbiotic stars are the progenitors of type Ia supernovae
(e.g., Hachisu & Kato 2001). On the other hand,
it has long been discussed that the efficiency, the ratio of the mass
captured by the white dwarf to the mass lost by the red giant, is very
small (say, a few per cent) and not enough to increase the white dwarf mass
to the Chandrasekhar mass limit (e.g., Kenyon et al.
1993).
Wind velocities in cool red giants are typically a few times 10 km s-1 and comparable to the orbital velocity in most symbiotic binary systems.
Therefore, flow patterns are probably something between Roche lobe
overflow (RLOF) and Bondi-Hoyle wind accretion kinds of flows.
The efficiency of capture in symbiotics should therefore not be estimated
by the Bondi-Hoyle picture but by direct simulations of intermediate,
complicated flow patterns.
Symbiotic stars are not the only systems in which wind accretion play a
significant role. The most adopted model for the formation of peculiar
red giants, barium, CH and S stars, require a binary system containing
an Asymptotic Giant Branch star (AGB) transferring mass via its stellar
wind to a main sequence companion which becomes polluted in carbon and
s-process elements (see e.g. Boffin & Jorissen 1988).
The AGB then evolve into a white dwarf while the companion will appear
as carbon or s-process rich and, when on the giant branch, as a peculiar
red giant. Boffin & Zacs (1994) have shown that an accretion
efficiency of only a few percent is enough to explain present Barium stars.
Objects related to these are the extrinsic S stars which also show
symbiotic activity (e.g. Carquillat et al. 1998) and bipolar
planetary nebulae (e.g. Mastrodemos & Morris 1998).
 Aurigae systems are another kind of system where wind accretion
plays a role. In these eclipsing double-lined binaries, a main sequence
star has an accretion wake produced by the wind of its K supergiant
companion. The eponymous system,
Aurigae systems are another kind of system where wind accretion
plays a role. In these eclipsing double-lined binaries, a main sequence
star has an accretion wake produced by the wind of its K supergiant
companion. The eponymous system,  Aur, is a binary with a 972 days
orbital period and containing a 5.8
Aur, is a binary with a 972 days
orbital period and containing a 5.8  K4 Ib and a 4.8
K4 Ib and a 4.8 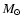 B5 V star (Bennett et al. 1996).
B5 V star (Bennett et al. 1996).
Finally, accretion wakes are also reported for high mass X-ray binaries (HMXB). These systems consist of a compact object, neutron star or black
hole, orbiting a massive OB primary star which has a strong stellar wind.
The X-ray emission is believed to be due to accretion of matter on the
compact companion.
There have been already many numerical studies of stellar wind in a close
binary system. Biermann (1971) computed
two-dimensional stellar wind using a characteristic method. Sorensen et al. (1975) performed two-dimensional
finite difference calculation of stellar wind emitted from a Roche lobe
filling secondary. They used the Fluid in Cell (FLIC) method with first
order of accuracy and a Cartesian grid. They computed Roche lobe overflow (RLOF) as well. Sawada et al. (1984)
calculated two-dimensional stellar wind from a contact binary using
a Beam-Warming time implicit finite difference scheme and a generalized
curvilinear coordinate. Their main goal was to compute the angular
momentum loss rate
from the system, which is an important factor to define the evolution of
the binary system. Sawada et al. (1986)
computed two-dimensional stellar wind from a semi-detached binary system
using the Osher upwind scheme and a generalized curvilinear coordinate.
They observed a transition from RLOF to stellar wind by increasing the wind
speed on the mass-losing star. The present study is a three-dimensional
version of their study. Matsuda et al.
(1987) also conducted a similar study and
discovered a flip-flop instability of the bow shock formed around a
compact mass accreting object (see also Boffin & Anzer 1994,
and on the stability issue, Foglizzo & Ruffert 1997, 1999, and
Pogolerov et al. 2000).
However, it was found that the phenomenon was characteristic to
two-dimensional case (Matsuda et al. 1992;
Ruffert 1996). In the present work we perform
three-dimensional calculation in which we do not observe the flip-flop
instability.
These simulations concerned the case of a compact object moving in a
wind and were mostly aimed at estimating the validity of the Bondi-Hoyle
accretion rate. Binary effects were partially simulated by including
velocity or density gradient in the wind. There are a few simulations
however which simulate in full mass transfer by wind in a binary system
(Blondin et al. 1991; Theuns & Jorissen 1993; Blondin & Woo 1995;
Theuns et al. 1996; Walder 1997; Mastrodemos & Morris 1998; Dumm et al.
2000; Boroson et al. 2001;
Gawryszczak et al. 2002).
Theuns & Jorissen (1993) and Theuns et al. (1996, TBJ96 in the following) performed
three-dimensional hydrodynamic simulations of a 3 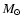 AGB transferring mass through its stellar wind to a 1.5
AGB transferring mass through its stellar wind to a 1.5 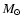 main
sequence companion, in order to test the wind accretion model for the
origin of peculiar red giants. They performed simulations using a
polytropic equation of state with
main
sequence companion, in order to test the wind accretion model for the
origin of peculiar red giants. They performed simulations using a
polytropic equation of state with
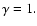 , 1.1 and 1.5 and found mass
accretion ratios (that is, mass accretion rate/mass loss rate)
of 1-2% for the
, 1.1 and 1.5 and found mass
accretion ratios (that is, mass accretion rate/mass loss rate)
of 1-2% for the
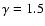 case and 8% for the
other models, i.e. about ten times smaller than the theoretical Bondi-Hoyle
estimate. They also observed that this value is dependent on resolution.
case and 8% for the
other models, i.e. about ten times smaller than the theoretical Bondi-Hoyle
estimate. They also observed that this value is dependent on resolution.
Walder (1997) presented simulations of wind accretion in well separated
binaries for three different cases: a HMXB, 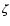 Aur and a barium star
progenitor. He obtains mass accretion ratio
(mass accretion rate/mass loss rate) of 0.6, 3 and 6%,
respectively. Walder & Folini (2000) also presented a nice review of
wind dynamics in symbiotics binaries, with an emphasis on the influence
of the radiation field of the accretor.
Aur and a barium star
progenitor. He obtains mass accretion ratio
(mass accretion rate/mass loss rate) of 0.6, 3 and 6%,
respectively. Walder & Folini (2000) also presented a nice review of
wind dynamics in symbiotics binaries, with an emphasis on the influence
of the radiation field of the accretor.
More recently, Dumm et al. (2000) presented three-dimensional
Eulerian isothermal simulations in order to represent the symbiotic system
RW Hya which seems to present an accretion wake, as indicated by the
reduced UV flux observed at phase
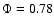 .
They found that 6% of
the M-giant wind is captured by the companion.
.
They found that 6% of
the M-giant wind is captured by the companion.
In this paper we perform three-dimensional numerical simulations of mass
transfer by wind in a binary system with a mass ratio of unity. The full
gravitational forces of the two components are taken into account.
This is therefore different from the e.g. TBJ96 or Dumm et al. (2000)
studies, where in order to account for the not very well known acceleration
mechanism of the wind, the gravitational force of the primary is partially
or totally reduced.
Here, we will concentrate on the derivation of the mass accretion
ratio.
We will leave for a following paper the physical discussion of the
flow, including a discussion of angular momentum loss from the system.
Consider a detached binary system of equal mass: one larger star
blows stellar wind which the other, more compact, component partly
accretes.
We normalize the length by the separation of the two stars, A, and the
time by 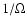 ,
where
,
where 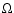 is the angular velocity of the binary
system. The surface of the mass-losing star is assumed to be an
equi-potential surface, whose mean radius is 0.25. The radius
of the mass accreting star is assumed to be 0.015 or smaller.
is the angular velocity of the binary
system. The surface of the mass-losing star is assumed to be an
equi-potential surface, whose mean radius is 0.25. The radius
of the mass accreting star is assumed to be 0.015 or smaller.
From an OB star, stellar wind is mainly accelerated by line
absorption of UV radiation. In symbiotic stars or in precursors of
peculiar red giants (PPRGs), the stellar wind mechanism
from the cool star is poorly known, and may imply radiation onto dust
grains. One needs however to still bring the matter far enough away from
the star so that dust grains can form. In more evolved red giants,
this may be done through the effect of pulsation. It is however still not
clear what
the mechanism could be in non-pulsating red giants, as they seem to exist
in some symbiotic or extrinsic S stars.
It is therefore clear that simplifying assumption have to be made.
In the present study, we will thus simply assume that
the wind is generated by thermal pressure, like in the solar wind.
More complicated wind structures will be studied in a forthcoming paper.
We assume that the gas is an ideal one and is characterized by the ratio of
specific heats, 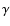 .
In the present work we consider two extreme
cases:
.
In the present work we consider two extreme
cases:
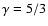 and
and
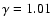 .
In the latter case, the gas is
almost isothermal except where there are shocks. This isothermality may
be explained as an outcome of good thermal conduction. We neglect other
complex effects like magnetic fields, radiation and viscosity
(except numerical one).
.
In the latter case, the gas is
almost isothermal except where there are shocks. This isothermality may
be explained as an outcome of good thermal conduction. We neglect other
complex effects like magnetic fields, radiation and viscosity
(except numerical one).
We have carried out our simulations for the case of a mass ratio unity.
Although this may not be representative for PPRGs, symbiotic stars or HMXBs, this should not change very much our results.
We solve the three-dimensional Euler equations using a finite volume
scheme. As Riemann solver, we use the SFS scheme and we apply the MUSCL method to interpolate physical variables in a cell; the details
on the scheme is described in Makita et al.
(2000), and RLOF simulations using the same method are
given in Fujiwara et al. (2001).
Calculations are done in the rotating frame of a binary and include the
gravity of the two stars, the centrifugal and Coriolis forces.
We use a Cartesian coordinate with the origin at the mass accreting star.
The computational region is
-1.5<x<0.5,
-0.5<y<0.5, 0<z<0.5 and
we assume symmetry around the orbital plane (Fig. 1).
The region is divided into
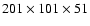 cells.
The mass accreting companion star is represented by a cubic hole with
cells of
cells.
The mass accreting companion star is represented by a cubic hole with
cells of
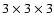 ,
including the lower half of the hole
under the orbital plane. Its physical dimension is
,
including the lower half of the hole
under the orbital plane. Its physical dimension is
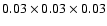 in our units.
in our units.
In order to study in details the structure of the flow near the mass
accreting object, we introduce a three levels nested grid. At the
second level, the region
-0.25<x<0.25,
-0.25<y<0.25 and 0<z<0.25 is
further divided into
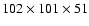 cells. At the third
level, the region
-0.125<x<0.125,
-0.125<y<0.125 and 0<z<0.125 is
once more divided into
cells. At the third
level, the region
-0.125<x<0.125,
-0.125<y<0.125 and 0<z<0.125 is
once more divided into
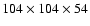 cells. The cell size
of the third level is thus 1/4 of the original first level cell. The hole
of
cells. The cell size
of the third level is thus 1/4 of the original first level cell. The hole
of
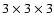 ,
in the first level, is represented
by a hole with
,
in the first level, is represented
by a hole with
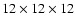 cells in the third level.
cells in the third level.
A typical symbiotic star, 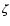 Auriga or PPRG has an orbital period of
a few years and a separation of a few AU. In this case, the cell size of 0.03 is of the order or even larger than a main sequence star.
This is thus applicable for
Auriga or PPRG has an orbital period of
a few years and a separation of a few AU. In this case, the cell size of 0.03 is of the order or even larger than a main sequence star.
This is thus applicable for 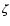 Aurigae or PPRGs. For S or symbiotic
stars, we should simulate the case of an accreting white dwarf. This would
require a hole about 100 times smaller. This is well beyond present days
numerical capabilities. This is also true if one would like to simulate
the compact accreting object in HMXBs.
Aurigae or PPRGs. For S or symbiotic
stars, we should simulate the case of an accreting white dwarf. This would
require a hole about 100 times smaller. This is well beyond present days
numerical capabilities. This is also true if one would like to simulate
the compact accreting object in HMXBs.
One should note however that the size of our accreting object is still
smaller than the one adopted by e.g. TBJ96. They have shown that the mass
accretion rate decreases with decreasing accreting size and our value is
similar to their highest resolution model. We thus also consider a case
of a hole having a size of
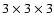 cells
(i.e. of physical dimensions
cells
(i.e. of physical dimensions 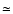
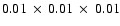 )
at the
third level in order to investigate the effect of the size of the mass
accreting object on the results.
)
at the
third level in order to investigate the effect of the size of the mass
accreting object on the results.
Table 1:
Model parameters. The parameters 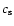 ,
,
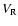 and f
are the sound speed on the surface of the mass losing star,
the normal velocity at the critical Roche surface and the
mass accretion ratio.
and f
are the sound speed on the surface of the mass losing star,
the normal velocity at the critical Roche surface and the
mass accretion ratio.
The outer parts of the mass-losing star is filled by a gas of
density 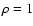 and sound speed
and sound speed 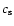 .
If the pressure inside the
mass-losing star is larger than that outside the mass-losing star,
gas is ejected from the surface. The velocity of the ejected gas is
computed by solving a Riemann problem between the two states.
.
If the pressure inside the
mass-losing star is larger than that outside the mass-losing star,
gas is ejected from the surface. The velocity of the ejected gas is
computed by solving a Riemann problem between the two states.
At t=0 the computational region except the mass-losing star is filled
by a tenuous gas with density
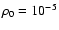 ,
velocity
u0=v0=w0=0
and pressure
,
velocity
u0=v0=w0=0
and pressure
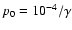 .
The computational region is gradually
filled with the gas ejected from the mass-losing star. The outside
of the computational region is filled by the initial gas all the time.
Mass outflow/inflow from the outer boundary can occur; the amount of
outflow/inflow is also calculated by solving Riemann problems between two
states. This (outside) boundary condition, which we call the ambient
condition, insures the stability of the computation.
The inside of the mass accreting hole is almost vacuum and the gas
approaching the hole is absorbed.
.
The computational region is gradually
filled with the gas ejected from the mass-losing star. The outside
of the computational region is filled by the initial gas all the time.
Mass outflow/inflow from the outer boundary can occur; the amount of
outflow/inflow is also calculated by solving Riemann problems between two
states. This (outside) boundary condition, which we call the ambient
condition, insures the stability of the computation.
The inside of the mass accreting hole is almost vacuum and the gas
approaching the hole is absorbed.
We start the calculation at t=0 and terminate it when the system becomes
steady. In the wind cases half an orbital period is enough to reach
a steady state, but in the RLOF cases we have to calculate at least
a few orbital periods.
As was described earlier, we adopt 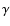 and the dimensionless sound
speed of gas in the mass-losing star,
and the dimensionless sound
speed of gas in the mass-losing star, 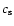 ,
as the model parameters.
In the present work, we consider the cases of
,
as the model parameters.
In the present work, we consider the cases of
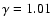 and
and
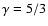 .
When
.
When 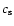 is less than some critical value, we expect
RLOF type flows, while in the other cases, we expect stellar wind kind
of flows. As is shown in Table 1, we study the cases of
is less than some critical value, we expect
RLOF type flows, while in the other cases, we expect stellar wind kind
of flows. As is shown in Table 1, we study the cases of
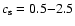 for
for
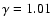 ,
and
,
and
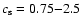 for
for
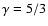 .
.
In PPRGs and symbiotic stars, the sound speed at the surface of the
mass-losing giant is of the order of 5-20 kms-1 while the orbital
velocity is of the order of 10-40 kms-1. In  Aurigae, both
these values are around 40-100 kms-1, while in HMXBs, the wind speed
is of the order of a few thousands of kms-1 while the orbital
velocity is several hundreds of kms-1.
Aurigae, both
these values are around 40-100 kms-1, while in HMXBs, the wind speed
is of the order of a few thousands of kms-1 while the orbital
velocity is several hundreds of kms-1.
The parameter 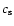 has no physical significance, because the mean radius,
0.25, of the mass losing star is chosen arbitrarily for numerical
purposes. Using the results of our numerical simulations, we therefore
calculate the mean value of the vertical component
of the gas speed on the critical Roche surface,
has no physical significance, because the mean radius,
0.25, of the mass losing star is chosen arbitrarily for numerical
purposes. Using the results of our numerical simulations, we therefore
calculate the mean value of the vertical component
of the gas speed on the critical Roche surface, 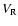 .
We classify the flow
pattern using
.
We classify the flow
pattern using 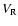 ,
which is shown in Table 1 as well.
It has to be emphasized that
,
which is shown in Table 1 as well.
It has to be emphasized that 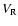 is not constant along
the critical Roche surface, especially in the Roche lobe type of flows. For
these, it may be better to use
is not constant along
the critical Roche surface, especially in the Roche lobe type of flows. For
these, it may be better to use 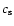 as a parameter. For the wind accretion
type of flow, which are more isotropic,
as a parameter. For the wind accretion
type of flow, which are more isotropic, 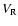 is more appropriate.
is more appropriate.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig2.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg79.gif) |
Figure 2:
Density contours in the orbital plane of the typical RLOF
case, but in a semi-detached binary system
(
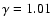 , ,
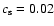 ). ). |
| Open with DEXTER |
In a typical Roche lobe overflow (RLOF), gas on the surface of the
companion flows through the L1 point and forms a narrow L1 stream. The L1 stream deflects its motion to the negative y direction in the present
configuration due to the Colioris force, and then circulates
counterclockwise around the mass-accreting star to form an accretion
disc.
We show an example of such typical ROLF flow in the case of
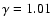 in Figs. 2 and 3. Here we assumed the star to fill its
Roche lobe, so this is not the main aim of this paper. They will serve as
comparison for the B-D and a cases discussed below.
in Figs. 2 and 3. Here we assumed the star to fill its
Roche lobe, so this is not the main aim of this paper. They will serve as
comparison for the B-D and a cases discussed below.
If the temperature of the surface of the companion star, 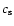 ,
is raised, the L1 stream becomes thicker (Fujiwara et al.
2001). We define the flow to be of the RLOF type if
the flow circulates around the accreting object in counterclockwise
direction.
,
is raised, the L1 stream becomes thicker (Fujiwara et al.
2001). We define the flow to be of the RLOF type if
the flow circulates around the accreting object in counterclockwise
direction.
If we raise 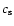 further, the gas escapes from the mass losing star in all
directions, and part of the gas rotates in a clockwise direction around the
companion. These two flows, rotating counterclockwise and clockwise,
collide behind (i.e. to the right) the accreting object to form
a bow shock. This is a typical wind accretion flow.
further, the gas escapes from the mass losing star in all
directions, and part of the gas rotates in a clockwise direction around the
companion. These two flows, rotating counterclockwise and clockwise,
collide behind (i.e. to the right) the accreting object to form
a bow shock. This is a typical wind accretion flow.
In the B-D cases for
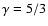 and the a case for
and the a case for
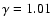 ,
we see from Table 1 that
,
we see from Table 1 that
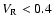 ,
i.e.
,
i.e. 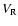 is smaller
than the escape velocity. The flow is of the RLOF type.
Similar types of flows have been obtained by other authors,
e.g. Bisikalo et al. (1998).
is smaller
than the escape velocity. The flow is of the RLOF type.
Similar types of flows have been obtained by other authors,
e.g. Bisikalo et al. (1998).
Figure 4 shows the density contours for model B
(
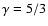 ,
,
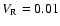 ), and Fig. 5 depicts the streamlines
for the same case.
In this case, since
), and Fig. 5 depicts the streamlines
for the same case.
In this case, since
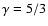 ,
the temperature
of the disc is so hot that the mass accretion ratio f, which is defined
in Sect. 3.6, is not 1 but 0.34. Spiral shocks, typical of RLOF flows (Makita et al. 2000; Matsuda et al.
2000; Fujiwara et al. 2001)
are not seen in this case.
,
the temperature
of the disc is so hot that the mass accretion ratio f, which is defined
in Sect. 3.6, is not 1 but 0.34. Spiral shocks, typical of RLOF flows (Makita et al. 2000; Matsuda et al.
2000; Fujiwara et al. 2001)
are not seen in this case.
One should note that contrarily to the impression one might have
when just looking at the figures, we have checked that there is no inflow
from the outer boundaries in these simulations.
Figure 6 shows the comparison of model a
(
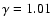 ,
,
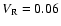 )
and D (
)
and D (
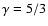 ,
,
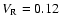 ).
We observe spiral shocks, although with a very much distorted shape.
).
We observe spiral shocks, although with a very much distorted shape.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig3.eps}
\par\end{figure}](/articles/aa/full/2004/19/aa2571/Timg81.gif) |
Figure 3:
Streamlines and Mach number counters of the typical RLOF case
(
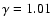 , ,
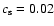 ). ). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig4.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg82.gif) |
Figure 4:
Density contours in the orbital plane of the RLOF type flow of
model B (
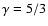 , ,
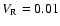 ). The left circle shows the
mass losing companion star with a radius of 0.25, and the
right black dot indicates the mass accreting object with
a radius of 0.015. ). The left circle shows the
mass losing companion star with a radius of 0.25, and the
right black dot indicates the mass accreting object with
a radius of 0.015. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig5.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg83.gif) |
Figure 5:
Streamlines and Mach number contours in the orbital
plane of the same model B as in Fig. 2. The Mach
number contours are represented by the shade, and the numbers
in the figure show typical Mach numbers. Streamlines are
generated from points separated by the same distance. We observe
that the flow rotates counterclockwise around the companion,
which is a typical feature of RLOF type flows. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig6.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg84.gif) |
Figure 6:
Comparison of two RLOF type flows. Density contours in the
orbital plane are shown. Left: model a (
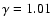 , ,
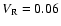 ); right: model D ( ); right: model D (
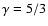 , ,
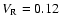 ).
We observe spiral shocks which are typical to RLOF. ).
We observe spiral shocks which are typical to RLOF. |
| Open with DEXTER |
In the cases E, b and b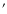 ,
we observe that
,
we observe that
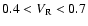 .
In these cases, the flow is not a typical RLOF or a wind accretion flow,
but rather a very complicated intermediate one. Figure 7 shows
the density contours of model E, and Fig. 8 depicts the
streamlines of the same model.
.
In these cases, the flow is not a typical RLOF or a wind accretion flow,
but rather a very complicated intermediate one. Figure 7 shows
the density contours of model E, and Fig. 8 depicts the
streamlines of the same model.
Figure 9 shows the density contours and the streamlines of the case b.
We find that the flow pattern and the shock structure
are very complicated in these intermediate flow.
We will now speculate on the possible cause of the complicated structure of
the intermediate flow. Gas
flows from the mass-losing star (left sphere) towards the mass accreting
object (right small sphere). The lower part of the flow experiences a
shock, and is decelerated to subsonic speed. A small accretion disc is
formed around the companion, but some part of the gas is accelerated to
supersonic velocity again. It collides with the gas coming from the
positive y side and forms a bow shock. The orientation of the bow shock
is rotated almost 90 degrees counterclockwise.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig7.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg86.gif) |
Figure 7:
Density contours in the orbital plane of the model E
(
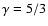 , ,
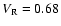 ). We observe very complicated shock
patterns. ). We observe very complicated shock
patterns. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig8.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg87.gif) |
Figure 8:
Streamlines and Mach number contours in the orbital
plane of the same model E as in Fig. 7. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig9.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg88.gif) |
Figure 9:
Density contours and stream lines in the orbital plane of
the model b (
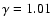 , ,
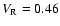 ). ). |
| Open with DEXTER |
For the cases with
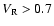 ,
which are all the other models than stated
above, the gas ejected from the mass-losing star is accelerated by
thermal pressure. Almost all the gas escapes from the system and only
a small part of the gas is accreted by the companion. We find a typical
conical bow shock attached to the accreting object. Figures 11 and 12 show the density distribution,
the streamlines and the magnitude of the velocity for model g
(
,
which are all the other models than stated
above, the gas ejected from the mass-losing star is accelerated by
thermal pressure. Almost all the gas escapes from the system and only
a small part of the gas is accreted by the companion. We find a typical
conical bow shock attached to the accreting object. Figures 11 and 12 show the density distribution,
the streamlines and the magnitude of the velocity for model g
(
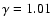 ,
,
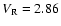 ).
).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig10.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg90.gif) |
Figure 10:
A schematic diagram of an intermediate flow model E. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig11.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg91.gif) |
Figure 11:
Density contours in the orbital plane of a typical wind
accretion flow model g (
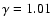 , ,
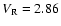 ). We observe
a conical bow shock attached to the accreting object, which is
a typical feature of the wind accretion flow. ). We observe
a conical bow shock attached to the accreting object, which is
a typical feature of the wind accretion flow. |
| Open with DEXTER |
In order to test the effect of resolution near the mass accreting
object, we calculate the flow using the nested grid described above. Figure 13 shows the density contours for model g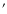 .
If we compare
the result of model g
.
If we compare
the result of model g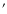 with that of model g, we can see a slight
oscillation on the bow shock for model g
with that of model g, we can see a slight
oscillation on the bow shock for model g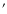 .
Nevertheless,
the essential features are unchanged except for the mass accretion
efficiency.
.
Nevertheless,
the essential features are unchanged except for the mass accretion
efficiency.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig12.eps} \end{figure}](/articles/aa/full/2004/19/aa2571/Timg92.gif) |
Figure 12:
Stream lines of the model g as in Fig. 11.
Numbers are magnitude of normalized velocity. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig13.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg93.gif) |
Figure 13:
Density contours of the model g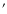 (
(
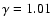 , ,
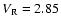 )
calculated on the nested grid.
Two blow-ups close to the accreting star are shown.
Compare the present figure with Fig. 11. We observe
that the bow shock is slightly jaggy compared with Fig. 10.
This is due to the reduced numerical viscosity. )
calculated on the nested grid.
Two blow-ups close to the accreting star are shown.
Compare the present figure with Fig. 11. We observe
that the bow shock is slightly jaggy compared with Fig. 10.
This is due to the reduced numerical viscosity. |
| Open with DEXTER |
3.6 Mass accretion ratio
We calculate the mass accretion ratio f, which is defined as the ratio
of the mass accreting rate onto the companion,
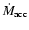 ,
to the mass loss rate from the mass losing star,
,
to the mass loss rate from the mass losing star,
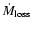 .
The mass accretion ratio as a function of
.
The mass accretion ratio as a function of 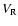 is shown in Fig. 14. The dash-dotted line is an empirical formula
is shown in Fig. 14. The dash-dotted line is an empirical formula
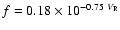 ,
which is valid in the range
,
which is valid in the range
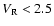 .
.
In typical wind case we found that f is less than 1%, and decreases
further with increasing 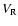 although it seems to saturate (but see below).
In the intermediate flow regime, f is about
a few% to 10%. For RLOF f is greater than 10% for
although it seems to saturate (but see below).
In the intermediate flow regime, f is about
a few% to 10%. For RLOF f is greater than 10% for
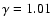 .
If we use the above empirical formula to the limit of
.
If we use the above empirical formula to the limit of
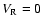 ,
we have f=0.18. Of course, this is not necessary true and f=1 is also possible.
Although a direct comparison is not possible, our values are in good
agreement with the results obtained by TBJ96, Walder (1997),
Mastrodemos & Morris (1998) or Dumm et al. (2000).
,
we have f=0.18. Of course, this is not necessary true and f=1 is also possible.
Although a direct comparison is not possible, our values are in good
agreement with the results obtained by TBJ96, Walder (1997),
Mastrodemos & Morris (1998) or Dumm et al. (2000).
The curve of the calculated accretion ratio based on the coarse grid has
a kink about
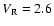 .
This may be due to the fact that the size of
the accreting cubic box may be comparable to or larger than the accretion
radius. In order to see the effect, we reduced the size of the inner box.
We found that the position of the kink is shifted towards larger
.
This may be due to the fact that the size of
the accreting cubic box may be comparable to or larger than the accretion
radius. In order to see the effect, we reduced the size of the inner box.
We found that the position of the kink is shifted towards larger 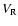 ,
and the accretion ratio is reduced. This again is in agreement with the
analysis done by TBJ96.
,
and the accretion ratio is reduced. This again is in agreement with the
analysis done by TBJ96.
![\begin{figure}
\par\includegraphics[width=8.8cm]{nagae-fig14.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg98.gif) |
Figure 14:
Mass accretion ratio, defined by the ratio of the mass
accretion rate to the mass loss rate, as a function of 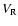 .
The horizontal axis is .
The horizontal axis is 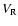 and the vertical one is
the mass accretion ratio. The dash-dotted line
is our empirical formula for the mass accretion ratio:
and the vertical one is
the mass accretion ratio. The dash-dotted line
is our empirical formula for the mass accretion ratio:
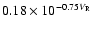 ,
while the upper line is the fit valid for large ,
while the upper line is the fit valid for large 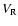 . .
|
| Open with DEXTER |
For high wind velocity, we expect the Hoyle-Lyttleton theory of wind accretion
(Hoyle & Lyttleton 1939), that is the case where pressure force is neglected, to be applicable.
If it is the case, then the mass accretion rate
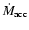 must be
proportional to the square of the mass accretion radius,
must be
proportional to the square of the mass accretion radius,
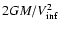 - with
- with 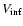 being the wind velocity at infinity,
and so we expect that
being the wind velocity at infinity,
and so we expect that
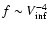 .
Assuming a spherical symmetric
wind around the mass-losing component, we have
.
Assuming a spherical symmetric
wind around the mass-losing component, we have
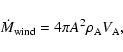 |
(1) |
near the mass-accreting component. For a high wind velocity, we may
expect that the accretion is determined by Hoyle & Lyttleton's
formula, i.e.,
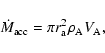 |
(2) |
and the accretion radius 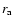 is given by
is given by
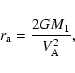 |
(3) |
where
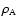 is the mass density,
is the mass density, 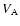 is the wind velocity
measured on the rotating flame,
both
at the mass accreting component, M1 is the mass of the mass-accreting
component. Therefore, the accretion ratio is calculated from
is the wind velocity
measured on the rotating flame,
both
at the mass accreting component, M1 is the mass of the mass-accreting
component. Therefore, the accretion ratio is calculated from
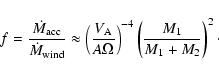 |
(4) |
Here, we use Kepler's relation of
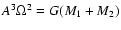 and M2 is the mass of the mass-losing component.
For the present case of equal mass, the accretion ratio becomes
and M2 is the mass of the mass-losing component.
For the present case of equal mass, the accretion ratio becomes
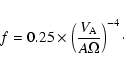 |
(5) |
Note that we checked that the wind velocity does not change by a noticeable amount between the
Roche lobe surface of the companion to the position of the primary. Hence, we can put
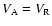 in the above equation.
in the above equation.
In Fig. 15 we show the accretion ratio as a function of
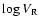 .
The upper line shows the simple Hoyle-Lyttleton formula as given by Eq. (5). The lower line
shows another experimental formula
.
The upper line shows the simple Hoyle-Lyttleton formula as given by Eq. (5). The lower line
shows another experimental formula
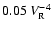 ,
which
agrees well with the calculated results for higher
,
which
agrees well with the calculated results for higher 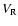 .
It appears thus
that the calculated mass accretion efficiency is about 20%
of the predicted one.
Such a comparison is however not fair for at least three reasons.
First, because we take into account pressure, one should not use
Hoyle-Lyttleton relation but rather the Bondi-Hoyle formula, and include
the sound speed.
Second, because our wind is thermally driven and we are in a binary
system, it is not obvious at all to determine which wind velocity should be
inserted in the equation.
In the Hoyle-Lyttleton formalism, the velocity which is inserted is the
upstream wind velocity at infinity. This is clearly meaningless in a close
binary where the wind may not have reached its terminal velocity while
close to the companion.
Third, our wind is a diverging flow from the mass losing star, which contradicts
the parallel upstream flow assumed in the Hoyle-Lyttleton or Bondi-Hoyle treatment.
Therefore the use of the Hoyle-Lyttleton or Bondi-Hoyle formalism can
be justified only qualitatively.
.
It appears thus
that the calculated mass accretion efficiency is about 20%
of the predicted one.
Such a comparison is however not fair for at least three reasons.
First, because we take into account pressure, one should not use
Hoyle-Lyttleton relation but rather the Bondi-Hoyle formula, and include
the sound speed.
Second, because our wind is thermally driven and we are in a binary
system, it is not obvious at all to determine which wind velocity should be
inserted in the equation.
In the Hoyle-Lyttleton formalism, the velocity which is inserted is the
upstream wind velocity at infinity. This is clearly meaningless in a close
binary where the wind may not have reached its terminal velocity while
close to the companion.
Third, our wind is a diverging flow from the mass losing star, which contradicts
the parallel upstream flow assumed in the Hoyle-Lyttleton or Bondi-Hoyle treatment.
Therefore the use of the Hoyle-Lyttleton or Bondi-Hoyle formalism can
be justified only qualitatively.
![\begin{figure}
\par\includegraphics[width=8.8cm]{nagae-fig15.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg115.gif) |
Figure 15:
Log-log plot of the Mass accretion ratio as a function of the
wind velocity at the position of the Roche lobe. The
upper line shows a simple Hoyle-Lyttleton formula as given
by Eq. (5).
The lower line shows another
empirical formula
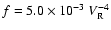 . . |
| Open with DEXTER |
We monitored the time variation of the mass accretion ratio. For
intermediate flows the amplitude of time variation is about 30% for
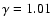 and it is about 70% for
and it is about 70% for
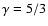 .
This trend that the
amplitude of oscillation is larger for larger
.
This trend that the
amplitude of oscillation is larger for larger 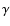 is applicable to
other cases. For larger
is applicable to
other cases. For larger 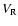 cases the oscillation is negligible. In Fig. 14, the error bars show the amplitude of the oscillation
of the mass accretion ratio. As was discussed above, the amplitude is
larger for the finer grid because of the reduction of the numerical
viscosity. By decreasing the size of the accreting box, we increase the
range in
cases the oscillation is negligible. In Fig. 14, the error bars show the amplitude of the oscillation
of the mass accretion ratio. As was discussed above, the amplitude is
larger for the finer grid because of the reduction of the numerical
viscosity. By decreasing the size of the accreting box, we increase the
range in 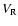 showing time variability. We Fourier analyzed the time
sequence of mass accretion and did not find any typical frequency.
showing time variability. We Fourier analyzed the time
sequence of mass accretion and did not find any typical frequency.
- 1.
- The flow pattern is classified by means of the normal speed of gas
on the critical Roche surface,
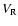 .
For
.
For
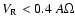 ,
we have a RLOF
type flow, while for
,
we have a RLOF
type flow, while for
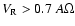 ,
wind accretion flows are realized.
In the intermediate parameter range,
,
wind accretion flows are realized.
In the intermediate parameter range,
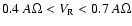 ,
we
observe very complex flows.
,
we
observe very complex flows.
- 2.
- We construct an
empirical formula for the mass accretion ratio given by
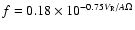 ,
valid for low
,
valid for low 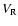 .
.
- 3.
- The calculated mass accretion ratio shows a kink at
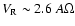 .
By using the nested grid, we found that this is
because the assumed size of the mass-accreting box is comparable to or
larger than the accretion radius. By reducing the size of the
mass-accreting box for the nested grid, the position of the kink is
shifted to larger
.
By using the nested grid, we found that this is
because the assumed size of the mass-accreting box is comparable to or
larger than the accretion radius. By reducing the size of the
mass-accreting box for the nested grid, the position of the kink is
shifted to larger 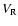 .
.
- 4.
- For larger
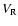 we obtain another empirical formula for the mass
accretion ratio
we obtain another empirical formula for the mass
accretion ratio
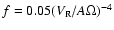 .
.
- 5.
- For typical wind accretion flow, the results based on the coarse
grid and those of the nested grid are essentially the same except the mass
accretion ratio described above. For intermediate flow, the computed flow
pattern depends on the resolution slightly. The amplitude of the
oscillation of the flow increases with increased resolution because of
reduced numerical viscosity.
Acknowledgements
We thank the anonymous referees for useful comments and remarks.
Calculations were performed on the Origin 3800 at the information
processing centre of Kobe University and on the NEC SX-5 at the Yukawa
Institute of Kyoto University.
K.O. was supported by the Research Fellowships of the Japan Society for
Promotion of Science for Young Scientists.
T.M. was supported by the grant in aid
for scientific research of the Japan Society of Promotion of Science
(13640241) and I.H. by (11640226). This work was supported by "The 21st Century COE Program of Origin and Evolution of Planetary Systems" in
Ministry of Education, Culture, Sports, Science and Technology (MEXT).
- Anupama, G. C., &
Mikolajewska, J. 1999, A&A, 344, 177 [NASA ADS]
- Bennett, P. D., Harper,
G. M., Brown, A., & Hummel, C. A. 1996, ApJ, 471, 454 [NASA ADS] [CrossRef] (In the text)
- Biermann, P. 1971,
A&A, 10, 205 [NASA ADS]
- Blondin, J. M., Stevens, I.
R., & Kallman, T. R. 1991, ApJ, 371, 684 [NASA ADS] [CrossRef] (In the text)
- Blondin, J. M., & Woo,
J. W. 1995, ApJ, 445, 889 [NASA ADS] [CrossRef] (In the text)
- Bisikalo, D. V.,
Boyarchuk, A. A., Chechetkin, V. M., Kuznetsov, O. A., &
Molteni, D. 1998, MNRAS, 300, 39 [NASA ADS]
- Boroson, B., Kallman,
T., Blondin, J. M., & Owen, M. P. 2001, ApJ, 550, 919 [NASA ADS] [CrossRef] (In the text)
- Boffin, H. M. J., &
Anzer, U. 1994, A&A, 284, 1026 [NASA ADS] (In the text)
- Boffin, H. M. J., &
Jorissen, A. 1988, A&A, 205, 155 [NASA ADS] (In the text)
- Boffin, H. M. J., &
Zàcs, L. 1994, A&A, 291, 811 [NASA ADS] (In the text)
- Bondi, H., & Hoyle,
F. 1944, MNRAS, 114, 195 [NASA ADS]
- Carquillat, J. M.,
Jorissen, A., Udry, S., & Ginestet, N. 1998, A&AS, 131,
49 [NASA ADS] (In the text)
- Dumm, T., Folini, D.,
Nussbaumer, H., et al. 2000, A&A, 354, 1014 [NASA ADS] (In the text)
- Foglizzo, T., &
Ruffert, M. 1997, A&A, 320, 342 [NASA ADS] (In the text)
- Foglizzo, T., &
Ruffert, M. 1999, A&A, 347, 901 [NASA ADS] (In the text)
- Fujiwara, H., Makita,
M., Nagae, T., & Matsuda, T. 2001, Prog. Theor. Phys., 106,
729 [NASA ADS]
- Gawryszczak, A. J.,
Mikolajewska, J., & Rózyczka, M. 2002, A&A, 385,
205 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Hachisu, I., &
Kato, M. 2001, ApJ, 558, 323 [NASA ADS] [CrossRef]
- Hoyle, F., & Lyttleton, R.
A. 1939, Proc. Camb. Phil. Soc., 35, 405 [NASA ADS] (In the text)
- Kenyon, S. J., Livio,
M., Mikolajewska, J., & Tout, C. A. 1993, ApJ, 407,
81 [NASA ADS] [CrossRef]
- Makita, M., Miyawaki,
K., & Matsuda, T. 2000, MNRAS, 316, 906 [NASA ADS] [CrossRef]
- Mastrodemos, N., &
Morris, M. 1998, ApJ, 497, 303 [NASA ADS] [CrossRef] (In the text)
- Matsuda, T., Inoue,
M., & Sawada, K. 1987, MNRAS, 226, 785 [NASA ADS]
- Matsuda, T., Ishii,
T., Sekino, N., et al. 1992, MNRAS, 255, 183 [NASA ADS]
- Matsuda, T.,
Makita, M., Fujiwara, H., et al. 2000, Ap&SS, 274, 259 [NASA ADS]
- Mikolajewska, J. 1997,
in Physical Processes in Symbiotic Binaries and Related Systems,
ed. J. Mikolajewska (Warsaw: Copernicus Foundation for Polish
Astronomy), 3
(In the text)
- Mürset, U.,
& Schmid, H. M. 1999, A&AS, 137, 473 [NASA ADS]
- Nussbaumer, H. 1991,
Evolution in Astrophysics, Proc. IUE Symp., Toulouse, FR
(Noordwijk: ESTEC)
(In the text)
- Pogorelov, N. V.,
Ohsugi, Y., & Matsuda, T. 2000, MNRAS, 313, 198 [NASA ADS] [CrossRef]
- Ruffert, M. 1996,
A&A, 311, 817 [NASA ADS] (In the text)
- Sawada, K., Hachisu,
I., & Matsuda, T. 1984, MNRAS, 206, 673 [NASA ADS]
- Sawada, K., Matsuda,
T., & Hachisu, I. 1986, MNRAS, 221, 679 [NASA ADS]
- Sion, E. M., &
Ready, C. 1992, PASP, 104, 87 [NASA ADS] [CrossRef]
- Sion, E. M., &
Starrfield, S. G. 1994, ApJ, 421, 261 [NASA ADS] [CrossRef]
- Sorensen,
S.-A., Matsuda, T., & Sakurai, T. 1975, Ap&SS, 33, 465 [NASA ADS]
- Theuns, T., & Jorissen,
A. 1993, MNRAS, 265, 946 [NASA ADS] (In the text)
- Theuns, T., Boffin, H. M.
J., & Jorissen, A. 1996, MNRAS, 280, 1264 [NASA ADS] (In the text)
- Walder, R. 1997, in
Accretion phenomena and related outflows, ed. D. T. Wichramasinghe,
L. Ferrario, & G. V. Bicknell, IAU Colloq., 163, ASP Conf.
Ser., 121, 822
(In the text)
- Walder, R., &
Folini, D. 2000, in Thermal and ionization Aspects of Flows from
Hot Stars, ed. H. Lamers, & A. Sapar, ASP Conf. Ser., 204,
331
(In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{nagae-fig1.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg47.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig2.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig3.eps}
\par\end{figure}](/articles/aa/full/2004/19/aa2571/Timg81.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig4.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg82.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig5.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg83.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig6.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig7.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig8.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig9.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig10.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig11.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg91.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig12.eps} \end{figure}](/articles/aa/full/2004/19/aa2571/Timg92.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{nagae-fig13.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{nagae-fig14.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg98.gif)
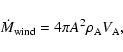
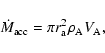
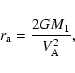
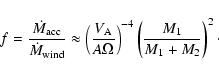
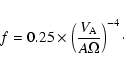
![\begin{figure}
\par\includegraphics[width=8.8cm]{nagae-fig15.eps}
\end{figure}](/articles/aa/full/2004/19/aa2571/Timg115.gif)