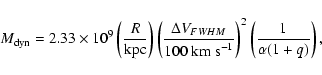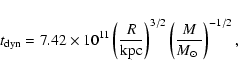A&A 419, 99-107 (2004)
DOI: 10.1051/0004-6361:20035788
Detection of CO J = 1-0 in the z = 3.79 radio galaxy 4C 60.07
T. R. Greve
1 -
R. J. Ivison
2 -
P. P. Papadopoulos
3,4
1 - Institute for Astronomy, University of Edinburgh,
Blackford Hill, Edinburgh EH9 3HJ, UK
2 -
UK ATC, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
3 -
Department of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
4 -
Sterrewacht Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
Received 2 December 2003 / Accepted 5 February 2004
Abstract
We report on the detection of the lowest CO
J=1 - 0 transition
in the powerful high-redshift radio galaxy 4C 60.07 at z = 3.79.
The CO emission is distributed in two spatially and
kinematically distinct components as was previously known from the observations
of the higher excitation CO
J=4 - 3 line.
The total molecular gas mass in 4C 60.07 inferred from the CO
J=1 - 0 emission is
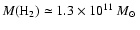 ,
sufficient to fuel the inferred star-formation rate of
,
sufficient to fuel the inferred star-formation rate of
 1600
1600
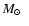 yr-1 for 108 yrs.
From our high-resolution CO
J=1 - 0 VLA maps we find the dynamical mass
of 4C 60.07 to be comparable
to that of a giant elliptical at the present time. A significant
fraction of the mass is in the form of molecular gas
suggesting that 4C 60.07 is in an early state of its evolution.
The merging nature of 4C 60.07 along with its large dynamical mass
imply that this system is a giant elliptical caught in its formative stages.
yr-1 for 108 yrs.
From our high-resolution CO
J=1 - 0 VLA maps we find the dynamical mass
of 4C 60.07 to be comparable
to that of a giant elliptical at the present time. A significant
fraction of the mass is in the form of molecular gas
suggesting that 4C 60.07 is in an early state of its evolution.
The merging nature of 4C 60.07 along with its large dynamical mass
imply that this system is a giant elliptical caught in its formative stages.
Key words: galaxies: individual: 4C 60.07 - galaxies: active - galaxies: formation - galaxies: ISM - cosmology: observations
High-redshift radio galaxies (HzRGs) are amongst the most luminous
objects known, and are believed to serve as tracers of the peaks of
the primordial density field around which giant elliptical galaxies and
clusters of galaxies form (Kauffmann 1996; West et al. 1994).
In the radio, HzRGs typically display a double-lobe
morphology and large radio luminosities (
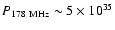 erg s-1 Hz-1),
indicating a highly active black hole.
erg s-1 Hz-1),
indicating a highly active black hole.
Recently, evidence
has been mounting that HzRGs are massive starburst galaxies.
This has come about from sub-millimetre detections of a number of HzRGs, implying large
rest-frame far-IR luminosities (
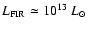 )
powered by intense star formation (SFR
)
powered by intense star formation (SFR
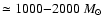 yr-1 -
Dunlop et al. 1994; Hughes et al. 1997; Ivison et al. 1998; Archibald et al. 2001). In a recent SCUBA survey of seven HzRGs and their surroundings,
Stevens et al. (2003) not only found the star formation in the radio galaxies themselves
to be extended on several tens of kilo-parsec scales but also found one or
more previously undetected submm
sources in the vicinity (50-250 kpc) of more than half of the targeted objects.
It is difficult to see how the Active Galactic Nucleus (AGN) could power
the far-IR luminosity on
yr-1 -
Dunlop et al. 1994; Hughes et al. 1997; Ivison et al. 1998; Archibald et al. 2001). In a recent SCUBA survey of seven HzRGs and their surroundings,
Stevens et al. (2003) not only found the star formation in the radio galaxies themselves
to be extended on several tens of kilo-parsec scales but also found one or
more previously undetected submm
sources in the vicinity (50-250 kpc) of more than half of the targeted objects.
It is difficult to see how the Active Galactic Nucleus (AGN) could power
the far-IR luminosity on 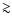 10 kpc scales, and a massive starburst seems
to be the natural explanation.
Indeed, adequate "fuel" for such large star formation rates has been found in the
four HzRGs which have been detected in CO to date (Papadopoulos et al. 2000;
De Breuck et al. 2003a,b).
These observations revealed the presence of massive (
10 kpc scales, and a massive starburst seems
to be the natural explanation.
Indeed, adequate "fuel" for such large star formation rates has been found in the
four HzRGs which have been detected in CO to date (Papadopoulos et al. 2000;
De Breuck et al. 2003a,b).
These observations revealed the presence of massive (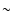 10
10
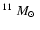 )
reservoirs of molecular gas, enough to fuel a
)
reservoirs of molecular gas, enough to fuel a 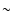 1000
1000
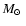 yr-1starburst for
yr-1starburst for 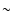 108 yr, and in in half of the cases the CO emission was found to be
extended on tens of kpc scales (Papadopoulos et al. 2000; De Breuck et al. 2003a).
Similar large molecular gas masses distributed in clumps on tens of kilo-parsec scales
has been found in a number of QSOs at high redshifts (Carilli et al. 2002a,b).
In general, HzRGs have the advantage over quasars that they are not
gravitationally lensed since they are usually
selected on the basis of extended lobe-emission whereas quasars
are often found to be lensed. Furthermore, HzRGs are known to be associated with
giant ellipticals in the local Universe (McLure & Dunlop 2000).
108 yr, and in in half of the cases the CO emission was found to be
extended on tens of kpc scales (Papadopoulos et al. 2000; De Breuck et al. 2003a).
Similar large molecular gas masses distributed in clumps on tens of kilo-parsec scales
has been found in a number of QSOs at high redshifts (Carilli et al. 2002a,b).
In general, HzRGs have the advantage over quasars that they are not
gravitationally lensed since they are usually
selected on the basis of extended lobe-emission whereas quasars
are often found to be lensed. Furthermore, HzRGs are known to be associated with
giant ellipticals in the local Universe (McLure & Dunlop 2000).
In this paper we present high-resolution observations of the CO
J=1 - 0
emission from 4C 60.07 at z=3.788 using the Very Large Array![[*]](/icons/foot_motif.gif) .
Throughout we have assumed
H0=65 km s-1 Mpc-1,
.
Throughout we have assumed
H0=65 km s-1 Mpc-1,
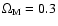 and
and
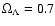 .
In
this cosmology the luminosity distance of 4C 60.07 is 36.2 Gpc and
.
In
this cosmology the luminosity distance of 4C 60.07 is 36.2 Gpc and
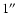 corresponds to 7.7 kpc.
corresponds to 7.7 kpc.
4C 60.07 is an ultra-steep-spectrum (USS) radio galaxy at redshift of
z=3.788 (Chambers et al. 1996; Röttgering et al. 1997). It displays a Fanaroff-Riley II (FR II)
edge-brightened double-radio morphology (Fanaroff & Riley 1974).
The radio morphology of 4C 60.07 is seen in Fig. 1 which shows a VLA C-band (6 cm)
archive image of 4C 60.07. The system consists of two main bright hot spots
separated by about
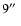 .
The south-eastern component is further comprised
of two components (B and C). Continuum emission is also seen from the radio core which
is located
.
The south-eastern component is further comprised
of two components (B and C). Continuum emission is also seen from the radio core which
is located  2
2
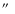 west-northwest of the C-component.
west-northwest of the C-component.
The CO
J=4 - 3 line and 1.25 mm continuum emission from 4C 60.07 have been imaged
using the IRAM Plateau de Bure Interferometer (Papadopoulos et al. 2000).
The CO emission was found to emerge
from two kinematically
distinct components separated in velocity space by 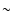 700 km s-1. The component with the narrowest line profile (
700 km s-1. The component with the narrowest line profile (
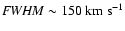 )
is offset by
)
is offset by
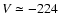 km s-1 from the systemic velocity
corresponding to z=3.788 and spatially coincident with the position of the
radio core. The broader component (
km s-1 from the systemic velocity
corresponding to z=3.788 and spatially coincident with the position of the
radio core. The broader component (
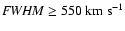 )
peaks
)
peaks 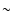 7
7
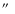 (
(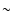 30 kpc) west of the radio core, and is offset by
30 kpc) west of the radio core, and is offset by
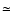 483 km s-1 from the systemic velocity. Such large offsets between the
redshift of the optical emission lines and the CO emission has been observed
in several other high redshift systems, and is commonly attributed to the optical
lines originating in strong outflows and winds (Guilloteau et al. 1999; Cox et al. 2002).
Strong gravitational lensing can be ruled out as
the origin of the double source and large apparent luminosity since not only do
the two components have different line widths but they are also offset in
velocity with respect to each other. Furthermore, there are no indications from
observations in the optical and radio suggesting that 4C 60.07 might be
lensed.
483 km s-1 from the systemic velocity. Such large offsets between the
redshift of the optical emission lines and the CO emission has been observed
in several other high redshift systems, and is commonly attributed to the optical
lines originating in strong outflows and winds (Guilloteau et al. 1999; Cox et al. 2002).
Strong gravitational lensing can be ruled out as
the origin of the double source and large apparent luminosity since not only do
the two components have different line widths but they are also offset in
velocity with respect to each other. Furthermore, there are no indications from
observations in the optical and radio suggesting that 4C 60.07 might be
lensed.
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{0788fig1.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg58.gif) |
Figure 1:
6 cm VLA map of 4C 60.07 overlaid on an I-band image
obtained with the William Herschel Telescope. The radio hot spots
are denoted by A, B and C. The cross marks the position of
the radio core: RA(J2000): 05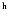 12 12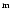 55 55
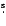 147, Dec(J2000): +60 147, Dec(J2000): +60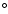 30 30 51 51
 0.
The insert in the bottom right corner shows the synthesized beam. 0.
The insert in the bottom right corner shows the synthesized beam. |
| Open with DEXTER |
In order to get a handle on the non-thermal contribution to the submm and CO fluxes,
we used C and X band images from the VLA Archive to measure the radio fluxes of the
various components in 4C 60.07 at 6 cm and 3.6 cm.
In Fig. 2 we have plotted the submm/far-IR spectral energy distribution (SED) of 4C 60.07
along with the radio spectra of the A-component and the radio core.
The A-component (the dotted line in Fig. 2) is the brightest component
in the radio and furthermore has the shallowest
spectral slope (
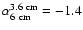 )
which means it provides a strict upper limit
on the non-thermal flux at submm wavelengths.
The 1.25 mm continuum emission from 4C 60.07 is likely to be thermal in origin,
i.e. from warm dust, since non-thermal processes are unable to account for the observed
flux, see Fig. 2. Furthermore, the 1.25 mm continuum emission is offset by
)
which means it provides a strict upper limit
on the non-thermal flux at submm wavelengths.
The 1.25 mm continuum emission from 4C 60.07 is likely to be thermal in origin,
i.e. from warm dust, since non-thermal processes are unable to account for the observed
flux, see Fig. 2. Furthermore, the 1.25 mm continuum emission is offset by
 4
4
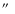 to the west from the radio core position, and does not appear
to be associated with the non-thermal emission.
to the west from the radio core position, and does not appear
to be associated with the non-thermal emission.
The radio core has a spectral slope of
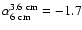 .
Extrapolating
to the frequency of the CO
J=1 - 0 line (
.
Extrapolating
to the frequency of the CO
J=1 - 0 line (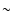 24 GHz)
we find that the radio continuum is expected to contribute a non-neglible
24 GHz)
we find that the radio continuum is expected to contribute a non-neglible
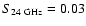 mJy. In comparison, the contribution from the
thermal dust spectrum seems completely neglible, see Fig. 2.
mJy. In comparison, the contribution from the
thermal dust spectrum seems completely neglible, see Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{0788fig2.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg62.gif) |
Figure 2:
The submm/far-IR spectral energy distribution (SED) of 4C 60.07 (red line) along with the
radio spectra of the A-component (blue dotted line) and the radio core (blue solid line).
The submm points are taken from SCUBA observations by Archibald et al. (2001) while the IRAM 30 m
Telescope data-points at 252 GHz (1.25 mm) and 100 GHz (3 mm) are from
Papadopoulos et al. (2000). The
radio points are measured from C and X band data of 4C 60.07 from the VLA Archive.
The positions and strengths of the CO
J=1 - 0 and
J=4 - 3 lines
relative to the SED are shown in yellow (based
on this paper and Papadopoulos et al. 2000). |
| Open with DEXTER |
The CO
J=1 - 0 line (
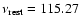 GHz) from 4C 60.07
is redshifted into the VLA's K-band (1.3-cm) receivers. Since
non-thermal continuum emission from the radio core was expected, we used two IF
pairs (right- and left-hand circular polarisation) centred on the two
kinematically distinct emission-line components, each pair set up such that one
IF pair was centred on the line and the other pair was offset from this by
100 MHz to measure the continuum. The IF set-up for both the broad and narrow component is
detailed in Fig. 3. The broad-line component was observed in continuum mode with a
50 MHz-wide IF centred at 24.035 GHz, which corresponds to a velocity
coverage of 624 km s-1. Not only does this not properly cover the broad component
but, since the observations were done in continuum mode, no
information on the line shape was available, and one therefore has to
rely on the IRAM CO
J=4 - 3 observations to infer a line width for the broad component.
The narrow component was observed in
spectral-line mode with a 7-channel IF centered at 24.095 GHz, each channel
being 3.125 MHz wide. This was to avoid under-resolving the narrow line
in velocity space. However, the line datasets from the 2002 December 20 and
2003 March 09 are centred at 24.089 GHz, corresponding to a shift of two
channels, in order to get a better spectral coverage at the low-frequency side
of the line. Thus nine channels (denoted channels 1,..., 9 in Fig. 3)
covered the line, corresponding to a velocity
coverage of 350 km s-1. 4C 60.07 was observed in the VLA's CD, D and C
configurations (see Table 1). The D-configuration data, however,
turned out not to have the spatial resolution required to properly separate the (B, C) component
from the radio core, and was therefore discarded.
The lack of D-array data is very unlikely to result in "filtering out"
any extended CO emission since such emission would have to be extended
over scales
GHz) from 4C 60.07
is redshifted into the VLA's K-band (1.3-cm) receivers. Since
non-thermal continuum emission from the radio core was expected, we used two IF
pairs (right- and left-hand circular polarisation) centred on the two
kinematically distinct emission-line components, each pair set up such that one
IF pair was centred on the line and the other pair was offset from this by
100 MHz to measure the continuum. The IF set-up for both the broad and narrow component is
detailed in Fig. 3. The broad-line component was observed in continuum mode with a
50 MHz-wide IF centred at 24.035 GHz, which corresponds to a velocity
coverage of 624 km s-1. Not only does this not properly cover the broad component
but, since the observations were done in continuum mode, no
information on the line shape was available, and one therefore has to
rely on the IRAM CO
J=4 - 3 observations to infer a line width for the broad component.
The narrow component was observed in
spectral-line mode with a 7-channel IF centered at 24.095 GHz, each channel
being 3.125 MHz wide. This was to avoid under-resolving the narrow line
in velocity space. However, the line datasets from the 2002 December 20 and
2003 March 09 are centred at 24.089 GHz, corresponding to a shift of two
channels, in order to get a better spectral coverage at the low-frequency side
of the line. Thus nine channels (denoted channels 1,..., 9 in Fig. 3)
covered the line, corresponding to a velocity
coverage of 350 km s-1. 4C 60.07 was observed in the VLA's CD, D and C
configurations (see Table 1). The D-configuration data, however,
turned out not to have the spatial resolution required to properly separate the (B, C) component
from the radio core, and was therefore discarded.
The lack of D-array data is very unlikely to result in "filtering out"
any extended CO emission since such emission would have to be extended
over scales 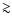 60
60
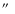 (
(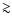 460 kpc).
The fact that we do not find any change in total flux
after including the D-array data verifies this point.
460 kpc).
The fact that we do not find any change in total flux
after including the D-array data verifies this point.
In total, after calibration overheads, we obtained 6.3 h of
integration time on source for both the
broad and narrow components.
Calibration and data reduction was done using standard recipes in the NRAO
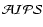 Cookbook.
The amplitude was calibrated with the quasars
3C 48 and 3C 286 at the beginning and/or end of each transit. The phase drift
was calibrated using a fast-switching technique in which we observed the nearby
source 04494+63322 every few minutes. The data were obtained in good weather
conditions, and the rms phase fluctuations after calibration was less than
Cookbook.
The amplitude was calibrated with the quasars
3C 48 and 3C 286 at the beginning and/or end of each transit. The phase drift
was calibrated using a fast-switching technique in which we observed the nearby
source 04494+63322 every few minutes. The data were obtained in good weather
conditions, and the rms phase fluctuations after calibration was less than
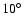 .
For the spectral-line mode observations of the narrow component, the
bandpass of the system was calibrated using 0319+415. In all cases the bandpass
calibration averaged over the 7 channels was better than 92%.
.
For the spectral-line mode observations of the narrow component, the
bandpass of the system was calibrated using 0319+415. In all cases the bandpass
calibration averaged over the 7 channels was better than 92%.
![\begin{figure}
\par\includegraphics[width=8.4cm,angle=0]{0788fig3.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg66.gif) |
Figure 3:
Velocity and frequency coverage of the IF set-up used in our VLA CO
J=1 - 0 observations. The dashed line
outlines the systemic velocity corresponding to z=3.788. In red is shown
the velocity-channels of the IRAM PdBI observations of Papadopoulos et al. (2000);
channels in which CO
J=4 - 3 emission was detected are marked in thick red. |
| Open with DEXTER |
Data taken at different times and in different
configurations were combined using DBCON, weighting each dataset with the its
total gridded weight.
Table 1:
VLA observations.
The radio morphology of 4C 60.7 in the broad and narrow component
IF set-ups is shown in Fig. 4.
Figures 4a and 4b show pure continuum emission and continuum emission plus the
broad CO line emission, respectively; similarly
for Figs. 4c and d but for the narrow component.
![\begin{figure}
\par\includegraphics[width=14.3cm,angle=0]{0788fig4ab.eps}\vspace*{2mm}
\includegraphics[width=14.3cm,angle=0]{0788fig4cd.eps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg72.gif) |
Figure 4:
Naturally weighted, untapered maps, showing the morphology of 4C 60.07 in
the two IF set-ups. Top row: the spatial resolution is
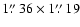 with
the major axis PA =
with
the major axis PA =
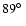 .
The rms noise is 0.030 mJy beam-1. Contours are shown at
-2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, and .
The rms noise is 0.030 mJy beam-1. Contours are shown at
-2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, and
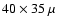 Jy beam-1.
Bottom row: the spatial resolution ( FWHM)
is Jy beam-1.
Bottom row: the spatial resolution ( FWHM)
is
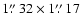 with the major axis PA =
with the major axis PA =
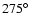 ,
and the rms noise level is 0.051 mJy beam-1. Contours are shown
at -2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, and ,
and the rms noise level is 0.051 mJy beam-1. Contours are shown
at -2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, and
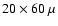 Jy beam-1.
The cross marks the position of the radio core RA(J2000): 05:12:55.147, Dec(J2000): +60:30:51.0. Jy beam-1.
The cross marks the position of the radio core RA(J2000): 05:12:55.147, Dec(J2000): +60:30:51.0. |
| Open with DEXTER |
In Fig. 4a, which shows the continuum emission at 23.935 GHz, we recognise
the two radio lobes seen in Fig. 4, although we have failed to separate the B and C components from the radio core, let alone to
resolve it into its two sub-components. The emission from the radio core is
clearly stronger and more extended in IF2 which, in addition to the continuum, contains the CO-emission from the
broad component (Fig. 4b).
A similar picture is seen for the narrow component in
Figs. 4c and d. Here, the radio core and B-component are separated in both
IFs.
The (large) negative spectral index (
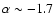 )
of the radio core rules out the possibility
that the excess emission seen in the IF2-maps is due to an increase in continuum emission,
since the IF2 maps are at a higher frequency than the IF1 maps.
The B and C radio hot spots have even larger negative spectral indices (Carilli et al. 1997)
and can therefore not be the cause of the increased emission either.
This suggests that what we are seeing in the IF2 maps is continuum emission
plus CO
J=1 - 0 emission from the emission features detected in the CO
J=4 - 3 maps.
)
of the radio core rules out the possibility
that the excess emission seen in the IF2-maps is due to an increase in continuum emission,
since the IF2 maps are at a higher frequency than the IF1 maps.
The B and C radio hot spots have even larger negative spectral indices (Carilli et al. 1997)
and can therefore not be the cause of the increased emission either.
This suggests that what we are seeing in the IF2 maps is continuum emission
plus CO
J=1 - 0 emission from the emission features detected in the CO
J=4 - 3 maps.
![\begin{figure}
\par\includegraphics[width=7.1cm,angle=0]{0788fig5a.eps}\hspace*{2mm} \includegraphics[width=7.1cm,angle=0]{0788fig5b.eps}\end{figure}](/articles/aa/full/2004/19/aa0788/Timg77.gif) |
Figure 5:
a) Naturally weighted CO
J=1 - 0 map of the broad component
obtained by combining the entire data-set and tapering
it with a Gaussian with a half-width at 0.30 amplitude of
200 k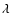 .
The spatial resolution is .
The spatial resolution is
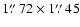 with the major axis PA =
with the major axis PA =
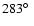 .
The contours are at
-2, 2, 3, 4, and .
The contours are at
-2, 2, 3, 4, and
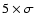 ,
where ,
where
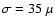 Jy beam-1.
b) The CO
J=1 - 0 emission tapered down to
60 k Jy beam-1.
b) The CO
J=1 - 0 emission tapered down to
60 k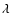 (
(
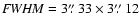 )
overlaid as contours
on a gray-scale representation of the
J=4 - 3 emission by
Papadopoulos et al. (2000). The contours are
-2, 2, 3, 4, 5, and )
overlaid as contours
on a gray-scale representation of the
J=4 - 3 emission by
Papadopoulos et al. (2000). The contours are
-2, 2, 3, 4, 5, and 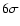 with
with
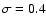 mJy beam-1,
and the gray-scale range is 0.6-2.0 mJy beam-1. mJy beam-1,
and the gray-scale range is 0.6-2.0 mJy beam-1. |
| Open with DEXTER |
In order to disentangle the broad CO emission from the continuum, a box was put
around the entire system and a CLEAN-component model of
the continuum emission shown in Fig. 4a was constructed. The CLEANing was stopped when
the rms of the residuals reached the noise level in the image. This was then
subtracted in uv-space from the IF2 data using the
 task UVSUB,
resulting in uv-data from which maps free of continuum emission could be
produced.
Figure 5a shows the resulting CO
J=1 - 0 map of the
broad component. The lack of residual emission at the positions of the
two radio lobes demonstrates the effectiveness of the continuum emission
subtraction.
The CO
J=1 - 0 emission is detected at
task UVSUB,
resulting in uv-data from which maps free of continuum emission could be
produced.
Figure 5a shows the resulting CO
J=1 - 0 map of the
broad component. The lack of residual emission at the positions of the
two radio lobes demonstrates the effectiveness of the continuum emission
subtraction.
The CO
J=1 - 0 emission is detected at 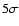 ,
peaking at a position which
is coincident with the radio core position but with emission appearing
to extend
,
peaking at a position which
is coincident with the radio core position but with emission appearing
to extend
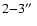 to the west.
In comparison, the broad component of the
CO
J=4 - 3 emission was found to peak
to the west.
In comparison, the broad component of the
CO
J=4 - 3 emission was found to peak 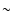 4
4
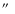 south-west of the radio core
(Papadopoulos et al. 2000).
south-west of the radio core
(Papadopoulos et al. 2000).
In Fig. 5b we have overlaid the CO
J=1 - 0 contours on top of a gray-scale image
of the
J=4 - 3 emission. The 1-0 map has been tapered down to 60 k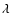 in order to
better match the resolution of the 4-3 data (
in order to
better match the resolution of the 4-3 data (
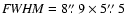 ).
The offset between the centroids of the 1-0 and 4-3 emission is within
the positional errors given the large
).
The offset between the centroids of the 1-0 and 4-3 emission is within
the positional errors given the large
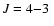 synthesized beam, and in general
there is good spatial correspondence between the two.
synthesized beam, and in general
there is good spatial correspondence between the two.
Assuming that the IF covers the entire line, we can estimate the velocity-integrated
J=1 - 0 flux density using
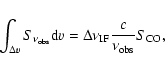 |
(1) |
where
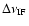 is the width of the IF and
is the width of the IF and
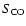 is the flux density.
We find
is the flux density.
We find
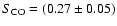 mJy which yields a velocity-integrated flux density
of
mJy which yields a velocity-integrated flux density
of
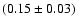 Jy km s-1, where we have used
Jy km s-1, where we have used
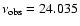 GHz
and an IF bandwidth of 45 MHz (560 km s-1) instead of 50 MHz due to bandpass rollover.
The CO
J=1 - 0 emission from the broad component
in the uvtaper 200 map appears to be somewhat extended in the north-west direction,
although the low signal-to-noise of the data does not warrant a firm conclusion on this
issue.
GHz
and an IF bandwidth of 45 MHz (560 km s-1) instead of 50 MHz due to bandpass rollover.
The CO
J=1 - 0 emission from the broad component
in the uvtaper 200 map appears to be somewhat extended in the north-west direction,
although the low signal-to-noise of the data does not warrant a firm conclusion on this
issue.
The continuum subtraction in the case of the narrow-line emission
was done in a similar fashion as for the broad component: a
continuum model was constructed by combining all IF1 channels
and then subtracted from the IF2 channels. Since channels 1 and 2 had
a different uv-coverage than channels 3 to 7 which again had a different
uv-coverage than channels 8 and 9, three different continuum models had to be
constructed, one for each of these three sets of channels.
In order to increase the signal-to-noise ratio we averaged neighbouring channels
during the imaging of the continuum-subtracted IF2 channels.
We then searched for any residual emission at the expected position
of the narrow component and used the task IMEAN to measure
the flux.
The resulting spectrum of the CO
J=1 - 0 emission is shown in Fig. 6
where we have also plotted the velocity-coverage of the two IRAM PdBI channels in which
J=4 - 3 emission from the narrow component was detected.
Note that channels 1-2 and 8-9 are somewhat more noisy than the other channels,
since the corresponding integration time is less. We detect CO
J=1 - 0 emission
in channels 3 to 6, which in velocity-space overlaps with the two IRAM PdBI channels
in which the strongest CO
J=4 - 3 emission is detected.
Only very weak CO
J=4 - 3 emission was found in the third
IRAM PdBI channel at 96.3095 GHz which is in agreement with the
J=1 - 0 line
profile. From a Gaussian fit to the line profile, we find the
1 - 0 spectrum to
peak at
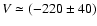 km s-1 offset from the
systemic velocity of 4C 60.07 which
is consistent with that found for the
4 - 3 line given the large velocity bins.
The formal linewidth is
km s-1 offset from the
systemic velocity of 4C 60.07 which
is consistent with that found for the
4 - 3 line given the large velocity bins.
The formal linewidth is
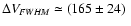 km s-1, again
in good agreement with that of the CO
J=4 - 3 line profile.
The fit yields a velocity-integrated flux density of
km s-1, again
in good agreement with that of the CO
J=4 - 3 line profile.
The fit yields a velocity-integrated flux density of
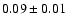 Jy km s-1, see also Table 2.
Jy km s-1, see also Table 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{0788fig6.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg94.gif) |
Figure 6:
The spectrum of the narrow CO
J=1 - 0 component in 4C 60.07. All channels maps
were tapered with a 200 k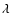 Gaussian. The rms noise
in channels 1-2 is 0.12 mJy beam-1 at a spatial resolution of
Gaussian. The rms noise
in channels 1-2 is 0.12 mJy beam-1 at a spatial resolution of
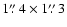 ;
the noise in channels 3-6 is 0.086 mJy beam-1 at a spatial resolution of ;
the noise in channels 3-6 is 0.086 mJy beam-1 at a spatial resolution of
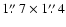 ,
and the noise in channels 7-8 is 0.09 mJy beam-1at a spatial resolution of ,
and the noise in channels 7-8 is 0.09 mJy beam-1at a spatial resolution of
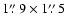 .
Above the line-profile we
have plotted the velocity coverage of the channels in which
J=4 - 3 emission was detected (Papadopoulos et al. 2000). The
vertical dashed line corresponds to the systemic velocity (z=3.788). .
Above the line-profile we
have plotted the velocity coverage of the channels in which
J=4 - 3 emission was detected (Papadopoulos et al. 2000). The
vertical dashed line corresponds to the systemic velocity (z=3.788). |
| Open with DEXTER |
Combining channels 3 to 6 we obtain the velocity-integrated
CO
J=1 - 0 emission map shown in Fig. 7a.
In Fig. 7b we have overlaid contours of the CO
J=1 - 0 emission
on a gray-scale image of the
J=4 - 3
emission where the latter has been tapered down to 60 k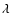 .
The
J=1 - 0 emission peaks at
.
The
J=1 - 0 emission peaks at 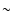
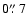 east of the radio core which is consistent with the
position of the narrow
J=4 - 3 component.
Similar to what was found for the
J=4 - 3
line, in
J=1 - 0 the narrow component appears to be more compact and less extended than the broad component.
east of the radio core which is consistent with the
position of the narrow
J=4 - 3 component.
Similar to what was found for the
J=4 - 3
line, in
J=1 - 0 the narrow component appears to be more compact and less extended than the broad component.
The observed CO
J=1 - 0 line fluxes for the broad and narrow components in
4C 60.07 imply intrinsic CO luminosities of
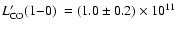 K km s-1 pc2 and
K km s-1 pc2 and
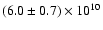 K km s-1 pc2, respectively. For the 4-3 line
Papadopoulos et al. (2000) found
K km s-1 pc2, respectively. For the 4-3 line
Papadopoulos et al. (2000) found
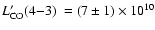 K km s-1 pc2 and
K km s-1 pc2 and
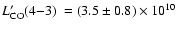 K km s-1 pc2 for the broad and narrow component,
respectively, where we have computed the luminosities in the cosmology adopted
here. From the CO
J=1 - 0 line the molecular gas mass can be found using the
well-known relation
K km s-1 pc2 for the broad and narrow component,
respectively, where we have computed the luminosities in the cosmology adopted
here. From the CO
J=1 - 0 line the molecular gas mass can be found using the
well-known relation
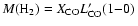 which relates the CO
J=1 - 0
luminosity with the molecular gas mass (e.g. Strong et al. 1988).
which relates the CO
J=1 - 0
luminosity with the molecular gas mass (e.g. Strong et al. 1988).
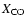 is the CO
J=1 - 0
line luminosity to H2-mass conversion factor which
in the extreme UV-intense environments found in local Ultra Luminous Infra-Red Galaxies,
and presumably also in high redshift galaxies such as 4C 60.07,
has a value of about 0.8 (K km s-1 pc2)
is the CO
J=1 - 0
line luminosity to H2-mass conversion factor which
in the extreme UV-intense environments found in local Ultra Luminous Infra-Red Galaxies,
and presumably also in high redshift galaxies such as 4C 60.07,
has a value of about 0.8 (K km s-1 pc2)
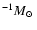 (Downes & Solomon 1998).
In doing so we find molecular gas masses of
(Downes & Solomon 1998).
In doing so we find molecular gas masses of
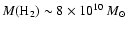 and
and
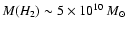 for the
broad and narrow CO emitting components, respectively.
Hence, even for a conservative, non-Galactic value of
for the
broad and narrow CO emitting components, respectively.
Hence, even for a conservative, non-Galactic value of
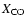 we find that about
we find that about 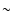
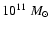 of molecular gas is
associated with 4C 60.07. The estimated gas masses are in very good
agreement with those of Papadopoulos et al. (2000).
of molecular gas is
associated with 4C 60.07. The estimated gas masses are in very good
agreement with those of Papadopoulos et al. (2000).
The total gas mass in 4C 60.07 will of course be larger once the
neutral hydrogen has been accounted for. Assuming a value
of
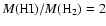 which is typically
found in IRAS galaxies (Andreani et al. 1995) we find
a total gas mass of
which is typically
found in IRAS galaxies (Andreani et al. 1995) we find
a total gas mass of
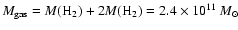 for the broad component and
for the broad component and
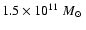 for the narrow component.
In case that metal-poor gas is also present the gas mass can be even higher.
for the narrow component.
In case that metal-poor gas is also present the gas mass can be even higher.
Table 2:
Observed and derived properties for 4C 60.07.
![\begin{figure}
\par\includegraphics[width=7.1cm,angle=0]{0788fig7a.eps}\hspace*{2mm} \includegraphics[width=7.1cm,angle=0]{0788fig7b.eps}\end{figure}](/articles/aa/full/2004/19/aa0788/Timg113.gif) |
Figure 7:
a) The narrow component tapered at 200 k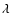 .
The resolution is .
The resolution is
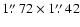 at PA =
at PA =
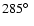 .
Contours are at -2, 2, 3, and .
Contours are at -2, 2, 3, and
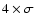 ,
where ,
where
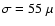 Jy beam-1.
b) The CO
J=1 - 0 emission tapered down to 60 k Jy beam-1.
b) The CO
J=1 - 0 emission tapered down to 60 k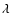 (
(
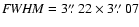 )
overlaid as contours on a gray-scale representation of the
J=4 - 3 detection by
Papadopoulos et al. (2000). The contours are -2, 2, 3, and )
overlaid as contours on a gray-scale representation of the
J=4 - 3 detection by
Papadopoulos et al. (2000). The contours are -2, 2, 3, and 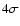 with
with
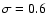 mJy beam-1, and the gray-scale range is
0.6 - 2.0 mJy beam-1. mJy beam-1, and the gray-scale range is
0.6 - 2.0 mJy beam-1. |
| Open with DEXTER |
In the case where the far-IR luminosity is powered by a starburst and not an AGN,
and all the stellar radiation is absorbed by dust, the
far-IR to CO luminosity ratio,
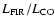 ,
provides a rough measure of the
integrated luminosity of massive stars responsible for heating the dust (
,
provides a rough measure of the
integrated luminosity of massive stars responsible for heating the dust (
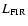 )
relative to the amount of fuel available for star formation (
)
relative to the amount of fuel available for star formation (
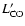 ).
We estimate the far-IR luminosity of 4C 60.07 to be
).
We estimate the far-IR luminosity of 4C 60.07 to be
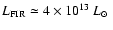 ,
where we have used the 850-
,
where we have used the 850-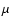 m flux measurement of Archibald et al. (2001) and adopted
a dust temperature and spectral index of
m flux measurement of Archibald et al. (2001) and adopted
a dust temperature and spectral index of
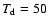 K and
K and
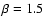 ,
respectively.
This yields a
,
respectively.
This yields a
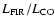 ratio of
ratio of 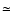
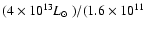 K km s-1 pc
K km s-1 pc
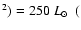 K km s-1 pc2)-1, which is similar to values found in ULIRGs (e.g. Solomon et al. 1997). Carilli et al. (2002a) found continuum-to-line ratios of 350 and 323 in the QSOs BRI 1202-0725 (z=4.70) and BRI 1335-0417 (z=4.41), respectively. A somewhat lower value of 200 was found in the z=4.12 QSO PSS J2322+1944 (Carilli et al. 2002b).
K km s-1 pc2)-1, which is similar to values found in ULIRGs (e.g. Solomon et al. 1997). Carilli et al. (2002a) found continuum-to-line ratios of 350 and 323 in the QSOs BRI 1202-0725 (z=4.70) and BRI 1335-0417 (z=4.41), respectively. A somewhat lower value of 200 was found in the z=4.12 QSO PSS J2322+1944 (Carilli et al. 2002b).
The current star-formation rate measured in
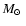 yr-1 is given by
yr-1 is given by
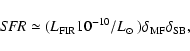 |
(2) |
where
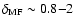 depends on the mass function of the stellar
population, and
depends on the mass function of the stellar
population, and
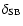 is the fraction of the far-IR luminosity which is
powered by the starburst and not the AGN (Omont et al. 2001). If we
adopt
is the fraction of the far-IR luminosity which is
powered by the starburst and not the AGN (Omont et al. 2001). If we
adopt
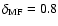 and conservatively assume that only 50% of
and conservatively assume that only 50% of
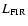 is powered
by the starburst (
is powered
by the starburst (
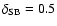 )
we find
)
we find
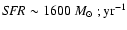 .
Assuming that the total amount of molecular gas observed towards 4C 60.07 ends up as fuel for the
starburst, we find that there is enough molecular gas to sustain the inferred star-formation rate
for
.
Assuming that the total amount of molecular gas observed towards 4C 60.07 ends up as fuel for the
starburst, we find that there is enough molecular gas to sustain the inferred star-formation rate
for 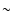
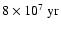 .
While this is short compared to the Hubble time it is still sufficient to produce a giant elliptical
with a stellar mass of
.
While this is short compared to the Hubble time it is still sufficient to produce a giant elliptical
with a stellar mass of
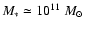 .
.
The efficiency with which stars are being formed,
i.e. the rate of star-formation per solar mass of molecular hydrogen, is given
by
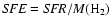 or equivalently
or equivalently
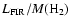 .
For 4C 60.07 we find
.
For 4C 60.07 we find
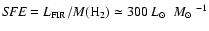 ,
which
is somewhat higher than the
,
which
is somewhat higher than the 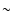 190
190
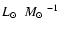 reported by
Papadopoulos et al. (2000) who derived their value based on their flux density
measurement of
reported by
Papadopoulos et al. (2000) who derived their value based on their flux density
measurement of
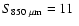 mJy. Here we have used the measurement by Archibald et al. (2001)
which yields a somewhat higher 850
mJy. Here we have used the measurement by Archibald et al. (2001)
which yields a somewhat higher 850 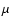 m flux density of 17 mJy, although still lower than
the 22 mJy reported by Stevens et al. (2003).
m flux density of 17 mJy, although still lower than
the 22 mJy reported by Stevens et al. (2003).
Local ULIRGs exhibit star-formation efficiencies comparable to that of 4C 60.07,
once the same
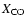 -factor has been used (Solomon et al. 1997).
It is worth stressing that our detection of CO
J=1 - 0 enables us to make a
direct comparison of SFEs with that of local ULIRGs since the same gas mass measure
(the
J=1 - 0 line) is used for ULIRGs.
-factor has been used (Solomon et al. 1997).
It is worth stressing that our detection of CO
J=1 - 0 enables us to make a
direct comparison of SFEs with that of local ULIRGs since the same gas mass measure
(the
J=1 - 0 line) is used for ULIRGs.
The apparently high star-formation efficiencies found for the above systems, could be
severely overestimated if the AGN contributes significantly to the far-IR luminosity.
However, the detection of CO together with the fact that 4C 60.07 and other HzRGs appear extended on several tens of
kilo-pc scales at submm-wavelengths (Ivison et al. 2000; Stevens et al. 2003) strongly suggests that the far-IR emission
is powered by large-scale starburst and not the AGN.
Here we must mention that while CO
J=1 - 0 may be a good indicator of the total
metal-rich H2 gas resevoir, it may be a poor one regarding the
dense gas phase (
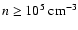 )
that "fuels" star-formation.
The latter could be particular true in the tidally disrupted giant molecular clouds (GMCs)
expected in ULIRGs
where a diffuse phase may dominate the CO
J=1 - 0 emission but has little
to do with star formation. This could be the reason why the
)
that "fuels" star-formation.
The latter could be particular true in the tidally disrupted giant molecular clouds (GMCs)
expected in ULIRGs
where a diffuse phase may dominate the CO
J=1 - 0 emission but has little
to do with star formation. This could be the reason why the
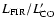 ratio is found to be such a strong function of
ratio is found to be such a strong function of
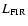 ,
increasing for the
merger systems associated usually with large far-IR luminosities. Interestingly,
recent work shows that the SFE of dense gas, parametrised by the
,
increasing for the
merger systems associated usually with large far-IR luminosities. Interestingly,
recent work shows that the SFE of dense gas, parametrised by the
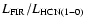 ratio (the HCN
J=1 - 0 critical density is
ratio (the HCN
J=1 - 0 critical density is
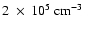 ), remains
constant from GMCs all the way to ULIRG system (Gao & Solomon 2003).
), remains
constant from GMCs all the way to ULIRG system (Gao & Solomon 2003).
From the detections of CO in 4C 60.07 we can infer the CO
(4-3)/(1-0)
velocity/area-averaged brightness temperature
ratio using
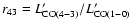 .
The global
line ratio, i.e. the line ratio obtained by combining the flux from the two components, is
r43=0.7+0.3-0.2. The line ratios for the broad and narrow
components are
0.7+0.3-0.2 and
0.6+0.2-0.2, respectively.
Hence, given the large uncertainties we find no significant difference
in the excitation conditions between the two components.
Thus in this case H2 mass estimates solely from CO
J=4 - 3 assuming
full thermalisation and optical thickness of the latter (i.e.
.
The global
line ratio, i.e. the line ratio obtained by combining the flux from the two components, is
r43=0.7+0.3-0.2. The line ratios for the broad and narrow
components are
0.7+0.3-0.2 and
0.6+0.2-0.2, respectively.
Hence, given the large uncertainties we find no significant difference
in the excitation conditions between the two components.
Thus in this case H2 mass estimates solely from CO
J=4 - 3 assuming
full thermalisation and optical thickness of the latter (i.e.
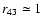 )
would not result in too large errors. However, the sub-thermal excitation of
such high-J CO lines remains a possibility even in starburst environments
(e.g. Papadopoulos & Ivison 2002; Greve et al. 2003).
)
would not result in too large errors. However, the sub-thermal excitation of
such high-J CO lines remains a possibility even in starburst environments
(e.g. Papadopoulos & Ivison 2002; Greve et al. 2003).
In Fig. 8 we plotted the velocity-integrated CO line flux
densities (normalised to
J=4 - 3) for the broad and narrow components in
4C 60.07 as well as the normalised line fluxes for PSS J2322+1944.
We have used a standard single-component large velocity gradient (LVG)
code to interpret the observed line ratio.
In fact, given the large range compatible with
our measurements we can only put a lower limit on the density. Indeed, for both
components the upper values for r43 are compatible with LTE and optically
thick emission where the ratio is no longer sensitive to the density.
A lower limit on the average gas density can be set by the lowest possible
value of
r43=0.4 allowed by the observations. Adopting a typical
CO abundance
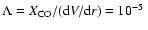 (km s-1 pc
-1)-1, a
(km s-1 pc
-1)-1, a
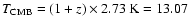 K and a
K and a
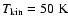 ,
which is a typical dust temperature in
starburst environments (Colbert et al. 1999; Hughes et al. 1997),
we find
,
which is a typical dust temperature in
starburst environments (Colbert et al. 1999; Hughes et al. 1997),
we find
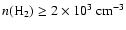 .
Adopting a higher
.
Adopting a higher
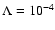 (unlikely in such kinematically
violent, UV-aggressive environments) lowers the aforementioned limit
to
(unlikely in such kinematically
violent, UV-aggressive environments) lowers the aforementioned limit
to 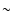 600 cm-3. A lower assumed temperature of
600 cm-3. A lower assumed temperature of
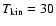 K
does not change these lower limits by much.
For the most likely value of
r43=0.7 we find
K
does not change these lower limits by much.
For the most likely value of
r43=0.7 we find
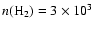 cm-3 (
cm-3 (
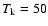 K,
K,
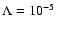 (km s-1 pc
-1)-1).
(km s-1 pc
-1)-1).
Comparing with the z=4.12 QSO PSS J2322+1944 which has
a (4-3)/(1-0) line ratio of 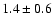 (Carilli et al. 2002b; Cox et al. 2002)
it appears that the excitation conditions in 4C 60.07 are less extreme.
Hence, these results may indicate that the molecular gas in 4C 60.07 is not as dense as
that seen in PSS J2322+1944.
(Carilli et al. 2002b; Cox et al. 2002)
it appears that the excitation conditions in 4C 60.07 are less extreme.
Hence, these results may indicate that the molecular gas in 4C 60.07 is not as dense as
that seen in PSS J2322+1944.
![\begin{figure}
\par\includegraphics[width=7.9cm,angle=0]{0788fig8.ps}\end{figure}](/articles/aa/full/2004/19/aa0788/Timg155.gif) |
Figure 8:
Velocity-integrated CO line flux densities from
4C 60.07 are shown as filled squares.
The integrated line fluxes have been normalised to the
J=4 - 3 line.
Also shown are the line fluxes
from the z=4.12 QSO PSS J2322+1944 (filled triangles - Carilli et al. 2002b; Cox et al. 2002),
the z=4.69 QSO BRI 1202-0725 (open circles - Omont et al. 1996; Carilli et al. 2002a),
the local starburst galaxy M 82 (open triangles - Mao et al. 2000), and
the integrated emission from within the solar radius of the the Milky Way (filled
circles - Fixsen et al. 1999).
The red dotted line shows the line flux increasing as frequency squared which is
expected for optically thick conditions. The green lines show results from
a LVG-model with
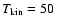 K, K,
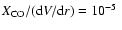 (km s-1 pc
-1)-1, and (km s-1 pc
-1)-1, and
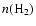 equal to
equal to
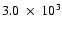 cm-3(solid line) and cm-3(solid line) and
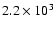 cm-3 (dashed line). cm-3 (dashed line). |
| Open with DEXTER |
Such a comparison, however, is prone to the effects of strong lensing.
While 4C 60.07 is unlikely to be a strongly lensed system because of its
CO components with widely different line widths, it is not the case for
PSS 2322+1944 which is known to be lensed (Carilli et al. 2003).
If the distribution of the
1 - 0 and
J=4 - 3 emitting gas
in the source plane differs, differential magnification of the two lines can
result in erroneous intrinsic line ratios.
A comparison between the molecular gas mass and the dynamical mass
allows for the determination of the evolutionary status of a galaxy, while a comparison
of its dynamical mass with that of present-day spiral or elliptical can point
toward its possible descendant. Typically, dynamical masses are calculated
assuming the gas is distributed in a disk in Keplerian rotation (e.g. Carilli et al. 2002a).
In the case of 4C 60.07, however, we have sufficient spatial and
kinematical information to conclude that the two gas components
do not belong to such a structure.
The detection of two kinematically distinct gas resevoirs in 4C 60.07,
each with a large gas mass, suggest a major merger event.
Hence, a more plausible scenario might be that the two clouds are part of
spherical system in the process of collapsing. Assuming the system is
virialised, one can apply the virial theorem to derive the following expression for the
dynamical mass
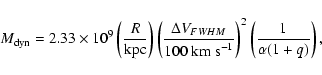 |
(3) |
where q is a factor which described the influence of non-gravitational forces
on the virial equilibrium, and 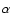 ranges from 0.55 to 2.4 with a typical
value of 1.5 which we shall adopt here (see Bryant & Scoville 1996 for details).
A possible caveat to this argument comes from the fact that if the assumption
of a virialised system is not true, Eq. (3) will tend to overestimate
the true dynamical mass.
Adopting a radius of the sphere corresponding to half the
separation between the two components, i.e.
ranges from 0.55 to 2.4 with a typical
value of 1.5 which we shall adopt here (see Bryant & Scoville 1996 for details).
A possible caveat to this argument comes from the fact that if the assumption
of a virialised system is not true, Eq. (3) will tend to overestimate
the true dynamical mass.
Adopting a radius of the sphere corresponding to half the
separation between the two components, i.e. 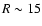 kpc (corresponding
to
kpc (corresponding
to
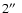 ), and a FWHM width equal
to the velocity offset between the line centers of the two gas resevoirs,
i.e.
), and a FWHM width equal
to the velocity offset between the line centers of the two gas resevoirs,
i.e.
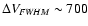 km s-1, leads to an enclosed
dynamical mass of
km s-1, leads to an enclosed
dynamical mass of
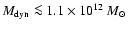 ,
where we have assumed that non-gravitational forces are negligible, i.e.
,
where we have assumed that non-gravitational forces are negligible, i.e. 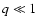 .
Note that since Bryant & Scoville (1996) derived Eq. (3) by examining
a large number of clouds filling up a spherical region, we have in the
above assumed that the velocity and spatial separation between the
two CO components is a fair approximation for
.
Note that since Bryant & Scoville (1996) derived Eq. (3) by examining
a large number of clouds filling up a spherical region, we have in the
above assumed that the velocity and spatial separation between the
two CO components is a fair approximation for
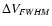 and R in
Eq. (3). Alternatively, we can do the more simple calculation of
finding the virial mass required to keep the two clouds bound by a spherical
potential. In this case the velocity dispersion becomes
and R in
Eq. (3). Alternatively, we can do the more simple calculation of
finding the virial mass required to keep the two clouds bound by a spherical
potential. In this case the velocity dispersion becomes
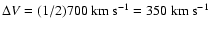 ,
and we find
,
and we find
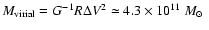 ,
where we have assumed R=15 kpc.
Projection effects will only tend to make R and
,
where we have assumed R=15 kpc.
Projection effects will only tend to make R and
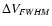 ,
and
therefore also the above mass estimates, larger.
Thus, 4C 60.07 is a massive system with a dynamical
mass comparable to that of giant elliptical galaxies
seen in the present day Universe.
The inferred ratio of the molecular-to-dynamic mass for
the system as a whole is
,
and
therefore also the above mass estimates, larger.
Thus, 4C 60.07 is a massive system with a dynamical
mass comparable to that of giant elliptical galaxies
seen in the present day Universe.
The inferred ratio of the molecular-to-dynamic mass for
the system as a whole is
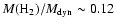 ,
and the total gas fraction is
,
and the total gas fraction is
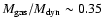 .
The high gas fraction, along with the large velocity dispersion of the system
suggest that 4C 60.07 is a very young system in its early stages of formation.
.
The high gas fraction, along with the large velocity dispersion of the system
suggest that 4C 60.07 is a very young system in its early stages of formation.
The fact that such a massive (
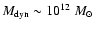 )
system
has assembled at z=3.8, which corresponds to a time when the Universe
was only
)
system
has assembled at z=3.8, which corresponds to a time when the Universe
was only  10% of its present age, seems to favour the monolithic collapse
model (e.g. Eggen et al. 1962; Tinsley & Gunn 1976)
of massive ellipticals over the hierarchical formation scenario
(e.g. Baron & White 1987; Baugh et al. 1996; Kauffmann & Charlot 1998).
Further in support of the monolithic collapse scenario is the large star-formation rate
(
10% of its present age, seems to favour the monolithic collapse
model (e.g. Eggen et al. 1962; Tinsley & Gunn 1976)
of massive ellipticals over the hierarchical formation scenario
(e.g. Baron & White 1987; Baugh et al. 1996; Kauffmann & Charlot 1998).
Further in support of the monolithic collapse scenario is the large star-formation rate
(
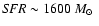 yr-1) we infer
from the far-IR luminosity. If such a large star-formation rate can
be sustained it is capable of producing a giant elliptical in a time scale
comparable to the dynamical time. The dynamical time-scale for
a system with a mass M within a radius R is
yr-1) we infer
from the far-IR luminosity. If such a large star-formation rate can
be sustained it is capable of producing a giant elliptical in a time scale
comparable to the dynamical time. The dynamical time-scale for
a system with a mass M within a radius R is
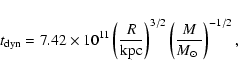 |
(4) |
where
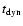 is measured in years (see p. 37 of Binney & Tremaine 1987). For a giant
elliptical with a mass
is measured in years (see p. 37 of Binney & Tremaine 1987). For a giant
elliptical with a mass
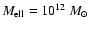 and a radius R=30 kpc, we find
and a radius R=30 kpc, we find
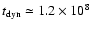 yr. Hence, in order to form a giant elliptical
within a dynamical time scale, star-formation rates of the order
yr. Hence, in order to form a giant elliptical
within a dynamical time scale, star-formation rates of the order
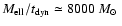 yr-1 are required,
which is comparable to what we find in 4C 60.07.
It is important to note that even if the true dynamical mass or the
star-formation rate of this system are less than the above estimates, the fact that
at z=3.8 about
yr-1 are required,
which is comparable to what we find in 4C 60.07.
It is important to note that even if the true dynamical mass or the
star-formation rate of this system are less than the above estimates, the fact that
at z=3.8 about
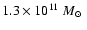 in H2 gas mass alone has assembled
within 15 kpc points towards a major galaxy forming merger rather than a gradual
accumulation of mass over time and redshift. This mass can only be revised
upwards and typically reach
in H2 gas mass alone has assembled
within 15 kpc points towards a major galaxy forming merger rather than a gradual
accumulation of mass over time and redshift. This mass can only be revised
upwards and typically reach 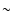
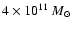 if HI is also
accounted for, thereby making the case for a monolithic collapse scenario even stronger.
if HI is also
accounted for, thereby making the case for a monolithic collapse scenario even stronger.
4C 60.07 is not the only system with extended CO emission.
Molecular gas distributed on tens of kpc scales, sometimes
in separate gas components, have been observed in high
redshifts quasars (e.g. Carilli et al. 2002a; Papadopoulos et al. 2001)
and radio galaxies (De Breuck et al. 2003; De Breuck et al., in preparation).
Thus, there is evidence to show that at least some
luminous active galaxies in the early Universe,
in addition to harbouring supermassive black holes in their centres, are
associated with massive reservoirs of molecular gas distributed
on tens of kpc scales which are in the process of merging.
This observed coevality between large scale mergers
of gaseous subsystems and the epoch of
AGN-activity might provide clues to the origin of the tight relationship observed locally
between the velocity dispersion of spheroids and the mass of their central
black holes (Ferrarese & Merritt 2000).
Acknowledgements
T.R.G. acknowledges support from the Danish Research Council and from the EU RTN
Network POE. PPP acknowledges a Marie Curie Individual Fellowship
HPMT-CT-2000-00875. We are grateful to Ignas Snellen and Philip Best for useful
advice on
 .
We are also greatly indebted to Carlos De Breuck and Michiel Reuland
for providing us with the IRAM PdBI CO
J=4 - 3 data.
.
We are also greatly indebted to Carlos De Breuck and Michiel Reuland
for providing us with the IRAM PdBI CO
J=4 - 3 data.
- Andreani, P.,
Casoli, F., & Gerin, M. 1995, A&A, 300, 43 [NASA ADS] (In the text)
- Archibald, E.
N., Dunlop, J. S., Hughes, D. H., et al. 2001, MNRAS, 323, 417 [NASA ADS] [CrossRef] (In the text)
- Baron, E., &
White, S. D. M. 1987, ApJ, 322, 585 [NASA ADS] [CrossRef] (In the text)
- Baugh, C. M., Cole,
S., & Frenk, C. S. 1996, MNRAS, 283, 136 [NASA ADS] (In the text)
- Binney, J., &
Tremaine, S. 1987, Galactic Dynamics, Princeton Ser. Astrophys.
(Princeton University Press)
(In the text)
- Bryant, P. M.,
& Scoville, N. Z. 1996, ApJ, 457, 678 [NASA ADS] [CrossRef] (In the text)
- Carilli, C. L.,
Röttgering, H. J. A., van Ojik, R., Miley, G. K., & van
Breugel, W. J. M. 1997, ApJS, 109, 1 [NASA ADS] [CrossRef] (In the text)
- Carilli, C. L.,
Kohno, K., Kawabe, R., et al. 2002a, AJ, 123, 1838 [NASA ADS] [CrossRef] (In the text)
- Carilli, C. L.,
Cox, P., Bertoldi, F., et al. 2002b, ApJ, 575, 145 [NASA ADS] [CrossRef] (In the text)
- Carilli, C. L.,
Lewis, G. F., Djorgovski, S. G., et al. 2003, Science, 300,
773 [NASA ADS] [CrossRef] (In the text)
- Chambers, K.
C., Miley, G. K., van Breugel, W. J. M., et al. 1996, ApJS, 106,
247 [NASA ADS] [CrossRef] (In the text)
- Colbert, J. W.,
Malkan, M. A., Clegg, P. E., et al. 1999, ApJ, 511, 721 [NASA ADS] [CrossRef] (In the text)
- Cox, P., Omont, A.,
Djorgovski, S. G., et al. 2002, A&A, 387, 406 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- De Breuck, C.,
Neri, R., Morganti, R., et al. 2003a, A&A, 401, 911 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- De Breuck, Neri,
R., & Omont, A. 2003b, Radio Galaxies: Past, present and
future, Leiden, 11-15 Nov. 2002, ed. M. Jarvis et al.
- Downes, D.,
Solomon, P. M., & Radford, S. J. E. 1993, ApJ, 414, L13 [NASA ADS] [CrossRef]
- Downes, D., &
Solomon, P. M. 1998, ApJ, 506, 615 [NASA ADS] (In the text)
- Dunlop, J. S.,
Hughes, D. H., Rawlings, S., Eales, S., & Ward, M. 1994,
Nature, 370, 347 [NASA ADS] [CrossRef] (In the text)
- Eggen, O. J.,
Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] (In the text)
- Fanaroff, B.
L., & Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] (In the text)
- Ferrarese,
L., & Meritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] (In the text)
- Fixsen, D. J.,
Bennett, C. L., & Mather, J. C. 1999, ApJ, 526, 207 [NASA ADS] [CrossRef] (In the text)
- Gao, Y., & Solomon,
P. M. 2003, in Star formation at high angular resolution (Sydney
Australia), IAU Symp., 221, 95
(In the text)
- Greve, T. R., Ivison,
R. J., & Papadopoulos, P. P. 2003, ApJ, in press
(In the text)
- Guilloteau,
S., Omont, A., Cox, P., McMahon, R., & Petitjean, P. 1999,
A&A, 349, 363 [NASA ADS] (In the text)
- Hughes, D. H.,
Dunlop, J. S., & Rawlings, S. 1997, MNRAS, 289, 766 [NASA ADS] (In the text)
- Ivison, R. J.,
Dunlop, J. S., Hughes, D. H., et al. 1998, ApJ, 494, 211 [NASA ADS] (In the text)
- Ivison, R. J.,
Dunlop, J. S., Smail, I., et al. 2000, ApJ, 542, 27 [NASA ADS] [CrossRef] (In the text)
- Kauffmann, G.
1996, MNRAS, 281, 487 [NASA ADS] (In the text)
- Kauffmann,
G., & Charlot, S. 1998, MNRAS, 294, 705 [NASA ADS] [CrossRef] (In the text)
- Mao, R. Q., Henkel, C.,
Schulz, A., et al. 2000, A&A, 358, 433 [NASA ADS] (In the text)
- McLure, R. J.,
& Dunlop, J. S. 2000, MNRAS, 317, 249 [NASA ADS] [CrossRef] (In the text)
- Omont, A., Petitjean,
P., Guilloteau, S., et al. 1996, Nature, 382, 428 [NASA ADS] [CrossRef] (In the text)
- Omont, A., Cox, P.,
Bertoldi, F., et al. 2001, A&A, 374, 371 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Papadopoulos, P. P., Röttgering, H. J. A., van der Werf, P.
P., et al. 2000, ApJ, 528, 626 [NASA ADS] [CrossRef] (In the text)
-
Papadopoulos, P. P., & Ivison, R. J. 2002, ApJ, 564, L9 [NASA ADS] [CrossRef] (In the text)
-
Papadopoulos, P. P., Ivison, R. J., Carilli, C. L., & Lewis, G.
2001, Nature, 409, 58 [NASA ADS] [CrossRef] (In the text)
-
Röttgering, H., van Oijk, R., Miley, G., et al. 1997, A&A,
326, 505 [NASA ADS] (In the text)
- Solomon, P. M.,
Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478,
144 [NASA ADS] [CrossRef] (In the text)
- Stevens, J. A.,
Ivison, R. J., Dunlop, J. S., et al. 2003, Nature, 425, 264 [NASA ADS] [CrossRef] (In the text)
- Strong, A. W.,
Bloemen, J. B. G. M., Dame, T. M., et al. 1988, A&A, 201,
1 [NASA ADS] (In the text)
- Tinsley, B. M.,
& Gunn, J. E. 1976, ApJ, 203, 52 [NASA ADS] [CrossRef] (In the text)
- West, M. J. 1994,
MNRAS, 268, 79 [NASA ADS] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{0788fig1.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{0788fig2.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg62.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,angle=0]{0788fig3.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg66.gif)
![\begin{figure}
\par\includegraphics[width=14.3cm,angle=0]{0788fig4ab.eps}\vspace*{2mm}
\includegraphics[width=14.3cm,angle=0]{0788fig4cd.eps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg72.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,angle=0]{0788fig5a.eps}\hspace*{2mm} \includegraphics[width=7.1cm,angle=0]{0788fig5b.eps}\end{figure}](/articles/aa/full/2004/19/aa0788/Timg77.gif)
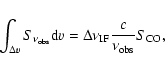
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{0788fig6.ps} \end{figure}](/articles/aa/full/2004/19/aa0788/Timg94.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,angle=0]{0788fig7a.eps}\hspace*{2mm} \includegraphics[width=7.1cm,angle=0]{0788fig7b.eps}\end{figure}](/articles/aa/full/2004/19/aa0788/Timg113.gif)
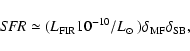
![\begin{figure}
\par\includegraphics[width=7.9cm,angle=0]{0788fig8.ps}\end{figure}](/articles/aa/full/2004/19/aa0788/Timg155.gif)