A&A 418, 1101-1115 (2004)
DOI: 10.1051/0004-6361:20034332
A multiwavelength study of solar flare waves
I. Observations and basic properties
A. Warmuth1
- B. Vrsnak2 - J. Magdalenic2 - A. Hanslmeier3 - W. Otruba4
1 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
2 -
Hvar Observatory, University of Zagreb, Kaciceva 26, 10000 Zagreb, Croatia
3 -
Institute for Geophysics, Astrophysics and Meteorology, University of Graz, Universitätsplatz 5, 8010 Graz, Austria
4 -
Sonnenobservatorium Kanzelhöhe, 9521 Treffen, Austria
Received 17 September 2003 / Accepted 26 January 2004
Abstract
Propagating wave-like disturbances associated with solar flares
- commonly observed in the chromosphere as Moreton waves - have
been known for several decades. Recently, the phenomenon has come
back into focus prompted by the observation of coronal waves with
the SOHO/EIT instrument ("EIT waves"). It has been suggested
that they represent the anticipated coronal counterpart to Moreton
waves, but due to some pronounced differences, this interpretation
is still being debated.
We study 12 flare wave events in order to determine their
physical nature, using H ,
EUV, He I 10 830 Å SXR and
radioheliographic data. The flare wave signatures in the various
spectral bands are found to lie on closely associated
kinematical curves, implying that they are signatures of the same
physical disturbance. In all events, and at all wavelengths, the flare waves are decelerating, which explains the apparent "velocity discrepancy" between Moreton and EIT waves which has been reported by various authors. In this paper, the focus of the study is on the morphology, the spatial characteristics and the kinematics of the waves. The characteristics of the common perturbation which causes the wave signatures, as well as the associated type II radio bursts, will be studied in companion Paper II, and a consistent physical interpretation of flare waves will be given.
,
EUV, He I 10 830 Å SXR and
radioheliographic data. The flare wave signatures in the various
spectral bands are found to lie on closely associated
kinematical curves, implying that they are signatures of the same
physical disturbance. In all events, and at all wavelengths, the flare waves are decelerating, which explains the apparent "velocity discrepancy" between Moreton and EIT waves which has been reported by various authors. In this paper, the focus of the study is on the morphology, the spatial characteristics and the kinematics of the waves. The characteristics of the common perturbation which causes the wave signatures, as well as the associated type II radio bursts, will be studied in companion Paper II, and a consistent physical interpretation of flare waves will be given.
Key words: shock waves - Sun: flares - Sun: radio radiation - Sun: corona - Sun: chromosphere
The first indication flare-associated globally traveling
disturbances in the low solar atmosphere were given by the activation
of distant filaments by flares, first discussed in detail by
Dodson (1949; see also Ramsey & Smith 1966). A second line of evidence for
propagating agents was provided by the analysis of
correlations between flares occurring close in time but at
different locations on the solar disk (e.g. Becker 1958; Valnicek 1964). However, the reality of this "sympathetic flaring"
has remained doubtful until today (for a recent study see
Biesecker & Thompson 2000).
In 1960 the existence of flare-associated disturbances
was proved by direct optical observations using H filtergrams (Moreton 1960; Moreton & Ramsey 1960; Athay &
Moreton 1961). The disturbances, which have since become known as
Moreton waves (a term referring primarily to H
filtergrams (Moreton 1960; Moreton & Ramsey 1960; Athay &
Moreton 1961). The disturbances, which have since become known as
Moreton waves (a term referring primarily to H observations) or - more generally - flare waves, appear as
arc-shaped fronts propagating away from the flare at speeds of the
order of 1000 km s-1. The fronts are seen in emission in
the center and in the blue wing of the H
observations) or - more generally - flare waves, appear as
arc-shaped fronts propagating away from the flare at speeds of the
order of 1000 km s-1. The fronts are seen in emission in
the center and in the blue wing of the H line, whereas in the red wing
they appear in absorption. This behavior was interpreted as a depression
of the chromosphere by an invisible agent (Moreton 1964). It was
also shown that flare waves can indeed cause the activation or
"winking" of filaments (Ramsey & Smith 1966).
line, whereas in the red wing
they appear in absorption. This behavior was interpreted as a depression
of the chromosphere by an invisible agent (Moreton 1964). It was
also shown that flare waves can indeed cause the activation or
"winking" of filaments (Ramsey & Smith 1966).
Uchida (1968) developed the theory that Moreton waves are just the
"ground track" of a flare-produced fast-mode MHD wavefront which
is coronal in nature and sweeps over the chromosphere
("sweeping-skirt" hypothesis). In numerical simulations, Uchida
(1970; Uchida et al. 1973) was able to show how the waves become
focused in regions of low Alfvén velocity, which produced
wavefronts that agreed reasonably well with the observations.
Type II solar radio bursts, which are seen in dynamic radio
spectra as narrow-band emission drifting from higher to lower
frequencies (e.g. Nelson & Melrose 1985), had already been
interpreted as the signature of a collisionless fast-mode MHD shock before (Uchida 1960), and it was now comparatively easy to integrate them
into the coronal shock scenario (Uchida 1974), especially since it
was also observationally shown that they are closely associated
with Moreton waves (e.g., Harvey et al. 1974).
Prompted by the study of type II bursts and coronagraphic
observations, a debate on the physical cause of propagating shock
waves on the sun developed in the 1980s. In the classical "blast
wave" scenario a flare produces an initial pressure pulse which
then propagates through the corona as a fast-mode shock (e.g. Vrsnak
& Lulic 2000a,b, and references therein), being observed as a Moreton
wave in the chromosphere and as a type II burst in the corona. The
new hypothesis which was proposed postulated that a CME acts as a
piston which generates a driven shock ("piston mechanism"; see
Cliver et al. 1999 and references therein). However, this
discussion was mainly focused on type II bursts and interplanetary shocks, whereas comparatively
little interest was directed towards Moreton waves.
Table 1:
Event overview and data coverage. Event gives the event label and date; NOAA No. the active
region number; flare loc. the coordinates of the flare; flare imp. the
optical and soft X-ray importance of the flare; SXR beg.-max. the time of
begin and maximum of the SXR flare;
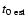 the estimated starting time of the disturbance; 1st Moreton the time of the first Moreton
wavefront; and n the number of identified wavefronts in the various spectral bands ( Nob. refers to the Nobeyama radioheliograph). "-" means
that no wave features could be detected, and a blank space indicates that no or
insufficient data were available.
the estimated starting time of the disturbance; 1st Moreton the time of the first Moreton
wavefront; and n the number of identified wavefronts in the various spectral bands ( Nob. refers to the Nobeyama radioheliograph). "-" means
that no wave features could be detected, and a blank space indicates that no or
insufficient data were available.
From 1997 onward, globally propagating wave-like features were
observed in the low corona (Thompson et al. 1998) with the Extreme
Ultraviolet Imaging Telescope (EIT) aboard the Solar and
Heliospheric Observatory (SOHO) spacecraft. Whether these
"EIT waves" are the coronal counterpart to Moreton waves as
anticipated by the Uchida model has remained a matter of debate
because the two phenomena show several remarkable differences. In
particular, EIT waves are on average 2-3 times slower than Moreton
waves (Smith & Harvey 1971; Klassen et al. 2000) and are
morphologically different.
Several recent studies (Thompson et al. 2000; Warmuth et al. 2001; Khan & Aurass 2002)
have shown that at least in certain cases Moreton and EIT waves
are closely related and may indeed be regarded as manifestations
of the same physical disturbance. In particular, it was shown by
Warmuth et al. (2001) that the mentioned velocity discrepancy
between Moreton and EIT waves can be straightforwardly explained
by the deceleration of the flare waves and several statistical selection effects. In H ,
the waves are observable only during the initial phase
of the propagation, when the velocities are still of the order of 1000 km s-1. On the other hand, EIT waves can be traced to
much larger distances, but are observed at the low cadence of EIT,
so their mean speed is significantly lower (in the order of
several 100 km s-1).
,
the waves are observable only during the initial phase
of the propagation, when the velocities are still of the order of 1000 km s-1. On the other hand, EIT waves can be traced to
much larger distances, but are observed at the low cadence of EIT,
so their mean speed is significantly lower (in the order of
several 100 km s-1).
Unfortunately, comparative studies of coronal and chromospheric
signatures of flare waves are seriously hampered by the low image
cadence of EIT (typically 15 min) and problems with EIT timing.
Therefore, it is very promising to use data from additional
spectral channels. A first step in this direction were soft X-ray
observations of coronal flare waves by the Soft X-ray Telescope (SXT) aboard the Yohkoh satellite. For
one event it has been shown that SXT, EIT and H wavefronts are quite consistent and may indeed be caused by the
same disturbance (Khan & Aurass 2002). In the same paper, it was shown that there is a fairly good
overlapping of the wavefront and the type II burst source observed by the Nançay
Radioheliograph (Kerdraon & Delouis 1997). The traces of traveling disturbances were also disclosed in He I 10 830 Å (He I hereafter) filtergrams (Gilbert et al. 2001; Vrsnak et al. 2002).
wavefronts are quite consistent and may indeed be caused by the
same disturbance (Khan & Aurass 2002). In the same paper, it was shown that there is a fairly good
overlapping of the wavefront and the type II burst source observed by the Nançay
Radioheliograph (Kerdraon & Delouis 1997). The traces of traveling disturbances were also disclosed in He I 10 830 Å (He I hereafter) filtergrams (Gilbert et al. 2001; Vrsnak et al. 2002).
Most of these studies suffer from a small sample of events, and a general lack of multi-wavelength data coverage. The results obtained by Warmuth et al. (2001), for example, were based on only two events, so it might be argued that the conclusions described above may not hold for all Moreton/EIT waves. Indeed, there have been claims that Moreton and EIT waves are distinct phenomena (Eto et al. 2002; Chen et al. 2002).
In order to resolve this question, we study an enlarged sample - 12 flare wave events - and use all available imaging data, including H ,
EUV, He I and SXR images, as well as radioheliograms. This allows us to check the conclusions reached in Warmuth et al. (2001) and derive more convincing and extensive results. In addition, we are now able to provide an overview of the characteristic parameters of flare waves, their ranges and average values.
,
EUV, He I and SXR images, as well as radioheliograms. This allows us to check the conclusions reached in Warmuth et al. (2001) and derive more convincing and extensive results. In addition, we are now able to provide an overview of the characteristic parameters of flare waves, their ranges and average values.
Our data sources, the principal analysis techniques and a brief description of the data set are given in Sect. 2. Morphological aspects of the waves are described in Sect. 3, while their spatial aspects and their kinematics are discussed in Sects. 4 and 5, respectively. The results are discussed in Sect. 6, and the conclusion is given in Sect. 7.
In the companion paper (Warmuth et al. 2004; henceforth Paper II), the evolution of the perturbation responsible for the creation of flare wave signatures will be studied, and the associated type II radio bursts (which were present in every event) will be analyzed. The outcome of these studies, combined with the results of this paper, will then be used to arrive at a consistent physical interpretation of flare waves.
The selection of suitable events started with an inspection of
full-disk H data. In order to reduce the number of flares
that had to be searched, in a first step only those flares which
were associated with a metric type II radio burst were considered,
since according to Pinter (1977), at least 77% of Moreton waves
are associated with type II bursts. To avoid a selection bias, all
other flares above a certain importance were also checked for associated Moreton
waves.
data. In order to reduce the number of flares
that had to be searched, in a first step only those flares which
were associated with a metric type II radio burst were considered,
since according to Pinter (1977), at least 77% of Moreton waves
are associated with type II bursts. To avoid a selection bias, all
other flares above a certain importance were also checked for associated Moreton
waves.
The data search started with March 1997, when EIT started to
operate at cadences that allow the detection of flare waves
(Biesecker et al. 2002). The search period covered a total of 54 months (or 4.5 years) and ended in August 2001, which corresponds
to the rising and the maximum phase of solar cycle 23.
The full-disk H data archives of Kanzelhöhe Solar
Observatory (KSO) and Big Bear Solar Observatory (BBSO) were
searched according to the scheme described above. Additionally, a
thorough search of the H
data archives of Kanzelhöhe Solar
Observatory (KSO) and Big Bear Solar Observatory (BBSO) were
searched according to the scheme described above. Additionally, a
thorough search of the H data from 1997 to 2000 has
been conducted by the staff of Hida Observatory (Shibata et al. 2002), and its results are used here, too. A
total of 12 Moreton events were found (KSO: 3; BBSO: 4; Hida: 4;
and an additional event observed by B. Reynolds which was first reported in
Thompson et al. 2000).
data from 1997 to 2000 has
been conducted by the staff of Hida Observatory (Shibata et al. 2002), and its results are used here, too. A
total of 12 Moreton events were found (KSO: 3; BBSO: 4; Hida: 4;
and an additional event observed by B. Reynolds which was first reported in
Thompson et al. 2000).
We stress that our only selection criterion was the observation of Moreton wavefronts that were defined clearly enough so that the kinematics of the waves could be measured accurately. This also means that we are studying a sub-category of flare waves, namely those associated with prominent H wavefronts. Possibly this represents the high amplitude limit of the phenomenon. In addition, we identified various events that showed some Moreton-like characteristics (i.e. propagating brightenings and winking filaments), but no coherent wavefronts. These events will be discussed in a future paper.
wavefronts. Possibly this represents the high amplitude limit of the phenomenon. In addition, we identified various events that showed some Moreton-like characteristics (i.e. propagating brightenings and winking filaments), but no coherent wavefronts. These events will be discussed in a future paper.
Table 1 gives an overview of the events and the
data coverage, introducing the event
labels E1 to E12![[*]](/icons/foot_motif.gif) . Note that the flare waves
are predominantly associated with active regions (ARs) that produced more than
one wave event. This could have important implications for the generation mechanism
of the disturbances and will be discussed in a forthcoming paper.
. Note that the flare waves
are predominantly associated with active regions (ARs) that produced more than
one wave event. This could have important implications for the generation mechanism
of the disturbances and will be discussed in a forthcoming paper.
We examine waves seen in five different spectral bands. In all
eight events where EIT data were available, EIT waves were really
observed, so it is reasonable to assume that all H Moreton
waves will have associated EIT waves. The association with
He I waves and waves seen in the 17 GHz radioheliograms
seems to be also quite high (67% and 75%, respectively). Due to
the peculiarities in the SXT data acquisition, it is difficult
to judge the occurrence rate of the X-ray waves (it is at least 50% in our sample)
Moreton
waves will have associated EIT waves. The association with
He I waves and waves seen in the 17 GHz radioheliograms
seems to be also quite high (67% and 75%, respectively). Due to
the peculiarities in the SXT data acquisition, it is difficult
to judge the occurrence rate of the X-ray waves (it is at least 50% in our sample)![[*]](/icons/foot_motif.gif) .
These high percentages of association suggest that, generally,
all of these different signatures will be present in a flare wave
event.
.
These high percentages of association suggest that, generally,
all of these different signatures will be present in a flare wave
event.
Table 2:
Imaging instruments. Spatial resolution is given in arcseconds per pixel, temporal cadence in minutes. Note that the Hida and NoRH data are available at much higher cadences, and that the cadence for SXT applies to each specific combination of filters and exposure times.
Table 2 gives an overview of the imaging instruments used in this study of flare waves. Our emphasis is on H (6563 Å) data, which is mainly due to their ready availability and
their high temporal cadence (typically 1 min). Data were provided by the KSO Digital H
(6563 Å) data, which is mainly due to their ready availability and
their high temporal cadence (typically 1 min). Data were provided by the KSO Digital H Camera (DHC; note that E3 was still recorded on film at KSO), the Singer telescope at BBSO, and the Flare Monitoring Telescope (FMT) at the Hida Observatory of Kyoto
University, which provides simultaneous images in H
Camera (DHC; note that E3 was still recorded on film at KSO), the Singer telescope at BBSO, and the Flare Monitoring Telescope (FMT) at the Hida Observatory of Kyoto
University, which provides simultaneous images in H line center and both line wings. E1 was observed in the red wing of H
line center and both line wings. E1 was observed in the red wing of H on film at a cadence of 2-3 min (see Thompson et al. 2000).
on film at a cadence of 2-3 min (see Thompson et al. 2000).
Additional chromospheric imaging data in the form
of He I 10 830 Å filtergrams were provided by the CHIP instrument at the Mauna Loa Solar
Observatory (MLSO). The He I absorption line is formed by the contribution of two distinct
processes (see Andretta & Jones 1997 and references therein): the
photoionization of helium by coronal UV and EUV radiation and
subsequent cascading back (PR mechanism), which is effective in
the upper chromosphere, and the direct excitation by collisions
from the ground state of parahelium, which dominates at the
boundary between the upper chromosphere and the transition region.
Therefore, He I filtergrams actually contain information
on three different height ranges. While this complicates
interpretation, it nevertheless provides us with an interesting
link between chromospheric and coronal observations.
As coronal imaging data, we mainly use EUV full-disk images provided by the
Extreme Ultraviolet Imaging Telescope (EIT) aboard the SOHO. It should be noted that
there are problems with the timing of the EIT images (A. Vourlidas, private
communication): the two different methods used to correct erroneous timing give
results that may disagree by up to 1 min. We therefore always use the mean of
the two corrected times.
A supplementary source of coronal data is the Soft X-ray Telescope (SXT) aboard Yohkoh. While the Fe XII images provided by EIT correspond to temperatures of 1.5-1.6 MK, SXT shows plasma at temperatures above 2 MK.
Radioheliograms in the microwave range (17 GHz) were available from the Nobeyama
radioheliograph (NoRH). Radio emission at this wavelength arises from both thermal
bremsstrahlung and non-thermal gyro-resonance radiation. In the quiet sun, the main
contribution is thermal bremsstrahlung from the chromosphere
(with a brightness temperature of
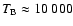 K).
K).
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig1.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg23.gif) |
Figure 1:
Overview of the Moreton and EIT waves of E1 to E12. The visually
determined H (black) and EIT wavefronts (white) are plotted on H
(black) and EIT wavefronts (white) are plotted on H images from the time of the wave onset (for E9, the He I fronts are shown instead of EIT). Also shown are parts of great circles
which define the sectors in which the distances of the wavefronts from the
calculated starting point were measured (for the cases where H images from the time of the wave onset (for E9, the He I fronts are shown instead of EIT). Also shown are parts of great circles
which define the sectors in which the distances of the wavefronts from the
calculated starting point were measured (for the cases where H and EIT waves were measured using different sectors, both of them are shown). In this and all subsequent images,
solar north is up, west is right, and times are given in UT.
and EIT waves were measured using different sectors, both of them are shown). In this and all subsequent images,
solar north is up, west is right, and times are given in UT. |
| Open with DEXTER |
We are studying the kinematics of flare waves by utilizing distance-time plots r(t) of their leading edge. To reduce possible sources of error, or at least
to get an indication for the accuracy of the derived values, we
employ two different measurement techniques. The first is based on
the visual determination of the leading edge of the wavefronts. We
then determine the distances of the wavefronts from a probable
starting location along ten paths which are parts of great circles
on the solar surface. They converge in the assumed starting
point and reflect the angle into which the wave propagates. Figure 1
shows large-scale H images for all events as an
overview. Overplotted are the visually determined H
images for all events as an
overview. Overplotted are the visually determined H and EIT wavefronts and the sector in which the measurements were
performed.
and EIT wavefronts and the sector in which the measurements were
performed.
With the second method, we obtain intensity profiles (using
differenced images) along a large number of paths, which are then
averaged laterally over the whole sector angle (for details see Vrsnak et al.
2002), giving the mean intensity as a function of distance for a given moment.
From these profiles we can derive the locations of the leading edge, and compare it with the "visual" values for r(t). Note that the profile method also can provide the location of the intensity maximum and the trailing edge, as well as the evolution of the intensity of the wavefront. These aspects will be discussed in Paper II.
What now remains to be determined is the location of the ignition
of the perturbation and its starting time. Usually, the center of
the flare is taken as a starting location. This assumption is
somewhat arbitrary, therefore, we use the earliest H wavefront for an extrapolation of the starting point by fitting a
circle to the visually determined leading edge of the front
(taking the curvature of the surface into account). This is not an
exact method (e.g., the central parts of the perturbation could be
slightly faster than those at the periphery, leading to an
elliptical shape of the front), but it makes no assumptions about
the initiation of the perturbation, in contrast to the usual
"flare center" approach.
wavefront for an extrapolation of the starting point by fitting a
circle to the visually determined leading edge of the front
(taking the curvature of the surface into account). This is not an
exact method (e.g., the central parts of the perturbation could be
slightly faster than those at the periphery, leading to an
elliptical shape of the front), but it makes no assumptions about
the initiation of the perturbation, in contrast to the usual
"flare center" approach.
The estimated starting time (
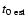 )
was usually taken as the time of the last H
)
was usually taken as the time of the last H image without a visible wavefront in all events where the H
image without a visible wavefront in all events where the H cadence was 1 min or better. In several cases, the time of the impulsive rise of the microwave burst and the evolution of the H
cadence was 1 min or better. In several cases, the time of the impulsive rise of the microwave burst and the evolution of the H flare (the presence of ejecta or a sudden expansion of the flaring area) were used to derive
flare (the presence of ejecta or a sudden expansion of the flaring area) were used to derive
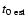 .
Note that our study of the kinematics does not depend on the exact starting times. A perhaps more objective estimation of the probable starting times will be presented in Sect. 5.1.
.
Note that our study of the kinematics does not depend on the exact starting times. A perhaps more objective estimation of the probable starting times will be presented in Sect. 5.1.
In Fig. 2, the morphology and evolution of the Moreton wave of E5 (which is the best-observed event in H )
is shown in
H
)
is shown in
H difference images. We note that the Moreton wavefronts
in fact consist of two distinct features: a diffuse arc of
more or less homogeneously increased emission, and a number of small
discrete brightenings. The wavefronts are not observed in the
immediate vicinity of the flare, but make their first appearance
at a considerable distance from the flare and the starting point.
difference images. We note that the Moreton wavefronts
in fact consist of two distinct features: a diffuse arc of
more or less homogeneously increased emission, and a number of small
discrete brightenings. The wavefronts are not observed in the
immediate vicinity of the flare, but make their first appearance
at a considerable distance from the flare and the starting point.
As the wave propagates away from the flare, the diffuse front
becomes progressively less intense and also less homogeneous,
while its thickness 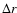 increases. As the diffuse front
travels over the surface, the localized brightenings light up and
then slowly fade over a period of several minutes, which means
that they still can be discerned after the diffuse wavefront has
passed over them. As the wave propagates farther, the newly
activated localized brightenings become progressively fainter and
more diffuse. Before the signatures of the disturbance become too
faint to be distinguished from the background, the wavefront has turned into
an inhomogeneous ensemble of small brightenings with some very faint remnants of the diffuse front.
increases. As the diffuse front
travels over the surface, the localized brightenings light up and
then slowly fade over a period of several minutes, which means
that they still can be discerned after the diffuse wavefront has
passed over them. As the wave propagates farther, the newly
activated localized brightenings become progressively fainter and
more diffuse. Before the signatures of the disturbance become too
faint to be distinguished from the background, the wavefront has turned into
an inhomogeneous ensemble of small brightenings with some very faint remnants of the diffuse front.
We emphasize that some of the localized brightenings light up even
before the wavefront has reached them. The distance to the leading
edge can range up to 25 Mm. This indicates that there is some
agent that can influence regions in the chromosphere before the
wavefront itself is actually passing over.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig2.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg25.gif) |
Figure 2:
Evolution of the flare wave of 1998 May 2 (E5) as shown by H a), b), d), e) and EIT c) difference images. The wavefronts are indicated by
arrows.
a), b), d), e) and EIT c) difference images. The wavefronts are indicated by
arrows. |
| Open with DEXTER |
In the wings of H ,
the overall morphology of the
wavefronts is the same as in the line center, and the waves seen
in the three spectral bands are also roughly cospatial. In the
blue wing (H
,
the overall morphology of the
wavefronts is the same as in the line center, and the waves seen
in the three spectral bands are also roughly cospatial. In the
blue wing (H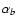 hereafter), the fronts are seen in emission, while they appear as
dark absorption features in the red wing (H
hereafter), the fronts are seen in emission, while they appear as
dark absorption features in the red wing (H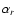 ). In all cases, the
contrast of the wavefronts is higher in the wings than in the line
center, especially in H
). In all cases, the
contrast of the wavefronts is higher in the wings than in the line
center, especially in H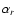 .
There, the absorption wavefronts are
followed by an emission feature of a larger thickness
.
There, the absorption wavefronts are
followed by an emission feature of a larger thickness 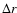 and a lower contrast. In H
and a lower contrast. In H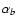 ,
similar trailing
disturbances are observed seen in absorption.
,
similar trailing
disturbances are observed seen in absorption.
In all events the excess emission clearly arises from an
enhancement of pre-existing chromospheric structures, and not from
matter propagating above the surface (e.g. H sprays).
sprays).
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig3.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg28.gif) |
Figure 3:
The flare wave of 1997 November 3
(E3) as shown by H a), SXT b), d) and EIT c) difference images. The black features in the SXT images
are artifacts of saturation. a), SXT b), d) and EIT c) difference images. The black features in the SXT images
are artifacts of saturation. |
| Open with DEXTER |
3.2 EIT
EIT waves show a wide range of morphological patterns (cf. Klassen
et al. 2000). Usually they are observed as diffuse and irregular
arcs of increased coronal emission, but about 7% of them display
sharp and bright wavefronts - the so-called S-waves (Biesecker
et al. 2002). Most of these events show also the more common
diffuse fronts in a later stage of the event, and it is reasonable
to suppose that the initially sharp fronts decay to the diffuse
fronts in the course of their propagation (as is observed in
the case of Moreton waves).
In two of the eight events that had EIT coverage - E1 and E5 -
such S-waves were found, and in both events the following EIT images showed the more usual diffuse fronts. Those two events were
also the only ones where an EIT wavefront could be observed within
the spatial and temporal range of the H Moreton
fronts, and they offer a unique opportunity to compare the
morphology and the exact location of EIT and Moreton fronts.
Moreton
fronts, and they offer a unique opportunity to compare the
morphology and the exact location of EIT and Moreton fronts.
In E1, the EIT front is very thin (
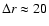 Mm) and has a sharp leading edge. Behind the front discrete
patches of increased emission are visible. The corresponding H
Mm) and has a sharp leading edge. Behind the front discrete
patches of increased emission are visible. The corresponding H front (observed in H
front (observed in H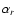 )
has a roughly
similar overall shape and angular extent. In the case of E5 (Fig. 2), the
S-wave is mainly visible due to localized brightenings that map a
continuous front. There is probably also a diffuse
part of the wave, but this is obscured by scattered light from the flare.
Many of the distinct brightenings
correspond remarkably well with the features seen in H
)
has a roughly
similar overall shape and angular extent. In the case of E5 (Fig. 2), the
S-wave is mainly visible due to localized brightenings that map a
continuous front. There is probably also a diffuse
part of the wave, but this is obscured by scattered light from the flare.
Many of the distinct brightenings
correspond remarkably well with the features seen in H ,
and also the overall shape and angular extent of the wavefronts
agree nicely. This supports the hypothesis that H
,
and also the overall shape and angular extent of the wavefronts
agree nicely. This supports the hypothesis that H and EIT waves are signatures of the same physical disturbance.
and EIT waves are signatures of the same physical disturbance.
The first EIT front in E3 (see Fig. 3c) was also an exception:
while it was not as thin as the S-waves (
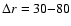 Mm), it was very bright and had a well defined leading
edge. In the other five events with EIT data coverage, only the
conventional diffuse EIT fronts were seen. This is probably due to
the low image cadence of EIT, since all of these fronts were
observed already at large distances (r > 300 Mm).
Mm), it was very bright and had a well defined leading
edge. In the other five events with EIT data coverage, only the
conventional diffuse EIT fronts were seen. This is probably due to
the low image cadence of EIT, since all of these fronts were
observed already at large distances (r > 300 Mm).
In general, there is a large range in relative intensity change
within the fronts (as obtained by applying the "profile method" to the EIT images and taking the difference of consecutive profiles). The brightness
increase averaged over the whole
wavefront ranges from more than 60% (the S-wave of E1) down to
below 10% (see also the discussion of the EIT intensity profiles in Paper II, Sect. 3.4). Several wavefronts (especially for r>600 Mm) were so faint that the brightness increase could not be measured by integrating over the front. These wavefronts were only marked by several smaller brightenings mapping out
an arc, which allowed the determination of the leading edge only with the "visual" method.
EIT waves, like Moreton waves, tend to avoid concentrations of magnetic fields,
such as ARs and polar coronal holes. This is nicely shown by E3, where the
wavefront splits into two parts before encountering a small AR in
the northern hemisphere. The influence of magnetic
structures on the wave propagation also explains the fact that the
EIT fronts that are far from the flaring AR generally have an
irregular shape, while the curvature of the fronts that are
observed near the wave origin agrees rather well with a circular
segment (cf. Fig. 1 and Sect. 4.1).
EIT waves can extend over a significant height range in the low
corona. This is demonstrated by EIT waves that are observed at the
solar limb, e.g. in E10 and E11, where the wavefront was
observable up to heights of more than 100 Mm (see also the EIT wave in Hudson et al. 2003). EIT waves that are
propagating on the disk are therefore observed as the integration
along the line of sight, projected onto the plane of sky. This
means that the apparent leading edge that is used to measure the
kinematics of the wave may not be identical to the "true" leading
edge of the wave at the height of the intersection between
chromosphere and corona. Nevertheless, since the majority of the
emission increase occurs relatively close to the surface, no
dramatic mismatches are expected. Indeed, the nearly cotemporal H and
EIT wavefronts in E1 and E5 are cospatial to within
and
EIT wavefronts in E1 and E5 are cospatial to within 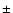 20 Mm.
20 Mm.
A discussion of the morphology of EIT waves would not be complete
without mentioning coronal dimming (see, e.g., Khan & Hudson 2000; Gopalswamy & Thompson 2000; Thompson et al. 2000). All EIT waves were associated with pronounced EUV dimming,
which is observed as a sudden significant decrease of emission behind the
EIT wavefronts. Initially, the dimming area is a rather compact region partially covering the space between the flaring AR and the EIT front (see, e.g. Figs. 2c and 3c). As the EIT wave expands, so does the dimming area behind it, though the area of significant dimming must not
necessarily expand with the wavefront during its whole
propagation. The dimming areas are rather inhomogeneous (smaller
patches within them may even show no dimming at all), they lack
sharp borders, and their average intensity relative to the emission of the quiet
corona (measured by applying the "profile method'' to the EIT frames) spans from 95% down to 65%, with a mean of 85%. The dimming areas remain stationary long after the EIT waves have vanished, and slowly return to their pre-event
brightness on a timescale of several hours.
Dimming is often associated with CMEs (e.g. Harrison et al. 2003), and indeed CMEs were detected in practically all events: no coronagraphic observations were available for E6, E7 and E9, but the observations of interplanetary type II bursts strongly suggest the presence of CMEs in E7 and E9, which leave E6 as the only event without any indication of a CME. Therefore, dimming may primarily be a result of the CME, and not of the flare waves. A closer examination of the wave-CME relation will be carried out in a forthcoming paper.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{0332fig4.eps}}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg32.gif) |
Figure 4:
The flare wave of 1998 August 24 (E9) as
shown by He I difference images a), c)
and H running difference images b), d).
The black circle in a) and c) indicates an area of decreased
He I absorption.
running difference images b), d).
The black circle in a) and c) indicates an area of decreased
He I absorption. |
| Open with DEXTER |
Figure 4 shows the He I wave of E9. The He I wave can
be seen as an expanding broad arc-shaped front of increased absorption. The
dark front has a much larger thickness 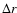 than the
corresponding H
than the
corresponding H front, it is inhomogeneous and lacks a
sharp edge. It consists of an extended diffuse component and a
number of discrete darker patches. These patches coincide with the
He I mottles that reproduce the chromospheric network,
and with the photospheric magnetic field. Thus, the patchy features
in the wavefront are caused by the increased absorption in
magnetic field concentrations (see Vrsnak et al. 2002).
front, it is inhomogeneous and lacks a
sharp edge. It consists of an extended diffuse component and a
number of discrete darker patches. These patches coincide with the
He I mottles that reproduce the chromospheric network,
and with the photospheric magnetic field. Thus, the patchy features
in the wavefront are caused by the increased absorption in
magnetic field concentrations (see Vrsnak et al. 2002).
Some regions behind the He I front show a weakening of
absorption, morphologically reminiscent of the coronal dimming
observed behind EIT waves. In E12, a comparison with the
contemporaneous EIT images shows that at the locations where the
dimming is strong in EIT, the He I absorption tends to
be reduced with respect to the pre-event state, although there is
no one-to-one correspondence (Vrsnak et al. 2002).
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig5.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg33.gif) |
Figure 5:
The flare wave of 1998 August 8 (E6) as shown by 17 GHz difference
images b)- e). a) is a pre-event direct radioheliogram showing the flaring
active region and the undisturbed chromosphere. |
| Open with DEXTER |
The two X-ray wavefronts that were observed in E3 are shown in Fig. 3.
They appear as homogeneous emission with a sharp leading
edge. Their overall shape and azimuthal extent agrees closely with
the single observed Moreton wavefront, and to a somewhat lesser
extent with the first EIT wavefront. The thickness 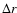 of
the X-ray wave could not be determined in this event since its
trailing edge is obscured by scattered light from the flare.
of
the X-ray wave could not be determined in this event since its
trailing edge is obscured by scattered light from the flare.
The X-ray wave in E2 (see Narukage et al. 2002) is very faint and
therefore not well suited for morphological studies. However, we
note that its overall shape and azimuthal extent again agrees reasonably well
with the Moreton wave. In E11, an arc-shaped propagating feature was detected, but since it has fixed footpoints, it is probably an erupting loop and not a wave.
3.5 17 GHz radioheliograms
A morphological study of flare wave signatures from
radioheliograms is complicated by the fact that many artifacts are
present in the images (due to the image synthesis algorithms)
which must not be confused with real features. Therefore, the
analysis will be restricted to the global appearance of the waves.
As an example, 17 GHz radioheliograms (in differenced form) are presented in Fig. 5 for E6. The wave is seen in emission and roughly resembles the accompanying Moreton wave in shape and
angular extent. However, it is more diffuse (which is at least
partly due to the limited resolution of the radioheliographic
data) and has a much larger thickness 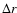 (up to 170 Mm). In the
limb events of E6 and E11, the excess emission does not extend
beyond the limb, which means that in this respect the waves
resemble more closely Moreton waves than EIT or X-ray waves.
(up to 170 Mm). In the
limb events of E6 and E11, the excess emission does not extend
beyond the limb, which means that in this respect the waves
resemble more closely Moreton waves than EIT or X-ray waves.
Since the primary contribution in the 17 GHz range is thermal
emission from the chromosphere and transition region, the wave
signature is probably due to the compression and/or heating of these
layers. In E6, the brightness temperatures 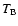 can be estimated: in the quiet chromosphere
can be estimated: in the quiet chromosphere 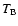 was about 10 000 K, while the maximum brightness temperature in the first clearly visible wavefront (03:17:01) was
was about 10 000 K, while the maximum brightness temperature in the first clearly visible wavefront (03:17:01) was
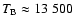 K.
K.
4.1 Wavefront shape
The leading edges of the earliest wavefronts (as determined with the "visual" method) agree very closely with a circular curvature. Figure 6 shows the deprojected leading edges of the first H wavefronts (excluding the limb events E6 to E8), together with the fitted circles (the center of the circles was used as the extrapolated wave source point). We have calculated a simple error estimate by measuring the mean absolute deviation between the actual front and the fitted circle, averaged across the whole wavefront angle, and normalized by the radius of the circle,
wavefronts (excluding the limb events E6 to E8), together with the fitted circles (the center of the circles was used as the extrapolated wave source point). We have calculated a simple error estimate by measuring the mean absolute deviation between the actual front and the fitted circle, averaged across the whole wavefront angle, and normalized by the radius of the circle,
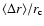 .
Excluding the limb events, where projection effects tend to increase the fitting errors,
.
Excluding the limb events, where projection effects tend to increase the fitting errors,
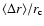 lies between 0.01 and 0.02 for the first Moreton wavefronts. An exception is E12 with
lies between 0.01 and 0.02 for the first Moreton wavefronts. An exception is E12 with
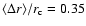 .
From Fig. 1, it is evident that E12 was the most irregular wave event. This may be due to the influence of the filament which can be seen lying in the middle of the wave's path.
.
From Fig. 1, it is evident that E12 was the most irregular wave event. This may be due to the influence of the filament which can be seen lying in the middle of the wave's path.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{0332fig6.eps}}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg38.gif) |
Figure 6:
Upper part: deprojected leading edges of the first observed H wavefronts ( black), shown together with a circular fit ( grey). Lower part: deprojected leading edges of the first EIT wavefronts in E1, E3, and E5, and of the first He I wavefront in E9. In all plots, solar north is up. The individual plots are not shown to scale. wavefronts ( black), shown together with a circular fit ( grey). Lower part: deprojected leading edges of the first EIT wavefronts in E1, E3, and E5, and of the first He I wavefront in E9. In all plots, solar north is up. The individual plots are not shown to scale. |
| Open with DEXTER |
With increasing distance, the leading edges of the wavefronts become more irregular (see Fig. 1), but generally, they retain a basic circular curvature - in many events,
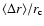 does not increase significantly. The first EIT wavefronts in E1, E3 and E5, as well as the first He I front in E9, also agree nicely with a circle (
does not increase significantly. The first EIT wavefronts in E1, E3 and E5, as well as the first He I front in E9, also agree nicely with a circle (
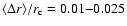 ;
see Fig. 6), whereas the EIT fronts which are farther from the flaring AR (say, r>300 Mm) show larger deviations from a circular shape (
;
see Fig. 6), whereas the EIT fronts which are farther from the flaring AR (say, r>300 Mm) show larger deviations from a circular shape (
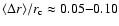 ). Still, the retention of a basic circular curvature over large distances is a strong indication of the wave-like nature of the disturbances.
). Still, the retention of a basic circular curvature over large distances is a strong indication of the wave-like nature of the disturbances.
In most events, the angular extent of the wavefronts changes with
time/distance. Therefore, an initial angular width 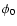 is defined, which
is the angle that the first wavefront spans, and an average propagation width
is defined, which
is the angle that the first wavefront spans, and an average propagation width 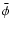 ,
which determines the angle within which the kinematics of the wave
is measured (
,
which determines the angle within which the kinematics of the wave
is measured (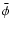 is the angle depicted in Fig. 1).
is the angle depicted in Fig. 1).
The angle 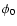 ranged from 56
ranged from 56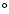 to 150
to 150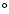 (excluding
the extreme limb events), with a mean of 99
(excluding
the extreme limb events), with a mean of 99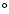 ,
while
,
while 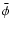 fell in the range between 15
fell in the range between 15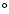 and 62
and 62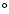 ,
with a mean value of 40
,
with a mean value of 40 .
These values agree reasonably
well with the mean Moreton angular width of 84
.
These values agree reasonably
well with the mean Moreton angular width of 84 found by
Smith & Harvey (1971), who did not make the distinction between
initial and average angle.
found by
Smith & Harvey (1971), who did not make the distinction between
initial and average angle.
In all events 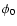 is larger than
is larger than 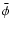 ,
which is due to two different reasons: since
,
which is due to two different reasons: since 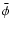 is the arc that all wavefronts have to cover, a single badly visible front (where only the central parts of the front could be identified) can significantly reduce
is the arc that all wavefronts have to cover, a single badly visible front (where only the central parts of the front could be identified) can significantly reduce 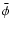 ,
although the other fronts have a consistently large angular width. On the other hand, in some events (e. g. E9 and E12) there seems to be a real physical reason behind
,
although the other fronts have a consistently large angular width. On the other hand, in some events (e. g. E9 and E12) there seems to be a real physical reason behind
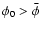 ,
because the later wavefronts really display a systematically smaller
,
because the later wavefronts really display a systematically smaller 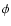 .
.
Due to their much more irregular shape, it is difficult to define the propagation
angles for EIT waves, especially since the second EIT fronts are usually too
ill-defined. It is more reasonable to compare the angular extents of the first
EIT fronts to the Moreton fronts in the three events where the EIT wave was
observed near the flaring AR. While the wavefronts in E3 and E5 agree in
angular extent, in E1 the EIT front was significantly more extended.
In E9, the only event where a direct comparison of H and He I wavefronts was possible, the initial angle
and He I wavefronts was possible, the initial angle 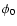 of the He I front was 115
of the He I front was 115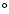 ,
whereas in H
,
whereas in H it was 150
it was 150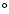 .
However, while the Moreton wave experienced very strong
shrinking (
.
However, while the Moreton wave experienced very strong
shrinking (
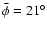 ), the He I wave remained
comparatively broad (
), the He I wave remained
comparatively broad (
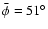 ).
).
The X-ray waves had similar angular extents as the accompanying
H waves and did not show signs of shrinking. The wavefronts seen in the radioheliograms were too
diffuse and noisy to allow a quantitative definition of the propagation angle, but they were broadly similar to the Moreton waves.
waves and did not show signs of shrinking. The wavefronts seen in the radioheliograms were too
diffuse and noisy to allow a quantitative definition of the propagation angle, but they were broadly similar to the Moreton waves.
In all nine cases where the starting location could be determined (excluding the
limb events E6, E7 and E8), the calculated origin of the wave was lying in the periphery of the flaring AR, clearly displaced from the central parts of the flare (see
Fig. 1). The distance between the starting point and the center of the
H flare amounted to 25-164 Mm, with a mean of 58 Mm. The two largest
offsets (in E9 and E12) could be accounted for by the fact that the wavefronts
were centered on remote flare brightenings of weaker intensity that might be
responsible for the wave launch. However, even when we exclude E9 and E12,
the mean value for the displacement from the flare center is 40 Mm.
flare amounted to 25-164 Mm, with a mean of 58 Mm. The two largest
offsets (in E9 and E12) could be accounted for by the fact that the wavefronts
were centered on remote flare brightenings of weaker intensity that might be
responsible for the wave launch. However, even when we exclude E9 and E12,
the mean value for the displacement from the flare center is 40 Mm.
It might be argued that the calculated starting points do not really
represent the true wave origins. In E1, E3 and E5, both the H and the
first EIT wavefronts are defined clearly enough so that they can be used to
extrapolate starting points independently. The same is true for the X-ray wave
in E3 and the He I wave in E9. The various calculated origins differ
on average by about 40 Mm. If we assume that all different signatures originate
from the same location, this in a way defines the accuracy of the extrapolation
method. The measured offsets of the starting locations from the associated
flares are of about this value, but since the calculated sources are
systematically displaced in the direction away from the flare, the offsets have
to be considered as real. Furthermore, Khan & Aurass (2002) and Hudson et al. (2003) also found these offsets using a totally different extrapolation technique.
and the
first EIT wavefronts are defined clearly enough so that they can be used to
extrapolate starting points independently. The same is true for the X-ray wave
in E3 and the He I wave in E9. The various calculated origins differ
on average by about 40 Mm. If we assume that all different signatures originate
from the same location, this in a way defines the accuracy of the extrapolation
method. The measured offsets of the starting locations from the associated
flares are of about this value, but since the calculated sources are
systematically displaced in the direction away from the flare, the offsets have
to be considered as real. Furthermore, Khan & Aurass (2002) and Hudson et al. (2003) also found these offsets using a totally different extrapolation technique.
5.1 H
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig7.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg48.gif) |
Figure 7:
The kinematics of the leading edges of the Moreton waves (visually
determined from H difference images) of the events E1 to E12 (excluding E3, where only one wavefront was observed). The distances r(t) ( crosses) are
plotted together with 2nd degree polynomial least-squares fits (thick
line) and power-law fits (thin line). The time t is counted from the
estimated starting time
difference images) of the events E1 to E12 (excluding E3, where only one wavefront was observed). The distances r(t) ( crosses) are
plotted together with 2nd degree polynomial least-squares fits (thick
line) and power-law fits (thin line). The time t is counted from the
estimated starting time
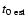 (t0 in these plots). Distances are given
in Mm (103 km).
(t0 in these plots). Distances are given
in Mm (103 km). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig8.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg49.gif) |
Figure 8:
The velocities v(t) ( crosses) derived from consecutive Moreton
wavefront pairs of events E1 to E12 (excluding E3). Also shown is the
derivative of the power-law fits of r(t) (thick line) and a 2nd degree polynomial fit of v(t) (thin line). Velocities are given in km s-1. |
| Open with DEXTER |
In Fig. 7 the distance r of the leading
edge of the H wavefronts from the calculated source point
is shown as a function of time t for all studied events except E3, where only a single Moreton wavefront was detected.
In all subsequent figures, the zero time t=0 corresponds to
the estimated starting time
wavefronts from the calculated source point
is shown as a function of time t for all studied events except E3, where only a single Moreton wavefront was detected.
In all subsequent figures, the zero time t=0 corresponds to
the estimated starting time
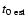 of the disturbances.
Overplotted are 2nd degree polynomial fits and power-law fits of the form
of the disturbances.
Overplotted are 2nd degree polynomial fits and power-law fits of the form
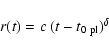 |
(1) |
where 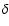 is the power-law exponent,
is the power-law exponent,
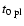 the starting
time given by the fit (t at r=0), and c is a constant.
the starting
time given by the fit (t at r=0), and c is a constant.
Figure 8
shows the velocities v derived from the consecutive wavefront
pairs. The rather large scatter in some of the v data points is due to two causes. Firstly, errors in the determination of the leading edge are amplified since each velocity is derived from a wavefront pair. Secondly, the propagation of the wavefronts often becomes inclined with respect to the great circles along which r(t) is measured, which leads to an increase in the range of measured velocities.
From the plots in Figs. 7 and 8, it is evident that all Moreton waves
experience significant deceleration during their propagation.
Table 3 shows the kinematical parameters for all events, measured
using the "visual" method. In E1, E2, E4, E6 and E12, images
taken in H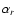 were used for deriving the
kinematical parameters since the waves have the highest contrast
in this spectral band. Table 3 includes the
measured first and last velocities v1 and vl (derived
from the first and the last wavefront pair), the velocity
were used for deriving the
kinematical parameters since the waves have the highest contrast
in this spectral band. Table 3 includes the
measured first and last velocities v1 and vl (derived
from the first and the last wavefront pair), the velocity
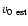 obtained
from the 2nd degree polynomial fit at
obtained
from the 2nd degree polynomial fit at
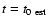 ,
the mean velocity
,
the mean velocity 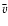 derived from a linear fit of r(t), the minimum and maximum distances
derived from a linear fit of r(t), the minimum and maximum distances
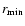 and
and
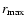 of the wavefronts, the average deceleration
of the wavefronts, the average deceleration 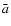 derived from the polynomial fits, and finally the power-law exponent
derived from the polynomial fits, and finally the power-law exponent 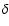 .
.
Table 3:
H Moreton wave kinematics derived with the "visual" method. v1
and vl are the measured first and last velocities,
Moreton wave kinematics derived with the "visual" method. v1
and vl are the measured first and last velocities,
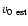 the
velocity obtained from the polynomial fit of r(t) at the estimated starting
time,
the
velocity obtained from the polynomial fit of r(t) at the estimated starting
time, 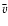 the mean velocity derived from a linear fit,
the mean velocity derived from a linear fit,
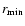 and
and
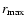 the minimum and maximum distances of the wavefronts,
the minimum and maximum distances of the wavefronts, 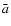 the
average deceleration derived from the polynomial fits, and
the
average deceleration derived from the polynomial fits, and 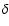 is the exponent of the power-law fits. The last four rows give the mean
values and standard deviations
is the exponent of the power-law fits. The last four rows give the mean
values and standard deviations 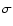 of the parameters obtained by the
"visual" and the "profile method", respectively. Values in brackets are
inaccurate and are not used for deriving the mean values. Decelerations are
given in m s-2, velocities in km s-1, and distances in Mm (103 km).
of the parameters obtained by the
"visual" and the "profile method", respectively. Values in brackets are
inaccurate and are not used for deriving the mean values. Decelerations are
given in m s-2, velocities in km s-1, and distances in Mm (103 km).
In the last four rows of Table 3 the results are summarized by
displaying the mean values and standard deviations of all parameters for the
visual and the profile method, respectively (the "profile-method" values for
the individual events are not shown in the table). The summary shows that the
kinematical parameters derived by the two different measurement techniques (note
that the average "profile" values do not include E1 due to the lack of a suitable pre-event image) are generally in a good agreement, and some of them agree exceptionally well, e.g. 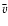 .
.
The good correspondence between the mean kinematical values given by the visual
and the profile method proves that both schemes generally reproduce the
true kinematics of the Moreton waves well. However, it seems that
usually the visual method is more accurate in determining the
leading edge of the disturbances, and henceforth we will refer
only to the "visual" parameters in our discussion.
The first measured velocities v1 have a mean of
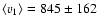 km s-1. The mean of the average velocities amounts to
km s-1. The mean of the average velocities amounts to
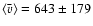 km s-1, which agrees very closely with the
value of
km s-1, which agrees very closely with the
value of
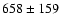 km s-1 found by Smith & Harvey (1971).
Evidently, Smith & Harvey were using linear fits and did not
detect the deceleration.
km s-1 found by Smith & Harvey (1971).
Evidently, Smith & Harvey were using linear fits and did not
detect the deceleration.
The average decelerations 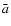 have a much larger scatter than the velocities, with a mean of
have a much larger scatter than the velocities, with a mean of
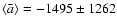 m s-2. The waves do not display
a constant deceleration, instead, the deceleration tends to become weaker
with increasing time and distance. For example, if only the first
three fronts are used to derive the polynomial fits, then the mean
of all decelerations is significantly larger at
m s-2. The waves do not display
a constant deceleration, instead, the deceleration tends to become weaker
with increasing time and distance. For example, if only the first
three fronts are used to derive the polynomial fits, then the mean
of all decelerations is significantly larger at
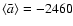 m s-2. Consequently, the kinematical paths of
the wavefronts are represented better by the power-law
fits. This is also evident from the calculated exponent
m s-2. Consequently, the kinematical paths of
the wavefronts are represented better by the power-law
fits. This is also evident from the calculated exponent 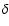 ,
which has a smaller scatter than
,
which has a smaller scatter than 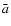 :
its average over all events was
:
its average over all events was
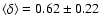 .
.
The Moreton waves could be tracked out to
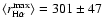 Mm, and were first observed at a
distance of
Mm, and were first observed at a
distance of
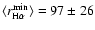 Mm (these averages
exclude the events where the starting location could not be back-extrapolated,
and also E3, which had a low image cadence in H
Mm (these averages
exclude the events where the starting location could not be back-extrapolated,
and also E3, which had a low image cadence in H ).
).
Interestingly, the extrapolated wavefront distance r0 at the
starting time
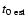 (not shown in Table 3) is rather large with a mean of
(not shown in Table 3) is rather large with a mean of
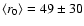 Mm. This means that either the waves are starting from
a location significantly farther out, the assumed starting times
are too late, or the disturbances are initially significantly
faster and suffer a strong initial deceleration. The first
possibility is unlikely since the extrapolation method is too
accurate to account for such large mismatches. Conversely, it might well be that the disturbances are only visible in H
Mm. This means that either the waves are starting from
a location significantly farther out, the assumed starting times
are too late, or the disturbances are initially significantly
faster and suffer a strong initial deceleration. The first
possibility is unlikely since the extrapolation method is too
accurate to account for such large mismatches. Conversely, it might well be that the disturbances are only visible in H after they have steepened sufficiently. The waves would have already been launched at
after they have steepened sufficiently. The waves would have already been launched at
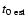 ,
but would only be detected on a later H
,
but would only be detected on a later H image. If that is the case, we can adopt a new starting time
image. If that is the case, we can adopt a new starting time
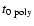 ,
which is the time at which the polynomial fit of r(t) reaches r=0.
,
which is the time at which the polynomial fit of r(t) reaches r=0.
On the other hand, we have seen that the power-law fits seem to represent the kinematics of the waves better, and they yield higher initial deceleration, which would reduce r0. An even stronger initial deceleration than the one predicted by the power-law fits may be caused by the denser medium close to the AR.
From the available data, it is not possible to determine which of the two effects is dominating, and therefore the "true'' launch time of the disturbances cannot be derived. However, for our present purposes, we have no need of more accurate starting times. Generally,
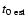 and
and
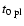 were in rough agreement (to
were in rough agreement (to 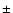 30 s), while
30 s), while
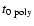 was systematically earlier by
was systematically earlier by  1 min.
1 min.
5.2 EIT
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig9.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg67.gif) |
Figure 9:
The combined kinematics of the Moreton and EIT wavefronts for all
events with EIT data coverage, except for E9 where H is
combined with He I.
is
combined with He I.
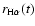 ( crosses) and
( crosses) and
 ( circles) are plotted together with 2nd degree polynomial fits
(thick line) and power-law fits (thin line) of the combined
distances r(t). For E3, the positions of the X-ray wave ( triangles) are
indicated, too, while for E9, both
( circles) are plotted together with 2nd degree polynomial fits
(thick line) and power-law fits (thin line) of the combined
distances r(t). For E3, the positions of the X-ray wave ( triangles) are
indicated, too, while for E9, both
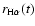 and
and
 ( diamonds) are plotted together with 2nd degree
polynomial fits of the two data types. For E12,
( diamonds) are plotted together with 2nd degree
polynomial fits of the two data types. For E12,
 (determined with the "profile" method) is shown together with the fits of the combined H
(determined with the "profile" method) is shown together with the fits of the combined H and EIT fronts.
and EIT fronts. |
| Open with DEXTER |
In Fig. 9 the distances r(t) for the
observed EIT wavefronts are plotted together with the distances of the H fronts for all events with EIT coverage, and for E9 (Fig. 9f), for which He I instead of EIT wavefronts are plotted. Also shown are 2nd degree
polynomial fits and power-law fits applied to the combinations of H
fronts for all events with EIT coverage, and for E9 (Fig. 9f), for which He I instead of EIT wavefronts are plotted. Also shown are 2nd degree
polynomial fits and power-law fits applied to the combinations of H and EIT r(t) data points. If Moreton waves and EIT waves are signatures of the
same physical disturbance, they should lie on closely associated kinematical
curves. Indeed, Fig. 9 shows that in most events EIT and H
and EIT r(t) data points. If Moreton waves and EIT waves are signatures of the
same physical disturbance, they should lie on closely associated kinematical
curves. Indeed, Fig. 9 shows that in most events EIT and H wavefronts agree quite well with the fitted curves. The agreement is best in E1
and E5, and worst in E10, which might be due to the poor H
wavefronts agree quite well with the fitted curves. The agreement is best in E1
and E5, and worst in E10, which might be due to the poor H data quality in
that event.
data quality in
that event.
In Table 4 the kinematical properties of the EIT waves are listed, as
well as the parameters derived from the combined EIT and H data (denoted
by the suffix cb). This includes
the mean EIT velocities
data (denoted
by the suffix cb). This includes
the mean EIT velocities
 ,
the minimum and
maximum EIT distances
,
the minimum and
maximum EIT distances
 and
and
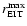 ,
the mean
combined velocities
,
the mean
combined velocities
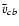 ,
the mean
combined decelerations
,
the mean
combined decelerations
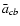 ,
and the exponent
,
and the exponent
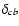 of the
power-law fits of the combined data.
of the
power-law fits of the combined data.
The EIT wave velocities
 are significantly
lower than the H
are significantly
lower than the H speeds. The mean value is
speeds. The mean value is
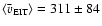 km s-1. In all events, the
fits of the combined H
km s-1. In all events, the
fits of the combined H and EIT data show significant decelerations, and
and EIT data show significant decelerations, and
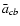 is smaller (i.e. less negative) than
is smaller (i.e. less negative) than
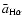 in every case. This is a consequence of the
decrease of the deceleration with increasing time and distance.
in every case. This is a consequence of the
decrease of the deceleration with increasing time and distance.
The power-law exponent is
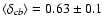 for
the combined data. When only the seven events that have EIT data
coverage and more than one Moreton wavefront are considered, so that the same
events are included in averaging, then
for
the combined data. When only the seven events that have EIT data
coverage and more than one Moreton wavefront are considered, so that the same
events are included in averaging, then
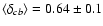 and
and
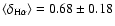 .
This close agreement of
.
This close agreement of
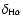 and
and
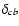 once more shows that Moreton and EIT waves are following kinematical curves that are closely associated.
once more shows that Moreton and EIT waves are following kinematical curves that are closely associated.
The EIT wave of E1 was the only one where three wavefronts could
be identified, and a deceleration of
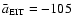 m s-2 could be derived. As a comparison, for the EIT waves of 1997 April 7 (Thompson et al. 1999) and 1997 May 12 (Thompson et al. 1998), decelerations were found of -242 m s-2 and -62 m s-2 (derived from the first three fronts), respectively. This shows that deceleration is also detectable in EIT wave events that are not associated with H
m s-2 could be derived. As a comparison, for the EIT waves of 1997 April 7 (Thompson et al. 1999) and 1997 May 12 (Thompson et al. 1998), decelerations were found of -242 m s-2 and -62 m s-2 (derived from the first three fronts), respectively. This shows that deceleration is also detectable in EIT wave events that are not associated with H signatures.
signatures.
The mean minimum and maximum observed distances of the EIT fronts
were
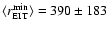 Mm and
Mm and
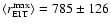 Mm, which are both significantly larger than
the corresponding values for the Moreton waves. Comparison of the values of
Mm, which are both significantly larger than
the corresponding values for the Moreton waves. Comparison of the values of
 clearly shows that EIT waves can be traced to much larger
distances than Moreton waves. On the other hand, the large
clearly shows that EIT waves can be traced to much larger
distances than Moreton waves. On the other hand, the large
 are the consequence of the low image cadence of EIT.
are the consequence of the low image cadence of EIT.
In Fig. 9f, r(t) of the He I and the H fronts
is plotted for E9 (in Fig. 9i, the He I fronts determined with the "profile" method are shown for E12, but the plot is quite crowded). Again the deceleration is evident. The He I and H
fronts
is plotted for E9 (in Fig. 9i, the He I fronts determined with the "profile" method are shown for E12, but the plot is quite crowded). Again the deceleration is evident. The He I and H perturbations are obviously related since they follow closely associated kinematical curves. Yet the
He I fronts are leading the H
perturbations are obviously related since they follow closely associated kinematical curves. Yet the
He I fronts are leading the H fronts by about 30 Mm. The same was found for E12. This behavior was interpreted by Vrsnak et al. (2002) in terms of a signal which reaches the chromosphere before the actual shock arrival, and we will return to discuss it in Paper II.
fronts by about 30 Mm. The same was found for E12. This behavior was interpreted by Vrsnak et al. (2002) in terms of a signal which reaches the chromosphere before the actual shock arrival, and we will return to discuss it in Paper II.
The He I velocities (e.g., E9:
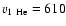 km s-1) as well
as the deceleration
km s-1) as well
as the deceleration
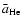 lie in between the usual values for H
lie in between the usual values for H and EIT waves. This is due to the fact that the
He I wavefronts are observed both close to the flaring AR (a consequence of the 3 min cadence of the He I filtergrams) and at large distances where H
and EIT waves. This is due to the fact that the
He I wavefronts are observed both close to the flaring AR (a consequence of the 3 min cadence of the He I filtergrams) and at large distances where H waves are no
longer detectable (E9:
waves are no
longer detectable (E9:
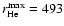 Mm,
Mm,
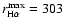 Mm). In that way, the He I disturbances may be regarded as a "missing link"
between Moreton and EIT waves.
Mm). In that way, the He I disturbances may be regarded as a "missing link"
between Moreton and EIT waves.
In E2, the X-ray fronts were very dim and diffuse, and no detailed
analysis was performed. However, the kinematics of the X-ray wave
is reported by Narukage et al. (2002), who found an average speed
of
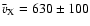 km s-1. The X-ray wavefronts were found to lead the Moreton fronts by
km s-1. The X-ray wavefronts were found to lead the Moreton fronts by 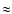 10-20 Mm.
10-20 Mm.
The two X-ray wavefronts of E3 yield a speed of
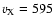 km s-1.
Figure 9c shows that the two X-ray fronts, the single H
km s-1.
Figure 9c shows that the two X-ray fronts, the single H front, and the first EIT front give a remarkably consistent kinematical picture. An
average deceleration of
front, and the first EIT front give a remarkably consistent kinematical picture. An
average deceleration of
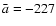 m s-2 is found for the combined
data.
m s-2 is found for the combined
data.
In both events, the maximum distance at which the X-ray wave was
observable was 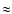 200 Mm, which is less than
200 Mm, which is less than
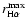 .
We
conclude that X-ray waves can also be attributed to the same disturbance that
creates the other signatures of flare waves.
.
We
conclude that X-ray waves can also be attributed to the same disturbance that
creates the other signatures of flare waves.
Due to their diffuse and noisy nature no detailed study of the
kinematics of the flare waves visible in the 17 GHz
radioheliograms has been carried out. However, as the morphological studies have
shown (see Sect. 3.5), the 17 GHz waves are closely associated with Moreton
waves, and it is reasonable to assume that their kinematical parameters will be
broadly similar, too. Indeed, the r(t) measurements in E6 show that the 17 GHz disturbance follows the same kinematical curve as the Moreton
wave, but it seems to lead by 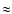 20 Mm (note that this value is highly
ambiguous due to the low accuracy of the distance measurements).
20 Mm (note that this value is highly
ambiguous due to the low accuracy of the distance measurements).
Table 4:
EIT and combined H /EIT wave kinematics.
/EIT wave kinematics.
 is the mean EIT velocity,
is the mean EIT velocity,
 and
and
 the minimum and maximum EIT distance,
the minimum and maximum EIT distance,
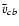 the
mean combined velocity,
the
mean combined velocity,
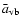 the mean combined deceleration, and
the mean combined deceleration, and
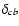 the exponent of the power-law fits
of the combined data.
the exponent of the power-law fits
of the combined data.
Signatures of flare waves were found in five different spectral
bands - H (line center and wings), EUV, He I,
SXR and 17 GHz. It seems that in a flare wave event of sufficient amplitude all signatures are present. The waves in the different channels were found to follow closely associated kinematical curves, which suggests that they are caused by the same physical disturbance. In the case of H
(line center and wings), EUV, He I,
SXR and 17 GHz. It seems that in a flare wave event of sufficient amplitude all signatures are present. The waves in the different channels were found to follow closely associated kinematical curves, which suggests that they are caused by the same physical disturbance. In the case of H and EIT waves, the close association is directly evident from the
observations of nearly cospatial (and morphologically similar)
H
and EIT waves, the close association is directly evident from the
observations of nearly cospatial (and morphologically similar)
H and EIT wavefronts in E1 and especially in E5 (see Sect. 3.2).
and EIT wavefronts in E1 and especially in E5 (see Sect. 3.2).
The presented analysis shows that all flare waves are decelerating. This causes
an artificial velocity discrepancy between EIT and H signatures: the EIT signatures must show lower mean velocities than their H
signatures: the EIT signatures must show lower mean velocities than their H counterparts
because they can be traced to much larger distances (
counterparts
because they can be traced to much larger distances (
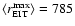 Mm, compared to
Mm, compared to
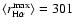 Mm). For example, the mean H
Mm). For example, the mean H wave speed is
wave speed is
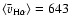 km s-1, while the mean EIT wave speed
km s-1, while the mean EIT wave speed
 is just 311 km s-1. The discrepancy is increased furthermore by the low cadence of the EIT observation, resulting in a poor coverage of fast events (i.e. a fast wave is recorded on only one image, which is insufficient for speed estimates).
is just 311 km s-1. The discrepancy is increased furthermore by the low cadence of the EIT observation, resulting in a poor coverage of fast events (i.e. a fast wave is recorded on only one image, which is insufficient for speed estimates).
It should be noted that Eto et al. (2002) conclude that Moreton
and EIT waves are not closely related. They studied E4 and found that a
small filament far from the AR started oscillating. They concluded
that the Moreton wave (assuming constant propagation speed) could
well have activated the filament, but the location of the EIT wave was
found to be inconsistent with this picture - the EIT wavefront
which was observed 2 min after the start of the filament
oscillation had not yet reached the filament.
While we find this inconsistency to be somewhat smaller than reported in Eto et al. (2002), the oscillation still seems to have been initiated before the EIT wave had reached the filament. This might be due to the fact that the wave is actually inclined to the solar surface (as is the case for the event studied by Hudson et al. 2003), and has already progressed farther at greater heights where the wave is not observable with EIT (at least not on the disk). Since the filament is also extended in height - it was a polar crown filament and their heights are typically several tens of Mm - the interaction with the flare wave could actually be initiated before the parts of the wave that are
propagating at the coronal base reach the filament.
Recently, Chen et al. (2002) found from a numerical simulation that an erupting flux rope would generate two distinct waves. A fast wave (a slightly supermagnetosonic shock) would be piston-driven by the expanding CME. This wave is identified with the Moreton wave, and referred to as "coronal Moreton wave". In addition, a slower wavefront would be generated by the successive opening of field lines, producing successive density enhancements. This disturbance (which is not a real wave) would correspond to the EIT wave and trail behind the fast wave at roughly one third of the velocity of the latter. Harra & Sterling (2003) provided some observational evidence for this model using a weak flare wave event.
However, among the class of events we are studying (which all showed initially fairly "sharp" disturbances), we do not find evidence supporting the Chen model. First, we do not observe two distinct wavefronts in any of our wavelength ranges. The two-part structure of the He I disturbances also cannot be interpreted in the framework of the Chen model, since they move basically at the same speeds. Lastly, the EIT wave in the Chen model decelerates much more strongly than the Moreton wave (see Fig. 2 in Chen et al. 2002), which is contrary to what we found (see Sect. 5.2).
Even though we cannot support the conclusions reached by Eto et al. (2002) and Chen et al. (2002), these studies again pose the question if EIT waves in general can be attributed to the same class of
disturbances as Moreton waves. The average EIT wave speed for the eight events
of this study is
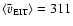 km s-1, while it is
slightly lower (
km s-1, while it is
slightly lower (
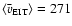 km s-1)
for the 20 events in Klassen et al. (2000), and much lower (
km s-1)
for the 20 events in Klassen et al. (2000), and much lower (
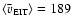 km s-1) for the 176 events in studied by Myers & Thompson (Thompson, private communications). Based on these velocities, we can conclude that the EIT waves of Klassen et al. (2000) belong to the same class of events as the EIT waves presented in this study. The sample of Myers & Thompson, on the
other hand, contains many events with speeds of just several tens of km s-1, i.e. one order of magnitude lower than the
characteristic speeds of flare waves. It is therefore probable
that this sample contains EIT disturbances that are not really
waves at all, but which are generated by a totally different
physical process than the "real" EIT waves which are produced by
the same disturbance that causes the flare waves in the
other spectral channels. Hence, we conclude that at least the EIT waves in our sample are caused by the same disturbance that creates the Moreton waves and the other signatures of flare waves in additional spectral channels.
km s-1) for the 176 events in studied by Myers & Thompson (Thompson, private communications). Based on these velocities, we can conclude that the EIT waves of Klassen et al. (2000) belong to the same class of events as the EIT waves presented in this study. The sample of Myers & Thompson, on the
other hand, contains many events with speeds of just several tens of km s-1, i.e. one order of magnitude lower than the
characteristic speeds of flare waves. It is therefore probable
that this sample contains EIT disturbances that are not really
waves at all, but which are generated by a totally different
physical process than the "real" EIT waves which are produced by
the same disturbance that causes the flare waves in the
other spectral channels. Hence, we conclude that at least the EIT waves in our sample are caused by the same disturbance that creates the Moreton waves and the other signatures of flare waves in additional spectral channels.
The He I waves have kinematical parameters that lie in between the values for H and EIT waves,
and can thus be regarded as a "missing link" between Moreton and EIT waves,
which further strengthens the argument that all signatures of
flare waves are caused by a common agent. However, the He I signatures lead the Moreton fronts by 20-40 Mm. Therefore some agent
must be present that creates the observed He I signatures even before
the shock arrives at a given point of the chromosphere (see Vrsnak et al. 2002). This could be also
related to the "premature" activation of the filament in E4.
and EIT waves,
and can thus be regarded as a "missing link" between Moreton and EIT waves,
which further strengthens the argument that all signatures of
flare waves are caused by a common agent. However, the He I signatures lead the Moreton fronts by 20-40 Mm. Therefore some agent
must be present that creates the observed He I signatures even before
the shock arrives at a given point of the chromosphere (see Vrsnak et al. 2002). This could be also
related to the "premature" activation of the filament in E4.
In the events with X-ray and radioheliographic flare waves, the
disturbances are found to be closely associated with the Moreton
waves. They follow basically the same kinematical curves,
and are either cospatial with the Moreton fronts, or are slightly ahead of them (by 10-20 Mm).
12 H Moreton wave events have been studied. For these events, wave signatures were also detected in EIT Fe XII images, in He I filtergrams, in Yohkoh/SXT images, and in 17 GHz
radioheliograms, and it seems that in an event of sufficient amplitude all of these signatures will be present. In H
Moreton wave events have been studied. For these events, wave signatures were also detected in EIT Fe XII images, in He I filtergrams, in Yohkoh/SXT images, and in 17 GHz
radioheliograms, and it seems that in an event of sufficient amplitude all of these signatures will be present. In H ,
it was evident that the signatures were created by an enhancement of pre-existing chromospheric structures, and at all wavelengths the leading edges of the wavefronts showed good agreement with a circular fit. These results confirm the wave-like nature of the disturbances, and rule out scenarios in which the wavefronts are directly created by propagating matter (e.g. ejected material impacting on the chromosphere) or other non-wave agents.
,
it was evident that the signatures were created by an enhancement of pre-existing chromospheric structures, and at all wavelengths the leading edges of the wavefronts showed good agreement with a circular fit. These results confirm the wave-like nature of the disturbances, and rule out scenarios in which the wavefronts are directly created by propagating matter (e.g. ejected material impacting on the chromosphere) or other non-wave agents.
The flare waves seen in the different spectral channels all follow closely associated kinematical curves, which implies that they are caused by a common physical disturbance. This notion is supported by morphological similarities between the different signatures. Furthermore, it was found that the waves do not propagate with constant velocities, instead, all flare waves are decelerating. This confirms the results obtained by Warmuth et al. (2001) and Vrsnak et al. (2002). The deceleration rate becomes smaller with increasing distance from their source point.
It was shown that there is no "velocity discrepancy" between Moreton and EIT waves. The differences in the measured speeds can be explained by the deceleration of the disturbance, combined with the fact that its signatures can be traced to much larger distances in EIT than in H ,
and with the low image cadence of EIT.
,
and with the low image cadence of EIT.
The main aim of this paper has been the establishment of the basic properties of the flare waves observed in the different spectral bands - their morphology, their spatial characteristics and their kinematics. In Paper II (Warmuth et al. 2004), we will combine these results with studies of the perturbation characteristics and the associated metric type II radio bursts to derive a consistent physical interpretation of the flare wave phenomenon.
Acknowledgements
The work of A.W. was supported by DLR under grant No. 50 QL 0001.
H data are used with permission of BBSO, New Jersey Institute of
Technology, and we thank the BBSO staff for their kind support. We are very
grateful to H. Kurokawa and K. Shibata for the provision of H
data are used with permission of BBSO, New Jersey Institute of
Technology, and we thank the BBSO staff for their kind support. We are very
grateful to H. Kurokawa and K. Shibata for the provision of H data from
Hida Observatory. He I data were provided by the High Altitude
Observatory of the National Center for Atmospheric Research, which is sponsored
by the National Science Foundation, and we thank T. Holzer, H. Gilbert and A.
Stanger for their support. Radioheliograms from the Nobeyama Radio Observatory
were kindly provided by K. Shibasaki. We thank B. J. Thompson for the provision
of H
data from
Hida Observatory. He I data were provided by the High Altitude
Observatory of the National Center for Atmospheric Research, which is sponsored
by the National Science Foundation, and we thank T. Holzer, H. Gilbert and A.
Stanger for their support. Radioheliograms from the Nobeyama Radio Observatory
were kindly provided by K. Shibasaki. We thank B. J. Thompson for the provision
of H data, A. Vourlidas for corrected EIT times, and G. Mann, H. Aurass, and A. Klassen for helpful discussions. SOHO is a project of international cooperation between ESA and NASA.
Yohkoh is a mission of the Institute of Space and Astronautical Sciences (Japan), with participation from the US (NASA) and UK (PPARC). A.W. and A.H. acknowledge the
support of the Austrian FWF Project P13653-PHY.
data, A. Vourlidas for corrected EIT times, and G. Mann, H. Aurass, and A. Klassen for helpful discussions. SOHO is a project of international cooperation between ESA and NASA.
Yohkoh is a mission of the Institute of Space and Astronautical Sciences (Japan), with participation from the US (NASA) and UK (PPARC). A.W. and A.H. acknowledge the
support of the Austrian FWF Project P13653-PHY.
- Andretta,
V., & Jones, H. P. 1997, ApJ, 489, 375 [NASA ADS] [CrossRef] (In the text)
- Athay, R. G.,
& Moreton, G. E. 1961, AJ, 133, 935 [NASA ADS] [CrossRef] (In the text)
- Becker, U.
1958, Z. Astrophys., 44, 243 [NASA ADS] (In the text)
-
Biesecker, D. A., & Thompson, B. J. 2000, J. Atmos. and
Sol.-Terr. Phys., 62, 1449 [NASA ADS] (In the text)
-
Biesecker, D. A., Myers, D. C., Thompson, B. J., Hammer, D. M.,
& Vourlidas, A. 2002, ApJ, 569, 1009 [NASA ADS] [CrossRef] (In the text)
- Cliver, E. W.,
Webb, D. F., & Howard, R. A. 1999, Sol. Phys., 187, 89 [NASA ADS] [CrossRef] (In the text)
- Chen, P. F., Wu, S.
T., Shibata, K., & Fang, C. 2002, ApJ, 572, L99 [NASA ADS] [CrossRef] (In the text)
-
Delaboudinière, J.-P., Artzner, G. E., Brunaud, J., et al.
1995, Sol. Phys., 162, 291 [NASA ADS]
- Denker, C.,
Johannesson, A., Marquette, W., et al. 1999, Sol. Phys., 184,
87 [NASA ADS] [CrossRef]
- Dodson, H. W.
1949, ApJ, 110, 382 [NASA ADS] [CrossRef] (In the text)
- Eto, S., Isobe, H.,
Narukage, N., et al. 2002, PASJ, 54, 481 [NASA ADS] (In the text)
- Gilbert, H.
R., Thompson, B. J., Holzer, T. E., & Burkepile, J. T. 2001,
AGU Fall Meeting 2001, abstract SH12B-0746
(In the text)
-
Gopalswamy, N., & Thompson, B. J. 2000, J. Atmos. and
Sol.-Terr. Phys., 62, 1457 [NASA ADS] (In the text)
- Harra, L. K.,
& Sterling, A. C. 2003, ApJ, 587, 429 [NASA ADS] [CrossRef] (In the text)
- Harrison,
R. A., Bryans, P., Simnett, G. M., & Lyons, M. 2003, A&A,
400, 1071 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Harvey, K. L.,
Martin, S. F., & Riddle, A. C. 1974, Sol. Phys., 36, 151 [NASA ADS] (In the text)
- Hudson, H. S.,
Khan, J. I., Lemen, J. R., Nitta, N. V., & Uchida, Y. 2003,
Sol. Phys., 212, 121 [NASA ADS] [CrossRef] (In the text)
- Kerdraon,
A., & Delouis, J.-M. 1997, in Coronal Physics from Radio and
Space Observations, ed. G. Trottet (Berlin: Springer), Lect. Notes
Phys., 483, 192
(In the text)
- Khan, J. I., &
Hudson, H. S. 2000, GRL, 27, 1083 (In the text)
- Khan, J. I., &
Aurass, H. 2002, A&A, 383, 1018 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Klassen, A.,
Aurass, H., Mann, G., & Thompson, B. J. 2000, A&AS, 141,
357 [NASA ADS] (In the text)
- Kurokawa,
H., Ishiura, K., Kimura, G., et al. 1995, J. Geomag Geoelecter, 47,
1043 [NASA ADS]
- MacQueen,
R. M., Blankner, J. G., Elmore, D. F., Lecinski, A. R., &
White, O. R. 1998, Sol. Phys., 182, 97 [NASA ADS] [CrossRef]
-
Messerotti, M., Otruba, W., Warmuth, A., et al. 1999, in Proc. ESA
Workshop on Space Weather, ed. N. Crosby, ESA WPP-155, 321
- Moreton, G.
E. 1960, AJ, 65, 494 [NASA ADS] [CrossRef] (In the text)
- Moreton, G.
E., & Ramsey, H. E. 1960, PASP, 72, 357 [NASA ADS] [CrossRef] (In the text)
- Moreton, G.
E. 1964, AJ, 69, 145 [NASA ADS] [CrossRef] (In the text)
- Nakajima,
H., Nishio, M., Enome, S., et al. 1994, Proc. IEEE, 82, 705 [NASA ADS] [CrossRef]
- Narukage,
N., Hudson, H. S., Morimoto, T., et al. 2002, ApJ, 572, L109 [NASA ADS] [CrossRef] (In the text)
- Nelson, G. S.,
& Melrose, D. B. 1985, in Solar Radiophysics, ed. D. J. McLean,
& N. R. Labrum (Cambridge: Cambridge Univ. Press), 333
(In the text)
- Pinter, S.
1977, Spec. Rep. AFGL-SR-209, Hanscom Air Force Base, 35
(In the text)
-
Pohjolainen, S., Maia, D., Pick, M., et al. 2001, ApJ, 556,
421 [NASA ADS] [CrossRef]
- Ramsey, H. E.,
& Smith, S. F. 1966, AJ, 71, 197 [NASA ADS] [CrossRef] (In the text)
- Shibata, K.,
Eto, S., Narukage, N., et al. 2002, in Proc. Yohkoh 10th
Anniversary Meeting, ed. P. Martens, Cospar Colloq., 13, 279
(In the text)
- Smith, S. F.,
& Harvey, K. L. 1971, in Physics of the Solar Corona, ed. C. J.
Macris (Dordrecht: Reidel), 156
(In the text)
- Thompson,
B. J., Plunkett, S. P., Gurman, J. B., et al. 1998, Geophys. Res.
Lett., 25, 2465 [NASA ADS] [CrossRef] (In the text)
- Thompson,
B. J., Gurman, J. B., Neupert, W. M., et al. 1999, ApJ, 517,
L151 [NASA ADS] [CrossRef] (In the text)
- Thompson,
B. J., Reynolds, B., Aurass, H., et al. 2000, Sol. Phys., 193,
161 [NASA ADS] [CrossRef] (In the text)
- Tsuneta, S.,
Acton, L., Bruner, M., et al. 1991, Sol. Phys., 136, 37 [NASA ADS]
- Uchida, Y.
1960, PASJ, 12, 676 [NASA ADS] (In the text)
- Uchida, Y.
1968, Sol. Phys., 4, 30 [NASA ADS] (In the text)
- Uchida, Y.
1970, PASJ, 22, 341 [NASA ADS] (In the text)
- Uchida, Y.,
Altschuler, M. D., & Newkirk, G., Jr. 1973, Sol. Phys., 28,
495 [NASA ADS] (In the text)
- Uchida, Y.
1974, Sol. Phys., 39, 431 (In the text)
- Valnicek, B.
1964, Bull. Astron. Inst. Czech., 15, 207 [NASA ADS] (In the text)
- Vrsnak, B., &
Lulic., S. 2000a, Sol. Phys., 196, 157 [NASA ADS] [CrossRef] (In the text)
- Vrsnak, B., &
Lulic., S. 2000b, Sol. Phys., 196, 181 [NASA ADS] [CrossRef]
- Vrsnak, B.,
Warmuth, A., Brajsa, R., & Hanslmeier, A. 2002, A&A, 394,
299 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Warmuth, A.,
Vrsnak, B., Aurass, H., & Hanslmeier, A. 2001, ApJ, 560,
L105 [NASA ADS] [CrossRef] (In the text)
- Warmuth, A.,
Vrsnak, B., Magdalenic, J., Hanslmeier, A., & Otruba, W. 2004,
A&A, 418, 1117 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig1.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig2.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg25.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig3.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg28.gif)
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{0332fig4.eps}}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg32.gif)
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{0332fig6.eps}}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg38.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig7.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig8.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg49.gif)
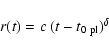
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0332fig9.eps}
\end{figure}](/articles/aa/full/2004/18/aa0332/Timg67.gif)