A&A 418, 1171-1178 (2004)
DOI: 10.1051/0004-6361:20034198
M. A. Bautista1 -
C. Mendoza1 -
T. R. Kallman2 -
P. Palmeri2,![]()
1 - Centro de Física, Instituto Venezolano de Investigaciones
Científicas (IVIC), PO Box 21827, Caracas 1020A, Venezuela
2 -
NASA Goddard Space Flight Center, Code 662, Greenbelt, MD 20771, USA
Received 14 August 2003 / Accepted 30 October 2003
Abstract
Photoabsorption cross sections across the K edge of
Fe XVII-Fe XXIII and electron impact K-shell
excitation effective collision strengths in Fe
XVIII-Fe XXIII have been computed with the Breit-Pauli
R-matrix method. The target models are represented with all the
fine-structure levels within the n=2 complex, built up from
single-electron orbital bases obtained in a Thomas-Fermi-Dirac
statistical model potential. The effects of radiation and
spectator Auger dampings are taken into account by means of an
optical potential. In photoabsorption, these effects cause the
resonances converging to the K thresholds to display symmetric
profiles of constant width that smear the edge, with important
implications in spectral analysis. In collisional excitation,
they attenuate resonances making their contributions to the
effective collision strength practically negligible.
Key words: atomic data - atomic processes - line: formation
Recent improvements in the spectral capabilities and sensitivity of satellite-borne X-ray telescopes (Chandra, XMM-Newton) have promoted the role of Fe K lines in plasma diagnostics, a trend that will continue to grow with the launch of future instruments such as Astro-E2 and Constellation-X. These diagnostics ultimately rely on the knowledge of the microphysics of line formation and hence on the accuracy of the atomic data. In this respect, Bautista et al. (2003) (hereafter Paper I), Palmeri et al. (2003a) (hereafter Paper II), Palmeri et al. (2003b) and Mendoza et al. (2004) have computed complete data sets of level energies, wavelengths, A-values and Auger rates for K lines in Fe II-Fe XXV. However, realistic spectral modeling also requires data for the population mechanisms, namely photoabsorption, photoionization and electron impact excitation cross sections. The K-resonance behavior in these continuum processes in both lowly and highly ionized species is somewhat different from that displayed by the outer-electron resonance series. For instance, Gorczyca (2000), Gorczyca & McLaughlin (2000) and Palmeri et al. (2002) (hereafter Paper III) have shown that the K-resonance widths are dominated by radiative and Auger dampings that make them independent of the principal quantum number and cause a smearing of the edge. Paper III shows the possibility of devising diagnostics based on K-edge broadening, but these would necessarily rely on accurate high-energy photoabsorption cross sections. Most previous close-coupling calculations of high-energy continuum processes in Fe ions (Berrington et al. 1997; Ballance et al. 2001; Berrington & Ballance 2001; Donnelly et al. 2000) have completely ignored spectator Auger decay, the main contributor of the K-resonance width.
In the present work we have carried out extensive calculations of the photoabsorption and photoionization of Fe XVII-Fe XXIII, considering both the total cross sections and partial cross sections where the daughter ion is left in a photoexcited K-vacancy state. Effective collision strengths for excitation by electron impact have also been computed. Calculations have been carried out with two relativistic numerical approaches: the Breit-Pauli R-matrix ( BPRM) method and AUTOSTRUCTURE based on a Thomas-Fermi-Dirac statistical model potential. In all these calculations, damping effects are given special care.
The present relativistic calculations are performed with a
Breit-Pauli Hamiltonian which for an N-electron system is given by
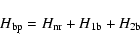 |
(1) |
The Breit-Pauli R-matrix package ( BPRM) is widely used
in electron-ion scattering and in radiative
bound-bound and bound-free calculations. It is based on the close-coupling
approximation of Burke & Seaton (1971) whereby the wavefunctions for states
of an N-electron target and a colliding electron with total angular momentum
and parity ![]() are expanded in terms of the target eigenfunctions
are expanded in terms of the target eigenfunctions
Breit-Pauli relativistic corrections have been introduced in the R-matrix suite by Scott & Burke (1980) and Scott & Taylor (1982), but the two-body terms (see Eq. (3)) have not as yet been implemented. Inter-channel coupling is equivalent to configuration interaction (CI) in the atomic structure context, and thus the BPRM method provides a formal and unified approach to study the decay properties of both bound states and resonances.
AUTOSTRUCTURE, an extension by Badnell (1997,1986) of the atomic
structure program
SUPERSTRUCTURE (Eissner et al. 1974), computes fine-structure
level energies, radiative and Auger rates in a Breit-Pauli
relativistic framework. Single electron orbitals, Pnl(r), are
constructed by diagonalizing the non-relativistic Hamiltonian,
![]() ,
within a statistical Thomas-Fermi-Dirac model
potential
,
within a statistical Thomas-Fermi-Dirac model
potential
![]() (Eissner & Nussbaumer 1969). The
(Eissner & Nussbaumer 1969). The
![]() scaling parameters are optimized variationally by minimizing a
weighted sum of the LS term energies. LS terms are
represented by CI wavefunctions of the type
scaling parameters are optimized variationally by minimizing a
weighted sum of the LS term energies. LS terms are
represented by CI wavefunctions of the type
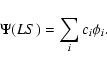 |
(5) |
When a K-vacancy state in an Fe ion with a partially filled L shell
is populated by dielectronic recombination or photon excitation
![$\displaystyle %
\left\{
\begin{array}{l}
{\rm Fe^{(\chi+1)+}}\ [2]^{p+1} + {\rm...
...ight\}
\rightarrow
\begin{array}{l}
{\rm Fe^{\chi+}}\ [1][2]^p\ nl,
\end{array}$](/articles/aa/full/2004/18/aa0198/img40.gif) |
(6) |
The present treatment of Auger and radiative dampings within the BPRM
framework uses the optical potential described by Gorczyca & Badnell (2000,1996)
where the resonance energy with respect to the threshold energy acquires
an imaginary component. For example, the energy of the
![]() closed channel is now expressed as
closed channel is now expressed as
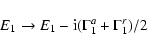 |
(11) |
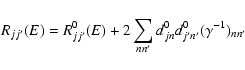 |
(12) |
The present BPRM calculations have been carried out with the standard R-matrix computer package of Berrington et al. (1995) for the inner region and with the asymptotic codes STGFDAMP (Gorczyca & Badnell 1996) and STGBF0DAMP (Badnell, unpublished) for determining photoabsorption and electron impact cross sections that take into account the effects of radiation and Auger dampings. This numerical approach has been previously used in Paper I to compute the high-energy photoabsorption cross section of the ground state of Fe XXIII and effective collision strengths for Fe XXIV.
Target representations include all the possible fine structure levels with
![]() ,
constructed in AUTOSTRUCTURE with single-electron orbital
bases obtained by minimizing the sum of the corresponding LS term energies.
Radiative and Auger widths have been taken from Paper II. The calculations for
all ions involve 30 continuum orbitals and R-matrix boundary radii that vary
from 1.0 au for Fe XXIII to 2.6 au in Fe XVII. The contributions
to the cross sections from long-range potentials in the outer region solutions
have been accounted for in all ions.
,
constructed in AUTOSTRUCTURE with single-electron orbital
bases obtained by minimizing the sum of the corresponding LS term energies.
Radiative and Auger widths have been taken from Paper II. The calculations for
all ions involve 30 continuum orbitals and R-matrix boundary radii that vary
from 1.0 au for Fe XXIII to 2.6 au in Fe XVII. The contributions
to the cross sections from long-range potentials in the outer region solutions
have been accounted for in all ions.
The photoabsorption cross sections of Fe XVII and Fe XXIII
computed with and without damping are shown in Fig. 1. They are
similar to those given in Papers I and III. It may be seen that
the cross sections near the K threshold are dominated by a
series of symmetric resonances of constant width that cause the
smearing of the edge. This unusual resonance behavior, as
explained in Paper III, is a consequence of the dominance of
K![]() and KLL dampings which are practically independent of the resonance
principal quantum number. The present target models are represented with
configuration levels within the n=2 complex that can only produce
accurate ab initio widths for the K
and KLL dampings which are practically independent of the resonance
principal quantum number. The present target models are represented with
configuration levels within the n=2 complex that can only produce
accurate ab initio widths for the K![]() resonances. For resonances
with n>2, they must be accounted for indirectly with the adjusted optical
potential described in Sect. 3.
resonances. For resonances
with n>2, they must be accounted for indirectly with the adjusted optical
potential described in Sect. 3.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0198fig1.eps}\end{figure}](/articles/aa/full/2004/18/aa0198/Timg58.gif) |
Figure 1: High-energy total photoabsorption cross sections of the ground level of: a) Fe XVII including radiative and Auger damping effects; b) Fe XVII excluding damping effects for resonances with n>2; c) Fe XXIII including damping; d) Fe XXIII excluding damping for resonances with n>2. It may be appreciated that when damping is included the resonance widths are constant for high n leading to a smearing of the K edge. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0198fig2.eps}\end{figure}](/articles/aa/full/2004/18/aa0198/Timg59.gif) |
Figure 2: High-energy total photoabsorption cross section of the ground levels of Fe XVII, Fe XVIII, Fe XIX and Fe XX. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0198fig3.eps}\end{figure}](/articles/aa/full/2004/18/aa0198/Timg60.gif) |
Figure 3: High-energy total photoabsorption cross section of the ground levels of Fe XXI, Fe XXII and Fe XXIII. |
| Open with DEXTER | |
Total photoabsorption cross sections of the ground states of
Fe XVII through Fe XXIII are displayed in
Figs. 2, 3. Regular absorption features in
ions with electron occupancy N<10 are the K![]() resonances.
They are absent, however, in Fe XVII due to the full L shell; therefore, the Fe K
resonances.
They are absent, however, in Fe XVII due to the full L shell; therefore, the Fe K![]() arrays are absorption spectral signatures of highly ionized species. Their energy positions shift
with ionic charge from 6.43 keV for Fe XVIII up to 6.63 keV
for Fe XXIII. Accurate and complete positions are given in Paper II.
arrays are absorption spectral signatures of highly ionized species. Their energy positions shift
with ionic charge from 6.43 keV for Fe XVIII up to 6.63 keV
for Fe XXIII. Accurate and complete positions are given in Paper II.
The K
![]() resonances are also distinctive absorption features in the
cross sections of Fe ions with 3p subshell vacancies, i.e. for species
with N<18. Unresolved transition arrays have been recently observed
at
resonances are also distinctive absorption features in the
cross sections of Fe ions with 3p subshell vacancies, i.e. for species
with N<18. Unresolved transition arrays have been recently observed
at ![]() 7.2 keV just below a smeared K edge in the MCG-6-30-15 spectrum
(Pounds & Reeves 2002) that can be assigned an Fe K
7.2 keV just below a smeared K edge in the MCG-6-30-15 spectrum
(Pounds & Reeves 2002) that can be assigned an Fe K![]() identification.
Moreover, the fitted ionization parameter value in Pounds & Reeves (2002) of
identification.
Moreover, the fitted ionization parameter value in Pounds & Reeves (2002) of
![]() obtained for
a warm absorber supports this identification.
obtained for
a warm absorber supports this identification.
As explained in Paper I, when radiation damping is taken into account photoabsorption and photoionization processes must be treated separately. In the former, the integrated cross section under the resonance must remain constant in spite of the broadening caused by damping so as to conserve oscillator strength. In the latter, the cross section is actually reduced since radiation damping leads to radiative de-excitation instead of photoionization. Unfortunately, there is as yet no formal procedure to separate the radiative de-excitation component in BPRM. We use AUTOSTRUCTURE to compute total photoionization cross sections by estimating a central-field background cross sections, representing resonances assuming Lorentzian profiles and computing resonance positions, radiative decay rates and Auger widths in the isolated resonance approximation. We have already shown in Paper I that the photoabsorption cross sections computed with this method closely resembles the cross sections obtained with BPRM.
Partial photoionization cross sections of the fine-structure levels
of the ground multiplets leaving the remnant ion in a K-vacancy level
have been computed for Fe XVII through Fe XXIII.
As an example, in Fig. 4 we plot the photoionization cross sections
for transitions from the
![]() ground level
of Fe XX to the first twelve K-vacancy levels of Fe XXI (levels 21 through 32 according Table 1 of Paper II). Similar cross sections have
been presented in Paper I for transitions from the ground level of
Fe XXIII to the K-vacancy levels of Fe XXIV.
Inspection leads to the finding that cross sections for transitions to
levels with angular momentum j within a given LS multiplet
do not split according to the (2j+1) statistical weights as previously
noted by Rau (1976). Also the dominant channels for K-shell
photoionization are those that comply with selection rules
between the initial and final levels of the remnant ion:
ground level
of Fe XX to the first twelve K-vacancy levels of Fe XXI (levels 21 through 32 according Table 1 of Paper II). Similar cross sections have
been presented in Paper I for transitions from the ground level of
Fe XXIII to the K-vacancy levels of Fe XXIV.
Inspection leads to the finding that cross sections for transitions to
levels with angular momentum j within a given LS multiplet
do not split according to the (2j+1) statistical weights as previously
noted by Rau (1976). Also the dominant channels for K-shell
photoionization are those that comply with selection rules
between the initial and final levels of the remnant ion:
| (13) |
![\begin{figure}
\par\includegraphics[angle=270,width=14.6cm,clip]{0198fig4.eps}\end{figure}](/articles/aa/full/2004/18/aa0198/Timg69.gif) |
Figure 4:
Partial photoionization cross sections from the
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[angle=270,width=14.6cm,clip]{0198fig5.eps}\end{figure}](/articles/aa/full/2004/18/aa0198/Timg70.gif) |
Figure 5:
Comparison of electron impact collision strengths computed with the
BPRM method for K-shell excitation of the
|
| Open with DEXTER | |
Collision strengths and Maxwellian averaged effective collision strengths
have been calculated for excitations to K-vacancy levels in
Fe XVIII-Fe XXIII. Collision strengths for Fe XXIV
were already reported in Paper I. Collision strengths have been computed up
to energies ![]() 2000 Ryd. At such high energies special care must be taken
to guarantee adequate convergence of the partial waves expansions. Following
the approach in Paper I, we compute partial waves up to
J=21/2 or 22/2 followed by non-exchange calculations for
higher partial waves up to
2000 Ryd. At such high energies special care must be taken
to guarantee adequate convergence of the partial waves expansions. Following
the approach in Paper I, we compute partial waves up to
J=21/2 or 22/2 followed by non-exchange calculations for
higher partial waves up to
![]() or 60/2. Topping up of partial waves up to
infinity for dipole allowed transitions is carried out with the Coulomb-Bethe
procedure of Burgess (1974).
or 60/2. Topping up of partial waves up to
infinity for dipole allowed transitions is carried out with the Coulomb-Bethe
procedure of Burgess (1974).
![\begin{figure}
\par\includegraphics[angle=270,width=14.7cm,clip]{0198fig6.eps}\end{figure}](/articles/aa/full/2004/18/aa0198/Timg72.gif) |
Figure 6:
A selection of collision strengths for Fe XX that shows the
contributions of high partial waves at high energies. Dotted lines depict
collision strengths obtained with J |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=15.1cm,clip]{0198fig7.eps}\end{figure}](/articles/aa/full/2004/18/aa0198/Timg73.gif) |
Figure 7:
Samples of electron impact effective collision strengths plotted with
the reduced scales of Burgess & Tully (1992).
a) Fe XX
|
| Open with DEXTER | |
In Fig. 5 collision strengths computed with and without damping
(radiative and Auger) are presented for the three
strongest transitions from the ground level of Fe XIX, i.e.
![]() .
It may be appreciated that when damping is taken into account
resonances are practically washed out. This effect, first reported in the
electron impact excitation of Fe XXIV in Paper I, is observed in the
collision strengths of all ions considered here, and it may be then concluded
that resonances are essentially irrelevant in electron impact K-shell
excitation of highly ionized Fe ions.
.
It may be appreciated that when damping is taken into account
resonances are practically washed out. This effect, first reported in the
electron impact excitation of Fe XXIV in Paper I, is observed in the
collision strengths of all ions considered here, and it may be then concluded
that resonances are essentially irrelevant in electron impact K-shell
excitation of highly ionized Fe ions.
To illustrate the convergence of collision strengths with the partial waves
expansion, we compare in Fig. 6 a sample of collision strengths
for Fe XX that include contributions up to J=22/2 with those topped
up to ![]() .
The plots show how the contributions from high partial waves
become increasingly important with electron energy. It may be also appreciated
that the partial waves expansion converges much more slowly for dipole
allowed transitions than for those of the forbidden type.
.
The plots show how the contributions from high partial waves
become increasingly important with electron energy. It may be also appreciated
that the partial waves expansion converges much more slowly for dipole
allowed transitions than for those of the forbidden type.
Excitation rates are given in terms of effective collision strengths which
are obtained by averaging the collision strengths over a Maxwellian electron
velocity distribution
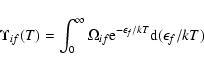 |
(14) |
| (15) | |||
| (16) |
| (17) | |||
| (18) |
| (19) | |||
| (20) |
| (21) | |||
| (22) |
As a part of a project to compute accurate atomic data for the spectral modeling of Fe K lines, electron impact collision strengths and total and partial photoionization cross sections have been computed for K-shell excitation in Fe XVII-Fe XXIII. Radiative and spectator Auger dampings are taken into account in detail which, confirming the findings in Paper III, cause the resonances converging to the K edge of the photoabsorption cross to display a peculiar behavior that leads to edge smearing. This edge behavior appears to have diagnostic potential in astrophysical plasmas. In agreement with previous conclusions by Rau (1976), we find that geometrical angular momentum factors combined with relativistic effect cause the level splitting of the LS photoionization cross sections to depart from statistical weight ratios. Also the prescribed selection rules for the dominant channels for K-shell photoionization are verified. These rules will help to simplify the computations for the lowly ionized members of the Fe isonuclear sequence that would otherwise prove computationally intractable.
With regards to electron impact excitation, resonances are shown to be practically washed out by the effects of radiative and Auger dampings, and thus contribute negligibly to the collisional excitation to n=2 K states. Instead, radiative decay of K states leaving the outer most electrons as spectators results in excitations of either highly excited bound states or high-n 2s vacancy states that tend to autoionize. Furthermore, spectator Auger decay of resonances enhances collisional ionization at the expense of excitation.
The data sets provided here together with the energy levels and
radiative and Auger rates reported in Paper II will help
modelers to carry out detailed studies of iron K emission for the
Fe ions reported so far. Similar calculations for the lower
ionization stages are in progress. All the data reported here are
being made available directly from TIPTOPbase![]() and from the XSTAR atomic
database (Bautista & Kallman 2001).
and from the XSTAR atomic
database (Bautista & Kallman 2001).
Acknowledgements
Support for this research was provided in part by grants from the NASA Astrophysics Theory Program and from FONACIT, Venezuela, under contract No. S1-20011000912.