All Figures

$\begin{figure} \par\rotatebox{270}{{\includegraphics[height=14cm,clip]{H4421.f1}}} \end{figure}$ Figure 1: The local radius ( upper left), local gravity ( upper right), local effective temperature ( lower left) and local luminosity $L(\theta )\equiv 4 \pi R^2(\theta )T_{\rm eff}^4(\theta )$ ( lower right) relative to the equatorial value of these quantities, for different ratios of the equatorial velocity to the critical velocity and as a function of co-latitude ( $\theta =0$ at the pole). The step in $y=v_{\rm eq}/v_{\rm crit}$ for the different curves is 0.1.
Open with DEXTER

In the text

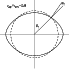$\begin{figure} \par\rotatebox{270}{\resizebox{6cm}{!}{\includegraphics{H4421.f2}}}\end{figure}$ Figure 2: A rotationally distorted star according to the Roche model for $v_{\rm eq}/v_{\rm crit}=0.8$ (full line). At a certain co-latitude $\theta _i$ the surface normal to the distorted star encloses an angle $\alpha _i$ with the radial vector, which is perpendicular to a spherical star with radius $r(\theta _i)$ (dashed line). The surface-integrated maximum mass loss calculated from Exp. (5) takes into account the maximum mass flux along the normal to the true stellar surface.
Open with DEXTER

In the text

$\begin{figure} \par\rotatebox{270}{{\includegraphics[height=16cm,clip]{H4421.f3}}} \end{figure}$ Figure 3: $z\equiv\dot{M}_{\rm max}^{\rm tot} (v_{\rm eq}/v_{\rm crit}) / \dot{M}_{\rm max}^{\rm tot} (0)$ as a function of $y\equiv v_{\rm eq}/v_{\rm crit}$ for rotating models including the Von Zeipel effect. The values are obtained from direct integration of the momentum equation at different co-latitudes and are indicated by filled boxes connected by a full line. The dotted line represents the empirical relation proposed by Langer (1998). The scaling law proposed by Maeder & Meynet (2000) for winds in rotating stars without instabilities is superimposed as a dashed line. The dashed-dotted line represents the multiple regression prediction formula given in Exps. (8) and (9).
Open with DEXTER

In the text

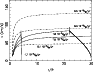$\begin{figure} \par\rotatebox{270}{\resizebox{6.3cm}{!}{\includegraphics{H4421.f4}}} \end{figure}$ Figure 4: Some velocity laws resulting from integration of the momentum equation for stellar parameters appropriate for $\eta~$ Car, allowing for different values of the velocity gradient at the sonic point. The full lines are solutions for the polar region while the dashed lines are valid for the equatorial regions. The mass-loss rates corresponding to the velocity laws are indicated. For a more detailed explanation we refer to Paper I and to the text.
Open with DEXTER

In the text