A&A 418, 387-392 (2004)
DOI: 10.1051/0004-6361:20040049

Flux-limited strong gravitational lensing and dark energy

D.-M. Chen

National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, PR China

Received 23 June 2003 / Accepted 15 January 2004

Abstract
In the standard flat cosmological constant ($\Lambda$) cold dark matter (CDM) cosmology, a model of two populations of lens halos for strong gravitational lensing can reproduce the results of the Jodrell-Bank VLA Astrometric Survey (JVAS) and the Cosmic Lens All-Sky Survey (CLASS) radio survey. In such a model, lensing probabilities are sensitive to three parameters: the concentration parameter c1, the cooling mass scale $M_{\rm c}$ and the value of the CDM power spectrum normalization parameter $\sigma_8$. The value ranges of these parameters are constrained by various observations. However, we found that predicted lensing probabilities are also quite sensitive to the flux density (brightness) ratio  $q_{{\rm r}}$of the multiple lensing images, which has been a very important selection criterion of a sample in any lensing survey experiments. We re-examine the mentioned above model by considering the flux ratio and galactic central Super Massive Black Holes (SMBHs), in flat, low-density cosmological models with different cosmic equations of state $\omega $, and find that the predicted lensing probabilities without considering  $q_{{\rm r}}$ are over-estimated. A low value of $q_{{\rm r}}$ can be compensated for by raising the cooling mass scale $M_{\rm c}$ in fitting the predicted lensing probabilities to JVAS/CLASS observations. To determine the cosmic equation of state $\omega $, the uncertainty in $M_{\rm c}$ must be resolved. The effects of SMBHs cannot be detected by strong gravitational lensing methods when  $q_{{\rm r}}\leq 10$.

Key words: cosmology: theory - cosmology: gravitational lensing

   
1 Introduction

Gravitational lensing provides us with a powerful probe of mass distribution of the universe. By comparing the lensing probabilities predicted by various cosmological models and the density profile of lenses with observations, we are able to test the mass distribution of dark matter halos and, in particular, the inner density slope because the Jodrell-Bank VLA Astrometric Survey (JVAS) and the Cosmic Lens All-Sky Survey (CLASS; Browne et al. 2000; Helbig 2000; Browne et al. 2002; Myers et al. 2002) has provided us with observed lensing probabilities at small image separations ( $0.3''<\Delta\theta<3''$).

In a standard flat $\Lambda$CDM cosmology, it is believed that a model of two populations of lens halos for strong gravitational lensing can reproduce the results of the JVAS/CLASS radio survey (Porciani & Madau 2000; Kochanek & White 2001; Keeton 2001; Keeton & Madau 2001; Sarbu et al. 2001; Li & Ostriker 2002; Oguri 2002; Oguri 2003; Oguri et al. 2003). The two populations of lens halos are distinguished by introducing an abrupt change in the structure of the objects at the cooling mass scale  $M_{\rm c}$ dividing galaxies and clusters. Some authors used Singular Isothermal Sphere (SIS) models below  $M_{\rm c}$ and Navarro-Frenk-White (NFW) models above  $M_{\rm c}$ and could fit the observed image separation distribution of JVAS/CLASS (Li & Ostriker 2002; Sarbu et al. 2001). Based on the fact that the image separation distribution of lenses below 1'' depends sensitively on both the inner mass profile of galactic halos and the faint end slope of the mass and luminosity functions, Ma (2003) compared the traditional approach that models the lenses as SIS and the Schechter luminosity function with a dark matter based approach that models the lenses with a certain halo mass profile and the Press-Chechter mass function. Constraints on the inner total mass profiles of halos are investigated by requiring the two approaches to give consistent predictions. Li & Ostriker (2003) further proposed a model of three populations of halos as lenses distinguished by the halos mass to calculate the lensing probability of image separation and time delay.

In this paper, we revisit the model of the two populations of lens halos to calculate the lensing probabilities in a flat quintessence cold dark matter (QCDM) cosmology with different cosmic equations of state $\omega $. The focus here is on the flux density ratio  $q_{{\rm r}}$ and cooling mass scale  $M_{\rm c}$, and their effects on the estimate of the equation of state of dark energy $\omega $. In spite of the fact that low mass lensing halos (galactic size or less) cannot all be SIS (Ma 2003; Li & Ostriker 2003; Benson et al. 2002; Somerville & Primack 1999; Kaufmann et al. 1993), we still model the galactic lens halos as SIS in our calculations based on the following considerations. On the one hand, evidence based on stellar dynamics of elliptical galaxies (e.g., Rix et al. 1997; Romanowsky & Kochanek 1999; Treu & Koopmans 2002), modeling of lensed systems (e.g., Cohn et al. 2001) and flux ratios of multiple images (Rusin & Ma 2001; Rusin 2002) all give an inner profile for lensing galaxies that is consistent with SIS. On the other hand, since the SIS lensing cross section is several orders of magnitude higher than that of the NFW, the lensing probabilities depend strongly on the cooling mass scale  $M_{\rm c}$ because a larger  $M_{\rm c}$ (and a smaller  $M_{\rm c}$ at the lower mass end of SIS lens halos, see Li & Ostriker 2003) allows more halos to be modeled as SIS. So the importance of the subdivision for low mass lens halos is lessened unless the large uncertainty of  $M_{\rm c}$ is sufficiently reduced. We thus ignore such a subdivision in this paper, and focus on the roles played by the flux density ratio  $q_{{\rm r}}$ and cooling mass scale  $M_{\rm c}$ in constraining the equation of state $\omega $.

In addition to  $q_{{\rm r}}$ and  $M_{\rm c}$, lensing probabilities estimated by the NFW halo are also sensitive to the concentration parameter c1. We use the mass-dependent fitting formula given by Bullock et al. (2001). For a given halo mass and redshift, there is a scatter in c1 that is consistent with a log-normal distribution with standard deviation $\sigma_c=\Delta(\log c)\approx 0.18$ (Jing 2000; Bullock et al. 2001). Taking into account the scatter in c1 by averaging the lensing probability with the lognormal distribution will increase the probabilities considerably at larger image separations and only slightly at smaller separations (Chen 2003b). Since the well-defined sample of JVAS/CLASS is limited to small image separations ( $0.3''<\Delta\theta<3''$), we thus ignore the scatter in c1 and our conclusions will not be affected. Another major uncertainty in predicting lensing probability arises from the considerable uncertainty regarding the value of the CDM power spectrum normalization parameter $\sigma_8$(Chen 2003b); we adopt  $\sigma_8=0.95$, suggested by the abundance of massive clusters at redshifts  $z=0.5\sim 0.8$(Bahcall & Bode 2003) which gives  $\sigma_8=0.98\pm 0.1$. Lensing probability increases quickly with the source redshift $z_{\rm s}$; since its distribution in the JVAS/CLASS survey is still poorly understood, we use the estimated mean value of $\langle z_{\rm s}\rangle =1.27$ (Marlow et al. 2000).

On the other hand, it should be pointed out that, like most authors, we use the spherical lensing profiles. Non-spherical lensing profiles do not change significantly the separation of observed multiple images, unless the profile deviates significantly from the spherical one. However, as pointed out by many authors (e.g. in a cluster environment, this has been discussed by Meneghetti et al. 2003a,b; for the importance of substructures see Mao & Schneider 1998), the elliptical lenses and their substructures do have significantly larger cross sections. A more realistic lensing model should include these effects, which will be discussed in another paper.

So in this paper we use the model of two populations of lens halos mentioned above to investigate the effect of image flux density ratio  $q_{{\rm r}}$ on lensing probabilities and find that the predicted lensing probabilities without considering  $q_{{\rm r}}$ are over-estimated. In flat, low-density cosmological models with different cosmic equations of state $\omega $, we show that when the flux density ratio $q_{{\rm r}}$changes from 10 to 104, the corresponding fit value of the cosmic equation of state will change from $\omega=-1$ to  $\omega=-1/2$. Also, in our flux-limited statistics of strong lensing image separations, the contributions from galactic central SMBHs can be safely ignored.

The paper is organized as follows: Sect. 2 provides a brief description of the cosmology model used in this paper, Sect. 3 presents the predicted integral lensing probabilities, Sect. 4 gives our results, the discussion and comparisons with previous work. Appendix A is devoted to a detailed deduction of lensing equations for galactic halos.

   
2 Cosmological model and mass function

In this section, we describe the cosmological model and dark halo mass function. More and more evidence shows that the Universe at present is dominated by a smooth component with negative pressure, the so called dark energy. So far, two kinds of dark energy have been proposed, quintessence and the so-called Chaplygin gas (e.g., Bento et al. 2002, 2003). We consider only the quintessence in this paper. It is assumed that quintessence offers an alternative to the cosmological constant as the missing energy in a spatially flat universe with a subcritical matter density  $\Omega_{\rm m}$ (Caldwell et al. 1998). In this paper, we study spatially flat QCDM models in which the cold dark matter and quintessence-field make up the critical density (i.e., $\Omega_{\rm m}+\Omega_{\rm Q}=1$). Throughout the paper, we choose the most generally accepted values of the parameters for flat, QCDM cosmology, in which, with the usual symbols, the matter density parameter, dark energy density parameter and Hubble constant are respectively:  $\Omega_{\rm m}=0.3$, $\Omega_{{\rm Q}}=0.7$, h=0.75. Four negative values of $\omega $ in equation of state $p_{\rm Q}=\omega\rho_{\rm Q}$, with $\omega=-1$(cosmological constant),  $\omega=-2/3$,  $\omega=-1/2$ and  $\omega=-1/3$, are chosen to see their effects on lensing probabilities. We use the conventional form to express the redshift z-dependent linear power spectrum for the matter density perturbation in a QCDM cosmology established by Ma et al. (1999)

 \begin{displaymath}P(k,z)=A_{\rm Q}k^nT^2_{\rm Q}(k,z) \left(\frac{g_{\rm Q}(z)}{g_{\rm Q}(0)(1+z)}\right)^2\cdot \end{displaymath} (1)

The normalization $A_{\rm Q}$ can be determined by $\sigma_8$for different values of $\omega $

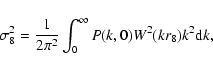\begin{displaymath}\sigma_8^2=\frac{1}{2\pi^2}\int^{\infty}_0P(k,0) W^2(kr_8)k^2{\rm d}k, \end{displaymath} (2)

in which  $W(x)=3[\sin(x)/x^3-\cos(x)/x^2]$ is the Fourier transformation of a top-hat window function, and $r_8=8~h^{-1}~{\rm Mpc}$. We choose the spectral index of the primordial adiabatic density perturbations to be n=1. $T_{\rm Q}$ is the transfer function for QCDM models, which is related to  $T_{\Lambda}$, the transfer function for $\Lambda$CDM models, with the relative transfer function

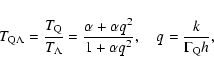\begin{displaymath}T_{{\rm Q}\Lambda}=\frac{T_{\rm Q}}{T_{\Lambda}}=\frac{\alpha+\alpha q^2}{1+\alpha q^2}, \ \ \ \ q=\frac{k}{\Gamma_{\rm Q}h}, \end{displaymath} (3)

where  $\Gamma_{\rm Q}$ is the shape parameter in QCDM models and $\alpha$ is a coefficient that quantifies the relative amplitude of the matter density field on large and small length scales, and is well approximated by
                              $\displaystyle \alpha$ = $\displaystyle (-\omega)^s,$  
s = $\displaystyle (0.012-0.036\omega-0.017/\omega)[1-\Omega_{\rm m}(z)]$  
    $\displaystyle +(0.098+0.029\omega-0.085/\omega) \ln\Omega_{\rm m}(z),$ (4)

where  $\Omega_{\rm m}(z)=\Omega_{\rm m}/[\Omega_{\rm m} +(1-\Omega_{\rm m})(1+z)^{3\omega}]$ is the matter density parameter. We use the fitting formula for $\Lambda$CDM transfer function given by Eisenstein & Hu (1999): $T_{\Lambda}=L/(L+Cq_{\rm eff}^2)$, with $L=\ln(e+1.84~q_{\rm eff})$, $q_{\rm eff}=k/(\Omega_{\rm m}~h^2~{\rm Mpc}^{-1})$ and $C=14.4+325/(1+60.5~q_{\rm eff}^{1.11})$.

Similarly, the linear growth suppression factor of the density field $g_{\rm Q}$ for QCDM in Eq. (1) is related to that for $\Lambda$CDM  $g_{\Lambda}$ with

                              $\displaystyle g_{\rm Q\Lambda}$ = $\displaystyle \frac{g_{\rm Q}}{g_{\Lambda}}=(-\omega)^{-t},$  
t = $\displaystyle -(0.255+0.305\omega+0.0027/\omega)[1-\Omega_{\rm m}(z)]$  
    $\displaystyle -(0.366+0.266\omega-0.07/\omega)\ln\Omega_{\rm m}(z),$ (5)

where the empirical fit of  $g_{\Lambda}$ is given by $g_{\Lambda}=2.5\Omega_{\rm m}(z)/\{\Omega_{\rm m}(z)^{4/7} -1+\Omega_{\rm m}(z)+[1+\Omega_{\rm m}(z)/2] [1+(1-\Omega_{\rm m}(z))/70]\}$ (Carroll et al. 1992).

We know that most of the consequences of quintessence follow from its effect on evolution of the expansion rate of the Universe, which in turn affects the growth of density perturbations (as described above) and the cosmological distances. From the first Friedmann equation d $(\rho_{\rm Q}a^3)=-p_{\rm Q}{\rm d}a^3$(a=1/(1+z) is the scale factor of the Universe), the expansion rate (Hubble constant) for a flat Universe and then the proper distance and the angular-diameter distance can be calculated in our QCDM models (Huterer & Turner 2001), which are needed in predicting lensing probabilities.

The physical number density  $\bar{n}(M,z)$ of virialized dark halos of masses between M and  $M+{\rm d}M$ is related to the comoving number density n(M,z) by  $\bar{n}(M,z)=n(M,z)(1+z)^3$, the latter originally given by Press & Schechter (1974), and the improved version is  $n(M,z){\rm d}M=(\bar{\rho}(0)/M)f(M,z){\rm d}M$, where  $\bar{\rho}(0)$ is the current mean mass density of the universe, and f(M,z) is the mass function for which we use the expression given by Jenkins et al. (2001).

   
3 Lensing probabilities

In this section, we first give a brief description of lensing equations for galaxies and clusters of galaxies, then present the predicted integral lensing probabilities. According to the model of two populations of halos, cluster-size halos are modeled as NFW profile:  $\rho_{\rm NFW}=\rho_{\rm s}r_{\rm s}^3/ [r(r+r_{\rm s})^2]$ , where  $\rho_{\rm s}$ and $r_{\rm s}$ are constants. We can define the mass of a halo to be the mass within the virial radius of the halo  $r_{\rm vir}$: $M_{\rm DM}=4\pi\rho_{\rm s}r_{\rm s}^3f(c_1)$, where $f(c_1)=\ln(1+c_1)-c_1/(1+c_1)$, and  $c_1=r_{\rm vir}/r_{\rm s}=9(1+z)^{-1}(M/1.5\times 10^{13}~h^{-1}~M_{\hbox{$\odot$ }})^{-0.13}$ is the concentration parameter, for which we have used the fitting formula given by Bullock et al. (2001). The lensing equation for NFW lenses is as usual $y=x-\mu_{\rm s} g(x)/x$ (Li & Ostriker 2002; Chen 2003a,b), where  $y=\vert\vec{y}\vert$, $\vec{\eta}=\vec{y}D_{\rm S}^{\rm A}/D^{\rm A}_{\rm L}$is the position vector in the source plane, in which  $D_{\rm S}^{\rm A}$ and  $D_{\rm L}^{\rm A}$ are angular-diameter distances from the observer to the source and to the lens respectively. $x=\vert\vec{x}\vert$ and  $\vec{x}=\vec{\xi}/r_{\rm s}$, $\vec{\xi}$ is the position vector in the lens plane. Since the surface mass density is circularly symmetric, we can extend both x and y to their opposite values in our actual calculations for convenience. The parameter  $\mu_{\rm s}=4\rho_{\rm s}r_{\rm s}/\Sigma_{\rm cr}$is x independent, in which  $\Sigma_{\rm cr}=(c^2/4\pi G)(D_{\rm S}^{\rm A}/D_{\rm L}^{\rm A} D_{\rm LS}^{\rm A})$ is the critical surface mass density, with c the speed of light, G the gravitational constant and  $D_{\rm LS}^{\rm A}$ the angular-diameter distance from the lens to the source. The function g(x) has an analytical expression originally given by Bartelmann (1996).

Since the observational evidence presented so far suggests the ubiquity of black holes in the nuclei of all bright galaxies regardless of their activity (Magorrian et al. 1998; Ferrarese & Merritt 2000; Ravindranath et al. 2001; Merritt & Ferrarese 2001a,b,c; Wandel 2002; Sarzi et al. 2002), we add a central supermassive black hole (SMBH) as a point mass to each SIS modeled galactic lens halo in its center(Keeton 2002; Chen 2003a,b). It is well known that the finite flux density ratio will definitely reduce the value of the lensing cross section (Schneider et al. 1992). In the model of one population of halos (NFW) combined with each galactic halo a central point mass, the lensing probabilities are shown to be sensitive to the flux density ratio (Chen 2003a,b). One may argue that this is the case only because we treat the galactic bulge as a point mass (some fraction of the bulge mass), since a point mass lens will always produce a larger flux density ratio  $q_{{\rm r}}$ of the multiple images. So it would be interesting to investigate the model of two populations of halos to see whether or not the lensing probabilities will be sensitive to  $q_{{\rm r}}$. We will show later that the answer is yes, and the contribution from an individual central galactic SMBH is detectable only if  $q_{{\rm r}}\geq 10^3$. When  $q_{{\rm r}}\leq 10$ (for the well-defined sample of JVAS/CLASS), the effect of SMBH can be safely ignored.

So, for galaxy-size lenses, we use an SIS+SMBH model. The surface mass density is

 \begin{displaymath}\Sigma(\vec{\xi})=M_{\bullet}\delta^2(\vec{\xi}) +\frac{\sigma^2_{v}}{2G\vert\vec{\xi}\vert}, \end{displaymath} (6)

where  $M_{\bullet}$ is the mass of a SMBH, $\vec{\xi}$ is the position vector in the lens plane,  $\delta^2(\vec{\xi})$ is the two dimensional Dirac-delta function, and  $\sigma_{v}$ is the velocity dispersion. Choosing certain length scales, the lensing equation can be written as  $y=x-x_{\rm h}/x-\vert x\vert/x$, where $x_{\rm h}$ is the scaled radius of the sphere of influence of a SMBH (see Appendix A for details).

When the quasars at the mean redshift  $<z_{{\rm s}}>~=1.27$ are lensed by foreground CDM halos of galaxies and clusters of galaxies, the lensing probability with image separations larger than  $\Delta \theta $ and flux density ratio less than  $q_{{\rm r}}$ is (Schneider et al. 1992)

 \begin{displaymath}P(>\Delta\theta, <q_{{\rm r}})=\int^{z_{{\rm s}}}_0\frac{{\rm... ...}{\rm d}z\int^{\infty}_0\bar{n}(M,z)\sigma(M,z)B(M,z){\rm d}M, \end{displaymath} (7)

where  $D_{{\rm L}}(z)$ is the proper distance from the observer to the lens located at redshift z. $\bar{n}(M,z)$ is the physical number density of virialized dark halos of masses between M and  $M+{\rm d}M$ at redshift z given by Jenkins et al. (2001). The cross section  $\sigma(M,z)$ is mass and redshift dependent, and is sensitive to the flux density ratio of multiple images $q_{{\rm r}}$ for SIS halos, as shown below in detail. For the magnification bias B(M,z), we use the results given by Li & Ostriker (2002) for both SIS+SMBH and NFW lense. For the former, if the contribution from a SMBH is ignored, the magnification bias for SIS only will be recovered (which is $B_{\rm SIS}\approx 4.76$).

The cross section for the cluster-size NFW lenses has been well studied (Li & Ostriker 2002). The lensing equation is $y=x-\mu_{\rm s} g(x)/x$ and the multiple images can be produced only if $\vert y\vert\leq y_{{\rm cr}}$, where  $y_{{\rm cr}}$ is the maximum value of y when x<0, which is determined by  ${\rm d}y/{\rm d}x=0$ and the cross section in the lens plane is simply  $\sigma(M, z)=\pi y_{\rm cr}^2r_{\rm s}^2$. We point out that the flux density ratio would also result in a reduction of the value of the cross section for NFW lenses if we apply it in our calculations. However, since we model the cluster-size lens halos as an NFW profile, which contributes to lensing probabilities mainly at larger image separations, where no confirmed lensing events are found (i.e. the null results of the JVAS/CLAS for  $6{''}\leq\Delta\theta\leq 15{''}$), if we adopt the mentioned above usual form of an NFW lens cross section, the predicted lensing probabilities will not be severely affected at smaller image separations.

For galaxy-size SIS+SMBH modeled lenses, two images will always be produced for all values of the source positions $\vert\vec{y}\vert$, and larger $\vert\vec{y}\vert$ will produce a higher flux density ratio $q_{{\rm r}}$. So a finite value of $q_{{\rm r}}$ will definitely limit the source within a certain corresponding position (which is also denoted by  $y_{{\rm cr}}$) and hence reduce the value of the cross section. The flux density ratio  $q_{{\rm r}}$ for the two images is the ratio of the corresponding absolute values of magnifications (Schneider et al. 1992; Wu 1996),  $q_{{\rm r}}=\vert\mu_+/\mu_-\vert$, where

\begin{displaymath}\mu_+(y)=\left[\left(\frac{y}{x}\frac{{\rm d}y}{{\rm d}x}\rig... ...c{y}{x}\frac{{\rm d}y}{{\rm d}x}\right)_{x<0}\right]^{-1}\cdot \end{displaymath} (8)

So  $y_{{\rm cr}}$ is determined numerically by $\vert\mu_+(y_{{\rm cr}})\vert=q_{{\rm r}}\vert\mu_-(y_{{\rm cr}})\vert$.


  \begin{figure} \par\resizebox{7.8cm}{!}{\includegraphics[clip]{4142_fig1.eps}} \end{figure} Figure 1: Image magnifications. Solid line: the brighter images ($\mu _+(y)$, x>0), dashed line: the fainter images ($\mu _-(y)$, x<0). The left vertical line (dot-dashed) indicates the source position $y_{{\rm cr}}$ at which  $q_{\rm r}=10$, and the right vertical line (dotted) indicates the position for $q_{\rm r}=10^{4}$.
Open with DEXTER

We plot the magnifications (each as a function of source position y) both for the brighter images and the fainter images in Fig. 1, with the source positions at which  $q_{\rm r}=10$ and  $q_{\rm r}=10^{4}$ explicitly indicated, and we have used a typical value  $x_{\rm h}=10^{-3}$. The sensitivity of the source position to the flux density ratio is obvious. The cross section for images with a separation greater than  $\Delta \theta $ and a flux density ratio less than  $q_{{\rm r}}$ in the lens plane is (Schneider et al. 1992; Chen 2003b)

 
$\displaystyle \sigma(M,z)=\pi\xi_0^2\vartheta(M-M_{{\rm min}}) \left\{\begin{ar... ...0,&{\rm for}~\Delta\theta\geq\Delta\theta_{y_{{\rm cr}}},\cr \end{array}\right.$     (9)

where  $\vartheta(x)$ is a step function, and  $M_{{\rm min}}$ is the minimum mass of halos above which lenses can produce images with separations greater than  $\Delta \theta $. From Eq. (A.5), an image separation for any y can be expressed as  $\Delta\theta(y)=\xi_0\Delta x(y)/D_{\rm L}^{\rm A}$, where  $\Delta x(y)$ is the image separation in lens plane for a given y. So in Eq. (9), the source position  $y_{\Delta\theta}$, at which a lens produces the image separation  $\Delta \theta $, is the reverse of this expression. $\Delta\theta_0=\Delta\theta(0)$ is the separation of the two images which are just on the Einstein ring; $\Delta\theta_{y_{{\rm cr}}}=\Delta\theta(y_{{\rm cr}})$ is the upper-limit of the separation above which the flux ratio of the two images will be greater than  $q_{{\rm r}}$. Note that since  $M_{{\rm DM}}$ (M15) is related to  $\Delta \theta $through $\xi_0$ in Eq. (6) and  $\sigma_v^2=GM_{\rm DM}/2r_{\rm vir}$, we can formally write $M_{{\rm DM}}=M_{{\rm DM}}(\Delta\theta(y))$ and determine $M_{{\rm min}}$ for galaxy-size lenses by $M_{{\rm min}}=M_{{\rm DM}}(\Delta\theta(y_{{\rm cr}}))$.

   
4 Discussion and conclusions

The lensing probabilities predicted by Eq. (7) and calculated from the combined JVAS/CLASS data are compared in Fig. 2. Four cases with different flux density ratios $q_{{\rm r}}$ or cooling scale $M_{\rm c}$ or with and without central SMBH are investigated to show their effects on lensing probabilities. In each case (see the corresponding panel of Fig. 2), four different values of the cosmic equation of state $\omega $: $\omega=-1$ (cosmological constant), $\omega=-2/3$,  $\omega=-1/2$ and  $\omega=-1/3$, are chosen to show the constraints from lensing probabilities. As in our previous work (Chen 2003b), the observed lensing probabilities are calculated by $P_{{\rm obs}}(>$ $\Delta\theta)=N(>$ $\Delta\theta)/8958$, where N(> $\Delta\theta)$ is the number of lenses with separation greater than  $\Delta \theta $ in 13 lenses.


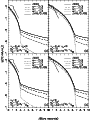  \begin{figure} \par\resizebox{7.8cm}{!}{\includegraphics{4142_fig2.eps}} \end{figure} Figure 2: The integral lensing probabilities with image separations larger than $\Delta \theta $ and flux density ratio less than  $q_{{\rm r}}$, for quasars at mean redshift  $\langle z_{\rm s}\rangle =1.27$ lensed by NFW ( $M_{\rm DM}>M_{\rm c}$) and SIS+SMBH ( $M_{\rm DM}<M_{\rm c}$) halos. The typically selected values of the cosmic equation of state $\omega $ for each curve, the flux density ratio $q_{{\rm r}}$ and cooling scale $M_{\rm c}$ are explicitly indicated. The observed lensing probabilities of JVAS/CLASS are plotted as a histogram in each panel.
Open with DEXTER

When flux density  $q_{\rm r}=10$ (as allowed by the JVAS/CLASS well-defined sample) and  $M_{\rm c}=10^{13}h^{-1}~M_{\hbox{$\odot$ }}$, one can see from the panel (a) of Fig. 2 that none of the four values of $\omega $ is able to predict enough lensing probabilities to match the observations. Note that the value of the cooling mass scale used in this case is preferred by Kochanek & White (2001) and Li & Ostriker (2002), and is also close to the cutoff mass of halos below which cooling of the corresponding baryonic component will lead to concentration of the baryons to the inner parts of the mass profile (Rees & Ostriker 1977; Blumenthal et al. 1986; Porciani &Madau 2000). So a larger value of $M_{\rm c}$ (> $10^{13}~h^{-1}~M_{\hbox{$\odot$ }}$) is needed for predictions to match observations. When we attribute too few predicted probabilities in panel (a) of Fig. 2 to the small value of $q_{{\rm r}}$ (=10), the quite large value of $q_{{\rm r}}$ (=104) also fails to match the observations, although the increment of the probabilities is also obvious, as shown in panel (c). The reason is that we have used different parameters and functions, e.g., the sensitive concentration parameter c1. Although it is not explicitly displayed in the figure, our calculations indeed show that if we set  $q_{\rm r}=10^{4}$ and  $M_{\rm c}=1.5\times 10^{13}~h^{-1}~M_{\hbox{$\odot$ }}$, the predicted lensing probabilities for $\omega=-1$ is able to match the observations quite well, which is in agreement with the result obtained by Sarbu et al. (2001), since we have used almost the same parameters and mass (and halo) functions. Note that when $q_{{\rm r}}$ is quite large (>103), the contribution from the central galactic SMBH cannot be ignored. In fact, it is just this contribution that compensates the finite value effect of  $q_{\rm r}=10^{4}$, which make our results obtained in this case be the same as that of Sarbu et al. (2001), whose flux density value is infinite.

If we persist in the flux density ratio allowed by the JVAS/CLASS sample in our calculations, the cooling mass scale $M_{\rm c}$ must have the value of  $3\times 10^{13}~h^{-1}~M_{\hbox{$\odot$ }}$ for the model with $\omega=-1$ to be able to match the observations, as shown in panel (b). Such a value of $M_{\rm c}$ is close to that used by Porciani & Madau (2000), however, they used different parameters and, especially, they did not consider the finite flux density ratio effect. Note that when  $q_{{\rm r}}\leq 10$, the contributions from a galactic central SMBH can be ignored, no matter what the value of $M_{\rm c}$ is, as shown in the top two panels of Fig. 2. This means that the finite small flux density ratio will reduce the cross section of SIS lenses considerably without a small central point mass. On the other hand, our calculations shows that the central SMBH can be detected only if  $q_{{\rm r}}\geq 10^3$, this value is possible for some confirmed radio-loud lens systems (Rusin & Ma 2001), but no sample suitable for analysis of the lens statistics is available with such a high flux density ratio. The sensitivity of lensing probability to the flux density ratio is obvious when we compare panel (b) with panel (d) of Fig. 2. In the latter,  $q_{\rm r}=10^{4}$, the effect of which is close to that when flux density ratio is assumed to be infinite (i.e., no constraints on the flux density ratio are taken into account, as in most previous work; see Fig. 1), and other parameters, including $M_{\rm c}$, are the same as panel (b). Obviously, for  $q_{\rm r}=10^{4}$, the "right" cosmic equation of state to match observations is  $\omega=-1/2$. The present time deceleration parameter for a flat, dark energy dominated Universe is  $q_0=1/2+(3/2)\omega\Omega_{\rm Q}$, and the accelerating Universe requires q0<0, which immediately gives  $\omega<-1/2.1$ (we are using  $\Omega_{{\rm Q}}=0.7$). So the fit value of  $\omega=-1/2$ in panel (d) is still within the range required by the accelerating Universe. Clearly, when flux density ratio $q_{{\rm r}}$ changes from 10 to 104, the corresponding fit value of the cosmic equation of state will change from $\omega=-1$ to  $\omega=-1/2$.

In summary, we revisit the two populations of lens halo model with mass distribution NFW ( $M_{\rm DM}>M_{\rm c}$) and SIS+SMBH ( $M_{\rm DM}<M_{\rm c}$), to calculate lensing probabilities in flat, low-density cosmological models with different cosmic equations of state $\omega $. The finite flux density ratio effect is significant. A low value of $q_{{\rm r}}$ can be compensated for by raising the cooling mass scale $M_{\rm c}$ in fitting the predicted lensing probabilities to JVAS/CLASS observations. To determine the cosmic equation of state $\omega $, the uncertainty in $M_{\rm c}$ must be resolved. The contributions from galactic central SMBHs can be safely ignored.

Acknowledgements
I'm grateful to the anonymous referee for helpful suggestions. This work was supported by the National Natural Science Foundation of China under grant No.10233040.

Appendix A: Lensing equation for SIS+SMBH

In this appendix, we give a detailed deduction of the lensing equation for SIS+SMBH model. Choose the length scales in the lens plane and the source plane to be

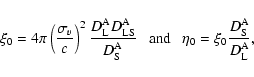\begin{displaymath}\xi_0=4\pi\left(\frac{\sigma_{v}}{c}\right)^2\frac{D_{\rm L}^... ...\ \ \ \eta_0=\xi_0\frac{D_{\rm S}^{\rm A}}{D_{\rm L}^{\rm A}}, \end{displaymath} (A.1)

then the position vector in the lens plane and source plane is, respectively,  $\vec{\xi}=\vec{x}\xi_0$ and $\vec{\eta}=\vec{y}\eta_0$. Note that we have used the different length scales between SIS and NFW lenses. The dimensionless surface mass density then is

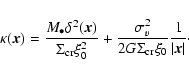\begin{displaymath}\kappa(\vec{x})=\frac{M_{\bullet}\delta^2(\vec{x})}{\Sigma_{\... ...2_{v}}{2G\Sigma_{\rm cr}\xi_0}\frac{1}{\vert\vec{x}\vert}\cdot \end{displaymath} (A.2)

So the lensing equation is

y=x-m(x)/x, (A.3)

with
 
                 m(x) = $\displaystyle 2\int^x_0\kappa(x')x'{\rm d}x'$  
  = $\displaystyle \frac{M_{\bullet}}{\pi\Sigma_{\rm cr}\xi^2_0}+x.$ (A.4)

$y=\vert\vec{y}\vert$ and  $x=\vert\vec{x}\vert$, and their values will be extended to the negative for convenience in later calculations. We have used the known formula  $\delta^2(\vec{x})=\delta(x)/2\pi x$ to derive the results in Eq. (A.4). In terms of the radius of the sphere of influence or Bondi accretion radius of a SMBH (e.g., Ferrarese & Merritt 2000; Melia & Falcke 2001; Zhao et al. 2002)  $r_{\rm h}=GM_\bullet/\sigma_v^2$, the lensing equation can be rewritten as

 \begin{displaymath}y=x-\frac{x_{\rm h}}{x}-\frac{\vert x\vert}{x} \ \ \ {\rm with} \ \ ~ x_{\rm h}=\frac{r_{\rm h}}{\pi\xi_0}\cdot \end{displaymath} (A.5)

The mass of each galactic central SMBH $M_{\bullet}$ is related to the mass of its host galaxy  $M_{{\rm DM}}$ with the formula given by Ferrarese (2002)

 \begin{displaymath}\frac{M_{\bullet}}{10^{15}~h^{-1}~M_{\hbox{$\odot$ }}}= 2.78\times 10^{-4}~M_{15}^{1.57}, \end{displaymath} (A.6)

here we have defined a reduced mass of the halos as $M_{15}=M_{\rm DM}/(10^{15}~{h}^{-1}~M_{\hbox{$\odot$ }})$. On the other hand, the mass of a SIS halo is defined the same way as for NFW:  $M_{\rm DM}=4\pi\int^{r_{\rm vir}}_0\rho(r)r^2{\rm d}r$. Since the mass density of a SIS halo is  $\rho(r)=\sigma_v^2/2\pi Gr^2$, the so-defined mass is related to the velocity dispersion by  $\sigma_v^2=GM_{\rm DM}/2r_{\rm vir}$. Generally, the virial radius  $r_{\rm vir}$ is cosmological model-dependent according to its definition  $M_{\rm DM}=4\pi\delta_{\rm vir}\bar{\rho}(z)r_{\rm vir}^3/3$, where  $\delta_{\rm vir}$ is the well-known density contrast of the virialized dark matter halos with the familiar value $\delta_{\rm vir}=18\pi^2\approx 178$ for a standard cold dark matter (SCDM) cosmology ( $\Omega_{\rm m}=1$), and  $\bar{\rho}(z)$ is the mean mass density of the universe at redshift z. We use  $\delta_{\rm vir}=200$ in our actual calculations, since Jenkins et al. (2001) specifically stated that their formula gives better fits to mass function f(M,z) with  $\delta_{\rm vir}=178$ regardless of the cosmological model (see Sarbu et al. 2001). So the scaled radius of the sphere of influence of the SMBH $x_{\rm h}$ can be written explicitly
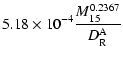                              $\displaystyle x_{\rm h}$ = $\displaystyle 5.18\times 10^{-4}\frac{M_{15}^{0.2367}}{D_{\rm R}^{\rm A}}$  
    $\displaystyle \times\left[\Omega_{\rm m}(1+z)^3+\Omega_{\rm Q}(1+z)^{3(1 +\omega)}\right]^{-2/3},$ (A.7)

where  $D_{\rm R}^{\rm A}= D_{\rm L}^{\rm A}D_{\rm LS}^{\rm A} /D_{\rm S}^{\rm A}$ and we have used (for a flat Universe)
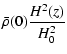                               $\displaystyle \bar{\rho}(z)$ = $\displaystyle \bar{\rho}(0)\frac{H^2(z)}{H^2_0}$  
  = $\displaystyle \bar{\rho}(0)\left[\Omega_{\rm m}(1+z)^3+\Omega_{\rm Q} (1+z)^{3(1+\omega)}\right].$ (A.8)

References


Copyright ESO 2004