A&A 418, 759-764 (2004)
DOI: 10.1051/0004-6361:20040038
S. M. Giuliatti Winter - O. C. Winter - A. H. F. Guimarães
Grupo de Dinâmica Orbital & Planetologia, UNESP, CP 205, Guaratinguetá, CEP 12500-000, SP, Brazil
Received 22 October 2002 / Accepted 31 December 2003
Abstract
In the present work we numerically simulated the motion
of particles coorbital to a small satellite under the
Poynting-Robertson light drag effect in order to verify the
symmetry suggested by Dermott et al. (1979, 1980) on their ring
confinement model. The results reveal a more complex scenario,
especially for very small particles (micrometer sizes), which
present chaotic motion. Despite the complexity of the
trajectories the particles remain confined inside the coorbital
region. However, the dissipative force caused by the solar
radiation also includes the radiation pressure component which can
change this configuration. Our results show that the inclusion of
the radiation pressure, which is not present in the original
confinement model, can destroy the configuration in a time much
shorter than the survival time predicted for a dust particle in a
horseshoe orbit with a satellite.
Key words: planets: rings - solar system: general
Goldreich & Tremaine (1979) have pointed out that the effects of
inter-particle collisions and Poynting-Robertson light drag on
unconstrained rings lead to radial spreading, disrupting a ring
in a time scale far shorter than the age of the solar system. This
would mean that the rings were formed recently or are being
continuously replenished. To avoid such a time scale constraint
two confinement models have been proposed. The concept of
shepherding satellites was proposed by Goldreich &
Tremaine (1979). This model consists of two small satellites, one
interior and other exterior to the ring, that would prevent
radial spreading by the gravitational torque on the ring in a
direction away from the perturbing satellites. The ring edges
would be located at the balance of these two torques. This
formalism assumes both satellites and ring particles to be on
circular orbits. The discovery of the satellites Cordelia and
Ophelia shepherding the Uranian ![]() ring confirmed this
model (Porco & Goldreich 1987). Murray & Thompson (1990)
proposed that unseen moonlets could be the shepherd satellites of
the other narrow rings of Uranus. The other mechanism for
confining narrow rings, proposed by Dermott et al. (1979,
1980), consists of one small satellite embedded within the ring.
The ring particles would be in stable horseshoe orbits about the
classical Lagrangian points L3, L4 and L5. An example of
this mechanism was found in the Encke Gap central ringlet where
the satellite Pan is claimed to be responsible for confining the
ring material (Showalter 1991). In this model, the mass ratio
between the satellite and the planet has to be
ring confirmed this
model (Porco & Goldreich 1987). Murray & Thompson (1990)
proposed that unseen moonlets could be the shepherd satellites of
the other narrow rings of Uranus. The other mechanism for
confining narrow rings, proposed by Dermott et al. (1979,
1980), consists of one small satellite embedded within the ring.
The ring particles would be in stable horseshoe orbits about the
classical Lagrangian points L3, L4 and L5. An example of
this mechanism was found in the Encke Gap central ringlet where
the satellite Pan is claimed to be responsible for confining the
ring material (Showalter 1991). In this model, the mass ratio
between the satellite and the planet has to be
![]() .
For very narrow rings the variation in the semi major axis of the
particle before and after the encounter with the satellite is
almost exactly equal and opposite (Dermott & Murray 1981).
Dermott et al. (1980), Dermott (1984) and Murray &
Dermott (1999) argue that the Poynting-Robertson light drag
(PRdrag) has little influence on the encounter with the satellite,
and the PRdrag forces acting on the particle were the same in
both halves of the horseshoe path. Then, the orbital decay of the
particle achieved in one half of the horseshoe path would in
effect be cancelled by that achieved in the other half. A
schematic diagram of this model, as proposed by Dermott (1984),
can be seen in Fig. 1. The path of a horseshoe particle as a
function of its angular position, in the rotating reference
frame, is shown by the dashed line, while the solid line shows the
change in this path due to the effects of the PRdrag force. The
satellite is located at r=1 and
.
For very narrow rings the variation in the semi major axis of the
particle before and after the encounter with the satellite is
almost exactly equal and opposite (Dermott & Murray 1981).
Dermott et al. (1980), Dermott (1984) and Murray &
Dermott (1999) argue that the Poynting-Robertson light drag
(PRdrag) has little influence on the encounter with the satellite,
and the PRdrag forces acting on the particle were the same in
both halves of the horseshoe path. Then, the orbital decay of the
particle achieved in one half of the horseshoe path would in
effect be cancelled by that achieved in the other half. A
schematic diagram of this model, as proposed by Dermott (1984),
can be seen in Fig. 1. The path of a horseshoe particle as a
function of its angular position, in the rotating reference
frame, is shown by the dashed line, while the solid line shows the
change in this path due to the effects of the PRdrag force. The
satellite is located at r=1 and
![]() .
In this
analysis the authors decoupled the effects of PRdrag on the
particle from the gravitational perturbation by the satellite. In
the present work we numerically simulated the coupled effect on
this dynamical system. The goal of this paper is to verify the
validity of the model proposed by Dermott et al. (1980).
This paper also takes a step further by including the radiation
pressure in this confinement model. Despite the fact that the
radiation pressure component causes a secular variation in the
eccentricity of the particle (Burns et al. 1979), this
effect can alter the dynamical system evolution. The paper is
organized as follows: in Sect. 2 we derive the equations of
motion for the particle in a horseshoe orbit with a satellite in
the presence of solar radiation, in Sect. 3 the
numerical simulations are presented and in the last section the
results are analysed.
.
In this
analysis the authors decoupled the effects of PRdrag on the
particle from the gravitational perturbation by the satellite. In
the present work we numerically simulated the coupled effect on
this dynamical system. The goal of this paper is to verify the
validity of the model proposed by Dermott et al. (1980).
This paper also takes a step further by including the radiation
pressure in this confinement model. Despite the fact that the
radiation pressure component causes a secular variation in the
eccentricity of the particle (Burns et al. 1979), this
effect can alter the dynamical system evolution. The paper is
organized as follows: in Sect. 2 we derive the equations of
motion for the particle in a horseshoe orbit with a satellite in
the presence of solar radiation, in Sect. 3 the
numerical simulations are presented and in the last section the
results are analysed.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3215_f1.eps}\end{figure}](/articles/aa/full/2004/17/aa3215/Timg12.gif) |
Figure 1: A diagram showing the paths of a horseshoe particle under the influence of the PRDrag (solid line) and without taking into account this perturbation (dashed line). |
| Open with DEXTER | |
Schuerman (1979) analysed the stability and location of the
Lagrangian points in the planar circular restricted three body
problem when some dissipative forces are taken into account. His
results show that the points L4 and L5 are linearly
unstable under the effects of PRdrag for particles in orbits
around the Sun. Nevertheless, his analysis cannot be applied
either to large-amplitude orbits, such as the horseshoe orbits,
or to particles in orbit around a planet. In the present work we
are interested in the effect of PRdrag on the orbital evolution of
a particle in horseshoe orbit with a satellite around a planet,
and also in the effects of the radiation pressure component (RP).
The dynamical system considered here is within the framework of
the restricted three-body problem, planet-satellite-ring particle,
with a time-dependent additional force, whose direction will
change regularly over the synodic period of the satellite. The
vectorial expression for the PRdrag and RP on a particle around a
planet is given by (Mignard 1984)
![$\displaystyle {\vec F}= \beta ~\bigg\{{{\vec r}_{\rm sp}\over {r_{\rm sp}}}\big...
...) \bigg ]-
\left({{{\vec v}_{\rm p}}\over c} + {{\vec v}\over c}\right)\bigg
\}$](/articles/aa/full/2004/17/aa3215/img13.gif) |
(1) |
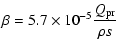 |
(2) |
The equations of motion for a ring particle in a planar orbit
around the planet (with mass m1), in a barycentric frame
rotating with the same angular velocity of the satellite (with
mass m2), under the effects of a dissipative force, are given
by (Murray & Dermott 1999)
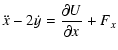 |
(3a) | ||
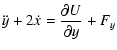 |
(3b) |
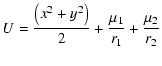 |
(4) |
| (5) |
| Fx | = | ||
| (6a) | |||
| Fy | = | ||
| (6b) |
In order to analyse the effects of the RP and PRdrag on a small particle initially in a horseshoe orbit with a satellite, we have numerically simulated the system adopting the equations of motion (Eq. (3)). We have used the Gauss-Radau numerical integrator (Everhard 1985).
The satellite is in circular orbit around the planet and the distance from the satellite to the planet is taken to be equal to the semi-major axis of the saturnian satellite Pan (Murray & Dermott 1999).
The initial conditions taken correspond to those particles which
perform a horseshoe orbit in the restricted three body problem
when the dissipative force is not considered. The particle is
initially located inside the horseshoe region and its initial
angular position is
![]() from the satellite.
The width of the horseshoe region is derived, for each satellite
mass, from the theory developed by Dermott & Murray (1981).
from the satellite.
The width of the horseshoe region is derived, for each satellite
mass, from the theory developed by Dermott & Murray (1981).
Dermott et al. (1979) proposed that the horseshoe
confinement model is verified when the satellite mass is such that
![]() .
We have chosen three different mass
ratios corresponding to known planetary ring-satellite systems of
Saturn. The
.
We have chosen three different mass
ratios corresponding to known planetary ring-satellite systems of
Saturn. The
![]() corresponds to a satellite mass
of the order of Pan. We have also analysed the limiting case,
corresponds to a satellite mass
of the order of Pan. We have also analysed the limiting case,
![]() ,
which corresponds to a satellite mass of the
order of
Prometheus, the inner satellite of the
F ring, and a satellite with
,
which corresponds to a satellite mass of the
order of
Prometheus, the inner satellite of the
F ring, and a satellite with
![]() .
The sizes of
the particles were chosen to be
.
The sizes of
the particles were chosen to be ![]() m,
m, ![]() m, and
m, and ![]() m. This sample of dust particles can be present in some
narrow rings, as has been proposed by Showalter et al. (1992) in the case of the F ring of Saturn.
m. This sample of dust particles can be present in some
narrow rings, as has been proposed by Showalter et al. (1992) in the case of the F ring of Saturn.
![\begin{figure}
\par\includegraphics[width=8cm,bb=93 206 221 280,clip]{3215_f2.ep...
...ps}\par\includegraphics[width=8cm,bb=93 16 221 95,clip]{3215_f2.eps}\end{figure}](/articles/aa/full/2004/17/aa3215/Timg41.gif) |
Figure 2:
Orbital evolution of a |
| Open with DEXTER | |
The results found in the numerical simulations show a different scenario from that proposed in the confinement model. A typical behaviour of the orbital evolution of a particle coorbital to a small satellite under PRDrag perturbation is given in Fig. 2. The evolution can be easily divided into two distinct stages. In the first stage a secular decrease of the radial and the angular amplitudes of oscillation occur. The particle evolves regularly in horseshoe orbits that keep getting smaller and smaller as time goes on. In the second stage the trajectory evolves in a chaotic way. The radial and angular amplitudes of oscillation evolve erratically, but bounded by the smallest amplitudes of the first stage. There is a critical radial amplitude of oscillation below which the orbital evolution is chaotic.
![\begin{figure}
\par\includegraphics[width=8cm,bb=93 206 221 278,clip]{3215_f3.ep...
...ps}\par\includegraphics[width=8cm,bb=93 16 221 95,clip]{3215_f3.eps}\end{figure}](/articles/aa/full/2004/17/aa3215/Timg42.gif) |
Figure 3:
Orbital evolution of a |
| Open with DEXTER | |
The critical radial amplitude of oscillation varies as a function of the the particle size and mass ratio. For smaller particle sizes and/or smaller mass ratios the critical radial amplitude of oscillation is larger. For particles with initial radial amplitude of oscillation larger than the critical value the orbital evolution is almost independent of the initial angular position.
The orbital evolution is chaotic in the case where the initial radial amplitude of oscillation is smaller than the critical value (Fig. 3), the first stage does not occur.
Therefore, the symmetry suggested by Dermott et al. (1979, 1980) in
their ring confinement model does not hold for micrometer-size
particles. For particles not too small (
![]() m) the
radial oscillation-amplitude decay is slow, so such
that for time scales that are not too long (
m) the
radial oscillation-amplitude decay is slow, so such
that for time scales that are not too long (
![]() years)
their orbital evolution in the rotating frame looks as in the
model proposed by Dermott (see an example in Fig. 4).
years)
their orbital evolution in the rotating frame looks as in the
model proposed by Dermott (see an example in Fig. 4).
![\begin{figure}
\par\includegraphics[width=8cm,bb=93 206 221 278,clip]{3215_f4.ep...
...*{2mm}
\includegraphics[width=8cm,bb=93 16 221 95,clip]{3215_f4.eps}\end{figure}](/articles/aa/full/2004/17/aa3215/Timg45.gif) |
Figure 4:
Orbital evolution of a |
| Open with DEXTER | |
The confinement model as it has been proposed does not include the component relative to the RP since it does not cause a secular variation in the semi-major axis of the particle in contrast to the PRdrag that causes its orbital decay (Burns et al. 1979). For a more general and realistic treatment of this problem we numerically simulated a sample of dust particles under the same conditions of the previous numerical simulations just adding the effects of the RP. Our results show that this confinement model is not valid for particles whitin the proposed size ranges of the size of the ring particles and the satellites. The orbit of the particle horseshoeing the satellite will be severely affected and the coorbital configuration will be lost completely. Some particles stay in orbit around the planet away from the derived width of the horseshoe region. Figures 5-7 show the evolution of the particle with the same initial conditions of Figs. 2-4, respectively, but with the inclusion of the radiation pressure component in the system. As we can see, the particles collide within the satellite in a very short time, less than 100 yr.
![\begin{figure}
\par\includegraphics[width=8cm,bb=93 205 221 281,clip]{3215_f5.ep...
...*{2mm}
\includegraphics[width=8cm,bb=93 16 221 97,clip]{3215_f5.eps}\end{figure}](/articles/aa/full/2004/17/aa3215/Timg46.gif) |
Figure 5:
Orbital evolution of a |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,bb=93 205 221 279,clip]{3215_f6.ep...
...*{2mm}
\includegraphics[width=8cm,bb=93 16 221 95,clip]{3215_f6.eps}\end{figure}](/articles/aa/full/2004/17/aa3215/Timg47.gif) |
Figure 6:
Orbital evolution of a |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,bb=93 203 221 279,clip]{3215_f7....
...2mm}
\includegraphics[width=8.3cm,bb=93 16 221 95,clip]{3215_f7.eps}\end{figure}](/articles/aa/full/2004/17/aa3215/Timg48.gif) |
Figure 7:
Orbital evolution of a |
| Open with DEXTER | |
Since the Poynting-Robertson drag is thought to be the main mechanism responsible for the decay of the dust particles Dermott et al. (1979) have proposed that a satellite can confine a ring particle in horseshoe orbit even in the presence of this dissipative force. In the present work we have tested this confinement model for a range of small particles and satellites.
In all the numerical simulation the particles, under the effects of the PRdrag and the gravitational influence of the satellite, remain confined in the horseshoe region. However, their orbital evolution in the rotating frame is much more complex than the symmetrical path formerly suggested. In general, the particles present two stages of orbital evolution. In the first stage there is a regular decrease of radial and angular amplitudes of oscillation. In the second stage the particles evolve chaotically with random amplitudes of oscillation.
However, since the radiation-pressure component is also present in the system, we have also included it in the numerical simulations. Although its effect does not cause a secular variation in the semi-major axis, the combined effects destroy the confinement mechanism for dust particles within the range of values mentioned in Sect. 3. Therefore, the timescale proposed for the decaying of dust ring particles is much shorter than the value expected from the confinement model.
Acknowledgements
We would like to thank the anonymous referee for the helpful review. This work was funded by Fapesp under the Grants 99/11965-8 and 99/11744-1, CNPq and Fundunesp. These supports are gratefully acknowledged.