A&A 418, 393-411 (2004)
DOI: 10.1051/0004-6361:20034158
T. Sanchis 1 - G. A. Mamon 2,3 - E. Salvador-Solé1,4 - J. M. Solanes1,4
1 - Departament d'Astronomia i Meteorologia, Universitat de Barcelona, Martí i
Franquès 1, 08028 Barcelona, Spain
2 -
Institut d'Astrophysique de Paris (CNRS UMR 7095), 98 bis Bd Arago,
75014 Paris, France
3 -
GEPI (CNRS UMR 8111), Observatoire de Paris, 92195 Meudon Cedex, France
4 -
CER on Astrophysics, Particle Physics, and Cosmology, Universitat de Barcelona, Martí i
Franquès 1, 08028 Barcelona, Spain
Received 5 August 2003 / Accepted 21 January 2004
Abstract
The origin of the deficiency in neutral hydrogen of 13
spiral galaxies lying
in the
outskirts of the Virgo cluster is reassessed.
If these galaxies have passed through the core of the cluster, their
interstellar gas should have been lost through ram pressure stripping by the
hot X-ray emitting gas of the cluster.
We analyze the positions of these H I-deficient and other spiral galaxies in
velocity-distance plots, in which we include our compilation of
velocity-distance data on 61 elliptical galaxies, and compare with
simulated velocity-distance diagrams
obtained from cosmological N-body simulations.
We find that ![]()
![]() relative Tully-Fisher
distance errors are consistent with the great majority of the spirals, except
for a small number of objects
whose positions in the velocity-distance diagram suggest grossly incorrect
distances, implying that the Tully-Fisher error distribution function
has non-Gaussian wings. Moreover, we find that
the distance errors may lead to an incorrect fitting of the
Tolman-Bondi solution that can generate significant errors in the
distance and especially the mass
estimates of the cluster.
We suggest 4 possibilities for the outlying H I-deficient spirals (in
decreasing frequency):
1) they
have large relative distance errors and
are in fact close enough (at distances between 12.7 and 20.9 Mpc from us)
to the cluster to have passed through its core and
seen their gas removed
by ram pressure stripping; 2) their gas is converted to stars by tidal
interactions with other galaxies;
3) their gas is heated during recent mergers with smaller galaxies;
and 4) they are not truly H I-deficient
(e.g. S0/a misclassified as Sa).
relative Tully-Fisher
distance errors are consistent with the great majority of the spirals, except
for a small number of objects
whose positions in the velocity-distance diagram suggest grossly incorrect
distances, implying that the Tully-Fisher error distribution function
has non-Gaussian wings. Moreover, we find that
the distance errors may lead to an incorrect fitting of the
Tolman-Bondi solution that can generate significant errors in the
distance and especially the mass
estimates of the cluster.
We suggest 4 possibilities for the outlying H I-deficient spirals (in
decreasing frequency):
1) they
have large relative distance errors and
are in fact close enough (at distances between 12.7 and 20.9 Mpc from us)
to the cluster to have passed through its core and
seen their gas removed
by ram pressure stripping; 2) their gas is converted to stars by tidal
interactions with other galaxies;
3) their gas is heated during recent mergers with smaller galaxies;
and 4) they are not truly H I-deficient
(e.g. S0/a misclassified as Sa).
Key words: galaxies: clusters: individual: Virgo - galaxies: evolution - galaxies: ISM - cosmology: distance scale - methods: N-body simulations
Over the last thirty years, substantial work has been carried out to quantify the effects of the environment on the properties of galaxies, i.e. to distinguish the characteristics of galaxies in dense, aggressive regions such as clusters, especially cluster cores, and low density zones away from clusters and groups. The nearby Virgo cluster is an excellent candidate for such studies, because its proximity allows 1) an easy comparison with field galaxies and 2) the measurement of distances independent of radial velocity, providing three-dimensional information on cluster properties (e.g. Solanes et al. 2002; Young & Currie 1995; Gavazzi et al. 1999) impossible to obtain in other clusters.
One particular characteristic of spiral galaxies is their neutral hydrogen (H I) gas content. It has been known for some time that a class of H I-deficient galaxies exists in the centers of clusters, such as the Virgo cluster (Chamaraux et al. 1980), and their deficiency, normalized to their optical diameter and morphological type, is anti-correlated with their clustercentric distance (Haynes & Giovanelli 1986; Solanes et al. 2001).
Chamaraux et al. (1980) considered ram pressure stripping of interstellar atomic hydrogen by the hot diffuse intracluster gas, first proposed by Gunn & Gott (1972), as one cause of the H I deficiency pattern of Virgo spirals. For galaxies moving face-on, ram pressure scales as the intracluster gas density times the square of the galaxy's velocity relative to this intracluster gas, so the role of ram pressure stripping was strengthened by the correlation of H I deficiency with the X-ray luminosity of clusters found by Giovanelli & Haynes (1985; see however Solanes et al. 2001) and by the presence of truncated H I disks observed by Cayatte et al. (1990).
It hence came as a surprise when Solanes et al. (2002) discovered spiral galaxies,
whose hydrogen content was deficient relative to other spiral galaxies of the
same morphological type, far away
from the core of Virgo, with several
deficient spirals in the
foreground of Virgo and particularly one group of spirals 7 to 10 Mpc
(depending on the adopted distance to Virgo) behind the cluster
with one-third of its 15 spirals displaying H I deficiencies deviating by more than ![]() from normalcy.
from normalcy.
In a followup study, Sanchis et al. (2002) explored the possibility that the group of deficient spirals behind Virgo might have plunged into the cluster core a few Gyr ago and lost their gas by interacting with the hot intracluster medium. Sanchis et al. applied a simple dynamical model that considered not only the classical deduction of the virgocentric infalling regime, but also the trajectories of galaxies that had already crossed once the center of the core. This model succeeded in explaining the overall characteristics of the observed velocity-distance diagram, including the envelope of the virialized cluster drawn by galaxies on first rebound. With the available data, they argued, from a statistical point of view, that one could not discard the possibility that some of the gas-deficient objects, including the background group in the outskirts of the Virgo Cluster Region, were not newcomers, but have passed through the cluster and lost their gas by ram pressure stripping.
We (Mamon et al. 2004) have recently estimated the maximum radius out to where galaxies falling into a cluster can bounce out. We found that this maximum rebound radius corresponds to 1 to 2.5 cluster virial radii. After estimating the virial radius of the Virgo cluster using X-ray observations, we concluded that the H I-deficient galaxies located in the foreground or background of the Virgo cluster appear to lie much farther from the center of the cluster than these maximum distances, and therefore that ram pressure stripping cannot account for the H I-deficiency of these outlying galaxies if their distances are correct.
In this paper, we investigate in further detail the origin of the H I-deficiency in the spiral galaxies that appear too far from the Virgo cluster to have suffered ram pressure stripping of their interstellar gas, by 1) adding to our four-dimensional (angular position, distance and radial velocity) sample of spiral galaxies, our compilation of the literature for elliptical galaxies towards Virgo, leading us to identify more precisely the density of the environment of the background deficient galaxies and estimate more accurately the distance to the center of Virgo, which is a crucial ingredient for the dynamical infall model, and 2) using cosmological N-body simulations that have the advantages of their lack of observational errors, completeness, and of defining a realistic infall pattern.
The sample of elliptical galaxies is described in Sect. 2. In Sect. 3, after describing the cosmological N-body simulations used here, we compare the simulated and observational samples to evaluate the influence of errors in distance estimates. Finally in Sect. 4, we discuss possible explanations for the H I deficiency of the outlying galaxies.
Using only late-type spirals, Sanchis et al. (2002) applied a spherical infall model to the velocity field of the Virgo Cluster Region and obtained two possible distances of 20 and 21 Mpc. Other distance estimates to the Virgo cluster, based upon spiral galaxies, produced distances in the range from 16 Mpc (Tully & Shaya 1984) to 21 Mpc (Ekholm et al. 2000).
An alternative way to estimate the cluster distance is by using the early-type components of the cluster, as they are thought to be better tracers of the center of the cluster due to morphological segregation (see e.g. Ferguson & Binggeli 1994). To do so, we have collected as many as possible early-type galaxies (E's, dE's and S0's) with redshift-independent distance measurements. Heliocentric velocities were extracted from the LEDA catalog of the HyperLEDA database and converted to the Local Group reference frame, while the direct distant measurements are obtained from a variety of sources.
Table 1: Datasets contributing to elliptical sample.
Table 1 summarizes the distance
datasets on the early-type galaxies towards Virgo.
Although
different authors use different methods
with different accuracy,
we have not found systematic deviations
between them, and furthermore found that the spread in differences of the
distance moduli was consistent with the quoted errors, for all sets of
early-type galaxies common to two authors.
Therefore, we estimated a global distance modulus
![]() for each
galaxy, using the maximum likelihood estimator (e.g. Bevington & Robinson 1992)
for each
galaxy, using the maximum likelihood estimator (e.g. Bevington & Robinson 1992)
Table 2 provides our final sample of 63 early-type galaxies. Columns (1)-(3) give the name of the galaxy, with its coordinates in Cols. (4) and (5). In Col. (6), we give the distance (in Mpc, from Eq. (1)) and its relative error (Eq. (2)) in Col. (7). Column (8) gives the velocity relative to the Local Group and Col. (9) provides the sources for the distance.
Table 2: Final sample of early-type galaxies.
Figure 1 shows a wedge diagram of the Virgo region with
the 61 early-types shown as circles and the 146 spirals shown as triangles.
One clearly notices the concentration of elliptical galaxies at a distance of
![]() ,
which is spread out in velocity space.
,
which is spread out in velocity space.
![\begin{figure}
\par\resizebox{12cm}{!}{\includegraphics[clip]{0158f1ac.ps}}\par\resizebox{12cm}{!}{\includegraphics[clip]{0158f1bc.ps}}
\end{figure}](/articles/aa/full/2004/17/aa0158/Timg162.gif) |
Figure 1:
Positions of 146 spiral (triangles) and 61 elliptical
(circles) galaxies in the Virgo field (within |
| Open with DEXTER | |
For a better understanding of the kinematics of galaxies in the direction of the Virgo cluster, we have simulated an observation of the velocity-distance relation using the dark matter particles in the GalICS cosmological simulation.
The N-body simulations used here to find N-body replica of the Virgo
cluster were carried out by Ninin (1999), as described by Hatton et al. (2003)
in the context of the GalICS hybrid
N-body/semi-analytic model of hierarchical galaxy formation.
Here, we are only
interested in the density and velocity fields directly traced by dark matter
particles. The N-body simulation contains 2563 particles of mass
![]() in a box of 150 Mpc size and it is run with a
softening length amounting to a spatial resolution of 29 kpc.
The simulation was run for a flat
universe with cosmological parameters
in a box of 150 Mpc size and it is run with a
softening length amounting to a spatial resolution of 29 kpc.
The simulation was run for a flat
universe with cosmological parameters
![]() ,
,
![]() ,
and
,
and
![]() .
Once the simulation is run,
halos of dark matter are detected with a "Friends-of-Friends'' (FoF) algorithm
(Davis et al. 1985),
with a variable linking length such that
the minimum mass of the FoF groups is
.
Once the simulation is run,
halos of dark matter are detected with a "Friends-of-Friends'' (FoF) algorithm
(Davis et al. 1985),
with a variable linking length such that
the minimum mass of the FoF groups is
![]() (20 particles) at any time step. With this method, over
(20 particles) at any time step. With this method, over
![]() halos are
detected at the final timestep, corresponding to the present-day (z=0)
Universe.
The GalICS halo finder does not allow halos within halos, so that a
cluster, to which is assigned a massive halo, cannot contain smaller halos
within it.
halos are
detected at the final timestep, corresponding to the present-day (z=0)
Universe.
The GalICS halo finder does not allow halos within halos, so that a
cluster, to which is assigned a massive halo, cannot contain smaller halos
within it.
Among the 12 halos that GalICS produces at z=0 with
![]() ,
we wish to choose those that resemble the Virgo cluster,
both in terms of mass and environment.
,
we wish to choose those that resemble the Virgo cluster,
both in terms of mass and environment.
As we can see in the radial phase space diagrams of dark matter halos
of the simulations (Fig. 1 of Mamon et al. 2004),
it is quite common to find small groups around the main
cluster halo, whereas the Virgo cluster is not known to have massive
neighbors,
except for the M 49 group just within the virial radius.
Note that the size of the simulation box,
![]() ,
implies,
given the periodic boundary condition, a maximum separation between halos of
,
implies,
given the periodic boundary condition, a maximum separation between halos of
![]() .
.
The effect of a neighboring halo will be from its tide on the
test halo. The ratio of the tidal acceleration on a particle of the test halo
at distance r from its center caused by a neighboring halo at distance Rfrom the center of the first halo
to the acceleration of this particle by the potential of its halo amounts to
a mean density criterion:
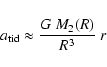 |
(3) |
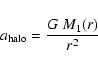 |
(4) |
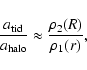 |
(5) |
The output from GalICS includes the mass of each halo obtained from the
FoF estimator, so that one can easily perform a first guess of which of the
halos with mass close to that of Virgo are as isolated as appears the Virgo
cluster.
Table 3
lists for the 10 most massive halos in the
simulation, the parameters of its most perturbing neighbor (that with the
lowest value of ![]() )
using FoF quantities for radii and masses.
Columns 2 to 4 list the virial radius, mass and circular velocity obtained
using the more precise spherical overdensity (SO) method, which allow a
direct comparison with the values we obtained for the Virgo cluster
in Mamon et al. (2004).
)
using FoF quantities for radii and masses.
Columns 2 to 4 list the virial radius, mass and circular velocity obtained
using the more precise spherical overdensity (SO) method, which allow a
direct comparison with the values we obtained for the Virgo cluster
in Mamon et al. (2004).
Table 3: Most perturbing neighbors of 10 most massive halos in GalICS simulation.
As seen in
Table 3,
the most perturbing halo is always inside r1.
Therefore, it is not clear
that we can easily estimate
the exact virial radius and mass of each perturbing halo
with the same spherical overdensity method as in Mamon et al. (2004) to
produce a better estimate of isolated halos. As we expect
![]() to be
approximately proportional to
to be
approximately proportional to
![]() ,
we take the results of
Table 3
as good indicators of the degree of isolation of halos in the
simulations.
,
we take the results of
Table 3
as good indicators of the degree of isolation of halos in the
simulations.
As shown in Table 3, the most isolated halo in the simulations is halo 1, the most massive halo. Picking the most massive halo also ensures that no other massive halos will distort the mock velocity-distance relation.
We now need to rescale
the simulated clusters to Virgo.
A reasonable way to put two halos in
comparable units is to normalize distances with the virial radius,
r100, and velocities
with the circular velocity of the halo at the virial radius, v100.
We therefore convert from the simulation frame to the
Virgo cluster frame by rescaling the terms related to distance with the
factor (omitting the "100'' subscripts for clarity)
![]() and the terms related to
velocities with the analogous factor
and the terms related to
velocities with the analogous factor
![]() ,
where superscripts "s'' and "V'' refer to the
simulation and the Virgo cluster, respectively.
We adopt the Virgo cluster
virial radius and circular velocity derived by Mamon et al. (2004) from X-ray
observations
,
where superscripts "s'' and "V'' refer to the
simulation and the Virgo cluster, respectively.
We adopt the Virgo cluster
virial radius and circular velocity derived by Mamon et al. (2004) from X-ray
observations
![]() ,
where
,
where
![]() ,
and
,
and
![]() .
.
Moreover, the N-body simulations give
us comoving velocities
![]() of dark matter particles, to
which we must add
the Hubble flow.
Therefore:
of dark matter particles, to
which we must add
the Hubble flow.
Therefore:
Inverting Eq. (8), we need to place the observer at a distance
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0158f2c.ps}
\end{figure}](/articles/aa/full/2004/17/aa0158/Timg204.gif) |
Figure 2:
Simulated and observed velocity-distance diagrams. The
observer is at (0,0) and sees a cone of angular radius |
| Open with DEXTER | |
It is interesting to check the peculiar velocities (or equivalently the
systemic velocities) found for the simulated
observer relative to the simulated cluster and compare them with that of our Local
Group of galaxies relative to the Virgo cluster, after rescaling the
simulation radial and velocity separations to the Virgo cluster attributes as
in Eqs. (8) and (9).
For 500 observers placed at a given distance from the halo, but in different
random directions, we find a systemic velocity between the halo and the
observer (i.e. the mean of 10 nearest halos)
in Virgo units of
![]() (errors are the
(errors are the ![]() dispersion) when we assume
dispersion) when we assume
![]() (as suggested by the positions of the
early-type
galaxies in Fig. 1, and especially of M 87,
which lies at the center of the X-ray emission)
and
(as suggested by the positions of the
early-type
galaxies in Fig. 1, and especially of M 87,
which lies at the center of the X-ray emission)
and
![]() when we
assume
when we
assume
![]() ,
as in Sanchis et al. (2002).
The values of the systemic velocity of the Virgo cluster in
the literature range approximately between 900 and 1000
,
as in Sanchis et al. (2002).
The values of the systemic velocity of the Virgo cluster in
the literature range approximately between 900 and 1000
![]() (Teerikorpi et al. 1992). Therefore, putting the Virgo cluster at 16.8 Mpc, as indicated by the early type galaxies,
gives a better match to the systemic velocity of the cluster.
In addition, if we calculate the number of all galaxies (early-type and
late-type ones) per distance bin, we found the maximum of the distribution
between
(Teerikorpi et al. 1992). Therefore, putting the Virgo cluster at 16.8 Mpc, as indicated by the early type galaxies,
gives a better match to the systemic velocity of the cluster.
In addition, if we calculate the number of all galaxies (early-type and
late-type ones) per distance bin, we found the maximum of the distribution
between
![]() .
Even if our sample lacks of completeness, this
result,
together with the previous ones, lead us to choose
.
Even if our sample lacks of completeness, this
result,
together with the previous ones, lead us to choose
![]() for the comparison between the N-body simulations and the Virgo cluster.
for the comparison between the N-body simulations and the Virgo cluster.
We take all the objects lying within a cone of half-opening ![]() aligned with the axis connecting the observer to the center of the halo.
aligned with the axis connecting the observer to the center of the halo.
Because observed galaxy catalogs, such as the VCC (Binggeli et al. 1985) catalog of Virgo cluster galaxies, are magnitude-limited, we imposed upon our simulated catalog (of dark matter particles) the same magnitude limit as the VCC, namely B < 18 (Binggeli et al. 1985). For this, we consider bins of distance to the observer, and, in each distance bin, we remove a fraction of dark matter particles equal to the predicted fraction of particles fainter than B = 18 given the distance and the Gaussian-shaped luminosity function of spiral galaxies derived by Sandage et al. (1985). This method supposes that the luminosity function is independent of environment (i.e. distance to the center of the Virgo cluster) and that those VCC galaxies with redshift-independent distance measurements have the same magnitude limit as the VCC galaxies in general. This luminosity incompleteness is only noticeable at large distances, where it amounts to reducing the number of particles by less than 10%.
Table 4: Spiral galaxies without H I data.
Figure 2 shows the velocity-distance plot of the simulated dark matter particles (small points), rescaled to Virgo units, and from which particles statistically fainter than the magnitude limit of the observed catalogs were removed. Superposed are the spiral galaxies (triangles) from Solanes et al. (2002) and the early-type galaxies (circles) compiled in Table 2. We have added to our sample the spiral galaxies compiled by Solanes et al. (2002) with reliable Tully-Fisher (Tully & Fisher 1977, hereafter TF) distances but no H I data. We list these galaxies in Table 4, with their coordinates, morphological type (from LEDA), systemic velocity and the final distance with errors assigned to it by Solanes et al. (2002), who estimated errors in distance as the mean deviation between the rescaled mean distance and the different estimates used (with this method, galaxies with only one estimator cannot be assigned an error and their distances are considered uncertain). We represent these objects as squares in Fig. 2.
Although Fig. 2 concerns a single observer and a single halo to represent the Virgo cluster (i.e. halo 1, which is the most isolated), the results are very similar for all halos studied as well as for any observer whose velocity with respect to the center of the main halo is similar to the mean of the 500 random trials. In other words, Fig. 2 provides a realistic general velocity-distance relation for a Virgo-like cluster in a flat Universe with a cosmological constant. Very recently, Klypin et al. (2003) have produced a similar plot for dark matter particles from their adaptive mesh refinement simulation. Note that the groups visible in the 3D phase space plot (Fig. 1 in Mamon et al. 2004) are much less visible here and the projection places them at smaller distances from the center of the main cluster.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{0158f3c.ps}
\end{figure}](/articles/aa/full/2004/17/aa0158/Timg233.gif) |
Figure 3:
Same as Fig. 2, but incorporating Gaussian relative
distance errors of
|
| Open with DEXTER | |
Figure 2 indicates that the velocity field drawn by the observed
spirals is noticeably different from the one followed by the dark matter
particles of the simulation. Nevertheless, the figure
shows that 1) the center of
the halo corresponds to the location of greater galaxy density
(not only for the early-type galaxies used to mark the center of the Virgo
cluster); 2) the
thickness of the halo in velocity space (the velocity dispersion)
corresponds to the corresponding thickness of the
central observed galaxies, and 3) the majority of the elliptical galaxies outside the cluster
also
appear to fit well the location of the particles in the outer
infalling/expanding locus.
These 3 facts suggest that both the
distance to the halo and the rescaling factors are well chosen and that the
differences between the Virgo cluster and the halo in the simulation should be
attributable to errors arising from the distance estimates (as the velocity errors
are negligible). It appears unlikely that the galaxies that, for a given
distance, lie within more than
![]() from the
locus of dark matter particles belong to the low- or high-velocity tails of
large velocity dispersion groups near the cluster, since in our simulations,
there are no such high velocity dispersion groups outside the main cluster.
from the
locus of dark matter particles belong to the low- or high-velocity tails of
large velocity dispersion groups near the cluster, since in our simulations,
there are no such high velocity dispersion groups outside the main cluster.
Given that most of the galaxies outside the velocity field drawn by dark matter
particles are spirals, we now build
a new velocity-distance diagram of our simulated particles incorporating the
mean relative distance error for the spiral galaxy sample.
Solanes et al. (2002) combined different studies of the TF relation to calculate
the distances of
spirals in the Virgo cluster. These studies give dispersions of the TF
relation of roughly 0.4 mag, corresponding to an uncertainty
of 18% in relative distance.
Figure 3 shows the corresponding velocity-distance plot for our
simulated Virgo line of sight, with inclusion of Gaussian relative distance
errors with
![]() (a slightly more conservative value than 0.18).
We omit particles beyond 40 Mpc, which corresponds to the distance (before
folding in the distance errors) where the
particles have a systemic velocity approximately equal to the maximum of the observed
galaxy sample.
(a slightly more conservative value than 0.18).
We omit particles beyond 40 Mpc, which corresponds to the distance (before
folding in the distance errors) where the
particles have a systemic velocity approximately equal to the maximum of the observed
galaxy sample.
Figure 3 indicates that the inclusion of distance errors, at the 20% relative rms level, allows us
to reproduce fairly well the observed velocity-distance diagram.
There are still several galaxies that lie far outside the general locus of
the dark matter particles. Among them are two galaxies
(VCC 319, which is part of a galaxy
pair and
![]() M~90 = NGC~4569 = Arp~76$">,
which is tidally
perturbed by a close neighbor) apparently in the foreground of the cluster
between 7 and 10 Mpc and with
M~90 = NGC~4569 = Arp~76$">,
which is tidally
perturbed by a close neighbor) apparently in the foreground of the cluster
between 7 and 10 Mpc and with
![]() ,
and four
galaxies (IC 3094,
NGC 4299, which is part of a pair, NGC 4253 and VCC 1644) in the background between 34 and 42 Mpc and
,
and four
galaxies (IC 3094,
NGC 4299, which is part of a pair, NGC 4253 and VCC 1644) in the background between 34 and 42 Mpc and
![]() .
Inspection of Fig. 2 indicates that these four
galaxies are
at more than
.
Inspection of Fig. 2 indicates that these four
galaxies are
at more than
![]() from the expected locus of the
Tolman-Bondi pattern given negligible distance errors. It is highly unlikely
that the peculiar velocities in interacting pairs can reach values as high as
from the expected locus of the
Tolman-Bondi pattern given negligible distance errors. It is highly unlikely
that the peculiar velocities in interacting pairs can reach values as high as
![]() ,
hence the distances to these galaxies appear to be grossly incorrect.
,
hence the distances to these galaxies appear to be grossly incorrect.
Table 5: Grossly incorrect galaxy distances.
We list the most discrepant galaxies in
Table 5.
Most of these galaxies have a single distance measurement (the elliptical
VCC 319 has a single Sérsic fit distance estimator, which is known
to be inaccurate - see Table 1).
However, it is a surprise to find a bright object such as NGC 4569
(M 90) in this list, especially since it has 6 different
Tully-Fisher distance measurements, 5 of which yield a distance between 7.9 and 10.2 Mpc and one (Gavazzi et al. 1999) giving
![]() ,
which is
what we expect from Fig. 2.
,
which is
what we expect from Fig. 2.
Since the 20% relative errors correctly reproduce the envelope of particles from the cosmological simulation, increasing the relative rms error to say 30% will not explain the distances to these discrepant spirals. We therefore conclude that the distances of the galaxies listed in Table 5 must be highly inaccurate.
In their dynamical, Tolman-Bondi, modeling of the Virgo region,
Sanchis et al. (2002) only used those spiral galaxies believed to trace the outer
envelope of galaxies expanding out of the Virgo cluster.
Figure 2 clearly indicates that the galaxies used by
Sanchis et al. (roughly aligned between distances of 34 and 45 Mpc) lie at typically
![]() lower
velocities for their distance than predicted by our simulated velocity-distance
model. Figure 3 suggests that the alignment of these galaxies
in the velocity-distance plot
may be fortuitous, given the
lower
velocities for their distance than predicted by our simulated velocity-distance
model. Figure 3 suggests that the alignment of these galaxies
in the velocity-distance plot
may be fortuitous, given the ![]()
![]() relative distance errors.
This fortuitous alignment forced the model of Sanchis et al.
to
shift the center of the Virgo cluster to greater distances.
relative distance errors.
This fortuitous alignment forced the model of Sanchis et al.
to
shift the center of the Virgo cluster to greater distances.
We now use the cosmological N-body simulations to quantify the errors on
the distance and mass to
the Virgo cluster obtained by fitting a Tolman-Bondi model to the
velocity-distance data outside the cluster core.
We construct simulated pseudo-galaxy samples
by randomly selecting as many points from the cosmological N-body
simulation as there are galaxies in the Virgo
cluster sample. We apply fixed relative distance errors in the range 0%-30% and, for each relative distance
error, we construct 50 realizations of the Virgo sample. We identify
pseudo-galaxies
presumably belonging to the core by building histograms of the number
of pseudo-galaxies
per 2 Mpc distance bin. Such histograms peak at the core of the
halo,
in a region of width ![]() 4 Mpc for the no error set and up
to
4 Mpc for the no error set and up
to ![]() 12 Mpc for
the 30% error set.
We avoid the virialized core by only considering pseudo-galaxies
lying on the back side of the identified cluster core.
12 Mpc for
the 30% error set.
We avoid the virialized core by only considering pseudo-galaxies
lying on the back side of the identified cluster core.
In the Tolman-Bondi
model used by Sanchis et al., galaxies are
treated as test particles
moving in a point-mass gravitational potential that is independent of time.
The model velocity-distance curve is a function of the age of the Universe,
t0, the distance to the cluster, ![]() ,
the point mass of the
cluster,
,
the point mass of the
cluster,
![]() ,
and the systemic velocity of the cluster relative to the
Local Group
of galaxies,
,
and the systemic velocity of the cluster relative to the
Local Group
of galaxies, ![]() .
Only three of these four parameters are independent, but
given the poor current velocity-distance data, it is better to use only two
free parameters and fix the third one.
Following Sanchis et al., we
have fixed
.
Only three of these four parameters are independent, but
given the poor current velocity-distance data, it is better to use only two
free parameters and fix the third one.
Following Sanchis et al., we
have fixed ![]() to the mean velocity of the main
halo for the 50 realizations (998
to the mean velocity of the main
halo for the 50 realizations (998
![]() for a distance of 16.8 Mpc,
see Sect. 3) and we have allowed
for a distance of 16.8 Mpc,
see Sect. 3) and we have allowed ![]() and
and ![]() to vary
freely. The resulting t0 will help us to see the viability of the results.
to vary
freely. The resulting t0 will help us to see the viability of the results.
Table 6 shows the results of the fits to the point-mass
Tolman-Bondi relation (see Sanchis et al. 2002) for the different sets.
For zero distance errors, the model
reproduces fairly well the input data of
![]() and
and
![]() (Mamon et al. 2004), as well as the age of
the Universe:
(Mamon et al. 2004), as well as the age of
the Universe:
![]() from the GalICS cosmological
simulations (which happens to perfectly match the age recently obtained by
Spergel et al. 2003 from the WMAP CMB experiment). The table also
clearly indicates that the errors in distance contribute to a slightly larger
distance to the cluster (by up to 2%), combined with a much larger mass for
the cluster (up to a factor 40!).
This dramatic rise in the mass decreases the resulting t0 to unacceptably
low values. Therefore, distance errors can cause the fitting of
Tolman-Bondi solutions to the velocity vs. distance of galaxies to yield
incorrect cluster parameters.
from the GalICS cosmological
simulations (which happens to perfectly match the age recently obtained by
Spergel et al. 2003 from the WMAP CMB experiment). The table also
clearly indicates that the errors in distance contribute to a slightly larger
distance to the cluster (by up to 2%), combined with a much larger mass for
the cluster (up to a factor 40!).
This dramatic rise in the mass decreases the resulting t0 to unacceptably
low values. Therefore, distance errors can cause the fitting of
Tolman-Bondi solutions to the velocity vs. distance of galaxies to yield
incorrect cluster parameters.
Table 6: Best fitting parameters for each dataset.
For the case
of real data on the Virgo cluster, the same fitting procedure leads to
![]() and
and
![]() ,
which imply
t0 = 5.2 Gyr.
Note that the present fitting procedure takes into account all galaxies
beyond the identified core of the cluster, whereas Sanchis et al.
only used those galaxies that are aligned between distances of 34 and 45 Mpc
in the velocity-distance plot, deducing a very different distance to the Virgo cluster (between 20 and 21 Mpc).
The comparison of the values of t0 from the real data and from the
simulated data convolved with different relative distance errors, suggests
that the TF distances may have up to 30% relative errors.
,
which imply
t0 = 5.2 Gyr.
Note that the present fitting procedure takes into account all galaxies
beyond the identified core of the cluster, whereas Sanchis et al.
only used those galaxies that are aligned between distances of 34 and 45 Mpc
in the velocity-distance plot, deducing a very different distance to the Virgo cluster (between 20 and 21 Mpc).
The comparison of the values of t0 from the real data and from the
simulated data convolved with different relative distance errors, suggests
that the TF distances may have up to 30% relative errors.
As shown above, the estimation of the distance to the cluster provided
by the point mass model is relatively good even for appreciable errors in
relative distances. Therefore, one could still obtain a reasonable value for
the mass of the cluster by taking ![]() from the fit (i.e., 17.4 Mpc),
together with
from the fit (i.e., 17.4 Mpc),
together with
![]() (Teerikorpi et al. 1992) and
t0 = 13.7 Gyr (Spergel et al. 2003)
as input parameters for the model and computing
(Teerikorpi et al. 1992) and
t0 = 13.7 Gyr (Spergel et al. 2003)
as input parameters for the model and computing ![]() as a
result. In this
way, we obtain a value of
as a
result. In this
way, we obtain a value of
![]() .
Notice
that the
effective mass of the point mass model does not have to coincide with the
virial mass of the cluster, as the latter one represents only the virialized
part of the cluster, while the former gives us an idea of the dynamical mass
of the whole Virgo region.
.
Notice
that the
effective mass of the point mass model does not have to coincide with the
virial mass of the cluster, as the latter one represents only the virialized
part of the cluster, while the former gives us an idea of the dynamical mass
of the whole Virgo region.
As mentioned in Sect. 1 and clearly seen in Fig. 2, there is a non-negligible number of H I-deficient galaxies distant from the cluster core, in particular at distances of 10 and 28 Mpc from the Local Group. We now examine different explanations for the presence of these H I-deficient galaxies outside the core of Virgo:
Table 7: H I-deficient galaxies possibly outside the Virgo cluster.
If one wishes to explain the outlying H I-deficient galaxies as galaxies that have lost their interstellar gas by its stripping by ram pressure from the hot intracluster gas, then these galaxies must have passed through the core of the Virgo cluster where the intracluster gas is dense and the galaxy velocities large so that the ram pressure is largest.
Mamon et al. (2004)
found
that objects that have passed through the
core of a structure in the past cannot be at distances greater than 1-2.5 virial radii from the cluster today. With their estimate of the distance (16.8 Mpc) and the virial radius (1.65 Mpc)
of Virgo, this means that galaxies that have passed through the core of Virgo
cannot lie at a distance from the Local Group greater than 18.5 or 20.9 Mpc (for
![]() or 2.5, respectively)
nor can they lie closer than 15.1 or 12.7 Mpc from the Local Group.
or 2.5, respectively)
nor can they lie closer than 15.1 or 12.7 Mpc from the Local Group.
For the 3 H I-deficient spirals at 28 Mpc to have passed through the core of
Virgo, one would require that their distances be each overestimated by 52% (34%), which corresponds to
![]() (
(
![]() )
events for their
distance moduli, for
)
events for their
distance moduli, for
![]() (2.5), respectively. Such
errors are possible, as shown in Sect. 3.5. Note that none of the
distances of the 13 galaxies listed in Table 7 are based upon Cepheid
measurements, which are much more precise than Tully-Fisher estimates.
On the
other hand, given the presence in our sample of some spirals with grossly
incorrect distances (see Sect. 3.5), one may wonder if the distances to
the 3 spirals at 28 Mpc could also be grossly incorrect: they could lie at the
cluster distance of 16.8 Mpc, thus leading in this case to distances
overestimated by 66%, which for 20% rms relative errors correspond to three
(2.5), respectively. Such
errors are possible, as shown in Sect. 3.5. Note that none of the
distances of the 13 galaxies listed in Table 7 are based upon Cepheid
measurements, which are much more precise than Tully-Fisher estimates.
On the
other hand, given the presence in our sample of some spirals with grossly
incorrect distances (see Sect. 3.5), one may wonder if the distances to
the 3 spirals at 28 Mpc could also be grossly incorrect: they could lie at the
cluster distance of 16.8 Mpc, thus leading in this case to distances
overestimated by 66%, which for 20% rms relative errors correspond to three
![]() events for their distance moduli, which appears unlikely,
unless the Tully-Fisher error distribution has non-Gaussian wings.
events for their distance moduli, which appears unlikely,
unless the Tully-Fisher error distribution has non-Gaussian wings.
Similarly, the three foreground
H I-deficient spirals at ![]() 10 Mpc could have bounced out of the core of
the Virgo cluster, as they lie on the outer edge of the envelope of the
particles after inclusion of 20% rms distance errors in Fig. 3.
Indeed, were they bouncing out of the Virgo cluster in the foreground at 15.1 (12.7) Mpc, one would then have three cases of 34% (21%) errors, each
corresponding to
10 Mpc could have bounced out of the core of
the Virgo cluster, as they lie on the outer edge of the envelope of the
particles after inclusion of 20% rms distance errors in Fig. 3.
Indeed, were they bouncing out of the Virgo cluster in the foreground at 15.1 (12.7) Mpc, one would then have three cases of 34% (21%) errors, each
corresponding to
![]() (
(
![]() )
events for their distance
moduli, for
)
events for their distance
moduli, for
![]() (2.5), respectively. Alternatively,
they could lie in the cluster proper, at 16.8 Mpc, which would correspond to
three
(2.5), respectively. Alternatively,
they could lie in the cluster proper, at 16.8 Mpc, which would correspond to
three
![]() events for their distance moduli, which again appears
unlikely, unless the Tully-Fisher error distribution has non-Gaussian wings.
events for their distance moduli, which again appears
unlikely, unless the Tully-Fisher error distribution has non-Gaussian wings.
The offset of a galaxy relative to the Tolman-Bondi locus in
Fig. 2 can be caused by a large distance error or a large peculiar
velocity relative to the general flow at that distance, or a combination of
both.
To see which effect is more important, one can consider the N simulated
particles with distance (with errors folded in) and velocity respectively
within 3 Mpc and
![]() of each galaxy in Table 7, as well as angular distance to the halo
center within
of each galaxy in Table 7, as well as angular distance to the halo
center within
![]() of that of the galaxy relative to M 87,
and
ask what fractions P1 and P2.5 of these particles were located
(before the distance errors were folded in)
within 1 or 2.5 times the virial radius of the halo, respectively.
of that of the galaxy relative to M 87,
and
ask what fractions P1 and P2.5 of these particles were located
(before the distance errors were folded in)
within 1 or 2.5 times the virial radius of the halo, respectively.
These fractions must be taken with caution, because the groups falling in or moving out of the Virgo cluster are at different distances and with different relative masses between the simulations and the observations. For example, a true group of galaxies in the background of the Virgo cluster will end up with too high values of P1 and P2.5 if there is no group at the same distance in the simulations, while a Virgo cluster galaxy with a measured distance of 10 Mpc or so beyond the cluster will have too low values of P1 and P2.5 if the simulations include a group at a distance close to this measured distance. Nevertheless, P1 and P2.5 should provide interesting first order constraints.
Of course, this method of locating galaxies, implies that galaxies
NGC 4064, NGC 4580 and NGC 4586, at angular
distances from M 87 beyond
![]() have P1
= 0.
Interestingly, all three galaxies are likely to be within
2.5 r100(i.e. P2 is close to unity).
have P1
= 0.
Interestingly, all three galaxies are likely to be within
2.5 r100(i.e. P2 is close to unity).
Among the 5 foreground galaxies with
![]() ,
NGC 4312, NGC 4438,
M 90
and NGC 4606
are all likely to be in the Virgo cluster
and all very likely to be close enough that they may have passed through its
core.
Only NGC 4424, apparently at distance 4.1 Mpc, is too close to
actually be located within 2.5 virial radii from the Virgo cluster.
,
NGC 4312, NGC 4438,
M 90
and NGC 4606
are all likely to be in the Virgo cluster
and all very likely to be close enough that they may have passed through its
core.
Only NGC 4424, apparently at distance 4.1 Mpc, is too close to
actually be located within 2.5 virial radii from the Virgo cluster.
Among the 5 background galaxies with
![]() ,
all but
NGC 4305, lying at 40 Mpc, have a non negligible probability of having
crossed the cluster. Only VCC 1569 measured at 23 Mpc is highly likely
to be located within the virial radius of the Virgo cluster.
Interestingly, the 3 galaxies at measured distances around 28 Mpc have very
different values of P1 and P2.5.
The closest one, NGC 4307, has one chance in two of being located
near the cluster and 40% probability of being within the cluster itself.
However, the farthest one, NGC 4356, has one chance in 5 of belonging
to the Virgo cluster and less than one chance in four of being within 2.5 virial radii.
The third one, NGC 4492, has only one chance in 9 of being within 2.5 virial radii of the Virgo cluster.
This low probability is not surprising, given that it is
located close to the infall/expansion zone of Fig. 2.
,
all but
NGC 4305, lying at 40 Mpc, have a non negligible probability of having
crossed the cluster. Only VCC 1569 measured at 23 Mpc is highly likely
to be located within the virial radius of the Virgo cluster.
Interestingly, the 3 galaxies at measured distances around 28 Mpc have very
different values of P1 and P2.5.
The closest one, NGC 4307, has one chance in two of being located
near the cluster and 40% probability of being within the cluster itself.
However, the farthest one, NGC 4356, has one chance in 5 of belonging
to the Virgo cluster and less than one chance in four of being within 2.5 virial radii.
The third one, NGC 4492, has only one chance in 9 of being within 2.5 virial radii of the Virgo cluster.
This low probability is not surprising, given that it is
located close to the infall/expansion zone of Fig. 2.
The alternative to ram pressure stripping of gas is removal of gas by tidal effects. One can envision various scenarios: 1) tidal stripping of gas beyond the optical radius; 2) tidal compression of gas clouds leading to gas transformation into stars; 3) tidal stripping of the gas reservoir infalling into the disk. Such tides can occur from interacting galaxies or from the cluster or group itself. We begin by asking whether the H I-deficient galaxies apparently outside of Virgo lie in groups.
Figure 4 shows the environment of the H I-deficient galaxies in
three equal logarithm distance bins, ![]()
![]() wide,
centered around 10 Mpc (the apparent distance to the foreground H I-deficient
galaxies), 16.8 Mpc (the distance to the Virgo cluster) and 28 Mpc (the
apparent distance to the background H I-deficient galaxies), as well as in
three radial velocity bins.
The log distance (velocity)
bins are chosen wide enough that if the parent distribution
function of the log distance (velocity) errors were Gaussian, one would have a
probability
wide,
centered around 10 Mpc (the apparent distance to the foreground H I-deficient
galaxies), 16.8 Mpc (the distance to the Virgo cluster) and 28 Mpc (the
apparent distance to the background H I-deficient galaxies), as well as in
three radial velocity bins.
The log distance (velocity)
bins are chosen wide enough that if the parent distribution
function of the log distance (velocity) errors were Gaussian, one would have a
probability
![]() of having a galaxy with a true
distance (velocity) within the
interval appearing to lie at the center of the interval.
of having a galaxy with a true
distance (velocity) within the
interval appearing to lie at the center of the interval.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0158f4.ps}
\end{figure}](/articles/aa/full/2004/17/aa0158/Timg336.gif) |
Figure 4:
Positions of galaxies within |
| Open with DEXTER | |
Among the 5 foreground H I-deficient spirals, 4 (NGC 4312, NGC 4438, M 90, which, as noted in Sect. 3.5, is far off the Tolman-Bondi relation, and NGC 4606), appear superposed (within dotted circle in upper-left plot) with the galaxies at the distance of the main structure of the Virgo cluster, which suggests that their distances may be seriously underestimated, unless there happens to be a group of galaxies precisely along the line of sight to the center of Virgo lying at 10 Mpc.
One may be tempted to identify the 3 H I-deficient spirals close to M 87 (NGC 4438, M 90, and NGC 4606)
with a group of ellipticals seen in the upper-left plot of
Fig. 4. The velocity dispersion of this group would explain
why these 3 galaxies are so far off the Tolman-Bondi solution given in Fig. 2. However, none of the ellipticals in this region have
accurate (<![]() )
relative distance estimates (cf. Table 2)
and some or all may actually belong to the Virgo
cluster.
)
relative distance estimates (cf. Table 2)
and some or all may actually belong to the Virgo
cluster.
Interestingly, 3 of the 4 H I-deficient spirals at 28 Mpc (NGC 4307, NGC 4356 and NGC 4492) lie in a dense region, extending to the SSW of the position of M 87 (lower-left plot), which is also seen in the middle distance bin (middle-left plot) corresponding to the distance to M 87, but with 3 times fewer galaxies. Although the eastern edge of the region, and particularly the H I-deficient NGC 4492, coincide with the position of M 49 (NGC 4472), it appears distinct from M 49, which roughly lies at the middle of a group of galaxies (middle-left plot) that does not seem to be associated with the dense region at 28 Mpc (lower-left plot).
We now compare the Tully-Fisher distance estimator with the redshift distance
estimator
Dv = v/H0.
If a structure outside of the Virgo cluster lies at a distance Dwithin a region with 1D velocity
dispersion ![]() ,
the error on the distance estimator
Dv = v/H0 will
be set by the dispersion of the peculiar velocities:
,
the error on the distance estimator
Dv = v/H0 will
be set by the dispersion of the peculiar velocities:
| (11) |
This change in optimal distance estimators is illustrated in Fig. 1, where only one of the background H I-deficient galaxies has a radial velocity much larger than the mean of the Virgo cluster. The plots on the right of Fig. 4 show that the structure to the south-southwest (SSW) of the Virgo cluster lies close to Virgo in velocity space (i.e. the concentration is in the right middle plot). In redshift space, the 3 background H I-deficient galaxies to the SSW of M 87 remain in a similar concentration of galaxies (middle right plot of Fig. 4) as in distance space (lower left plot), but this concentration is at similar radial velocities as the Virgo cluster. However, only one (NGC 4307) has a reasonably high chance (P1 in Table 7) of being located in or near the Virgo cluster, while one (NGC 4356) has less than one chance in 4 of being in or near the cluster (from the analysis of Sect. 4.1), and one (NGC 4492) has a radial velocity indicative of a background object expanding away from the Virgo cluster (this galaxy shows up as the empty triangle in Fig. 2 very close to the Tolman-Bondi locus), and has only roughly one chance in 9 of being even close to the cluster. But the analysis of P1 and P2.5 of Sect. 4.1 should be superior to the analysis of Fig. 4, because it takes into account the correlation of distance and velocity. In summary, the 3 background H I-deficient galaxies to the SSW of M 87 may be suffering from tidal effects of a background group of galaxies.
Table 8: Companions to H I-deficient galaxies in the outskirts of Virgo.
Table 8 shows the properties of the companions to these 4 galaxies.
Column 5 is the difference in velocity relative to the Local Group;
Col. 6 is the difference in extinction-corrected total I-band magnitude;
Col. 7 is the angular distance between the two components, in units of the
optical radius (D25/2) of the major member;
Cols. 8 and 9 are indicators for morphological and kinematical
(Rubin et al. 1999) disturbances (R ![]() regular, I
regular, I ![]() irregular) for the major
component.
Table 8 indicates that NGC 4438 has a very close major companion,
which is likely to be responsible for its irregular morphology and internal
kinematics.
NGC 4305 and NGC 4606 have moderately close major
companions.
M 90 has a close very minor (
irregular) for the major
component.
Table 8 indicates that NGC 4438 has a very close major companion,
which is likely to be responsible for its irregular morphology and internal
kinematics.
NGC 4305 and NGC 4606 have moderately close major
companions.
M 90 has a close very minor (![]() 1/50 in mass) companion.
1/50 in mass) companion.
Moreover, NGC 4307 and NGC 4356 are close in 4D space: their
projected separation (at the distance of M 87) is 215 kpc and their velocity
difference is
![]() ,
so they may constitute an interacting
pair.
Similarly, NGC 4580 and NGC 4586 are at a projected
separation of 311 kpc with a velocity difference of
,
so they may constitute an interacting
pair.
Similarly, NGC 4580 and NGC 4586 are at a projected
separation of 311 kpc with a velocity difference of
![]() ,
so they too may constitute an interacting pair.
,
so they too may constitute an interacting pair.
Finally, two other galaxies in Table 7 have unusually low inner rotation (Rubin et al. 1999): NGC 4064 and NGC 4424. Kenney et al. (1996) argue that NGC 4424 has undergone a merger with a galaxy 2 to 10 times less massive and presumably the same can be said for NGC 4064.
We can obtain some clues about the origin of the H I deficiency of the
outlying galaxies by studying their star formation rates.
We adopt the,
obviously simplified, point of view that tidal
interactions are believed to enhance star formation
(e.g. Liu & Kennicutt 1995),
while ram pressure stripping should reduce star formation.
We therefore verify the tidal interaction hypothesis by checking for enhanced
star formation rates.
Because tidal interactions operate on scales of order the orbital times of
interacting pairs, typically 250 Myr or more, we do not use the H![]() star formation rate indicator, as it is only sensitive to very recent star
formation, but focus instead on the broad-band color B-H.
We have taken B and H magnitudes from the GOLDMine database
(Gavazzi et al. 2003).
star formation rate indicator, as it is only sensitive to very recent star
formation, but focus instead on the broad-band color B-H.
We have taken B and H magnitudes from the GOLDMine database
(Gavazzi et al. 2003).
![\begin{figure}
\par\resizebox{13cm}{!}{\includegraphics[clip]{0158f5.ps}}
\end{figure}](/articles/aa/full/2004/17/aa0158/Timg353.gif) |
Figure 5: Color-luminosity diagram for 12 of the 13 H I-deficient galaxies of Table 7 (VCC 1569 was excluded because it is not bright enough to be included in GOLDMine), possibly outside the Virgo cluster (large filled symbols) or placed at the distance of the Virgo cluster (large open symbols). Other Virgo galaxies are shown as small open symbols. Triangles, squares and pentagons (respectively in red, green, and blue in the electronic version of the journal) refer to galaxies of morphological type 1-2, 3-4 and 5-6, respectively. The data is taken from the GOLDMine (Gavazzi et al. 2003) database, and dereddened using the internal and Galactic extinctions from LEDA with the selective extinctions of Cardelli et al. (1989). |
| Open with DEXTER | |
Figure 5 shows the B-H colors as a function of H-band luminosity for the 12 NGC galaxies of Table 7 (we have omitted VCC 1569, which is too underluminous to be in GOLDMine) and for other Virgo galaxies. The colors and luminosities in this figure were corrected for absorption using internal and galactic (Schlegel et al. 1998) absorption obtained from LEDA, assuming selective extinction coefficients from Cardelli et al. (1989). Figure 5 clearly displays a general color-luminosity relation, i.e. the trend that more luminous galaxies are redder. Comparing galaxies of similar mophological types, one checks that among the four candidates for possessing tidal companions, NGC 4305, NGC 4438, NGC 4569 (M 90), and NGC 4606 (see Table 8), the first three are blue for their luminosities, assuming their Tully-Fisher distances, but given that the latter three might well lie in Virgo (see Col. P1 in Table 7), we also check that at the distance to the Virgo cluster these 3 galaxies are very blue (NGC 4438), extremely blue (M 90) and just blue (NGC 4606). The blue colors for these 4 galaxies, given their luminosity and morphological type, confirms the tidal hypothesis for all four objects.
Interestingly, the possibly interacting galaxies NGC 4307 and NGC 4356 have blue colors confirming their interaction if they are indeed in the background of Virgo as their Tully-Fisher distances suggest, but have red colors as expected for ram pressure stripped galaxies if they lie in the Virgo cluster. The values of P1 in Table 7 cannot distinguish between these two possibilities. The situation is even more uncertain for the possibly interacting galaxies NGC 4580 and NGC 4586, whose Tully-Fisher distances place them slightly behind and in front of the Virgo cluster, respectively. If they both lie at the distance of the Virgo cluster, the first one would have a normal color, while NGC 4586 would be blue as expected if it is indeed interacting with NGC 4580.
The situation is also confusing for the two galaxies with possible recent minor merging: NGC 4064 appears normal or red if it lies in the foreground as suggested by its Tully-Fisher distance, but blue if it lies at the distance of the Virgo cluster, and NGC 4424 appears normal or red if it lies as close as its Tully-Fisher distance suggests but quite blue if it lies at the distance of Virgo. One would expect the minor merger to generate a blue nucleus if the merging took place recently enough, but this may have little effect on the overall color of the galaxy.
Moreover,
one may contest that tides will remove stars as well as gas from the disk of
a spiral galaxy.
However,
the estimates of H I-deficiency presented here are based upon single-dish (Arecibo) radio
observations, which often do not have sufficient angular resolution to map the gas
(the half-power beam of Arecibo subtends
![]() ,
close to
the typical optical angular diameters of the H I-deficient galaxies - see
Table 7).
One can therefore easily imagine that fairly weak tidal effects will deplete
the neutral hydrogen gas beyond the optical radius without affecting the stars in the
spiral disk, thus leading to an H I-deficiency when normalized relative to
the size of the optical disk.
,
close to
the typical optical angular diameters of the H I-deficient galaxies - see
Table 7).
One can therefore easily imagine that fairly weak tidal effects will deplete
the neutral hydrogen gas beyond the optical radius without affecting the stars in the
spiral disk, thus leading to an H I-deficiency when normalized relative to
the size of the optical disk.
Two galaxies among our H I-deficient Virgo outliers listed in Table 7 (NGC 4438 and M 90) have been studied by Cayatte et al. (1994), who computed H I-deficiencies of Virgo spirals, based upon high resolution 21 cm VLA observations. Both galaxies present very small 21 cm to optical diameter ratios, indicating that the gas deficiency sets in at small radii and cannot be caused by tidal effects. Additional high-resolution 21 cm observations at the VLA of the other galaxies in Table 7 will obviously allow confirmation of this result.
The H I-deficiency estimator has been defined by several authors
(e.g. Chamaraux et al. 1980; Haynes & Giovanelli 1984; Solanes et al. 1996) as
the hydrogen mass relative to the
mean for galaxies of the same morphological type and optical
diameter:
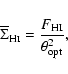 |
(15) |
Could the seemingly H I-deficient galaxies in the foreground and background
of Virgo have normal gas content according to Eq. (13) but
appear deficient with Eq. (14)?
Solanes et al. checked the statistical agreement of these two
H I-deficiency estimators by fitting a linear model between the two parameters and found a regression line with slope and intercept close to the
unit and zero respectively, with a scatter of 0.126.
Figure 6 shows this correlation, where those galaxies possible
located outside the Virgo cluster are
shown as solid circles. The plot clearly indicates that the outliers are also
deficient with the
![]() definition of H I-deficiency.
definition of H I-deficiency.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{0158f6.ps}}
\end{figure}](/articles/aa/full/2004/17/aa0158/Timg363.gif) |
Figure 6:
Comparison of H I-deficiency estimators.
Galaxies possibly located outside the Virgo cluster
are shown as filled circles. The vertical and horizontal dashed lines shows the |
| Open with DEXTER | |
However, Table 7 clearly shows that 7 out of our 13 H I-deficient possible outliers appear to be Sa galaxies (T=1), some of which might be misclassified S0/a or even S0 galaxies, which are known to have little cold gas. The stronger H I-deficiency of early-type spirals in the Virgo cluster has been already noticed by Guiderdoni & Rocca-Volmerange (1985). Some of these Sa galaxies may not be deficient relative to field S0/a or S0 galaxies. Indeed, the most recent study (Bettoni et al. 2003) of the H I content of galaxies as a function of morphological type indicates that the logarithm of the H I mass normalized to luminosity or to square optical diameter decreases increasingly faster for earlier galaxy types, therefore its slope for Sa's is considerably larger than for Sc's, and hence S0/a galaxies misclassified as Sa's will appear more H I-deficient than later-type galaxies misclassified by one-half of a morphological type within the Hubble sequence.
Moreover, independent estimates of morphological types by experts led to
![]() (rms) for galaxies with optical diameters >2'(Naim et al. 1995). The galaxies listed in
Table 7
have optical diameters ranging
from 2' to 10' plus one (VCC 1569) with
(rms) for galaxies with optical diameters >2'(Naim et al. 1995). The galaxies listed in
Table 7
have optical diameters ranging
from 2' to 10' plus one (VCC 1569) with
![]() .
There
are two galaxies (NGC 4305 and NGC 4492) with T = 1 and
.
There
are two galaxies (NGC 4305 and NGC 4492) with T = 1 and ![]() ,
i.e. where the uncertainty on T is probably as high as 1.5.
,
i.e. where the uncertainty on T is probably as high as 1.5.
For example, NGC 4424 and NGC 4492 are marginally
H I-deficient and are prime candidates for losing their status of gas-deficient
if they are misclassified lenticulars (by
![]() ,
the typical scatter
given by LEDA).
,
the typical scatter
given by LEDA).
![\begin{figure}
\par\resizebox{17cm}{!}{\includegraphics[clip]{0158f7.ps}}
\end{figure}](/articles/aa/full/2004/17/aa0158/Timg368.gif) |
Figure 7: POSS I snapshots of the T=1 H I-deficient galaxies of Table 7. The box size is 6' and North points upwards. |
| Open with DEXTER | |
We must thus resort to visualizing the possibly misclassified galaxies. Figure 7 displays the snapshots of the 7 H I-deficient outliers classified as Sa (T=1). We now discuss the morphologies of these 7 galaxies.
Given that between types S0/a and Sa, the compilation of Bettoni et al. (2003) (left
plots of their Fig. 2) indicates that the normalized H I content varies as
![]() ,
an overestimate
of 1 (0.5) in T will lead to an underestimate in H I-deficiency of 0.25 (0.125).
The H I-deficiency of NGC 4064 is sufficiently high that a
correction of 0.25 will still keep it among the
,
an overestimate
of 1 (0.5) in T will lead to an underestimate in H I-deficiency of 0.25 (0.125).
The H I-deficiency of NGC 4064 is sufficiently high that a
correction of 0.25 will still keep it among the ![]() cases using both DEF1 and DEF2 criteria.
On the other hand, if the morphological type of NGC 4424
is S0/a (T=0), it would still be H I-deficient
with criterion DEF1, but no longer among the
cases using both DEF1 and DEF2 criteria.
On the other hand, if the morphological type of NGC 4424
is S0/a (T=0), it would still be H I-deficient
with criterion DEF1, but no longer among the ![]() cases with DEF2.
cases with DEF2.
Note, however, that if most H I-deficient outliers classified as Sa's were in fact S0/a's, we would find ourselves with the new problem of justifying the presence of S0/a's so far away from the cluster core and apparently not within groups (see Sect. 5.3). We also have to keep in mind that Koopmann & Kenney (1998) argued that spirals in the Virgo cluster could have also been misidentified as early-type objects, an opposite trend to the above suggested.
We now focus on each of the 13 galaxies, one by one.
M 90 is extremely isolated in projected phase space.
Among the galaxies with
![]() ,
it appears associated with a group
of ellipticals, none of which has accurate distance measurements, with
sky coordinates associated with the central ellipticals with accurate
distance measurements in the center of the Virgo cluster.
Given its bright corrected total blue magnitude of 9.63 (Table 7),
its absolute magnitude would correspond to
MB = -20.24 at 9.4 Mpc or
MB = -21.5 at 16.8 Mpc.
The latter absolute magnitude is very bright for a spiral galaxy.
This can be quantified by comparing with the turnover luminosity, L*,
of the field galaxy
luminosity function. Unfortunately, the surveys used to derive the field
galaxy luminosity function do not employ the Johnson B band used here.
However, the 2MASS survey has measured a total K-band magnitude of K
= 6.58 for M 90. For a turnover absolute magnitude (Kochanek et al. 2001)
,
it appears associated with a group
of ellipticals, none of which has accurate distance measurements, with
sky coordinates associated with the central ellipticals with accurate
distance measurements in the center of the Virgo cluster.
Given its bright corrected total blue magnitude of 9.63 (Table 7),
its absolute magnitude would correspond to
MB = -20.24 at 9.4 Mpc or
MB = -21.5 at 16.8 Mpc.
The latter absolute magnitude is very bright for a spiral galaxy.
This can be quantified by comparing with the turnover luminosity, L*,
of the field galaxy
luminosity function. Unfortunately, the surveys used to derive the field
galaxy luminosity function do not employ the Johnson B band used here.
However, the 2MASS survey has measured a total K-band magnitude of K
= 6.58 for M 90. For a turnover absolute magnitude (Kochanek et al. 2001)
![]() for h=2/3 adopted here, the K-band
luminosity of M 90 corresponds to 0.4 L* if M 90 is at 9.4 Mpc but 1.3 L* if it lies at the distance of the Virgo cluster, which
is a large luminosity for a spiral galaxy.
Moreover, at the distance of Virgo, M 90 would be extremely blue for
its luminosity (Fig. 5).
for h=2/3 adopted here, the K-band
luminosity of M 90 corresponds to 0.4 L* if M 90 is at 9.4 Mpc but 1.3 L* if it lies at the distance of the Virgo cluster, which
is a large luminosity for a spiral galaxy.
Moreover, at the distance of Virgo, M 90 would be extremely blue for
its luminosity (Fig. 5).
Finally, the contours of continuum radio emission seen from the NVSS survey taken at the VLA are compressed in the East-Northeast direction, which is opposite to the direction towards the center of the Virgo cluster. This suggests that M 90 may be bouncing out of the cluster, which would also explain the galaxy's negative radial velocity.
The H I-deficient galaxies apparently lying well in front and behind of the Virgo cluster must have passed through the core of the cluster to have shed their gas by stripping by the ram pressure of the intracluster gas. As shown by Mamon et al. (2004), galaxies cannot bounce out beyond 1 to 2.5 virial radii, which according to their estimate of the virial radius of Virgo, amounts to 1.7 to 4.1 Mpc. Therefore, given a distance to the Virgo cluster of 16.8 Mpc, we suggest that only galaxies with distances between 12.7 and 20.9 Mpc could have passed through Virgo.
One
possibility, discussed in Sect. 4.1, is that the true 3D locations
of the outlying
H I-deficient galaxies are in fact within the Virgo cluster's virial radius
or at most within 4 Mpc from its center, which is possible (although not likely) given the typical 20% relative distance errors for the spiral galaxies in Virgo, expected from
the Tully-Fisher relation, and from our comparison of the observed velocity
distance relation with that derived from cosmological N-body simulations.
Indeed, of the 13 H I-deficient spirals appearing in the outskirts of the
Virgo cluster, 4 to 5 (depending on how to place the distance to M 90) are highly likely to be located in 3D within the virial radius
of the
Virgo cluster (Table 7) and one other galaxy (NGC 4307) has one
chance in two of being in the cluster or near it. Three others are at an
angular radius >
![]() from M 87, but appear to be within 2.5 virial
radii of it in 3D.
Finally, two galaxies (NGC 4356 and NGC 4492)
in the direction of the cluster have low but non
negligible probability of being in or near the cluster, while the last two
are definitely foreground (NGC 4424) and background (NGC 4305) galaxies.
Hence, between 4 and 11 of these 13 galaxies may have passed through the core
of the Virgo cluster and seen their neutral gas ram pressure swept by the hot
intracluster gas.
from M 87, but appear to be within 2.5 virial
radii of it in 3D.
Finally, two galaxies (NGC 4356 and NGC 4492)
in the direction of the cluster have low but non
negligible probability of being in or near the cluster, while the last two
are definitely foreground (NGC 4424) and background (NGC 4305) galaxies.
Hence, between 4 and 11 of these 13 galaxies may have passed through the core
of the Virgo cluster and seen their neutral gas ram pressure swept by the hot
intracluster gas.
The presence of a few discrepant distance measurements suggests that the nearly Gaussian parent distribution function for measurement errors in the distance modulus (or relative distance) has extended non-Gaussian wings.
It is also possible that highly inaccurate (at the 30% level or more) Tully-Fisher distance measurements may arise from physical biases. If galaxies are H I-deficient because of strong interactions with the cluster (through ram pressure stripping or tides) or with neighboring galaxies (through collisional tides), their Tully-Fisher distances may be biased and/or inefficient. Indeed, our analysis of Sect. 4.3 indicates that, among the galaxies likely or possibly within the Virgo cluster, one (NGC 4438) shows clear tidal perturbations from a close major companion, while 2 others (M 90 and NGC 4606) are probably tidally perturbed by close companions, and the one possible Virgo cluster member (NGC 4307) may have interacted with a fairly close major companion in the past.
Moreover, there are general arguments, independent of these case-study tidal
effects, that suggest that
abnormal Tully-Fisher distances may be
caused by H I-deficiency.
For example, Stauffer et al. (1986) noted that H I-deficient spirals in the direction
of the Virgo cluster tend to have
smaller line-widths for their H-band luminosity, and, similarly,
Rubin et al. (1991) found that the maximum rotation velocity of spiral
galaxies within compact groups of galaxies
tend to be smaller for their luminosity than
for normal spirals.
Such small line-widths or maximum rotation velocities
imply that distances are underestimated.
Using 2D (Fabry-Perot) spectroscopy,
Mendes de Oliveira et al. (2003) have refined the analysis of Rubin et al.
and find that the lowest luminosity galaxies in their sample (
![]() )
have lower
maximum rotation velocities than field spirals of the same
luminosity. Moreover, they find that compact group galaxies display a more
scattered Tully-Fisher relation than that of field spirals.
)
have lower
maximum rotation velocities than field spirals of the same
luminosity. Moreover, they find that compact group galaxies display a more
scattered Tully-Fisher relation than that of field spirals.
For galaxies lying in or very near the Virgo cluster,
an alternative to ram pressure gas stripping would be tidally stripped gaseous
reservoirs that prevent subsequent gas infall to the disk, which quenches
subsequent star formation (Larson et al. 1980).
However, if a spiral galaxy lies in a cluster, it may well be on its first
infall, provided that the effective ram pressure stripping of its neutral gas
quickly converts it into an S0 galaxy.
It seems reasonable to expect that
tidally stripped gas reservoirs will not have time to have a large effect on
the gas content, so that such galaxies with tidally stripped gas reservoirs
will not be as severely H I-deficient as the 13 ![]() cases of Table 7.
cases of Table 7.
The H I-deficient galaxies that are truly outside of the cluster may have lost their gas by the tides generated during close encounters with other galaxies within a group or small cluster of galaxies. Indeed, the efficiency of tidal perturbations of galaxies from close encounters with other galaxies is stronger in groups and small clusters than in rich clusters (see Fig. 5 of Mamon 2000), basically because the rapid motions in rich clusters decrease the efficiency of tides. Three of the four H I-deficient galaxies at 28 Mpc lie within a significant concentration of galaxies (Figs. 1 and 4) that ought to create such collisional tides, even with the estimates of distance using the more precise radial velocities (for these distant objects, see Eq. (12)).
The 3 galaxies outside the virial angular radius (NGC 4064,
NGC 4580 and NGC 4586) all probably lie
closer than 2.5 virial radii from M 87, and may be in the process of bouncing
out of the cluster after having lost their H I gas through ram pressure
stripping by the intracluster gas, if the maximum rebound radius is closer to
the upper limit of 2.5 virial radii found by Mamon et al. (2004), than to their
lower limit of 1 virial radius.
One of these galaxies
(NGC 4064) is a candidate for a recent merger as witnessed by its
very low inner rotation, while the other two (NGC 4580 and NGC 4586) may have interacted in the past, given their proximity in
phase space.
In the case of recent merging, the neutral gas may have been shock heated
with that of the galaxy being swallowed up, and should shine in H![]() or X-rays depending on its temperature.
or X-rays depending on its temperature.
Of the 4 galaxies likely or certainly far outside
the Virgo cluster (in 3D), one (NGC 4305) may be tidally perturbed
by a close major companion, one (NGC 4424) has suffered a recent
merger (given its very low inner rotation velocity), one may have interacted
with another galaxy (NGC 4307) in the past, and one (NGC 4492) may be a misclassified S0/a (with T=0), implying a lower expected
H I content, hence a less than ![]() H I-deficiency upon the estimator DEF1 and just at
H I-deficiency upon the estimator DEF1 and just at ![]() upon DEF2, although the bulge/disk ratio
derived by Gavazzi et al. (2000) suggests that the galaxy is indeed an Sa.
upon DEF2, although the bulge/disk ratio
derived by Gavazzi et al. (2000) suggests that the galaxy is indeed an Sa.
Although we can provide at least one explanation for each case of H I-deficiency in the 13 spiral galaxies that 1) appear to be located in the foreground or background of the Virgo cluster or 2) lie just outside the projected virial radius of the cluster, there is certainly room for an improved analysis. In particular, accurate distances obtained with Cepheids would be most beneficial, as well as VLA maps for 11 of the 13 galaxies to distinguish tidal stripping from ram pressure stripping.
Acknowledgements
We wish to thank Philippe Amram, Hector Bravo-Alfaro, Véronique Cayatte, Avishai Dekel, Peppo Gavazzi, Gopal Krishna, and Gilles Theureau for useful discussions, and the anonymous referee for very useful comments. We also thank François Bouchet, Bruno Guiderdoni and coworkers for kindly providing us with their N-body simulations, and Jeremy Blaizot for answering our technical questions about the design and access to the simulations. T.S. acknowledges hospitality of the Institut d'Astrophysique de Paris where most of this work was done, and she and G.A.M. acknowledge Ewaokas for hosting them at the CAMK in Warsaw, where part of this work was also done. T.S. was supported by a fellowship of the Ministerio de Educación, Cultura y Deporte of Spain. We have used the HyperLEDA database (http://leda.univ-lyon1.fr) operated at the Observatoire de Lyon, France, SIMBAD (http://simbad.u-strasbg.fr), operated by the CDS in Strasbourg, France, the NASA/IPAC Extragalactic Database (NED, http://nedwww.iap.caltech.edu), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, and the GOLDMine database operated by the Universita' degli Studi di Milano-Bicocca.
For a single measurement of variable X of value x with uncertainty ![]() ,
assuming Gaussian errors,
the probability of measuring xi is
,
assuming Gaussian errors,
the probability of measuring xi is
For simplicity, one can assume a uniform f(x).
The probability of the true X being less than some value x is then
| P(<x) | = | 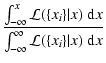 |
|
| = | ![$\displaystyle {
\int_{-\infty}^x \exp \left [-{x^2/ 2}~\sum_i {1/ \sigma_i^2} +...
...2/ 2}~\sum_i {1/ \sigma_i^2} +
x~\sum_i {x_i / \sigma_i^2} \right ] ~{\rm d}x }$](/articles/aa/full/2004/17/aa0158/img385.gif) |
||
| = | 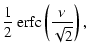 |
(A.5) |
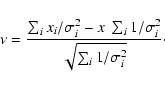 |
(A.6) |
Alternatively, one could
adopt an underlying physical model for f(x).
If X is the distance modulus, for which
the Gaussian p.d.f. of Eq. (A.1) should be adequate, one could use
a Virgocentric model, where the probability f(x) stems from a density
distribution around Virgo, using for example an NFW model.
If the angle between the galaxy and Virgo, as seen by the observer, is ![]() ,
one has
,
one has
| f(d) | (A.10) | ||
| = | 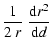 |
||
| = | 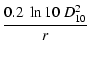 |
||
| (A.11) |