A model of meteor ablation in the atmosphere has been developed for meteoroids in the mass range 10-12 kg to
A&A 418, 751-758 (2004)
DOI: 10.1051/0004-6361:20041001-1
M. D. Campbell-Brown - D. Koschny
European Space Agency, ESTEC, Keplerlaan 1, Noordwijk, 2201 AZ, The Netherlands
Received 9 January 2004 / Accepted 27 January 2004
Abstract
A model of meteor ablation in the atmosphere has been developed for meteoroids in the mass range 10-12 kg to
![]() kg (size range 10
kg (size range 10 ![]() m to 2 mm). The model builds on the classical model of meteor ablation, and adds a thermal fragmentation mechanism. The goal of the model is to characterize the physical structure (fundamental grain sizes) and chemical composition of meteoroids.
m to 2 mm). The model builds on the classical model of meteor ablation, and adds a thermal fragmentation mechanism. The goal of the model is to characterize the physical structure (fundamental grain sizes) and chemical composition of meteoroids.
Key words: solar system: general - earth - meteor, meteoroids
Meteoroids in the mass range 10-9 kg to
![]() kg (size range approximately 100
kg (size range approximately 100 ![]() m to 2 mm) are commonly studied with radar and image intensified video. This is especially true of Leonid meteors during the outbursts of the last few years, when many thousands of optical light curves have been obtained by various groups (cf. Brown et al. 2000).
m to 2 mm) are commonly studied with radar and image intensified video. This is especially true of Leonid meteors during the outbursts of the last few years, when many thousands of optical light curves have been obtained by various groups (cf. Brown et al. 2000).
Meteoroids in this size range are particularly interesting because they represent particles not easily studied in space. In general, they are too large to be studied by dust detectors or infrared emission, and too small to be seen optically from the Earth. They are most easily investigated using the atmosphere as a detector, i.e. by recording their collision with atmospheric molecules, when they vaporize and produce light and ionization.
The majority of objects in this size range are probably cometary in origin, and many shower meteoroids, like those of the Leonid stream, have known parent bodies (Comet 55P/Tempel-Tuttle). Thus, by studying meteoroids we may gain valuable insights into cometary structure and composition.
Meteoroids are also important because of the impact hazard they pose to spacecraft. While the particles themselves are small, the impact velocities (up to 72 km s-1 for particles bound to the sun) are very large, so the potential damage to satellites and other spacecraft is significant. Understanding the structure of a meteoroid is important in assessing the hazard in case of a collision: a solid, compact object will produce different impact damage than a fluffy, extended particle (see Auer 2001, for a review). It is also a key parameter needed to estimate accurately the mass of meteoroids.
The most revealing observations of meteors involve measurements of their luminous intensity as a function of height. These light curves provide constraints on a meteoroid's physical structure and chemical composition. Many studies of the light curves of faint meteors have been done, notably by Jacchia (1955), who proposed fragmentation of fragile particles as the cause of the discrepancy between masses measured by deceleration (dynamic mass) and those measured by light emission (photometric mass) (cf. Ceplecha et al. 1998).
In order to determine the physical and chemical nature of the meteoroid, one must understand the interaction between the meteoroid and the atmosphere. Computer modeling is the most obvious way to do this. Because many effects come into play during meteor ablation, a numerical model, rather than an analytical model, is most appropriate. The classical model of meteor ablation uses conservation of energy and momentum, together with the evaporation rate, to determine the light produced by a meteoroid as a function of time.
In addition to the basic equations of ablation for a single particle, fragmentation must be taken into account. Major studies of the light curves of faint meteors (e.g. Fleming et al. 1993; Koten & Borovicka 2001; Jones & Hawkes 1975; Koschny et al. 2002; Campbell et al. 2000; Murray et al. 1999; Jacchia 1955) have shown that light curve shapes are extremely variable, and do not match the light curve predicted by the classical, single-body model.
Development of a good model is the first necessary step to unravelling meteoroid structure from light curve observations. Here we present details of such a numerical model, which incorporates processes not previously taken into account in earlier models.
While inadequate to explain the light curves of faint meteors, a model of the ablation of a single particle is the necessary basis of a model of a fragmenting meteoroid. The model described in the following section can be used individually on each grain as it separates from the meteoroid. This may introduce error, since there may be interactions among adjacent fragments, but we believe it is a good first order approximation to the real process.
In order to construct a model, one must know which flow regime applies. The Knudsen number, K, is defined as l/r, where l is the mean free path in the atmosphere and r is a characteristic dimension of the body moving through it; for a sphere, r is the radius. When the Knudsen number is high (greater than 10), a particle interacts with individual atmospheric atoms: there are no secondary collisions between meteor vapor atoms. In particular, the meteoroid surface is not shielded from the atmosphere by a layer of vapor. This is the free molecular flow regime and it is often assumed to apply for faint meteors. For larger atmospheric densities (lower heights), Knudsen numbers between 10 and 0.01, a transition region forms in front of the meteoroid, which modifies the interaction between it and the atmosphere. This transition or slip flow regime has not been extensively modeled: at present there is no analytic way to calculate the dynamics of a meteoroid in this type of flow. At large atmospheric densities, when the Knudsen number is less than 0.01, a shock forms in front of the object. This is the continuum flow regime, which is used to model the ablation of large meteoroids (e.g. Ceplecha et al. 2000).
The mean free path at 100 km is 12 cm, and 83 cm at 110 km. Clearly, for particles less than a centimeter in size, any meteoroid above 100 km is in the free molecular flow regime. However, the ablation of the meteoroid complicates the determination of regime: meteoroids ablate very rapidly and the production of vapor increases the density in the immediate vicinity of the particle. It is necessary to take this into account when determining the height at which the vapor cloud must be taken into consideration. Popova (2000) have estimated that the density in front of a meteoroid undergoing intensive evaporation is of order 100 times the atmospheric density at the same height, which would shift the flow regime heights as shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{0040fig1.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg4.gif) |
Figure 1: Top plot: flow regimes for meteoroids between 10-5 m and 1 m diameter, assuming no increase in density over the atmospheric density. Bottom plot: flow regimes assuming intensive ablation increases the density by a factor of 100. The actual regime over 100 km is probably closer to the first plot (see text). |
| Open with DEXTER | |
However, the density of the cloud alone cannot be used to determine the flow regime, since the vapor cloud is moving away from the meteoroid surface at thermal velocities and an atom in this cloud will not impact the surface unless it undergoes a collision with an atmospheric atom.
To determine whether the free molecular flow assumption is valid for meteoroids in our size range, the evolution of the vapor cloud was simulated using a simple collisional model. Ablation rates and meteoroid temperatures were approximately calculated using a free molecular flow model (described below) - any shielding by the vapor cloud would tend to reduce the rate of ablation, and therefore the regions identified as free molecular flow will be conservative estimates. Each ablating atom was released after a time interval determined by the instantaneous rate of ablation, and was assumed to travel along the normal to the surface at a thermal velocity corresponding to the surface temperature of the meteoroid. The ablated atom encountered an atmospheric atom at an average distance equal to the mean free path, and the two atoms were assumed to collide elastically with a random impact parameter. The position of the meteoric atom was marked at the end of certain time intervals, and it was noted if a meteor atom collided with the meteoroid surface or if an atmospheric atom on course to collide with the meteoroid surface was deflected by a collision with a vapor atom. To reduce the simulation time, each atom was taken to represent
![]() atoms; densities and numbers of colliding atoms were multiplied accordingly.
atoms; densities and numbers of colliding atoms were multiplied accordingly.
Of the three light curves which were simulated for this study, only the largest was tested for vapor cloud interactions. Since the others are smaller, they do not penetrate as far into the atmosphere, and have lower ablation rates and therefore less interaction between vapor and meteoroid. The simulation was done in two parts. Between 140 and 119 km altitude, the total mass of the body was used,
![]() kg. Below 119 km, after the body has completely fragmented, only one fragment was simulated, with a mass of
kg. Below 119 km, after the body has completely fragmented, only one fragment was simulated, with a mass of
![]() kg. In principle, the vapor clouds of different fragments may interact, but this was neglected for the current work. The fragments generally spread during the course of the simulation for distances between meters and tens of meters, and therefore interactions among the fragments may not be very important.
kg. In principle, the vapor clouds of different fragments may interact, but this was neglected for the current work. The fragments generally spread during the course of the simulation for distances between meters and tens of meters, and therefore interactions among the fragments may not be very important.
None of the ablated atoms were reflected in such a way as to collide with the meteoroid surface, and out of
![]() atmospheric atoms expected to collide (on average) with the meteoroid,
atmospheric atoms expected to collide (on average) with the meteoroid,
![]() were deflected by the vapor cloud. Zero collisions with the meteoroid seems surprising, until one considers that even at 96 km, the mean free path is roughly 6 cm. Since by the time the meteoroid reaches this height, the fragment has a radius less than one tenth of a millimeter, the chances of a random collision resulting in a meteoroid atom being reflected onto the surface is equal to the solid angle subtended by a 0.1 mm circle at a radius of 6 cm, chance of collision is less than 1 in 106. Since only one of every million atmospheric atoms is prevented from reaching the meteoroid surface, shielding is negligible. We can therefore conclude that the vapor cloud can be neglected for meteoroids smaller than
were deflected by the vapor cloud. Zero collisions with the meteoroid seems surprising, until one considers that even at 96 km, the mean free path is roughly 6 cm. Since by the time the meteoroid reaches this height, the fragment has a radius less than one tenth of a millimeter, the chances of a random collision resulting in a meteoroid atom being reflected onto the surface is equal to the solid angle subtended by a 0.1 mm circle at a radius of 6 cm, chance of collision is less than 1 in 106. Since only one of every million atmospheric atoms is prevented from reaching the meteoroid surface, shielding is negligible. We can therefore conclude that the vapor cloud can be neglected for meteoroids smaller than
![]() kg, at heights above 96 km.
kg, at heights above 96 km.
In order to model the interaction between the atmosphere and the meteoroid, a model of the atmospheric density, temperature and pressure must be adopted.
The density was taken from the MSIS-E 90 model Hedin (1991). The mass density was calculated at heights between 60 and 200 km, at 2 km intervals, for the geographic location and date of the observations. A fifth order polynomial fit was performed to the log of the density to obtain a function which could be used to calculate the density at any given height. The error in densities for the MSIS-E 90 model is estimated to be of order 5% (Hedin 1991), and measurements of atmospheric density by the shuttle, rockets and falling spheres tend to differ from the model by less than 20%.
To estimate the effects of errors in the density on the model results, the same meteor was simulated twice, with the atmospheric density in one case 20% higher than the other. The height of fragmentation was found to differ by 2 km, and the height of maximum luminosity by 1 km. There was less than a 0.1 mag change in the maximum luminosity, and less than 1 km change in the ending height. Errors in the atmospheric density will have a small effect on the temperature at which fragmentation occurs, but virtually no effect on the size of the component grains or on the measured mass.
The atmosphere was assumed to be isothermal, at 280 K. Because of the very low atmospheric density in meteor regions, the radiative heat transfer from the atmosphere to the meteoroid is negligible.
The pressure was taken from the US Standard Atmosphere. Since the pressure is very low above 100 km, this value has very little effect on the simulation results, so no effort was made to characterize the errors in it.
In the following sections, the heat transferred to the meteoroid is assumed to be distributed over the whole surface. For this to be strictly true, the meteoroid would have to be rapidly and randomly rotating. While it is unlikely that a meteoroid would be tumbling freely, rapid rotation of the body is likely (Hawkes & Jones 1978). If the body is rotating slowly or if the axis of rotation is parallel to the direction of travel, only the front surface will be heated by the atmosphere. Since the meteoroids dealt with in this work are small and therefore heat through quickly, the rapid and random rotation approximation has been kept.
The temperature of the meteoroid can be calculated by conservation of energy. The change in meteoroid surface temperature d![]() in a time interval dt can be calculated from the change in energy over the same time interval (dE) as d
in a time interval dt can be calculated from the change in energy over the same time interval (dE) as d
![]() ,
where c is the specific heat of the meteoroid material and
,
where c is the specific heat of the meteoroid material and
![]() is the mass affected by the heating. This may be the mass of the outer layer of the meteoroid, if the object is large enough to have a thermal gradient. There are three sources and sinks of energy considered in the model.
is the mass affected by the heating. This may be the mass of the outer layer of the meteoroid, if the object is large enough to have a thermal gradient. There are three sources and sinks of energy considered in the model.
Energy is imparted to the meteoroid by collisions with atmospheric atoms. In the reference frame of the meteoroid, the atmosphere has energy
![]() /2, where v is the speed of the meteoroid, and
/2, where v is the speed of the meteoroid, and ![]() is the total mass of atmospheric atoms. The mass encountered by the meteoroid in a time interval dt is
is the total mass of atmospheric atoms. The mass encountered by the meteoroid in a time interval dt is
![]() ,
where
,
where
![]() is the atmospheric density, m is the meteoroid mass,
is the atmospheric density, m is the meteoroid mass,
![]() is the meteoroid density, and A is the shape factor of the meteoroid, defined so that
is the meteoroid density, and A is the shape factor of the meteoroid, defined so that
![]() is the effective cross sectional area of the meteoroid. For a sphere, A is 1.2, and any rotating body will have a mean A of approximately unity. A dimensionless coefficient
is the effective cross sectional area of the meteoroid. For a sphere, A is 1.2, and any rotating body will have a mean A of approximately unity. A dimensionless coefficient ![]() (heat-transfer coefficient) is used to describe the fraction of the kinetic energy which is used in heating the meteoroid. This can vary between 0 and 1, and will be assumed to be 0.5.
(heat-transfer coefficient) is used to describe the fraction of the kinetic energy which is used in heating the meteoroid. This can vary between 0 and 1, and will be assumed to be 0.5.
Energy is lost from the meteoroid by radiation. This effect is particularly important for small particles: Leonids smaller than about
![]() kg do not reach intensive ablation, but are slowed and actually survive passage through the atmosphere. The energy lost by the meteoroid from this mechanism is
kg do not reach intensive ablation, but are slowed and actually survive passage through the atmosphere. The energy lost by the meteoroid from this mechanism is
![]() ,
where
,
where ![]() is the atmospheric temperature,
is the atmospheric temperature, ![]() is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and ![]() is the emissivity of the meteoroid, assumed to be 0.9.
is the emissivity of the meteoroid, assumed to be 0.9.
Energy is also lost through evaporation of the meteor material. The energy required to ablate mass dm is by definition
![]() ,
where L is the heat of ablation, which includes the heat of fusion and the heat of vaporization of the meteoroid material. Energy is lost by the meteoroid at the rate
,
where L is the heat of ablation, which includes the heat of fusion and the heat of vaporization of the meteoroid material. Energy is lost by the meteoroid at the rate
![]() .
The complete differential equation for temperature is therefore:
.
The complete differential equation for temperature is therefore:
For the drag coefficient, error is, not surprisingly, negligible. For Leonid meteors, the deceleration is virtually indetectable, and a wide variation in ![]() produces extremely small changes in the height of ablation. For a single fragment of mass
produces extremely small changes in the height of ablation. For a single fragment of mass
![]() kg, changing the drag coefficient from 0.1 to 2 changed the height of maximum luminosity by 40 m and the maximum magnitude by 0.02 mag. Both of these are much smaller than errors in these data; therefore any errors in the drag coefficient will have no sensible effect on conclusions drawn from the model.
kg, changing the drag coefficient from 0.1 to 2 changed the height of maximum luminosity by 40 m and the maximum magnitude by 0.02 mag. Both of these are much smaller than errors in these data; therefore any errors in the drag coefficient will have no sensible effect on conclusions drawn from the model.
The heat transfer coefficient is much more important. Changing ![]() from 0.1 to 1 changed the magnitude at the peak of the curve by only one quarter of a magnitude, but the height of maximum was altered by 14 km. Any error in the heat transfer coefficient will therefore lead to significant inaccuracies in the results of the model, most notably in the thermal properties of the meteoroid material or in the size of the component particles. It is likely, in fact, that
from 0.1 to 1 changed the magnitude at the peak of the curve by only one quarter of a magnitude, but the height of maximum was altered by 14 km. Any error in the heat transfer coefficient will therefore lead to significant inaccuracies in the results of the model, most notably in the thermal properties of the meteoroid material or in the size of the component particles. It is likely, in fact, that ![]() is not constant over the meteor's flight path: this matter bears further examination in future work.
is not constant over the meteor's flight path: this matter bears further examination in future work.
Classical meteor ablation theory assumes that the mass loss is proportional to the kinetic energy imparted to the meteoroid. In the classical model, ablation begins when the surface of the meteoroid reaches the boiling temperature (e.g. Bronshten 1983); at this point, the temperature is assumed to remain constant and the change in mass is given by:
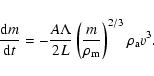 |
(3) |
The Clausius-Clapeyron equation gives the vapor pressure of a substance at a given temperature (see, e.g. Bronshten 1983):
where ![]() is the saturated vapor pressure,
is the saturated vapor pressure, ![]() the mass of a meteor atom,
the mass of a meteor atom, ![]() is the Boltzmann constant and K is a constant which can be determined from experiment. For an approximate solution, one can determine K from the boiling temperature of the meteoroid substance,
is the Boltzmann constant and K is a constant which can be determined from experiment. For an approximate solution, one can determine K from the boiling temperature of the meteoroid substance, ![]() ,
at sea level pressure
,
at sea level pressure ![]() :
:
which produces:
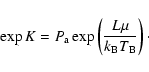 |
(6) |
where ![]() is the vapor pressure of the meteoroid substance and
is the vapor pressure of the meteoroid substance and ![]() is the condensation coefficient, which gives the probability that an ablated meteor atom colliding with the surface will condense. For metals,
is the condensation coefficient, which gives the probability that an ablated meteor atom colliding with the surface will condense. For metals, ![]() is 1: following Bronshten (1983) we will assume the
is 1: following Bronshten (1983) we will assume the ![]() of stone to be 0.5.
of stone to be 0.5.
Combining Eqs. (7) and (8), we have:
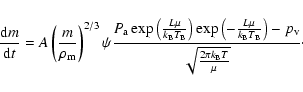 |
(9) |
For the vast majority of video meteors, the vapor pressure is negligible (see Sect. 2.1).
At high temperatures, meteoroids may lose mass not only though evaporation, but also through spraying of the melted layer on the surface (Bronshten 1983, Chap. III). To simulate this effect, when the surface of the meteoroid reaches the melting temperature at sea level pressure (
![]() ), an extra term is added to the mass loss equation, with the form of the classical mass loss equation. To prevent oscillations in the numerical integration at the sudden change in
), an extra term is added to the mass loss equation, with the form of the classical mass loss equation. To prevent oscillations in the numerical integration at the sudden change in
![]() ,
a variable factor is added in front of this term:
,
a variable factor is added in front of this term:
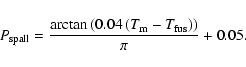
This term is equal to zero when the meteoroid surface temperature is much less than the melting point of the meteoroid material, and increases rapidly to one as the temperature becomes greater than the melting temperature. At this point, the temperature of the meteoroid will flatten out, since most of the energy being absorbed by the meteoroid is used in the ablation of mass. In practice, this term becomes active only at the very end of a typical meteor's trajectory, and has little effect on the height of maximum luminosity.
Since the classical equation of mass loss has been extensively used in the past, it is interesting to compare results obtained with the classical and Clausius-Clapeyron equations. The ablation of a
![]() kg solid meteoroid was simulated twice using identical parameters, and altering only the mass loss equation. The results are shown in Fig. 2. For the classical equation, using a typical meteoroid boiling point of 1900 K, the height of maximum luminosity was 0.7 km higher than the model using the Clausius-Clapeyron equation, and the peak magnitude was brighter by 0.2 mag. The most significant difference between the two models was in the early part of the trail, where the classical equation predicts no luminosity and the Clausius-Clapeyron model predicts a gradually brightening meteor.
kg solid meteoroid was simulated twice using identical parameters, and altering only the mass loss equation. The results are shown in Fig. 2. For the classical equation, using a typical meteoroid boiling point of 1900 K, the height of maximum luminosity was 0.7 km higher than the model using the Clausius-Clapeyron equation, and the peak magnitude was brighter by 0.2 mag. The most significant difference between the two models was in the early part of the trail, where the classical equation predicts no luminosity and the Clausius-Clapeyron model predicts a gradually brightening meteor.
| |
Figure 2:
Light curve of a solid meteoroid, mass
|
| Open with DEXTER | |
The production of light is the most uncertain portion of the model. Meteors emit light in spectral bands, rather than as a thermal continuum (cf. Ceplecha et al. 1998), so the amount of light produced depends on the composition and size of the meteoroid, the speed of the meteoroid, and the atmospheric density. A full treatment of the problem is complicated by the fact that meteoritic speeds are difficult to simulate in the laboratory, so very little experimental data are available.
In this model we use the classical assumption that the luminous intensity is proportional to the kinetic energy lost by the meteoroid: for small particles this is effectively proportional to the mass loss rate, since the velocity is nearly constant. The equation for the luminous intensity is:
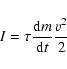 |
(10) |
where ![]() is the luminosity coefficient. There is a wide scatter in the values of
is the luminosity coefficient. There is a wide scatter in the values of ![]() used in various studies, which reflects the uncertainty in this value. Whipple (1938) proposed a simplification of the form
used in various studies, which reflects the uncertainty in this value. Whipple (1938) proposed a simplification of the form
![]() ,
based on photographic data, but there is doubt as to whether this applies to fainter meteors. Öpik (1963) found that for fainter meteors
,
based on photographic data, but there is doubt as to whether this applies to fainter meteors. Öpik (1963) found that for fainter meteors ![]() actually decreased with velocity above 24 km s-1. We have adopted a constant value of
actually decreased with velocity above 24 km s-1. We have adopted a constant value of
![]() for
for ![]() .
This is somewhere in the middle of proposed values of
.
This is somewhere in the middle of proposed values of ![]() (Bronshten 1983).
(Bronshten 1983).
It is worth noting that the ![]() used in this study is dimensionless, and the intensity I has units of Watts. The magnitude is given by:
used in this study is dimensionless, and the intensity I has units of Watts. The magnitude is given by:
| (11) |
If the above model is used to simulate a solid particle, the light curve produced has a certain characteristic shape (Fig. 3). The height at which the maximum luminosity occurs may change as the thermal properties of the object are changed, or as the size is altered, but the overall light curve will always consist of a slow rise to maximum, followed by a rapid decrease.
![\begin{figure}
\par\includegraphics[width=6.7cm,height=4.9cm,clip]{0040fig3.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg58.gif) |
Figure 3: Light curve of a solid meteoroid. |
| Open with DEXTER | |
Actual meteor light curves rarely match this shape: on average, faint meteors have symmetric light curves, with the point of maximum luminosity occurring early for some meteors and late for others (Figs. 4 and 5). It is necessary for any good model to explain this fact. As we shall see, fragmentation can account for it.
![\begin{figure}
\par\includegraphics[width=6.9cm,height=4.6cm,clip]{0040fig4.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg59.gif) |
Figure 4: Light curve of a Leonid meteor, showing a peak in the middle of the curve. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm,height=4.9cm,clip]{0040fig5.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg60.gif) |
Figure 5: Light curve of a Leonid meteor, showing a peak toward the end of the curve. |
| Open with DEXTER | |
The dustball model (formulated by Hawkes & Jones 1975, after the proposal by Öpik 1958) proposed that meteoroids are composed of solid grains held together with a volatile "glue''. This volatile substance melts first while the meteoroid is heating, releasing the solid grains which then ablate individually. The nature of the volatile substance is not known: it may be a heavy organic such as n-octadecane (C18H38) (Steel 1998) or a light metal such as sodium. In this model we ignore any light produced by the volatile component, and simulate it by allowing solid meteoroid grains to separate from the surface when it reaches a certain temperature. This temperature will depend on the nature of the volatile substance: it will be fitted in the simulation.
A meteoroid, even one only 1 mm in size, will not heat uniformly: the surface receives all the heat and over short timescales this is not transferred to the interior. To determine the temperature at the surface, it is assumed that a shell of the meteoroid, thickness x0, heats uniformly, while the interior remains cool. When this outer shell has heated to the limiting temperature of the volatile "glue'', the grains in this layer are released.
The size of the outer layer is determined from the "heating depth", calculated by Bronshten (1983). Using the standard model to calculate the heat flux into the meteoroid, one finds that the depth at which the temperature is 1/e of the surface temperature is:
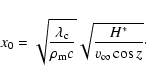 |
(12) |
Here
![]() is the thermal conductivity of the meteoroid, H* is the scale height in the atmosphere,
is the thermal conductivity of the meteoroid, H* is the scale height in the atmosphere, ![]() is the meteoroid speed outside the atmosphere, and z the zenith angle of the meteor radiant. Since the scale height changes rapidly at meteor heights, H* was calculated at every step, using the atmospheric density at the height being considered, and at a point 2 km lower. Any core that is left is assumed to have a temperature of 1/e the surface temperature.
is the meteoroid speed outside the atmosphere, and z the zenith angle of the meteor radiant. Since the scale height changes rapidly at meteor heights, H* was calculated at every step, using the atmospheric density at the height being considered, and at a point 2 km lower. Any core that is left is assumed to have a temperature of 1/e the surface temperature.
To apply the model, it is also necessary to determine the distribution of fragments in the meteoroid. The structure of meteoroids in the size range observed is not known, so several distributions have been simulated. The first is a Gaussian distribution where the grains have some average mass and standard deviation. In order to access a wide variety of light curve shapes, the second distribution is a power law distribution, where there are many more small grains than large ones. The third distribution used is a combination of the first two.
Gaussian distributions of grains produce light curves with classical, late-skew curves, but these curves can be shorter than those for single bodies. The width of the curve and the height of the maximum can be varied by changing the average grain size (Fig. 6). Power law distributions can match many different shapes, depending on the choice of grain mass distribution index sf. Values of sf less than 2 (an excess of mass in large grains) produce curves which peak late, while values greater than 2 (indicating an excess of mass in small grains) give curves which peak early (Fig. 7). Some combination of these two may be able to explain all light curves.
![\begin{figure}
\par\includegraphics[width=7.4cm,height=5.1cm,clip]{0040fig6.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg64.gif) |
Figure 6: Simulated light curve using a Gaussian distribution of grains, with average grain size 10-8 kg. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,height=5cm,clip]{0040fig7.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg65.gif) |
Figure 7: Simulated light curve using a power law distribution, sf=2.4. |
| Open with DEXTER | |
The model was implemented in IDL 5.6. This allowed the results to be plotted automatically for each run.
The numerical integration of the three differential equations was performed using a Runge-Kutta 4 integrator (see Press et al. 1992, for a C implementation). This is a relatively fast, accurate integrator, and was found to be stable at time steps of 0.001 s. A variable stepsize was also implemented as an experiment, but there was no significant gain in accuracy and the speed of the code was significantly reduced, so a fixed stepsize was used in the final model.
The masses of individual fragments in the meteoroid were calculated according to the specified size distribution prior to the beginning of the simulation. Grains were then released in random order as needed.
One approximation was made in order to increase the processing speed. Each time a group of fragments were separated from the meteoroid, those with masses within 1% of each other were grouped. The integration was performed for one particle with a mass equal to the average mass of particles in that bin, and the light produced was multiplied by the number of fragments in the group. The power law distribution in particular produces many small grains with similar sizes, so this approach decreased the processing time by up to a factor of 200.
It is important to check that the model can reproduce, within estimated errors, the light curves of observed meteors. Three Leonid meteor light curves for which heights are available have been simulated to test the model.
The measured heights of these meteors have errors less than 1 km (see Koschny & Diaz 2002, for details of the analysis), but the magnitudes are less precise, with errors estimated to be in the vicinity of 1 astronomical magnitude. The error is estimated to be greatest in the absolute values of the magnitudes: the relative magnitudes probably have much lower errors. These errors will be improved before detailed modeling is done and conclusions are drawn about the physical and chemical nature of the meteoroids. The absolute magnitudes of the meteors, or apparent magnitudes if the meteors were observed from a range of 100 km, were calculated.
For each simulation, the appropriate radiant zenith angle and velocity was used. The thermal properties of porous stone were used prior to fragmentation, to emphasize the fragile structure of the meteoroid, while each grain, after detaching from the main body, was assumed to be solid stone. The density of the main body was taken to be 1500 kg/m3, while individual fragments had densities of 3500 kg/m3. The boiling point of both was set at 2100 K, and the melting point at 1900 K. The specific heat was 1000 J/kg K, the condensation coefficient 0.5 (after Bronshten 1983), and the average atomic mass was taken to be 23 atomic units. The thermal conductivity of the porous stone was taken to be 0.5 J/m s K, while the solid stone had a higher thermal conductivity, 3.0 J / m s K. The heat of ablation used for both the porous and solid stone was
![]() J/kg.
J/kg.
The first meteor (LC182415) was well fit using a Gaussian distribution of stone grains with average mass
![]() kg. The temperature at which the glue released the grains was 1100 K, and the total mass required was
kg. The temperature at which the glue released the grains was 1100 K, and the total mass required was
![]() kg. The fragmentation can be seen in the rapid rise of the light curve between 120 and 115 km (Fig. 8).
kg. The fragmentation can be seen in the rapid rise of the light curve between 120 and 115 km (Fig. 8).
![\begin{figure}
\par\includegraphics[width=7cm,height=5cm,clip]{0040fig8.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg69.gif) |
Figure 8: Fit to observed Leonid light curve. |
| Open with DEXTER | |
The second meteor (Fig. 9, LC183020) is also well fit with a Gaussian distribution, with larger grains averaging
![]() kg. The grain release temperature that best matched the curve was slightly lower, 1000 K: the fragmentation of this meteoroid took place entirely before the meteor became visible. The total mass required in the model was higher than the first meteor,
kg. The grain release temperature that best matched the curve was slightly lower, 1000 K: the fragmentation of this meteoroid took place entirely before the meteor became visible. The total mass required in the model was higher than the first meteor,
![]() kg.
kg.
![\begin{figure}
\par\includegraphics[width=7.1cm,height=5cm,clip]{0040fig9.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg70.gif) |
Figure 9: Fit to observed Leonid light curve. |
| Open with DEXTER | |
The third meteor (Fig. 10, LC191717) is not well fitted with a Gaussian: the best fit was obtained using a power law distribution with an sf value of 2.1. The smallest grain size used was
![]() kg; including smaller grains made the peak intensity at the point of fragmentation too high and too narrow. The grains separated at a temperature of 1150 K, close to the first meteor simulated: the fragmentation is the reason for the initial rise of the meteor's brightness. The total mass of the meteoroid was
kg; including smaller grains made the peak intensity at the point of fragmentation too high and too narrow. The grains separated at a temperature of 1150 K, close to the first meteor simulated: the fragmentation is the reason for the initial rise of the meteor's brightness. The total mass of the meteoroid was
![]() kg. The first two points on this curve are particularly intriguing, since they seem to match the slow rise just before fragmentation; however the uncertainty in the magnitudes does not allow firm conclusions to be drawn from this.
kg. The first two points on this curve are particularly intriguing, since they seem to match the slow rise just before fragmentation; however the uncertainty in the magnitudes does not allow firm conclusions to be drawn from this.
![\begin{figure}
\par\includegraphics[width=6.9cm,height=4.9cm,clip]{0040fg10.eps}\end{figure}](/articles/aa/full/2004/17/aa0040/Timg73.gif) |
Figure 10: Fit to observed Leonid light curve. |
| Open with DEXTER | |
The grain distribution of meteoroids is of great interest, as is the question of whether all meteoroids are alike (implying that the comet's surface is relatively homogenous) or whether they differ. While the chemical composition cannot be uniquely determined from light curve observations, it can be determined whether particular substances are consistent with the observed light curves. If one particular model can be found which matches the observations better than any other, it would be of great interest to investigate this further.
The current model is valid only in the free molecular flow regime, and will not apply to large meteoroids which penetrate farther into the atmosphere. The exact size at which this occurs will have to be determined. The physics in this regime is complicated, since the simplifications which can be used in free molecular flow will not apply, nor will those for the continuum flow regime, where some sort of equilibrium can be assumed. It is likely that detailed simulations of the region around the meteoroid will be needed before a model of this regime can be constructed.
In the current model, fragmentation occurs when the temperature of the surface reaches a temperature sufficient to disrupt the binding of the meteoroid. Meteoroids may also fragment due to mechanical crushing when the force of the atmosphere (ram pressure) on the leading surface becomes large. At heights above 100 km, the force is too small to disrupt even the most fragile of particles, but at lower heights this force will become significant and larger meteoroids may fragment in this way.
Data exist for some spectral emissions of certain elements when they collide with nitrogen or oxygen (Boitnott & Savage (1971), magnesium and calcium; Boitnott & Savage (1970), sodium). These can be used with a chemical model of the meteoroid to determine the light produced in given spectral bands. Using these calculated luminous efficiencies, a meteor spectrum may be generated which could be compared to observed meteor spectra, to determine the relative concentration of different elements in the meteoroid.
For this, the thermal properties of many substances likely occurring in meteoroids will be needed, so that each can be simulated accurately. This approach will also impose more constraints on the model, improving its reliability.
The model of meteor ablation outlined above should be a valuable tool for examining the physical structure and chemical composition of meteoroids. In the preliminary fits described above, the heights of maximum luminosity for each meteor could be accurately reproduced using stone grains, implying that meteoroids are composed of something thermally similar to stone. The grain distributions derived for these three Leonids are similar to the results of Murray et al. (2000). That study concluded that most Leonid light curves could be fit with a power law distribution of grains, some of them accompanied by single, large grains. Firm conclusions about the composition cannot be drawn until more models have been tested.
The greatest sources of uncertainty in the model are the coefficient of luminous intensity and the heat transfer coefficient. The former can alter the photometric mass computed from light curves by up to one order of magnitude. The latter will alter the maximum height of a particular grain: this means that if the heat transfer coefficient is in error, the grain sizes calculated from the model will be too large or too small.
Acknowledgements
Thanks to Armand Jongen for help with optimizing the IDL code.