Department of Pure and Applied Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland, UK

Abstract
Energy levels and radiative rates for transitions among the lowest 97 fine-structure levels belonging to the (1s²2s²2p⁶) 3s²3p², 3s3p³, 3s²3p3d, 3p⁴, 3s3p²3d and 3s²3d² configurations of Fe XIII have been calculated using the fully relativistic GRASP code. Additionally, collision strengths for transitions among these levels have been computed using the Dirac Atomic R-matrix Code (DARC) of Norrington & Grant (2004). Radiative rates and oscillator strengths are tabulated for all allowed transitions among the 97 fine-structure levels, while collision strengths are reported for some transitions at a few energies above thresholds. Comparisons are made with the available results, and the accuracy of the data is assessed.

Earlier calculations for Fe XIII have been performed by many workers, but the most recent and comprehensive results available today are those of Gupta & Tayal (1998). They have reported energy levels, radiative rates, and collision strengths ( $\Omega$ ) for transitions among 26 fine-structure levels of the 3s²3p², 3s3p³ and 3s²3p3d configurations. Furthermore, they have resolved resonances in thresholds region and have reported results for effective collision strengths ( $\Upsilon$ ) at temperatures below $5\times 10^6$ K, which is sufficient for applications in plasma diagnostics. In their calculations they have included configuration interaction (CI) for generating wavefunctions, and one-body relativistic operators for calculating $\Omega$ . Therefore, their results should be the most reliable available today. However, in a recent paper Landi (2002) has emphasized a need for fresh calculations (for both transition rates and collision rates), because electron densities derived from line ratios calculated from the recent atomic data of Gupta & Tayal (1998) and earlier data of Fawcett & Mason (1989) differ by a factor of two, and hence provide different results for plasma diagnostics.

Apart from the above reason, we find that there is scope for extension as well as improvement over the results of both Fawcett & Mason (1989) and Gupta & Tayal (1998). We achieve this by extending the calculations to 97 levels, and hence including resonances arising from the higher lying levels, mainly from the 3p⁴, 3s3p²3d and 3s²3d² configurations. Apart from this, we are adopting an independent approach for calculating the wavefunctions as well as the collision strengths. To be specific, we are employing the GRASP (General-purpose Relativistic Atomic Structure Program) of Dyall et al. (1989) and DARC (Dirac Atomic R-matrix Code) of Norrington & Grant (2004) for the computations of wavefunctions and $\Omega$ , respectively. This is in contrast to the use of the CIV3 (Hibbert 1975) and Breit-Pauli R-matrix (Scott & Taylor 1982) programs by Gupta & Tayal (1998), and SuperStructure (SS: Eissner et al. 1974) and Distorted-Wave (DW: Eissner & Seaton 1972) codes by Fawcett & Mason (1989). Thus our calculations are fully relativistic in the jj coupling scheme, in comparison to their semi-relativistic approach of the ${\it LSJ}$ coupling scheme.

2 Energy levels

The (1s²2s²2p⁶) 3s²3p², 3s3p³, 3s²3p3d, 3p⁴, 3s3p²3d and 3s²3d² configurations of Fe XIII give rise to 97 fine-structure levels, listed in Table 1. To calculate level energies, and oscillator strengths and radiative rates for allowed transitions among these levels, we have adopted the GRASP code of Dyall et al. (1989). Thus relativistic effects have been fully taken into account, unlike earlier calculations which have neglected the two-body relativistic operators.

In Table 1 we list our energy levels obtained with above 6 configurations. Also included in this table are the CIV3 energies of Gupta & Tayal (1998) and the experimentally compiled energies by NIST (http://www.physics.nist.gov/PhysRefData). The experimental values for all levels are not yet available, but for common levels the agreement between theory and experiment is better than 5% for most of the levels, and the discrepancy is up to 8% for two levels, namely 3s3p³ ¹D⁰₂ (13) and 3s3p³ ³S⁰₁ (15). The agreement between the experimental and theoretical CIV3 energies is slightly better for some levels, although discrepancy between the two is up to 9% - see level 2 i.e. 3s²3p² ³P₁. In the absence of experimental results for most of the levels listed in Table 1, one way to improve energy levels is to include additional CI. The 3p³3d, 3s3p3d² and 3s3d³ configurations generate 38, 90 and 38 additional levels, respectively. These additional levels lie in the energy range 9.80 to 13.20 Ryd, which is towards the higher end of the energy levels in Table 1. Hence CI with these levels does make a difference for some of the levels. Similarly, the 3s²3p4 $\ell$ configurations give rise to 76 additional levels in the energy range of 12.60 to 16.50 Ryd. Levels of other configurations (such as: 3p²3d² and 3d⁴) lie in a much higher energy range, and hence do not make any appreciable impact on the energies of the levels listed in Table 1. Therefore, we have performed a larger calculation with 301 levels of the 3s²3p², 3s3p³, 3s²3p3d, 3p⁴, 3s3p²3d, 3s²3d², 3p³3d, 3s3p3d², 3s3d³ and 3s²3p4 $\ell$ configurations, and the level energies so obtained are also listed in Table 1. These results from a larger CI calculation improve energy levels up to 7%, and reduce the discrepancy with the corresponding experimental results. Also level orderings are slighly different, between our 6 and 13 configurations calculations, in a few instances such as levels 14/15 and 21/22. In conclusion we may state that apart from relativistic effects, CI is still important for Fe XIII, which has a comparatively high nuclear charge with Z = 26.

In spite of observing the effect of additional CI on energy levels of Fe XIII, we are restricting our calculations to 97 levels among the first six configurations listed above, because levels of other configurations cross over with the levels of the 3s3p²3d and 3s²3d² configurations, and inclusion of a significantly large additional levels in a collision calculation is beyond the limit of our available computational resources.

3 Radiative rates and oscillator strengths

The absorption oscillator strength (f_ij) and radiative rate A_ji (in s^-1) for an allowed transition $i \to j$ are related by the following expression:

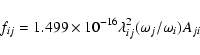$\begin{displaymath}f_{ij} = 1.499 \times 10^{-16} \lambda^2_{ij} (\omega_j/\omega_i) A_{ji} \end{displaymath}$

(1)

In Table 3 we compare our oscillator strengths for those transitions for which Gupta & Tayal (1998, henceforth GT) have reported their results. This will facilitate a comparison with their corresponding results of $\Omega$ in the next section. Also included in this table are results from our other two GRASP calculations, which have been performed with 6 configurations (namely, 3s²3p², 3s3p³, 3s²3p3d, 3p⁴, 3s3p3d² and 3p³3d), and all 13 (listed in the previous section) configurations, and will be referred to as GRASP6 and GRASP13, respectively. The six configurations listed above are those which were included by Fawcett & Mason (1989, henceforth FM) in their calculations of collision strengths, and hence will facilitate a comparison with their $\Omega$ values in the next section. The 13 configuration calculations have been included here just to demonstrate that CI is very important for Fe XIII.

Table 3: Comparison of oscillator strengths for some transitions of Fe XIII. ( $a \pm b \equiv a \times 10^{\pm b}$ ).

The CIV3 results of GT agree with the corresponding GRASP6 and GRASP13 f-values within a factor of two, for most of the transitions listed in Table 3. However, for a few weaker transitions whose f-values are comparatively small, the differences between the two calculations can be up to several orders of magnitude - see, for example, 2-20, 3-8, 3-22 and 4-12 transitions. Similarly, the f-values from our GRASP6 and GRASP13 calculations agree to better than 50% for most of the transitions, but differences for weaker transitions can be up to several orders of magnitude - see, for example, 3-22, 3-28, 4-12, 4-28 and 5-23 transitions. Our results listed in Table 2 and referred to as GRASP in Table 3 agree with those of GRASP13 within a factor of two, but differences for some of the transitions (such as: 2-18, 4-19, 4-24 and 5-15) are up to a factor of three. Furthermore, for very weak transitions (such as: 2-20, 4-12 and 4-28) the two sets of f-values differ by up to several orders of magnitude. This is due to the effect of cancellation among mixing coefficients, but we may emphasize here that such weak transitions do not play any significant role in plasma diagnostics. The other results available in the literature are of Bromage et al. (1978) for a few transitions. Their f-values (not listed in Table 3) agree with those of GRASP6 within a factor of two for many common transitions, but are higher by a factor of 5 for the 3-20 transition. In conclusion, we may state that CI (apart from relativistic effects) is very important for Fe XIII, and results have not (truly) converged within the 13 configurations considered in the present work. To improve the calculations further, more extensive CI needs to be included. This may be possible to achieve with available resources, but will make the collisional calculations intractable, as discussed in Sect. 1. Therefore, the results for radiative rates and oscillator strengths listed in Table 2 for transitions in Fe XIII are probably the best available under the circumstances, although scope remains for improvement.

We now briefly comment on the accuracy assessment of our radiative rates presented in Table 2. It is clear from the discussion above that the present radiative rates have enough scope for improvement by including further CI. Successive inclusion of more and more configurations generally provides converging results for a majority of transitions, especially those whose f-values are not insignificant. Because of cross over of the levels of many configurations, this approach is not very practical for the Fe XIII ion. A criterion which is generally adopted for the accuracy assessment of a calculation such as the present one, is the agreement achieved between the length and velocity forms of the f-values and/or the radiative rates. For about 20% of strong transitions ( $f \ge 0.01$ ) the two forms of f-values differ by more than 20%, whereas they differ by more than 50% for only 6% of such transitions. In our opinion, such a result is highly satisfactory considering the large number of transitions involved in the calculations.

4 Collision strengths

On the other hand, GT included CI among configurations of the n = 3 complex plus 3s²3p4f, and one-body relativistic operators in the Breit-Pauli approximation. Furthermore, they extended the partial waves and energy ranges of FM from L = 7 and E = 45 Ryd to L = 25 and E = 60 Ryd, respectively, and included resonances in thresholds region in order to calculate results for $\Upsilon$ up to $T_e = 5\times 10^6$ K. They excluded the 3s3p³ ⁵S⁰₂ level from their calculations, which should not seriously affect their results for a majority of transitions. However, a comparison of $\Omega$ values shown in their Table 4 makes a few anomalies obvious. For example, their $\Omega$ values differ from those of FM by more than two orders of magnitude for some transitions, such as: 1-5 (3s²3p² ³P₀-3s²3p² ¹S₀) and 2-20 (3s²3p² ³P₁-3s²3p3d ³P⁰₁). The 1-5 is a 0-0 forbidden transition whose $\Omega$ value is expected to be small, but GT's results are higher than those of FM by over two orders of magnitude. This could be a result of their choice of the earlier version of the R-matrix program (Scott & Taylor 1982) they adopted, which is known to have some errors, as their similar results for Fe XI also suffer from the same problem - see Aggarwal & Keenan (2003) for details and examples. However, 2-20 is an allowed transition, whose $\Omega$ value is not only expected to be significant, but should also increase with increasing energy. The GT results for this transition are in total contrast with those of FM, mainly because their f-value is very small, i.e. 0.0001. However, the f-value of FM calculations for this transition should be even smaller (see Table 3, especially column GRASP6). Such allowed transitions with very small f-values generally behave as forbidden transitions, and hence their $\Omega$ values are insignificantly small. However, the corresponding results of FM appear to be contrary. This could be a result of some levels mixing, as often SS, DW and JAJOM follow different levels ordering, and therefore level identification sometimes becomes ambiguous, as discussed by Aggarwal et al. (2003) for transitions in Fe XVII.

The other anomaly is that the GT values of $\Omega$ for almost all strong allowed transitions, such as 1-20 (3s²3p² ³P₀-3s²3p3d ³P⁰₁), 2-19 (3s²3p² ³P₁-3s²3p3d ³P⁰₂) and 3-25 (3s²3p² ³P₂-3s²3p3d³D⁰₃), are up to 50% lower than those of FM - see Table 4 of Gupta & Tayal (1998), or the present Table 4. This could be a direct consequence of their (up to 25%) lower f-values, as seen in Table 3. However, for some other strong transitions, such as: 1-15 (3s²3p² ³P₀-3s3p³ ³S⁰₁), 2-15 (3s²3p² ³P₁-3s3p³ ³S⁰₁), 2-22 (3s²3p² ³P₁-3s²3p3d ¹D⁰₂), 4-19 (3s²3p² ¹D₂-3s²3p3d ³P⁰₂), 5-18 (3s²3p² ¹S₀-3s3p³ ¹P⁰₁), and 5-28 (3s²3p² ¹S₀-3s²3p3d ¹P⁰₁), the f-values of GT should be comparable with those of FM (see Table 3), yet the GT values of $\Omega$ are lower by up to a factor of two. These large differences in the two sets of $\Omega$ have been attributed by GT to the possibility of overestimation by FM. However, such large differences for strong transitions (for both f and $\Omega$ ) are bound to affect the calculations of line ratios, and subsequently of plasma diagnostics. Therefore, it will be useful to assess the accuracy of these calculations by another independent one.

For the computations of collision strengths, we have employed the DARC program of Norrington & Grant (2004). This program includes the relativistic effects in a systematic way, in both the target description and the scattering model. It is based on the jj coupling scheme, and uses the Dirac-Coulomb Hamiltonian in the R-matrix approach. However, because of the inclusion of fine-structure in the definition of channel coupling, the matrix size of the Hamiltonian increases substantially, making the calculations computationally more expensive. The R-matrix radius has been adopted to be 3.0 au, and 15 continuum orbitals have been included for each channel angular momentum for the expansion of the wavefunction. This allows us to compute $\Omega$ up to an energy of 120 Ryd. The maximum number of channels for a partial wave is 475, and the corresponding size of the Hamiltonian matrix is 7138. In order to obtain convergence of $\Omega$ for all transitions and at all energies, we have included all partial waves with angular momentum $J \le 39.5$ , although a higher range would have been preferable for the convergence of allowed transitions, especially at higher energies. Unfortunately however, given the resources available to us, this was not possible. Nevertheless, to account for the inclusion of higher neglected partial waves, we have included a top-up, based on the Coulomb-Bethe approximation for allowed transitions and geometric series for forbidden transitions.

In Figs. 1a and 2a we show the variation of $\Omega$ with angular momentum J at three energies of 15, 30 and 45 Ryd, and for two transitions, namely 2-3 (3s²3p² ³P₁-3s²3p² ³P₂) and 4-5 (3s²3p² ¹D₂-3s²3p² ¹S₀), respectively. The corresponding results at three higher energies of 60, 90 and 120 Ryd are shown in Figs. 1b and 2b. Both of these are forbidden transitions, but have comparatively higher magnitude. For both of these (beside similar other) transitions, values of $\Omega$ have (almost) fully converged including the highest energy of our calculations, i.e. 120 Ryd. In Figs. 3a-5a we show similar results for three allowed transitions, namely 1-20 (3s²3p² ³P₀-3s²3p3d ³P⁰₁), 2-23 (3s²3p² ³P₁-3s²3p3d ³D⁰₁), and 3-19 (3s²3p² ³P₂-3s²3p3d ³P⁰₂), at three energies of 15, 30 and 45 Ryd. These transitions have particularly been selected, because our GRASP and earlier CIV3 f-values of GT are in total agreement, and those of FM also agree within 15%. This satisfactory agreement among different sets of f-values will facilitate a direct comparison among the $\Omega$ values, which we will discuss below. However, it is clear from these figures that for all these (and other similar) transitions, values of $\Omega$ have fully converged within the partial waves range of our calculations (i.e. $J \le 39.5$ ), at energies below $\sim$ 45 Ryd. Therefore, the contribution of higher neglected partial waves will be insignificant. However, even this large range of partial waves is not sufficient for the convergence of $\Omega$ at higher energies, as can be seen in Figs. 3b-5b for the same 1-20, 2-23, and 3-19 transitions, at three energies of 60, 90 and 120 Ryd.

In Table 4 we compare our results of $\Omega$ with those of FM and GT for transitions from the levels of the 3s²3p² configuration to those of the 3s3p³ and 3s²3p3d configurations, because these are the only transitions common among the three calculations. Similarly, the three energies of 15, 30 and 45 Ryd are the only common energies. However, a complete list of $\Omega$ for all 4656 inelastic transitions among the lowest 97 fine-structure

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig1a.ps} \end{figure}$	Figure 1: a) Partial collision strengths for the 3s²3p² ³P₁-3s²3p² ³P₂ (2-3) transition of Fe XIII, at three energies of 15 Ryd (circles), 30 Ryd (triangles), and 45 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14.1cm,clip]{564fig1b.ps} \end{figure}$	Figure 1: b) Partial collision strengths for the 3s²3p² ³P₁-3s²3p² ³P₂ (2-3) transition of Fe XIII, at three energies of 60 Ryd (circles), 90 Ryd (triangles), and 120 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig2a.ps} \end{figure}$	Figure 2: a) Partial collision strengths for the 3s²3p² ¹D₂-3s²3p² ¹S₀ (4-5) transition of Fe XIII, at three energies of 15 Ryd (circles), 30 Ryd (triangles), and 45 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig2b.ps} \end{figure}$	Figure 2: b) Partial collision strengths for the 3s²3p² ¹D₂-3s²3p² ¹S₀ (4-5) transition of Fe XIII, at three energies of 60 Ryd (circles), 90 Ryd (triangles), and 120 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14.2cm,clip]{564fig3a.ps} \end{figure}$	Figure 3: a) Partial collision strengths for the 3s²3p² ³P₀-3s²3p3d ³P₁⁰ (1-20) transition of Fe XIII, at three energies of 15 Ryd (circles), 30 Ryd (triangles), and 45 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14.2cm,clip]{564fig3b.ps} \end{figure}$	Figure 3: b) Partial collision strengths for the 3s²3p² ³P₀-3s²3p3d ³P₁⁰ (1-20) transition of Fe XIII, at three energies of 60 Ryd (circles), 90 Ryd (triangles), and 120 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig4a.ps} \end{figure}$	Figure 4: a) Partial collision strengths for the 3s²3p² ³P₁-3s²3p3d ³D₁⁰ (2-23) transition of Fe XIII, at three energies of 15 Ryd (circles), 30 Ryd (triangles), and 45 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig4b.ps} \end{figure}$	Figure 4: b) Partial collision strengths for the 3s²3p² ³P₁-3s²3p3d ³D₁⁰ (2-23) transition of Fe XIII, at three energies of 60 Ryd (circles), 90 Ryd (triangles), and 120 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig5a.ps} \end{figure}$	Figure 5: a) Partial collision strengths for the 3s²3p² ³P₂-3s²3p3d ³P₂⁰ (3-19) transition of Fe XIII, at three energies of 15 Ryd (circles), 30 Ryd (triangles), and 45 Ryd (stars).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig5b.ps} \end{figure}$	Figure 5: b) Partial collision strengths for the 3s²3p² ³P₂-3s²3p3d ³P₂⁰ (3-19) transition of Fe XIII, at three energies of 60 Ryd (circles), 90 Ryd (triangles), and 120 Ryd (stars).
Open with DEXTER

Table 4: Comparison of collision strengths for some transitions of Fe XIII. ( $a \pm b \equiv a \times 10^{\pm b}$ ).

$\begin{figure} \par\includegraphics[angle=-90,width=14cm,clip]{564fig6.ps} \end{figure}$	Figure 6: Partial collision strengths for the 3s²3p² ¹S₀-3s²3p3d ¹P₁⁰ (5-28) transition of Fe XIII, at three energies of 15 Ryd (circles), 30 Ryd (triangles), and 45 Ryd (stars).
Open with DEXTER

levels of Fe XIII in a wider energy range (10.5 to 120.0 Ryd) will be reported in a later publication along with results for $\Upsilon$ . As stated above, the $\Omega$ values of GT for the 1-5 (0-0) transition are higher by over two orders of magnitude, and are in total disagreement with the other two calculations. However, for all forbidden transitions there is a general agreement between our present and their earlier calculations, although differences for three transitions (namely, 1-4, 3-4 and 3-5) are up to a factor of two. Similarly, differences between the two calculations for allowed transitions are up to a factor of four (see, for example, 1-18, 1-28, 2-15 and 2-18 transitions), but are in accordance with the differences in the wavefunctions, i.e. in the f-values, as seen in Table 3. This satisfactory agreement between the two independent R-matrix calculations is mainly because both calculations have included a wide range of partial waves, which are fully sufficient for the convergence of $\Omega$ for the forbidden transitions, and are nearly sufficient for the allowed transitions, as shown earlier in Figs. 1a-5a.

However, the other results of FM listed in Table 4 differ with the other two calculations for many transitions. Their results of $\Omega$ are underestimated, by up to a factor of four, for many forbidden transitions, such as: 2-17, 2-25, and 5-22. Moreover, the differences increase with increasing energy. This is clearly a result of a limited range of partial waves ( $L \le 7$ ) included by them, which is not sufficient for the convergence of $\Omega$ as shown in Figs. 1a and 2a. Similarly, their results of $\Omega$ also differ for many allowed transitions, such as: 1-15, 2-15, 2-22, 3-24, 4-19 and 5-18, by up to a factor of six. Some of these differences in $\Omega$ are a result of the corresponding differences in the f-values. However, there are many transitions for which the three calculations produce nearly the same values of oscillator strengths, see, for example, transitions 1-7, 2-8, 3-26, 4-25, and 5-28, yet the $\Omega$ values of FM are higher by up to 50%. For many of these transitions, $\Omega$ have nearly converged within $J \le$ 39.5, as shown earlier in Figs. 3a-5a, and hence the contribution of higher neglected partial waves is almost negligible. As a further example, we show our partial $\Omega$ in Fig. 6 for the 5-28 (3s²3p² ¹S₀-3s²3p3d ¹P⁰₁) transition, because the three sets of f-values agree within 10% - see Table 3. Our present and earlier results of GT agree to better than 5% at all three energies of 15, 30 and 45 Ryd, but the corresponding $\Omega$ of FM are higher by up to 30%. Clearly, FM have overestimated the contribution of higher neglected partial waves with $L \ge 8$ . Moreover, for some of the transitions, such as 1-23 and 2-20, the FM values of $\Omega$ are lower and higher by factors of 2 and 50, respectively, and are not in accordance with their corresponding f-values.

5 Conclusions

In this paper we have reported a consistent set of results for energy levels, radiative rates, and collision strengths for transitions among 97 fine-structure levels of Fe XIII. Relativistic effects and CI have been included while generating the wavefunctions, and a large range of partial waves has been included to ensure the convergence of $\Omega$ . Apart from performing our calculations in the jj coupling scheme, we have attempted to make an overall improvement over the existing results. These improvements have mainly been achieved by the inclusion of: (i) a larger number of levels, (ii) a wider range of partial waves, and (iii) a higher range of energy.

Our results of collision strengths are in broad agreement with those of GT, and the differences, if any, are in accordance with the wavefunctions. However, the corresponding results of FM are found to be deficient. For forbidden transitions, their values of $\Omega$ are underestimated, whereas for the allowed transitions they are overestimated. Additionally, for some of the allowed transitions their results of $\Omega$ are not in accordance with their corresponding f-values.

Our results for energy levels are assessed to be accurate to $\sim$ 5%, whereas for radiative rates and collision strengths the accuracy should be better than 20%, for a majority of transitions. The accuracy of our present results can be further improved by the inclusion of additional CI, which may be possible in future calculations. Regarding the discrepancies observed by Landi (2002) in applying the atomic data of FM and GT in plasma diagnostics, we may state that the results of FM are deficient for almost all transitions. For forbidden transitions their results of $\Omega$ are underestimated, and for the allowed ones are overestimated. Therefore, any agreement between experimental observations and parameters derived from their data will probably be fortuitous. However, the corresponding results of GT are almost as accurate as presented in this work, but are confined to a limited number of levels only. Furthermore, it may not be appropriate at this stage to give any accuracy assessments of their results for effective collision strengths ( $\Upsilon$ ), which were employed by Landi (2002). To obtain results for $\Upsilon$ we need to resolve resonances in thresholds region, because their contribution is often significant, if not dominant, especially for the forbidden transitions. These calculations will take a significantly long time to conclude, but we hope to resolve the discrepancy in future.

Electron impact excitation of Fe XIII

1 Introduction

2 Energy levels

3 Radiative rates and oscillator strengths

4 Collision strengths

5 Conclusions

References