A&A 417, 115-133 (2004)
DOI: 10.1051/0004-6361:20031733
S. J. Williams1 - G. A. Fuller1 - T. K. Sridharan2
1 - Department of Physics, UMIST, PO Box 88, Manchester, M60 1QD, UK
2 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, MS 78, Cambridge, MA 02138, USA
Received 27 March 2003 / Accepted 3 December 2003
Abstract
We present maps of the 850 ![]() m and 450
m and 450 ![]() m continuum emission
seen towards a sample of 68 high-mass protostellar candidates with
luminosities ranging from 10
m continuum emission
seen towards a sample of 68 high-mass protostellar candidates with
luminosities ranging from 10
![]() to
to
![]()
![]() .
Most of these candidate high-mass stars are in the earliest
stages of evolution, and have not yet developed an ultra-compact HII region.
We observe a variety of continuum emission morphologies, from compact
symmetric sources through to multiple cores embedded in long filaments of
emission. We find on average there is a 65% probability of an IRAS
point-source having a companion detection at submillimetre wavelengths. The
ratio of integrated flux to peak flux for our detections shows no strong
dependence on distance, suggesting the emission we have observed is
primarily from scale-free envelopes with power-law density structures.
Assuming a near kinematic distance projection, the clumps we detect vary in
mass from
.
Most of these candidate high-mass stars are in the earliest
stages of evolution, and have not yet developed an ultra-compact HII region.
We observe a variety of continuum emission morphologies, from compact
symmetric sources through to multiple cores embedded in long filaments of
emission. We find on average there is a 65% probability of an IRAS
point-source having a companion detection at submillimetre wavelengths. The
ratio of integrated flux to peak flux for our detections shows no strong
dependence on distance, suggesting the emission we have observed is
primarily from scale-free envelopes with power-law density structures.
Assuming a near kinematic distance projection, the clumps we detect vary in
mass from
![]() to over 1000
to over 1000 ![]() ,
with a mean clump
mass of 330
,
with a mean clump
mass of 330 ![]() ,
column density of
,
column density of
![]() cm-2 and
diameter of
cm-2 and
diameter of ![]() pc. The high luminosity and low mass of the smallest
clumps suggests they are accompanied by a minimal number of stellar
companions, while the most massive clumps may be examples of young
protogroups and protoclusters. We measure the spectral index of the dust
emission (
pc. The high luminosity and low mass of the smallest
clumps suggests they are accompanied by a minimal number of stellar
companions, while the most massive clumps may be examples of young
protogroups and protoclusters. We measure the spectral index of the dust
emission (![]() )
and the spectral index of the dust grain opacity
(
)
and the spectral index of the dust grain opacity
(![]() )
towards each object, finding clumps with morphologies suggestive
of strong temperature gradients, and of grain growth in their dense inner
regions. We find a mean value for
)
towards each object, finding clumps with morphologies suggestive
of strong temperature gradients, and of grain growth in their dense inner
regions. We find a mean value for ![]() of 0.9, significantly smaller
than observed towards UCHII regions.
of 0.9, significantly smaller
than observed towards UCHII regions.
Key words: stars: formation - stars: circumstellar matter - ISM: clouds - ISM: dust, extinction
Until recently, most young high-mass stars were first identified through the detection of a radio-bright ultra-compact HII (UCHII) region, considered a beacon pointing to the presence of a young high-mass star. As high-mass protostars increase in mass and luminosity, they emit an ever larger number of high energy UV photons which ionize the protostar's immediate surroundings, hence the small, compact nature of a UCHII region is usually considered evidence of the youthful status of the driving source (although debate continues about the exact timescale of the UCHII stage; for a review, see Kurtz et al. 2000).
Unfortunately, a powerful protostar and UCHII region soon act to disrupt and confuse their surroundings, so the initial conditions of the natal cloud and the mechanisms that led to the formation of the massive protostar cannot be unambiguously reconstructed. As a result, many questions about high-mass protostars remain - in particular, do they form via processes similar to their low-mass counterparts? To address the mechanisms that create and shape high-mass stars, we must observe before they have formed a UCHII region, during the initial collapse of the star-forming core.
Observations of these preliminary samples of HMPOs have allowed the first glimpses of high-mass protostars in their earliest evolutionary states: a typical core not yet associated with an ionised region is found to be larger, more massive, and more turbulent than a UCHII-class protostar, with a typical diameter of around 0.5-1.0 pc and a mass that may range from a few tens to a few thousand solar masses (Brand et al. 2001; Beuther et al. 2002a). They are cooler, with typical dust temperature averaging around 30-40 K (Sridharan et al. 2002; Molinari et al. 2000), while the dust opacity usually has a spectral index of around 2, suggestive of silicate dust grains (Molinari et al. 2000). Self-absorption profiles towards a number of candidate HMPOs suggest infall may be an important part of the formation mechanism (e.g. Brand et al. 2001; Fuller et al. 2004), while outflow observations suggest that accretion is a significant process (Zhang et al. 2001; Beuther et al. 2002b; Molinari et al. 2002). Water maser emission has also been detected towards candidate protostars, a feature thought to be missing from more evolved sources (e.g. Palla et al. 1993; Sridharan et al. 2002). Despite these advances, there is still much to be learned about the pre-UCHII stage of high-mass star formation, and there remains a need for additional candidates and further observations.
In total, sixty-nine IRAS point sources satisfied these cumulative criteria, identifying these sources as potentially among the most massive and deeply embedded pre-UCHII protostars in our Galaxy. The SBSMW sample has been studied in detail over the last few years, and their status as high-mass candidate protostars has been supported through observations of 1.2 mm and 3.6 cm continuum emission (Beuther et al. 2002a; SBSMW), molecular line emission (CS, CO and NH3), and H2O and CH3OH maser transitions (SBSMW) towards the sources.
This paper presents the results of a new set of submillimetre (submm) observations of the SBSMW sample of candidate high-mass protostars. All but one (IRAS 18517+0437) of the SBSMW candidate HMPOs were observed. An additional source, IRAS 18449-0158, was observed but this source does not satisfy the SBSMW criteria and is not included in any analysis. Our observations are detailed in Sect. 2, with maps of the reduced data found in Sect. 3. We measure the multiplicity of the detections in Sect. 3.1, commenting on the position and morphologies of the sample in Sect. 3.4. We analyse the dust optical depth in Sect. 4, and use the spectral index of the emission to investigate the nature of the dust in Sect. 4.1. We calculate the mass characteristics of our sample in Sect. 5, and consider the implications of the cumulative mass spectrum in Sect. 5.1. After a brief discussion and comparison of our results with the IRAM 1.2 mm continuum observations of Beuther et al. (2002a) in Sect. 6.1, we conclude in Sect. 7 with a summary of our results.
This paper presents the first half of our study and analysis of the dust emission; the companion to this paper presents the results of radiative transfer modelling of the clumps (Williams et al. 2004).
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{figures/postscripts/850psf...
...
\includegraphics[width=6.4cm,clip]{figures/postscripts/450psf.eps}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg28.gif) |
Figure 1:
Jiggle-maps of Uranus measured at 850 |
| Open with DEXTER | |
The data were reduced using the SCUBA User Reduction Facility (SURF; Jenness & Lightfoot 1998). Correlated sky noise was removed using the REMSKY routine, based on the signal from a hand-picked sample of bolometers considered free from source emission. Maps were extinction calibrated from skydips and flux calibrated in terms of Jy beam-1 from maps of Uranus, IRAS 16293-2422, CRL 618, and CRL 2688, following the procedures defined by Sandell et al. (2001).
Zenith opacities at 225 GHz ranged from 0.05-0.12 during the observations, but
usually averaged around 0.10. Telescope pointing was calibrated many times
during each observing run, and telescope drift was minimal, requiring very
small (
![]() )
corrections overall. We measured the JCMT beam size
from observations of Uranus, finding a full-width half-maximum of
)
corrections overall. We measured the JCMT beam size
from observations of Uranus, finding a full-width half-maximum of
![]() at 450
at 450 ![]() m and
m and
![]() at 850
at 850 ![]() m.
An average 1-
m.
An average 1-![]() rms noise level of 0.03 Jy beam-1 and 0.69 Jy beam-1 was found at 850
rms noise level of 0.03 Jy beam-1 and 0.69 Jy beam-1 was found at 850 ![]() m and 450
m and 450 ![]() m respectively. The rms noise
level measured in each jigglemap is listed in Table 2 as the
uncertainty in the peak flux.
m respectively. The rms noise
level measured in each jigglemap is listed in Table 2 as the
uncertainty in the peak flux.
Clumps were identified using object detection routines in the software package
GAIA (Chipperfield & Draper 2001). We define a positive detection as
a group of pixels subtending at least the area of the JCMT beam with emission
above a 3-![]() level, where
level, where ![]() is the rms noise level of the
jigglemap. The validity of each detection was also confirmed manually. Clumps
not quite bright enough to be automatically detected were examined, and if
deemed worthy of inclusion, added to the list of detections. These lower
sigma detections are labelled by a note in Table 2.
is the rms noise level of the
jigglemap. The validity of each detection was also confirmed manually. Clumps
not quite bright enough to be automatically detected were examined, and if
deemed worthy of inclusion, added to the list of detections. These lower
sigma detections are labelled by a note in Table 2.
We list the peak flux per beam and the integrated flux for each detection.
The peak flux per beam gives the peak flux level averaged in a 14.4'' beam
for 850 ![]() m maps and in an 8.0'' beam for 450
m maps and in an 8.0'' beam for 450 ![]() m maps, while the
integrated flux of a detection measures the total flux inside an isophote
tracing the 3-
m maps, while the
integrated flux of a detection measures the total flux inside an isophote
tracing the 3-![]() rms noise level around the detection. We quote the
position of each detection as the location of peak emission, not as the
centroid of the 3-
rms noise level around the detection. We quote the
position of each detection as the location of peak emission, not as the
centroid of the 3-![]() isophote.
isophote.
Calibrating the integrated flux of a detection required additional consideration, as the JCMT beam structure is complex (Fig. 1), so the number of detector counts recovered within an aperture is also a function of aperture size. We quantified the extent of this relationship using maps of Uranus (which we consider a point source), calibrating detector counts recovered inside circular apertures of increasing radius. We did not include the small number of non-planetary flux calibrators in the calibration of integrated flux. The resulting function measures increasing counts with aperture size, asymptotically reaching maximum counts once the aperture has expanded to encompass the JCMT beam and its primary error beam. For each detection, we then converted n counts recovered inside an isophote of area A to Janskys by multiplying n by the counts-to-Jy conversion factor derived from a circular aperture of equivalent area.
Our observations were performed on seven nights over a period of three months.
Despite the protracted nature of our observations, a comparison of the
counts-to-Jy conversion factor calculated for each night showed it usually
remained consistent with the published JCMT
response![]() .
Where the conversion factor appeared inconsistent and no other recent flux
calibrator maps were available, we assumed a conversion factor equal to the
mean value for our run. A comparison with the independent 1.2 mm continuum
observations of Beuther et al. (2002a) shows the data to be
consistently calibrated (Sect. 6.1), and we estimate
the absolute flux uncertainty to be
.
Where the conversion factor appeared inconsistent and no other recent flux
calibrator maps were available, we assumed a conversion factor equal to the
mean value for our run. A comparison with the independent 1.2 mm continuum
observations of Beuther et al. (2002a) shows the data to be
consistently calibrated (Sect. 6.1), and we estimate
the absolute flux uncertainty to be ![]() 10% at 850
10% at 850 ![]() m and
m and ![]() 30% at
450
30% at
450 ![]() m.
m.
Our observations used a 120'' chop to sky to measure and remove the background emission. However, in crowded regions, the 120'' chop-throw sometimes points the telescope towards an occupied region of sky rather than an empty field. When this occurs, emission from objects in the sky reference beam is subtracted from the target field emission, resulting in negative images of clumps seen towards the reference position superimposed onto the final map. Some of our maps contain these artefacts, which are usually seen away from regions of interest (e.g. IRAS 18151-1208, IRAS 18431-0312), but chopping onto emission altered the map of IRAS 18454-0158 to such an extent that no reliable measurement was possible, and this source was removed from our analysis.
We occasionally observed additional jigglemaps offset from the target position
to map fields with emission continuing outside the
![]() SCUBA field of
view. These additional maps were calibrated as individual jigglemaps before
they were combined into a mosaic, weighting the contribution of each map to
intersecting areas by 1/
SCUBA field of
view. These additional maps were calibrated as individual jigglemaps before
they were combined into a mosaic, weighting the contribution of each map to
intersecting areas by 1/
![]() ,
where
,
where ![]() is the rms noise level in
the map. Detections within the mosaic are still defined as clumps with
emission above a 3-
is the rms noise level in
the map. Detections within the mosaic are still defined as clumps with
emission above a 3-![]() limit over an area the size of the JCMT beam, but
using the rms local to the section of mosaic being measured.
limit over an area the size of the JCMT beam, but
using the rms local to the section of mosaic being measured.
![\begin{figure}
\par\includegraphics[angle=270,width=17.cm,clip]{figures/postscri...
...idth=17.cm,clip]{figures/postscripts/jigglemaps/18089-1732-combined}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg35.gif) |
Figure 2:
Maps of S850, S450, and the |
| Open with DEXTER | |
The target sources IRAS 19266+1745 and IRAS 18553+0414 displayed a gas+dust mass incompatible with the luminosity of the driving protostar, unless these sources are projected to the far kinematic distance (Sect. 6.2). Therefore, we reject the near kinematic distance for these objects and consider them resolved to the far kinematic distance for all subsequent analysis.
The CCF for our sample is
![]() ,
where the uncertainty comes from
,
where the uncertainty comes from
![]() counting statistics. In reality, the absolute value of the CCF and
the quoted uncertainty are both lower limits, as they are calculated assuming
we have detected, and are uniformly sensitive, to all companions. This is not
the case, as our limited angular resolution precludes the detection of
companions closer than around a beamsize, plus the finite field of view means
companions of greater than
counting statistics. In reality, the absolute value of the CCF and
the quoted uncertainty are both lower limits, as they are calculated assuming
we have detected, and are uniformly sensitive, to all companions. This is not
the case, as our limited angular resolution precludes the detection of
companions closer than around a beamsize, plus the finite field of view means
companions of greater than
![]() separation (assuming a clump central in
the jigglemap) will not be detected. Additionally, when coupled with the large
difference in projected distance (the most distant sources being more than 15
times further away than the closest sources), our companion mass sensitivity
also bears a dependence on distance.
separation (assuming a clump central in
the jigglemap) will not be detected. Additionally, when coupled with the large
difference in projected distance (the most distant sources being more than 15
times further away than the closest sources), our companion mass sensitivity
also bears a dependence on distance.
We examined the effect of different distance projections by sorting our candidate HMPOs into four bins, containing sources <2 kpc, 2 to 4 kpc, 4 to 8 kpc and >8 kpc distant, respectively. The CCF of these subsamples remains remarkably consistent, each section in agreement with the full sample CCF within the uncertainty limits. This is true regardless of whether distance-unresolved sources are projected to the near or far kinematic distance, with the exception of the <2 kpc bin projected to the far kinematic distance, and suggests clumps have a similar number of companions over a wide range of distance scales.
The expression of multiplicity given in Eq. (1) is usually used as a diagnostic of more evolved stars, in particular to quantify the number of companions a low-mass star is born with (e.g. Beck et al. 2003; Patience et al. 2002), whereas in this study the CCF can be interpreted as the likelihood of finding additional potentially star-forming clumps when observing Galactic HMPOs identified by a similar flux-limited criteria. While it remains difficult to constrain the statistics of such a disparate sample, the CCF does emphasise that most clumps do not form in isolation, and that a single IRAS detection is usually resolved into several submm clumps. New samples of protostars comparable to our sample are hard to compile, but the strong likelihood of detecting additional clumps in the locality of our sample suggests that wide-field surveys towards existing high-mass protostars may also be a productive way of locating new protostellar candidates.
In Fig. 3 we plot the Y distribution for our
submm detections, dividing our sample into two groups: subsample A,
containing detections with a high confidence of being solitary cores (having
just one detection within an IRAS, MSX, SCUBA and IRAM field of view) and
subsample B, the remainder. While the solitary detections in sample A do
not display the extended distribution tail seen in subsample B, we see both
groups peak at an intensity ratio of
![]() ,
which in light of the factor
15 range in distance suggests that the envelope structures may be scale-free.
,
which in light of the factor
15 range in distance suggests that the envelope structures may be scale-free.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{figures/postscripts/fluxratio_histogram.eps}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg43.gif) |
Figure 3:
A histogram of the
|
| Open with DEXTER | |
The large scatter in Fig. 4 means we do not
find any strong correlation with distance at the near distance projection
(which is the most likely projection for our sample), although considering the
distance-resolved sources alone does reveal a trend beyond d=4 kpc, where
![]() .
This fall-off does not reveal a physical change, but
reflects the diminishing level of integrated emission as the 3-
.
This fall-off does not reveal a physical change, but
reflects the diminishing level of integrated emission as the 3-![]() isophote encloses less of the envelope for more distant sources.
isophote encloses less of the envelope for more distant sources.
We must qualify a number of uncertainties that could affect the distribution
of Y, not least our variable sensitivity to additional embedded sources.
While the large-scale envelope structures appear to be scale-free, on the
small scale there are indications that we are still undersampling the number
of companions separated by less than a beam width. A number of apparently
single detections at 850 ![]() m are barely resolved as multiple sources at 450
m are barely resolved as multiple sources at 450 ![]() m (e.g. IRAS 05490+2658); a reminder that further clustering on size
scales less than a 450
m (e.g. IRAS 05490+2658); a reminder that further clustering on size
scales less than a 450 ![]() m beam width may also be present. Overall, it is
inevitable that with limited resolution we misclassify some multiple cores as
solitary detections, a point demonstrated in Fig. 5, where all sources (bar one) with 850
m beam width may also be present. Overall, it is
inevitable that with limited resolution we misclassify some multiple cores as
solitary detections, a point demonstrated in Fig. 5, where all sources (bar one) with 850 ![]() m flux ratios larger than 7
are resolved as multiple detections at 450
m flux ratios larger than 7
are resolved as multiple detections at 450 ![]() m. IRAS 22551+6221 provides
the most visible demonstration of this effect, where the high 850
m. IRAS 22551+6221 provides
the most visible demonstration of this effect, where the high 850 ![]() m flux
ratio arises from the inclusion of flux from a bright neighbouring source that
is only fully resolved at 450
m flux
ratio arises from the inclusion of flux from a bright neighbouring source that
is only fully resolved at 450 ![]() m.
m.
We also tend to overestimate the flux of multiple detections, as the elliptical apertures used for photometry could include emission shared with a companion source. Although the intersection of apertures around adjacent components was minimised where possible, it remains a potential cause of uncertainty. Finally, the ratio for extended sources is likely to be a lower limit, as emission from a large, extended envelopes is more likely to project emission onto a noisy bolometer, and flux incident on these noisy bolometers is masked during jigglemap reduction. As a result, the quoted integrated emission is a lower limit, and the flux ratio is underestimated.
To conclude, while these concerns affect the quantative results, qualitatively we still observe that a significant fraction of the total mass lies outside the central "core'' at this stage of evolution.
| |
Figure 4:
A plot of
|
| Open with DEXTER | |
The MSDC of our detections is shown in Fig. 6. The
MSDC was calculated by measuring the linear separation r of each detection
to its companions. The separation of each companion pair was binned into
annuli of separation r to
![]() .
The number of pairs N within each
annulus was then divided by the area of the annulus and the total number of
sources N* to give the MSDC,
.
The number of pairs N within each
annulus was then divided by the area of the annulus and the total number of
sources N* to give the MSDC, ![]() ,
as
,
as
| (2) |
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{figures/postscripts/integrated_vs_peak.eps}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg53.gif) |
Figure 5:
A comparison of the peak flux and integrated flux of each 850 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{figures/postscripts/surface_density_all} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg55.gif) |
Figure 6:
MSDC for single power-law distribution models (light dotted
lines), with
|
| Open with DEXTER | |
We examined the significance of variable sensitivity using a procedure similar to that used for the CCF (Sect. 3.1), comparing the MSDC slope of groups of sources with similar distances, finding the slope of each MSDC segment agrees with the MSDC of the whole sample within the uncertainty limits. We suggest the MSDC as calculated provides at least a basic estimate of the clustering properties of these clumps. Ultimately, the scarcity of high-mass protostars means there will always be a large range of distances in samples of HMPOs, and we may never be able to construct a set of uniformly sampled observations to the extent possible with low-mass protostars.
Considering each clump as a protocluster may explain displaced IRAS/MSX and submm detections, as additional stars embedded in the less dense, more transparent outer reaches of the envelope will not encounter the same degree of opacity, providing a mechanism for shorter wavelength photons to pass. To examine this possiblity and resolve whether MSX and SCUBA detections trace the same body of material will require further high-resolution IR observations.
To calculate the dust optical depth for our detections using Eq. (3) we assumed dust temperatures equal to the SBSMW cold-component
dust temperatures. In the SBSMW study, the spectral energy distribution (SED)
of each IRAS source was successfully modelled as a composite of two
greybodies: one greybody representing a cold dust component, accounting for
the >60 ![]() m flux, while a separate hot dust component contributes the
majority of near-IR flux. As SCUBA is only sensitive to emission from the cold
dust greybody, we set T equal to the temperature of the cold component
(
m flux, while a separate hot dust component contributes the
majority of near-IR flux. As SCUBA is only sensitive to emission from the cold
dust greybody, we set T equal to the temperature of the cold component
(
![]() )
as given in Table 1 of SBSMW.
)
as given in Table 1 of SBSMW.
The beam-averaged optical depth and other parameters derived from the flux
density are listed in Table 3. While our sources consist of
very dense clumps, the beam-averaged 450 ![]() m and 850
m and 850 ![]() m optical depths
show that they are usually optically thin at submm wavelengths. The optical
depth at 850
m optical depths
show that they are usually optically thin at submm wavelengths. The optical
depth at 850 ![]() m spans almost two orders of magnitude, from
m spans almost two orders of magnitude, from
![]() .
At 450
.
At 450 ![]() m,
m,
![]() is found within the range
is found within the range
![]() with three exceptions: detection #8 (IRAS 18089-1732) appears optically thick at 450
with three exceptions: detection #8 (IRAS 18089-1732) appears optically thick at 450 ![]() m with
m with
![]() but this is by far the brightest detection of our survey. Two
other detections (#16: IRAS 18182-1433 and #19: IRAS 18264-1152) have high
S450, leading to higher
but this is by far the brightest detection of our survey. Two
other detections (#16: IRAS 18182-1433 and #19: IRAS 18264-1152) have high
S450, leading to higher
![]() than the majority of the detections,
but they remain with
than the majority of the detections,
but they remain with
![]() .
.
Table 3:
Derived
parameters of the submm detections resolved by this survey. The mass of
each clump is calculated from the 850 ![]() m integrated flux value,
assuming the dust grains have thin ice mantles, and using a 100:1
gas-to-dust ratio. The column density refers to the total gas column
density (i.e. n(H+H2)).
m integrated flux value,
assuming the dust grains have thin ice mantles, and using a 100:1
gas-to-dust ratio. The column density refers to the total gas column
density (i.e. n(H+H2)).
We have modelled the submm emission seen towards our sample using a
one-dimensional radiative-transfer code (details and results can be found in
the companion to this paper: Williams et al. 2004). These
models assume a fixed dust grain chemical composition, with a
silicon-to-graphite ratio half that of the interstellar medium (Mathis et al.
1977) and a standard Draine & Lee (1984) dust grain size
distribution. We used these model dust grains to predict the optical depth of
the cores as a function of wavelength, which when scaled to match the observed
850 ![]() m and 450
m and 450 ![]() m optical depths gives an estimate of the wavelength
at which the submm detections become optically thick (listed in Col. 7 of
Table 3). We find that for the average clump,
m optical depths gives an estimate of the wavelength
at which the submm detections become optically thick (listed in Col. 7 of
Table 3). We find that for the average clump, ![]() for
wavelengths shorter than
for
wavelengths shorter than ![]() 90
90 ![]() m.
m.
However, first we must take into account the different JCMT response and beam
patterns at 850 ![]() m and 450
m and 450 ![]() m, for as seen in Fig. 1,
more flux lies outside the main beam at 450
m, for as seen in Fig. 1,
more flux lies outside the main beam at 450 ![]() m compared to the response at
850
m compared to the response at
850 ![]() m. We accounted for these differences by following the procedures
defined in Hogerheijde & Sandell (2000), normalizing the images
to a common response before finally determining
m. We accounted for these differences by following the procedures
defined in Hogerheijde & Sandell (2000), normalizing the images
to a common response before finally determining ![]() as the ratio of
images. In detail, we described the JCMT beam at each wavelength as a
superposition of three Gaussians, the parameters of which were found by a fit
to the azimuthal average response to Uranus. The amplitude and FWHM of these
components are listed in Table 4. We then
deconvolved the 850
as the ratio of
images. In detail, we described the JCMT beam at each wavelength as a
superposition of three Gaussians, the parameters of which were found by a fit
to the azimuthal average response to Uranus. The amplitude and FWHM of these
components are listed in Table 4. We then
deconvolved the 850 ![]() m and 450
m and 450 ![]() m SCUBA images with the corresponding
beam model, smoothing the deconvolved images with a single Gaussian to achieve
a final, uniform, spatial resolution of 15.0'' before forming
m SCUBA images with the corresponding
beam model, smoothing the deconvolved images with a single Gaussian to achieve
a final, uniform, spatial resolution of 15.0'' before forming ![]() as
given in Eq. (4).
as
given in Eq. (4).
![\begin{figure}
\par\mbox{\includegraphics[angle=0,width=8.8cm,clip]{figures/post...
...cs[angle=-90,width=8.8cm,clip]{figures/postscripts/alpha_dip.eps} }
\end{figure}](/articles/aa/full/2004/13/aa3777/Timg76.gif) |
Figure 7:
A plot of the typical cross-sections seen for peaked |
| Open with DEXTER | |
The spectral index measured at the position of peak 850 ![]() m emission varies
from
m emission varies
from
![]() (IRAS 19411+2306) to
(IRAS 19411+2306) to
![]() (IRAS
20293+3952), though overall this index is fairly uniform with a sample mean of
(IRAS
20293+3952), though overall this index is fairly uniform with a sample mean of
![]() .
Averaging all spectral index data
around a detection slightly reduces the statistical variability, so that
.
Averaging all spectral index data
around a detection slightly reduces the statistical variability, so that
![]() ranges from 1.1 to 3.5, and the sample mean falls to
ranges from 1.1 to 3.5, and the sample mean falls to
![]() .
As implied by these statistics, the
majority of detections display an
.
As implied by these statistics, the
majority of detections display an ![]() distribution that peaks towards the
location of maximum 850
distribution that peaks towards the
location of maximum 850 ![]() m emission, although some sources display an
anticorrelation with intensity.
m emission, although some sources display an
anticorrelation with intensity.
Cross-sections of the ![]() distributions towards IRAS 05358+3543 and IRAS 05490+2658 are presented in Fig. 7. Although these
sources display very different
distributions towards IRAS 05358+3543 and IRAS 05490+2658 are presented in Fig. 7. Although these
sources display very different ![]() morphologies, we note that the
positive and negative features seen towards the location of peak submm
emission are roughly comparable in depth and width. As these sources are at
roughly the same kinematic distance, the cause of these features could
potentially occur on a similar spatial scale.
morphologies, we note that the
positive and negative features seen towards the location of peak submm
emission are roughly comparable in depth and width. As these sources are at
roughly the same kinematic distance, the cause of these features could
potentially occur on a similar spatial scale.
Table 4: Parameters used for a three Gaussian component description of the JCMT beam.
The spectral index of the dust emission depends on a combination of the
beam-averaged values of dust temperature, opacity, and spectral index of the
dust opacity (![]() ,
defined in the sense
,
defined in the sense
![]() ). As a
result, there are three mechanisms which may explain the spatial distributions
we observed:
). As a
result, there are three mechanisms which may explain the spatial distributions
we observed:
Single-dish NH3 observations have also been conducted towards our sample,
tracing gas within the cooler, extended envelope (SBSMW). From these
observations, SBSMW found a mean temperature of
![]() K, around 25 K
lower than the dust temperature in an average core. However, a core containing
warm dust and an extended envelope characterised by cool gas does not prove
the existence of a temperature gradient, for it is very difficult to make the
gas temperature close to that of warm dust, even with the high densities
(
K, around 25 K
lower than the dust temperature in an average core. However, a core containing
warm dust and an extended envelope characterised by cool gas does not prove
the existence of a temperature gradient, for it is very difficult to make the
gas temperature close to that of warm dust, even with the high densities
(
![]() cm-3) seen towards typical protostellar candidates
(Goldsmith et al. 1997). However, CH3OH and CH3CN
molecular tracers, pointing to high temperature, high density regions and
indicating the presence of a hot core, have been detected towards a number of
our candidate HMPOs (SBSMW). These detections imply that there are regions
within the clumps of much higher temperature than the beam-averaged dust
temperature alone would suggest, so we expect a strong temperature gradient
must be present towards at least some of our sources.
cm-3) seen towards typical protostellar candidates
(Goldsmith et al. 1997). However, CH3OH and CH3CN
molecular tracers, pointing to high temperature, high density regions and
indicating the presence of a hot core, have been detected towards a number of
our candidate HMPOs (SBSMW). These detections imply that there are regions
within the clumps of much higher temperature than the beam-averaged dust
temperature alone would suggest, so we expect a strong temperature gradient
must be present towards at least some of our sources.
We examined the significance of a temperature gradient by forming simulated
![]() maps using the 450
maps using the 450 ![]() m and 850
m and 850 ![]() m continuum images created by
our best-fit radiative transfer models (Williams et al. 2004).
These models assume a single luminous protostar embedded in a dense, dusty
envelope, and form excellent fits to the observed emission while maintaining
constant dust grain characteristics (i.e. opacity and variable grain
composition are not a factor in the simulated
m continuum images created by
our best-fit radiative transfer models (Williams et al. 2004).
These models assume a single luminous protostar embedded in a dense, dusty
envelope, and form excellent fits to the observed emission while maintaining
constant dust grain characteristics (i.e. opacity and variable grain
composition are not a factor in the simulated ![]() map). In general, our
best fit models suggest the presence of dust envelopes with temperatures
around 300-500 K at the inner boundary, falling to around 10-15 K at the
outer boundary. With a temperature gradient as the only factor, the simulated
map). In general, our
best fit models suggest the presence of dust envelopes with temperatures
around 300-500 K at the inner boundary, falling to around 10-15 K at the
outer boundary. With a temperature gradient as the only factor, the simulated
![]() distribution peaks towards the hottest, densest, most central
regions. These centrally peaked
distribution peaks towards the hottest, densest, most central
regions. These centrally peaked ![]() morphologies are similar to those
seen towards the majority of our sample (e.g. IRAS 18247-1147; IRAS 18306-0835), suggesting the observed
morphologies are similar to those
seen towards the majority of our sample (e.g. IRAS 18247-1147; IRAS 18306-0835), suggesting the observed ![]() features are dominated by
temperature gradients across the envelope. This result emphasises that we
must know the spatial temperature distribution of the clumps if we are to
refine our investigation and accurately quantify the contribution of other
factors towards these sources.
features are dominated by
temperature gradients across the envelope. This result emphasises that we
must know the spatial temperature distribution of the clumps if we are to
refine our investigation and accurately quantify the contribution of other
factors towards these sources.
On the other hand, peaked ![]() distributions are not the only morphology
observed: the IRAS sources 05490+2658, 18290-0924, 18530+0215, 19413+2332 and
20051+3435 form notable exceptions where
distributions are not the only morphology
observed: the IRAS sources 05490+2658, 18290-0924, 18530+0215, 19413+2332 and
20051+3435 form notable exceptions where ![]() falls towards the location
of maximum 850
falls towards the location
of maximum 850 ![]() m emission. In terms of temperature gradients, these
m emission. In terms of temperature gradients, these
![]() morphologies run counter to the
morphologies run counter to the ![]() distribution expected for an
internally heated core: if no other factors are involved, they imply that the
inner core must be cooler than the surrounding envelope. But is the formation
of a hot envelope and cool inner core a realistic possibility? To form a
typical negative dip morphology with an
distribution expected for an
internally heated core: if no other factors are involved, they imply that the
inner core must be cooler than the surrounding envelope. But is the formation
of a hot envelope and cool inner core a realistic possibility? To form a
typical negative dip morphology with an ![]() valley depth of
valley depth of
![]() ,
while maintaining an average dust temperature of 44 K, would
require an inner core temperature of around 26 K with a surrounding envelope
of
,
while maintaining an average dust temperature of 44 K, would
require an inner core temperature of around 26 K with a surrounding envelope
of ![]() K. It would be hard to explain such low inner temperatures in the
presence of large, luminous protostars when "hot-cores'' associated with
typical pre-UCHII protostars have temperatures of >100 K (Kurtz et al.
2000). Alternatively, external heating could warm the outer
layers of the clump relative to the inner core, but the interstellar radiation
field alone is not capable of heating such dense dust to such high
temperatures, and while nearby luminous stars could conceivably heat the
exterior to higher temperatures our radiative transfer modelling shows the
submm emission profiles are well matched by low temperatures
(
K. It would be hard to explain such low inner temperatures in the
presence of large, luminous protostars when "hot-cores'' associated with
typical pre-UCHII protostars have temperatures of >100 K (Kurtz et al.
2000). Alternatively, external heating could warm the outer
layers of the clump relative to the inner core, but the interstellar radiation
field alone is not capable of heating such dense dust to such high
temperatures, and while nearby luminous stars could conceivably heat the
exterior to higher temperatures our radiative transfer modelling shows the
submm emission profiles are well matched by low temperatures
(
![]() K) at the external envelope boundary (Williams et al.
2004). Furthermore, low core temperatures may preclude the very
formation of a massive protostar, as the Jeans mass becomes much lower within
cooler cores, suggesting that a series of lower mass protostars would form
instead. This does not exclude the possiblity that a massive star could form
through the coalescence of discrete low-mass protostars, but considering the
weight of evidence it is hard to envisage how "cool cores'' may cause the
observed variations.
K) at the external envelope boundary (Williams et al.
2004). Furthermore, low core temperatures may preclude the very
formation of a massive protostar, as the Jeans mass becomes much lower within
cooler cores, suggesting that a series of lower mass protostars would form
instead. This does not exclude the possiblity that a massive star could form
through the coalescence of discrete low-mass protostars, but considering the
weight of evidence it is hard to envisage how "cool cores'' may cause the
observed variations.
An alternative explanation is that these ![]() -dip cores are optically
thick. This possibility is unlikely, as Sect. 4 shows
that all cores (with the exception of Source #8, the main component towards
IRAS 18089-1732) are optically thin even at 450
-dip cores are optically
thick. This possibility is unlikely, as Sect. 4 shows
that all cores (with the exception of Source #8, the main component towards
IRAS 18089-1732) are optically thin even at 450 ![]() m. Even so, we recognise
that this statement is based on the beam-averaged values, and there may be
much denser, optically thick regions present on scales smaller than our
observations can probe. For example, a circumstellar disk would lead to a
large density concentration in the very inner envelope, but would remain
unresolved by our observations. Then again, the presence of circumstellar
disks has been confirmed towards IRAS 20126+4104 (Cesaroni et al.
1997) and IRAS 05553+1631 (Shepherd & Kurtz
1999), and the
m. Even so, we recognise
that this statement is based on the beam-averaged values, and there may be
much denser, optically thick regions present on scales smaller than our
observations can probe. For example, a circumstellar disk would lead to a
large density concentration in the very inner envelope, but would remain
unresolved by our observations. Then again, the presence of circumstellar
disks has been confirmed towards IRAS 20126+4104 (Cesaroni et al.
1997) and IRAS 05553+1631 (Shepherd & Kurtz
1999), and the ![]() distribution towards these sources
remains strongly peaked. Overall, we conclude that optically thick regions do
not significantly affect the
distribution towards these sources
remains strongly peaked. Overall, we conclude that optically thick regions do
not significantly affect the ![]() distribution at the spatial resolution
of our measurements.
distribution at the spatial resolution
of our measurements.
Finally, variations in the properties of the dust-grains themselves could help
explain the trends. The optical properties of dust grains can be quantified by
![]() ,
the spectral index of the dust opacity. This is often a quantity of
interest as it may give information on the composition and evolutionary
history of dust grains within the envelope. There are many models that predict
,
the spectral index of the dust opacity. This is often a quantity of
interest as it may give information on the composition and evolutionary
history of dust grains within the envelope. There are many models that predict
![]() for different grain characteristics, and the majority of grain
compositions result in a spectral index of
for different grain characteristics, and the majority of grain
compositions result in a spectral index of
![]() (e.g. Gezari et al. 1973; Draine & Lee 1984; Krügel &
Siebenmorgen 1994), although it may range from
(e.g. Gezari et al. 1973; Draine & Lee 1984; Krügel &
Siebenmorgen 1994), although it may range from
![]() (Mathis
& Whiffen 1989) up to
(Mathis
& Whiffen 1989) up to ![]() (Aannestad 1975). To
observe an
(Aannestad 1975). To
observe an ![]() -dip morphology, dust grains within the central core must
be of lower
-dip morphology, dust grains within the central core must
be of lower ![]() than grains in the surrounding envelope. Low
than grains in the surrounding envelope. Low ![]() and
and
![]() distributions that fall towards regions of high density are usually
attributed to grain growth in these dense, innermost regions (e.g. Mannings &
Emerson 1994; Beckwith & Sargent 1991; Goldsmith et al. 1997), and our observed
distributions that fall towards regions of high density are usually
attributed to grain growth in these dense, innermost regions (e.g. Mannings &
Emerson 1994; Beckwith & Sargent 1991; Goldsmith et al. 1997), and our observed ![]() -dip morphologies are
generally consistent with this grain growth interpretation, as
-dip morphologies are
generally consistent with this grain growth interpretation, as ![]() (and
thus
(and
thus ![]() )
fall preferentially towards the center of the dense cores we
have observed.
)
fall preferentially towards the center of the dense cores we
have observed.
However, the models of Ossenkopf & Henning (1994) predict that
![]() will only change if the dust grains do not have ice mantles, which
would require inner cores with dust temperatures
will only change if the dust grains do not have ice mantles, which
would require inner cores with dust temperatures ![]() 100 K. The detection
of CH3OH and CH3CN towards the
100 K. The detection
of CH3OH and CH3CN towards the ![]() -dip detections IRAS 19413+2332 and IRAS 18530+0215 signifies the presence of a hot core of
sufficient temperature to melt ice mantles, thus permitting grain growth.
However, the detection of CH3OH and CH3CN towards a large number of
candidate protostars with centrally peaked
-dip detections IRAS 19413+2332 and IRAS 18530+0215 signifies the presence of a hot core of
sufficient temperature to melt ice mantles, thus permitting grain growth.
However, the detection of CH3OH and CH3CN towards a large number of
candidate protostars with centrally peaked ![]() morphologies raises an
interesting question: these molecular tracers imply a high central temperature
- certainly high enough to melt ice mantles and permit changes in
morphologies raises an
interesting question: these molecular tracers imply a high central temperature
- certainly high enough to melt ice mantles and permit changes in ![]() ,
so
why are there no signs of grain growth? Why do the majority of these sources
have positively peaked
,
so
why are there no signs of grain growth? Why do the majority of these sources
have positively peaked ![]() morphologies? The strongly peaked
morphologies? The strongly peaked ![]() distributions we observe suggests that the temperature gradient effect
outweighs any contribution from grain evolution. On the other hand, as it
takes time for ice mantles to melt, perhaps these icy grains remain towards
cores only recently heated, and perhaps these cores are younger than those
associated with
distributions we observe suggests that the temperature gradient effect
outweighs any contribution from grain evolution. On the other hand, as it
takes time for ice mantles to melt, perhaps these icy grains remain towards
cores only recently heated, and perhaps these cores are younger than those
associated with ![]() -dip distributions.
-dip distributions.
Also, CH3OH and CH3CN have not been detected towards IRAS 05490+2658
and IRAS 18290-0924, suggesting a hot core has not formed, yet these objects
are still found with ![]() -dip morphologies. Clearly, neither temperature
gradients or variable dust grain composition taken alone can fully explain
the observed
-dip morphologies. Clearly, neither temperature
gradients or variable dust grain composition taken alone can fully explain
the observed ![]() morphologies. It is not clear that hot cores are
strongly correlated with grain growth nor with
morphologies. It is not clear that hot cores are
strongly correlated with grain growth nor with ![]() -dip morphologies, and
accurate high-resolution measurements of the temperature of the clumps are
vital if we are to determine the magnitude of grain growth towards our sample.
-dip morphologies, and
accurate high-resolution measurements of the temperature of the clumps are
vital if we are to determine the magnitude of grain growth towards our sample.
| (5) |
The value of ![]() at the location of peak 850
at the location of peak 850 ![]() m submm emission is
listed individually for each detection in Table 3. The
average grain opacity index for our sample is
m submm emission is
listed individually for each detection in Table 3. The
average grain opacity index for our sample is
![]() .
This index is smaller than for that seen towards high-mass stars
associated with UCHII regions (Hunter 1997), and the
.
This index is smaller than for that seen towards high-mass stars
associated with UCHII regions (Hunter 1997), and the ![]() distribution is substantially shifted to lower indices compared to the more
evolved objects (Fig. 8). Low
distribution is substantially shifted to lower indices compared to the more
evolved objects (Fig. 8). Low ![]() is often
associated with young, less evolved sources, which would point to further
evidence that our sample of young high-mass stars are at an earlier stage of
evolution than their UCHII counterparts. An inadequate Rayleigh-Jeans
correction could raise our estimate of
is often
associated with young, less evolved sources, which would point to further
evidence that our sample of young high-mass stars are at an earlier stage of
evolution than their UCHII counterparts. An inadequate Rayleigh-Jeans
correction could raise our estimate of ![]() ,
but even if we have globally
overestimated core temperatures by 20 K,
,
but even if we have globally
overestimated core temperatures by 20 K,
![]() would only to rise
to
would only to rise
to
![]() ,
still lower than
,
still lower than ![]() towards more evolved UCHII sources. No
relationship is found between
towards more evolved UCHII sources. No
relationship is found between ![]() ,
,
![]() and distance (Fig. 9), suggesting resolution is not an issue.
and distance (Fig. 9), suggesting resolution is not an issue.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{figures/postscripts/beta_histogram.eps}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg110.gif) |
Figure 8:
A histogram of the
|
| Open with DEXTER | |
| |
Figure 9:
A plot of
|
| Open with DEXTER | |
Figure 10 shows that despite the absence of any
correlation between ![]() and
and
![]() or
or ![]() ,
,
![]() ,
,
![]() or
or
![]() and source distance, there is significant
correlation between
and source distance, there is significant
correlation between ![]() and
and
![]() ,
albeit with a large scatter.
Our estimate of
,
albeit with a large scatter.
Our estimate of ![]() is dependent on the SBSMW dust temperature, which was
calculated assuming
is dependent on the SBSMW dust temperature, which was
calculated assuming ![]() .
Had SBSMW used lower values of
.
Had SBSMW used lower values of ![]() ,
they
would have derived higher dust temperatures, which in turn both reduces the
Rayleigh-Jeans correction and decreases the implied dust optical depth. As a
result, low-
,
they
would have derived higher dust temperatures, which in turn both reduces the
Rayleigh-Jeans correction and decreases the implied dust optical depth. As a
result, low-![]() points in Fig. 10 would move
down (due to the smaller Rayleigh-Jeans correction) and to the left (due to
decreased optical depth), a shift greatest for points towards the bottom-left
quadrant as these objects would be associated with the largest dust
temperature increase, hence strengthening the correlation between
points in Fig. 10 would move
down (due to the smaller Rayleigh-Jeans correction) and to the left (due to
decreased optical depth), a shift greatest for points towards the bottom-left
quadrant as these objects would be associated with the largest dust
temperature increase, hence strengthening the correlation between ![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{figures/postscri...
...ngle=-90,width=8.7cm,clip]{./figures/postscripts/peakbeta_vs_tau850}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg114.gif) |
Figure 10:
A plot of the relationship of
|
| Open with DEXTER | |
Low values of ![]() are typically attributed to growth and evolution of the
dust grains within dense, dusty regions, so the observed trend of low values
of
are typically attributed to growth and evolution of the
dust grains within dense, dusty regions, so the observed trend of low values
of ![]() at low optical depths is initially surprising. We would expect the
densest, most massive clumps to undergo the most significant grain growth,
resulting in lowest
at low optical depths is initially surprising. We would expect the
densest, most massive clumps to undergo the most significant grain growth,
resulting in lowest ![]() for these cores, whereas actually we seem to
observe the opposite trend. In addition, Ossenkopf & Henning
(1994) found that dust grains within a protostellar core remain
below the Rayleigh scattering size limit after 105 years (the typical age
expected for our sample; Behrend & Maeder 2001), with the dust
grain opacity changing only by a factor of
for these cores, whereas actually we seem to
observe the opposite trend. In addition, Ossenkopf & Henning
(1994) found that dust grains within a protostellar core remain
below the Rayleigh scattering size limit after 105 years (the typical age
expected for our sample; Behrend & Maeder 2001), with the dust
grain opacity changing only by a factor of ![]() at 850
at 850 ![]() m. However,
the results in Fig. 10 suggest a change of close to
an order of magnitude in opacity: for values of
m. However,
the results in Fig. 10 suggest a change of close to
an order of magnitude in opacity: for values of ![]() around 0.5,
around 0.5,
![]() has a value of around
has a value of around
![]() ,
increasing to
,
increasing to
![]() for dust grains with
for dust grains with
![]() .
Only in
the extremely dense and cold regions within circumstellar disks is it believed
that a significant number of grains can grow beyond the Rayleigh limit,
allowing the large shift in opacity (e.g. Schmitt et al. 1997).
.
Only in
the extremely dense and cold regions within circumstellar disks is it believed
that a significant number of grains can grow beyond the Rayleigh limit,
allowing the large shift in opacity (e.g. Schmitt et al. 1997).
These inconsistencies can be understood by considering the inhomogeneous
nature of our sample, and how the clumps we have observed vary in mass
(Sect. 5) and most probably evolutionary status (SBSMW). Sources
within the high
![]() ,
high
,
high ![]() quadrant of Fig. 10 show considerable "excess'' mass compared to the mass of an
equivalent luminosity main-sequence star (cf. Fig. 11),
suggesting these clumps could easily be forming protogroups or protoclusters
(Sect. 5.1). In any case, the majority of dust
grains within these high-mass clumps will not be intimately associated with
the high-mass protostar, and will most likely remain outside the T > 100 K
boundary necessary to melt ice mantles and allow large variations in
quadrant of Fig. 10 show considerable "excess'' mass compared to the mass of an
equivalent luminosity main-sequence star (cf. Fig. 11),
suggesting these clumps could easily be forming protogroups or protoclusters
(Sect. 5.1). In any case, the majority of dust
grains within these high-mass clumps will not be intimately associated with
the high-mass protostar, and will most likely remain outside the T > 100 K
boundary necessary to melt ice mantles and allow large variations in ![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm]{figures/postscripts/mass_vs_beta.eps}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg119.gif) |
Figure 11:
A comparison of detection mass and |
| Open with DEXTER | |
In contrast, the much lower mass of the low
![]() ,
low
,
low ![]() detections means these clumps may be forming solitary high-mass stars
(solitary for high-mass stars being a relative term, which we interpret as
existing with only a small number of lower-mass stellar companions), with
fractionally much more dust lying inside the massive protostar's sphere of
influence. This distinction becomes important when we consider that the
detections means these clumps may be forming solitary high-mass stars
(solitary for high-mass stars being a relative term, which we interpret as
existing with only a small number of lower-mass stellar companions), with
fractionally much more dust lying inside the massive protostar's sphere of
influence. This distinction becomes important when we consider that the
![]() and
and ![]() we observe are actually the optical depth and dust
opacity index averaged along the line of sight. Within the largest
clumps, low
we observe are actually the optical depth and dust
opacity index averaged along the line of sight. Within the largest
clumps, low ![]() grains in the vicinity of the high-mass protostar will be
rendered less detectable, swamped by the higher
grains in the vicinity of the high-mass protostar will be
rendered less detectable, swamped by the higher ![]() dust grains lying
within the envelope of the proto-group/cluster, whereas fractionally there
will be many more low-
dust grains lying
within the envelope of the proto-group/cluster, whereas fractionally there
will be many more low-![]() grains along the line of sight towards low mass,
low
grains along the line of sight towards low mass,
low
![]() cores, making these evolved grains appear more prominently
towards less massive cores.
cores, making these evolved grains appear more prominently
towards less massive cores.
Secondly, grain growth will occur in parallel with evolution of the high-mass protostar. The mass of material in the core will decrease as material either collapses to form stars or has been removed from the core by the action of stellar jets and winds. These mechanisms will act to reduce the opacity towards more evolved cores by removing dust and gas. For example, the outflows of high-mass stars may disperse up to eight times the mass of material that falls onto the star (Churchwell 1997), allowing the dust opacity to change by a larger degree than that possible via grain growth alone.
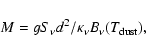 |
(7) |
Figure 12 shows the histogram of clump mass, where we
see the majority of clumps have a mass of less than 500 ![]() ,
regardless of whether distance-unresolved cores are projected to the near
kinematic distance or the far kinematic distance. The distance-resolved
detections in our sample have a mean clump mass of around 350
,
regardless of whether distance-unresolved cores are projected to the near
kinematic distance or the far kinematic distance. The distance-resolved
detections in our sample have a mean clump mass of around 350 ![]() ,
although the median mass is less at around 100
,
although the median mass is less at around 100 ![]() .
Assuming the near
kinematic distance for distance-unresolved sources results in a mean clump
mass of
.
Assuming the near
kinematic distance for distance-unresolved sources results in a mean clump
mass of ![]() 330
330 ![]() ,
with a median roughly half this value at 143
,
with a median roughly half this value at 143 ![]() ,
while projecting to the far kinematic distance results in a mean
clump mass of 1120
,
while projecting to the far kinematic distance results in a mean
clump mass of 1120 ![]() and a median mass of 460
and a median mass of 460 ![]() .
.
The mass of the distance-resolved and near distance-projected clumps are
comparable to other continuum-derived mass estimates of similar massive
protostars. For example, Mueller et al. (2002) find an average clump
mass of 209 ![]() ,
while Molinari et al. (2002) measure
,
while Molinari et al. (2002) measure
![]()
![]() .
These values support claims that natal clumps
bearing massive stars may contain up to 100 times the mass of the most massive
adult star that emerges (Churchwell 1997). This is a very
different scenario to that seen in the primarily low-mass star-forming region
of Rho Ophiucus (Motte et al. 1998), where a high fraction of the
initial clump mass is seen to transfer onto the resulting low-mass protostars.
.
These values support claims that natal clumps
bearing massive stars may contain up to 100 times the mass of the most massive
adult star that emerges (Churchwell 1997). This is a very
different scenario to that seen in the primarily low-mass star-forming region
of Rho Ophiucus (Motte et al. 1998), where a high fraction of the
initial clump mass is seen to transfer onto the resulting low-mass protostars.
Using the mass and column density relationships defined in Hildebrand
(1983), we can also translate the mass of each detection to a
beam-averaged gas column density. The values we derive are presented in Table 3, where we find an average H+H2 column density of
![]() cm-2. With an average clump diameter of 0.6 pc and
projected distance of 4 kpc, this translates to a mean hydrogen number density
of
cm-2. With an average clump diameter of 0.6 pc and
projected distance of 4 kpc, this translates to a mean hydrogen number density
of
![]() cm-3 through the clump.
cm-3 through the clump.
| |
Figure 12:
A histogram of the object mass, assuming the near
kinematic distance (left-hand and center plot) and far kinematic distance
(right-hand plot) for distance-unresolved IRAS fields. The contribution of
distance resolved detections to each histogram is plotted by an outlined
histogram. The mass of each detection is calculated from 850 |
| Open with DEXTER | |
Figure 13 presents the cumulative mass spectrum of our
850 ![]() m detections, distance-limited to IRAS fields less than 5 kpc distant
to increase the region of complete sampling. We estimate a completeness limit
of 10
m detections, distance-limited to IRAS fields less than 5 kpc distant
to increase the region of complete sampling. We estimate a completeness limit
of 10 ![]() ,
calculated by determing the mass of a 3-
,
calculated by determing the mass of a 3-![]() detection
at the upper distance limit of 5 kpc, assuming the dust temperature of the
detection equals that of the sample average dust temperature, with
detection
at the upper distance limit of 5 kpc, assuming the dust temperature of the
detection equals that of the sample average dust temperature, with
![]() K. The best fit power-law to the mass spectrum is
fairly flat below
K. The best fit power-law to the mass spectrum is
fairly flat below ![]()
![]() ,
with
,
with
![]() .
A
break in the spectrum is seen around 100
.
A
break in the spectrum is seen around 100 ![]() ,
above which the mass
spectrum steepens to
,
above which the mass
spectrum steepens to
![]() .
The mass distribution
breakpoint is found comfortably above the completeness limit, suggesting this
is not an observational artefact.
.
The mass distribution
breakpoint is found comfortably above the completeness limit, suggesting this
is not an observational artefact.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{figures/postscripts/massspec.eps}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg135.gif) |
Figure 13:
Cumulative mass distribution of all detections found at a
kinematic distance of <5 kpc, incorporating 65 clumps when assuming the
near kinematic distance (upper curve) and 32 clumps for the far kinematic
distance (lower curve). The mass of each object is calculated from the 850
|
| Open with DEXTER | |
We compared the index of these power-law fits to other observations, finding
the distribution below 100 ![]() to be significantly flatter than that
seen in other studies. This points to either an absence or accelerated
evolution of the lower-mass clumps, both of which would reduce the submm
emission observed in the lower mass range. Most likely, this reflects an
absence of low-mass clumps as we have only observed high-mass candidates,
preferentially sampling only the high-mass tail of the initial mass
distribution, and additionally many close low-mass clumps undoubtedly lie
unresolved. Correcting for these factors could raise the power-law index to a
more typical IMF-like power-law slope, whereas at the moment the most similar
power-law index for this region is that of clumps within molecular clouds,
where the index averages around -0.60 (Kramer et al. 1998; Kramer
et al. 1996). This is still a factor of four greater than our
study, and without knowing how far we can minimize this difference we must
question their true degree of similarity.
to be significantly flatter than that
seen in other studies. This points to either an absence or accelerated
evolution of the lower-mass clumps, both of which would reduce the submm
emission observed in the lower mass range. Most likely, this reflects an
absence of low-mass clumps as we have only observed high-mass candidates,
preferentially sampling only the high-mass tail of the initial mass
distribution, and additionally many close low-mass clumps undoubtedly lie
unresolved. Correcting for these factors could raise the power-law index to a
more typical IMF-like power-law slope, whereas at the moment the most similar
power-law index for this region is that of clumps within molecular clouds,
where the index averages around -0.60 (Kramer et al. 1998; Kramer
et al. 1996). This is still a factor of four greater than our
study, and without knowing how far we can minimize this difference we must
question their true degree of similarity.
Above the 100 ![]() breakpoint, the slope of our sample becomes very
similar to that of the field star IMF (
breakpoint, the slope of our sample becomes very
similar to that of the field star IMF (
![]() for
for
![]() ;
Kroupa 2001). If the IMF-like
distribution is valid, the apparently similar power-law index of main-sequence
and massive pre-stellar clumps would suggest the star formation efficiency
within these protoclusters is relatively mass invariant; it would appear that
just the breakpoint shifts to lower mass as the core fragments and additional
stars form.
;
Kroupa 2001). If the IMF-like
distribution is valid, the apparently similar power-law index of main-sequence
and massive pre-stellar clumps would suggest the star formation efficiency
within these protoclusters is relatively mass invariant; it would appear that
just the breakpoint shifts to lower mass as the core fragments and additional
stars form.
Assuming the multiple power-law IMF of Kroupa 2001, we may
estimate the number of sources within an average 350 ![]() clump. Even
if the star-formation efficiency
clump. Even
if the star-formation efficiency ![]() for a 10
for a 10 ![]() star is as low
as 5%, this still leaves sufficient mass to form an additional
star is as low
as 5%, this still leaves sufficient mass to form an additional
![]() lower-mass objects created with efficiency
lower-mass objects created with efficiency
![]() ,
distributed via
the IMF number ratios given in Table 5. With a typical clump
radius of
,
distributed via
the IMF number ratios given in Table 5. With a typical clump
radius of
![]() ,
this would result in a typical stellar volume density of
,
this would result in a typical stellar volume density of
![]() stars pc-3.
stars pc-3.
Table 5: Stellar IMF, taken from Kroupa (2001). The third and fourth columns tabulate the contribution of each object type to the population and mass total.
With a median mass of ![]() 143
143 ![]() ,
the typical median clump could
easily form at least one >8
,
the typical median clump could
easily form at least one >8 ![]() star assuming an average 50%
star-formation efficiency and an IMF-like mass distribution, assuming a
high-mass star accounts for 17% of the total cluster mass (Table
5). However, the limited mass reservoir of the lowest-mass
companionless clumps means the star-formation efficiency
star assuming an average 50%
star-formation efficiency and an IMF-like mass distribution, assuming a
high-mass star accounts for 17% of the total cluster mass (Table
5). However, the limited mass reservoir of the lowest-mass
companionless clumps means the star-formation efficiency ![]() within
these objects must be fairly high, as the total mass of gas and dust is close
to that of a high-luminosity protostar. The limited residual mass reservoir
would also mean that not many lower-mass protostars can co-exist within the
clumps. As a result, the stellar mass spectrum within these clumps must be
skewed compared to the IMF of field stars or that within higher mass clumps.
Although an isolated high-mass protostar has yet to be found, we suggest these
clumps form ideal candidates of high-mass protostars with a minimal number of
stellar companions.
within
these objects must be fairly high, as the total mass of gas and dust is close
to that of a high-luminosity protostar. The limited residual mass reservoir
would also mean that not many lower-mass protostars can co-exist within the
clumps. As a result, the stellar mass spectrum within these clumps must be
skewed compared to the IMF of field stars or that within higher mass clumps.
Although an isolated high-mass protostar has yet to be found, we suggest these
clumps form ideal candidates of high-mass protostars with a minimal number of
stellar companions.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{figures/postscri...
...angle=-90,width=8.8cm,clip]{figures/postscripts/flux_comparison.eps}\end{figure}](/articles/aa/full/2004/13/aa3777/Timg143.gif) |
Figure 14:
A plot displaying the correlation between mass (upper plot)
and peak flux (lower plot) of coincident IRAM 1.2 mm detections and
JCMT 850 |
| Open with DEXTER | |
The mass of coincident 850 ![]() m detections and 1.2 mm detections correlate
well when the same gas and dust characteristics are assumed, as can be seen in
the upper plot of Fig. 14. Points lying away from the
main trend generally represent sources with companions lying in extended
emission, suggesting the difference originates in the different techniques
used to measure the integrated emission around extended and multiple component
sources. Admittedly, the choice of where once source ends and another begins
can be subjective, and we do not consider this a cause for concern.
m detections and 1.2 mm detections correlate
well when the same gas and dust characteristics are assumed, as can be seen in
the upper plot of Fig. 14. Points lying away from the
main trend generally represent sources with companions lying in extended
emission, suggesting the difference originates in the different techniques
used to measure the integrated emission around extended and multiple component
sources. Admittedly, the choice of where once source ends and another begins
can be subjective, and we do not consider this a cause for concern.
There is good agreement in the peak flux of 850 ![]() m and 1.2 mm detections,
which implies there is no large optical depth gradient between these
wavelengths, and additionally that the studies are calibrated consistently
with respect to one another, measuring approximately 7 Jy/14.4'' beam at
850
m and 1.2 mm detections,
which implies there is no large optical depth gradient between these
wavelengths, and additionally that the studies are calibrated consistently
with respect to one another, measuring approximately 7 Jy/14.4'' beam at
850 ![]() m per 1 Jy/11'' beam measured at 1.2 mm (lower plot of Fig. 14). This is another indication that the 850
m per 1 Jy/11'' beam measured at 1.2 mm (lower plot of Fig. 14). This is another indication that the 850 ![]() m
and 1.2 mm observations are detecting the same material and thus trace the same
amount of mass. By confirming the mass of the clumps, we may place more
confidence in the mass-luminosity relationship derived by Sridharan et al.
(2002).
m
and 1.2 mm observations are detecting the same material and thus trace the same
amount of mass. By confirming the mass of the clumps, we may place more
confidence in the mass-luminosity relationship derived by Sridharan et al.
(2002).
The greybody analysis of SBSMW also gives an estimate of the bolometric
luminosity of each IRAS source. Assuming
![]() (where
M* is the mass of the protostar and
(where
M* is the mass of the protostar and
![]() is the SBSMW luminosity),
similar to the mass-luminosity relationship for massive stars on the main
sequence, it is simple to calculate the mass of the illuminating source. In
comparing M* to the mass of the clump at both the near and far kinematic
distance projections, we found the luminosity of detections #64 (IRAS 18553+0414) and #74 (IRAS 19266+1745) to be incompatible with their
near-distance clump mass, suggesting that these sources are actually located
at the far kinematic distance.
is the SBSMW luminosity),
similar to the mass-luminosity relationship for massive stars on the main
sequence, it is simple to calculate the mass of the illuminating source. In
comparing M* to the mass of the clump at both the near and far kinematic
distance projections, we found the luminosity of detections #64 (IRAS 18553+0414) and #74 (IRAS 19266+1745) to be incompatible with their
near-distance clump mass, suggesting that these sources are actually located
at the far kinematic distance.
We observed a sample of candidate high-mass protostars with the JCMT.
Dust continuum emission was detected towards all sources, and from
analysis of the 850 ![]() m and 450
m and 450 ![]() m maps we reach the following
conclusions:
m maps we reach the following
conclusions:
The degree of coincidence may point to evidence of evolution, from the oldest, most evolved sources with MSX detections and no coincident submm flux, to MSX detections with some degree of submm flux, to the youngest, most embedded sources with potentially no MSX detection and high IR optical depth. Further investigation of these possibilities will require high resolution observations at submm and far infra-red wavelengths.
Peaked ![]() morphologies can be reproduced with simple internal
heating of a dusty envelope, with the observed
morphologies can be reproduced with simple internal
heating of a dusty envelope, with the observed ![]() gradient
resulting from the corresponding temperature gradient through the
envelope.
gradient
resulting from the corresponding temperature gradient through the
envelope.
An ![]() -dip morphology could occur if the inner region of the
clumps are cool with respect to their surroundings or if substantial
grain growth occurs in these dense central regions. Although we
suggest grain growth is the most likely factor, identifying the
dominant mechanism will require high-resolution observations of
temperature tracers towards the regions.
-dip morphology could occur if the inner region of the
clumps are cool with respect to their surroundings or if substantial
grain growth occurs in these dense central regions. Although we
suggest grain growth is the most likely factor, identifying the
dominant mechanism will require high-resolution observations of
temperature tracers towards the regions.
Acknowledgements
We would like to thank Claire Chandler for her insight and invaluable comments that helped improve this paper. The James Clerk Maxwell Telescope is operated on a joint basis between the United Kingdom Particle Physics and Astronomy Research Council (PPARC), The Netherlands Organization for the Advancement of Pure Research (ZWO), the Canadian National Research Council (NRC), and the University of Hawaii (UH). This research has made use of NASA's Astrophysics Data System Bibliographic Services and the SIMBAD database, operated at CDS, Strasbourg, France.
Table 1:
Positions of the IRAS point sources satisifying the Sridharan et al. (2002) criteria, precessed to J2000 co-ordinates, alongside the kinematic distance of the IRAS source and date(s) of observation. All sources were observed during the spring and summer of 2000. All distances are taken from Sridharan et al. 2002 with the exception of IRAS 18449-0158, for which we derive the kinematic distance using
![]() from the CS(2-1) observations of Bronfman et al. (1996). Candidates with only the far kinematic distance listed have had their distance uncertainty resolved.
from the CS(2-1) observations of Bronfman et al. (1996). Candidates with only the far kinematic distance listed have had their distance uncertainty resolved.
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/18159-1550-0511-064} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg153.gif) |
Figure 2:
continued. Maps of the 850 |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/18264-1152-0511-070} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg154.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/18308-0841-0511-075} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg155.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/18348-0616-0511-084} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg156.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/18431-0312-0523-039} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg157.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=17.6cm,clip]{figures/postscripts/...
...th=17.6cm,clip]{figures/postscripts/jigglemaps/18447-0229-0530-054} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg158.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/18470-0044-0613-081} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg159.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=17.6cm,clip]{figures/postscripts/...
...th=17.6cm,clip]{figures/postscripts/jigglemaps/18530+0215-0613-084} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg160.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/19012+0536-0523-050} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg161.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/19217+1651-0523-054} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg162.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/19403+2258-0613-092} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg163.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/19471+2641-0613-094} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg164.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/20205+3948-combined} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg165.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=17.3cm,clip]{figures/postscripts/...
...th=17.3cm,clip]{figures/postscripts/jigglemaps/20332+4124-0523-058} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg166.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/22570+5912-combined} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg167.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{figures/postscripts/ji...
...idth=16cm,clip]{figures/postscripts/jigglemaps/23545+6508-combined} \end{figure}](/articles/aa/full/2004/13/aa3777/Timg168.gif) |
Figure 2: continued. |
| Open with DEXTER | |