A&A 416, 853-864 (2004)
DOI: 10.1051/0004-6361:20031757

Numerical study of halo concentrations in dark-energy cosmologies

K. Dolag1 - M. Bartelmann2 - F. Perrotta3,4 - C. Baccigalupi3,4 - L. Moscardini5 - M. Meneghetti1 - G. Tormen1


1 - Dipartimento di Astronomia, Università di Padova, Italy
2 - Max-Planck-Institut für Astrophysik, PO Box 1317, 85741 Garching, Germany
3 - SISSA, Trieste, Italy
4 - Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA
5 - Dipartimento di Astronomia, Università di Bologna, Italy

Received 18 August 2003 / Accepted 2 December 2003

Abstract
We study the concentration parameters, their mass dependence and redshift evolution, of dark-matter halos in different dark-energy cosmologies with constant and time-variable equation of state, and compare them with "standard'' $\Lambda $CDM and OCDM models. We find that previously proposed algorithms for predicting halo concentrations can be well adapted to dark-energy models. When centred on the analytically expected values, halo concentrations show a log-normal distribution with a uniform standard deviation of $\sim$0.2. The dependence of averaged halo concentrations on mass and redshift permits a simple fit of the form $(1+z)~c=c_0~(M/M_0)^\alpha$, with $\alpha\approx-0.1$ throughout. We find that the cluster concentration depends on the dark energy equation of state at the cluster formation redshift $z_{\rm coll}$ through the linear growth factor $D_+(z_{\rm coll})$. As a simple correction accounting for dark-energy cosmologies, we propose scaling c0 from $\Lambda $CDM with the ratio of linear growth factors, $c_0\rightarrow c_0~D_+(z_{\rm coll})/D_{+,~\Lambda{\rm CDM}}(z_{\rm coll})$.

Key words: galaxies: clusters: general - galaxies: halos - cosmology: theory

1 Introduction

The properties of dark-matter halos have been shown in many earlier studies to depend in characteristic ways on their formation history. The dark-matter density profile consistently found in numerical simulations by Navarro et al. (1997,1996) has a radial scale, $r_{\rm s}$, which is smaller than the virial radius  $r_{\rm vir}$ by the concentration parameter $c=r_{\rm vir}/r_{\rm s}$. Although there is an ongoing discussion as to the exact density-profile slope in halo cores, there is agreement that the density profile steepens substantially going outward across the scale radius.

The central density in halo cores was found to reflect the mean density of the Universe at the time of halo formation. Since halos of increasing mass form at increasingly late cosmic epochs in hierarchical models of structure formation, the concentration parameter of halos at fixed redshift decreases with mass. For halos of fixed mass, the concentration parameter increases with decreasing redshift because the background density drops.

Structure growth in the Universe is thus reflected by the core densities, or concentrations, of dark-matter halos. Haloes thus establish a connection between principally measurable quantities, like their central densities, and the cosmological framework model because the latter dictates how structures form.

We have shown in an earlier paper (Bartelmann et al. 2002) that halos of given mass and redshift are predicted to have higher concentrations in dark-energy cosmologies than in models with cosmological constant because they tend to form earlier and thus acquire a higher core density. For that study, we used analytic algorithms for predicting halo properties which were assumed, but never shown, to hold true in dark-energy cosmologies. In this paper, we describe numerical simulations undertaken with the specific aim of studying how halo properties change in dark-energy models, and whether the analytic algorithms proposed for other cosmologies can be adopted or adapted to dark-energy models.

Klypin et al. (2003) also studied the properties of clusters simulated in the framework of cosmological models with dynamical dark energy, which were recently extended to the case of a coupling with the dark matter (Mainini et al. 2003). However, their cosmological models differ from ours for the choice of many parameters. Moreover, we will analyse here a larger sample of individually simulated clusters, covering a completely different range of halo masses.

We describe the dark-energy models used in Sect. 2 and our numerical simulations in Sect. 3. Section 4 details the determination of halo concentrations, their comparison with analytic expectations, and their statistical properties. We identify an interesting dependence between average halo concentrations and the density of dark energy at halo formation in Sect. 5, and conclude with a summary in Sect. 6.

  
2 Dark-energy models

In this paper, we study and compare results obtained for the following cosmological models: an open Cold Dark Matte (OCDM) and four flat dark-energy cosmogonies. The latter are a cosmological constant ($\Lambda $CDM) model, a dark-energy model with constant equation of state (DECDM), and two quintessence models, one with inverse power-law Ratra-Peebles potential (RP, see Peebles & Ratra 2002, and references therein) and one with SUGRA potential (SUGRA, see Brax & Martin 2000, and references therein).

In all cases, the matter density parameter today is $\Omega_0=0.3$. In the flat cosmologies, the remaining $70\%$ of the critical density is assigned to the dark energy at present. The remaining cosmological parameters are h=0.7, $\Omega_{\rm b}~h^{2}=0.022$, a Gaussian density fluctuations with scale-invariant power spectrum, and no gravitational waves.

Particularly important for us is the normalisation of the perturbation power spectrum, which we set by defining the rms density fluctuation level within spheres of $8~h^{-1}~{\rm Mpc}$ radius, $\sigma _8$. In this respect, we follow two approaches, which are normalising the perturbation amplitude either on large scales with the observed Cosmic Microwave Background (CMB) anisotropies (e.g. Bennett et al. 2003), or on small scales using the observed cluster abundance. In the second case, we choose $\sigma _8=0.9$ in all the models, while the $\sigma _8$ derived from the CMB is generally slightly smaller because of the Integrated Sachs Wolfe (ISW) effect affecting the large scale CMB anisotropies in the cosmologies we consider (see Bartelmann et al. 2002, and references therein): we take 0.86, 0.82 and 0.76 for DECDM, RP and SUGRA, respectively. These numbers as well as all the inputs from the linear evolution of cosmological perturbations to the N-body procedure described later are computed using our dark energy oriented cosmological code (Perrotta & Baccigalupi 1999), based on CMB fast (Seljak & Zaldarriaga 1996).

We briefly describe now the dark energy cosmologies we will adopt. The equation of state w is a key parameter, describing the ratio between the dark energy pressure  $p_{\rm DE}$ and energy density  $\rho_{\rm DE}$, and it must be negative in order to effectuate cosmic acceleration today. The continuity equation for the dark energy is

 \begin{displaymath} \dot{\rho}_{\rm DE}+3H(\rho_{\rm DE}+p_{\rm DE})=0, \end{displaymath} (1)

where the dot means derivative with respect to the ordinary cosmic time t, $H=\dot{a}/a$ is the Hubble expansion rate and a=1/(1+z)is the cosmic scale factor. In the limit of constant w, the dark energy density evolves in redshift proportionally to (1+z)3(1+w). That is the case for both the $\Lambda $CDM model, whose w=-1 yields a constant dark energy density, and the DECDM model, which we choose to have w=-0.6. Note that the latter case is an effective scenario in the sense that it is obtained simply by replacing the cosmological-constant equation of state, assuming it to be constant and neglecting any other dark energy features such as its cosmological perturbations. Also, it is useful to note that from the point of view of the Friedmann equation, the curvature term in the OCDM model behaves as a dark energy component with constant w=-1/3(see Bartelmann et al. 2002, and references therein). In the general case in which w depends on z, the dark energy density evolves as

 \begin{displaymath}\rho_{\rm DE}(z)=\rho_{\rm DE,0}~ \exp\left[3\int_0^z{\rm d} z'\frac{1+w(z')}{1+z'}\right], \end{displaymath} (2)

which is easily verified solving the continuity Eq. (1).

The dark energy is consistently described by means of the quintessence scalar field $\phi$. The dynamics of its unperturbed value and of the linear fluctuation  $\delta\phi$ obey the Klein-Gordon equation

 \begin{displaymath}\Box{\phi}+V'=0,\quad\delta(\Box{\phi})+V''\delta\phi=0, \end{displaymath} (3)

where $\Box$ is the d'Alambert operator in a Friedmann-Robertson-Walker (FRW) cosmology, and $V(\phi)$ is the quintessence potential. Note that the unperturbed Klein-Gordon equation above is equivalent to the continuity Eq. (1) with $\rho_{\rm DE}=\dot{\phi}^2/2+V$ and $p_{\rm DE}=\dot{\phi}^{2}-V$.

The RP and SUGRA potentials are given by

 \begin{displaymath}V_{\rm RP}=\frac{M^{4+\alpha_Q}}{\phi^{\alpha_Q}},\quad V_{\... ...ha_Q}}{\phi^{\alpha_Q}}\cdot \exp{\left(4\pi G\phi^2\right)}, \end{displaymath} (4)

respectively. The exponential in $V_{\rm SUGRA}$ comes from super-gravity corrections (Brax & Martin 2000) and induces significant changes in the trajectories with respect to the RP case, as we explain now.

The trajectories $\phi(z)$ solving the unperturbed equation of motion (3) with the potentials (4) are attractors, called tracking solutions: they allow reaching the present field value $\phi_0$, of the order of the Planck mass  $M_{\rm Planck}$, starting from a wide set of initial conditions for $\phi$ and  $\dot{\phi}$, with the only relevant condition that $\phi_i\ll M_{\rm Planck}$. For both RP and SUGRA, the tracking regime holds until the quintessence energy density is subdominant compared to the other cosmological components, yielding a constant equation of state obeying the simple relation

 \begin{displaymath}w=-\frac{2}{2+\alpha_Q}\cdot \end{displaymath} (5)

When the quintessence comes to dominate the expansion, the tracking regime represented by (5) is abandoned. At that point, the dark energy equation of state tends to the cosmological constant case because in most dark energy models the potential has to be flat in order to mimic a cosmological constant. The flatter the potential is, the faster is the convergence to this regime.

The key difference between the RP and SUGRA scenarios is precisely in this aspect. With respect to the RP case, the SUGRA exponential correction flattens the potential shape noticeably at $\phi\simeq M_{\rm Planck}$, i.e. at the end of the tracking trajectory. That brings the present-day SUGRA equation of state close to -1 even for steep potentials, i.e. with large values of  $\alpha_{Q}$. In other words, a given equation of state at present is obtained for noticeably higher values of $\alpha_{Q}$ than for RP; this implies that the dark energy dynamics and thus the cosmological expansion rate as a function of redshift are generally much different in the two scenarios. In our particular case, the RP and SUGRA quintessence models have the same equation of state at the present epoch, w=-0.83, with $\alpha_{Q}=-0.6$ and $\alpha_{Q}=-6.7$, respectively. According to Eq. (5), this yields $w_{\rm SUGRA}\simeq -0.23$ and $w_{\rm RP}\simeq -0.77$ in the tracking regime. Thus, these models well represent the diversity that dark energy cosmologies can have in the past, even if they reproduce the same amount of cosmic acceleration today. The redshift behaviour of w in the two cases is illustrated in Fig. 1. Correspondingly, the Hubble expansion rate in the two models is different and is represented in Fig. 2. In the SUGRA case, the dark energy density increases more rapidly with z, making H higher. Note that the difference between the two scenarios is greatly reduced with respect to Fig. 1. The reason is that as z increases the dark energy becomes less and less relevant with respect to matter, greatly diluting the effect of the different w(z). Indeed, at redshifts higher than those shown in the plot, the dark energy is completely negligible and the two curves for H(z)join. As we shall see in the next Section, the expansion rate is the relevant quantity with accounts for the effect of the quintessence on galaxy cluster scales, also affecting the linear perturbation growth rate. By looking at Fig. 2, we expect variations of a few percent level between the two quintessence models considered.

Summarising, the cosmological scenarios we study here are mutually very different. The differences are relevant even between the flat dark energy models: for DECDM, the equation of state is far from -1, while RP and SUGRA have the same equation of state today, but differ strongly in the past, as we emphasised above. These pronounced differences allow us to recognise their imprint in the properties of the dark non-linear halos which we study next. In this respect, we obtain the most interesting results when the cosmologies above are compared by keeping everything else fixed, including $\sigma _8$.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f7.eps} \end{figure} Figure 1: Equation of state for the RP and SUGRA quintessence models studied in this work.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f7a.eps} \end{figure} Figure 2: Hubble expansion rate for the RP and SUGRA quintessence models studied in this work, represented by a solid and dashed line, respectively.
Open with DEXTER

3 Numerical simulations

3.1 The simulation code

We adapted the cosmological code GADGET (Springel et al. 2001c) for simulating a set of 17 galaxy clusters in various dark-energy cosmologies with constant and time-variable equations of state. This section describes the code used, the modifications required for dark-energy models, and the initial conditions we set up.

In total we performed 136 cluster simulations. The simulations were performed in parallel on 8 CPUs on an IBM-SP4 located at the CINECA Super Computing Centre in Bologna, Italy.

3.1.1 GADGET

The cosmological code GADGET (Springel et al. 2001c) is well tested and used for simulating a wide range of cosmological scenarios from the interaction of galaxies (Springel 2000) to large-scale structure formation (Springel et al. 2001a). GADGET is based on a tree-SPH code using co-moving coordinates. The new version (P-GADGET-2, kindly provided by Volker Springel) allows the computation of long-range forces with a particle-mesh (PM) algorithm, with the tree algorithm supplying short-range gravitational interactions only. This "TreePM'' method can substantially speed up the computation while maintaining the large dynamic range and flexibility of the tree algorithm. It also differs in the choice of internal variables for time and velocity, in its time-stepping algorithm and in its parallelisation strategy (see Springel 2003, in preparation). The modifications necessary for performing simulations within cosmologies with dark-energy within P-GADGET-2 do not differ in principle from the modifications necessary for the earlier version of GADGET, but appear in slightly different places due to the changes in design of the code.

3.1.2 Including dark-energy in GADGET

Within the co-moving coordinate scheme of GADGET, the only place where the dark energy has to be taken care of is the calculation of the Hubble function, or some combination of the Hubble function with the scale factor a. This is used when ever a conversion to physical quantities is needed, like converting the internal time variable $\log a$ to physical time t, or in the equation of motion in a cosmological context. Thus, for running cosmological simulations including dark-energy, once can rewrite the usual Hubble function

\begin{displaymath}H(a)=H_0~\left[ \frac{\Omega_0}{a^3}+ \frac{1-\Omega_0-\Omega_\Lambda}{a^2}+ \Omega_\Lambda \right]^{1/2}, \end{displaymath} (6)

for a flat cosmology with cosmological constant using Eq. (2) as
 
$\displaystyle H(a)=H_0~\left[ \frac{\Omega_0}{a^3}+ \frac{1-\Omega_0-\Omega_{\r... ...Omega_{\rm Q}~ \exp\left(-3\int_a^1\frac{1+w(a')}{a'}{\rm d} a'\right) \right].$     (7)

Within the new integration scheme of P-GADGET-2, this is also done within the calculation of the drift and kick factors (Springel et al., in preparation).

For reasons of timing and precision, we tabulate the integral in Eq. (7) at the beginning of a run, and then interpolate within the table during the run.


  \begin{figure} \par\includegraphics[width=16.7cm]{h4738fc.eps} \end{figure} Figure 3: One individual cluster is shown at different redshifts (z=2 to z=0 in steps of 0.5 from bottom to top) in different cosmologies (columns as labelled) all normalised to $\sigma _8=0.9$ today. The panels illustrate that the clusters in different cosmological models arose from the same initial conditions and thus appear morphologically similar, but subtle differences are visible in detail.
Open with DEXTER

3.2 Initial conditions

Regarding the initial conditions, we concentrate on creating a set of identical clusters in all cosmologies studied. Thus, we started from a set of 17 clusters in the $\Lambda $CDM cosmology and adapted their initial conditions to the different dark-energy cosmologies investigated.

3.2.1 The original set of initial conditions

For the present analysis, we use cluster models obtained using the so called re-simulation technique. It consists of re-simulating at higher resolution regions selected from an existing large-scale cosmological simulation. For this work, we selected as a parent simulation an N-body run with 5123 particles in a box of $479~h^{-1}~{\rm kpc}$ (Jenkins et al. 2001; Yoshida et al. 2001). Its background cosmological model is spatially flat with $\Omega_{\rm m,0}= 0.3$and $\Omega_\Lambda=0.7$ at the final epoch, identified with redshift zero. The Hubble constant is h=0.7 in units of $100~{\rm km~s^{-1}~Mpc^{-1}}$, and the power spectrum normalisation was set to $\sigma _8=0.9$. The particle mass was $6.8\times10^{10}~h^{-1}~M_\odot$, and the gravitational softening was chosen as $30~h^{-1}~{\rm kpc}$. From the output of this simulation at z=0, we randomly selected ten spherical regions of radius between 5 and $10~h^{-1}~{\rm Mpc}$, each containing either one or a pair of dark matter haloes, with mass larger than $3\times10^{14}~M_\odot$. The total number of cluster-sized objects turns out to be 17.

We constructed new initial conditions for each of these regions using the ZIC software package (Zoomed Initial Conditions; Tormen et al. 1997). The procedure for this construction is as follows. The initial positions of the particles in the simulation run define a Lagrangian region. The initial density field in this Lagrangian region is resampled by placing a larger number of particles than were originally present; on average, the number of high-resolution (HR), dark-matter (DM) particles is 106 for our simulations. In this way, the spatial and mass resolution can be increased at will. The mass resolution of the re-simulation ranges from $2\times 10^9$ to $6\times 10^9 ~{h}^{-1}~M_\odot$ per DM particle so as to have each cluster consists of approximately the same number of particles. The gravitational softening is given by a $5~h^{-1}~{\rm kpc}$ cubic spline smoothing for all HR particles.

The number of particles outside the HR Lagrangian region was reduced by interpolating them onto a spherical grid centred on the geometrical centre of the HR region. An angular resolution of the grid between 3 and 5 degrees in both angular directions produces on the order of 100 000 macro particles of varying mass and gravitational softening. Extensive testing has shown that this number is enough to guarantee an overall good description of the original tidal field on large scales.

The distribution of high resolution particles in the new initial conditions samples all the fluctuations of the matter power spectrum realization of the original cosmological run, plus a new and independent realization of high frequency fluctuations from the original spectrum; in this way the power spectrum is extended up to the Nyquist frequency of the new HR particle distribution.

The ZIC package has been widely tested and was used to produce initial conditions for many resimulations at medium to extremely high resolution (e.g. Yoshida et al. 2002; Springel et al. 2001b; Tormen et al. 1997; Stoehr et al. 2002).

3.2.2 Modifying the initial conditions for dark-energy models

Since the goal of this work is studying the evolution of the same set of clusters in different cosmologies, we decided to adapt the initial conditions from the $\Lambda $CDM cosmology to all the dark energy cosmologies we wish to investigate. This is done in two steps. In the first step, the initial redshift is adapted such that the rms density fluctuation amplitude today is the same in all models despite their different dynamics. The initial redshift  $z_{\rm ini}$ for any model is thus implicitly determined by the ratio of linear growth factors D+(z),

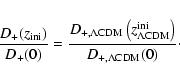\begin{displaymath}\frac{D_+(z_{\rm ini})}{D_+(0)}= \frac{D_{\rm +,\Lambda CDM}... ...ini}_{\rm\Lambda CDM}\right)} {D_{\rm +,\Lambda CDM}(0)}\cdot \end{displaymath} (8)

In a second step, the peculiar velocities of the particles in their Lagrangian initial region have to be modified such as to reflect the change in initial redshift. At early times $\tau$, they can be described by the Zel'dovich (1972) approximation,

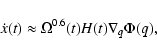\begin{displaymath}\dot{x}(t)\approx\Omega^{0.6}(t)H(t)\nabla_q\Phi(q), \end{displaymath} (9)

where q is the Lagrangian particle position, and $\Phi(q)$ is the velocity potential in Lagrangian space. Thus, the new velocities can be calculated starting from the displacement field $\nabla_q\Phi(q)$ and scaling them to the new initial redshift and the new cosmological model we wish to adapt them to. The velocities are thus given by

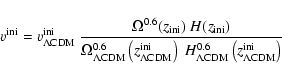\begin{displaymath}v^{\rm ini}= v_{\rm\Lambda CDM}^{\rm ini}~ \frac{\Omega^{0.6... ...\Lambda CDM}^{0.6} \left(z_{\rm\Lambda CDM}^{\rm ini}\right)} \end{displaymath} (10)

Table 1 summarises the initial redshifts and the velocity scalings used for the different cosmologies.

Table 1: Parameters used for adapting the initial conditions of the $\Lambda $CDM model to the other cosmological models used in this paper. Models marked with superscript $^\dagger $ have their rms fluctuation amplitude $\sigma _8$ adapted to the COBE normalisation, see Table 2.

3.3 Post-processing

We applied a halo finder and constructed the merger tree as described in Tormen et al. (2003).

3.3.1 Finding the halos

The halo finder adopts the spherical overdensity criterion to define collapsed structures in the simulations. This is done for each snapshot of each resimulation, estimating the local dark matter density at the position of each particle, $\varrho_{i,~{\rm DM}}$, by calculating the distance di,10 to the tenth closest neighbour, and assuming $\varrho_{i,~{\rm DM}}\propto d_{i,10}^{-3}$. We then sort the particles by density and take as centre of the first halo the position of the particle embedded into the highest density. Around this centre, we grow spherical shells of matter, recording the total mean overdensity inside the sphere as it decreases with increasing radius. We stop the growth and cut the halo when the overdensity first drops below 200 times the mean (as opposed to critical) background density, and denote the radius so defined as r200. The particles selected in this way belong to the same halo and are used to compute its virial properties (mass, radius, etc.). We tag all halo particles as engaged in the list of sorted densities, and selected the centre of the next halo at the position of the densest available (unengaged) particle. We continue in this manner until all particles are screened. We include in our catalogue only such halos which have at least n=10 dark-matter particles within their virial radius. All other particles are considered field particles.

We found that our 17 clusters contain on average $N_V\approx200~000$dark matter particles within their virial radii. The corresponding virial masses range between $M_{\rm V}=3.1\times10^{14}$ to $1.7\times10^{15}~h^{-1}~M_\odot$.

3.3.2 Constructing merger trees

For each of these cluster-sized halos we build a merging history tree using the halo catalogs at all time outputs. Starting with a halo at any given z, we define its progenitors at the previous output $z+\Delta z$ to be all haloes containing at least one particle that by z will belong to the first halo. We call the main progenitor at $z+\Delta z$ the one giving the largest mass contribution to the halo at z.

3.3.3 Fitting halo concentrations

For determining halo concentrations and their change with time, we only took the main progenitor of each of the 17 massive halos into account. Using the centres from the halo finder, we construct radial profiles by binning the particles within r200 in logarithmic radial bins with at least 132 particles each. For low-mass halos, this number is reduced to be 1/20 of the total number of particles within r200 to ensure enough points for the fitting procedure. Our choice in number of particles is smaller than suggested by Power et al. (2003) but still reasonable, as we are interested in the local density at the innermost point, and not in the enclosed over-density. Also the global fit does not strongly depend on the innermost data-points. We checked, that the largest contribution to the scatter of the concentration parameter within a redshift bin comes from the dynamical state of the halo. The changes in the concentration parameters inferred from the fits when changing then number of particles within the innermost bin by a factor of five is still one order of magnitude smaller than the intrinsic scatter due to the dynamical state of the halo.

We then fit the NFW profile

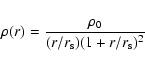\begin{displaymath}\rho(r) = \frac{\rho_0}{(r/r_{\rm s})(1+r/r_{\rm s})^2} \end{displaymath} (11)

(Navarro et al. 1997) to the binned profiles obtained. The concentration is then defined as usual, $c=r_{200}/r_{\rm s}$. Note, however, that Navarro et al. (1997) defined r200 as enclosing a mean density of 200 times the critical rather than the mean background density as we do here.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f6.eps} \end{figure} Figure 4: Halo-mass histograms in the $\Lambda $CDM model for four of the eight equidistant redshift bins between redshifts zero and three introduced in Sect. 4 below. The distributions in the missing bins fall in between those in the adjacent bins and are left out for clarity. As halos merge and new halos form, the histograms shift towards higher masses.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f3a.eps}\hspace*{2mm} \includegraphics[width=8.8cm,clip]{h4738f4a.eps} \end{figure} Figure 5: Concentrations of halos formed in the $\Lambda $CDM model binned by redshift before ( left panel) and after ( right panel) determining halo-prescription parameters. While the ENS algorithm fits the measured halo concentrations very well, concentrations according to the Navarro et al. and Bullock et al. algorithms deviate significantly. Changing the algorithm parameters yields very good agreement also for the Bullock et al. algorithm, while the Navarro et al. algorithm has too shallow redshift evolution. The right panel also shows the good quality of the simple polynomial fit. The error bars indicate the approximate 1-$\sigma $ range of halo concentrations within the redshift bins. Concentrations are defined relative to the radius r200 of spheres around halo centres containing 200 times the mean background density.
Open with DEXTER

  
4 Halo concentrations

Given the numerically determined halo concentrations, we can now proceed to compare them with expectations from analytic algorithms. Three such algorithms have been proposed:

The algorithms by Navarro et al. (1997) and Bullock et al. (2001) involve two parameters, a mass fraction $f_{\rm NFW,B}$ and a constant factor $C_{\rm NFW,B}$, while Eke et al. (2001) introduce a single parameter only.

Before we can apply these algorithms to our simulated halos, we have to introduce a common definition of virial radii and masses. While Navarro et al. (1997) define the virial radius r200 as enclosing an overdensity of 200 times the critical density of the Universe, Bullock et al. (2001) and Eke et al. (2001) refer to $\Delta$ times the mean background density instead, where $\Delta$ is the cosmology-dependent mean overdensity within virialised spherical halos rather than the factor 200. Since the mean is lower than the critical density, r200 is larger when referred to the mean density.

In our numerical simulations, we use the radius enclosing 200 times the mean background density as virial radius, which we call r200 throughout. We adapt the numerical algorithms by Navarro et al. (1997), Bullock et al. (2001) and Eke et al. (2001) such that they use the same definition of r200. This requires iterative solutions because converting masses from one definition of the virial radius to another requires the density profile, and thus concentrations, to be known.

Given the masses and redshifts of all individual halos, we compute the analytically expected concentrations for each halo according to the three algorithms listed above. We thus have for each halo four concentration values, viz. the three analytic expectations and the value obtained by fitting the NFW profile to the numerically determined density profile. We then bin halos by redshift into eight bins between redshifts three and zero. Each redshift bin thus contains halos with a range of masses. In each bin, we determine the median and the 33- and 68-percentiles of the distribution of the four types of concentration. The left panel of Fig. 5 shows results for the $\Lambda $CDM model as an example.

The solid curve shows the numerically determined halo concentrations, with the error bars giving the 33- and 68-percentiles centred on the median within each bin. The other curves show results obtained from the three algorithms as indicated in the figure. Error bars attached to those reflect the mass ranges of halos within the respective redshift bins. While the algorithm by Eke et al. (2001) describes the numerically fitted halo concentrations very well within the error bars, concentrations obtained according to Navarro et al. (1997) and Bullock et al. (2001) fall consistently above and below the numerical concentrations, respectively. The curve for the NFW algorithm reflects the earlier finding that it reproduces halo concentrations well at redshift zero, but under-predicts their decrease with increasing redshift. Concentrations according to Bullock et al. (2001) are somewhat too small in all redshift bins.

The error bars on the simulated curve are larger than those on the analytically determined curves because of halo mergers, which change halo masses much more abruptly than halo concentrations.

Since all three algorithms have one or two free parameters, we now investigate whether their agreement with the numerical results can be improved modifying the parameters. We thus define a measure for the quadratic deviation of analytical from numerical halo concentrations,

 \begin{displaymath}\chi^2=\sum_{\rm halos}\left[\left( c_{\rm analytic}-c_{\rm numerical} \right)^2\right], \end{displaymath} (12)

and minimise $\chi ^2$ varying the parameter(s). Figure 6 shows $\chi ^2$ contours obtained for the $\Lambda $CDM model from the algorithms by Navarro et al. (1997) (left panel) and Bullock et al. (2001) (right panel). Both algorithms have two parameters, a mass fraction and a factor, which are shown along the horizontal and vertical axes, respectively.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f1a.eps}\hspace*{3mm} \includegraphics[width=8.8cm,clip]{h4738f1b.eps} \end{figure} Figure 6: $\chi ^2$ contours in the space of parameters contained in the halo-concentration prescriptions by Navarro et al. ( left panel) and Bullock et al. ( right panel). Both contour plots show extended valleys in the $\chi ^2$ surface with very flat bottoms. The dotted curves indicate approximate relations for the directions of these valleys.
Open with DEXTER

Both contour plots share the feature of having a shallow, degenerate valley along which the mass fraction changes by orders of magnitude, while the factor changes very little. Approximately, these valleys follow the relations indicated by dashed lines in the two panels of Fig. 6. This near-insensitivity to the exact mass fraction allows fixing it at $f_{\rm NFW,B}=0.001$, say, and then determining the $\chi ^2$ minimum along the perpendicular axis only.

Figure 7 shows cuts through the contour plots in Fig. 6, and also $\chi ^2$ according to the one-parameter algorithm proposed by Eke et al. (2001). The abscissa shows the factors $C_{\rm NFW,B}$ divided by their values at the $\chi ^2$ minima for fixed $f_{\rm NFW,B}=0.001$, i.e.  $C_{\rm NFW}=1500$ and $C_{\rm B}=3.5$, while $C_{\rm ENS}$ is divided by the originally proposed value, i.e.  $C_{\rm ENS}=1/28$. The curves show pronounced minima for the algorithms proposed by Bullock et al. (2001) and Eke et al. (2001), and a very shallow minimum for the Navarro et al. (1997) algorithm.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f2.eps} \end{figure} Figure 7: Cuts through the $\chi ^2$ contours at constant mass fraction for three different halo-concentration prescriptions.
Open with DEXTER

Using these parameters, we now return to the comparing the numerically determined and analytically expected halo concentrations and find the results shown in the right panel of Fig. 5. The agreement between the numerical results and the Bullock et al. (2001) concentrations has improved substantially, while the Navarro et al. (1997) algorithm still predicts too high halo concentrations at moderate and high redshifts.

We repeated this procedure for all cosmological models used and found that the algorithm by Bullock et al. (2001) reproduces the numerical concentrations well in all of them if its parameters are modified to $f_{\rm B}=0.001$ and $C_{\rm B}=3.5$, while the algorithm by Eke et al. (2001) performs very well throughout with the factor $C_{\rm ENS}=1/28$ which was originally proposed. The agreement achieved for dark-energy models is illustrated for the Ratra-Peebles and SUGRA models in the left and right panels of Fig. 8, respectively.

Our first conclusion is thus that the halo-concentration algorithms proposed by Bullock et al. (2001) performs very well also in dark-energy cosmologies, provided its two parameters are modified, while the algorithm by Eke et al. (2001) does not require any adaptation. The algorithm originally proposed by Navarro et al. (1997) has the same weakness in dark-energy as in $\Lambda $CDM models of under-predicting the redshift evolution. This can be remedied to some degree, but not removed, by modifying its two parameters.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f4b.eps}\hspace*{3mm} \includegraphics[width=8.8cm,clip]{h4738f4d.eps} \end{figure} Figure 8: Examples for the agreement between numerically simulated and analytically expected halo concentrations for two dark-energy models, Ratra-Peebles ( left panel) and SUGRA ( right panel). The agreement is very good, except for the Navarro et al. prescription whose redshift evolution is too shallow.
Open with DEXTER

These algorithms have the advantage of relating halo properties to the physical mechanism of halo formation. The gentle changes of halo concentrations with mass and redshift suggest, however, that they can be described in a much more simplified fashion by a fitting formula. Since concentrations of halos with fixed mass increase with decreasing redshift as the background density decreases, we attempt fitting the two-parameter functional relationship

 \begin{displaymath}c(M,z)=\frac{c_0}{1+z}~ \left(\frac{M}{10^{14}~h^{-1}~M_\odot}\right)^\alpha \end{displaymath} (13)

to the numerically determined halo concentrations. Best-fitting values for c0 and $\alpha $ are listed for all eight cosmological models in Table 2. The uncertainties of c0 and $\alpha $ given there are 1-$\sigma $ bootstrap errors obtained from 1024 bootstrap halo samples. Although Eq. (13) does not reflect the physics of halo formation, it is useful for conveniently summarising the numerical results.

Table 2: Parameters c0 and $\alpha $ for the different cosmological models.

The agreement between the numerically determined concentrations and those obtained from the fitting formula (13) are illustrated for $\Lambda $CDM in the right panel of Fig. 5 and for two dark-energy models in both panels of Fig. 8. While the constant factor c0 changes quite appreciably across cosmological models, the exponent $\alpha\approx-0.1$ is approximately constant for all models, except perhaps for the dark-energy model with constant w=-0.6 and reduced $\sigma _8$. Recently, Zhao et al. (2003) found that the dependence of halo concentrations on halo mass becomes shallower with increasing redshift. Since we are focusing on how halo properties vary across cosmologies, our halo sample is currently too small for confirming this result.

Remarkably, halo concentrations are distributed about their mean values $\bar{c}$ in a way which is virtually independent of the cosmological model. Figure 9 shows the distribution of $c/\bar{c}$ for all eight cosmologies, where separate curves are shown for $\bar{c}$ determined according to the algorithms by Bullock et al. (2001), Eke et al. (2001) and the fitting formula (13).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f5.eps} \end{figure} Figure 9: Normalised halo-concentration distributions across all cosmological models for three halo-concentration algorithms. The curves are very close to log-normal distributions whose standard deviations are almost independent of the cosmological model.
Open with DEXTER

These curves closely resemble log-normal distributions, as found earlier in $\Lambda $CDM and OCDM cosmologies (e.g. Bullock et al. 2001; Jing 2000) . We thus attempt fitting them with distributions of the form

 \begin{displaymath}p(c)=A~\exp\left[ -\frac{(\ln c-\ln\bar{c}-\ln\mu)^2}{2\sigma^2} \right]\cdot \end{displaymath} (14)

The amplitude A is fixed by normalisation, and the parameters $\mu$and $\sigma $ are determined from fitting to the measured distributions, using $\bar{c}$ as obtained from the different algorithms and the polynomial of (13).

Any deviation of $\mu$ from unity indicates that the respective distribution is not centred on $\bar{c}$. Since the algorithms and Eq. (13) were adapted such as to optimise the agreement between $\bar{c}$ and the measured mean values, $\mu$ is determined for cross-checking only. Table 3 shows the results for the three algorithms and the polynomial (13).

Table 3: Means and standard deviations of log-normal distributions fitted to normalised halo concentration distributions for four different halo-concentration prescriptions in the eight different cosmological models.

The table shows that the mean $\mu$ scatters slightly about unity for all algorithms except for Navarro et al. (1997), for which it is consistently below unity. This reflects the well-known inability of that algorithm to model the redshift evolution correctly: it over-predicts concentrations $\bar{c}$ at redshifts above unity, and thus shifts the distribution of $c/\bar{c}$ systematically to values below unity. Perhaps more surprising is that the standard deviation of the log-normal distribution is quite independent of the cosmological model and of the algorithm used for describing the halo concentrations, $\sigma\approx0.22$. This result agrees well with the scatter found in a variety of CDM models with and without cosmological constant (Bullock et al. 2001; Jing 2000).

  
5 Dependence on w(z)

In this section, we focus on the models with fixed $\sigma _8=0.9$, in order to study the dependence of the halo concentration on the behaviour of w(z). As we saw in the previous section, c0 for fixed normalisation $\sigma _8$ increases for the following order of cosmologies: $\Lambda $CDM, RP, SUGRA, DECDM, and OCDM. This is not accidental, but expresses one of our major results. As we stressed in the introduction, the different candidates for explaining the dark energy and cosmological acceleration are different in the redshift dependence of their equation of state. The models we study here, in particular the RP and SUGRA quintessence scenarios, well represent this issue, having the same w0 but a markedly different w(z), as is obvious from Fig. 1. Thus, it is worthwhile studying the difference between these models in a phenomenological context. In Fig. 10, we plot the linear perturbation growth factor divided by the scale factor, $g(z)\equiv D_+(z)/a(z)$, for the cosmologies studied here. D+ is the growing solution of the general linear perturbation equation

 \begin{displaymath}\ddot\delta+2\frac{\dot a}{a}\dot\delta-4\pi G\rho\delta=0 \end{displaymath} (15)

which can, for w=-1 and w=-1/3, be integrated once to yield $D_+\propto\dot{a} a^{-1}\int_0^a \dot{a}^{-3} {\rm d} a \;$. We normalise D+ to unity at present.

The asymptotic behaviour $D_+\propto a$ for $a\to0$ means that the growth factor at early times in all cosmologies converges to the behaviour in a flat CDM Einstein-de Sitter case, with $\Omega_0=1$. On the other hand, the growth factor normalised by the scale factor, g(z), behaves differently for the different cosmologies. Most importantly, it turns out to reflect the behaviour of c0 in the different cosmologies studied here above.

The curves in Fig. 10 display g(z) for the different cosmological models, normalised to unity at present: the higher g(z) is at a given redshift z, the higher was the perturbation amplitude at that epoch, and the earlier was the epoch when structures formed (Bartelmann et al. 2002). Since at high redshifts all cosmologies approach the flat CDM Einstein-de Sitter limit in which $D_+\propto a$, the structures acquire their fluctuation amplitude at redshifts determined by the ratio of the asymptotic values of g(z) as shown in Fig. 10.

It is thus natural to expect that the concentration parameters c0of our halos are affected similarly in the different cosmologies, since they parametrise the central density contrast of the halos. This is indeed what we find, as Table 4 shows.

Table 4: Concentration and perturbation asymptotic growth factor in the different cosmologies.

The table has four columns. The first abbreviates the cosmological model. The second gives the c0 parameters relative to $c_0^{\rm\Lambda CDM}$ for the $\Lambda $CDM model, with error bars obtained from the bootstrap errors of c0 as given in Table 2. The third column shows the linear growth factors at infinity relative to the $\Lambda $CDM model, and the fourth column gives the same ratio taken at the average collapse redshifts of our numerically simulated halos. Error bars on the values in the fourth column are due to the mass range of halos which implies a range of collapse redshifts.

The collapse redshifts were obtained using the prescription by Eke et al. (2001) because their algorithm for computing halo concentrations turned out to reflect our numerical results best. We draw three main conclusions from the results in Table 4. First, the concentration parameters c0 relative to $\Lambda $CDM are quite close to the linear growth factors at high redshift relative to $\Lambda $CDM, although the match is not perfect. We may be affected by cosmic variance because the number of halos per cosmology is relatively small. Second, using different definitions of the collapse redshift yields different ratios of the linear growth factor. In particular, such definitions according to which the collapse redshifts are small fail in reproducing the trend in c0 with different cosmological models. Third, since the asymptotic ratio of growth factors towards infinite redshift is rather close to the ratios of the c0 parameters, the final halo concentrations are apparently determined at very high redshift already even though the halos are quite massive and thus completely assembled late in cosmic history.

We thus propose to interpret the c0 parameter as composed of a factor valid for to the $\Lambda $CDM cosmology, multiplied by a correction which takes into account the asymptotic behaviour of the linear growth factors at high redshift for the given dark-energy cosmology,

 \begin{displaymath}c_0\rightarrow c_0^{\rm\Lambda CDM}\cdot \frac{D_+(z_{\rm coll})} {D_+^{\rm\Lambda CDM}(z_{\rm coll})}\cdot \end{displaymath} (16)

This result is particularly important since it demonstrates that quintessence cosmologies having the same equation of state at present but a different redshift behaviour can produce relevant and predictable differences in the central regions of clusters.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h4738f8.eps} \end{figure} Figure 10: Linear density perturbation growth dynamics in the different cosmologies considered.
Open with DEXTER

6 Summary

We used cosmological numerical simulations to study the concentration parameters of massive dark-matter halos in cosmological models with dark energy, and compared them to results obtained in cosmological-constant ($\Lambda $CDM) and low-density, open (OCDM) models.

We investigate three different dark-energy cosmologies. One has a constant ratio w=-0.6 between pressure and density of the dark energy, the other two have equations of state which change over time. The Ratra-Peebles (Peebles & Ratra 2002) model describes the dark-energy scalar field with an inverse power-law potential, the SUGRA (Brax & Martin 2000) model modifies the power-law potential with an exponential factor.

Dark energy with non-constant density, and more generally with non-constant equation of state, modifies terms in Friedmann's equation. We modified and extended the proprietary GADGET-2 code accordingly, which is an extension of the publically available GADGET code (Springel et al. 2001c).

Cluster-sized halos were selected from a large cosmological simulation volume and re-simulated at substantially higher resolution. Since the large-scale simulation was originally prepared for a cosmological-constant ($\Lambda $CDM) cosmology, the initial conditions used for re-simulation needed to be carefully adapted in two ways to the other cosmological models. First, microwave-background (CMB) observations on large angular scales constrain the amplitude of dark-matter fluctuations, conventionally expressed by the rms fluctuation level $\sigma _8$ within spheres of $8~h^{-1}_,{\rm Mpc}$radius. Due to the enhanced dynamics of the gravitational potential in dark-energy cosmologies, the integrated Sachs-Wolfe effect increases and thus the amount of primordial fluctuations on large scales needs to be reduced in order to remain compatible with observed CMB fluctuations on large angular scales. This reduction of $\sigma _8$requires the redshift of the initial conditions to be adapted. Second, the particle velocities in the initial data need to be scaled according to the modified cosmological dynamics in dark-energy cosmologies.

It should be noted that the correction of $\sigma _8$ tries to adapt the density-fluctuation level in the simulations to CMB observations on large angular scales, while we are interested in the formation of cluster-sized halos on much smaller scales. How cluster-sized fluctuations are related to large-scale fluctuations depends sensitively on the primordial slope of the dark-matter power spectrum, which we assume to unity here.

We ran simulations for two sets of normalisations. As $\sigma _8=0.9$for the original $\Lambda $CDM model, we first ran simulations with the same $\sigma _8$ for the OCDM and the three dark-energy models in order to arrive at cluster samples which could most directly be compared to each other. We then ran three additional sets of simulations after adapting the normalisation of the dark-energy models to account for the enhanced integrated Sachs-Wolfe effect. There are thus in total eight sets of simulations. Each of those contained 17 massive halos re-simulated at high resolution.

Concentrations for these halos were determined by fitting the NFW density profile at 78 redshifts between z=5.8 and z=0. Comparing these fitted values to analytical expectations on halo concentrations, we found the following results:

Similar findings on the log-normal distribution of halo concentrations and its standard deviation have be achieved before for CDM models with and without cosmological constant (see, e.g., Bullock et al. 2001; Jing 2000). Our study extends these investigations to dark-energy models. Our two most important conclusions are that (1) mean halo concentrations and their distribution about those mean values are as in low-density open and cosmological-constant models except that (2) halos are systematically more concentrated in dark-energy models in a way closely reflecting the linear density-fluctuation amplitude at high redshifts.

Acknowledgements
We are deeply indebted to Volker Springel for providing access to, and support in using and modifying P-GADGET-2 prior to release. Simon White's comments helped improving the paper substantially. The simulations were carried out on the IBM-SP4 machine at the "Centro Interuniversitario del Nord-Est per il Calcolo Elettronico'' (CINECA, Bologna), with CPU time assigned under an INAF-CINECA grant. K. Dolag acknowledges support by a Marie Curie Fellowship of the European Community program "Human Potential´´ under contract number MCFI-2001-01227.

References


Copyright ESO 2004