S. Bagnulo ^1, - H. Hensberge² - J. D. Landstreet³ - T. Szeifert¹ - G. A. Wade⁴

1 - European Southern Observatory, Casilla 19001, Santiago 19, Chile
2 - Royal Observatory of Belgium, Ringlaan 3, 1180 Brussel, Belgium
3 - Department of Physics and Astronomy, University of Western Ontario, London, Ontario N6A 3K7, Canada
4 - Department of Physics, Royal Military College of Canada, PO Box 17000, Station "Forces'', Kingston, Ontario K7K 7B4, Canada

Abstract
During a survey of field strengths in upper main sequence stars in open clusters, we observed the star NGC 2244-334 in the Rosette Nebula cluster and discovered an extraordinarily large mean longitudinal field of about -9 kG, the second largest longitudinal field known in a non-degenerate star. This star appears to be a typical Ap He-wk (Si) star of about $4~M_\odot$ . Spectrum synthesis using a line synthesis code incorporating the effects of the strong magnetic field indicates that He is underabundant by about 1.5 dex, and C, O and Mg by about 0.1-0.4 dex, while Si, Mn and Fe are overabundant by about 1 dex, and Cr and Ti are nearly 2 dex overabundant.

Cluster membership for this star is secure, so its age is about $2\times 10^6$ yr, which is less than 3% of its main sequence lifetime. This star is one of the very youngest magnetic upper main sequence stars with a well-determined age, and confirms that both magnetic fields and strong chemical peculiarity can appear in stars which are both extremely young and very close to the ZAMS.

Key words: polarization - stars: abundances - stars: chemically peculiar - stars: magnetic fields - stars: individual: NGC 2244-334

1 Introduction

Strong magnetic fields occur in a few percent of the stars of the upper main sequence ( $T_{\rm e} \geq 7000$ K or so). Fields are generally found in stars having Ap SrCrEu, Ap Cr, Ap Si, He-weak and He-strong (collectively Ap-Bp) classification peculiarities, and corresponding atmospheric abundance anomalies.

These fields are usually first detected by observation of a significant mean line-of-sight field component $\langle B_z \rangle$ (e.g. Landstreet 1992), but in some stars the mean field modulus $\langle B \rangle$ can also be measured (Mathys et al. 1997). Typical values of $\langle B \rangle$ are measured or inferred to be in the range of $3\times 10^2$ - $3\times 10^4$ G. The measured ( $\langle B_z \rangle$ and/or $\langle B \rangle$ ) field usually varies periodically with time with a period which may lie anywhere in the range of about 0.5 d up to a century. It is typically found that the brightness of the star as measured photometrically varies (by a few percent) with the same period, and this is also often true of spectral line profiles.

The fields observed in upper main sequence (UMS) stars are well described by the rigid rotator model. The field is frozen into the star, but is not symmetric with respect to the rotation axis. The overall topological structure of the field may be crudely modelled using a dipolar field structure, and it is generally found that the axis of the dipole is inclined to the rotation axis at some angle $\beta \neq 0$ . Thus as the star rotates, the field structure on the visible hemisphere changes periodically, leading to the observed periodic $\langle B_z \rangle$ variations: the period of variation is the stellar rotation period. Note that the observed periods are typically an order of magnitude or more longer than those inferred for normal A and B UMS stars; the magnetic UMS stars have on average only a few percent of the normal specific angular momentum of non-magnetic A and B stars.

The magnetic field structure somehow leads to both the quite unusual surface chemical abundances and to the occurrence of strong horizontal variations in these abundances, which in turn cause the spectrum and photometric variations. The chemical peculiarities are thought to be produced by the selective action of radiative levitation of low-abundance elements with rich spectra, an effect which competes with gravitational settling of atoms more massive than H, and with various hydrodynamical effects such as stellar winds, meridional circulation, turbulent diffusion, and perhaps convection zones. However, no detailed models yet exist which can predict either the overall abundance patterns observed, or the occurrence of the observed horizontal abundance variations, in spite of serious efforts (e.g. Babel & Michaud 1991) to explain these phenomena.

Furthermore, the origin and evolution of the strong magnetic fields of UMS stars are not yet understood. We do not know with certainty when in an UMS star's evolution it develops a magnetic field stronger by some orders of magnitude than those that might be present in normal A and B stars, although it has been argued by Stepien (2000) that the fields of Ap-Bp stars are already present during the pre-main sequence phase. Theoretical models of the structure and evolution of UMS stellar fields are still rather uncertain, but it is widely thought that the fields are probably fossils, left from the pre-main sequence evolution of the star, rather than dynamo fields being generated during the main sequence phase (e.g. Moss 2001). If this is the case, the observed fields are expected to evolve through a combination of (slow) ohmic decay together with field distortion produced by evolutionary structural changes and by meridional circulation currents. The surface field of such a fossil field would be expected to be observable throughout the whole main sequence lifetime of a magnetic star.

Observations have not yet provided clear guidance on field evolution. Early studies used the characteristic Ap-Bp chemical peculiarities as a means of identifying magnetic stars. Observations by Hartoog (1976, 1977) and Abt (1979) showed clearly that Ap-Bp stars are found in numerous open clusters. The relatively massive Bp stars are found in clusters of all ages in which such stars are expected to be on the main sequence. The presence of detectable fields in Bp stars with ages from a few Myr to about 20 Myr has been directly confirmed by magnetic observations of cluster and association members by Landstreet & Borra (1978), Borra (1981), and Bohlender et al. (1993), but little is known observationally about the fields of older cluster Bp stars.

In contrast, observational evidence for the lower mass Ap stars was found only in older clusters (Hartoog 1976; Abt 1979), and in fact Abt suggested that low-mass Ap stars are found only in clusters of about 10⁸ yr or more in age. Recent searches (e.g. by Maitzen and collaborators) have tended to confirm this lack of low-mass Ap stars in young clusters. A recent study of four nearby young clusters by Pöhnl et al. (2003) underlines this situation: among 13 Ap-Bp cluster members, they found none with masses less than 1.95 $M_\odot$ , so that this collection is without any of the cooler Ap stars, which extend down to about 1.6 or 1.7 $M_\odot$ . This situation is very puzzling in the context of the fossil field theory. It is very difficult to see why a fossil field would only become visible after a low-mass magnetic star has been on the main sequence for 10⁸ yr. Furthermore, if low-mass Ap stars are not found in young clusters because fields are not yet present at the surfaces of these stars, it is hard to understand how the stars, when older, could have slowed to their generally low rotation rates, a situation which probably requires magnetic braking (Stepien 2000).

However, the apparent lack of young Ap stars may be primarily due to observational selection effects. (1) Photographic classification spectra were harder to obtain for the relatively faint A stars in the (mostly rather distant) young clusters, so observations have tended to concentrate on the numerous B stars. (In fact, in such clusters the A stars also often seem to be under-represented even in membership studies, perhaps because of their faintness relative to the brighter B stars.) (2) The $\Delta a$ photometry of Maitzen is relatively insensitive to the cooler Ap stars (Maitzen & Vogt 1981), and until recently this photometry was carried out one star at a time, with photoelectric photometers, providing the same temptation to concentrate on the brightest stars in each cluster, and again providing little information about A stars in young clusters.

There have in fact been occasional reports of low-mass Ap stars in young clusters. According to Warren & Hesser (1977) the Ap CrEu(Sr) star HD 290665 (= WH 257) is probably a member of Ori OB1. Data compiled by Thompson et al. (1987) suggests that Ap Sr star HD 147105 is a member of the Sco-Cen association, as discussed by North (1987). Two Ap Sr stars seem to be members of the young Per OB2 association (Guetter 1977). This confused situation underlines the shortage of relevant observations.

Two more recent studies of Ap stars have again come to contradictory conclusions concerning the evolution of fields during the main sequence phase. Gomez et al. (1998) used Hipparcos parallaxes to study the distribution in the Hertzsprung-Russell diagram of the various classes of Ap-Bp stars, and found that all the classes, including the low-mass Ap SrCrEu stars, are distributed approximately uniformly from the ZAMS to the TAMS. In contrast, Hubrig et al. (2000) examined the positions in the HR diagram of the particular sample of stars that have both sufficiently large fields and sufficiently slow rotation that $\langle B \rangle$ can be measured, and found that none of the stars in this sample appear to lie close to the ZAMS. They proposed that strong fields do not appear on the surfaces of magnetic Ap stars of $M < 3~M_\odot$ until about 30% of the main sequence lifetime has elapsed. (However, this hypothesis has been contradicted by the discovery of a large magnetic field in a $2.1~M_\odot$ Ap star in NGC 2516 that has completed only 16 $\pm$ 5% of its main sequence life; see Bagnulo et al. 2002.)

The fundamentally important general problem of field evolution, and the very confusing observational situation, has led us to begin a systematic study of the magnetic fields of Ap-Bp stars in clusters. In this way we hope to characterize the magnetic fields of a substantial sample of stars for which the age and evolutionary state are known with little ambiguity. These data are expected to fundamentally improve our understanding of the evolution of fields in magnetic UMS stars.

We now have magnetic measurements of stars in about a dozen open clusters. These data are still being analyzed, but during the reduction process we identified one star, NGC 2244-334, as a star with an extraordinarily large magnetic field. In this paper we present a first report on this star. The next section discusses our magnetic observations, the third section presents a simple abundance analysis of the star, and the final section discusses the significance of our discovery.

2 Magnetic field measurements

2.1 Field measurements using FORS1

To obtain statistically useful information about the evolution of magnetic fields in UMS stars through their main sequence lives from a survey of magnetic fields in UMS open cluster stars, it is necessary to characterize the fields of at least 30 or 40 magnetic stars of various masses and ages. Since at most a few magnetic stars occur in each cluster, this requires observing stars in some 10 to 20 clusters. The most widely applicable method of detecting fields in UMS stars is by detection of circular polarization in line profiles, either in metallic lines or in the Balmer lines, so we must use a spectropolarimeter that can reach clusters at several hundred pc. This clearly requires a large telescope. We have shown (Bagnulo et al. 2002, 2003) that the combination of the FORS1 multi-object spectropolarimeter on the ESO 8-m VLT telescope Antu, used as a Balmer line Zeeman analyzer, provides the capability needed. With this instrument, we can make usefully precise ( $\sigma \sim$ 50-300 G) field measurements out to distances of well over 1 kpc, thus reaching a sufficiently large volume of space to study stars in some dozens of clusters.

We are currently surveying fields in cluster stars using this instrument. Since fields are generally found in UMS stars that are also chemically peculiar, we are focusing at first on stars that have been identified through previous spectroscopic or photometric surveys for chemical peculiarity. We have chosen candidate stars to observe using spectroscopic surveys such as those of Hartoog (1976) and Abt (1979), and have also relied heavily on the wide-ranging survey for Ap-Bp star in clusters by means of $\Delta a$ photometry that has been carried out by Maitzen and collaborators (e.g. Maitzen & Hensberge 1981; numerous later papers). In addition to observing known Ap-Bp stars, we try to obtain field measurements of a number of other A and B stars in each cluster, in order to see whether - even in very young clusters - all the magnetic stars show obvious chemical peculiarities.

Our observing procedure currently is to obtain spectra of each target star that are analyzed for circular polarization, using FORS1 in polarimetric mode with grism 600B. For isolated stars, we use the instrument in single-slit mode; for cluster regions where several stars of comparable brightness are available, we use the instrument in multi-object mode, placing up to nine slits in the $6.8' \times 6.8'$ FORS1 field of view, so as to observe as many stars as possible at once. The combination of the FORS1 polarimetric mode with the 600B grating enables us to obtain both Stokes I and V/I as function of wavelength in a spectral window that typically extends from below the Balmer jump to beyond H $\beta$ . We thus obtain useful circular polarimetry across six or seven Balmer lines. With a 1'' slit width, GRISM 600B provides a resolution of about 780. For NGC 2244-334 (as for most of our targets) we used a 0.5''slit width (thus reaching a resolving power of about 1500).

In the polarimetric mode of FORS1, starlight passes through a quarter-wave plate followed by a linearly polarizing beam-splitter (Wollaston prism) with principal axes at $45^\circ$ to those of the wave plate, producing two parallel spectra from each observing slit on the CCD detector, one in right and one in left circularly polarized light. (Which of the two spectra from a given slit is right circularly polarized, and which is left, depends on the orientation of the wave plate, and can be reversed by changing between wave plate orientations of $+45^\circ$ and $-45^\circ$ .) These spectra are obtained from the raw data using standard data reduction procedures, with bias subtraction, and wavelength calibration of each pair of spectra (but with no flat-field correction). In the ideal case, the Stokes I spectrum is obtained by adding these two spectra, and the Stokes V spectrum is the difference between them.

However, two principal systematic errors must be considered in obtaining Stokes V as a difference of the spectra observed in opposite senses of circular polarization. First, differences in transmission between the two beams from a given slit would lead to spurious non-zero values of continuum circular polarization. Secondly, possible systematic errors can arise from errors in the implicitly assumed or calibrated wavelength scale of each of the two analyzed spectra; if an error is present, the line profiles in the two spectra will not be precisely aligned even for a completely non-magnetic (unpolarized) spectrum, leading to spurious polarization signals in every line.

Actually, the small errors due both to an imperfect flat-fielding, and to the wavelength calibrations of the two polarized spectra, lead to spurious polarization that changes sign as the wave plate is rotated. Thus both problems described above can be minimized by rotating the retarder wave-plate, and obtaining Stokes V through

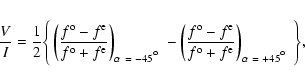
$\begin{eqnarray*}\frac{V}{I} = \frac{1}{2} \Bigg\{ \left(\frac{\ensuremath{f^{{\... ...th{f^{{\rm e}}} }\right)_{\alpha~=~+45\hbox{$^\circ$ }} \Bigg\}, \end{eqnarray*}$

We have also carried out these reductions using ratios of fluxes in the ordinary and extraordinary beams, as described by Donati et al. (1997). The results are very similar to those found with the method described here. A comparison of these two methods will be discussed in a future paper.

In practice, several exposures are taken following to the sequence $\alpha = +45\hbox{$^\circ$ }$ , $-45\hbox{$^\circ$ }$ , $-45\hbox{$^\circ$ }$ , $+45\hbox{$^\circ$ }$ , $+45\hbox{$^\circ$ }$ , $-45\hbox{$^\circ$ }$ , $-45\hbox{$^\circ$ }$ , $+45\hbox{$^\circ$ }$ , where $\alpha$ indicates the orientation of the retarder wave-plate. Stokes V and I profiles are obtained by averaging the individual exposures of a series of four.

An estimate of the noise in the spectrum can be obtained by averaging the spectra in such a way that half have the signs of V reversed, so that any real V signal is cancelled out; the remaining scatter of the signal around 0, which Donati et al. (1997) call the N spectrum, gives a measure of the actual noise of the data. Comparison of the V/I and N spectra provides a visual measure of the S/N ratio of the polarization data.

Field detection is achieved by measuring the circular polarization (of the order of 0.1%) of opposite sign induced in the two wings of each Balmer line by the Zeeman effect. The circular polarization in a spectral line due to the longitudinal Zeeman effect has been discussed by several authors (for a recent review, see Mathys 1989). It has been shown (e.g. Landstreet 1982) that the observed circular polarization in a broad line such as a Balmer line is related to the line-strength weighted mean longitudinal field approximately by

$\begin{displaymath}% \frac{V}{I} = - g_{{\rm eff}} \ \ensuremath{C_z}\ \lambda^{... ...{I} \ \frac{{\rm d}I}{{\rm d}\lambda} \ \langle B_z \rangle, \end{displaymath}$

(1)

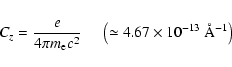
$\begin{eqnarray*}\ensuremath{C_z} = \frac{e}{4 \pi m_{\rm e} c^2} \ \ \ \ \ \left(\simeq 4.67 \times 10^{-13}~{\rm\AA}^{-1}\right) \end{eqnarray*}$

Using this relation, we have adopted the simple strategy of computing for each point in the spectrum the value of V/I and of $({\rm d}I/{\rm d}\lambda )/I$ , plotting one against the other, and solving for the slope of the fitted line, which yields an approximate value of $\langle B_z \rangle$ . The uncertainty in the slope provides one estimate of the uncertainty of the field measurement. This field measurement technique has been shown to be both accurate and efficient by test measurements of the known magnetic star HD 94660 (Bagnulo et al. 2002), by the first large field discovered in a cluster Ap-Bp star (HD 66318 in NGC 2516; see Bagnulo et al. 2003) as a result of this project, and by numerous nulls observed for normal A and B stars not expected to exhibit detectable fields.

2.2 Field measurement of NGC 2244-334

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{0283fig1.ps}\end{figure}$

Figure 1: The reduced FORS1 I ( top), V ( middle), and N ( bottom, moved downward by 1% for clarity) spectra of NGC 2244-334. The Si II lines at $\lambda \lambda$ 4128-4130 are visible, and the numerous Fe II lines around 5200 Å that contribute to the absorption detected by Maitzen's $\Delta a$ photometry are prominent. A strong Zeeman signature is also seen in the three very strong lines of multiplet 42 of Fe II at 4923, 5018 and 5169 Å.

Open with DEXTER

NGC 2244-334 was included in our cluster sample because of the discovery by Hensberge et al. (1998), using synthetic $\Delta a$ photometry, that this star is a strongly peculiar Ap-Bp member of the very young open cluster NGC 2244. The open cluster NGC 2244 is estimated to be less than $3 \times 10^6$ yr old (Hensberge et al. 2000), and is one of the youngest open clusters known. Thus NGC 2244-334 is one of the youngest Ap-Bp stars so far identified. In view of the conflicting results described in Sect. 1, it seemed worthwhile to observe this extremely young star in spite of its faintness (V = 12.88, Ogura & Ishida 1981), which led us to spend almost three hours of 8-m telescope time (out of a total allocation of two nights) obtaining a polarized spectrum of the star.

A FORS1 polarized spectrum of NGC 2244-334 was obtained on 8/9 Feb. 2003, with mid-exposure at JD 2452679.662. The total observation lasted 2.8 h. When these data were reduced, we found that the star exhibited the enormous longitudinal field strength of $\langle B_z \rangle = -9.0 \pm 0.2$ kG. This is the second strongest $\langle B_z \rangle$ value ever found in an UMS star. It is exceeded only by the longitudinal field of 12-22 kG measured in HD 215441 = Babcock's star (Borra & Landstreet 1978), and is slightly larger than the largest value of $\langle B_z \rangle$ observed in HD 178892, which reaches $\langle B_z \rangle \approx 8.5$ kG (El'Kin et al. 2003).

Figure 1 shows the Stokes I and Stokes V spectra of NGC 2244-334, as well as the N (noise level) spectrum produced by averaging the V spectra in such a way as to cancel out the real magnetic signal. The I spectrum reveals a star which might be classified as a peculiar late B star: the stellar Ca II line $\lambda 3933$ is narrow and weak enough to be largely masked by the interstellar line, but the He I lines expected for a B star are not seen. The spectrum shows fairly strong lines of Si II at $\lambda \lambda 3853 {-} 3862$ and 4128-4130 and numerous lines of Fe II longward of H $\beta$ . The V spectrum below shows the very strong circular polarization at each of the Balmer lines, changing sign across each line and close to 1% in amplitude (which indicates a $\langle B_z \rangle$ value of order 10⁴ G). There are also many weaker but very suggestive Zeeman signatures that coincide with the stronger metallic lines, especially the Fe II lines beyond H $\beta$ . The reality of the Zeeman signatures seen in the V spectrum is confirmed by the N spectrum at the bottom of the figure, which shows the level of noise in the V spectrum; many of the features in the V spectrum are several times larger than the typical noise level.

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{0283fig2.ps}\end{figure}$	Figure 2: The correlation diagram of V/I versus $({\rm d}I/{\rm d}\lambda )/I$ , from which the value of $\langle B_z \rangle$ is deduced. The points in this diagram are obtained only from the wings of the Balmer lines, using a window that corresponds roughly to the observed width of each line. The windows used range in (full) width from about 50 Å at H $\beta$ to 25 Å at H11 (3770 Å).
Open with DEXTER

The V/I versus ${\rm d}I/{\rm d}\lambda$ figure is shown in Fig. 2. This figure confirms the strong correlation of V with ${\rm d}I/{\rm d}\lambda$ and is the basis for determination of $\langle B_z \rangle$ . An alternative view of these data is shown in Fig. 3, where the observed circular polarization spectrum in several Balmer lines is compared to the spectrum of ${\rm d}I/{\rm d}\lambda$ scaled by the factor corresponding to our deduced field strength.

3 Spectrum of NGC 2244-334

The enormous field detected in NGC 2244-334 prompted us to apply for Director's Discretionary Time to obtain a high-resolution ( R = 40 000) spectrum of the star with the UVES spectrograph on the VLT telescope Kueyen. A spectrum was obtained on 8 March 2003 with mid-exposure at JD 2452706.587. The spectrum covers virtually the complete wavelength window between 3200 Å and 1.04 $\mu$ m. The signal-to-noise ratio varies considerably over the spectrum, from a low of about 10 at the shortest wavelength to a high of a little more than 100 from H $\delta$ to H $\alpha$ . The spectrum is useful for modelling between about 3400 and 8000 Å, where the SNR is at least about 30.

The spectrum shows a rich variety of light element (C, O, Mg, Si) and iron peak (Ti, Cr, Mn, Fe) lines, as well as strong interstellar Na I and Ca II lines. As noted above, the H lines are quite strong, but even the strongest He lines ( $\lambda \lambda$ 4026, 4471, 5876) are only marginally detectable. All lines are rather broad, indicating a projected rotational velocity $v \sin i \approx 50$ km s^-1.

To model the spectrum and obtain information on abundances, we need to determine the effective temperature $T_{\rm e}$ and the gravity $\log g$ . From the observed UBV colours and estimated E(B-V) (Ogura & Ishida 1981), and the value of E(U-B)/E(B-V) = 0.72 provided by Massey et al. (1995), we find the intrinsic colours of NGC 2244-334 to be approximately (B-V)₀ = -0.10 and (U-B)₀ = -0.61. There is no calibration of UBV colours versus $T_{\rm e}$ available for Ap-Bp stars for this colour range, but we may estimate the value of $T_{\rm e}$ by comparison with effective temperatures determined for Bp stars of similar UBV colours by Hauck & North (1993; HD 34452, HD 92664, HD 175362, HD 142301) and by Stepien (1994; HD 34452, HD 92664, HD 175362). From these comparisons, we estimate that the temperature of NGC 2244-334 is $T_{\rm e} = 15~000$ $\pm$ 1000 K.

$\begin{figure} \par\includegraphics[width=13.6cm,clip]{0283fig3.ps}\end{figure}$	Figure 3: This figure shows the unscaled I FORS1 spectrum of NGC 2244-334 (dotted), the observed V/I spectrum (error bars), and the ${\rm d}I/{\rm d}\lambda$ spectrum derived from the I spectrum by numerical differentiation and scaled by the factor appropriate for $\langle B_z \rangle$ = -9 kG (Eq. (1)).
Open with DEXTER

Alternatively, photo-electric photometry of NGC 2244 in the Walraven system by Verschueren (1991) may be used to estimate the temperature. The Walraven system uses five passbands (VBLUW) with effective wavelengths (fwhm in parentheses) of 5441 Å (708 Å), 4298 Å (423 Å), 3837 Å (221 Å), 3623 Å (232 Å) and 3236 Å (157 Å). Verschueren concluded $T_{\rm e} = 16~250$ K, log g = 4.2 from comparison of the reddening-free indices [B-U] and [B-L] with a grid computed from Kurucz models, assuming that the colours are not peculiar. Again comparing with the VBLUW photometry of other hot Bp stars (HD 175362, HD 142301; de Geus et al. 1990), we find #334 to be marginally cooler than these stars, in agreement with the temperature estimate from the UBV colours. Its reddening-corrected visual magnitude is not brighter than the B8V stars in NGC 2244.

We could determine $\log g$ from the Balmer lines, but in the absence of clear experimental evidence that this provides accurate values of $\log g$ for Ap-Bp stars, we believe that we obtain a more accurate estimate of the value of $\log g$ from comparison with stellar models. NGC 2244-334 is a definite member of NGC 2244, so its age is at most a few million years. Comparing our derived value of $T_{\rm e}$ with the models of Schaller et al. (1992), we deduce that the star has a mass of about $4 \pm 0.5~M_\odot$ , and has $\log g = 4.3 \pm 0.1$ .

We have two spectra of NGC 2244-334 taken at different times, but the FORS1 spectrum is of such low resolution that even features that are resolved in the UVES spectrum are often blended together. Comparison of the two spectra shows that most significant features seen in the UVES spectrum are present in the FORS1 spectrum, but the degree of blending in the FORS1 spectrum makes it very hard to achieve the same continuum normalization in the two spectra, so it is very difficult to see if significant spectral variation has occurred between the two spectra. Similarly, modelling of the FORS1 spectrum is found to be quite difficult. Hence we limit our efforts at spectral synthesis to modelling the single UVES spectrum.

With only a single I spectrum available, modelling must be based on numerous simplifying assumptions. We assume that the atmosphere is chemically homogeneous both horizontally and vertically. Because of the strong rotational broadening of spectral lines, we have little information about the magnetic field except from the observed value of $\langle B_z \rangle$ , which of course was not obtained at the same time as the observation with UVES. However, with a measured $\langle B_z \rangle$ value of nearly 10 kG, the field at the surface of the star must be of the order of 20 kG or more, and so will have a very strong effect on the local spectral line profiles. The $\pi$ and $\sigma$ components of optical spectral lines will be separated by roughly 0.2 Å or more, and thus completely resolved. With typical spacings of the order of 0.03 Å, about the same as the thermal width of the local line profile, even the individual Zeeman subcomponents of most spectral lines will be marginally resolved. In strong lines with several $\pi$ and $\sigma$ components, this splitting will have the same effect as a very large microturbulence - the equivalent width of saturated lines will be substantially increased over the values they would have without the field. Thus it is essential to include the effects of the field if derived abundances are to be at all realistic, and to do this a field model must be adopted.

Assuming that the field is very roughly dipolar (and quite arbitrarily adding a small reversed octupole component to reduce the pole-to-equator variation, making the field structure somewhat more uniform than that of a pure dipole), we find that polar values of $B_{\rm d} = -23~000$ and $B_{\rm o} = 5~000$ G provides a strong enough global field to produce a $\langle B_z \rangle$ value of close to -9 kG when the field is seen nearly pole-on. The field strength at the stellar surface may well be larger than the general value provided by this model, but it is unlikely to be much smaller. In fact, since even with this field the Zeeman subcomponents are nearly resolved, the field could be considerably larger without greatly changing the strength of lines. In other words, the field is so large that we do not really need to know about it in detail to incorporate its effects into the abundance analysis with useful accuracy.

We have no information about the actual value of $\langle B_z \rangle$ at the time that UVES spectrum was obtained, but there is marginal evidence in the line profiles (which are slightly more pointed than one would expect from rotation alone) that the field is observed from near the pole. With no more justification than this, but in order to have a definite magnetic model, we take the axis $\beta$ of the field components to make an angle of 80 $^\circ$ to the rotation axis, and the angle i between the line of sight and rotation axis to be 90 $^\circ$ . Although this is certainly not an accurate model of the magnetic field at the time the UVES spectrum was obtained, it at least means that the spectrum synthesis will include the effects of a field of the right order of magnitude.

With these assumptions, we may estimate the abundances of several elements in the atmosphere of NGC 2244-334. We carry out spectrum synthesis with the computer code ZEEMAN.F, described by Landstreet (1988) and Landstreet et al. (1989), which has recently been compared to other codes by Wade et al. (2001). The spectrum of NGC 2244-334 is fairly rich in lines, but these are mostly (except for the Balmer lines) less than 0.1 of the continuum deep because of rotational broadening. Nevertheless, it is possible to identify lines of C II, O I, Mg II, Al II, Si II and III, Ti II, Cr II, Mn II, and Fe II. The strong lines of Ca II are possibly present, blended with deep and wide interstellar lines. Lines of He are not really visible, but on fitting the strongest lines appear to be very weakly present.

Abundances relative to H were determined by fitting a few lines of each element that appear to be relatively unblended and for which gf values seem to be satisfactory. The quality of the derived abundance for a particular element then tested, if possible, on other lines of that element, and also (in the case of the elements Ti, Cr, and Fe, which have many lines throughout the UVES spectrum) by synthesizing several 100 Å long stretches of the spectrum. In general, Landé factors were taken from the VALD compilation; when values were not available there (mostly for light elements such as Si and Al), we used values computed in LS coupling. A Kurucz model atmosphere for $T_{\rm e}$ = 15 000 K and $\log g = 4.3$ , built with normal solar abundances, has been assumed.

From the fits obtained, we find $v \sin i = 50$ $\pm$ 5 km s^-1. The uncertainty is evaluated from the typical line-to-line scatter (due perhaps to patchy element or incorrectly modelled magnetic field distributions). Using the mass and surface gravity deduced above, the stellar radius is found to be about $R = 2.4~R_\odot$ . Combining this with the derived value of $v \sin i$ , we conclude that the rotation period of NGC 2244-334 is less than about 2.4 d. The period is thus likely to be very similar to those of other Bp stars of similar mass; the periods of the four stars mentioned above in connection with determination of $T_{\rm e}$ have periods between 1.45 and 3.67 d.

The radial velocity of NGC 2244-334 at the time the UVES spectrum was obtained was about $v_{\rm r, obs} = + 55$ $\pm$ 2 km s^-1 (again, the uncertainty is evaluated from line-to-line scatter probably caused by the same limitations of the model that lead to variations in measured $v \sin i$ ). When this is corrected to the heliocentric frame of reference, we find $v_{\rm r, helio} = 28$ $\pm$ 2 km s^-1. This is consistent with the mean cluster radial velocity of $33.7 \pm 3$ km s^-1 obtained by Perez (1991).

The abundance of He was determined using the strong He I lines $\lambda \lambda$ 4026, 4471, 4921, and 5876 Å, all of which appear to be weakly present. He is underabundant by about 1.5 dex.

The C abundance is based on the three C II features at $\lambda \lambda$ 3918, 3920 and 4267 Å. All three lines are fairly strong but only the 4267 Å (composed of two strong lines separated by 0.26 Å) appears largely unblended. The strength of these high-excitation lines provides confirmation that the high temperature indicated by the unreddened colours is approximately correct. The abundance of C appears to be close to solar.

Oxygen is only very weakly present. The derived abundance is based on the 7775 Å triplet of O I, which is in a noisy part of the spectrum and less than 0.1 of the continuum deep. O appears to be underabundant compared to the sun by about a factor of two.

The lines of Ne are expected to be too weak to be measured in NGC 2244-334 even if Ne has solar abundance, and none are found.

The only usable line of Mg is the Mg II doublet at 4481 Å. This line provides a good measurement of $v \sin i$ ; a value near 50 km s^-1 fits the observed profile well. Mg appears to be underabundant compared to the sun by about a factor of two.

Many strong lines of Si II are present throughout the spectrum, and the Si III triplet lines at $\lambda \lambda$ 4552, 4567, and 4574 are weakly present in about the expected relative strengths. A subtlety in fitting particularly the Si lines is that some observed features, such as $\lambda \lambda$ 4130 and 4200 Å, are actually blends of two closely spaced Si lines of similar strength. In this case, the equivalent width computed is fairly sensitive to the local field strength, since as the field strength varies the Zeeman subcomponents of the lines overlap in rapidly changing ways. In contrast, as discussed above, single lines have nearly resolved subcomponents and so their equivalent widths vary rather slowly with increasing field strength. Thus we rely on isolated lines as far as possible. It is found that a single abundance does not accurately fit all the lines. Most of the blue lines ( $\lambda \lambda$ 3853, 3856, 3862, and 4128 are reasonably well fit with $\log n_{\rm Si}/ n_{\rm H} = -3.7$ $\pm$ 0.2, but the red lines $\lambda \lambda$ 5979, 6347 and 6371 Å require an abundance of about -3.3. The principal discrepancy, between red and blue lines, may well be an effect due to vertical stratification of Si; the continuous opacity in the atmosphere of NGC 2244-334 is dominated by H bound-free opacity, which increases by roughly a factor of 3 between 4000 and 6000 Å, so that the red lines are formed about one scale height (roughly 600 km) higher in the atmosphere than the blue lines. In any case, it is clear that Si is overabundant by a factor of several over the solar value.

We cannot derive an abundance for Ca as the H and K lines are blended with strong and broad interstellar lines, and the infrared triplet is not present in the UVES spectrum.

Ti has a number of reasonably clean lines in the near UV between 3300 and 3500 Å, and others scattered through the blue between 4290 and 4575 Å. These lines are generally well fit with about 50 times higher abundance than in the sun.

Cr has fairly strong lines in many parts of the spectrum. Lines of numerous multiplets (e.g. 2, 3, 4, 12, 13, 21, 30, 31, 44) are easily identified. Most of these lines are fit reasonably well with Cr overabundant by a factor of nearly 2 dex compared to the solar abundance. In the high signal-to-noise regions of the spectrum there are clear differences between the shapes of the observed Cr lines and those resulting from our model. This is presumably due either to the oversimplified magnetic model, or to surface abundance variations of Cr.

The abundance of Mn may be derived from three reasonably clean UV lines at $\lambda \lambda$ 3442, 3460, and 3474 Å. The abundance found is not accurately determined because of some residual blending, but is about one dex above solar.

Iron is present in strong lines throughout the spectrum, and requires about one dex of overabundance to fit the observed lines. Unlike Cr, the observed and computed line profiles are quite similar in shape.

In spite of careful inspection and modelling, we are unable to securely identify any lines of elements heavier than Fe, such as Sr, Ba, Zr, or any of the rare earths. Synthesis of several hundred Å of spectrum does not reveal a significant population of lines not included in our line list (which essentially contains only lines of elements no heavier than Fe).

Experiments were also carried out to determine what level of overabundance of some of the most commonly observed rare earths could be excluded by our spectra. Abundances of La, Ce, Pr and Nd were increased until the strongest lines of doubly ionized atoms (which are expected to be one of the dominant ion states for all these atoms) were too strong when compared with the observed spectrum. This did not provide evidence of the presence of any of these ions, but allowed us to set approximate overabundance limits (compared to solar abundances) of about +4 dex for La, Ce, and Pr, and about +5 dex for Nd.

$\begin{figure} \par\includegraphics[width=15.8cm,clip]{0283fig4.eps}\end{figure}$

Figure 4: Representative synthesis of three 50-Å regions of the UVES spectrum of NGC 2244-334. The actual spectra are the curves with noise in the continuum; fits are smoother. Note that there is no real evidence for missing lines in the synthesis, although not all the lines are well fit. Identification of dominant contributors to the stronger features is given underneath the spectra. Although the ultraviolet spectral regions have relatively low signal-to-noise ratio, they are still rich in information.

Open with DEXTER

The actual derived abundances are listed in Table 1, together with estimated uncertainties, and with the solar abundances for comparison. In interpreting these values, recall that our model is based on a very rough estimate of the magnetic field configuration, and completely ignores possible lateral and vertical abundance inhomogeneities. Nevertheless, the model indicates clearly that the light elements He, C, O and Mg are either underabundant or approximately normal when compared to solar values, while Si and the iron peak elements Ti, Cr, Mn and Fe are all between about 10 and 100 times overabundant.

Fits to several representative spectral regions with our simple model are displayed in Fig. 4.

4 Discussion

NGC 2244-334 is a secure member of NGC 2244 in which it is seen. Marschall et al. (1982) and Sabogal-Martínez et al. (2001) assign membership probabilities of between 92 and 96% based on proper motions and photometry. Furthermore, our radial velocity measurement from the UVES spectrum is consistent with the cluster radial velocity.

The cluster NGC 2244, embedded in the famous Rosette Nebula, NGC 2237, is extremely young. The most massive star in the cluster is an O4 V (with a mass of about $70~M_\odot$ ), and Massey et al. (1995) estimate the age of the massive stars in this cluster to be 1-3 Myr, which makes it one of the youngest clusters known in the Milky Way. A more precise age has been derived by Hensberge et al. (2000) from a detailed analysis of the eclipsing binary V578 Mon in NGC 2244. They find the binary (and hence the cluster) to have an age of $2.3 \pm 0.2$ Myr. Presumably the age of NGC 2244-334 is very similar to this number (although in such a young cluster a significant spread in ages may occur).

The only Ap-Bp stars known (through membership in young clusters or associations) to have ages comparable to that of NGC 2244-334 are the magnetic stars that have been observed in the Orion OB 1 association (e.g. Landstreet & Borra 1978; Borra 1981; Thompson & Landstreet 1985; Bohlender et al. 1987; Romanyuk et al. 1999; Donati et al. 2002). (HD 92664 has a magnetic field - see Bohlender et al. 1993 - and is a probable member of the young cluster IC 2602, but with an age of at least 10 Myr, this cluster is significantly older than NGC 2244. The magnetic stars in the Sco-Cen association probably also have ages of 10 Myr or more; see Thompson et al. 1987. A current list of known magnetic stars, including proposed cluster membership identifications, has been compiled by Romanyuk & Kudryavtsev, and is available online from http://www.sao.ru/hq/lizm/catalogue)

Some 18 or 19 stars in the Ori OB 1 association are known to have magnetic fields (the Hipparcos parallax of HD 36916 is marginally inconsistent with membership). Almost all these stars are found in subgroups a-c of the association. The only known magnetic star in the youngest subgroup of Ori OB 1d = the Orion Nebula Cluster (ONC) is $\theta^1$ Ori C, an O7 V and the brightest and most massive star in the cluster. With a mass of about $50~M_\odot$ (Hillenbrand 1997), $\theta^1$ Ori C is by far the most massive main sequence magnetic star known, and is substantially more massive than the classical Ap-Bp stars, even including their extension to the massive He-rich stars ( $M \sim 10~M_\odot$ ) with spectral types near B2 V. $\theta^1$ Ori C is somewhat later spectral type, and lower mass, than HD 46150 [O4 V ((f)), about $70~M_\odot$ ) and HD 46223 [O4 V ((f)), about $60~M_\odot$ ; see Massey et al. 1995], the two most massive stars in NGC 2244, which suggests that the ONC is slightly older than NGC 2244. $\theta^1$ Ori C and NCG 2244-334 probably have very similar ages.

The other known magnetic stars in Orion are in parts of the association that have significantly older ages than the ONC (see e.g. Warren & Hesser 1978). The youngest part of Ori OB 1 outside of the ONC is subgroup c, which has an estimated age in the range of 1.6-5.6 Myr. (However the most massive star in this subgroup is a B0 V, significantly lower in mass than the most massive star in either the ONC or NGC 2244, so this subgroup is probably closer to 4 or 5 Myr than 2 Myr in age.) Subgroup c includes the He-rich star HD 37017 and the He-weak stars HD 36540, 36629, 37058, 37210, and 37642 (and possibly HD 36916 if its Hipparcos distance is wrong); these stars are probably slightly older than NGC 2244-334. Of the stars in Ori OB 1c, HD 36629 and 37058 are significantly hotter and more massive than NGC 2244-334, but from its colours HD 37642 should be quite similar in mass to NGC 2244-334. The magnetic stars in subgroups b and a, with ages of about 5 and 8 Myr respectively, are almost certainly somewhat older than NGC 2244-334.

Thus NGC 2244-334 emerges as possibly the very youngest known Ap-Bp star, rivaled only by $\theta^1$ Ori C (which at present is a completely unique star, and is certainly very dissimilar to the classical Ap-Bp stars) and possibly by some of the stars in Ori OB 1c. From the comparison of the age of NGC 2244 with the main sequence lifetime of a star of $4~M_\odot$ , NGC 2244-334 has completed about $2 \pm 1$ % of its main sequence life. Note that although we do not know the rotation period of NGC 2244-334, the value of $v \sin i = 50$ km s^-1 deduced for this star suggests that it rotates several times slower than a typical normal B star. It thus appears to have lost most of its angular momentum before reaching the main sequence phase, as discussed by Stepien (2000).

NGC 2244-334 is more massive than any of the stars in the sample considered by Hubrig et al. (2000), so its extreme youth does not directly contradict their hypothesis that Ap-Bp stars less massive than $3~M_\odot$ begin to show magnetic fields only after about 30% of the main sequence lifetime has elapsed. However, the existence of the huge magnetic field found in NGC 2244-334 clearly confirms that magnetic Bp stars can be detectably magnetic virtually from birth on.

With its unreddened colours near those of a B5 V star, but almost undetectable He lines, NGC 2244-334 would be classified as a He-weak B star. Three types of chemical peculiarities are recognized in such stars, the Si, SrTi and PGa types (Borra et al. 1983). Only the first two types are found to have fields. In NGC 2244-334, two weak features at roughly the wavelengths of the two classification lines of Sr II at $\lambda \lambda$ 4077 and 4215 are apparently due to Cr II, and Ti is also not very prominent visually, although it is substantially overabundant. In contrast, a number of Si II lines are very strong and obvious in the spectrum. It seems likely that NGC 2244-334 would be classified as a He-weak Si star. Thus it conforms to the conclusion of Abt (1979) that Si-type Ap-Bp stars are found in very young clusters. The presence of peculiarities sufficient to lead to large $\Delta a$ values in the Orion magnetic stars, and to the strongly peculiar composition we deduce for NGC 2244-334, confirms that magnetic Bp stars can develop anomalous surface compositions within only a couple Myr of arriving on the main sequence, if not sooner.

We have already noted that NGC 2244-334 has the second largest value of $\langle B_z \rangle$ ever observed in a main sequence star, smaller only than that found in HD 215441 = Babcock's star. It is notable that in other respects the two stars are rather similar. Both have nearly the same effective temperature (the surface gravity of HD 215441 is not known with any accuracy). Abundances have been accurately determined for only a few elements in HD 215441 (see Landstreet et al. 1989) because of the limited spectral coverage available at the time this star was modelled, but - like NGC 2244-334 - HD 215441 exhibits large overabundances of Si, Ti, Cr and Fe.

To summarize, NGC 2244-334 is found to host a huge magnetic field, one of the very largest known, and is an extremely young star, both absolutely and relative to its main sequence lifetime, but otherwise appears to be a fairly typical He-wk Bp Si star.