A&A 416, 391-401 (2004)
DOI: 10.1051/0004-6361:20034619

Automatic detection of arcs and arclets formed by gravitational lensing

F. Lenzen1 - S. Schindler2 - O. Scherzer1


1 - Institute of Computer Science, University of Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria
2 - Institute for Astrophysics, University of Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria

Received 10 July 2003 / Accepted 13 November 2003

Abstract
We present an algorithm developed particularly to detect gravitationally lensed arcs in clusters of galaxies. This algorithm is suited for automated surveys as well as individual arc detections. New methods are used for image smoothing and source detection. The smoothing is performed by so-called anisotropic diffusion, which maintains the shape of the arcs and does not disperse them. The algorithm is much more efficient in detecting arcs than other source finding algorithms and the detection by eye.

Key words: methods: data analysis - techniques: image processing - galaxies: clusters: general - gravitational lensing

1 Introduction

Gravitational lensing has turned out to be a universal tool for very different astrophysical applications. In particular, lensing by massive clusters of galaxies is extremely useful for cosmology. The measurement of various properties of the magnified and distorted images of background galaxies ("arcs and arclets'') provides information on the cluster as well as on the population of faint and distant galaxies. Many of these distant background galaxies (up to redshifts of $z \approx 5$, Franx et al. 1997) could not be studied with the largest telescopes if they were not magnified by the gravitational lensing effect. Some of these distant galaxies are particularly useful for the study of galaxy evolution (Pettini et al. 2000; Seitz et al. 1998). As these background galaxies are free of selection effects, because they lie serendipitously behind massive clusters, they are ideal targets for a population study of distant galaxies (Fort et al. 1997). Gravitationally lensed arcs also provide a way to measure the total mass and the dark matter in clusters (Fort & Mellier 1994; Mellier 1999; Wambsganss 1998). As galaxy clusters can be considered to be fair samples of the universal mass fractions, such determinations probe cosmological parameters like $\Omega_{\rm tot}$, $\Omega_{\rm matter}$, and  $\Omega_{\rm baryon}$. A third, very important application of gravitational lensing in clusters is the determination of the frequency of arcs (=arc statistics). This is a strong criterion in order to distinguish between different cosmological models (Kaufmann & Straumann 2000; Bartelmann et al. 1998). Therefore detections of gravitationally lensed arcs are of high importance for astrophysics and cosmology.

Ideal for cosmological studies are systematic searches. A successful arc search was performed with the X-ray luminous cluster sample of the EMSS (Luppino et al. 1999). More searches are under way, which not only cover larger areas than the previous survey, but they also go much deeper, i.e. fainter galaxies can be detected.

The first arcs were detected only in 1986 (Soucail et al. 1987; Lynds & Petrosian 1986) because they are very faint and very thin structures. Under non-ideal observing conditions (e.g. bad seeing) they are easily dispersed and disappear into the background. Even with ideal conditions they are not easy to detect because they are often just above the background level. In order to remove the noise and make faint structures better visible usually smoothing is applied. Unfortunately in the case of such thin structures as arcs the smoothing procedure often leads to a dispersion of the few photons so that the arcs are difficult to detect at all. To prevent this dispersing we suggest an algorithm that automatically smooths only along the arcs and not perpendicular to them, so-called "anisotropic diffusion''. The subsequently applied source finding procedure extracts all the information from the sources necessary to distinguish arcs from other sources (i.e. edge-on spirals or highly elliptical galaxies). This new algorithm is much more efficient in finding gravitationally lensed arcs than existing source detection algorithms, because it is optimized just for this purpose.

In Sect. 2 the algorithm is explained with its four different steps. In Sect. 3 examples of detected arcs are presented. Section 4 outlines the differences to existing source finding software and the advantages for arc detection. In Sect. 5 we draw conclusions on the applicability and usefulness of the new algorithm.

2 The algorithm

We propose a  four level strategy for numerical detection of arcs in astronomical data sets consisting in the successive realization of

1.
histogram modification;
2.
anisotropic diffusion filtering;
3.
object finding;
4.
selection of arcs.
The algorithm described in detail below has been implemented in the programming language C.

The image data are given by a 2D matrix of intensity values I. For the sake of simplicity of presentation we assume that the intensity matrix is of dimension $N \times N$. The set of indexes

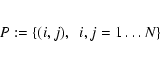
\begin{eqnarray*}P:=\{(i,j),\;~i,j=1\dots N\} \end{eqnarray*}


are referred to as pixels and identify the position of the recorded intensity I(i,j).

   
2.1 Histogram modification

Astronomical image data contain objects on a variety of brightness scales. Frequently stars and galaxies show up relatively bright; arcs however are small elongated objects of only marginally higher intensity than the surrounding background. In order to detect such arcs it is necessary to correct for the dominance of extremely bright objects. This is done by histogram modification. Here, we use a nonlinear transformation

 \begin{displaymath}% \mathcal{S}(x)=\left\{ \begin{array}{cl} 0&\mbox{ if }x<a\\... ...\mbox{ if } x\in [a,b]\\ 1&\mbox{ if } x>b \end{array}\right. \end{displaymath} (1)

which is applied to the pixel intensities I(i,j), giving a new intensity matrix $I^0(i,j)=\mathcal{S}(I(i,j))$. The transformation $\mathcal{S}$ maps the pixel intensity distribution, which originally varied from 0 to the maximum pixel value, onto the interval [0,1] by the use of a bijective transformation s from the interval [0,1] to [0,1].

The interval [a,b] specifies the level of intensities where arcs are to be detected. The lower bound a is considered the intensity value of the background. By analyzing several different astronomical data sets we have learned that a and b have to be chosen relatively close to each other for optimal visualization of arcs (cf. Fig. 1).


  \begin{figure} \par\includegraphics[width=8.8cm]{h4662f1.eps} \end{figure} Figure 1: Distribution of pixel values of an astronomical test image. A typical parameter setting for a and b (low and high cut) is marked in gray. A good choice for parameter a is the maximum of the distribution and can be easily computed, whereas a general optimum for parameter b can not be prescribed. In the considered example a good choice is: a=0 and b=1.
Open with DEXTER

In the interval [a,b] we have to distinguish between noise and real sources such as stars, galaxies and arcs. To ease this separation process we apply nonlinear intensity transformations such as $s(x)= \sqrt{x}$, or alternatively s(x)=x.

Some astronomical data set may contain arcs in different intensity ranges. In this case choosing the value for the parameter b of about the intensity of the brightest arcs is appropriate.

2.2 Anisotropic diffusion filtering

2.2.1 Introduction to diffusion processes

By interpolation the scaled image I0(i,j) can by interpreted as a function in  $\mathbb{R}^2$ and is now denoted by $u^0(x,y),\;(x,y)\in \mathbb{R}^2$.

By applying Gaussian convolution with a kernel $K_t(x,y):=\frac{1}{4\pi t}\exp \left(-\frac{x^2+y^2}{4t} \right)$ depending on t one gets a smoothed image

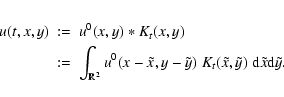
\begin{eqnarray*}u(t,x,y)&:=&u^0(x,y)\ast K_t (x,y)\\ &:=&\int_{\mathbb{R}^2} ... ...y})\;K_t(\tilde{x},\tilde{y})\;{\rm d}\tilde{x}{\rm d}\tilde{y}. \end{eqnarray*}


The parameter t controls the amount of smoothing. A larger value of t corresponds to a higher filtering.

In the following $\partial_t u(t,x,y)$ denotes the first derivative of u with respect to t, $\partial_{xx} u(t,x,y)$ and $\partial_{yy} u(t,x,y)$ the second derivatives with respect to x and y and  $\Delta u(t,x,y):=\partial_{xx} u(t,x,y)+\partial_{yy} u(t,x,y)$ the Laplacian.

It is well known that u(t,x,y) solves the diffusion (resp. heat) equation

 \begin{displaymath}% \partial_t u(t,x,y) -\Delta u(t,x,y)=0 \mbox{ for all } (x,y)\in\mathbb{R}^2 \end{displaymath} (2)

with the initial condition u(0,x,y)=u0(x,y).

To simplify the notation we write $u(t,x),\;x\in\mathbb{R}^2$ instead of u(t,x,y).

Equation (2) can be restricted to a rectangular domain $\Omega\subset \mathbb{R}^2$, the domain of interest, typically the set of pixels where intensity information has been recorded.

In order to achieve existence and uniqueness of the solution  $u(t,x),\;x\in\Omega$ it is necessary to prescribe boundary conditions such as

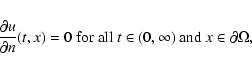
\begin{eqnarray*}\frac{\partial u}{\partial n}(t,x) = 0 \mbox{ for all } t\in(0,\infty) \mbox{ and } x\in\partial\Omega, \end{eqnarray*}


where $\partial \Omega$ denotes the boundary of the domain $\Omega$, n is the outer normal vector on $\partial \Omega$ and $\frac{\partial}{\partial n}$ denotes the derivative in direction of n.

Applying the diffusion process up to a fixed time T>0 smooths the given data u0and spurious noise is filtered. The parameter T defines the strength of the filtering process. Thus in the following we refer to T as the filter parameter.

The disadvantage of Gaussian convolution is that edges in the filtered image u(T,x) are blurred and the allocation and detection of object borders is difficult. To settle this problem several advanced diffusion models have been proposed in the literature (Catte et al. 1992; Weickert 1998).

In the next section we define the general model of a diffusion process and in Sect. 2.2.3 we describe the specific model used in our algorithm.

2.2.2 The general diffusion equation

Anisotropic diffusion filtering consists in solving the time dependent differential equation

 \begin{displaymath}% \partial_t u(t,x) - \mbox{div}\Big(D(x,u,\nabla u)\nabla u(t,x)\Big) =0 \end{displaymath} (3)

up to a certain time T > 0.

Here $D(x,u,\nabla u)$ is the $2~\times~ 2$ diffusion matrix depending on x and u,

We prescribe the same initial and similar boundary conditions as mentioned above. Setting $D(x,u,\nabla u)=1$ results in the heat Eq. (2).

Two classes of anisotropic diffusion models are considered in the literature: if $D(x,u,\nabla u)$ is independent of u and $\nabla u$ then Eq. (3) is called linear anisotropic diffusion filtering, otherwise it is called nonlinear filtering.

For a survey on the topic of diffusion filtering we refer to Weickert (1998).

  
2.2.3 The specific model

In anisotropic models the diffusion matrix D is constructed to reflect the estimated edge structure. That is to prefer smoothing in directions along edges, or in other words edges are preserved or even enhanced and simultaneously spurious noise is filtered.

Consequently this kind of filtering eases a subsequent edge-based object detection.

In the following D will only depend on the gradient $\nabla u$, which reflects the edge structure of the image.

To accomplish the diffusion matrix $D(\nabla u)$ we note that

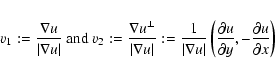
\begin{eqnarray*}v_1:=\frac{\nabla u}{\vert\nabla u\vert} \mbox{ and } v_2:=\f... ...\partial u}{\partial y}, -\frac{\partial u}{\partial x} \right) \end{eqnarray*}


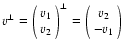denote the directions perpendicular and parallel, respectively, to edges. (By  $v^\bot=\left( \begin{array}{c} v_1\\ v_2\\ \end{array}\right)^\bot =\left( \begin{array}{c} v_2\\ -v_1\\ \end{array}\right) $ we denote the vector perpendicular to v.)

By selecting

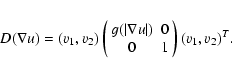
\begin{eqnarray*}D(\nabla u) = (v_1,v_2) \left(\begin{array}{cc} g(\vert\nabla u\vert) & 0\\ 0 & 1 \end{array} \right) (v_1,v_2)^T. \end{eqnarray*}


with

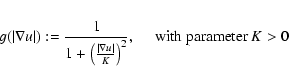
\begin{eqnarray*}g(\vert\nabla u\vert):=\frac{1}{1+\left(\frac{\vert\nabla u\vert}{K}\right)^2}, \quad \mbox{ with parameter }K>0 \end{eqnarray*}


the diffusion filtering method (3) prefers filtering parallel to edges.

Figure 3 highlights the diffusion directions: arrows indicate the main directions of diffusion (v1,v2) and their thickness relates to the diffusion coefficient determining the strength of diffusion. Parallel to the edge the diffusion coefficient is constantly 1 (strong diffusion), where as the diffusion coefficient  $g(\vert\nabla u\vert)$ in normal direction decreases rapidly (cf. Fig. 2) as $\vert\nabla u\vert$ increases (weak diffusion on edges).

The dependence of $g(\vert\nabla u\vert)$ on $\vert\nabla u\vert$ is controlled by parameter K (cf. Fig. 2). We therefore refer to K as the edge sensitivity parameter.

We use the following common variation of the diffusion matrix D:

To limit the effect of noise the diffusion tensor is chosen to be dependent on the pre-smoothed image $u_\sigma(t,x)=u(t,x)\ast K_\sigma$obtained by Gaussian convolution with pre-filter parameter $\sigma>0$. In the following to determine the diffusion matrix we exploit the gradient of the pre-filtered image  $u_\sigma(T,.)$ instead of u(T,.).

Let $v_1^\mu,v_2^\mu$ be the eigenvalues of the filtered structure tensor

\begin{eqnarray*}J_\mu(x):=\left(K_\mu * \left[\left(\nabla u_\sigma\right) \left(\nabla u_\sigma\right)^T\right]\right)(x). \end{eqnarray*}


We refer to $\mu\ge 0$ as the pre-filter parameter for the structure tensor.

Note that in the case $\mu=0$ the eigenvectors of J0 are $\frac{\nabla u_\sigma}{\vert\nabla u_\sigma\vert}$ and $\frac{\nabla u_\sigma^\bot}{\vert\nabla u_\sigma\vert}$. If $\sigma$ and $\mu$ are small, the effect of Gaussian filtering is negligible, and consequently $v_1^\mu,v_2^\mu$and v1,v2 refer to similar edge structures.

The purpose of filtering of the structure tensor is to average information about edges in the image.

Taking into account the approximation we are led to the following diffusion matrix

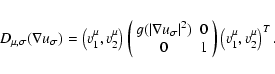
\begin{eqnarray*}D_{\mu,\sigma}(\nabla u_\sigma) = \left(v_1^\mu,v_2^\mu\right) ... ...0\\ 0 & 1 \end{array} \right) \left(v_1^\mu,v_2^\mu\right)^T. \end{eqnarray*}


Besides the fact that $D_{\mu,\sigma}(\nabla u_\sigma)$ is less noise sensitive there are several advantages of using the approximation $D_{\mu,\sigma}(\nabla u_\sigma)$ instead of  $D(\nabla u)$:
1.
The numerical calculation of $D(\nabla u)$ is unstable; if $\mu$ and $\sigma$ are chosen appropriately $D_{\mu,\sigma}(\nabla u_\sigma)$ can be determined in a stable way;
2.
For our particular application, in a neighborhood of arcs the vector field $v_2^\mu$ is nearly parallel to the arcs. Thus filtering is performed in arc orientation enhancing the geometrical structure of arcs. A side effect which is very useful for our particular application is that small gaps between elongated structures are closed, merging nearby objects.
This is the anisotropic diffusion filtering method used in our numerical calculations.


  \begin{figure} \par\includegraphics[width=7.3cm,clip]{h4662f2.eps} \end{figure} Figure 2: Graph plot of function g(x) used for weakening the diffusion orthogonal to edges to archive edge enhancing. For parameter K values K=0.1 resp. K=0.001 are used.
Open with DEXTER

In order to solve the differential Eq. (3) it is discretized using a finite element method in space and an implicit Euler method in time. (Within the finite element method the width of the quadratic elements is set to 1.) For each time step the resulting system of linear equations is solved by a conjugate gradient method. For a survey on solving parabolic differential equations with finite element methods we refer to Thomee (1984). The conjugate gradient method is discussed in Hanke-Bourgeois (1995,2002).

Anisotropic diffusion filtering requires to select parameters  $T,K,\sigma$ and $\mu$.


  \begin{figure} \par\includegraphics[width=5.15cm,clip]{h4662f3.eps} \end{figure} Figure 3: Diffusion (smoothing) near edges: the thickness of the arrows indicate the strength of diffusion. Parallel to the edge a strong diffusion occurs whereas in orthogonal direction a weak diffusion leads to an enhancing of the edge. Due to the averaging of the structure tensor these directions are also determine the diffusion in a surrounding area of the edge and in particular at the vertices yielding a diffusion mainly parallel to the direction of elongation.
Open with DEXTER

2.3 Object finding

In this section we discuss a partitioning algorithm to separate different image data, i.e. disjoint subsets of connected objects and background (partitions). The algorithm uses only the anisotropic diffusion filtered data $u(\cdot):=u(T,\cdot)$and not the initial data u0.

In order to save computational effort we restrict our attention to segment objects of interest, i.e. isolated objects exceeding a certain brightness. We search for local intensity maxima exceeding a certain intensity  $c_{\rm min}$ (referred to as the intensity threshold for detection).

Each maximum serves as seed for the partitioning algorithm: starting from the seed pixel the region to which this pixel belongs has to be determined.

To outline this concept we use the following notation. For a given pixel  $p =(i,j)\in P$ we denote by N(p)the set of the eight neighboring pixels.

The neighborhood of a set $R \subseteq P$ is the set

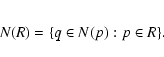
\begin{eqnarray*}N(R)=\{q \in N(p) : p \in R\}. \end{eqnarray*}


For two pixels $p,q\in P$ a path connecting p to q is any sequence $(p=p_0,p_1,p_2,\dots p_n=q)$ satisfying $p_i \in N(p_{i-1})$, $i=1\dots n$.

The partitioning algorithm consists of two loops.

1.
Set j=0 and P0:=P for initialization;
2.
 Update $j \to j+1$.

A pixel p $\in$ Pj-1 is selected where the intensity of the filtered image u(p) attains a local maximum exceeding the intensity threshold for detection: $u(p)>c_{\rm min}>0$.
A numerical procedure for detection of local maxima is described in Sect. 2.3.2.

If no such pixel can be found the algorithm is terminated and Pj-1 is called "background'';

3.
  The second step is a region growing algorithm.
(a)
It is initialized with i = 0, the seed p0:=p and the region $R_0:=\{p_0\}$. For p0 a threshold parameter $c_{\rm thres}>0$ is selected, which is used to terminate the region growing algorithm. The determination of this parameter is explained in Sect. 2.3.1;
(b)
Update $i \to i+1$.

Ri consists of Ri-1 and the neighboring pixels $N(R_{i-1})\cap P_{j-1}$ satisfying that

  • the according intensity exceeds ${c_{{\rm thres}}}$ and
  • the intensity is smaller than the intensities of neighboring pixels in Ri-1.
(c)
The iteration is terminated when Ri+1 = Ri and we denote R(p0) := R(i). This region corresponds to an object.
4.
Updating $P_{j}= P_{j-1} \backslash R(p_0)$ and repeating steps 2 and 3, completely determines the algorithm.


  \begin{figure} \par\includegraphics[width=6cm,clip]{h4662f4.eps} \end{figure} Figure 4: Segmentation of an elliptical object (the theoretical object boundary is indicated by the black ellipse, gray squares indicate pixels with high intensities / white squares indicate pixels with low intensities): Assuming that the region growing starts with the pixel numbered by zero the neighboring pixels with numbers 1 to 7 are successively added to the region until the intensities of the next pixels to be added (here: white colored ) fall below a certain threshold intensity.
Open with DEXTER

Figure 4 illustrates the process of region growing for an elliptical objects.

A detailed overview over segmentation methods is given in Rosenfeld & Kak (1993) or Soille (2003).

In the following we describe numerical procedures for calculation of local maxima and the determination of  ${c_{{\rm thres}}}$ in the object finding algorithm.

   
2.3.1 Determination of ${c_{{\rm thres}}}$

Let p0 be a local maximum within an arc, which is used as an initialization for the region growing algorithm. The anisotropic diffusion filtering method calculates the two eigenvalues $v_1^\mu$ and $v_2^\mu$ of the structure tensor $J_\mu$. Thinking of an arc as an elliptically shaped region $v_1^\mu$ and $v_2^\mu$ approximate the axes of the ellipse. $v_1^\mu$, $v_2^\mu$ denote the principal, respectively cross-sectional axis. Let  $u_{-n},u_{-n+1},\dots u_0,\dots u_n$ be the intensities along the cross-sectional axes. Figure 5 shows such a typical intensity distribution along a cross-sectional axes of an object. The points on the cross sectional axis with maximal gradient are natural candidates for object boundaries. In the discrete setting these points are

\begin{eqnarray*}&& j^-=\arg \max_{i=-1\dots -n}\{\vert u_{i}-u_{i+1}\vert\},\\ && j^+=\arg \max_{i=1\dots n}\{\vert u_{i}-u_{i-1}\vert\}. \end{eqnarray*}


As threshold intensity for the region growing algorithm we choose:

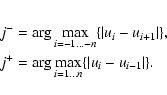
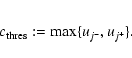
\begin{eqnarray*}c_{\rm thres}:=\max\{{u_{j^-},u_{j^+}}\}. \end{eqnarray*}


   
2.3.2 Detection of local maxima

For the detection of local maxima which exceed the intensity threshold for detection, $c_{\rm min}$, we proceed in a similar way as in the implementation of watershed algorithms (cf. Stoev 2000). The strategy for finding a local maximum is to choose an initial pixel p and to look for a pixel q neighboring to p with higher intensity and then with $p\leftarrow q$ reinitialized to proceed iteratively until a local maximum is reached.


  \begin{figure} \par\includegraphics[width=8cm,clip]{h4662f5.eps} \end{figure} Figure 5: Typical intensity distribution along a cross-section through an object.
Open with DEXTER

Applying this procedure we have to deal with the case, that a local maximum may not be a single pixel but a connected set of pixels with the same intensity (a plateau). In the sequel, for simplicity of presentation, we also refer to a single pixel as a plateau.

Taking this into account we use the following procedure.

We use markers (+), (-), and (0) to denote if a pixel is a local maximum, not a local maximum, or if it is not yet considered in the algorithm, respectively. Initially every pixel is marked by (0).

1.
Search for a pixel p marked with (0). If no such pixel exists, the algorithm is terminated.
If the intensity u(p) lies below $c_{\rm min}$ mark p with (-) and repeat this step with another pixel;
2.
Start segmentation of the plateau including pixel p by applying a region-growing algorithm. During this process we monitor the following occurrences:
(a)
A pixel q neighboring the plateau is found with u(q) > u(p): Mark the pixels of the plateau with (-), set p = q and repeat step 2;
(b)
A pixel of the plateau is found which is already marked with (-): Mark the pixels of the plateau with (-) and go to step 1;
(c)
All neighboring pixels of the plateau have less intensity: Mark the pixels of the plateau with (+) and go to step 1.

After finding a local maximal plateau we choose one pixel of the plateau as seed for the later object detection.

Note that the identification of local maximal plateaus can not be carried out by investigating the first and second derivatives of the intensity function.

Threshold $c_{\rm min}$ correlates to the parameters a and b. The latter should be chosen such that a is about the background intensity and b is about the intensity of the arcs to be detected. As the arc intensities are only very little higher than the noise amplitude, $c_{\rm min}$ serves as a threshold between the noise level and arcs intensity range and is of high importance for the object detection.

Choosing $c_{\rm min} \approx 0$ guarantees detection of most objects but many of them may result from noise amplification. On the other hand a choice $c_{\rm min}\approx 1$ real arcs with intensity below  $c_{\rm min}$are obviously not detected.

2.4 Selection of arc candidates

   
2.4.1 Selection of source candidates

Due to blurring effects on the CCD, in a neighborhood of bright stars and galaxies, the background shows up bright, amplifying the intensity of the noise. In these regions several local intensity maxima above the threshold  $c_{\rm min}$ occur and regions are detected, which clearly are artificial and belong to the background. Such regions are singled out by a comparison of the mean intensities along a cross section within an object and the background. To this end let

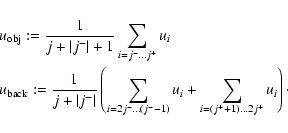
\begin{eqnarray*}&& u_{\rm obj}:=\frac{1}{j+\vert j^-\vert+1}\sum_{i=j^-\dots j^... ...j^-\dots (j^--1)} u_i+\sum_{i=(j^++1)\dots 2j^+} u_i\right)\cdot \end{eqnarray*}


The artificial objects (e.g. resulting from the diffusion filtering of noise) satisfy the condition that $u_{\rm obj}-u_{\rm back}$ is small. Consequently we further restrict our attention to objects satisfying

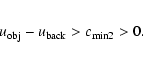
\begin{eqnarray*}u_{\rm obj}-u_{\rm back}>c_{\rm min2} > 0. \end{eqnarray*}


The parameter $c_{\rm min2}$ denotes the minimal difference of the objects intensity from the background. We refer to it as the parameter of minimal intensity difference from background.

By taking into account only pixels with indices between 2j- and 2j+, $u_{\rm back}$ averages the intensities in a small neighborhood of the object.

We assume that the object is isolated, i.e. that there are no other objects in this neighborhood and  $u_{\rm back}$ reflects the local average background intensity.

   
2.4.2 Selection of arcs

The last step of our algorithm consists in selecting arcs from the detected objects. For deriving the following features of the objects the image resulting from applying the histogram modification is used.

Let R be an object, consisting of the set of pixels

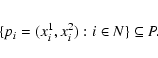
\begin{eqnarray*}\{ p_i=(x^1_i,x^2_i) : i\in N\} \subseteq P. \end{eqnarray*}


The light intensity of such an object can be interpreted as mass resp. density and thus regarding the object as an rigid body we define the total intensity

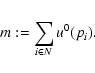
\begin{eqnarray*}m:=\sum_{i\in N} u^0(p_i). \end{eqnarray*}


The object's center is given by

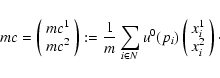
\begin{eqnarray*}mc=\left( \begin{array}{c} mc^1\\ mc^2 \end{array}\right) :=\f... ...i)\left( \begin{array}{c} x^1_i\\ x^2_i \end{array}\right)\cdot \end{eqnarray*}


We define the 2nd moment M as the $2 \times 2$ matrix with components

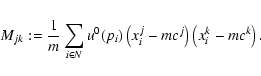
\begin{eqnarray*}M_{jk}:=\frac{1}{m} \sum_{i\in N} u^0(p_i) \left(x_i^j-mc^j\right)\left(x_i^k-mc^k\right). \end{eqnarray*}


The eigenvalues $\lambda_1 \geq \lambda_2$ of M indicate the length and the thickness of the object.

The eccentricity of R

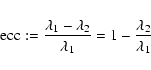
\begin{eqnarray*}{\rm ecc}:=\frac{\lambda_1-\lambda_2}{\lambda_1}=1-\frac{\lambda_2}{\lambda_1} \end{eqnarray*}


is a measure of elongation of R (Jähne 2002). We identify arcs as thin and elongated objects, which in mathematical terms requires that

\begin{eqnarray*}{\rm ecc} \geq c_{\rm ecc}\in[0,1] \mbox{ and } \lambda_2 \leq c_{\rm thick}. \end{eqnarray*}


For given thresholds $c_{\rm ecc}$ (eccentricity threshold and  $c_{\rm thick}$ (thickness threshold).

The detection and selection of arcs is controlled by the three parameters  $c_{\rm min2}$, $c_{\rm ecc}$ and  $c_{\rm thick}$:

It has to be taken into account, that an object may contain several local maxima and the region growing procedure detects adjacent parts of this object. These parts can be merged into one object after the selection process easily. Note that our sequence of selection and merging prevents objects of different shape from being merged.

In most cases the criteria described above are sufficient to detect arcs. The selection process can be refined by incorporating a priori information, like for instance information on the center of mass of a gravitational lens (galaxy cluster). For a spherically symmetric ideal gravitational lens with center gc=(gc1,gc2), the arcs occur tangentially around the center. Let mc denote the center of mass of an arc. Then the vectors p=mc-gc (position relative to center) and $v_2^\mu$ (approx. direction of elongation) have to be orthogonal, giving an additional selection criterion for arcs. However, note that user interaction is required to incorporate a priori information on the position of the gravitational lens.

The algorithm might be also used for detection of strings, if additional post-processing steps are applied using alternative selection criteria which take into account alignment information (instead of shape information as above).

3 Results

3.1 Quality of detections

The quality of the results provided by our algorithm depends mostly on noise variance present in the data.

Arcs may not be detected (false negative detection) by the algorithm if their intensity is within the scale of the noise. As we have seen in Sect. 2.1 the intensity range of the arcs is in general close to the background intensity. The choice of parameter  $c_{\rm min}$ determines whether a weak structure is interpreted as background noise (ignored) or is segmented (feasible local maxima). Corresponding the choice of a high value for  $c_{\rm min}$ increases the risk of a false negative detection.

Another case leading to a false negative detection is the joining of close-by objects.

A false positive detection may occur if the noise level exceeds the intensity  $c_{\rm min}$. In such case the edge enhancing anisotropic diffusion may recover structures present in the noise, which may be segmented as elongated objects afterwards. Thus the choice of a low value for  $c_{\rm min}$ increases the risk of a false positive detection.

In the neighborhood of bright sources the background intensity increases and the noise may lead to several local maxima above  $c_{\rm min}$. As a result the risk of a false positive detection increases in these areas. To reduce these kinds of false positive detections we utilize the parameter  $c_{\rm min2}$ prescribing the minimal intensity difference of a detection in comparison with its surrounding. Again the quality of detection depends on the adaption of  $c_{\rm min2}$ to the noise variance.

3.2 Test images

To highlight the properties of our algorithm we applied the algorithm to three astronomical test images. The first data set is an image of size 2285 $\times $ 2388 pixels with intensity range [-8.49,700.49], the second and third are of size 2048 $\times $ 2048 pixels with intensity ranges [0,19559.8] and  [0,9314.26], respectively. We plotted in Fig. 1 the histogram of the first data set, the histograms of the second and third test image look similar.

Figures 6-8 show galaxy clusters with gravitationally lensed arcs, which have been treated with histogram transformation; we have used $s(x)= \sqrt{x}$ and  (a,b)=(0,1), (149,200) and (141,170), respectively. The histogram modification is already useful to visualize arcs.


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{h4662f6.eps} \end{figure} Figure 6: Detail of a VLT observation of the galaxy cluster RX J1347-1145 (from Miralles et al., in prep.). The image has a size of 2285 $\times $ 2388 pixels. This is the first test image.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{h4662f7.eps} \end{figure} Figure 7: Detail of an HST observation of the galaxy cluster A1689. The image has a size of 2048 $\times $ 2048 pixels. This is the second test image.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{h4662f8.eps} \end{figure} Figure 8: Detail of an HST observation of the galaxy cluster A1689. The image has a size of 2048 $\times $ 2048 pixels. This is the third test image.
Open with DEXTER

3.3 Computational effort

Figure 9 shows the computation time[*] for anisotropic diffusion filtering, object finding (including the search for local maxima, segmentation and selection) and the total computational time in dependence of the size of the image data (number of pixels) in typical astronomical data sets.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{h4662f9.eps} \end{figure} Figure 9: Computation time versus image size for the different steps of the algorithm.
Open with DEXTER

Numerically, the pre-filtering step is most expensive as a large system of linear equations has to be solved. The number of iterations performed by the conjugate gradient solver increases slowly with growing data size. Thus the computational effort is approximately linearly correlated to the number of pixels (cf. Fig. 9).

During the detection of local maxima each pixel is invoked a fix number of times:

1.
to check if it is already marked;
2.
to check if it has to be included into a plateau during the region growing process (once for each of its eight neighbors);
3.
to mark it as being (or not being) a local maximum.
Therefore the computational effort for detecting the local maxima is linearly depending on the number of pixels. As the segmented area is small in comparison with the image size, the effort for object finding strongly depends on the number of objects resp. local maxima. The same holds for the selection process.

Overall the total computation effort grows linearly with the image size (cf. Fig. 9).

3.4 Anisotropic diffusion filtering

Figure 10 shows the result of the anisotropic diffusion filtering for the first test data set.

  \begin{figure} \par\includegraphics[width=8.15cm,clip]{h4662f10.eps} \end{figure} Figure 10: Image of the cluster RX J1347-1145 with anisotropic diffusion filtering applied. Compared to the unsmoothed image in Fig. 6 the noise is considerably reduced. Parameter setting for the filtering: filter parameter T=15, edge sensitivity K=0.0001, pre-filter parameter $\sigma =2$ and pre-filter parameter for structure tensor $\mu =9$.
Open with DEXTER

To examine the effect of enhancing elongated structures we zoom in the filtered image. Figure 11 shows the histogram modified image, i.e. the cuts of the image are set to the steep region of the distribution of the pixel values (top), the Gaussian filtered image (middle) and the image filtered with anisotropic diffusion (bottom). Both filters were applied separately to the histogram modified image.


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{h4662f11.eps} \end{figure} Figure 11: Zoom of Fig. 6. Top: histogram modified data, middle: Gaussian filtered image (Kernel $K_\sigma $with $\sigma =5$), bottom: image filtered with anisotropic diffusion with the parameters: filter parameter T=15, edge sensitivity K=0.0001, pre-filter parameter $\sigma =2$ and pre-filter parameter for structure tensor $\mu =9$. In the Gaussian filtered image (middle) the edges are not preserved well, i.e. the arcs get dispersed, while anisotropic diffusion (bottom) maintains the edges and reduces the noise at the same time.
Open with DEXTER

The filter parameters were chosen to remove noise up to nearly the same signal-to-noise ratio[*], which is about 6.1% in the Gaussian filtered image and about 6.3% in the image filtered with anisotropic diffusion.

In comparison to Gaussian convolution, anisotropic filtering is able to preserve accurately the edges of the objects both of high and of weak intensities. Anisotropic diffusion therefore is ideal as preprocessing for object finding based on edge detection.

3.5 Detected objects

In the first test image (Fig. 6) after applying the histogram modification about four arcs can be recognized at first glance. These arcs are grouped around a center of the cluster of galaxies, which appears in the middle of the image.

In Fig. 12 shows selected objects with thickness  $\lambda_2\le 16$ and eccentricity  ${\rm ecc} \ge 0.7$. The eccentricity is color coded: green, yellow, and red corresponds to an eccentricity in the ranges  [0.7, 0.8], [0.8,0.9] and [0.9,1]. The higher the eccentricity and the smaller the thickness are, the higher is the probability that the detected object is an arc. Incorporating a priori information on the center of the gravitational lens, unreasonable arcs candidates can be filtered out further (Fig. 13). Table 1 lists the coordinates of the detected objects with an eccentricity greater than or equal to 0.84 (referring to Fig. 12). Besides the arcs already mentioned the algorithm detects a significant amount of arc candidates which are not obviously recognizable to the naked eye.

Figures 15 and 16 show the results of our algorithm applied to the second and third test image.


  \begin{figure} \par\includegraphics[width=8cm,clip]{h4662f12.eps} \end{figure} Figure 12: Result of segmentation and selection applied to the first test image - cluster RX J1347-1145. Only the objects which are detected as being arcs with high probability are shown. Settings: intensity threshold for detection $c_{\rm min}=0.1$, minimal intensity difference from background  $c_{\rm min2}=0.1$, eccentricity threshold  $c_{\rm ecc}=0.7$ and thickness threshold  $c_{\rm thick}=16$.
Open with DEXTER

Table 1: List of objects detected in the first data set (cf. Figs. 6 and 12) with eccentricity larger than 0.84, i.e. good arc candidates. Objects with an eccentricity larger than 0.9, i.e. objects 1 to 6 are very good candidates.

Table 2: Parameter settings used for the three test data sets.

4 Comparison with software for source extraction

In this section we compare our algorithm with the software package "SExtractor'' by E. Bertin (Bertin 1994; Bertin & Arnouts 1996). SExtractor is a general purpose astronomical software for the extraction of sources such as stars and galaxies, while our software is particularly designed to extract gravitationally lensed arcs. Although the main areas of applications are rather different, several levels of implementation are similar, although quite different in details: SExtractor uses background estimation which in our program is performed by histogram modification. For Detection, SExtractor used Gaussian convolution filtering; this step relates to the object finding process. Deblending and filtering of deblending are related to our merging strategy described at the second last paragraph of the last section.

To compare both algorithms we single out five specific arcs in the first test image. Figure 14 shows these objects as they are detected by the proposed algorithm (upper row) and as they are segmented by SExtractor (lower row).

Concerning the SExtractor's results a possible adaption of the SExtractor's algorithm for detection of arcs would be to perform a selection process afterwards as described in Sect. 2.4.2. However we did not apply such a selection process to the SExtractor's output. Beside the arcs under investigation several other objects with only small elongations show up when applying SExtractor. To distinguish close-by objects we use two different colors.


  \begin{figure} \par\includegraphics[width=8cm,clip]{h4662f13.eps} \end{figure} Figure 13: Result of segmentation and selection by taking into account a priori information on the center of the gravitational lens. The colors encode the objects eccentricity: [0.7,0.8] - green, [0.8,0.9] - yellow, [0.9,1.0] - red, i.e. the red objects are most likely arcs. The assumed center of the cluster is marked with a red cross.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{h4662f14.eps} \end{figure} Figure 14: To illustrate the features of the new algorithm we compare some specific objects detected by both algorithms, the proposed algorithm (first row) and the segmentation by SExtractor (second row). The images of each column show the same part of the image. The pixels detected by the according algorithm as belonging to the arc are plotted in red. In order to distinguish between close-by objects we use green color in addition. In Cols. 1 and 4 SExtractor has connected pixels to the arc which do actually come from various other sources. Therefore the arc may not satisfy the required elongation and hence may not be selected. Column 5 shows that the new algorithm has detected many more pixels of the faint structure than SExtractor.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{h4662f15.eps} \end{figure} Figure 15: Result of segmentation and selection applied to the second test image. Parameter settings: Diffusion: filter parameter T=30, edge sensitivity K=0.0001, pre-filter parameter $\sigma =2$ and pre-filter parameter for structure tensor $\mu =30$; Selection: intensity threshold for detection $c_{\rm min}=0.1$, minimal intensity difference from background  $c_{\rm min2}=0.2$, eccentricity threshold  $c_{\rm ecc}=0.7$ and thickness threshold  $c_{\rm thick}=9$. Colors as in Fig. 13.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{h4662f16.eps} \end{figure} Figure 16: Result of segmentation and selection applied to the third test image. Parameter settings: Diffusion: filter parameter T=20, edge sensitivity K=0.0001,pre-filter parameter $\sigma =2$ and pre-filter parameter for structure tensor $\mu =15$; Selection: intensity threshold for detection  $c_{\rm min}=0.3$, minimal intensity difference from background  $c_{\rm min2}=0.2$, eccentricity threshold $c_{\rm ecc}=0.7$ and thickness threshold  $c_{\rm thick}=9$. Colors as in Fig. 13.
Open with DEXTER

The first remarkable difference is that SExtractor in order to measure the objects total magnitudes uses a far lower segmentation threshold and thus it segments larger parts of bright objects than our algorithm as can be realized in columns one to three in Fig. 14. The evaluation of the objects elongation then depends on the segmented shape.

The results of our algorithm show a more regular border due to the edge parallel diffusion and the edge enhancement. Using SExtractor one may choose a higher threshold for detection (DETECT_THRES) and yield a better shape of the segmented objects. However, since this is a global threshold SExtractor tends to loose fainter objects. Our algorithm overcomes this problem by using a local adaptive threshold.

The forth arc in Fig. 14 segmented by SExtractor is an example for a failure of the deblending procedure. The arc is not separated from the nearby galaxy and since the composition of both sources is not much elongated it would be refused by the selection process. On the other hand tuning the parameter for deblending, which is supplied by SExtractor for this specific arc allows a separate detection of both sources but leads to an undesired splitting of other objects.

In the fifth arc our algorithm reveals a far larger part of the weak structure than SExtractor due to the use of anisotropic diffusion and detects its direction of elongation correctly. SExtractor does also find an elongated part of this arc but the direction of elongation of this part differs from the exact direction. Thus our algorithm provides a better quality of detection.

To summarize the new algorithm for detecting arcs presented here has two main advantages.

The method of filtering, e.g. anisotropic diffusion is chosen with regard to the kind of objects to be detected. The filtering process provides a closure of gaps in between objects as well as edge enhancing.

The use of object dependent thresholds based on edge detection leads to an improved segmentation even of weak sources. A deblending procedure is not required. Moreover the new algorithm is able to detect close-by objects of different scale, for which the SExtractor's deblending procedure fails.

5 Summary and conclusions

We proposed a new algorithm for the detection of gravitationally lensed arcs on CCD images of galaxy clusters, performing an edge-based object detection on the filtered image together with an automatic selection of arcs.

The algorithm consists of several steps:

1.
Histogram modification: we focus on the typical range of the arcs intensities.
2.
Filtering: we use anisotropic diffusion, which enhances thin and elongated objects such as arcs.
3.
Segmentation: the principal directions as determined in the diffusion process are exploited in the later segmentation process and the edge enhancing eases border allocation.
4.
Selection: after detection thin and elongated objects are selected.
Comparing our algorithm with the software package "SExtractor'' we find that both algorithms rely on multi-level strategies for feature extraction in astronomical data. The emphasis in SExtractor lies on the extraction of stars and galaxies while our algorithm is designed to extract elongated arcs. Both multi-level strategies are implemented rather differently; the major differences are the filtering methods used and the determination of the segmentation threshold: SExtractor relies on Gaussian convolution filtering; the threshold for segmentation depends on the estimated background. Our algorithm relies on anisotropic diffusion filtering; the segmentationthreshold is determined by border allocation using the same principal directions as in the diffusion process and avoiding the effect of merging close-by objects.

The new algorithm is particularly well suited for the detection of arcs in astronomical images. It can be both applied to automated surveys as well as to individual clusters.

The algorithm (implemented in C) will be provided to the public. Feel free to contact Frank Lenzen (Frank.Lenzen@uibk.ac.at).

Acknowledgements
We thank Thomas Erben and Peter Schneider for kindly providing the HST image of A1689. We are grateful to Joachim Wambsganss and Thomas Erben for valuable comments to the manuscript.

The work of F.L. is supported by the Tiroler Zukunftsstiftung. The work of O.S. and S.S. is partly supported by the Austrian Science Foundation, Projects Y-123INF and P15868, respectively.

References


Copyright ESO 2004