We measure the variance in the distribution of off-plane (
A&A 416, 1-7 (2004)
DOI: 10.1051/0004-6361:20031718
M. López-Corredoira1 - J. E. Betancort-Rijo2,3
1 - Astronomisches Institut der Universität Basel, Venusstrasse 7, 4102 Binningen, Switzerland
2 -
Instituto de Astrofísica de Canarias, C/. Vía Láctea, s/n,
38200 La Laguna (Tenerife), Spain
3 -
Departamento de Astrofísica, Universidad de La Laguna, Tenerife, Spain
Received 15 May 2003 / Accepted 31 October 2003
Abstract
We measure the variance in the
distribution of off-plane (
![]() )
galaxies with mK<13.5 from the 2MASS K-band survey
in circles of diameter between 0.344
)
galaxies with mK<13.5 from the 2MASS K-band survey
in circles of diameter between 0.344![]() and 57.2
and 57.2![]() .
The use of a near-infrared survey makes the contribution of
Galactic extinction to these fluctuations negligible.
We calculate these variances within
the standard
.
The use of a near-infrared survey makes the contribution of
Galactic extinction to these fluctuations negligible.
We calculate these variances within
the standard ![]() CDM model assuming that the sources are
distributed like halos of the corresponding mass,
and it reproduces qualitatively the galaxy count variance.
Therefore, we conclude that the counts can be
explained in terms only of the large
scale structure. A second result of this paper is a new method to determine
the two point correlation function obtained by forcing
agreement between model and data. This method does not
need the knowledge of the two-point angular
correlation function, allows an estimation of the errors (which are low
with this method), and can be used even with incomplete surveys.
CDM model assuming that the sources are
distributed like halos of the corresponding mass,
and it reproduces qualitatively the galaxy count variance.
Therefore, we conclude that the counts can be
explained in terms only of the large
scale structure. A second result of this paper is a new method to determine
the two point correlation function obtained by forcing
agreement between model and data. This method does not
need the knowledge of the two-point angular
correlation function, allows an estimation of the errors (which are low
with this method), and can be used even with incomplete surveys.
Using this method we get
![]() ,
which is the first measure of the amplitude of
,
which is the first measure of the amplitude of ![]() in the local Universe for the K-band.
It is more or less in agreement with those
obtained through red optical filter selected samples, but it is
larger than the amplitude obtained for blue optical filter selected samples.
in the local Universe for the K-band.
It is more or less in agreement with those
obtained through red optical filter selected samples, but it is
larger than the amplitude obtained for blue optical filter selected samples.
Key words: cosmology: large-scale structure of Universe - infrared: galaxies - galaxies: statistics - cosmology: theory
The distribution of the number of galaxies or clusters of galaxies in a certain volume V can be used to test the large-scale structure of the universe. The calculation of probabilities of finding different structures in a clustering model are sometimes amenable to analytical techniques: for instance, for voids (Betancort-Rijo 1990), density of Abel clusters (Betancort-Rijo 1995), number of galaxies in a randomly placed sphere and cluster density profiles (Betancort-Rijo & López-Corredoira 1996), etc. The calculation of variance of the number of galaxies within the cones corresponding to the circles in the sky, or another 2D figure, (i.e., galaxy counts) is another possibility, and even easier to compare with the observations since we do not need any information about the redshifts of the individual galaxies. This is precisely the purpose of this paper: the calculation from a model of the variance of the number of galaxies in the different regions of the sky, and to see how well they fit real data obtained directly from a sky survey. This will allow us to determine some parameters of the two-point correlation function independent of any other method.
One disadvantage of galaxy counts is that they are affected by Galactic
extinction, and it is difficult to separate the fluctuations due to this
extinction from the real fluctuation in the galaxy distribution.
However, the arrival of near-infrared galaxy surveys such as DeNIS or
2MASS provides a way to avoid this problem, since the extinction
in K-band, the one to be used in this paper, is 10 times lower than in
V-band. In V-band, the dispersion of
galaxy counts due only to the fluctuations of extinction in scales
around 1 degree is around 30%
(see Eq. (4) and the parameters given in the paragraph
before Eq. (4)) at galactic latitudes
![]() ,
while in K-band is only
,
while in K-band is only ![]() 3%.
Since the fluctuations we measure due to the large-scale structure
are 25-80% in the explored scales,
calculation of the structure
parameters are very sensitive to the exact knowledge of the galactic extinction
in visible bands; however, in the near-infrared, the calculation of the parameters is
much less sensitive to the extinction and we can be sure that the
measured fluctuations correspond to the real distribution of galaxies.
Moreover, in the K-band
we have an important advantage: the K-correction is nearly independent
of galaxy type (Mannucci et al. 2001), and this will allow us to make
the K-corrections without knowing the galaxy type of the sources in
the survey.
3%.
Since the fluctuations we measure due to the large-scale structure
are 25-80% in the explored scales,
calculation of the structure
parameters are very sensitive to the exact knowledge of the galactic extinction
in visible bands; however, in the near-infrared, the calculation of the parameters is
much less sensitive to the extinction and we can be sure that the
measured fluctuations correspond to the real distribution of galaxies.
Moreover, in the K-band
we have an important advantage: the K-correction is nearly independent
of galaxy type (Mannucci et al. 2001), and this will allow us to make
the K-corrections without knowing the galaxy type of the sources in
the survey.
Maps of galaxy counts have been available for quite a long time and have been used for several purposes. Zwicky (1957, p. 84), for instance, produced them from the available catalogues in visible bands, with a smooth correction of galactic extinction as a function of b, to explore intergalactic extinction.
The purpose of this paper is first to show that the count variances are
in qualitative good agreement with those obtained assuming that the source
correlation function is equal to that obtained in the standard ![]() CDM model for virialized objects with circular velocity larger than 120 km s-1. Then, by
considering a slightly modified power law (the correlation of the those haloes
is almost exactly a power law in the most relevant region) and determining the values of the amplitude and exponent leading to best agreement with the actual counts. This have proved to
be an accurate way of determining the correlation function of the sources.
Cumulative galaxy counts (in optical) versus the limiting magnitude have been
used to constrain the departure from homogeneity-fractal distribution-at
large scales (Sandage et al. 1972). A
CDM model for virialized objects with circular velocity larger than 120 km s-1. Then, by
considering a slightly modified power law (the correlation of the those haloes
is almost exactly a power law in the most relevant region) and determining the values of the amplitude and exponent leading to best agreement with the actual counts. This have proved to
be an accurate way of determining the correlation function of the sources.
Cumulative galaxy counts (in optical) versus the limiting magnitude have been
used to constrain the departure from homogeneity-fractal distribution-at
large scales (Sandage et al. 1972). A
![]() indicates
total homogeneity and this is more or less observed in near infrared counts
too: with 2MASS data for low redshift (Schneider et al. 1998, Fig. 5) or
other surveys.
Here, we will not explore further the homogeneity at very large scales but focus
on the clustering at small scales in the local Universe (z<0.4).
The use of galaxy counts to derive the two-point angular
correlation function has been considered by Porciani & Giavalisco (2002); however,
we will recover directly (under some assumptions) the two-point correlation
function of the sources, and, therefore, their relative biasing with respect to the mentioned halos.
indicates
total homogeneity and this is more or less observed in near infrared counts
too: with 2MASS data for low redshift (Schneider et al. 1998, Fig. 5) or
other surveys.
Here, we will not explore further the homogeneity at very large scales but focus
on the clustering at small scales in the local Universe (z<0.4).
The use of galaxy counts to derive the two-point angular
correlation function has been considered by Porciani & Giavalisco (2002); however,
we will recover directly (under some assumptions) the two-point correlation
function of the sources, and, therefore, their relative biasing with respect to the mentioned halos.
The paper is divided as follows: Sect. 2 describes the observational data and how to measure the variance in the distribution of galaxies; Sect. 3 explains how to calculate this variance within a model of the large scale structure; and Sect. 4 makes the comparison between data and model predictions and derives the parameters of the two-point correlation function necessary to get an agreement between model and data.
The data used in this work have been taken from the extended sources
of the 2MASS-project (Jarrett et al. 2000), All-sky release
(http://www.ipac.caltech.edu/2mass/releases/docs.html).
Completeness limit: mK=13.5 (Schneider et al. 1998; Jarrett et al. 2000;
Maller et al. 2003, Sect. 2).
Assuming an average color of
![]() ,
this is equivalent to an
optical limit of 17.5 (Schneider et al. 1998), deep enough for
statistical studies of the large scale structure, the local structures
are not too predominant, but shallow enough to exclude
high redshift [the galaxies have redshifts z< 0.3-0.4
(Cole et al. 2002), and an average
,
this is equivalent to an
optical limit of 17.5 (Schneider et al. 1998), deep enough for
statistical studies of the large scale structure, the local structures
are not too predominant, but shallow enough to exclude
high redshift [the galaxies have redshifts z< 0.3-0.4
(Cole et al. 2002), and an average
![]() (see
below for details)].
We do not analyze samples of galaxies below this limit of mK(for instance, mK<12.0 or mK<11.0, etc.) because this would represent
the very local Universe rather than the large scale structure.
(see
below for details)].
We do not analyze samples of galaxies below this limit of mK(for instance, mK<12.0 or mK<11.0, etc.) because this would represent
the very local Universe rather than the large scale structure.
In Fig. 1, we see a representation of the fluctuations
at a scale of ![]() in the whole sky (with on average
around 150 galaxies per area with complete coverage).
In the zone of avoidance,
in the whole sky (with on average
around 150 galaxies per area with complete coverage).
In the zone of avoidance,
![]() ,
there is a clear deficit
of galaxies due to the extinction,which is small compared to the optical but
not negligible in near plane regions.
The reliability is larger than 99% in
,
there is a clear deficit
of galaxies due to the extinction,which is small compared to the optical but
not negligible in near plane regions.
The reliability is larger than 99% in
![]() (Schneider et al. 1998).
(Schneider et al. 1998).
![\begin{figure}
\par\includegraphics[height=13.45cm,width=13.5cm,clip]{cuen_aitoff.1.eps}\end{figure}](/articles/aa/full/2004/10/aa3993/Timg19.gif) |
Figure 1:
Aitoff projection in galactic coordinates (up) and equatorial
coordinates (down) of the 2MASS/"All-sky release''
galaxy counts with mK<13.5; average: 14.4 galaxies/deg2.
Galaxies were counted in square regions of 3 deg |
| Open with DEXTER | |
In order to quantify the fluctuations, we count the number of galaxies
in each circle of the sky with angular radius r0. In 3D space,
we count the galaxies within the corresponding cone in the line of sight.
We select only the circular regions in
![]() which were covered more than 90%. The cumulativecounts up to magnitude 13.5 are expressed per unit area (we divide the number of galaxies
per region by the area, S, of the region).
We measure the counts in randomly placed circular areas instead
of a regular mesh. Since the number of random circles in which we
measure the galaxy counts is around 8 times larger than the total area divided
by the area of the circle, the information lost is
very low (0.033% of the galaxies would not be in any circle if the
distribution were Poissonian).
Once we have these counts for each of the n regions containing
respectively ni galaxies, we calculate the average,
which were covered more than 90%. The cumulativecounts up to magnitude 13.5 are expressed per unit area (we divide the number of galaxies
per region by the area, S, of the region).
We measure the counts in randomly placed circular areas instead
of a regular mesh. Since the number of random circles in which we
measure the galaxy counts is around 8 times larger than the total area divided
by the area of the circle, the information lost is
very low (0.033% of the galaxies would not be in any circle if the
distribution were Poissonian).
Once we have these counts for each of the n regions containing
respectively ni galaxies, we calculate the average,
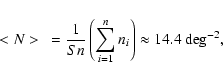 |
(1) |
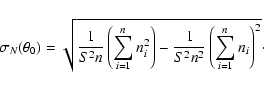 |
(2) |
The fluctuations due to the intrinsic clustering of galaxies,
![]() ,
will be the total fluctuations minus the other independent
sources of fluctuation subtracted quadratically:
,
will be the total fluctuations minus the other independent
sources of fluctuation subtracted quadratically:
The Poissonian fluctuations are the most important contribution, other than those due to large scale structure, and it can be exactly determined:
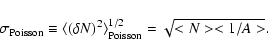 |
(5) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{histo.eps}\end{figure}](/articles/aa/full/2004/10/aa3993/Timg30.gif) |
Figure 2:
Distribution of frequencies of cells with N galaxies for circular
cells of angular radius
|
| Open with DEXTER | |
The calculation of the fluctuations
![]() due to the
clustering of the galaxies is carried out in the following way:
due to the
clustering of the galaxies is carried out in the following way:
![\begin{displaymath}%
\langle N\rangle=A \overline{n}\int _{\theta<\theta_0} r^2 \Phi
[M_K<M_{K,{\rm limit}}(r)]{\rm d}r,
\end{displaymath}](/articles/aa/full/2004/10/aa3993/img32.gif) |
(6) |
| |
= | ||
| (7) |
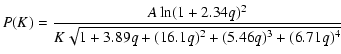 |
|||
| (10) |
Two questions arise as to the suitability of Eq. (9):
1) is the assumption of a power-law for non-linear scales appropriate?
2) could we apply a power-law for all scales instead of a ![]() CDM model
for the linear regime? Both questions are answered in other papers but
they will also be answered by the result of the fit of the
counts itself, shown in Sect. 4 (see Fig. 3).
As to the first question, the fit of the power law with
r0=6.66 h-1 Mpc,
CDM model
for the linear regime? Both questions are answered in other papers but
they will also be answered by the result of the fit of the
counts itself, shown in Sect. 4 (see Fig. 3).
As to the first question, the fit of the power law with
r0=6.66 h-1 Mpc,
![]() is remarkably good for low
is remarkably good for low ![]() (which is nearly independent of the
linear part of
(which is nearly independent of the
linear part of ![]() ), a power law in the non-linear
regime gives a very good fit.
The answer to the second question is provided by the following consideration:
a power-law in all scales gives more structure at r>40 h-1 Mpc
than the power-law in the non-linear regime +
), a power law in the non-linear
regime gives a very good fit.
The answer to the second question is provided by the following consideration:
a power-law in all scales gives more structure at r>40 h-1 Mpc
than the power-law in the non-linear regime + ![]() CDM model in the linear regime. The first option gives further fluctuations at large
CDM model in the linear regime. The first option gives further fluctuations at large ![]() ;
the difference is not high enough
to reject the first option (we have already said that the fit is not
very sensitive to the parameters in the linear power spectra),
but the
;
the difference is not high enough
to reject the first option (we have already said that the fit is not
very sensitive to the parameters in the linear power spectra),
but the ![]() CDM model in the linear regime (solid
line in Fig. 3) is considerably better
than the power-law at all scales (long dashed line
in Fig. 3).
CDM model in the linear regime (solid
line in Fig. 3) is considerably better
than the power-law at all scales (long dashed line
in Fig. 3).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fluct_area.eps}\end{figure}](/articles/aa/full/2004/10/aa3993/Timg64.gif) |
Figure 3: Log-log plot: fluctuations of the mean density of counts as a function of the radius of the circular regions. The error bar of the models is less than 1%. |
| Open with DEXTER | |
There are also theoretical reasons to use expression (9)
for ![]() .
.
![]() CDM simulations lead to a correlation function for
virialized halos with circular velocity >120 km s-1 with this form and
CDM simulations lead to a correlation function for
virialized halos with circular velocity >120 km s-1 with this form and
![]() (Primack 2001, Fig. 1). This function turns out to be almost
exactly equal to that for APM galaxies. For K-selected galaxies the correlations
do not need to be equal to that for halos; there may exist some biasing.
However, the biasing (
(Primack 2001, Fig. 1). This function turns out to be almost
exactly equal to that for APM galaxies. For K-selected galaxies the correlations
do not need to be equal to that for halos; there may exist some biasing.
However, the biasing (
![]() )
is expected to be a mild function of r.
So, it seems plausible to use expression (9) with different amplitudes
and slightly different
)
is expected to be a mild function of r.
So, it seems plausible to use expression (9) with different amplitudes
and slightly different ![]() with respect to the halos (or APM galaxies).
with respect to the halos (or APM galaxies).
With this in mind, we shall see in next section that with the assumed
shape (that for the mentioned haloes) in Eq. (9), there is qualitative agreement with the
observed variances. We consider this result as a confirmation of the
assumption that the measured variances are due to the large scale
structure. We consider that large scale structure should explain not only the
main part of the variances, but the whole of them. Forcing this by choosing
the appropriate values for r0, ![]() leads us to an alternative
method for determining the correlation function.
leads us to an alternative
method for determining the correlation function.
The evolution of the correlation function depends on
![]() and
and
![]() through
through ![]() .
In our case, since the average redshift
.
In our case, since the average redshift
![]() (for mK<13.5 using the aforementioned luminosity function and
K-correction), the exact value of
(for mK<13.5 using the aforementioned luminosity function and
K-correction), the exact value of ![]() is not so important, and
small variations will not significantly affect the results of the
model. The evolutionary corrections in this small range of redshifts
are also negligible, especially in K-band (Carlberg et al. 1997).
We take the value
is not so important, and
small variations will not significantly affect the results of the
model. The evolutionary corrections in this small range of redshifts
are also negligible, especially in K-band (Carlberg et al. 1997).
We take the value
![]() ,
which comes from the approximation
of
,
which comes from the approximation
of
![]() ,
for comoving coordinates
(which holds provided that the shape of
,
for comoving coordinates
(which holds provided that the shape of ![]() does not evolve, i.e.
does not evolve, i.e.
![]() is constant with respect to z, proved by Carlberg et al. 1997),
where D, the growing factor of the linear density fluctuations, is given by
(Heath 1977; Carroll et al. 1992)
is constant with respect to z, proved by Carlberg et al. 1997),
where D, the growing factor of the linear density fluctuations, is given by
(Heath 1977; Carroll et al. 1992)
![\begin{displaymath}%
D(z)=\frac{5\Omega _{\rm mat}(t_0)(1+z)}{2f[R(z)]}
\int _0^{R}f^3(R){\rm d}R,
\end{displaymath}](/articles/aa/full/2004/10/aa3993/img74.gif) |
(11) |
![\begin{eqnarray*}&& R=\frac{1}{1+z} \\
&& f(R)=\left[1+\Omega _{\rm mat}(t_0)\l...
...-1\right)
+\Omega _{\rm\Lambda}\left(R^2-1\right)\right]^{-1/2}.
\end{eqnarray*}](/articles/aa/full/2004/10/aa3993/img75.gif)
In the previous section, the only non-specified parameters are
![]() and r0, on which the fluctuations strongly depend.
These will be fitted in this section.
Through the comparison between model and data,
we have a new method to obtain
the two point correlation function, which does not
explicitly require the two-point angular
correlation function, does not suffer from
edge problems, allows an estimation of the errors,
and can be used even with incomplete surveys.
Porciani & Giavalisco (2002) have also used galaxy counts for this purpose,
but they derive the two-point angular correlation function
and then insert it in the Limber equation (which assumes power law
two point correlation function in all ranges), so it is halfway between our
method and the standard one.
and r0, on which the fluctuations strongly depend.
These will be fitted in this section.
Through the comparison between model and data,
we have a new method to obtain
the two point correlation function, which does not
explicitly require the two-point angular
correlation function, does not suffer from
edge problems, allows an estimation of the errors,
and can be used even with incomplete surveys.
Porciani & Giavalisco (2002) have also used galaxy counts for this purpose,
but they derive the two-point angular correlation function
and then insert it in the Limber equation (which assumes power law
two point correlation function in all ranges), so it is halfway between our
method and the standard one.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.5cm,clip]{chi2.ps}\end{figure}](/articles/aa/full/2004/10/aa3993/Timg81.gif) |
Figure 4:
Modified |
| Open with DEXTER | |
Table 1:
![]() as a function of
as a function of ![]() for the 2MASS-data
and the models (same as Fig. 3).
for the 2MASS-data
and the models (same as Fig. 3).
Figure 3 shows the data and some model predictions.
The numbers are given in Table 1.
The best fit is for r0=6.66 h-1 Mpc,
![]() .
Lower values of r0 for the same
.
Lower values of r0 for the same ![]() ,
such as
r0=4.9 h-1 Mpc, give considerably less structure than observed
for the present sample of galaxies. For example,
the two-point correlation function derived from the APM optical survey (equal to
that for the mentioned halos):
,
such as
r0=4.9 h-1 Mpc, give considerably less structure than observed
for the present sample of galaxies. For example,
the two-point correlation function derived from the APM optical survey (equal to
that for the mentioned halos):
![]() ,
r0=4.5 h-1 Mpc (Baugh 1996), shows substantialy smaller values than that obtained for the blue band. This leads us to agree with Carlberg et al. (1997),
that optically (blue) selected surveys appear to be significantly less
correlated than K-selected galaxies.
,
r0=4.5 h-1 Mpc (Baugh 1996), shows substantialy smaller values than that obtained for the blue band. This leads us to agree with Carlberg et al. (1997),
that optically (blue) selected surveys appear to be significantly less
correlated than K-selected galaxies.
The values of the parameters ![]() and r0 which are compatible
with the data are shown in Fig. 4, derived from a
modified
and r0 which are compatible
with the data are shown in Fig. 4, derived from a
modified ![]() -test for correlated data (Rubiño-Martín &
Betancort-Rijo 2003, Sect. 4) applied to the data for
-test for correlated data (Rubiño-Martín &
Betancort-Rijo 2003, Sect. 4) applied to the data for
![]() (the other points have very large error bars and are not useful for
constraining the parameters; moreover, they are more dependent on the
values of
(the other points have very large error bars and are not useful for
constraining the parameters; moreover, they are more dependent on the
values of ![]() in the linear regime).
in the linear regime).
In the simplest version of this test (
![]() ,
see
Rubiño-Martín & Betancort-Rijo 2003), which for the present
type of problem cannot be far from the best one (determined by
an optimal set of Pi), the ordinary uncorrelated
,
see
Rubiño-Martín & Betancort-Rijo 2003), which for the present
type of problem cannot be far from the best one (determined by
an optimal set of Pi), the ordinary uncorrelated ![]() ,
,
![]() ,
and the number of degrees of freedom are rescaled by
a certain factor, A, which is a function of the correlations:
,
and the number of degrees of freedom are rescaled by
a certain factor, A, which is a function of the correlations:
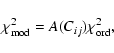 |
(12) |
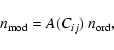 |
(13) |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{a_samp.eps}\end{figure}](/articles/aa/full/2004/10/aa3993/Timg95.gif) |
Figure 5: Value of A(Cij) as a function of the number of resamplings. |
| Open with DEXTER | |
The inferred values of the two parameters are:
| (14) |
![\begin{displaymath}%
r_0^\gamma=29.8\pm 0.3 \ {\rm (68\% \ C. L.)}\ [\pm 1.1 \ {\rm (95\% \ C. L.)]}.
\end{displaymath}](/articles/aa/full/2004/10/aa3993/img97.gif) |
(15) |
These values are in excellent agreement
with the estimations of ![]() in near-infrared
surveys by other means: the angular correlation function is at small scales
proportional to
in near-infrared
surveys by other means: the angular correlation function is at small scales
proportional to
![]() in K-band
(Baugh et al. 1996; Carlberg et al. 1997), which through Limber's equation
gives
in K-band
(Baugh et al. 1996; Carlberg et al. 1997), which through Limber's equation
gives
![]() .
Kümmel & Wagner (2000) give an angular correlation
in K-band proportional to
.
Kümmel & Wagner (2000) give an angular correlation
in K-band proportional to
![]() which would
give through Limber's equation
which would
give through Limber's equation
![]() ,
again consistent
with our value. Maller et al. (2003) with 2MASS K-band data derive
an angular correlation proportional to
,
again consistent
with our value. Maller et al. (2003) with 2MASS K-band data derive
an angular correlation proportional to
![]() which gives
which gives
![]() ,
very close to our preferred value.
The value of
,
very close to our preferred value.
The value of ![]() is also in agreement
with some simulations of
is also in agreement
with some simulations of
![]() (Primack 2001, Fig. 1:
(Primack 2001, Fig. 1:
![]() )
and the exponents in optical surveys such as APM (
)
and the exponents in optical surveys such as APM (
![]() ,
Baugh 1996).
,
Baugh 1996).
We get an amplitude
![]() (68% C.L.), more or less in agreement
with the R-selected Las Campanas Redshift Survey which finds
(68% C.L.), more or less in agreement
with the R-selected Las Campanas Redshift Survey which finds
![]() (Jing et al. 1998),
equivalent (through Eq. (8) with
(Jing et al. 1998),
equivalent (through Eq. (8) with
![]() )
to
)
to
![]() .
This is also in agreement with the extrapolation
down to z=0 of the evolution of
.
This is also in agreement with the extrapolation
down to z=0 of the evolution of
![]() in K-band selected galaxies at high redshift
(see Fig. 8 of Carlberg et al. 1997).
However, the blue band selected surveys give a lower amplitude
of the correlations by a factor of two
(Carlberg et al. 1997, Sect. 6 and references therein).
At high redshifts (
in K-band selected galaxies at high redshift
(see Fig. 8 of Carlberg et al. 1997).
However, the blue band selected surveys give a lower amplitude
of the correlations by a factor of two
(Carlberg et al. 1997, Sect. 6 and references therein).
At high redshifts (
![]() ),
this difference of amplitude between K-band selected
galaxies and blue-optical selected galaxies is even larger: a factor 3-4 (Daddi et al. 2003). This is consistent because
the correlation length r0 is not independent of the range of
luminosities of the selected sample (Colombo & Bonometto
2001). Locally it follows roughly a dependence
),
this difference of amplitude between K-band selected
galaxies and blue-optical selected galaxies is even larger: a factor 3-4 (Daddi et al. 2003). This is consistent because
the correlation length r0 is not independent of the range of
luminosities of the selected sample (Colombo & Bonometto
2001). Locally it follows roughly a dependence
![]() h-1 Mpc +0.4DL with the scale
h-1 Mpc +0.4DL with the scale
![]() (Colombo & Bonometto 2001).
(Colombo & Bonometto 2001).
Figure 3 shows that
the fluctuations of galaxy counts may be accurately predicted by
an expression of the form given in (9) for the correlation. It must be noted
that our method uses a frequentist statistical analysis that not
merely determines the best correlation function but also tells us
how good the best one is. The fact that the best values (of r0,
![]() )
are within the 68% C.L. region tells us that expression
(9) is as good as it can possibly be.
)
are within the 68% C.L. region tells us that expression
(9) is as good as it can possibly be.
No effect other than the large scale structure itself, for instance intergalactic
extinction, is necessary to explain the variances.
When Zwicky (1957, chap. 3)
observed that
![]() increased with
increased with ![]() even for large angles, he interpreted this result as
proof of the presence of significant intergalactic extinction.
However, as we see in Fig. 3,
the fact that
even for large angles, he interpreted this result as
proof of the presence of significant intergalactic extinction.
However, as we see in Fig. 3,
the fact that
![]() decreases slowly with increasing
decreases slowly with increasing ![]() is due to the large scale structure itself, that produces extra fluctuations
in large scales over those expected from a Poissonian distribution
for scales of several degrees or tens of degrees.
is due to the large scale structure itself, that produces extra fluctuations
in large scales over those expected from a Poissonian distribution
for scales of several degrees or tens of degrees.
We have tested that the ![]() CDM model
of large scale structure is consistent with the observed
galaxy count variance. This consistency is obtained for
particular values of the parameters of the
two point correlation function, giving a new method to obtain it indirectly
without making use of the two-point angular correlation function.
In the application of this method to 2MASS K-band galaxies with mK<13.5we get
CDM model
of large scale structure is consistent with the observed
galaxy count variance. This consistency is obtained for
particular values of the parameters of the
two point correlation function, giving a new method to obtain it indirectly
without making use of the two-point angular correlation function.
In the application of this method to 2MASS K-band galaxies with mK<13.5we get
![]() (68% C.L.).
(68% C.L.).
Acknowledgements
We thanks the referee, A. Maller, for rather helpful comments and suggestions. Thanks are also given to N. Sambhus for proof-reading help. This publication makes use of data products from: 2MASS, which is a joint project of the Univ. of Massachusetts and the Infrared Processing and Analysis Center (IPAC), funded by the NASA and the NSF. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA. We thank the Swiss National Science Foundation for support under grant 20-64856.01.