A&A 416, 297-310 (2004)
DOI: 10.1051/0004-6361:20034511

Comparative study of the two large flares from SGR1900+14 with the BeppoSAX Gamma-Ray Burst Monitor

C. Guidorzi1 - F. Frontera1,2 - E. Montanari1,3 - M. Feroci4 - L. Amati2 - E. Costa4 - M. Orlandini2


1 - Dipartimento di Fisica, Università di Ferrara, via Paradiso 12, 44100 Ferrara, Italy
2 - Istituto di Astrofisica Spaziale e Fisica Cosmica, CNR, Sezione di Bologna, via Gobetti 101, 40129 Bologna, Italy
3 - ISA "A. Venturi'', Modena, Italy
4 - Istituto di Astrofisica Spaziale e Fisica Cosmica, CNR, Sezione di Roma, via Fosso del Cavaliere, 00133 Roma, Italy

Received 14 October 2003 / Accepted 26 November 2003

Abstract
We report on spectral and temporal results of the 40-700 keV observations, obtained with the Gamma-Ray Burst Monitor (GRBM) on board BeppoSAX, of the two large flares from the Soft Gamma-ray Repeater SGR 1900+14 occurred on August 27, 1998 and April 18, 2001. From their intensity, fluence and duration, the first one was classified as "giant'' and the second as "intermediate''.The spectral results have been obtained with an improved response function of the GRBM. We find that the two events have similar spectral properties, but different temporal properties. The major difference concerns the time profiles of the light curves, whereas the lack of evidence in the 2001 flare for the erratic time variability found at high frequencies (10-1000 Hz) in the 1998 flare could be ascribed to lower counting statistics. We discuss these results in the light of the magnetar model proposed for SGR sources.

Key words: stars: pulsars: individual: SGR1900+14 - X-rays: bursts - stars: magnetic fields

   
1 Introduction

Soft-Gamma Repeaters (SGRs, see Hurley 2000 and Woods 2003 for reviews) are X-/gamma-ray transient sources that unpredictably undergo periods of bursting activity, separated by sometimes long intervals (from years to decades) of quiescence.

To date, the SGR class includes four sources (SGR0525-66, SGR1627-41, SGR1806-20 and SGR1900+14) plus two candidates, SGR1801-23 (only two bursts detected; Cline et al. 2000) and SGR1808-20 (one SGR-like burst observed; Lamb et al. 2003). All confirmed SGRs, on the basis of their early determined positions, appeared to be associated with young supernova remnants (SNRs) of ages $\le$104 yr. However, basing on more precise locations, in most cases this association has been questioned (Lorimer & Xilouris 2000; Hurley et al. 1999a; Kaplan et al. 2002a) and in some cases attributed to random chance (Gaensler et al. 2001). All SGRs appear to be in our galaxy, except for SGR0525-66 which is in the Large Magellanic Cloud.

Typically, bursts from SGRs have short durations($\sim $0.1 s), recurrence times of seconds to years, energies of $\sim $10 41 D210 ergs ( D = 10 D10 kpc). Their hard X-ray spectra (>25 keV) are analytically consistent with an Optically Thin Thermal Bremsstrahlung ( OTTB) with temperatures of 20-40 keV. During quiescence, persistent X-ray emission (<10 keV) has been observed from all of them with luminosities of $\sim $1035- 1036 D210 erg s-1 and power-law spectral shapes. In the case of SGR1900+14, an additional blackbody ( BB) component ( $kT_{\rm bb} \sim 0.5$ keV) is requested (Woods 2003). SGR1806-20 and SGR1900+14, during quiescence, show X-ray pulsations with periods in the range from 5 to 8 s and spin-down rates of $\sim $ 10-11-10-10 s/s (see, e.g., Hurley et al. 1999b; Kouveliotou et al. 1999). From these sources, also evidence of X-ray lines has been reported during bursts: an emission line at $\sim $6.4 keV from the former source (Strohmayer &Ibrahim 2000) and an absorption-like feature at $\sim $5 keV from the latter (Ibrahim et al. 2002).

Rarely, "giant'' flares of hard X-/$\gamma$-rays have been observed from SGR0525-66 (Mazets et al. 1979) and SGR1900+14 (Cline et al. 1998; Feroci et al. 1999; Hurley et al. 1999a; Mazets et al. 1999b). They show durations of hundreds of seconds, pulsations during most part of the event, and peak luminosities in excess of 1044 D210 erg s-1.

After large bursts fading afterglow emission has been observed. A fading X-ray afterglow, visible for several days, has been discovered after the large flares from SGR1900+14 (i.e., the giant flare of August 1998 and the intermediate flare of April 2001, see below). The X-ray afterglow decays as a power-law ( $F(t)\propto t^{-\alpha}$) with temporal index $\alpha\sim0.7$ after the August 1998 event (Woods et al. 2001) and $\alpha\sim0.9$ after the April 2001 event (Feroci et al. 2003). The X-ray afterglow spectrum is the combination of a power-law ( PL) and a BB, with the BB not visible at early times when the PL component is predominant, but emerging at later times, when the PL component becomes weaker (Woods et al. 1999a; Feroci et al. 2003), suggesting that the non-thermal component fades more rapidly than the thermal one (see also Lenters et al. 2003, for the X-ray tail that followed the short burst occurred on April 28, 2001). The presence of X-ray afterglow emission from the other SGR sources is still an open question. Radio afterglow has also been observed from SGR1900+14 after the August 1998 event by Frail et al. (1999), who detected a transient radio source with the Very Large Array telescope at the source position following the giant flare. This is the only point-like radio source associated to an SGR to date.

On the basis of their locations and temporal properties and the absence of companion stars, SGRs have been proposed to be young (<104 yrs) isolated neutron stars (NS) with ultra-strong magnetic fields ( $B_{\rm dipole} > 10^{14}$ gauss), a.k.a. "magnetars''. The magnetar model (Duncan & Thompson 1992; Thompson & Duncan 1993; Thompson & Duncan 1995) considers a young neutron star with a very strong magnetic field ($\sim $10 14-1015 G), whose decay powers the quiescent X-ray emission through heating of stellar crust, while the low-level seismic activity and the persistent magnetospheric currents (Thompson et al. 2002) occasionally cause big crustquakes which trigger short bursts and large flares. In the magnetar scenario, the absorption feature from SGR1806-20 can be interpreted as ion-cyclotron resonance in the huge magnetic field of the NS (Ibrahim et al. 2002).

SGRs share some properties (pulse period distribution, spin-down rate, lack of a companion star, quiescent X-ray luminosity) with a peculiar class of neutron stars, the so-called anomalous X-ray pulsars (AXPs, see, e.g., Mereghetti 1999 for a review). Additional evidence for a link between the two classes has been provided by the detection of SGR-like bursting activity also from the AXPs 1E 2259+586 (Kaspi et al. 2002, 2003), and 1E 1048.1-5937 (Gavriil et al. 2002), and from the recent discovery of an absorption-like feature at $\sim $8.1 keV from the AXP 1RXS J170849-400910 (Rea et al. 2003).

1.1 SGR1900+14

SGR1900+14 was discovered in 1979 following three bursts in two days (Mazets et al. 1979). After its discovery, the source was found bursting again in 1992 (Kouveliotou et al. 1993) and, after five years of quiescence, in May 1998, when it entered an extremely active bursting period, that reached its maximum with the above mentioned giant flare of August 27, 1998. A precise localization of the source with IPN (Hurley et al. 1999c) showed that SGR1900+14 lays just outside a Galactic SNR, G042.8+00.6 and could be associated with it. However, recently Kaplan et al. (2002b) found three new candidate SNRs (G043.5+00.6, G042.0-00.1 and G041.5+00.4), that could be related to SGR1900+14 as well. Observations of the quiescent soft X-ray counterpart (Vasisht et al. 1994) have shown a 5.16-s periodicity with a spin-down rate of 10-10 s/s (Hurley et al. 1999b; Kouveliotou et al. 1999).

Several measurements of the quiescent spectrum have been performed (e.g., Hurley et al. 1999b; Kouveliotou et al. 1999). An X-ray observation with the BeppoSAX satellite (Woods et al. 1999a) shows that the 0.1-10 keV quiescent spectrum can be described by a photoelectrically absorbed ( $N_{\rm H} \sim 1.8 \times 10^{22}$ cm-2) BB ( $kT_{\rm bb} \sim 0.5$ keV) plus a PL with a photon index $\Gamma = 1.1 \pm 0.2$.

The source spectrum during the standard bursting activity has been mainly observed in the hard (>20 keV) X-/gamma-ray band. Results reported by Mazets et al. (1999a) from Konus-Wind observations show that the burst photon spectra can be analytically described by an OTTB model ( $I(E)\propto E^{-1} \exp{(-E/kT)}$) with $kT \sim 20{-}30$ keV with no significant spectral evolution within a single event or from event to event. Only in the case of a few bursts, discussed by Woods et al. (1999b), the spectrum is better described by the smoothly broken power-law, widely used to describe GRB spectra (Band et al. 1993). In these cases also a soft-to-hard spectral evolution has been observed, with hardness/intensity anticorrelation.

The giant flare occurred on 1998 August 27 (here after GF98) was observed with the Konus-Wind spectrometer (Cline et al. 1998; Mazets et al. 1999b), the Ulysses burst monitor (Hurley et al. 1999a) and the BeppoSAX GRBM (Feroci et al. 1999). The 5.16-s periodicity, along with its harmonics (e.g., Feroci et al. 1999, 2001, hereafter F99 and F01, respectively), was clearly detected during the flare. Mazets et al. (1999b) find the spectrum well described with an OTTB model with temperature kT evolving rapidly (in about 1 s and in a non-monotonic way) from >300 keV to $\sim $20 keV. Feroci et al. (1999) find a more complex 40-700 keV spectrum ( OTTB, with $kT\sim 31$ keV, plus PL with photon index $\Gamma \sim 1.5$) in the early part (first 68 s) of the event which evolves to an OTTB-like shape ( $kT \sim 29$ keV) at late times (last 128 s). At that time, as pointed out by F99, the response function of the BeppoSAX GRBM was not well known at large instrumental off-axis angles, in the direction of which the source was observed, and thus a systematic error of 10% was tentatively added to the statistical uncertainties. By joining together the BeppoSAX GRBM spectra with the 20-150 keV Ulysses data (F01), also affected by similar systematics, the first 128-s spectrum after the 68 s from the flare onset was fit by two BB, with $kT_{\rm bb1} \sim$ 9 keV and $kT_{\rm bb2} \sim 20$ keV, plus a PL model with photon index $\Gamma \sim$ 2.8, while the later 128-s spectrum was better described by an OTTB model with $kT \sim 29$ keV, consistent with the F99 results.

After the giant flare of 1998 August 27 and the recurrent bursting activity prolonged until 1999 (Mazets et al. 1999a), the source entered a period of quiescence for more than two years, which ended on 2001 April 18, when another large flare (hereafter IF01) with a shorter duration and intermediate intensity occurred. Due to a simultaneous proton solar burst, both the Ulysses burst monitor and the Konus-Wind spectrometer were overwhelmed by a high count rate. The only instrument which provided high-time resolution data of the event was the BeppoSAX GRBM (Guidorzi et al. 2001a,b).

An improved response function of the BeppoSAX GRBM is now available (see below) for all off-axis angles. In this paper we present the results of the spectral analysis of the 2001 flare, the reanalysis of the spectral data of the 1998 giant flare with the new GRBM response function, and the results of the Power Spectral Density (PSD) estimate of the high-frequency (up to 1 kHz) flux variations of the source during the two flares. Preliminary results of this analysis were reported elsewhere (Guidorzi et al. 2003a).

   
2 The BeppoSAX GRBM

The Gamma-Ray Burst Monitor (GRBM; Frontera et al. 1997; Feroci et al. 1997) is one of the instruments on board the BeppoSAX satellite (Boella et al. 1997) operative through June 1996 and April 30, 2002. The GRBM consisted of four optically independent CsI(Na) units forming a square box: each unit had a geometric area of $\sim $1136 cm2. GRBM units No. 1 and 3 were co-aligned with the Wide Field Cameras (WFC's; Jager et al. 1997). The data continuously available from the GRBM included 1-s ratemeters in the 40-700 keV and >100 keV energy channels, 225-channel spectra in the 40-700 keV band integrated over 128 s and, in the case of burst trigger, 7.8125-ms ratemeters for 96 s and, for 10 s after the trigger, $\sim $0.5-ms count rates, both in the 40-700 keV band. From the 1-s ratemeters, it is possible to extract the source 40-100 keV and 100-700 keV count rates under the assumption that the source flux above 700 keV is negligible (see Amati et al. 1999).

The detection units, except for the units 1 and 3 within small off-axis directions (Amati et al. 1999), were surrounded, in a complex way, by materials of the BeppoSAX payload. In order to exploit the capabilities of the GRBM units 2 and 4 and those of units 1 and 3 at large off-axis angles, the complete GRBM response function was derived with Monte Carlo methods (Rapisarda et al. 1997; Calura et al. 2000). Recently the complete response has been tested with the Crab Nebula and with several GRBs which were observed, at different instrument off-axis angles, with both the GRBM and the BATSE experiment (e.g., Guidorzi 2002; Guidorzi et al. 2003b; Costa & Frontera 2003) with the limitation of a generally smaller statistical accuracy of the GRBM data, with respect to the BATSE data. The deconvolution results of the GRBs, in terms of derived GRB direction and photon spectrum, are in excellent agreement with those obtained with BATSE. Thus we expect that systematic errors, also for possible terrestrial albedo effects, are similar to those which affect the deconvolution of the BATSE data (e.g., Paciesas et al. 1999). Actually, we must point out that the total counts measured for the brightest GRBs detected with both GRBM and BATSE and used to test the GRBM response function, amount to a few 105 cts in the most illuminated GRBM unit (e.g., $\sim $250 000 for GRB990123, $\sim $140 000 for GRB991216, $\sim $130 000 for GRB971110), while about $8\times 10^5$ cts were collected in the GRBM unit 1 due to GF98. Due to the smallest statistical uncertainties in the latter case, the systematics could have a major influence on deconvolution results.

3 Observations and data analysis

GF98 triggered the GRBM on August 27, 1998 at 10:22:15.7 UT, while IF01 triggered the GRBM on April 18, 2001 at 07:55:11.5 UT. IF01 occurred when the SGR1900+14 line of sight was only $\sim $11$^{\circ}$ off-axis from the detection unit No. 1 (indeed the flare was initially observed also with the WFC No. 1; Guidorzi et al. 2001a,b; Feroci et al. 2003). GF98 occurred when the line of sight to the source was at high off-axis angles: an elevation angle of 48$^{\circ}$ with respect to the GRBM equatorial plane, an azimuthal angle of 29$^{\circ}$ with respect to the GRBM unit 1 axis, and 61$^{\circ}$ with respect to unit 4 axis. All GRBM units detected the event, with the best signal given by unit 1. Our results, except when expressly stated, will be based on the data obtained from this unit.


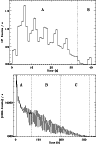  \begin{figure} \par\resizebox{8.3cm}{!}{\includegraphics{0511_01a.eps}}\par\vspace*{2mm} \resizebox{8.3cm}{!}{\includegraphics{0511_01b.ps}} \end{figure} Figure 1: 1-s background subtracted light curves of the two flares in the 40-700 keV energy band. Top: 2001 April 18 event; bottom: 1998 August 27 event. The 5.2-s modulation is apparent in both cases. Vertical dotted lines mark the 128-s intervals during which 225-channel spectra were accumulated on board.
Open with DEXTER

The background subtracted light curves of both flares are shown in Fig. 1, where the onset time is used as zero time. Details of the observation of the GF98 event can be found in the paper by F01. Feroci et al. 1999 The time duration of IF01 was 40 s, whereas GF98 lasted about 300 s. The 7.8125-ms ratemeters cover the entire IF01. The 0.5-ms ratemeters are available for the interval 0.69-10.69 s from the flare onset. During IF01, the background level was fairly stable and was evaluated by linear interpolation of the background levels in time intervals [-50, -10] s and [+50, +150] s, before and after the flare, respectively.

For the spectral analysis of IF01, the available data are two 225-channel 128-s contiguous spectra. The start and end times of these spectra are reported in Table 1. The interval A covers $\sim $97% of the flare fluence; the interval B includes little more than the isolated pulse at $t\sim40$ s from the flare onset (see Fig. 1).

The available data for the spectral analysis of GF98 are three spectra in three contiguous 128-s intervals (A, B, C) described in Table 1. The A spectrum includes both the initial hard spike and the intermediate smooth decay, whereas the B and C spectra include the 5.16-s pulsation modulated decay (see Fig. 1).

To get the source spectra, we subtracted from the above data a background spectrum of the same duration (128 s) interpolated between those measured before and after the flare.

The spectra were analyzed with the XSPEC software package (Arnaud 1996). The quoted errors are given at 90% confidence level (CL) for one parameter ( $\Delta \chi^2 = 2.7$), except when otherwise specified.

Table 1: Time intervals of the available 128-s count spectra.

4 Results

4.1 Light curves

The light curves of both flares are complex and different from each other. As it can be seen from Fig. 1, unlike GF98, IF01 does not shows any initial spike; the time duration of IF01 is much shorter than GF98, ending after about 40 s when a four-peaked repetitive pattern sets up in GF98 (F01). The light curves show measured counts, that do not account for the different effective areas of the two flares: actually, the effective area corresponding to the direction of GF98 was about 1/3 that of IF01.


  \begin{figure} \par\includegraphics[width=8cm,clip]{0511_02.ps} \end{figure} Figure 2: Background subtracted light curve of IF01 compared with the corresponding first 40 s of GF98 in the 40-700 keV energy band. Top: IF01; bottom: GF98. Vertical dotted lines mark the 5.2-s intervals and are synchronized with the IF01 pulsations.
Open with DEXTER

In order to better compare the time behaviour of IF01 with that of GF98 during the early phase, in Fig. 2 we show the light curves of both events in the first 40 s. Even if some similarities between the two light curves could be found, in the first 8 s they are markedly different. Apart from the GF98 initial spike, which is not observed in IF01, in the first 3 s, IF01 shows a first weak peak, which does not have a correspondence with any peak of the GF98 light curve. From the two light curves it is also unclear to which phase of the IF01 light curve the GF98 initial spike corresponds. We have considered two possible correspondence cases: i) the GF98 initial spike time corresponds to the fast rise of the IF01 light curve (duration $\Delta~t_{\rm rise} = 0.25\pm0.05$ s) at 3 s from the flare onset (Fig. 3), ii) the dips corresponding to the interpulses in both light curves are aligned (see Fig. 4). In the first case (see Fig. 3), we find that all IF01 dips soon after each peak are separated from the assumed main rise at multiple distances of $\sim $5.2 s. Using Fourier techniques, after detrending the data stretch by fitting with a trapped-fireball model (see Fig. 19), the best estimate of this periodicity in the time intervals from 2 to 7, is $P_{01} = 5.21 \pm 0.05$ s (negligible barycenter correction), a value which is consistent with that measured from the observation of the X-ray quiescent source soon after the event ( $P_{\rm quiesc} = 5.17284268$ s) (Woods et al. 2003). In GF98 the dips have period P98 circa 5.16 s (F99), but they are out of phase with respect to the initial spike.

In the second case (see Fig. 4), the result is that the GF98 initial spike corresponds to the peak of the weak pulse preceding the first dip (and the main rise) of the IF01 light curve.

In both cases, it is possible to see that, when the pulse peak fades away (slice 7 of Fig. 3 or 4), the corresponding dip is no more visible. The pattern completely changes soon before IF01 ends (slice 8): while the continuum level seems to fade under the GRBM sensitivity, a pulse rises up to a peak count rate of about 160 counts in 31.25 ms, the same level as the early pulse. The pulse does not seem to have properties similar to the preceding regular pulses: it neither occurs in phase with them nor exhibits a similar structure.

The complexity of the GF98 and IF01 light curves and their mutual differences are better apparent in Fig. 6, which, for correspondence case ii), shows them split into 9 panels, each displaying a single pulsation cycle, with 125 ms time resolution. The pulse shape of the IF01 pulsation and its evolution are apparent in the panels from 2 to 7. Two pulses and two dips nearly equally spaced are visible in the pulse shape, with the second pulse stronger and fading later and almost suddenly in panel 7. The pulse shape of the first 40 s of GF98 appears more complex than that of IF01. In the same panels, it exhibits, from phase 0 to $\sim $0.6, a single, broad pulse instead of the pulse and dip exhibited by IF01 in the same phase interval. The difference is more marked in the first two and last two panels.


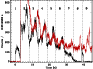  \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{0511_03.eps}} \end{figure} Figure 3: Light curves of the first $\sim $40 s of both IF01 ( black) and GF98 ( red) superposed to each other assuming that the two steepest rises correspond to the onset of the flares.
Open with DEXTER


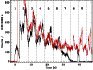  \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{0511_04.ps}} \end{figure} Figure 4: Light curves of the first $\sim $40 s of both IF01 ( black) and GF98 ( red) superposed to each other, with the first interpulses aligned. The slices' boundaries have been chosen to mark the first minima.
Open with DEXTER


  \begin{figure} \par {\includegraphics[width=8.8cm,clip]{0511_05.eps} }\end{figure} Figure 5: Precursor in the 40-700 keV light curve of GF98 at $t\sim -0.45$ s, followed by a slow increase in intensity just before the initial pulse. We added the counts of all GRBM units to improve the statistical quality.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16.3cm,clip]{0511_06.eps} \end{figure} Figure 6: Pulse shape evolution of both flares (IF01: black, GF98: red) during the first nine slices. The time offset between the two events was chosen in order to align the first interpulses (see also Fig. 4). Horizontal scale: phase of rotation cycle; vertical scale: counts per 125 ms.
Open with DEXTER

   
4.2 Precursors

The precursor of GF98, at $\sim $0.4 s before the main event, is well established. It was reported by Hurley et al. (1999a) in the 25-150 keV energy band and by Mazets et al. (1999b) in the 15-50 keV band. In the 7.8125-ms GRBM data, we also find this precursor in the range 40-700 keV. It also occurs at t = -0.45 s and lasts about 0.1 s (see Fig. 5). The pulse is even better apparent by rebinning the original 7.8125-ms data from all the 4 GRBM units in new 62.5-ms bins, from which an excess of ($100\pm 23$ cts) can be established. From the same figure, it is also visible the slow increase in the count rate just before the initial spike, similar to the rise of a typical short burst (see also Mazets et al. 1999a).

In the case of IF01, the nature of the first peak is more difficult to understand. It may be a precursor candidate. However its duration (about 3 s) is much longer than that exhibited by the GF98 precursor, is not separated from the main rise of the flare, and, more important, it shows a much harder spectrum than that of the GF98 precursor. Indeed the latter was not detected by Konus (Mazets et al. 1999b) in the energy channels above 50 keV, while the IF01 pulse is detected by the GRBM even above 100 keV (see Fig. 7).


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{0511_07.eps} \end{figure} Figure 7: IF01 light curve in the >100 keV energy band. The fact that the pulse preceding the main rise is also apparent in this band, seems to suggest that it is unlikely to be a precursor.
Open with DEXTER

4.3 Erratic time variability

A temporal analysis of the 40-700 keV data with Fourier techniques was performed for each of the two flares. In the case of the 1998 flare, we limited the analysis to the first 38 s when the 5.2-s periodicity was not well set up yet. We exploited both available time binnings of 7.8125 ms and, for the first 10 s, $\sim $0.5 ms.

Using the longer time binning, for IF01 we estimated the PSD function of the entire light curve in the 0.031-64 Hz frequency range. The resulting PSD, inclusive of the Poissonian variance, is shown in Fig. 8. We adopted the Leahy et al. (1983) normalization, such that the Poissonian noise level has a PSD value of 2. As can be seen from this figure, apart from two apparent peaks at 0.2 and 0.4 Hz due to the $\sim $5.2-s periodicity, the main PSD feature is its strong decrease with frequency. It mainly depends on the fact that the light curve we are analyzing is a non-stationary process.


  \begin{figure} \par\includegraphics[height=7.0cm,width=5.0cm,angle=270,clip]{0511_08.ps} \end{figure} Figure 8: Measured PSD of IF01 using as time binning 7.8125 ms. Solid line: PSD of the best-fit exponential function used to describe the mean light curve of IF01, excluding the precursor (see text). Dashed line: Poissonian level corrected for the dead time.
Open with DEXTER

Indeed, in the null hypothesis that the light curve is a non-stationary Poisson process x(t) of duration T and mean value given by the deterministic function $\lambda(t)$, the mean PSD of the process at frequency f, $\overline{S}_x(f)$, is given by (Frontera & Fuligni 1979):

 \begin{displaymath}\overline{S}_x(f) = S_\lambda(f) + 2 \end{displaymath} (1)

where $S_\lambda(f)$ is the power spectrum of $\lambda(t)$ (Leahy et al. 1983 normalization adopted). Actually, the PSD of a non-stationary process can also be influenced by other effects, like the detector dead time ( $\tau=4 \mu$s in our case), and the binning time (coincident with the sampling time). For low frequencies ( $f\ll f_\tau$ where $f_\tau = 1/2\pi\tau$), as in our case (Nyquist frequency fN= 64 Hz), the dead time changes the PSD level by a factor $(1 - \mu~\tau)^2$, where $\mu$ is the average measured count rate (Frontera & Fuligni 1978; see also van der Klis 1989). The dead time effect, consistently with an expected correcting factor of 0.949 (from the mean count rate $\mu=6412$ cts s-1) is visible in the Poissonian level shown in Fig. 8.

Following the working scheme adopted by Frontera & Fuligni (1979), we have tested the null hypothesis that the measured PSD can be entirely explained in terms of a non-stationary process. Assuming that the average behaviour of the IF01 light curve can be described by an exponential $\lambda(t) = A U(t) {\rm e}^{-k t}$, where U(t) is the step function (time origin at the main rise of the flare, see discussion above), and A and k are free parameters, the expected PSD is $S_\lambda(f) = 2 A^2/[\mu T (k^2 + (2\pi f)^2)]$. From the fit to the light curve, we derived the best-fit parameters of the exponential and thus the PSD of the function $S_\lambda(f)$. After the addition of the Poissonian statistics corrected for the dead time, the expected PSD is shown in Fig. 8 as continuous line. As can be seen from this figure, $S_\lambda(f)$ dominates the PSD up to $\sim $10 Hz where it achieves the Poissonian level. We have found that the power in excess of $S_\lambda(f)$ is negligible even above 10 Hz, with no evidence of a non-Poissonian noise up to 64 Hz. A similar analysis, performed in the first 10 s after the trigger using the high-time resolution binning of $\sim $0.5 ms, has also given a negative result up to 1 kHz (see Fig. 9), with the conclusion that up to a frequency of 1 kHz no significant non-Poissonian noise is present in the time variability of IF01.


  \begin{figure} \par\includegraphics[height=7.0cm,width=5.0cm,angle=270,clip]{0511_09.ps} \end{figure} Figure 9: 20 Hz-1 kHz PSD of IF01 measured in the time interval [+0.7,+10.7] s after subtraction of the non-stationary Poissonian noise dead-time corrected.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=7.0cm,width=5.0cm,angle=270,clip]{0511_10.ps} \end{figure} Figure 10: PSD of the first 38 s of GF98 with time origin 1 s after the onset, in order to exclude the spike. The time binning used is 7.8125 ms. Solid line: PSD of the best-fit exponential function used to describe the mean light curve. Dashed line: Poissonian level corrected for the dead time.
Open with DEXTER

Following the same guidelines adopted above for IF01, we performed the PSD estimate of the first 38 s of GF98 after the initial spike. The resulting PSD is shown in Fig. 10 along with the $S_\lambda(f)$(continuous line), obtained from the best-fit of the exponential function $\lambda(t)$ to the data, plus the Poissonian level corrected for the dead time. As it can be seen, also in this case $S_\lambda(f)$ dominates the measured power spectrum up to $\sim $10 Hz, even if some evidence of an excess power over the non stationary Poissonian noise is visible.

To avoid a contamination of the PSD from the non-stationary component, we focused on the high-frequency domain deriving the PSD of the first 8 s after the spike, with high-time resolution binning ($\sim $0.5 ms). The resulting PSD is shown in Fig. 11, where it can be seen that, above 20 Hz, $S_\lambda(f)$ gives a small contribution to the total power and, above 100 Hz, does not contribute at all (see also the inset in Fig. 11).


  \begin{figure} \par\includegraphics[height=7.0cm,width=5.0cm,angle=270,clip]{0511_11.ps} \end{figure} Figure 11: PSD of GF98 in the time interval [+1, +9] s. Continuum line: PSD of the best-fit exponential function used to describe the first 10 s of the mean light curve. Dashed line: Poissonian level corrected for dead time. Inset: zoomed high-frequency PSD.
Open with DEXTER

The excess power with respect to the non-stationary Poisson model in the 6-1000 Hz for the GRBM unit 1 is shown in Fig. 12. As can be seen, this time a relevant residual power is apparent up to 1 kHz. The non-Poissonian spectrum $S_{\rm np}(f)$ in the range 10-1000 Hz is well fit with a power law ( $S_{\rm np}(f) \propto f^{-\alpha}$) with $\alpha = 0.74 \pm 0.18$. An excess power has also been found in the PSD of the other GRBM units (2, 3, and 4). The cumulative result is shown in Fig. 13. A power-law still gives the best description of the non-Poissonian spectrum with a best-fit power-law index of $0.75\pm 0.15$, even though also a flicker noise ( $S_{\rm np} \propto 1/f$) gives an acceptable fit ( $\chi^2/{\rm d.o.f.} = 10.6/9$). Using the power-law best-fit values, the total fractional variation (in rms units) in the range 10-1000 Hz comes out to be around 1%. Concerning IF01, as far as we assume similar fractional variability, we could not detect it because of the worse statistics; therefore, we cannot rule out the presence of similar non-Poissonian noise with comparable power for IF01.


  \begin{figure} \par\includegraphics[height=7.0cm,width=5.0cm,angle=270,clip]{0511_12.ps} \end{figure} Figure 12: PSD of the residual noise of GF98 in the time interval [1-9] s. Solid line: best-fit power-law (see text).
Open with DEXTER

   
4.4 Spectral properties

The two available source count rate spectra (A and B) of IF01 and the three (A, B, and C) source spectra of GF98 are shown in Figs. 14 and 15, respectively. For GF98, the A spectrum (inclusive of the initial spike) is well determined up to 700 keV, the B spectrum up to $\sim $500 keV and the C spectrum up to 200 keV. As far as IF01 is concerned, the spectrum A is well determined up to 700 keV, while the B spectrum can only be estimated up to 100 keV. In the following, we limited our analysis to the energy bands where significant source counts were detected.


  \begin{figure} \par\includegraphics[height=7.0cm,width=5.0cm,angle=270,clip]{0511_13.ps} \end{figure} Figure 13: PSD of GF98 for the interval [+1-+9] s averaged over the four GRBM units. Solid line: best-fit power law (see text).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=5.0cm,angle=270,clip]{0511_14a.ps}\par... ...ace*{2mm} \includegraphics[width=5.0cm,angle=270,clip]{0511_14b.ps} \end{figure} Figure 14: Count rate spectra of IF01 and their fit with a BB + BKNPL during the interval A, and with a BB model during the interval B. The residuals to the models are shown as well.
Open with DEXTER

Table 2: Best-fit parameters of the IF01 and GF98 photon spectra.

Several single, two-component and three-component models were tested to fit these spectra. In the case of the A spectrum of IF01, models like a power-law PL, a cutoff power law ( CUTOFFPL), a single BB, an OTTB with or without a power-law PL, are unsatisfactory, even in the 40-300 keV energy band. Up to 300 keV, a BKNPL plus either a BB or an OTTB give a good fit ( $\chi^2/{\rm d.o.f.} =56/65$ with BB and $\chi^2/{\rm d.o.f.} =61/65$ with OTTB). Also the sum of two BB cannot be ruled out ( $\chi^2/{\rm d.o.f.}=72.6/66$). In the top panel of Fig. 14 we show the fit of the A spectrum with the BB plus BKNPL model. Clearly, an excess to the model is apparent in the 300-700 keV band. The best fit of the entire spectrum is obtained when a PL is added to either a BB + BKNPL model or an OTTB + BKNPL model. The best-fit parameters along with the $\chi^2$ values are reported in Table 2, while in Fig. 16 (top) the EF(E) spectrum along with one of the best models ( BB + BKNPL + PL) and the residuals to the model are shown. By adding a PL to the double BB, the fit goodness ( $\chi^2/{\rm d.o.f.}=83/74$) is also acceptable, even though worse than the fit with the two previous models, with the following best-fit parameters: $kT_{\rm bb1}=13.5^{+0.2}_{-0.2}$ keV, $kT_{\rm bb2}=33^{+2}_{-3}$ keV, and $\Gamma=-1.06^{+0.64}_{-0.03}$.

The B spectrum (derived up to only 100 keV) can be fit with either a BB or an OTTB ( $\chi^2/{\rm d.o.f.} = 17.6/14$ and $\chi^2/{\rm d.o.f.} = 16.7/14$, respectively). The best-fit parameters are also reported in Table 2, while the EF(E) spectrum and its best-fit model are shown in Fig. 16 (bottom panel). The multi-component models adopted for the A spectrum also yield acceptable fits of this spectrum.


  \begin{figure} \par\includegraphics[width=5.0cm,angle=270,clip]{0511_15a.ps}\par... ...ace*{2mm} \includegraphics[width=5.0cm,angle=270,clip]{0511_15c.ps} \end{figure} Figure 15: Count rate spectra of GF98 and their fit with a BB + BKNPL during the interval A and B, and with a BB model during the interval C. The residuals to the model are shown as well.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=5.0cm,angle=270,clip]{0511_16a.ps}\par... ...ace*{2mm} \includegraphics[width=5.0cm,angle=270,clip]{0511_16b.ps} \end{figure} Figure 16: EF(E) spectra of IF01. Top panel: A spectrum along with the best fit with a BB+BKNPL+PL model. Bottom panel: B spectrum along with the fit with a BB. Also the single model components and the residuals (in units of $\sigma $) to the best-fit models are shown.
Open with DEXTER

As far as the GF98 spectra are concerned, first of all we caution that the results of the fits of the A spectrum can be can be influenced by the dramatic dead-time and pile-up effects due to the hard initial spike contribution, the hardness of which rapidly changes with time (see Mazets et al. 1999b and also F99).

In spite of that, the best fit of the A spectrum is obtained using as input the three-component models which best fit the A spectrum of IF01: either a BB plus BKNPL plus PL or an OTTB plus BKNPL plus PL. The best-fit parameters along with the $\chi^2$ values are also reported in Table 2, while in Fig. 17 (top) the EF(E) spectrum along with one of the best models ( BB + BKNPL + PL) and the residuals to the model are shown. The simple BB + PL or the OTTB + PL models, which were found to provide a good fit of the same spectrum with the preliminary GRBM response function and the 10% systematic error adopted by F99, with the improved response function provide unsatisfactory fits ( $\chi^2/{\rm d.o.f.} > 2$ with ${\rm d.o.f.} = 189$).


  \begin{figure} \par\includegraphics[width=5.0cm,angle=270,clip]{0511_17a.ps}\par... ...ace*{2mm} \includegraphics[width=5.0cm,angle=270,clip]{0511_17c.ps} \end{figure} Figure 17: EF(E) average spectra of GF98. Top panel: A spectrum with superposed the best-fit model BB+BKNPL+PL. Middle panel: B spectrum with superposed the best-fit model BB+BKNPL. Bottom panel: C spectrum with superposed the best-fit model BB+PL. Also the model components and the residuals to the best-fit models are shown.
Open with DEXTER

The fit of the B spectrum was limited to the 40-500 keV energy band. The best-fit model is obtained with either a BB+BKNPL ( $\chi^2/{\rm d.o.f.} = 50.3/69$) or an OTTB+BKNPL ( $\chi^2/{\rm d.o.f.} = 50.7/69$). However, in the latter case, the lower limit to the photon index $\Gamma_1$ cannot be constrained (see Table 2). In agreement with the results by F01, we find that the OTTB + PL model, the BB + PL and the Band model (Band et al. 1993) are definitely unacceptable (e.g., $\chi^2/{\rm d.o.f.}= 860/70$ for the former model). However, we find that also the double BB plus PL model, which was found by F01 to provide the best fit to the GRBM plus Ulysses spectral data, does not provide a good fit to the 40-500 keV GRBM data alone with the improved response function ( $\chi^2/{\rm d.o.f.}=99/69$). The best-fit parameters are reported in Table 2, while in Fig. 17 (middle panel) we show the EF(E) spectrum with superposed the best-fit BB + BKNPL model and the residuals to the model.

The C spectrum could be estimated in an even more restricted energy band (40-200 keV), due to the poor statistics above 200 keV. The fit with a simple BB gives a $\chi^2/{\rm d.o.f.} = 52/38$, with a chance probability of 6.5%. By adding a PL component, the fit improves ( $\chi^2/{\rm d.o.f.} = 41.3/36$) even if the photon index cannot be strongly constrained (<2.6 at 90% CL). However, this component is needed to model the high-energy excess with respect to the BB component. The best-fit parameters of the BB + PL model are reported in Table 2, while the EF(E) spectrum along with the best-fit model and the residuals to the model are shown in Fig. 17 (bottom panel).

The 40-700 keV fluence in each of the time intervals is shown in Table 2. For the interval A of GF98 we have estimated only the lower limit of the 40-700 keV fluence due to the high dead-time and pile-up effects during the initial spike.

The contribution to the fluence from the BKNPL component is the most relevant in most of the time of the GF98 event and for almost the entire time duration of the IF01 (see Figs. 16 and 17). In the case of GF98, assuming BB as thermal component, the fractional contribution of the BKNPL component is 86% in the interval A and 75% in the interval B, while it is 68% in the time interval A of IF01. These values decrease if the BB is replaced by an OTTB. Instead the fractional contribution of the high-energy PL component, which is apparent only in the time interval A of both GF98 and IF01 (and, perhaps, in GF98 C as well), is only 2%. It is interesting the fact that this component, which in the case of GF98 could be attributed to the initial spike, is also present even in the case of IF01, which does not exhibit any spike.

The total 40-700 keV fluence of the IF01 event is $S_{01} = 1.2 \times 10^{-4}$ erg cm-2 to be compared with a value $S_{98} = 1 \times 10^{-3}$ erg cm-2 derived for GF98, which must be considered a lower limit of the real fluence as explained above.

4.5 Spectral evolution

Given that only two energy channels are available on 1-s integration time, the only way to investigate how the spectrum evolves with time is the ratio between the counting rates in the 100-700 keV channel and those in the 40-100 keV channel (Hardness Ratio, HR). However, since the two flares occurred at different directions with respect to the BeppoSAX local frame, the differences in the HRmight be at least partially ascribed to the different instrumental response. Because of this, in order to compare the absolute hardnesses, we studied the equivalent kT of an OTTB model, although in principle it does not provide us with an acceptable fit of the time-averaged spectra.

The time behaviour of kT for the entire duration of GF98 is already reported (F01). Limiting the kT of GF98 to the first 40 s, for a comparison with IF01 (see Fig. 18), we see that the kT of IF01 is significantly lower than that of GF98. In addition it does not exhibit any significant variations throughout the event. In particular, there is no clear indication of correlation between kT and the modulation observed in the flare profile. However, a slight trend of the kT to increase with time and then to decrease before the end of the event is apparent.


  \begin{figure} \par {\hspace*{2mm}\includegraphics[width=5.0cm,angle=270,clip]{0... ...ace*{2mm} \includegraphics[width=5.0cm,angle=270,clip]{0511_18b.ps} \end{figure} Figure 18: Time behaviour of the equivalent kT of an OTTB model for the entire duration of IF01 and for the early part of GF98. Error bars are 90% CL. Top panel: GF98; bottom panel: IF01.
Open with DEXTER

5 Discussion

The two large flares were classified on the basis of their energetics and durations as giant (GF98) and intermediate (IF01) (Kouveliotou et al. 2001). We find this classification appropriate when their 40-700 keV fluence is considered ( $S_{98} > 1 \times 10^{-3}$ erg cm-2, $S_{01} = 1.2 \times 10^{-4}$ erg cm-2), which give a ratio of >10. However, in the next sections we discuss other similarities and distinctive features of the two events on the basis of their spectra and temporal variability.

5.1 Light curves

For the duration of IF01 ($\sim $40 s), both light curves of GF98 and IF01 are characterized for most part of the time by a $\sim $0.2 Hz pulsation, with complex and variable shape of the periodic pulses. The pulse shapes are different in the two cases. Only dips between pulses appear the common feature of both light curves. The most distinguishing feature of the GF98 light curve is the presence of an initial spike, which is not observed in the case of IF01. In fact, given the difficulty of justifying the first weak pulse in the IF01 light curve as a precursor (see Sect. 4.2), it appears that the initial GF98 spike corresponds to this pulse (if the two events are assumed to be "phased'' by their dips). This is one of the most important results of our comparative analysis.

The periodicity found in the IF01 light curve ( $P_{01} = 5.21 \pm 0.05$ s) is consistent with that measured during the source quiescence before and soon after the event ( $P_{\rm quiesc} = 5.17284268$ s) (Woods et al. 2003).

Within the magnetar model scenario (see F01, Thompson & Duncan 2001), the 1998 giant flare is triggered by a distortion of the internal magnetic field in the neutron star core, that induces large-scale fractures in the crust and strong magnetic shears in the magnetosphere, that drive reconnection and conversion to Alfvén waves. According to this view, the initial spike is the signature of a relativistic outflow with a very low baryon load, as also suggested by the radio transient observed by Frail et al. (1999) and corroborated by the highly structured temporal profile of the spike, with peaks as narrow as $\sim $10-2 s (Mazets et al. 1999b), whereas the pulsating tail would be due to the fraction (about 50%) of energy trapped in the magnetosphere in the form of a photon-pair plasma. A similar scenario for the IF01 time profile is clearly problematic: we do not see the spike. The spike absence could be explained in several ways. We focus on three possibilities: first, no huge energy release comparable to that of GF98 occurred; second, the spiking event occurred, but the beamed outflow was not directed toward our line of sight; third, a comparable or slightly less energetic release really occurred, but the permanent changes undergone by the magnetosphere after the global reconfiguration further to GF98 (Woods et al. 2001) are responsible for the unusual time profile of IF01. The first explanation seems the most natural, since it easily accounts for the lower X- and $\gamma$-ray fluence of IF01 and seems to agree with the minor changes observed in the trend of the pulsation profile after the flare against what occurred after GF98 (Gögüs et al. 2002; Woods et al. 2003). However the light curve of IF01 shows some similarities (e.g., dips at the same phase in the correspondence case of Fig. 4) to the initial stage of GF98. Furthermore, the pulse profile during IF01 appears far more complex than it appeared at the later stages of GF98 (Mazets et al. 1999b) and than that of the quiescent pulsar after 1998 (Gögüs et al. 2002; Woods et al. 2003). This suggests that a transient reconfiguration of the magnetic field took place related to this event, that caused the complex pulse profile evolution during the burst. In addition, the detection of a non-thermal X-ray afterglow after this event raises the issue of a possible GRB-like mechanism for explaining this emission (Feroci et al. 2003; Ioka 2001), that in turn would imply an outflow of relativistic particles (whose signature is missing in IF01, however).

In the context of the magnetar model, F01 pointed out that the envelope of the light curve can give an important clue about the radiation emission mechanisms and/or the geometry during the flares. Thompson & Duncan (2001), assuming that the emitted luminosity is the result of a cooling fireball trapped on the closed magnetic field lines of a neutron star, expect that it varies as a power of the remaining fireball energy Ea. As a consequence the fading law of the radiation is expected to vary as $L(t) = L(0) (1-t/t_{\rm evap})^{a/(1-a)}$, where $t_{\rm evap}$ is the time at which the fireball evaporates and its radius shrinks to zero, while adepends on the trapped fireball geometry and temperature distribution (a=2/3or a=1/2 in the case of spherical or cylindrical geometry, respectively). F01 found, for GF98, $t_{\rm evap}=(501\pm 13)$ s and $a= 0.828\pm0.005$ in the 40-100 keV range, and $t_{\rm evap}=(545\pm 62)$ s and $a= 0.85\pm0.01$in the 100-700 keV band. We find for the 40-700 keV the result shown in Fig. 19 with the following best fit parameters: $t_{\rm evap}=(35.25\pm0.11)$ s, $a= 0.413\pm0.004$. This result shows that, in contrast to the spherical-like geometry of GF98, the trapped fireball responsible for the pulsating tail of IF01 had probably a cylinder-like geometry ($a\sim 1/2$), with a non uniform temperature distribution (that has the effect of decreasing the value of the fireball index a).


  \begin{figure} \par\includegraphics[height=7.5cm,angle=270,clip]{0511_19.ps} \end{figure} Figure 19: Light curve of IF01; the dashed line is the best fit with a fireball model obtained for the time interval [7.46875-38.5] s, rebinned at 5.171875 s; the solid line shows the best fit applied to the interval [3-38] s, whose parameters have been constrained to vary within 1$\sigma $ around the best fit of the tail.
Open with DEXTER

5.2 Erratic time variability

From the PSD estimates, it clearly emerges that GF98 has time properties which are not observed in the case of IF01. A significant power above the Poissonian level is apparent up to 1 kHz in the PSD of GF98, with a power-law shape (index $\alpha = 0.75 \pm 0.15$) with frequency. Even if the 10-1000 Hz fractional variation (in rms units) is only 1%, the PSD shows the clear presence of a flicker-like noise, similar to that observed in many accreting compact X-ray sources.

Barat et al. (1983) found evidence of timing noise in the X-ray decay of the March 5 burst from SGR0526-66, although in that case it was identified as due to $\sim $23 ms quasi-periodic oscillations. An interpretation of the flicker-like noise in the light of the magnetar model is needed, although it could be possibly explained invoking the mechanisms described by Duncan (1998) and by Ioka (2001): they account for the ms quasi-periodicity as due to the excitation of global seismic oscillations of the crust coupling strongly to Alfvén modes in the lower magnetosphere.

A possible phenomenological interpretation of the detected noise is in terms of clustering of elementary pulses. In this case the noise dependence on frequency is determined by the distribution of waiting times between subsequent pulses and, possibly, by the distribution of the pulse intensity. There is a big variety of mechanisms that, in principle, may generate power-law noise with $\alpha\approx1$: see, e.g., Kaulakys & Meskauskas (1998) and references therein. Davidsen & Schuster (2002) propose a simple mechanism for generating pulse sequences with $S(f) \propto f^{-\alpha}$ in systems whose dynamics is driven by a variable threshold, like for earthquakes. This kind of mechanism is also known as an integrate-and-fire (IAF) model. It requires a threshold C(t) evolving with time according to a Brownian motion with diffusion constant D within a defined interval $C_{\rm l}<C(t)<C_{\rm u}$. Assuming a function V(t) which linearly increases with time, as soon as V(t) matches the threshold C(t), it is reset to a starting value V0 and a single pulse is produced, leaving C(t)unaltered. Under proper choices of the threshold boundaries, diffusion constant and reset value, the PSD of the resulting pulse train is characterized by a PSD with a power-law shape with index $\alpha$, which is typically between 0.5 and 1.1. The similarity of the high-frequency noise with that of earthquakes was also discussed by Cheng et al. (1996), who showed that for a set of bursts from SGR1806-20 the distribution of size and cumulative waiting times are similar to those of earthquakes. These properties have also been verified for the SGR1900+14 short bursts (Gögüs et al. 1999).

In the light of the magnetar model, the observed noise could be the consequence of the dramatic energy release during the initial spike. Likely, the engine which powered the spike is far from equilibrium and the magnetic field lines probably undergo rapid and complex variations. If a threshold-controlled mechanism, like that above described, is at work, unstable fireballs could be created, that burst whenever a particular threshold is exceeded, that might depend on quantities like energy density, magnetic field and its twist. In this scenario, the observed high-frequency noise might be suggestive of how fractures in the crust propagate with time.

5.3 Energy spectra

At first glance, we notice that the GF98 spectrum of the first 40 s is significantly harder than that of IF01, as shown by the comparison of the equivalent temperatures of an OTTB model. However, unlike the discussed differences between the two events, the spectral properties of GF98 and IF01 show striking similarities. In the time interval A, which covers most of the IF01 light curve and during the first 68 s of the GF98 light curve, both 40-700 keV spectra are best fit with the same three-component models ( BB + BKNPL + PL or OTTB + BKNPL + PL; see Table 2). Assuming the former of these models, both the BB temperatures and break energies of the BKNPL model are similar: $kT_{\rm bb}^{98} = 19^{+4}_{-3}$ keV and $E_{\rm break}^{98} = 75^{+1}_{-2}$ keV, $kT_{\rm bb}^{01} = 14.4^{+1.2}_{-0.8}$ keV and $E_{\rm break}^{01} = 73^{+2}_{-2}$ keV, respectively. However the centroids of the BKNPL indices are only marginally consistent at 90% CL, and we remind that the A spectrum of GF98 is likely distorted by dramatic dead-time and pile-up effects suffered during the initial spike.

The BB + BKNPL (+PL) model better agrees with the trapped fireball+corona scenario (Thompson & Duncan 2001), at least in the case of GF98: the BB flux remains almost constant throughout the flare, whereas the BKNPL and PL fade exhibiting a small spectral evolution. This is confirmed also by the temporal evolution of the equivalent kT: while GF98 exhibits a slow decrease during the first 40 s, after which it softens even more slowly, IF01 shows a mild increase followed at the end by a small drop, with no strong spectral evolution. In this scenario, the BB component is due to the outer layer of a trapped fireball, while the BKNPL can partially come from the surrounding corona, and, probably, from the reprocessing of the radiation coming from the inner fireball. Indeed such component, although it decreases, does not disappear in the time interval B of GF98, where the corona should already have evaporated. The BB temperature value in both GF98 and IF01 are above the minimum photospheric temperature of a trapped fireball expected in $B>B_{\textrm{\sc qed}}$ magnetic fields (Eq. (133) from Thompson & Duncan 1995).

While a possible interpretation can be given for the BKNPL, the origin of the high-energy (>300 keV) power-law component, with positive index at least for the A spectra of both events, is more mysterious.

5.4 The last isolated pulse of IF01

The 1.5-s long isolated pulse of IF01 has a shape apparently different from that of the previous pulses. It is narrower and is not in phase with the previous ones. Thus, we are led to think about a different origin for it. A possibility is that, unlike the periodic light curve before it, whose likely origin is in the outer layer of the transient corona, the last pulse could originate in the nearby of the neutron star surface and/or with the same mechanism of typical short bursts. We note that, the occurrence of short bursts during the tail of bright bursts was noted also in the tail of the August 29 event (Palmer 2002). Actually, its average energy spectrum does not appear significantly different from the A spectrum, and Fig. 18 shows that its kTis consistent with general behaviour at previous times. Thus, the last pulse mainly differs from the first part of the flare for its temporal properties rather than for its energy spectrum.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{0511_20.eps} \end{figure} Figure 20: 40-700 keV time profiles of the last isolated pulse of IF01 ( blue) and of the August 29, 1998 burst ( red).
Open with DEXTER

Actually, if we compare this pulse with the peculiar burst of August 29, 1998 (Ibrahim et al. 2001), also detected with the GRBM (see Fig. 20), we find a similar light curve, even if the fluence of the IF01 last pulse ($\sim $ $5\times 10^{-6}$ erg cm-2) is about twice as high as that of the August 29 burst fluence in the 40-700 keV band. Curiously, the duration of the subpulse of the August 29 burst is similar to that of the last pulse of IF01. This similarity could suggest a common origin of the last pulse of IF01 with some of the brightest short bursts recorded from SGR1900+14.

6 Conclusions

The BeppoSAX GRBM was the only instrument that in the same 40-700 keV energy band allowed a detailed study of the two large X-/gamma-ray flares from SGR1900+14 occurred on 1998 August 27 and 2001 April 18. In this paper we have compared the spectral and temporal properties of both flares to study their similarities and distinctive features. Apart from the different time durations of the two flares ($\sim $40 s for IF01 and $\sim $300 s for GF98) and a higher (>10) 40-700 keV fluence of GF98, other distinctive features have also been derived from our analysis. The light curve of IF01 does not show the initial spike exhibited by GF98, and shows a periodicity ( $5.21~ \pm~ 0.05$ s) consistent with the value measured for the quiescent X-ray source soon after IF01 (Woods et al. 2003), with no evidence for a glitch like in the case of GF98 (Woods et al. 1999c). Moreover, it does not show the high-frequency (10-1000 Hz) erratic variability which is detected from GF98, although this might be due to lower counting statistics. However the two flares show also similar spectral properties. The photon spectrum of IF01 and the corresponding spectrum of GF98 during the first 40 s (corresponding to the time duration of IF01) are both best fit with a three-component ( BB + BKNPL + PL) model, with similar BB temperature ($\sim $15 keV) and break energy ( $E_{\rm break} \sim 73$ keV) of the BKNPL model. However, the power-law indices of the BKNPL are different, resulting higher (and the spectrum softer) for IF01. The highest energy sections of the spectra (>300 keV) are both well fit with a power-law with marginally similar positive photon indices. This power-law component contributes, in both cases, to $\sim $2% of the 40-700 keV fluence of the two flares.

In the magnetar model scenario, the entire 2001 flare and the intermediate stage of GF98 (before the pulsation is set up clearly) could be both interpreted as radiation coming from a transient pair-dominated corona surrounding a trapped fireball anchored to the neutron star surface, although other interpretations can be possible. The high-frequency noise, detected during the intermediate stage of GF98, could directly trace the evolution of fractures propagating throughout the neutron star crust soon after the dramatic spike. The PSD of the non-Poissonian noise is in agreement with the expectations of the "Integrate And Fire'' (IAF) model (Davidsen & Schuster 2002), according to which, similarly to earthquakes, discrete energy releases occur when a variable threshold is exceeded.

The appearance of a last isolated pulse at the end of IF01 might point to a different origin from what caused the flare: its peculiar time profile is similar to that of short bursts from the same source. While the main time profile of IF01 could have come from the outer layer of the pair corona, the last pulse might have originated close to the surface.

Acknowledgements
We thank Sandro Mereghetti for carefully reading this manuscript and for his comments. This research is supported by the Italian Space Agency (ASI) and Ministry of University and Scientific Research of Italy. We wish to thank the Mission Director L. Salotti and the teams of the BeppoSAX Operation Control Center, Science Operation Center and Scientific Data Center for their support.

References


Copyright ESO 2004