A&A 415, 617-625 (2004)
DOI: 10.1051/0004-6361:20031640
Monte Carlo radiative transfer
in molecular cloud cores
J. Gonçalves1,2 - D. Galli2 -
M. Walmsley2
1 - Centro de Astronomia e Astrofísica
da Universidade de Lisboa, Tapada da Ajuda, 1349-018
Lisboa, Portugal
2 - INAF-Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5, 50125 Firenze, Italy
Received 15 August 2003 / Accepted 21 October 2003
Abstract
We present the results of a three-dimensional Monte Carlo
radiative transfer code for starless molecular cloud cores heated by an
external isotropic or non-isotropic interstellar radiation field. The
code computes the dust temperature distribution inside model clouds
with specified but arbitrary density profiles. In particular we examine
in detail spherical (Bonnor-Ebert) clouds, axisymmetric and
non-axisymmetric toroids, and clouds heated by an external stellar
source in addition to the general interstellar field. For these
configurations, the code also computes maps of the emergent intensity
at different wavelengths and arbitrary viewing angle, that can be
compared directly with continuum maps of prestellar cores. In the
approximation where the dust temperature is independent of interactions
with the gas and where the gas is heated both by collisions with dust
grains and ionization by cosmic rays, the temperature distribution of
the gas is also calculated. For cloud models with parameters typical
of dense cores, the results show that the dust temperature decreases
monotonically from a maximum value near the cloud's edge (14-15 K) to
a minimum value at the cloud's center (6-7 K). Conversely, the gas
temperature varies in a similar range, but, due to efficient dust-gas
coupling in the inner regions and inefficient cosmic-ray heating in the
outer regions, the gradient is non-monotonic and the gas temperature
reaches a maximum value at intermediate radii. The emission
computed for these models (at 350  m and 1.3 mm) shows that
deviations from spherical symmetry in the density and/or temperature
distributions are generally reduced in the simulated intensity maps
(even without beam convolution), especially at the longer wavelengths.
m and 1.3 mm) shows that
deviations from spherical symmetry in the density and/or temperature
distributions are generally reduced in the simulated intensity maps
(even without beam convolution), especially at the longer wavelengths.
Key words: radiative transfer - ISM: clouds, dust, extinction
Understanding the structure of pre-protostellar cores is an essential
step towards an understanding of protostellar evolution. The density
distribution immediately prior to the onset of gravitational collapse
defines the initial conditions for collapse and hence one has a strong
motivation to attempt to derive this density distribution from the
observations. Since these objects are most commonly observed by means
of their millimeter dust emission, one has a strong interest in
understanding the temperature distribution of the dust in the
pre-protostellar core and its influence on the emergent intensity
distribution at millimeter-submillimeter wavelengths. In this article,
we present a radiative transport code which has the interpretation of
mm-submm maps of pre-protostellar cores as its main goal.
The approach which we have adopted is influenced by the fact that, as a
rule, the density structure of these objects shows evidence for large
deviations from spherical symmetry. More precisely, the maps of the
millimeter dust emission show clear departures from circular symmetry
(see e.g. André et al. 2000; Caselli et al. 2002a,b; Tafalla et al.
2002). In some cases there also evidence for polarization and hence for
a magnetic field (Ward-Thompson et al. 2000). It seems likely to us
that such behaviour is caused by magnetic fields of energy densities
sufficiently large to influence the core structure (see also Shu et al.
1987) and cause flattening along field lines (Basu 2000; Jones &
Basu 2002). We can attempt to infer the density distribution on the
basis of mm-submm continuum maps if we can derive the temperature
distribution in regions where departures from spherical symmetry are
important. A first attempt in this direction was made by Zucconi et al. (2001, hereafter ZWG)
but these authors neglected heating of dust
grains due to re-absorption of photons emitted by the cloud itself.
Here we present a Monte-Carlo code without this limitation but which
is capable of handling a variety of geometries. We expect that this
type of analysis will be especially useful as a tool for the
interpretation of the high class data we expect to come from future
instruments like ALMA and HERSCHEL.
Some high quality data are already available and are consistent with a
picture in which the dust temperature of pre-protostellar cores
decreases towards the center (Ward-Thompson et al. 2002; Bianchi et al. 2003). ISO observations in the mid-IR (Bacmann et al. 2000) and in
the far-IR (Ward-Thompson et al. 2002) suggest dust temperature
gradients consistent with heating from the external interstellar
radiation field (ISRF). The available models predict a factor of 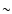 2 increase in temperature from center to edge, with the gradient
dependent on the cloud structure (see, e.g. ZWG, Evans et al. 2001;
André et al. 2003). The predicted emission of several cores is in
reasonable accord with the data, and implies that the assumed
equilibrium configurations are either unstable or maintained by a
magnetic field.
2 increase in temperature from center to edge, with the gradient
dependent on the cloud structure (see, e.g. ZWG, Evans et al. 2001;
André et al. 2003). The predicted emission of several cores is in
reasonable accord with the data, and implies that the assumed
equilibrium configurations are either unstable or maintained by a
magnetic field.
Additional observational constraints on the thermal structure of
prestellar cores are given by spatially resolved measurements of the
gas temperature from NH3 observations. Low-mass cores show fairly
uniform gas temperature (e.g. Tafalla et al. 2002 for L1517B and L1498), whereas massive quiescent cores in Orion show significant
temperature drops from edge to center (Li et al. 2003). Thus another
check on our understanding of core structure is possible if radiative
transfer models are also able to predict the gas temperature
distribution resulting from the balance of the relevant heating and
cooling mechanisms. We therefore have also developed the capability to
predict gas temperature distributions for our model cores.
While techniques have been developed for the study of radiative
transfer in cold cores in one dimension (e.g. Leung 1976;
Rowan-Robinson 1980; Ivezic et al. 1997), their extension to
three-dimensional geometries is not straightforward. A Monte Carlo
technique has the advantage that it deals easily with any general
geometry, independently of the density distribution and the anisotropy
of the incident radiation field. The increasingly faster workstations
available render this technique very useful, and fully 3-D Monte Carlo
radiative transfer codes have been developed recently (e.g. Wolf et al. 1999; Niccolini et al. 2003). However, in these latter studies the
radiative sources are internal, and this is a computationally distinct
problem from a core heated from the outside for two main reasons.
First, as we are interested in cold cores, it is reasonable to expect
that they will be optically thin to their own emission, and therefore,
for methods that use iteration, the temperature distribution quickly
relaxes to the final value; alternatively, for methods that follow
individual packets until they exit the domain, each individual packet
will interact with the dust often only once. Second, as packets are
launched from the outside, a wide range of spatial scales demands a
prohibitively large number of incident photons, as the probability of a
packet being launched in the direction of the innermost cells becomes
increasingly small.
In general, our paper confirms and supports the results recently
obtained for embedded prestellar cores by Stamatellos &
Whitworth (2003) with an independent but similar Monte Carlo radiative
transfer code. While Stamatellos & Whitworth (2003) focus on the
important effect of the ambient medium in which (spherical) cores are
embedded, our paper mostly emphasizes the consequences of deviations
from spherical symmetry in the density distribution and anisotropies of
the ISRF. The two papers represent therefore complementary attempts to
model radiative transfer in molecular cloud cores in less idealized
situations than those considered so far.
The structure of this paper is as follows. In Sect. 2, we set the
general problem of radiative transfer in a dusty cloud. In Sect. 3,
we describe the Monte Carlo method we have used. In Sect. 4, we
present our choice of opacities and interstellar radiation field and
briefly discuss their effect on the results. In Sects. 5 and 6 we
present our results for two- and three-dimensional models,
respectively. Finally, in Sect. 7 we summarize our conclusions.
In local thermodynamic equilibrium and ignoring the effects of
scattering of radiation by dust grains, the radiation field in a dusty
cloud satisfies the equation of transfer
![\begin{displaymath}{\hat{\vec n}}\cdot\nabla I_\nu({\vec r},{\hat{\vec n}})=
\rh...
...[T_{\rm d}({\vec r})]- I_\nu({\vec r},{\hat{\vec n}})\right\},
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img15.gif) |
(1) |
where
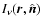 is the specific intensity of
radiation (in Jy ster-1) at position
is the specific intensity of
radiation (in Jy ster-1) at position 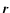 in the direction
in the direction
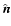 at frequency
at frequency 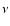 ,
,
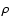 is the total (gas plus dust)
density,
is the total (gas plus dust)
density,
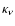 the total absorption opacity,
the total absorption opacity, 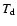 is the
dust temperature, and
is the
dust temperature, and 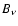 is the Planck function,
is the Planck function,
![\begin{displaymath}B_\nu(T_{\rm d})=\frac{2h \nu^3}{c^2}
\left[\exp\left(\frac{h\nu}{kT_{\rm d}}\right)-1\right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img24.gif) |
(2) |
The dust temperature distribution
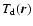 is obtained by
solving the equation of balance of emitted and absorbed radiation,
is obtained by
solving the equation of balance of emitted and absorbed radiation,
![\begin{displaymath}\int^\infty_0 \kappa_\nu B_\nu [T_{\rm d}({\vec r})]\;{\rm d}\nu =
\int^\infty_0 \kappa_\nu J_\nu({\vec r})\;{\rm d}\nu,
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img26.gif) |
(3) |
where
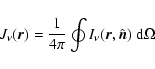 |
(4) |
is the mean intensity of radiation (in Jy).
ZWG made the simplifying assumption that the dust grains are only
heated by the incident interstellar radiation field
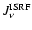 (assumed isotropic), neglecting re-emission of radiation
absorbed by the grains themselves. That is to say, they assumed that
the cloud is optically thin to its own radiation. Under this
hypothesis, the equation of radiative transfer has the solution
(assumed isotropic), neglecting re-emission of radiation
absorbed by the grains themselves. That is to say, they assumed that
the cloud is optically thin to its own radiation. Under this
hypothesis, the equation of radiative transfer has the solution
![\begin{displaymath}J_\nu({\vec r})=\frac{J_\nu^{\rm ISRF}}{4\pi}\oint
\exp[-\tau_\nu({\vec r},{\hat{\vec n}})]\;{\rm d}\Omega,
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img29.gif) |
(5) |
where
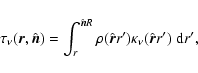 |
(6) |
is the optical depth from a point 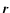 inside the cloud to a point
inside the cloud to a point
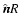 on the cloud boundary, in the direction
on the cloud boundary, in the direction
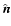 .
The calculation of the radiation field inside the cloud is thus
reduced to a large number of integrations along different directions
(rays) defined at each grid point. This simplification allowed ZWG to
model axisymmetric non-spherical density distributions, but has the
disadvantage of slightly underestimating the dust temperature,
particularly at the cold center of the cloud.
.
The calculation of the radiation field inside the cloud is thus
reduced to a large number of integrations along different directions
(rays) defined at each grid point. This simplification allowed ZWG to
model axisymmetric non-spherical density distributions, but has the
disadvantage of slightly underestimating the dust temperature,
particularly at the cold center of the cloud.
Our general approach is the following. First, for a given ISRF we
compute the radiation field at any point inside the cloud core and
solve the equation of balance of radiation emitted and absorbed by dust
grains to obtain the dust temperature distribution
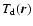 .
Second, we compute the flux emitted in a given view direction at
different wavelengths and we compare the results with observed spectral
energy distributions and monochromatic maps for specific objects.
.
Second, we compute the flux emitted in a given view direction at
different wavelengths and we compare the results with observed spectral
energy distributions and monochromatic maps for specific objects.
In several cases we have also considered the effect of a spherical
envelope surrounding the cloud core on the resulting temperature
distribution. The rationale for this is that these objects are always
embedded in a photon-dominated region (PDR) which transforms the
incident optical-UV field into mid and far IR radiation. Often in
practice, this is radiation from transiently heated particles, either
very small grains or polycyclic aromatic hydrocarbons, emitting in the 3-30  m range. Since we wish to focus on the temperature
structure of the high density core interior, we have decided to assume
that the radiation field incident on embedded cores is cut off in the
optical-UV wavelength range and that the radiation absorbed in the PDR is reradiated in the infrared. We thus incorporate the photons
reradiated by the PDR in the external field. The error involved here
can be estimated by varying the form of the ISRF and appears to be
small (though see the discussion of André et al. 2003). Our focus
here is on the effects of the core geometry upon temperature structure
and we place minor emphasis on the spectral energy distribution of the
incident field.
m range. Since we wish to focus on the temperature
structure of the high density core interior, we have decided to assume
that the radiation field incident on embedded cores is cut off in the
optical-UV wavelength range and that the radiation absorbed in the PDR is reradiated in the infrared. We thus incorporate the photons
reradiated by the PDR in the external field. The error involved here
can be estimated by varying the form of the ISRF and appears to be
small (though see the discussion of André et al. 2003). Our focus
here is on the effects of the core geometry upon temperature structure
and we place minor emphasis on the spectral energy distribution of the
incident field.
We stress that our approach is general: the density distribution, the
optical properties of the dust grains, the intensity and spectral
energy of the radiation source(s) are input parameters that can be
freely specified and can be adapted to model various astrophysical
situations.
In the Monte Carlo technique, the computational domain is divided in a
large number of cells of mass mi that absorb and emit radiation. The
energy that enters the computational domain is divided in 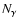 monochromatic packets of equal energy, that are launched stochastically
from the boundary and followed until they exit the cloud. These packets
may be absorbed by the dust particles, resulting in a temperature
increase of the cells where they are absorbed, and are immediately
reemited to enforce radiative equilibrium. If the cell i absorbs Ni packets, the energy absorbed by the cell per unit time is
monochromatic packets of equal energy, that are launched stochastically
from the boundary and followed until they exit the cloud. These packets
may be absorbed by the dust particles, resulting in a temperature
increase of the cells where they are absorbed, and are immediately
reemited to enforce radiative equilibrium. If the cell i absorbs Ni packets, the energy absorbed by the cell per unit time is
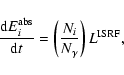 |
(7) |
where
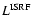 is the luminosity of the ISRF at the
cloud's surface, obtained integrating the mean intensity of the
(anisotropic) ISRF over the cloud's surface and over frequency,
is the luminosity of the ISRF at the
cloud's surface, obtained integrating the mean intensity of the
(anisotropic) ISRF over the cloud's surface and over frequency,
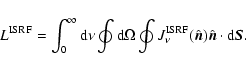 |
(8) |
Assuming LTE conditions, the energy emitted by the ith cell per unit time is
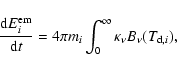 |
(9) |
where
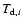 is the dust temperature of the ith cell,
obtained by equating the absorbed and emitted energies per unit time,
is the dust temperature of the ith cell,
obtained by equating the absorbed and emitted energies per unit time,
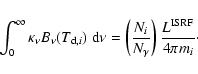 |
(10) |
The integral on the left-hand side of this equation can be tabulated
for a grid of values of the dust temperature and opacity. The solution
of Eq. (10) can then be easily obtained by iteration and
interpolation. In the limit to the continuum,
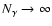 and
and
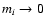 ,
Eq. (10) is equivalent
to Eq. (3), but differs from the approximation adopted
in ZWG, Eq. (5), because in Ni are included the packets
that may have been absorbed more than once in the cloud, and
subsequently re-emitted.
,
Eq. (10) is equivalent
to Eq. (3), but differs from the approximation adopted
in ZWG, Eq. (5), because in Ni are included the packets
that may have been absorbed more than once in the cloud, and
subsequently re-emitted.
We handled re-radiation (and, therefore, energy conservation) using the
method devised by Bjorkman & Wood (2001): once a packet is absorbed,
it is immediately re-emitted (to conserve energy) at a new frequency
determined by the local dust temperature. To achieve this, one starts
by noting that if a cell has emissivity
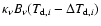 prior to absorbing a wave packet, then
after packet absorption its temperature increases by an amount
prior to absorbing a wave packet, then
after packet absorption its temperature increases by an amount
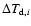 ,
and the cell emissivity becomes
,
and the cell emissivity becomes
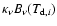 .
Thus, the increment in the cell emissivity is
.
Thus, the increment in the cell emissivity is
A photon packet is immediately reemitted with
a frequency obtained from a probability distribution having the same
spectral shape as
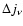 ,
,
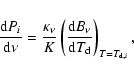 |
(12) |
where
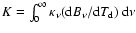 is a
normalization constant. The re-emitted photon packet is then followed
until a new interaction occurs, and the procedure is repeated until the
photon leaves the cloud. This method ensures energy conservation in a
statistical sense. Due to the low temperature of the cores, energy is
generally re-radiated at long wavelengths, to which the core has a low
optical depth, and the overall effect of re-emission on the dust
temperature is more significant in the core's cold interior but is
generally very small.
is a
normalization constant. The re-emitted photon packet is then followed
until a new interaction occurs, and the procedure is repeated until the
photon leaves the cloud. This method ensures energy conservation in a
statistical sense. Due to the low temperature of the cores, energy is
generally re-radiated at long wavelengths, to which the core has a low
optical depth, and the overall effect of re-emission on the dust
temperature is more significant in the core's cold interior but is
generally very small.
We have tested our Monte Carlo code in different ways. Here we present
the results of two complementary tests, one checking the accuracy of
the packet propagation procedure and one checking the equality of
emitted and absorbed energy.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{H4706f1.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg51.gif) |
Figure 1:
Comparison of dust temperature profiles obtained with
different methods for a BE sphere with central density
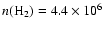 cm-3, gas temperature cm-3, gas temperature
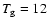 K, and radius
R=0.1 pc. The solid and dotted curves shows the result
obtained with the ray integration method of ZWG and the Monte Carlo
code, without including the effects of re-emission. The two results are
in excellent agreement. The short-dashed curve shows the dust
temperature computed with the Monte Carlo code including re-emission.
In all three cases the cloud has no envelope. K, and radius
R=0.1 pc. The solid and dotted curves shows the result
obtained with the ray integration method of ZWG and the Monte Carlo
code, without including the effects of re-emission. The two results are
in excellent agreement. The short-dashed curve shows the dust
temperature computed with the Monte Carlo code including re-emission.
In all three cases the cloud has no envelope. |
| Open with DEXTER |
To test the packet propagation procedure, we have computed dust
temperatures profiles for spherically symmetric clouds, for which
results can also be obtained with the ray integration method of ZWG.
Specifically we have assumed the density profile of a Bonnor-Ebert (BE)
sphere, an isothermal, pressure-bounded, equilibrium model, that
reproduces the centrally flattened density distribution and the rapid
density decrease at large radii observed in most cloud cores.
Figure 1 shows the dust temperature as function of radius
for a BE with radius R=0.1 pc, central density
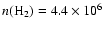 cm-3, and isothermal gas temperature
cm-3, and isothermal gas temperature
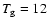 K
(note that the gas temperature here is merely for the purpose of
specifying the assumed density distribution). As shown in
Fig. 1, the result obtained using the ray integration
method (solid line), is identical to the Monte Carlo result using the
same approximation of optically thin re-emission (dotted line). We also
notice that when re-emission is taken into consideration (dashed line),
there is only a small increase of the central temperature, even in this
case, when the extinction through the core center is
K
(note that the gas temperature here is merely for the purpose of
specifying the assumed density distribution). As shown in
Fig. 1, the result obtained using the ray integration
method (solid line), is identical to the Monte Carlo result using the
same approximation of optically thin re-emission (dotted line). We also
notice that when re-emission is taken into consideration (dashed line),
there is only a small increase of the central temperature, even in this
case, when the extinction through the core center is
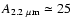 ,
and the central dust temperature is little more than 6 K.
,
and the central dust temperature is little more than 6 K.
To test energy conservation, we have computed the energy emitted per
unit time by an arbitrary area element on the cloud's surface by
integrating 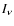 (the solution of Eq. (1)) and
(the solution of Eq. (1)) and
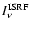 over solid angles and frequencies, finding a very
small discrepancy between the two values (less than 1%). This test
shows that for the given number and size of cells, the accuracy of
Eqs. (10) and (12), that contain
approximations introduced by the discretization of the computational
volume, is very good.
over solid angles and frequencies, finding a very
small discrepancy between the two values (less than 1%). This test
shows that for the given number and size of cells, the accuracy of
Eqs. (10) and (12), that contain
approximations introduced by the discretization of the computational
volume, is very good.
Following ZWG and Evans et al. (2001), we adopt as a reference the ISRF
given by Black (1994), which is an average for the solar
neighbourhood. Scaling the intensity of the ISRF by a factor G0leads to a change in the dust temperature at all radii by a factor of
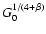 ,
where
,
where
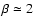 is the power law index for
the long wavelength opacity. Actually the radiation incident on
molecular cloud cores may differ not only in intensity but also in
spectral shape, depending on the degree of embedding of the cores in
the ambient cloud and on the possible vicinity to hot stars. It
appears for example to be the case that many cores associated with the
is the power law index for
the long wavelength opacity. Actually the radiation incident on
molecular cloud cores may differ not only in intensity but also in
spectral shape, depending on the degree of embedding of the cores in
the ambient cloud and on the possible vicinity to hot stars. It
appears for example to be the case that many cores associated with the
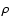 Oph star forming regions are subjected to an incident ISRF
roughly an order of magnitude larger than the solar neighbourhood ISRF.
An example of what can happen is given by a recent study by André et al. (2003) of a particular core, heated by a ISRF higher than the Black
field by an order of magnitude in both the mid-IR and far-IR. This
resulted in a higher central temperature and a sharper gradient at the
edge than in our models for a similar density distribution. Thus
observers attempting to infer density distributions from maps of the
mm-submm dust emission must bear in mind the fact that both the
radiation field and the geometry can play a role.
Oph star forming regions are subjected to an incident ISRF
roughly an order of magnitude larger than the solar neighbourhood ISRF.
An example of what can happen is given by a recent study by André et al. (2003) of a particular core, heated by a ISRF higher than the Black
field by an order of magnitude in both the mid-IR and far-IR. This
resulted in a higher central temperature and a sharper gradient at the
edge than in our models for a similar density distribution. Thus
observers attempting to infer density distributions from maps of the
mm-submm dust emission must bear in mind the fact that both the
radiation field and the geometry can play a role.
In this paper however, our objective is to study the effects of
geometry rather than those of the spectral characteristics or intensity
of the incident radiation field. Geometry in this context can mean
the geometry of the density distribution or that of the radiation
field. We thus also consider a case where we use our Monte Carlo model
to consider an anisotropic incident ISRF as exists in many galactic
reflection nebulae.
We adopt the dust opacities tabulated by Ossenkopf & Henning (1994,
hereafter OH) in the wavelength range 1  m-1.3 mm. Recent work by
Bianchi et al. (2003) and by Kramer et al. (2003) has shown that these
theoretically derived opacities are consistent with the observed ratio
of mm dust continuum intensity and near infrared extinction. It is
also clear from the study by OH that one can expect the dust opacity to
vary between the lower density outer layers of a core and the high
density interior where most of the heavy element content of the core is
in the form of ice of various sorts. We neglect such effects in this
study mainly because, as shown below, the variation between different
OH dust models is relatively mild.
m-1.3 mm. Recent work by
Bianchi et al. (2003) and by Kramer et al. (2003) has shown that these
theoretically derived opacities are consistent with the observed ratio
of mm dust continuum intensity and near infrared extinction. It is
also clear from the study by OH that one can expect the dust opacity to
vary between the lower density outer layers of a core and the high
density interior where most of the heavy element content of the core is
in the form of ice of various sorts. We neglect such effects in this
study mainly because, as shown below, the variation between different
OH dust models is relatively mild.
We label the opacity according to the column number in Table 1 of OH:
OH1, standard MRN distribution; OH4, MRN with thin ice mantles; OH5,
MRN with thin ice mantles, after 105 yr of coagulation at density 106 cm-3; OH8, MRN with thick ice mantles, after 105 yr of
coagulation at density 106 cm-3.
The OH opacities are tabulated for wavelengths between 1  m and 1.3 mm. Within this range we have obtained values of the opacity at
arbitrary wavelengths by four-point interpolation and above 1.3 mm, we
have used a power law extrapolation based on the last two tabulated
values. We neglect scattering completely as we are interested in the
transport of infrared photons.
m and 1.3 mm. Within this range we have obtained values of the opacity at
arbitrary wavelengths by four-point interpolation and above 1.3 mm, we
have used a power law extrapolation based on the last two tabulated
values. We neglect scattering completely as we are interested in the
transport of infrared photons.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{H4706f2.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg58.gif) |
Figure 2:
Dust temperature profiles (including re-emission) for the cloud
model shown in Fig. 1 for different choices of the dust opacity:
solid curve, OH1; dotted curve, OH4; short-dashed curve, OH5; long-dashed curve, OH8 (see text for the definitions). The
gas-to-dust ratio was varied so that the total extinction at
2.2  m is the same in all cases. The cloud is embedded in a spherical
outer envelope with total extinction m is the same in all cases. The cloud is embedded in a spherical
outer envelope with total extinction
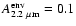 . . |
| Open with DEXTER |
The effect of the various opacities on the temperature profile of a
cloud is shown in Fig. 2, for the reference case of a
BE sphere with central density
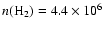 cm-3,
radius 0.1 pc, gas temperature
cm-3,
radius 0.1 pc, gas temperature
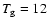 K, embedded in a
spherical envelope with total extinction
K, embedded in a
spherical envelope with total extinction
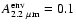 .
In this particular example, the gas-to-dust ratio was varied for
each opacity prescription in order to keep fixed the total extinction
at 2.2
.
In this particular example, the gas-to-dust ratio was varied for
each opacity prescription in order to keep fixed the total extinction
at 2.2  m.
m.
As Fig. 2 shows, temperature variations due to
different choices of the opacity are generally small. The opacities OH1, OH4 and OH5 have a similar dependence on wavelength, and the
resulting temperature difference is equivalent to scaling the intensity
of the ISRF by about 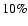 .
The OH8 opacity, having a slightly
different dependence on wavelength, results in a the temperature
profile slightly different from the other three cases. In all remaining
models presented in this study we have used OH5.
.
The OH8 opacity, having a slightly
different dependence on wavelength, results in a the temperature
profile slightly different from the other three cases. In all remaining
models presented in this study we have used OH5.
In this section we consider two particular situations that require a
two-dimensional modeling of the radiative transfer. In the first
example, the external radiation field is isotropic but the density
distribution is not spherically symmetric. In the second example, the
density profile is spherically symmetric but the incident radiation
field is anisotropic, as the cloud is heated by an external stellar
source. Both situations are easily handled by our Monte Carlo code.
As a first application of our Monte Carlo code, we consider the
radiative transfer in a singular isothermal toroid (Li & Shu 1996), a
scale-free, axisymmetric equilibrium configuration of an isothermal
cloud under the influence of sef-gravity, gas pressure and magnetic
forces. These toroids are characterized by a single parameter, H0,
representing the fractional amount of support provided by the magnetic
field. We choose the particular value H0=0.5 to model a cloud with
moderate axial ratio (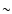 2.5) intermediate between a spherical
unmagnetized cloud and a magnetically dominated disklike
configuration.
2.5) intermediate between a spherical
unmagnetized cloud and a magnetically dominated disklike
configuration.
It should be noticed that, in all models presented, we are simply
computing the dust temperature of pre-defined core density
distributions, and therefore the resulting core is not the solution of
the equilibrium equation if gas-dust coupling is assumed. Also, the
practical definition of the boundary as an isobaric surface is only
possible for spherical clouds, as in this case the isopycnic and
isobaric surfaces necessarily coincide. In all other geometries, we
take the boundary as the isopycnic surface corresponding to a specified
value of the density.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270,clip]{H4706f3.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg61.gif) |
Figure 3:
The top panel shows the dust temperature ( top
half) and density distribution ( bottom half) of a singular
isothermal toroid with H0=0.5, seen edge-on. The density on the
boundary is
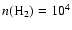 cm-3 and the isopycnic curves are
logarithmically spaced by 0.5. The density distribution is azimuthally
symmetric and also symmetric with respect to the midplane. The maximum
outer temperature is 15 K and the isothermal curves are spaced by 1 K.
The bottom panel shows the emission at 1.3 mm ( top half)
and at 350 cm-3 and the isopycnic curves are
logarithmically spaced by 0.5. The density distribution is azimuthally
symmetric and also symmetric with respect to the midplane. The maximum
outer temperature is 15 K and the isothermal curves are spaced by 1 K.
The bottom panel shows the emission at 1.3 mm ( top half)
and at 350  m ( bottom half). The isophotal curves are
logarithmically spaced by 0.2 starting from the lower value m ( bottom half). The isophotal curves are
logarithmically spaced by 0.2 starting from the lower value
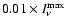 .
With the adopted opacity law (OH5), the peak values
are .
With the adopted opacity law (OH5), the peak values
are
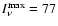 MJy sr-1 at 1.3 mm and 382 MJy sr-1at 350 MJy sr-1 at 1.3 mm and 382 MJy sr-1at 350  m (in this and in the following figures, the maps have not
been convolved with an observing beam). m (in this and in the following figures, the maps have not
been convolved with an observing beam). |
| Open with DEXTER |
In Fig. 3 are shown both the density distribution of the
toroid and the resulting temperature distribution. The boundary of the
configuration is defined as the isopycnic surface with
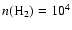 cm-3. Notice that the temperature varies over the
boundary surface by a factor of about two from the origin to the
maximum radius, and this difference is due to an increase of grain
exposure to the ISRF as the radius increases, an effect known also for
disks of low aspect ratio (e.g. Spagna et al. 1991), and is
particularly enhanced in a toroid. It is also evident from
Fig. 3 that the temperature decreases outward both in the
horizontal and vertical directions.
cm-3. Notice that the temperature varies over the
boundary surface by a factor of about two from the origin to the
maximum radius, and this difference is due to an increase of grain
exposure to the ISRF as the radius increases, an effect known also for
disks of low aspect ratio (e.g. Spagna et al. 1991), and is
particularly enhanced in a toroid. It is also evident from
Fig. 3 that the temperature decreases outward both in the
horizontal and vertical directions.
In Fig. 3, we also show synthetic (unconvolved with an
observing beam) maps of the expected dust emission at 350  m and 1.3 mm. In particular at 1.3 mm, the "observed contours'' reflect
fairly faithfully the projected column density and hence the density
distribution. At 350
m and 1.3 mm. In particular at 1.3 mm, the "observed contours'' reflect
fairly faithfully the projected column density and hence the density
distribution. At 350  m however, the intensity distribution is much
more extended than at 1.3 mm. The half-power dimensions are
m however, the intensity distribution is much
more extended than at 1.3 mm. The half-power dimensions are 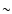
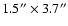 at 1.3 mm (in angular
size at a distance of 140 parsec) but
at 1.3 mm (in angular
size at a distance of 140 parsec) but
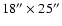 at 350
at 350  m. Thus the effect of heating from the
exterior is mainly observable as an increase in size with frequency.
m. Thus the effect of heating from the
exterior is mainly observable as an increase in size with frequency.
While the above discussion concerns cores of non-spherical geometry
subject to an isotropic incident radiation field, it should be noted
that one expects often to find cases where the incident radiation field
is anisotropic. Most obviously, this is the case in galactic reflection
nebulae where the radiation field from single early type stars may be
dominant. We therefore here (in a slight parenthesis to the discussion
elsewhere in this paper) demonstrate the application of our code to
such a case and compute the expected temperature distribution in a
core subject to radiation from a nearby B star (note earlier work in
this field by Natta et al. 1981).
The vicinity of a star to a prestellar core results in an anisotropic
radiation field, leading to a 2-D radiation transfer problem in the
case of a spherically symmetric core. It should be noted that this is a
case where the approximation of ZWG (Eq. (5)) may not hold, as
the expected increase in dust temperature may make the core no longer
optically thin to its own radiation.
To study the effect of such a field, we start by considering a system
composed of a prestellar core represented as a BE sphere, with the
physical parameters given in Sect. 3.1, and a B3 star at a distance
of 0.15 pc from the edge of the core. The large range of spatial
scales involved makes it difficult for a Monte Carlo program to solve
this problem consistently, by emitting packets from the star, and
following them through the ISM and the prestellar core. We avoid this
problem by assuming that the stellar radiation is reprocessed by a
tenuous but spatially extended photodissociation region (PDR)
surrounding the core, and use a fit to the spectral emission of the PDR computed by Désert et al. (1990). In this way, the situation is
reduced to the case treated in Sect. 3.1, with the difference that
the incident radiation is characterized by a PDR spectrum, instead of
the standard ISRF, and a variable intensity over the surface of the
core. We further assume that the total luminosity over any area
element on the cloud's surface is the same as that obtained assuming
no attenuation between the star and envelope. Thus, the luminosity of
a surface element in spherical coordinates is
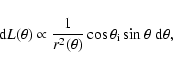 |
(13) |
where 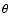 is the angle between the point on the
surface of the core and the star as seen from the core's center,
is the angle between the point on the
surface of the core and the star as seen from the core's center,
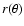 is the distance of that point to the star, and
is the distance of that point to the star, and
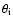 is the angle of incidence of the radiation. The proportionality
constant is obtained by setting the total incident luminosity equal to
is the angle of incidence of the radiation. The proportionality
constant is obtained by setting the total incident luminosity equal to
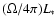 ,
where
,
where 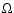 is the solid angle of the core
as seen from the star.
is the solid angle of the core
as seen from the star.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270,clip]{H4706f4.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg70.gif) |
Figure 4:
Model results for a spherical (Bonnor-Ebert) cloud core heated by the standard ISRF and a B3 star located at 0.15 pc from the surface of the cloud (on
the left side in this figure). The core has central
density
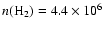 cm-3, gas temperature cm-3, gas temperature
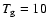 K, and radius R=0.1 pc. The top panel shows the
dust temperature ( top half) and the density ( bottom
half). Isopycnic curves are logarithmically spaced by 0.5 and the
boundary density is K, and radius R=0.1 pc. The top panel shows the
dust temperature ( top half) and the density ( bottom
half). Isopycnic curves are logarithmically spaced by 0.5 and the
boundary density is
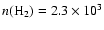 cm-3. Isothermal
curves are spaced by 2 K starting from cm-3. Isothermal
curves are spaced by 2 K starting from
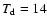 K. The
middle and bottom panels show the emission at 1.3 mm,
350 K. The
middle and bottom panels show the emission at 1.3 mm,
350  m, 100 m, 100  m and 60 m and 60  m. Isophotes are logarithmically
spaced by 0.2 starting from m. Isophotes are logarithmically
spaced by 0.2 starting from
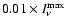 .
The peak
intensity .
The peak
intensity
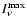 is 78 MJy sr-1 at 1.3 mm,
3347 MJy sr-1 at 350
is 78 MJy sr-1 at 1.3 mm,
3347 MJy sr-1 at 350  m, 1404 MJy sr-1 at 100 m, 1404 MJy sr-1 at 100  m and 200 MJy sr-1 at 60 m and 200 MJy sr-1 at 60  m. m. |
| Open with DEXTER |
The resulting temperature distribution is shown in the top panel of
Fig. 4. As expected, the cloud is hotter on the side
facing the star, and the temperature decreases both radially and
azimuthally, with the lowest temperature close to the centre of the
core, which is almost twice higher than the minimum temperature of the
Black ISRF heated core with the same density profile
(Fig. 1). The ratio
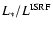 is
is 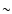 20,
and the inverse square dependence of dL (see Eq. (13)) that
makes this ratio over a surface element be much larger close to the
star, has the consequence that the isotropic ISRF is negligible almost
everywhere. The exception to this is on the core's side opposite to the
star, where the shielding provided by the cloud's center suffices to
make the isotropic ISRF the dominant heating field.
20,
and the inverse square dependence of dL (see Eq. (13)) that
makes this ratio over a surface element be much larger close to the
star, has the consequence that the isotropic ISRF is negligible almost
everywhere. The exception to this is on the core's side opposite to the
star, where the shielding provided by the cloud's center suffices to
make the isotropic ISRF the dominant heating field.
In Fig. 4 we show the simulated emission maps at 1.3 mm,
350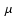 m, 100
m, 100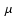 m and 60
m and 60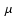 m. The 1.3 mm map shows slight
distortions due to the temperature structure but clearly allows a
reasonable determination of the mass distribution in the BE sphere. As
one goes to shorter wavelengths however, the distortions become extreme
and at 60 microns, one sees essentially the heated surface of the
cloud. Thus maps at different wavelengths may allow the identification
of a heating source and show where the star is along the line of sight
relative to the cloud. In such situations, there will often be mid-IR
data available which will additionally define the geometry of the
"envelope'' or PDR layer hypothesised in our analysis.
m. The 1.3 mm map shows slight
distortions due to the temperature structure but clearly allows a
reasonable determination of the mass distribution in the BE sphere. As
one goes to shorter wavelengths however, the distortions become extreme
and at 60 microns, one sees essentially the heated surface of the
cloud. Thus maps at different wavelengths may allow the identification
of a heating source and show where the star is along the line of sight
relative to the cloud. In such situations, there will often be mid-IR
data available which will additionally define the geometry of the
"envelope'' or PDR layer hypothesised in our analysis.
As an application of our code to fully 3-D density distributions, we
consider the radiative transfer in a model built on the results of
Galli et al. (2001) for magnetized disks with uniform mass-to-flux
ratio
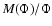 (isopedic). A computationally convenient
characteristic of these model is the existence of non-axisymmetric but
analytical solutions of the equations of magnetostatics, corresponding
to surface density distributions
(isopedic). A computationally convenient
characteristic of these model is the existence of non-axisymmetric but
analytical solutions of the equations of magnetostatics, corresponding
to surface density distributions 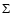 separable in polar coordinates
separable in polar coordinates
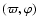 :
:
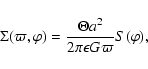 |
(14) |
where
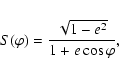 |
(15) |
with 0<e<1. Here,
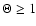 and
and
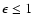 represent the
increase of gas pressure and the reduction of the gravitational constant
due to magnetic pressure and magnetic tension, respectively, related to
the nondimensional mass-to-flux ratio
represent the
increase of gas pressure and the reduction of the gravitational constant
due to magnetic pressure and magnetic tension, respectively, related to
the nondimensional mass-to-flux ratio
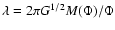 by the relations (Shu & Li 1997)
by the relations (Shu & Li 1997)
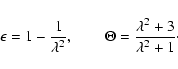 |
(16) |
We construct, in a rather ad hoc way, a 3-D model assuming a
vertical stratification of gas in hydrostatic equilibrium and imposing the
condition that the column density of the resulting density distribution
reproduces Eq. (14), obtaining
![\begin{displaymath}\rho(\varpi,\varphi,z)=\frac{a^2 \Theta^2}{8\pi \epsilon^2 G\...
...varphi)\;{\rm sech}^2\left[\frac{z}{H(\varpi,\varphi)}\right],
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img82.gif) |
(17) |
where
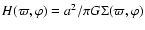 .
.
As a specific example, we adopt the parameters derived by Galli et al. (2001) to match the thermal dust emission map obtained by
Ward-Thompson et al. (1999) for the starless core L1544. We assume an
effective sound speed a= 0.21 km s-1, a nondimensional
mass-to-flux ratio 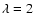 ,
an eccentricity e=0.54, and we define
the core boundary by the isopycnic surface
,
an eccentricity e=0.54, and we define
the core boundary by the isopycnic surface
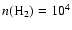 cm-3. We choose this value of the density because it
represents the threshold value that characterizes typical dense
("ammonia") cores. For a density profile characterized by a r-2 law, the visual extinction of the cloud material with density below
this threshold value corresponds to about
cm-3. We choose this value of the density because it
represents the threshold value that characterizes typical dense
("ammonia") cores. For a density profile characterized by a r-2 law, the visual extinction of the cloud material with density below
this threshold value corresponds to about
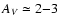 .
.
For this model we have also computed the gas temperature. To do this,
we first notice that the energy deposited in the gas by cosmic ray
ionization is negligible when compared to the energy absorbed by the dust,
so that the energy transfer between gas and dust will not significantly
affect the grain temperature. Therefore, it is only necessary to solve
the equation of thermal equilibrium of the gas,
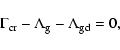 |
(18) |
with
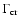 the cosmic-ray heating rate,
the cosmic-ray heating rate,
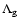 the gas cooling rate by molecular and atomic transitions, and
the gas cooling rate by molecular and atomic transitions, and
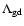 the gas-dust energy transfer rate. For these
quantities, we assume the values given by Goldsmith (2001). We also
assume a CO depletion factor of the form
the gas-dust energy transfer rate. For these
quantities, we assume the values given by Goldsmith (2001). We also
assume a CO depletion factor of the form
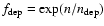 ,
where the critical density for CO depletion is taken to be
,
where the critical density for CO depletion is taken to be
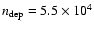 cm-3. Figure 5 shows the
density, dust temperature and gas temperature of our model, with the
top half presenting the y=0 semiplane, and the bottom half showing
the z=0 semiplane, both of which possess reflection simmetry.
cm-3. Figure 5 shows the
density, dust temperature and gas temperature of our model, with the
top half presenting the y=0 semiplane, and the bottom half showing
the z=0 semiplane, both of which possess reflection simmetry.
![\begin{figure}
\par\resizebox{14cm}{!}{\includegraphics[angle=270,clip]{H4706f5.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg92.gif) |
Figure 5:
Density and temperature distribution in the magnetic 3-D model.
Panels on the left (right) side show results in the y=0 (z=0) plane,
respectively.
The top panels show the gas density,
with isopycnic curves logarithmically spaced by 0.5, and density on the
boundary
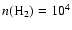 cm-3. The middle panels shows
the dust temperature distribution, with isothermal curves spaced by 1 K
between the minimum (7 K) and maximum (14 K) values. The bottom
panels shows the gas temperature, with isothermal levels ranging from 7
to 14 K. cm-3. The middle panels shows
the dust temperature distribution, with isothermal curves spaced by 1 K
between the minimum (7 K) and maximum (14 K) values. The bottom
panels shows the gas temperature, with isothermal levels ranging from 7
to 14 K. |
| Open with DEXTER |
This 3-D model and the 2-D toroidal model presented in the previous
section show qualitatively similar temperature distributions, but the
mismatch between isopycnic and dust isothermal surfaces is enhanced in
the 3-D model, particularly in the y=0 plane where the geometry is
more complex.
The gas temperature, as it depends on both the dust temperature and on
the gas density, shows a different distribution from either
(Fig. 5). At the dense center, the temperatures of the gas
and the dust are well coupled, but they are partially decoupled at the
lower density boundary. This results in a non-monotonic behaviour of
the gas temperature, which reaches a maximum at an intermediate density
(an effect that also occurs in 1D geometry, as shown by Galli et al. 2002). It is also evident, from Fig. 5 that the gas
temperature has a slightly higher value on the right side of the
singularity than on the left, which is a consequence of the different
dust temperature values at the density where the turnover in the gas
temperature occurs on the two sides of the singularity.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270,clip]{H4706f6.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg93.gif) |
Figure 6:
Normalized emission for the 3-D model, seen edge-on (top panel) and face-on (bottom panel). Each panel shows the
emission at 1.3 mm (top half) and at 350  m (bottom
half). Isophotal curves are logarithmically spaced by 0.2 starting from
the lower value m (bottom
half). Isophotal curves are logarithmically spaced by 0.2 starting from
the lower value
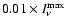 .
With the adopted opacity
law (OH5), the peak values are: .
With the adopted opacity
law (OH5), the peak values are:
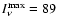 MJy sr-1 at 1.3 mm and 460 MJy sr-1 at 350 MJy sr-1 at 1.3 mm and 460 MJy sr-1 at 350  m (edge-on case); m (edge-on case);
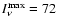 MJy sr-1 at 1.3 mm and 307 MJy sr-1 at 350 MJy sr-1 at 1.3 mm and 307 MJy sr-1 at 350  m
(face-on case). m
(face-on case). |
| Open with DEXTER |
Figure 6 shows simulated dust emission maps at 1.3 mm and 350  m for the side view and top view. The flattening towards the
center due to the dust temperature gradient is evident from the
comparison between the emission at the two wavelengths. The vertical
density stratification has a fairly strong effect on the shape of the
map seen from the side, but is not noticeable from the top. In general,
one notes a slight "bottleneck'' deviation from a purely elliptical
shape of the singular isothermal disk model present in Galli et al. (2001). We note also that the "cometary shape'' of the edge-on
1.3 mm map is rather similar to that observed towards L1544 and L63
by Ward-Thompson et al. (1999).
m for the side view and top view. The flattening towards the
center due to the dust temperature gradient is evident from the
comparison between the emission at the two wavelengths. The vertical
density stratification has a fairly strong effect on the shape of the
map seen from the side, but is not noticeable from the top. In general,
one notes a slight "bottleneck'' deviation from a purely elliptical
shape of the singular isothermal disk model present in Galli et al. (2001). We note also that the "cometary shape'' of the edge-on
1.3 mm map is rather similar to that observed towards L1544 and L63
by Ward-Thompson et al. (1999).
In this paper we have presented a Monte Carlo model for radiative
transfer applicable to the study of the physical conditions in starless
molecular cloud cores. The method described is able to compute
accurately and efficiently the dust and gas temperature distribution in
clouds of specified but arbitrary density profiles heated by the ISRF,
an external stellar source, or a combination thereof. In addition, the
method allows the computation of synthetic maps of the emission at
near-infrared and submillimeter wavelengths for arbitrary viewing
angles, and to predict the emergent spectral energy distribution. We
have successfully tested our code by detailed comparison with
one-dimensional calculations in spherical symmetry (ZWG, Galli et al.
2002) and have shown that the assumption of effective optical thinness
is a good one for prestellar cores. As preliminary applications of our
code, we have considered the radiative transfer in model clouds of
increasing degrees of asymmetry and in a spherical cloud core heated by
a neighbouring star.
With our method, we confirm the results of ZWG, Evans et al. (2001),
and Stamatellos & Whitworth (2003) that the dust temperature in cloud
models with physical characteristics typical of dense cores varies
monotonically between a minimum value at the center (6-7 K) and a
maximum value near the cloud's edge (14-15 K) for the standard ISRF.
In general, maps at submillimeter wavelengths closely reproduce the
column density distribution, even for the most non-isothermal
configurations. In the Rayleigh-Jeans regime, in fact, temperature
differences of a factor 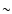 2 along the line-of-sight are washed out
by the much larger variation of the density. However, the decrease of
the dust temperature at the cloud center has the consequence that
submillimeter maps sample preferentially the low-density envelope of
prestellar cores, and are therefore unable to distinguish centrally
peaked (pivotal) configurations from more flattened density profiles.
We also note that our three-dimensional model based on the work of
Galli et al. (2001) produces in natural fashion the cometary structure
observed towards many prestellar cores.
2 along the line-of-sight are washed out
by the much larger variation of the density. However, the decrease of
the dust temperature at the cloud center has the consequence that
submillimeter maps sample preferentially the low-density envelope of
prestellar cores, and are therefore unable to distinguish centrally
peaked (pivotal) configurations from more flattened density profiles.
We also note that our three-dimensional model based on the work of
Galli et al. (2001) produces in natural fashion the cometary structure
observed towards many prestellar cores.
For a spherical core heated by an external stellar source close to the
cloud's surface, the temperature distribution is non-spherical, but the
submillimeter emission generally reproduces the core's column density
profile. Deviations from circular symmetry become extremely apparent
on the other hand shortward of 100  m where one samples mainly the
heated surface layer.
m where one samples mainly the
heated surface layer.
Acknowledgements
We thank the referee S. P. Goodwin for useful comments and A. Natta for
constructive criticism. We acknowledge financial support from the EC
Research Training Network "The Formation and Evolution of Young
Stellar Clusters'' (HPRN-CT-2000-00155). JG acknowledges support from
the scholarship SFRH/BD/6108/2001 awarded by the Fundação para a
Ciência e Tecnologia (Portugal).
- André, P., Ward-Thompson, D., & Barsony, M. 2000, in
Protostars & Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell
(Tucson: The University of Arizona Press), 59
In the text
- André, P., Bouwman, J., Belloche, A., & Hennebelle, P. 2003,
in Chemistry as a diagnostic of star formation, ed.
C. L. Curry, & M. Fich, in press
In the text
- Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A, 361, 555
In the text
NASA ADS
- Bianchi, S., Gonçalves, J., Albrecht, M., et al. 2003, A&A, 399, L43
In the text
NASA ADS
- Black, J. H. 1994, in The First Symposium on the
Infrared Cyrrus and Diffuse Interstellar Clouds, ed. R. M. Cutri, & W. B. Latter,
ASP Conf. Ser., 58, 355
In the text
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615
In the text
NASA ADS
- Basu, S. 2000, ApJ, 540, L103
In the text
NASA ADS
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002a, ApJ, 565, 331
In the text
NASA ADS
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002b, ApJ, 565, 344
NASA ADS
- Désert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215
In the text
NASA ADS
- Evans, N. J., Rawlings, J. M. C., Shirley, Y., & Mundy, L. G. 2001, ApJ, 557, 193
In the text
NASA ADS
- Galli, D., Shu, F. H., Laughlin, G., & Lizano, S. 2001, ApJ, 551, 367
In the text
NASA ADS
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275
In the text
NASA ADS
- Goldsmith, P. F. 2001, ApJ, 557, 763
In the text
- Ivezic, Z., Groenewegen, M. A. T., Men'schikov, A.,
& Szczerba, R. 1997, MNRAS, 291, 121
In the text
NASA ADS
- Jones, C. E., & Basu, S. 2002, ApJ, 569, 280
In the text
NASA ADS
- Kramer, C., Richer, J., Mookerjea, B., Alves, J., & Lada, C. 2003, A&A, 399, 1073
In the text
NASA ADS
- Leung, C. M. 1976, ApJ, 209, 75
In the text
NASA ADS
- Li, D., Goldsmith, P. F., & Menten, K. 2003, ApJ, 587, 262
In the text
NASA ADS
- Li, Z.-Y., & Shu, F. H. 1996, ApJ, 472, 211
In the text
NASA ADS
- Natta, A., Palla, F., Preite-Martinez, A., & Panagia, N. 1981,
A&A, 99, 289
In the text
NASA ADS
- Niccolini, G., Woitke, P., & Lopez, B. 2003, A&A, 399, 703
In the text
NASA ADS
- Olofsson, H., Johansson, L. E. B., Hjalmarson, A.,
& Nguyen- Quang-Rieu, Mr. 1982, A&A, 107, 128
NASA ADS
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 (OH)
In the text
NASA ADS
- Rowan-Robinson, M. 1980, ApJS, 44, 403
In the text
NASA ADS
- Shirley, Y., Evans, N. J., Rawlings, J. M. C., & Gregersen, E. M. 2000, ApJS, 131, 249
NASA ADS
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 31
In the text
- Shu, F. H., & Li, Z.-Y. 1997, ApJ, 475, 251
In the text
NASA ADS
- Spagna, G. F. Jr., Leung, C. M., & Egan, M. P. 1991, ApJ,
379, 232
In the text
NASA ADS
- Stamatellos, D., & Whitworth, A. P. 2003, A&A, 407, 941
In the text
NASA ADS
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M.,
& Comito, C. 2002, ApJ, 565, 331
In the text
NASA ADS
- Ward-Thompson, D., Motte, F., & André, P. 1999, MNRAS,
305, 143
In the text
NASA ADS
- Ward-Thompson, D., Kirk, J. M., Crutcher, R. M., et al. 2000, ApJ, 537, L35
In the text
NASA ADS
- Ward-Thompson, D., André, P., & Kirk, J. M. 2002, MNRAS,
329, 257
In the text
NASA ADS
- Wolf, S., Henning, Th., & Stecklum, B. 1999, A&A, 349, 839
In the text
NASA ADS
- Zucconi, A., Walmsley, C. M., & Galli, D. 2001, A&A, 376,
650 (ZWG)
In the text
NASA ADS
Copyright ESO 2004
![\begin{displaymath}B_\nu(T_{\rm d})=\frac{2h \nu^3}{c^2}
\left[\exp\left(\frac{h\nu}{kT_{\rm d}}\right)-1\right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img24.gif)
![\begin{displaymath}\int^\infty_0 \kappa_\nu B_\nu [T_{\rm d}({\vec r})]\;{\rm d}\nu =
\int^\infty_0 \kappa_\nu J_\nu({\vec r})\;{\rm d}\nu,
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img26.gif)
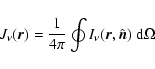
![\begin{displaymath}J_\nu({\vec r})=\frac{J_\nu^{\rm ISRF}}{4\pi}\oint
\exp[-\tau_\nu({\vec r},{\hat{\vec n}})]\;{\rm d}\Omega,
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img29.gif)
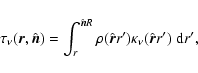
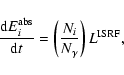
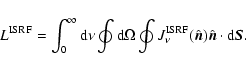
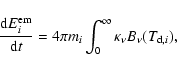
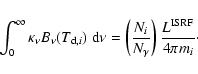
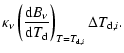
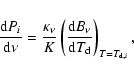
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{H4706f1.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg51.gif)
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{H4706f2.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg58.gif)
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270,clip]{H4706f3.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg61.gif)
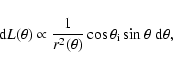
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270,clip]{H4706f4.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg70.gif)
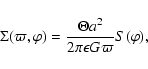
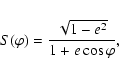
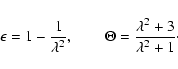
![\begin{displaymath}\rho(\varpi,\varphi,z)=\frac{a^2 \Theta^2}{8\pi \epsilon^2 G\...
...varphi)\;{\rm sech}^2\left[\frac{z}{H(\varpi,\varphi)}\right],
\end{displaymath}](/articles/aa/full/2004/08/aah4706/img82.gif)
![\begin{figure}
\par\resizebox{14cm}{!}{\includegraphics[angle=270,clip]{H4706f5.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg92.gif)
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270,clip]{H4706f6.ps}}
\end{figure}](/articles/aa/full/2004/08/aah4706/Timg93.gif)