A&A 415, 771-775 (2004)
DOI: 10.1051/0004-6361:20035603
Size estimates of some optically bright KBOs
W. J. Altenhoff - F. Bertoldi - K. M. Menten
Max-Planck-Institut für Radioastronomie (MPIfR),
Auf dem Hügel 69, 53121 Bonn, Germany
Received 30 October 2003 / Accepted 10 November 2003
Abstract
Seven recently detected optically "bright''
Kuiper-Belt-Objects (KBOs) were observed at 250 GHz using the
Max-Planck Millimeter Bolometer (MAMBO) array at the IRAM 30 m
telescope. Only the optical binary KBO (47 171) 1999 TC36
was detected, whose components differ optically by
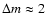 mag. Assuming that the derived mean geometric
albedo of p = 0.05 is identical for both,
the component diameters become 566 and 225 km.
For the other six objects upper limits to their sizes and
lower limits for their albedos were obtained. The geometric albedo,
p, for (28978) Ixion is surprisingly large,
mag. Assuming that the derived mean geometric
albedo of p = 0.05 is identical for both,
the component diameters become 566 and 225 km.
For the other six objects upper limits to their sizes and
lower limits for their albedos were obtained. The geometric albedo,
p, for (28978) Ixion is surprisingly large, 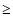 0.15. For a consistent
comparison all published radio photometric data of KBOs and Centaurs
were analyzed again: the average geometric albedo
is found to be
0.15. For a consistent
comparison all published radio photometric data of KBOs and Centaurs
were analyzed again: the average geometric albedo
is found to be 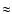 0.08.
0.08.
Key words: minor planets - radio continuum: solar system
The outer regions of the solar system are occupied by three
distinct groups of distant minor planets: the Kuiper
Belt Objects (KBOs), the Scattered Disk Objects (SDOs), and the
Centaurs. The KBOs move in the ecliptic plane in dynamically stable
orbits at heliocentric distances larger than 30 AU. Through
close encounters KBOs can be forced into less stable
highly eccentric orbits within
a scattered disk, with typical perihelia of 35 AU, mean heliocentric
distances of 85 AU, or into the domain of
Centaurs, the "major planet crossers''.
If the Centaurs and SDOs, treated also by the Minor Planet Center/CBAT
(2003)
as one group, are really forced "recently'' into their new
orbits, their physical constitution should be unchanged since their origin.
The first KBO was detected less than a decade ago. By now (September 2003)
722 KBOs and 132 Centaurs are catalogued (Parker 2003),
and many of the brighter ones have been
investigated intensively. Their reflection spectra differ from those
of the main belt asteroids (MBAs), and they can not be classified in the
schema of the MBAs. Tegler & Romanishin (2003) and Peixinho et al.
(2003) debate whether the bimodality of the color population
is statistically confirmed only for the Centaurs or globally for Centaurs
and KBOs. Even the one dimensional continuous color distribution
may become
a first classification criterion for KBOs. Sheppard & Jewitt
(2002) report that 32% of the observed KBOs show (peak
to peak) light variations greater 15%, with periods comparable with
the average MBA rotation period of 9 hours.
They suggest that the light curves
are caused by rotationally distorted shapes (the rubble pile model).
Hainaut et al. (2000) and Sheppard & Jewitt (2003)
report amplitude variations of the light curves of (19 308) 1996 TO66
and (24 835) 1995 SM55, respectively, which might be explained by
cometary activity between the observing sessions.
Whether the low brightness variations of the majority of the KBOs
is an indication of their sphericity or of their attitude
distribution remains to be investigated
(Lacerda & Luu 2003).
Nine KBOs were confirmed as binaries (e.g. Noll et al.
2002). The components of these binaries typically have a
comparable size and a wide separation, while binary components of the
MBAs show a small separations and very different sizes.
Observations of 7 KBOs by Sheppard & Jewitt (2002)
show a striking similarity of their phase functions, indicating
comparative uniformity
of their surface composition, which is very
different from that of the Pluto-Charon Binary and also from the MBAs.
The different properties of the distant minor planets compared to the MBAs
add weight to the claim that they are remnants of the pristine
material of the original solar accretion disk.
From all observable parameters of KBOs the size and albedo information is
scarce:
only one angular size could be measured directly (Brown & Trujillo
2002), and two indirectly by the sensitivity-limited radio photometric
method, measuring their
thermal emission: the observed flux density is proportional
to the cross section of the KBO and to the independently known brightness
temperature (Altenhoff et al. 2001).
Here we want to extend the radio photometric size determinations of
minor planets (Altenhoff et al. 1994, 1995, 2001)
to more distant minor planets and compare the results systematically
with other published radio size measurements for an improved set of
sizes and albedos.
Table 1:
Distant minor planets observed at 250 GHz.
The millimeter observations were made with the IRAM 30 m telescope on
Pico Veleta, Spain, using the 37- or 117-channel versions of the
Max-Planck Millimeter Bolometer (MAMBO), which was built at the
Max-Planck-Institut für Radioastronomie (Kreysa et al.
1999). For our observations
the performance of both
bolometer versions is about identical with respect to angular
resolution and sensitivity.
MAMBO is a hexagonally close-packed array operating at 0.3 K.
It has a half-power spectral bandwidth between 210 and 290 GHz with
an effective frequency for steep thermal spectra of 250 GHz. The beam
size on the sky is 10.7 arcsec. The sources were observed with a
single channel using the standard on-off mode with the telescope
secondary chopping in azimuth by 32
 at a rate of 2 Hz; after each integration of 10 s the telescope is moved to
the preceding off position.
The data were analysed using the MOPSI software created by Zylka (1998), which allows to subtract
the mean correlated sky noise observed in the
off-source channels from the
on-source channel.
For absolute flux calibration a number of calibration
sources were observed, resulting in an estimated absolute flux
uncertainty of
at a rate of 2 Hz; after each integration of 10 s the telescope is moved to
the preceding off position.
The data were analysed using the MOPSI software created by Zylka (1998), which allows to subtract
the mean correlated sky noise observed in the
off-source channels from the
on-source channel.
For absolute flux calibration a number of calibration
sources were observed, resulting in an estimated absolute flux
uncertainty of 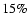 (1
(1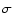 ). Considering the number of
observing periods for each distant minor planet, listed in Table 1,
the statistical error of the absolute calibration becomes negligible
compared to the observing accuracy.
). Considering the number of
observing periods for each distant minor planet, listed in Table 1,
the statistical error of the absolute calibration becomes negligible
compared to the observing accuracy.
For our observations we had selected the optically brightest KBOs
known at the time (Table 1). The integrations were deep enough for
each object so that it could have been detected if its geometric albedo
was near that expected,
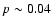 .
Only one KBO could be detected; it is evident that the typical albedo
of the KBOs is therefore higher.
Each KBO was observed at many different dates, thus
reducing systematic errors like confusion by
background sources, or undersampling of the light curve
from a non-spherical, rotating object.
.
Only one KBO could be detected; it is evident that the typical albedo
of the KBOs is therefore higher.
Each KBO was observed at many different dates, thus
reducing systematic errors like confusion by
background sources, or undersampling of the light curve
from a non-spherical, rotating object.
All distant minor planets were observed with ephemerides based on the latest
orbital elements provided by CBAT (2003). We expect
their quality to have been better than the accuracy of 1 arcsec (i.e. 1/10 of the beam width) required for accurate
flux density observations.
Under the assumption that distant minor planets do not have a significant
internal heat source
the observed emission is in radiation equilibrium with the insolation.
Using Stefan's law and the known solar constant the equilibrium
temperature
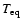 at the sub-solar point of a non-rotating body with low heat
conductivity and no atmosphere (see e.g. Kellermann 1966;
Weigert & Wendker 1996) is described by:
at the sub-solar point of a non-rotating body with low heat
conductivity and no atmosphere (see e.g. Kellermann 1966;
Weigert & Wendker 1996) is described by:
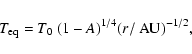 |
(1) |
where A, r, and T0 = 392 K are the Bond albedo (fraction of
reflected light by a spherical body), the heliocentric distance,
and the black body equilibrium temperature at 1 AU, respectively.
The solar energy absorbed by the surface of the body per unit area is:
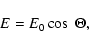 |
(2) |
where 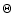 is the zenith angle of the sun. The temperature
distribution on the sun-lit surface becomes
is the zenith angle of the sun. The temperature
distribution on the sun-lit surface becomes
 |
(3) |
and the disk averaged equilibrium temperature becomes
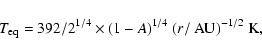 |
(4) |
with T0 = 329 the disk averaged temperature of the black body at 1 AU.
The emitted energy is described by the Planck law,
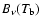 ,
,
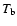 is the brightness temperature.
The diameter of the KBO, d, is then determined from
is the brightness temperature.
The diameter of the KBO, d, is then determined from
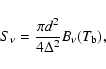 |
(5) |
where 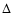 is the geocentric distance.
It should be noted that at mm-wavelengths the observed flux density
is proportional to the product of brightness temperature and the
solid angle of the body, thus facilitating the interpretation of
radiation equilibrium.
is the geocentric distance.
It should be noted that at mm-wavelengths the observed flux density
is proportional to the product of brightness temperature and the
solid angle of the body, thus facilitating the interpretation of
radiation equilibrium.
The emission of a KBO can possibly be better described
as a grey body with the
brightness temperature 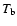 and emissivity e. The equilibrium,
brightness, and physical temperatures of the surface relate as
and emissivity e. The equilibrium,
brightness, and physical temperatures of the surface relate as
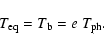 |
(6) |
The equality of the
equilibrium and brightness temperature was noticed
in mm observations by Webster et al. (1988), Johnston et al. (1989), and Altenhoff et al. (1994). The radiation
equilibrium was first applied to the interpretation of
planetary radio observations by Kellermann (1966).
The Bond albedo is related to the geometric albedo, p, by A = p q,
where q is the phase integral. For KBOs the phase integral
is poorly determined because for distant minor planets the solar phase
varies only by about 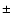 2 deg, it therefore needs extrapolation
(e.g. Stumpff 1948).
2 deg, it therefore needs extrapolation
(e.g. Stumpff 1948).
3.2 Rotation
The black body equivalent temperature T0 is model dependent:
for a non-rotating sphere it assumes a value of 392 K at its subsolar point, and averaged over the illuminated
disk it is 329 K. This simplistic thermal model, in which
the sub-solar and the sub-Earth point coincide, is named (especially
in IR-astronomy) the standard thermal model (STM).
In case of fast rotation (insolation on a
hemisphere, emission from the total sphere) the disk-averaged
temperature becomes
T0 = 329/21/4 K =277 K. This model, in which
the Sun and Earth are in the equatorial plane and which assumes an
isothermal distribution in longitude, is also called the isothermal
latitude model (ILM). Both models are the limiting cases for
the equilibrium temperature. In principle an "intermediate latitude
model'' would be needed, if the Sun and Earth are not in the equatorial
plane. But because the spin axis of most distant minor
planets are thought to be nearly in the direction of the ecliptic pole
(which still needs confirmation), the fast rotation model should
approximate the equilibrium temperature at 250 GHz.
For a rotating body the actual rotation model depends
not only on the rotation period but on the observing frequency as well,
because the emission originates in a
surface layer with a depth proportional to the wavelength; the
thermal inertia of this layer, and with it the time delay between
absorption and re-emission, is wavelength dependent.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{AA2003.603.eps}
\end{figure}](/articles/aa/full/2004/08/aa0603/Timg25.gif) |
Figure 1:
Observed disk-averaged temperature
of MBA and planetary
satellites, normalized to a standard distance r = 1 AU,
as a function of rotation time, t. For fast
rotation, 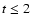 days, days,
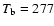 K; for t>
12 days, the observed K; for t>
12 days, the observed
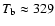 K, corresponding to the
slow rotation model.
The values of the two rotation models are indicated by thin
horizontal lines. References for the 250 GHz data used: Vesta
& Hebe (Altenhoff et al. 1994), Ceres (Altenhoff et al. 1996), Mars (prime calibrator),
Callisto & Titan (Altenhoff et al. 1988),
Moon, scaled to the disk averaged temperature (Krotikov &
Pelyushenko 1987). K, corresponding to the
slow rotation model.
The values of the two rotation models are indicated by thin
horizontal lines. References for the 250 GHz data used: Vesta
& Hebe (Altenhoff et al. 1994), Ceres (Altenhoff et al. 1996), Mars (prime calibrator),
Callisto & Titan (Altenhoff et al. 1988),
Moon, scaled to the disk averaged temperature (Krotikov &
Pelyushenko 1987). |
| Open with DEXTER |
Table 2:
Radio photometric sizes of distant minor planets.
We used existing measurements of planetary objects with accurately known
diameters to derive 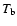 (Eq. (3)) and scaled them to
the heliocentric distance r = 1; they are shown as function of the
rotation period in Fig. 1. These brightness temperatures
are compared with the equilibrium temperature (Eq. (1)) for non-rotation
with T0 = 329 K and for fast-rotation with T0 = 277 K.
For periods
below two days
(Eq. (3)) and scaled them to
the heliocentric distance r = 1; they are shown as function of the
rotation period in Fig. 1. These brightness temperatures
are compared with the equilibrium temperature (Eq. (1)) for non-rotation
with T0 = 329 K and for fast-rotation with T0 = 277 K.
For periods
below two days 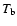 agrees well with
agrees well with
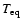 for fast rotation, and
for periods above 12 days
for fast rotation, and
for periods above 12 days 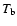 corresponds to the non-rotation model.
corresponds to the non-rotation model.
For periods smaller than 2 days
the fast rotation model is applicable, for periods above 12 days
the slow rotation model is valid.
All known rotation periods of KBOs and of single MBAs are well below 2 days (see e.g. Shor 2002),
thus in the range of applicability of the fast rotation model.
The most precise data in Fig. 1 is that of Mars,
the prime calibrator at mm-wavelengths; the agreement of its
brightness and equilibrium temperatures is strongly supporting
the fast rotation model.
An independent argument against the slow motion model for Mars is the
missing radio phase. Its disk averaged brightness temperature, 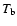 ,
should vary
with the phase angle, as we know it from the millimetric phase of the moon.
But neither for Mars nor for any MBA such phase effect was
observed. Since Mars is the body with the longest rotation period in the
sample of the fast rotators, we can safely apply this model to
our distant minor planets, which seem to have shorter rotation periods.
,
should vary
with the phase angle, as we know it from the millimetric phase of the moon.
But neither for Mars nor for any MBA such phase effect was
observed. Since Mars is the body with the longest rotation period in the
sample of the fast rotators, we can safely apply this model to
our distant minor planets, which seem to have shorter rotation periods.
Jewitt et al. (2001)
used
the slow-rotator model and the Rayleigh-Jeans approximation, while Lellouch et al. (2000) used the fast-rotator model but a millimeter emissivity of 0.7,
leading to different sizes and albedos.
In Table 2 the derived sizes and albedos for the KBOs we observed
are compared with other published radio
photometric results, adjusted to our photometry. For all objects the
fast rotation model was assumed, and the systematic flux density
underestimate due to the microwave background,
even though at 250 GHz only about 3% of the observed signal, was corrected. For the phase integral
we assume q = 0.28. The absolute optical magnitudes, H, were
taken from information provided by the
Central Bureau for Astronomical Telegrams (CBAT) (2003).
The Pluto-Charon Binary, often considered the
prototype of KBOs, we exclude from
consideration, because it differs in all relevant aspects from the distant
minor planets. Because KBOs, Centaurs, and SDOs seem to be of similar
constitution (see above), they will be discussed together.
(2060) Chiron.
Luu & Jewitt (1990) found an optically thin coma with a mass loss rate
of order 1 kg/s around this Centaur.
This is much too small to transport big dust particles into
the coma, which could contaminate
the observed thermal emission of the disk of Chiron.
This is confirmed by the agreement of the radio photometric diameter
with that derived from an occultation (Bus et al. 1996).
Luu (1993) and others have stressed the "true cometary identity'' of
Chiron. However, Stern (1995) called Chiron a "hybrid object'',
in between a planet and a comet. For the analysis of distant minor planets
the cometary activity is only a side aspect, so no
Centaur should be excluded.
(24835) 1995 SM55.
The quoted rotation period is taken from Jewitt & Sheppard (2003);
the optical light curve may be variable.
(19308) 1996 TO66.
Hainaut et al. (2000) report a change from a double peaked light
curve to a single peaked one, connected with an change of amplitude. Their
preferred explanation is cometary activity between observing sessions.
(47171) 1999 TC36.
This KBO was recognized as a binary by Trujillo & Brown (2002),
which was confirmed by Marchis et al. (2002). The brightness
difference between the components is about 2 mag,
its orbital period is not yet known. The quoted rotation period was
observed by Ortiz et al. (2003) with a high confidence level,
but it could not be confirmed in a subsequent observation. If real, it might
belong to the brighter component.
Assuming the same
albedo and a fast rotation model, our flux measurement implies the components'
diameters to be 566 km and 225 km, respectively.
(28978) Ixion.
Bertoldi (2002) initially reported an apparently
spurious, marginal 250 GHz detection, which was not
confirmed by later observations.
Hahn et al. (2001) cite observations with
"Astrovirtel'' that resulted in an object size 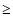 1200 km,
based apparently on the observed absolute
optical magnitude H (not quoted) and an assumed geometric
albedo p = 0.07. Lately, Boehnhardt (private communication) reported
that the visual absolute magnitude is close to 3.8; this would reduce
the geometric red albedo to p > 0.08.
We were not able to detect Ixion, which, given its
optical brightness, yields a very high lower limit to its geometric albedo.
1200 km,
based apparently on the observed absolute
optical magnitude H (not quoted) and an assumed geometric
albedo p = 0.07. Lately, Boehnhardt (private communication) reported
that the visual absolute magnitude is close to 3.8; this would reduce
the geometric red albedo to p > 0.08.
We were not able to detect Ixion, which, given its
optical brightness, yields a very high lower limit to its geometric albedo.
(50000) Quaoar.
The size of the KBO Quaoar was measured directly
by Brown & Trujillo (2002). The radio photometric
observations are not yet fully published.
The re-evaluation of observations, e.g., by
Jewitt et al. (2001), Lellouch et al. (2002),
Margot et al. (2002) leads to sizes and geometric albedos,
differing by 10 and 20%, respectively, compared with the original
publications. For the observations under discussion these differences
are within the observational
uncertainties. For measurements with
higher intensity resolution, e.g., of MBAs, the selection of the appropriate
thermal model is vital.
The re-evaluated geometric albedos for the three groups of distant
minor planets in Table 2 vary between 0.06 and 0.16.
The mid-infrared observations of
Centaurs by Fernandez et al. (2002)
show a similar distribution of the geometric albedo; compared with
the cometary albedo, p = 0.04, the distant minor planets
have a significantly higher albedo,
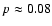 .
.
For 6 of the 10 KBOs in our sample McBride et al. (2002) provide
absolute magnitudes, H, and (V-J) colors. For 4 distant minor planets
the absolute magnitudes of CBAT and McBride et al.
agree very well, for
two objects there is a difference of about 0.5 mag - this
should be followed up.
This uncertainty of the absolute magnitude hardly
affects the radio photometric size determination, but the derived
geometric albedo, p,
depends linearly on the optical brightness.
We find no apparent
correlation between the optical color and the geometric albedo for
the objects in Table 2
due also to the small number of objects
and the large errors on the albedos. Therefore more
precise measurements, especially of the KBOs with high upper
limits of the albedo, are urgently needed.
Acknowledgements
We acknowledge the information of Dr. Boehnhardt on the optical
absolute magnitude of Ixion.
We sincerely thank Drs. U. Lisenfeld
and A. Weiss for organizing the pooled observations.
The support for this project by Prof. M. Grewing and Dr. C. Thum is much
appreciated.
- Altenhoff, W. J., Chini, R., Hein, H., et al. 1988,
A&A, 190, L15
In the text
NASA ADS
- Altenhoff, W. J., Johnston, K. J., Stumpff, P.,
& Webster, W. J. 1994, A&A, 287, 641
In the text
NASA ADS
- Altenhoff, W. J., & Stumpff, P. 1995, A&A,
293, L41
In the text
NASA ADS
- Altenhoff, W. J., Baars, J. W. M., Schraml, J. B.,
et al. 1996, A&A, 309, 953
In the text
NASA ADS
- Altenhoff, W. J., Menten, K. M., &
Bertoldi, F. 2001, A&A, 366, L9
In the text
NASA ADS
- Bertoldi, F., Carilli, C. L., Menten, K. M.,
et al. 2000, A&A, 360, 92
NASA ADS
- Bertoldi, F. 2002, MPIfR press release
In the text
- Brown, M. E., & Trujillo, C. 2002, AJ, submitted
In the text
- Bus, S. J., Buie, M. W., Schleicher, D. G., et al. 1996,
Icarus, 123, 478
In the text
NASA ADS
- CBAT, Central Bureau for Astronomical Telegrams, 2003
In the text
- Fernandez, Y. R., Jewitt, D. C.,
& Sheppard, S. S. 2002, AJ, 123, 1050
In the text
NASA ADS
- Hahn, G., Muinonen, K., Lagerkvist, C.-I.,
Christensen, L. L., & West, R. 2001, ESO Press Release Aug., 23
In the text
- Hainaut, O. R., Delahodde, C. E.,
Boehnhardt, H., et al. 2000, A&A, 356, 1076
In the text
NASA ADS
- Jewitt, D., & Luu, L. 1992, AJ, 104, 398
NASA ADS
- Jewitt, D., Aussel, H., & Evans, A. 2001,
Nature, 411, 446
In the text
NASA ADS
- Johnston, K. J., Lamphear, E. J., Webster, W. J.,
et al. 1989, AJ, 98, 335
In the text
NASA ADS
- Kellermann, K. I. 1966, Icarus, 478
In the text
- Kreysa, E., Gmünd, H.-P., Gromke, J., et al. 1999,
Infrared Phys. Technol., 40, 191
In the text
NASA ADS
- Krotikov, V. D., & Pelyushenko, S. A. 1987,
Astron. Z., 64, 417
In the text
- Lacerda, P., & Luu, J. 2003, Icarus, 161, 174
In the text
NASA ADS
- Lellouch, E., Paubert, G., Moreno, R.,
& Schmitt, B. 2000, Icarus, 147, 580
In the text
NASA ADS
- Lellouch, E., Moreno, R., Ortiz, J. L.,
et al. 2002, A&A, 1133
In the text
- Luu, J. X., & Jewitt, D. C. 1999, AJ, 100, 913
In the text
- Luu, J. X. 1993, PASP, 105, 946
In the text
NASA ADS
- Marchis, F., Berthier, J., et al. 2002, IAUC, 7807
In the text
- Margot, J. L., Trujillo, C., Brown, M. E.,
& Bertoldi, F. 2002, BAAS, 34, 871
In the text
NASA ADS
- McBride, N., Green, S. F., Davies, J. K., et al. 2002,
Icarus
In the text
- Noll, K. S., Stephens, C., Grundy, W. M., et al.
2003, AJ, 124, 3424
In the text
NASA ADS
- Ortiz, J. L., Gutiérrez, P. J., Casanova, V.,
& Sota, A. 2003, A&A, 407, 1149
In the text
NASA ADS
- Parker, J. W. 2003, DISTANT EKO's, No. 31, 2
In the text
- Peixinho, N., Doressoundiram, A., Delsanti, A.,
et al. 2003, A&A, in press
In the text
- Russel, N. N., Dugan, R. S., & Steward, J. Q. 1938,
Astron. Ginn (Boston), II, 541
- Sheppard, S. S., & Jewitt, D. C. 2002,
AJ, 124, 1757
In the text
NASA ADS
- Sheppard, S. S., & Jewitt, D. C. 2003,
Earth, Moon and Planets, in press
In the text
- Shor, V. A. 2002, Ephemerides of Minor
planets for 2003, Russ. Academy of Sciences, St. Petersburg
In the text
- Stern, S. A. 1995, Nature, 373, 23
In the text
NASA ADS
- Stumpff, K. 1948, AN, 276, 118
In the text
NASA ADS
- Tegler, S. C., & Romanishin, W. 2003,
Icarus, 161, 181
In the text
NASA ADS
- Trujillo, C. A., & Brown, M. E. 2002, IAUC # 7787
In the text
- Webster, W. J., Johnston, K. J., Hobbs, R. W.,
et al. 1988, AJ, 95, 1263
In the text
NASA ADS
- Weigert, A., & Wendker, H. J.
1996, Astronomie und Astrophysik (Weinheim: VCH Verlag)
In the text
- Zylka, R., The MOPSI Cookbook 1998 (Bonn: Bolometer group)
In the text
Copyright ESO 2004
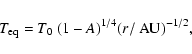
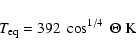
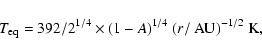
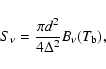
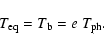
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{AA2003.603.eps}
\end{figure}](/articles/aa/full/2004/08/aa0603/Timg25.gif)