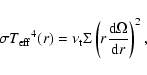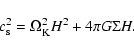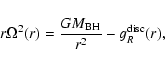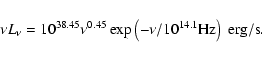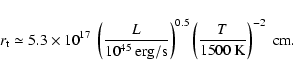A&A 415, 47-54 (2004)
DOI: 10.1051/0004-6361:20034613
The origin of optical emission from super-Eddington
accreting Active Galactic Nuclei: The case of Ton S 180
T. Kawaguchi1,2 -
A. Pierens1 -
J.-M. Huré1,3
1 - LUTh/Observatoire de Paris-Meudon et CNRS UMR 8102,
Place Jules Janssen, 92195 Meudon Cedex, France
2 -
Postdoctoral Fellow of the Japan Society for the
Promotion of Science
3 -
Université Paris 7 Denis Diderot, 2 place Jussieu,
75251 Paris Cedex 05, France
Received 2 May 2003 / Accepted 17 October 2003
Abstract
Self-gravitating accretion discs have only been studied in a
few nearby objects using maser spots at the parsec-scale.
We find a new spectral window for observing the self-gravitating
accretion disc in super-Eddington accreting Active Galactic Nuclei
(AGNs).
This window is determined by calculating the outermost radius
(
 )
of a non self-gravitating disc and the corresponding
emission wavelength (
)
of a non self-gravitating disc and the corresponding
emission wavelength (
 )
as a function of various disc parameters.
We find that
)
as a function of various disc parameters.
We find that
 reaches
reaches
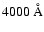 for
for
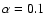 ,
when
,
when
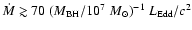 (where
(where 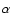 ,
,
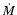 ,
,
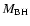 and
and
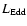 are, respectively,
the viscosity parameter, gas accretion rate onto the central black hole (BH),
the BH mass and the Eddington luminosity).
Moreover,
are, respectively,
the viscosity parameter, gas accretion rate onto the central black hole (BH),
the BH mass and the Eddington luminosity).
Moreover,
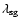 is as small as
is as small as 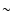
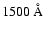 for
for
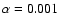 ,
which is
the smallest
,
which is
the smallest 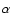 case in this study.
Therefore,
the window for observing the self-gravitating part of an
AGN accretion disc is from
case in this study.
Therefore,
the window for observing the self-gravitating part of an
AGN accretion disc is from 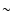
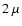 m to
m to
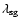 .
Incidentally,
.
Incidentally,
 can be less than the photon trapping radius
for
can be less than the photon trapping radius
for
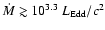 .
Namely, a self-gravitating,
optically-thick, advection-dominated accretion disc
is expected to appear in the extremely high accretion rate regime.
.
Namely, a self-gravitating,
optically-thick, advection-dominated accretion disc
is expected to appear in the extremely high accretion rate regime.
Next, we demonstrate that the Mid-Infrared to X-ray spectrum
of a bright, well-studied Narrow-Line Seyfert 1 galaxy, Ton S 180,
is indeed well fitted by the spectrum arising from
the following three components: an inner slim disc (with a corona),
an outer, self-gravitating non-Keplerian disc
and a dusty torus.
The total mass, BH mass plus the entire disc mass,
is found to be about
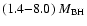 .
If the surface density varies with radius r in proportion to
r-0.6, the total mass
is consistent
with the central mass estimated by H
.
If the surface density varies with radius r in proportion to
r-0.6, the total mass
is consistent
with the central mass estimated by H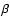 and [O III] widths.
and [O III] widths.
Key words: accretion, accretion disks -
radiation mechanisms: thermal -
galaxies: active -
galaxies: individual: Ton S 180 -
galaxies: nuclei -
galaxies: Seyfert
The Optical/UV/X-ray emission from
Active Galactic Nuclei (AGNs) is thought to arise from a hot
accretion disc around a super-massive Black Hole
(BH; e.g., Mushotzky et al. 1993;
Koratkar & Blaes 1999),
while the Mid- and Near Infrared (IR) radiation comes
from a cold, dusty torus (e.g., Telesco et al. 1984; Thatte et al. 1997;
Pier & Krolik 1993).
Disc self-gravity can generally be ignored in the innermost region
where the high energy spectrum is formed. At large distances
(typically 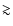 103 - 104 Schwarzschild radii, depending on
accretion parameters), the disc mass is expected to play a significant
role.
Disc self-gravity has been tested only at the parsec-scale via
maser spots detected in a few nearby objects
(e.g. Nakai et al. 1993; Miyoshi et al. 1995;
Huré 2002; Lodato & Bertin 2003).
103 - 104 Schwarzschild radii, depending on
accretion parameters), the disc mass is expected to play a significant
role.
Disc self-gravity has been tested only at the parsec-scale via
maser spots detected in a few nearby objects
(e.g. Nakai et al. 1993; Miyoshi et al. 1995;
Huré 2002; Lodato & Bertin 2003).
Narrow Line Seyfert 1 galaxies (NLS1s) and their high luminosity
analogue,
Narrow-Line QSOs, are supposed to have high accretion rates
among the AGN population (e.g., Brandt & Boller 1998;
Mineshige et al. 2000).
The gas accretion rate 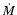 for those objects
is expected to
be comparable to or larger than
for those objects
is expected to
be comparable to or larger than
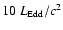 ,
where
,
where
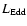 is the Eddington luminosity.
For such super-Eddington accretion rates,
the outer edge of the non self-gravitating part of the accretion disc
radiates optical continuum
emission (
is the Eddington luminosity.
For such super-Eddington accretion rates,
the outer edge of the non self-gravitating part of the accretion disc
radiates optical continuum
emission (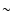
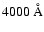 )
for a certain
parameter set (Kawaguchi 2003).
Thus, they are potentially good candidates to study the
self-gravitating part of the disc observationally at longer wavelengths
(Collin et al. 2002; Kawaguchi 2003).
)
for a certain
parameter set (Kawaguchi 2003).
Thus, they are potentially good candidates to study the
self-gravitating part of the disc observationally at longer wavelengths
(Collin et al. 2002; Kawaguchi 2003).
In this paper, we qualitatively describe
the wavelength corresponding to the emission from the outer edge of
a non self-gravitating disc for various accretion parameter sets.
This is done in Sect. 2.
We present in Sect. 3
a Mid-IR to X-ray spectral modeling of a bright, well-studied
NLS1, Ton S 180 (PHL912),
for which numerous, multi-waveband observations
are available (e.g., Wisotzki et al. 1995; Turner et al. 2002;
Vaughan et al. 2002).
In Sect. 4, several discussions are presented.
The final section is devoted to a summary.
In this section, we calculate the radius of the
outer edge of the non self-gravitating slim disc (
 ), i.e.
inner edge of the self-gravitating disc,
as a function of the BH mass
), i.e.
inner edge of the self-gravitating disc,
as a function of the BH mass
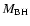 ,
,
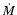 and
viscosity parameter
and
viscosity parameter 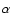 .
We will then show the
corresponding wavelength (
.
We will then show the
corresponding wavelength (
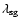 )
that is relevant to emission from
)
that is relevant to emission from
 .
We define M7 for
.
We define M7 for
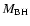 in the unit of
in the unit of
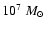 .
.
Figure 1 illustrates the configuration considered
in this study.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3925f1.eps}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg48.gif) |
Figure 1:
Schematic configuration (not to scale) of the three
relevant components surrounding the black hole: a slim disc,
a self-gravitating disc and a torus.
For Ton S 180 (Sect. 3), the characteristic radii are found to be the
followings:
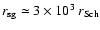 , ,
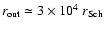 and
and
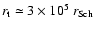 .
The broad-line region is located at .
The broad-line region is located at
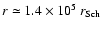 (Sect. 4).
(Sect. 4). |
| Open with DEXTER |
For super-Eddington accretion rates (i.e.
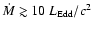 ), an optically-thick, advection-dominated regime appears (Abramowicz et al. 1988). Inside a certain radius
), an optically-thick, advection-dominated regime appears (Abramowicz et al. 1988). Inside a certain radius
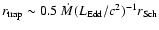 (Begelman & Meier 1982; Kawaguchi 2003),
the timescale for photon diffusion is larger than the accretion timescale,
and thus most of the photons emitted inside the flow are trapped within it.
Thus, advection cooling becomes dominant over radiative cooling
at
(Begelman & Meier 1982; Kawaguchi 2003),
the timescale for photon diffusion is larger than the accretion timescale,
and thus most of the photons emitted inside the flow are trapped within it.
Thus, advection cooling becomes dominant over radiative cooling
at
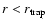 .
.
We define
 as the radius where the mass density in the disc mid-plane
(
as the radius where the mass density in the disc mid-plane
(
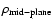 )
equals
)
equals
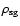 .
Here,
.
Here,
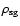 is a critical density above
which
self-gravity of the disc
must be considered:
is a critical density above
which
self-gravity of the disc
must be considered:
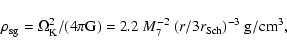 |
(1) |
where
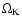 is the Keplerian rotation frequency
(e.g., Goldreich & Lynden-Bell 1965; Huré 1998).
Inside
is the Keplerian rotation frequency
(e.g., Goldreich & Lynden-Bell 1965; Huré 1998).
Inside
 ,
,
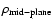 is smaller than
is smaller than
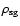 ,
thus the disc self-gravity is negligible there.
,
thus the disc self-gravity is negligible there.
Many authors have tried to derive
 (e.g., Shore & White 1982).
Actually,
(e.g., Shore & White 1982).
Actually,
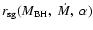 derived and used in this
study is qualitatively consistent with that in Huré (1998).
derived and used in this
study is qualitatively consistent with that in Huré (1998).
In order to derive
 ,
we use analytical formulae for the mass density
(
,
we use analytical formulae for the mass density
(
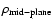 )
given for a Newtonian gravitational potential
(e.g., Kato et al. 1998).
We confirm that these standard-disc formulae for various physical quantities
are consistent with numerical computations (Kawaguchi 2003) within a factor
of
)
given for a Newtonian gravitational potential
(e.g., Kato et al. 1998).
We confirm that these standard-disc formulae for various physical quantities
are consistent with numerical computations (Kawaguchi 2003) within a factor
of 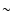 1.5 at any radius larger than
1.5 at any radius larger than
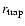 .
In other words, the flow behaves like a standard disc
(Shakura & Sunyaev 1973) outside
.
In other words, the flow behaves like a standard disc
(Shakura & Sunyaev 1973) outside
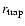 ,
even for a super-Eddington accretion rate.
,
even for a super-Eddington accretion rate.
In a standard disc, the following
three regions must be distinguished according to
the sources of the pressure and opacity
(e.g., Shakura & Sunyaev 1973; Kato et al. 1998).
In which region
 appears is determined by
appears is determined by 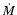 (see Fig. 2).
(see Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3925f2.eps}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg59.gif) |
Figure 2:
Classification of the region where
 appears (Sect. 2.1).
Region (c) harbors
appears (Sect. 2.1).
Region (c) harbors
 when
when 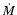 is less than
is less than
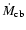 ,
while regions (b) and (a) are, respectively, in charge of ,
while regions (b) and (a) are, respectively, in charge of
 when
when 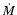 is smaller and larger than
is smaller and larger than
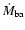 .
Around the radius .
Around the radius
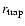 ,
the flow undergoes a change from
radiation cooling-dominated regime to advection-dominated
regime (optically-thick ADAF). ,
the flow undergoes a change from
radiation cooling-dominated regime to advection-dominated
regime (optically-thick ADAF). |
| Open with DEXTER |
Given
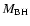 and
and 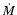 ,
the critical radius
,
the critical radius
 can be
written as Max(
can be
written as Max(
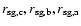 ),
for the whole range of accretion rates.
Instead of a piece-wise function, we employ a simple formula:
),
for the whole range of accretion rates.
Instead of a piece-wise function, we employ a simple formula:
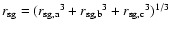 .
Figure 3 (upper panels) shows
.
Figure 3 (upper panels) shows
 for
various
for
various
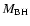 ,
,
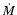 and
and 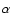 .
Until the accretion rate reaches
.
Until the accretion rate reaches
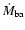 ,
,
 decreases with an increasing
decreases with an increasing 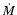 ,
while
,
while
 changes the sign of its
changes the sign of its 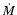 -dependency at
-dependency at
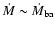 .
.
We find that with
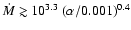
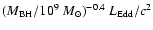 ,
,
 can be less than
can be less than
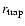 .
The above expressions are no longer valid in
the regime in which
.
The above expressions are no longer valid in
the regime in which
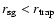 .
In that case,
a self-gravitating,
optically-thick, advection-dominated accretion disc appears.
Therefore, we restrict ourselves to
accretion rates lower than
.
In that case,
a self-gravitating,
optically-thick, advection-dominated accretion disc appears.
Therefore, we restrict ourselves to
accretion rates lower than
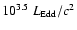 ,
in order to ensure that
,
in order to ensure that
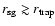 .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm,clip]{MS3925f3.epsi}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg76.gif) |
Figure 3:
Critical radius and wavelength
[
 (upper) and
(upper) and
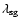 (lower)] for various
(lower)] for various
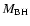 , ,
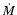 and
and 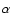 .
Here, .
Here,
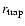 (dashed lines in the upper panels) is the
radius inside which photon trapping plays a role.
The dotted lines in the lower panel are computed based on
the assumption that the radiation from
(dashed lines in the upper panels) is the
radius inside which photon trapping plays a role.
The dotted lines in the lower panel are computed based on
the assumption that the radiation from
 is blackbody,
while solid lines take the effect of electron scattering (modified
blackbody) into account.
If
is blackbody,
while solid lines take the effect of electron scattering (modified
blackbody) into account.
If
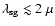 m, it means that we are able to observe
the self-gravitating accretion disc as Near-IR/optical continuum
radiation. m, it means that we are able to observe
the self-gravitating accretion disc as Near-IR/optical continuum
radiation. |
| Open with DEXTER |
Next, we evaluate the effective temperature at
 ,
and subsequently a critical wavelength
,
and subsequently a critical wavelength
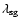 corresponding to the
emission from
corresponding to the
emission from
 .
At
.
At
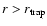 ,
the effective temperature
,
the effective temperature
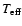 at radius r is given by
at radius r is given by
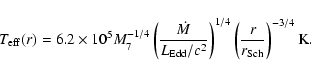 |
(5) |
The simplest procedure to estimate
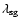 is to use the
Wien displacement law assuming that the emission is close to a blackbody
radiation:
namely
is to use the
Wien displacement law assuming that the emission is close to a blackbody
radiation:
namely
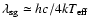 (see Rybicki & Lightman 1979).
It follows that the critical wavelength is
(see Rybicki & Lightman 1979).
It follows that the critical wavelength is
![\begin{displaymath}
{\lambda_{\rm sg}}= \frac{h c}{4 k {T_{\rm eff}}({r_{\rm sg...
...frac{{T_{\rm eff}}({r_{\rm sg}})}{\rm K}\right]^{-1} {\rm cm}.
\end{displaymath}](/articles/aa/full/2004/07/aa3925/img80.gif) |
(6) |
The results are shown by
the dotted lines in Fig. 3 (lower panels).
The effects of electron scattering (opacity and Comptonization)
must be considered in studying the emergent
spectra from a super-Eddington accreting disc
(Shimura & Manmoto 2003; Wang & Netzer 2003; Kawaguchi 2003).
Comptonization is important at radius less than 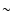
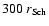 for
for
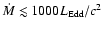 ,
and thus it has no effect
on the emission beyond
,
and thus it has no effect
on the emission beyond
 .
On the other hand, the ratio of electron-scattering opacity to
absorption opacity is larger than unity at
.
On the other hand, the ratio of electron-scattering opacity to
absorption opacity is larger than unity at
![$r \lesssim 2500 [{\dot{M}}/({L_{\rm Edd}/c^2})]^{2/3}~r_{\rm Sch}$](/articles/aa/full/2004/07/aa3925/img83.gif) (see Kato et al. 1998),
and thus the effect of electron-scattering opacity
is still important at
(see Kato et al. 1998),
and thus the effect of electron-scattering opacity
is still important at
 .
.
![\begin{figure}
\par\includegraphics[angle=0,width=12.9cm,clip]{MS3925f4.eps}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg86.gif) |
Figure 4:
Mid-IR to X-ray spectral modeling of Ton S 180.
Open squares and thick striped lines are the observed data and
the power-law fits described in Turner et al. (2002).
Two solid lines are the spectral components of the dusty torus
(left) and the non self-gravitating disc with a corona (right;
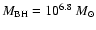 , ,
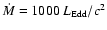 ,
and ,
and
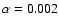 ).
Two dotted lines mean the spectrum (from ).
Two dotted lines mean the spectrum (from
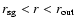 )
of the self-gravitating disc
for )
of the self-gravitating disc
for
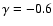 (where
(where
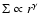 )
and )
and
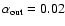 (upper; one of the successful
fits shown in Table 2) and
that of a Keplerian, standard disc (lower).
Total spectra of those three components are indicated
by dashed lines:
thick line is the spectrum with the self-gravitating
disc mentioned above, while the case with a standard disc is
indicated by a lower curve.
The upper dashed line exhibits a total
spectrum with a different parameter set for the outer
self-gravitating disc (
(upper; one of the successful
fits shown in Table 2) and
that of a Keplerian, standard disc (lower).
Total spectra of those three components are indicated
by dashed lines:
thick line is the spectrum with the self-gravitating
disc mentioned above, while the case with a standard disc is
indicated by a lower curve.
The upper dashed line exhibits a total
spectrum with a different parameter set for the outer
self-gravitating disc (
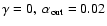 ). ). |
| Open with DEXTER |
Due to the electron-scattering opacity, the emergent spectrum (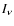 )
is distorted towards higher energy (i.e. shorter wavelength),
and is close to the so called modified blackbody
(Rybicki & Lightman 1979;
Czerny & Elvis 1987;
Wandel & Petrosian 1988):
)
is distorted towards higher energy (i.e. shorter wavelength),
and is close to the so called modified blackbody
(Rybicki & Lightman 1979;
Czerny & Elvis 1987;
Wandel & Petrosian 1988):
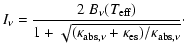 |
|
|
(7) |
Here, 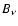 ,
,
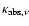 and
and
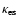 (=0.4 cm2/g) are, respectively,
the Planck function, absorption opacity and
electron-scattering opacity.
The spectral shift due to this effect is roughly estimated as
follows (Madej 1974):
(=0.4 cm2/g) are, respectively,
the Planck function, absorption opacity and
electron-scattering opacity.
The spectral shift due to this effect is roughly estimated as
follows (Madej 1974):
![$\displaystyle \Delta\log_{10}{\lambda_{\rm sg}}
\simeq \frac{1}{8}
\log_{10}\le...
...m sg}})}
{\kappa_{\rm abs}({r_{\rm sg}})+\kappa_{\rm es}({r_{\rm sg}})}\right],$](/articles/aa/full/2004/07/aa3925/img92.gif) |
|
|
(8) |
where
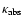 is the Rosseland mean opacity for
absorption (bound-bound, bound-free and free-free processes).
In assessing
is the Rosseland mean opacity for
absorption (bound-bound, bound-free and free-free processes).
In assessing
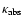 ,
we take 30 times the free-free
absorption opacity,
as is done in Czerny & Elvis (1987) and Kawaguchi (2003):
,
we take 30 times the free-free
absorption opacity,
as is done in Czerny & Elvis (1987) and Kawaguchi (2003):
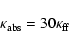 |
(9) |
with the free-free absorption opacity,
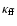 ,
as follows
,
as follows
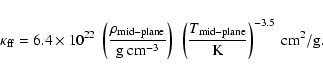 |
(10) |
Here,
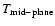 is the temperature at the mid-plane of the disc
(Kato et al. 1998).
is the temperature at the mid-plane of the disc
(Kato et al. 1998).
Finally,
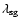 modified from Eq. (6) by Eq. (8)
are plotted in the lower panels of Fig. 3 as
solid lines.
As far as
modified from Eq. (6) by Eq. (8)
are plotted in the lower panels of Fig. 3 as
solid lines.
As far as
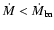 ,
,
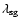 is roughly
proportional to
is roughly
proportional to
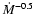 .
For
.
For
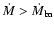 and
and
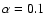 ,
,
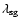 reaches and stays at
reaches and stays at 
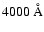 ,
and interestingly it can be as small as
,
and interestingly it can be as small as 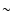
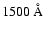 for
the lowest
for
the lowest 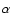 case here (i.e.
case here (i.e.
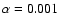 ).
Because of dust sublimation at
).
Because of dust sublimation at
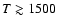 K,
emission of dust falls within the Mid-IR-Near-IR spectral range
and can not contribute to the optical component (see Sect. 3.3).
Therefore, emission from
K,
emission of dust falls within the Mid-IR-Near-IR spectral range
and can not contribute to the optical component (see Sect. 3.3).
Therefore, emission from 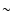
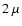 m to
m to
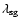 arises
from the self-gravitating part of the super-Eddington accreting disc.
In other words, this is
a discovery of a spectral window for observing the self-gravitating
disc, which has solely been studied by maser spots.
arises
from the self-gravitating part of the super-Eddington accreting disc.
In other words, this is
a discovery of a spectral window for observing the self-gravitating
disc, which has solely been studied by maser spots.
We note that
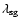 for
for
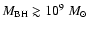 is also
small even with sub-Eddington accretion rates.
In the sub-Eddington regime, however,
heating by central radiation onto an outer
region at
is also
small even with sub-Eddington accretion rates.
In the sub-Eddington regime, however,
heating by central radiation onto an outer
region at
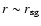 may not be negligible.
An uncertainty of physical quantities (such as the gas density)
in the outer region of the disc
(e.g., Hoshi & Inoue 1988) will lead to
uncertainties of
may not be negligible.
An uncertainty of physical quantities (such as the gas density)
in the outer region of the disc
(e.g., Hoshi & Inoue 1988) will lead to
uncertainties of
 and
and
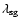 .
On the contrary, a super-Eddington accreting disc is not flared,
i.e. it has a maximum of
the aspect ratio at
.
On the contrary, a super-Eddington accreting disc is not flared,
i.e. it has a maximum of
the aspect ratio at
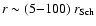 (Kawaguchi 2003),
when such irradiation is considered to be less important.
For this reason,
(Kawaguchi 2003),
when such irradiation is considered to be less important.
For this reason,
 and
and
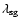 obtained for high
obtained for high 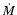 are more reliable than for the sub-Eddington cases.
Therefore, we concentrate on the
super-Eddington cases.
are more reliable than for the sub-Eddington cases.
Therefore, we concentrate on the
super-Eddington cases.
We now demonstrate that the broad-band spectrum
of a bright, well-studied NLS1, Ton S 180,
is indeed well fitted by the spectrum arising from
three components: a slim disc (with a coronal, hard X-ray spectrum),
a self-gravitating non-Keplerian disc
and a dusty torus.
The configuration we consider is schematically shown in Fig. 1.
The Near-IR to X-ray data are taken from Fig. 7 and Table 6 of
Turner et al. (2002).
The IRAS data for Far-IR and Mid-IR flux are derived from the NED database.
The luminosity is calculated from observed flux assuming
isotropic radiation, zero cosmological constant,
deceleration parameter q0 = 0.5, and Hubble
constant H0 = 75 km s-1 Mpc-1.
Data are plotted in Fig. 4
as open squares.
Ton S 180 has low Galactic and intrinsic extinction
(Turner et al. 2002).
Since Ton S 180 is a nearby object (z=0.06),
we have not taken any spectral shifts or K-corrections into account.
The BH mass estimated from the H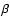 width and optical
luminosity (Wandel et al. 1999; Kaspi et al. 2000)
is
width and optical
luminosity (Wandel et al. 1999; Kaspi et al. 2000)
is
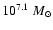 .
This value is comparable to
.
This value is comparable to
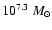 inferred from the [O III] width using Eq. (2) in Wang & Lu (2001).
Its B-band luminosity,
inferred from the [O III] width using Eq. (2) in Wang & Lu (2001).
Its B-band luminosity,
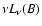 ,
is about 1044.6 erg/s,
implying that
,
is about 1044.6 erg/s,
implying that
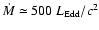 (see Kawaguchi 2003).
Thus, this object is expected to be one of the
highest
(see Kawaguchi 2003).
Thus, this object is expected to be one of the
highest
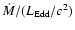 objects among NLS1s and Narrow-Line QSOs.
objects among NLS1s and Narrow-Line QSOs.
The structure and emergent spectrum of the inner disc around
a non-rotating BH is computed
numerically following the same procedure as in Kawaguchi (2003).
The theoretical background of the numerical method is described in
Matsumoto et al. (1984) and in Honma et al. (1991a,b).
The model employs the standard prescription for turbulent viscosity
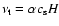 (Shakura & Sunyaev 1973) where
(Shakura & Sunyaev 1973) where
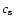 is the sound speed and H the semi-thickness.
The input parameters are
is the sound speed and H the semi-thickness.
The input parameters are
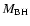 ,
,
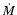 and viscosity parameter
and viscosity parameter 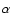 .
Given a set of these parameters, we integrate the differential equations
for the flow from
.
Given a set of these parameters, we integrate the differential equations
for the flow from
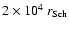 down to the inner free
boundary at
down to the inner free
boundary at
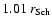 .
.
The best parameters for this object have been selected by
the least-square procedure,
comparing the predicted spectrum
(with a hard X-ray power-law due to a corona) to
the power-law fits for the optical/UV/X-ray spectrum
(thick striped lines in Fig. 4;
see Table 7 in Turner et al. 2002).
First,
the following parameter region is surveyed;
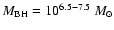 ,
,
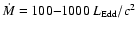 ,
and
,
and
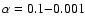 with
with
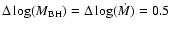 ,
and
,
and
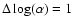 .
Among them, one parameter set (
.
Among them, one parameter set (
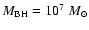 ,
,
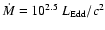 and
and
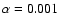 )
exhibits
the best fit.
Next, we compute the spectra in more detail around
this parameter set,
with
)
exhibits
the best fit.
Next, we compute the spectra in more detail around
this parameter set,
with
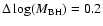 ,
,
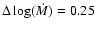 ,
and
,
and
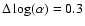 .
Finally, we selected two best sets of parameters
as listed in Table 1,
with
.
Finally, we selected two best sets of parameters
as listed in Table 1,
with
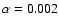 in both cases.
The mass of this inner disc
in both cases.
The mass of this inner disc
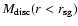 is
is
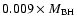 for set 1,
and
for set 1,
and
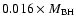 for set 2, respectively.
Values at
for set 2, respectively.
Values at
 (
( and H) are used
as the inner boundary conditions for the
self-gravitating part.
and H) are used
as the inner boundary conditions for the
self-gravitating part.
Table 1:
Best parameter sets for the non self-gravitating disc.
The emergent spectrum from
 (for set 2) is shown
in Fig. 4 by a solid line (right),
while
relevant physical quantities are shown in Fig. 5.
For a presentation purpose, a simple
(for set 2) is shown
in Fig. 4 by a solid line (right),
while
relevant physical quantities are shown in Fig. 5.
For a presentation purpose, a simple
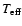 profile
(i.e.
profile
(i.e.
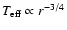 )
is also drawn as a dotted line.
)
is also drawn as a dotted line.
As to the broken power-law description for the X-ray data,
different combinations of the photon index 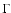 and breaking energy
are deduced for different observations.
In order to assess how the different combinations
affect the generation of the best sets of parameters,
we have also performed the same least-square procedure with
the X-ray data replaced by the broken power-law description
in Vaughan et al. (2002).
The following four parameter sets provide best fits;
and breaking energy
are deduced for different observations.
In order to assess how the different combinations
affect the generation of the best sets of parameters,
we have also performed the same least-square procedure with
the X-ray data replaced by the broken power-law description
in Vaughan et al. (2002).
The following four parameter sets provide best fits;
![$[\log ({M_{\rm BH}}/ {M_\odot}), \ {\dot{M}}/({L_{\rm Edd}/c^2}), \ \alpha] =
(6.8, 1000, 0.002), (6.8, 1000, 0.004), (7.0, 562, 0.002)$](/articles/aa/full/2004/07/aa3925/img131.gif) ,
and
(7.2, 178, 0.002).
The goodness of the fit to the data
shows a slightly shallower distribution than the fit to the
Turner et al. (2002) data.
In the rest of this study, we emphasize the fit to
the data in Turner et al. (2002), where the broadband data
were obtained quasi simultaneously.
,
and
(7.2, 178, 0.002).
The goodness of the fit to the data
shows a slightly shallower distribution than the fit to the
Turner et al. (2002) data.
In the rest of this study, we emphasize the fit to
the data in Turner et al. (2002), where the broadband data
were obtained quasi simultaneously.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{MS3925f5.eps}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg132.gif) |
Figure 5:
Variation with radius of some disc parameters
(the inner, non self-gravitating part is based on set 2);
half surface density 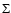 ,
rotational frequency
normalized to the Keplerian value ,
rotational frequency
normalized to the Keplerian value
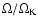 ,
effective temperature ,
effective temperature
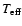 ,
and Toomre Q-parameter.
The solid lines are computed with ,
and Toomre Q-parameter.
The solid lines are computed with
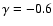 and
and
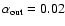 ,
while dot-dashed and dashed ones
are computed for ,
while dot-dashed and dashed ones
are computed for
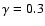 with a constant
with a constant 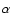 and
and
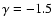 with
with
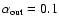 ,
respectively.
Two accretion regimes are detached at ,
respectively.
Two accretion regimes are detached at
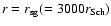 . . |
| Open with DEXTER |
In the standard theory of radiatively cooled accretion discs
(e.g., Pringle 1981), the effective temperature
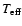 (close to the surface temperature) is given by
(close to the surface temperature) is given by
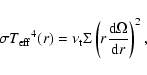 |
(11) |
where  is the rotation frequency.
Again, the turbulent viscosity is chosen to be the standard
prescription:
is the rotation frequency.
Again, the turbulent viscosity is chosen to be the standard
prescription:
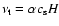 (Shakura & Sunyaev 1973).
The sound speed
(Shakura & Sunyaev 1973).
The sound speed 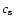 is found from the requirement of hydrostatic
equilibrium, namely
is found from the requirement of hydrostatic
equilibrium, namely
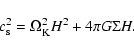 |
(12) |
At
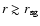 ,
the disc becomes self-gravitating,
namely
,
the disc becomes self-gravitating,
namely 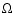 is expected to depart from its Keplerian
value
is expected to depart from its Keplerian
value
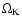 .
In order to compute
.
In order to compute 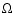 ,
we assume that the rotation
curve has only a gravitational origin, that is
,
we assume that the rotation
curve has only a gravitational origin, that is
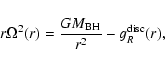 |
(13) |
where
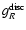 is the contribution due to
the whole disc, including the inner slim disc.
In general, at large distances, we expect
is the contribution due to
the whole disc, including the inner slim disc.
In general, at large distances, we expect
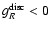 with the consequence that
with the consequence that
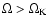 .
This means a possible reduction of the gradient,
.
This means a possible reduction of the gradient,
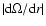 ,
and subsequently a change of the effective
temperature (Eq. (11)) with respect to a standard disc.
It is worth noting that a similar idea has been proposed by Lodato
& Bertin (2001) in order to explain the IR-excess of T Tauri stars.
,
and subsequently a change of the effective
temperature (Eq. (11)) with respect to a standard disc.
It is worth noting that a similar idea has been proposed by Lodato
& Bertin (2001) in order to explain the IR-excess of T Tauri stars.
Since the self-gravitating disc should be gravitationally unstable,
other sources of heating, e.g., heating by gravitational
instabilities (Adams et al. 1988; Lodato & Bertin 2001),
may overcome the heating by turbulent viscosity (see Lodato & Rice 2003).
To take into account this possibility, we allow the parameter 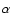 in the self-gravitating part to increase linearly with r,
from 0.002 (the value used for the inner disc in Sect. 3.1)
at
in the self-gravitating part to increase linearly with r,
from 0.002 (the value used for the inner disc in Sect. 3.1)
at
 to
to
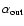 at the outermost radius of the
self-gravitating disc
at the outermost radius of the
self-gravitating disc
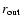 .
.
Since there is no simple formula for radial self-gravity, we
have determined
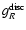 numerically using the accurate Poisson
3D-solver, which is described in Huré (2003) for discs with various
shapes, sizes and surface density profiles.
This has been performed assuming
that
numerically using the accurate Poisson
3D-solver, which is described in Huré (2003) for discs with various
shapes, sizes and surface density profiles.
This has been performed assuming
that
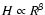 and
and
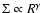 ,
where
,
where 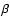 and
and 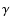 are input parameters.
Here, H and
are input parameters.
Here, H and 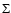 are continuous at the transition between
the two regimes of the disc.
The radial extension of the self-gravitating disc
are continuous at the transition between
the two regimes of the disc.
The radial extension of the self-gravitating disc
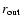 and the viscosity parameter
and the viscosity parameter 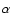 at that radius
at that radius
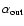 are also input parameters.
Those values (
are also input parameters.
Those values (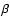 ,
,
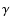 ,
,
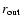 ,
and
,
and
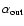 )
are determined so that the total spectra (Sect. 3.4) provide acceptable
fits to the observed one.
)
are determined so that the total spectra (Sect. 3.4) provide acceptable
fits to the observed one.
For each model, the effective temperature
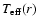 is
derived from the resultant rotation frequency using Eq. (11).
The spectrum of the self-gravitating disc is then computed
in the same way as the inner slim disc (i.e., with
the effect of electron scattering, even though the effect is small
in the outer self-gravitating part).
is
derived from the resultant rotation frequency using Eq. (11).
The spectrum of the self-gravitating disc is then computed
in the same way as the inner slim disc (i.e., with
the effect of electron scattering, even though the effect is small
in the outer self-gravitating part).
When we add the spectra of the
outer, self-gravitating disc onto the inner disc spectrum,
it is found that
the combined spectra based on set 2 (Table 1)
generally provide a better fit
to the observed optical/UV spectrum than those based on
set 1.
Thus,
we hereafter discuss the models obtained for set 2 alone
as an example.
For set 2, three possible combinations of parameters
are shown in Table 2.
The best parameters for 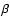 and
and
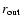 are common to
them:
are common to
them:
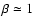 and
and
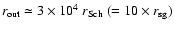 .
For one case (
.
For one case (
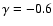 and
and
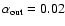 ),
the spectra from the self-gravitating part (upper dotted line)
and the total spectrum (thick dashed line) are presented in
Fig. 4.
Those three combinations exhibit almost identical spectra
(deviation of
),
the spectra from the self-gravitating part (upper dotted line)
and the total spectrum (thick dashed line) are presented in
Fig. 4.
Those three combinations exhibit almost identical spectra
(deviation of 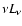 is 0.05 dex at most).
Other combinations are also acceptable.
The cumulative disc mass
is 0.05 dex at most).
Other combinations are also acceptable.
The cumulative disc mass
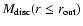 is not negligible,
ranging from
is not negligible,
ranging from
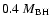 to
to
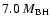 .
For the intermediate case, for instance,
the total mass,
.
For the intermediate case, for instance,
the total mass,
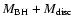 ,
is about
,
is about
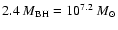 ,
which is consistent
with the central mass estimated by H
,
which is consistent
with the central mass estimated by H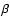 and [O III] line widths.
It indicates that
and [O III] line widths.
It indicates that
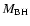 -estimations using line widths
overestimate the BH mass systematically.
To assess how the spectrum changes with different
-estimations using line widths
overestimate the BH mass systematically.
To assess how the spectrum changes with different 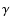 ,
the total spectrum obtained with
,
the total spectrum obtained with
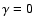 ,
which is less preferable,
is indicated by the upper dashed line.
,
which is less preferable,
is indicated by the upper dashed line.
Table 2:
Successful solutions for the self-gravitating disc.
Figure 5 presents several physical quantities
of the disc
for the three successful parameter sets (Table 2)
as a function of radius;
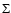 ,
,
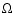 (Eq. (13)) and
(Eq. (13)) and
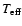 .
Vertical optical thickness of the flow,
.
Vertical optical thickness of the flow, 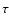 [
[
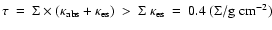 ]
is much larger than unity
everywhere.
For the case with a very massive disc (
]
is much larger than unity
everywhere.
For the case with a very massive disc (
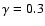 ),
),
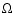 becomes flat and even starts to increase with radius
due to the strong radial self-gravity.
This produces a local decrease in
becomes flat and even starts to increase with radius
due to the strong radial self-gravity.
This produces a local decrease in
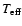 [
[
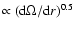 ;
Eq. (11)]
at a small range of radius.
However, the temperature profiles
;
Eq. (11)]
at a small range of radius.
However, the temperature profiles
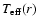 for the three
cases are mostly the same, and thus they produce almost identical
spectra.
for the three
cases are mostly the same, and thus they produce almost identical
spectra.
The dusty torus component
is supposed to be responsible for the Mid-IR (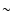
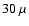 m)
to
m)
to 
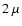 m emission.
In general, the Near-IR flux from AGN varies with time following the
optical flux with a time lag of about a month-year (e.g.,
Clavel et al. 1989; Glass 1992; Nelson 1996).
This implies that the dusty torus is located quite far from the BH,
and that it is heated by the radiation from
the vicinity of the central BH.
m emission.
In general, the Near-IR flux from AGN varies with time following the
optical flux with a time lag of about a month-year (e.g.,
Clavel et al. 1989; Glass 1992; Nelson 1996).
This implies that the dusty torus is located quite far from the BH,
and that it is heated by the radiation from
the vicinity of the central BH.
A detailed modeling of the emission of the torus is beyond
the scope of this paper. Here, we adopt a simple power-law
description with a cut-off. Theoretical arguments on the dust
sublimation as well as
observational data (as a spectral bump around 3 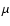 m)
indicate that the maximum temperature of the torus
is
m)
indicate that the maximum temperature of the torus
is 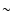 1000-1500 K (e.g. Efstathiou et al. 1995;
Kobayashi et al. 1993; Pier & Krolik 1993).
It corresponds to wavelength of
1000-1500 K (e.g. Efstathiou et al. 1995;
Kobayashi et al. 1993; Pier & Krolik 1993).
It corresponds to wavelength of 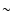
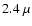 m
(i.e.
h c / (4 k T) with
m
(i.e.
h c / (4 k T) with
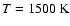 ),
or
),
or
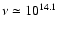 Hz (i.e. 4 k T / h).
Hz (i.e. 4 k T / h).
We assume that the fluxes at
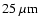 and
and
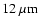 come from
the dusty torus alone, while the near-IR flux is partly due to
the self-gravitating disc.
Then, the simple model we apply is
come from
the dusty torus alone, while the near-IR flux is partly due to
the self-gravitating disc.
Then, the simple model we apply is
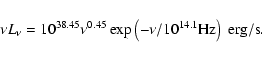 |
(14) |
We are confident that this is neither the only nor the best
possible description.
The spectral index inferred for this object differs
from the typical mid-IR-near-IR index of bright AGNs
(
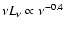 ;
Neugebauer et al. 1987;
Polletta & Couvoisier 1999; see also Grupe et al. 1998).
;
Neugebauer et al. 1987;
Polletta & Couvoisier 1999; see also Grupe et al. 1998).
We can specify the location 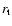 of the inner torus
(see Fig. 1) by considering that the torus is
in thermal balance (heating by radiation from the inner disc
is balanced by radiative cooling):
of the inner torus
(see Fig. 1) by considering that the torus is
in thermal balance (heating by radiation from the inner disc
is balanced by radiative cooling):
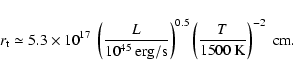 |
(15) |
where L and T are the bolometric luminosity of the central
disc, and the gas temperature at the innermost radius of the torus,
respectively.
For the set 2, we have
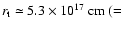
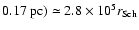 ,
which is about 10 times
larger than the outer radius of the self-gravitating disc
,
which is about 10 times
larger than the outer radius of the self-gravitating disc
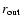 .
Thus, gravitational attraction on the self-gravitating disc by
the torus should not be crucial, unless the torus mass exceeds
the BH mass by some order of magnitude.
.
Thus, gravitational attraction on the self-gravitating disc by
the torus should not be crucial, unless the torus mass exceeds
the BH mass by some order of magnitude.
The thick dashed line in
Fig. 4 shows the broad-band, mid-IR to X-ray
spectral modeling for Ton S 180,
comprised of the three components described in the
subsections above.
We see that the
optical component can be interpreted as the thermal emission
from the self-gravitating, non-Keplerian disc.
The models for the self-gravitating disc with 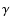 and
and
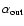 listed in Table 2
provide equally good fits to the observed spectrum.
The upper dashed line (for
listed in Table 2
provide equally good fits to the observed spectrum.
The upper dashed line (for
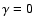 and
and
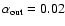 )
is drawn to show to what extent a different
value of
)
is drawn to show to what extent a different
value of 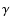 changes the total spectrum.
changes the total spectrum.
If the outer self-gravitating disc is replaced by
a Keplerian, standard disc, the resultant total
spectrum (lower dashed curve)
is not adequate to explain the observed optical/near-IR spectrum.
In other words, flux enhancement at the outer region
is necessary.
This enhancement depends on the resultant rotation law,
as well as
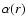 ,
at the outer self-gravitating disc.
,
at the outer self-gravitating disc.
We demonstrate that a broadband spectrum of one NLS1, Ton S 180,
is indeed well fitted by a summation of
an inner, non self-gravitating disc, an outer, self-gravitating
disc and a dusty torus.
Detailed mid-near-IR observations, including temporal
studies (e.g. Glass 1992; Nelson 1996), will
provide a more accurate model of the dusty torus.
Subtraction of the torus component from the total (disc and torus)
spectrum will enable us to
derive stronger constraints on the size of the self-gravitating
part, and mass of the whole disc, etc.
High spatial resolution obtained with ground-based,
mid- to near-IR interferometers with the large
telescopes, such as OHANA (Mariotti et al. 1996; Perrin et al. 2000)
and VLTI, will contribute to solving these problems.
As is obtained in Sect. 3.2,
the integrated disc mass is about
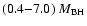 (Table 2).
Although
the Toomre Q parameter
[=
(Table 2).
Although
the Toomre Q parameter
[=
![$\Omega c_{\rm s}/ (\pi \Sigma G)]$](/articles/aa/full/2004/07/aa3925/img176.gif) remains greater than one
in the whole disc (Fig. 5),
it is quite close to unity at outer radius for larger
remains greater than one
in the whole disc (Fig. 5),
it is quite close to unity at outer radius for larger 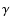 .
This fact supports the introduction of the additional heating
due to gravitational instabilities (e.g., increasing
.
This fact supports the introduction of the additional heating
due to gravitational instabilities (e.g., increasing 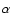 used
here; see Lodato & Rice 2003).
Consensus on the amount of such heating has not yet been reached.
Further understanding on this topic, which is related to
used
here; see Lodato & Rice 2003).
Consensus on the amount of such heating has not yet been reached.
Further understanding on this topic, which is related to
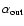 in this study, will allow us to constrain
in this study, will allow us to constrain 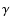 (where
(where
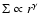 )
and the disc mass more severely.
)
and the disc mass more severely.
The size of the broad-line region (BLR),
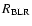 ,
for Ton S 180 is
expected to be of the order of 100 lt.d.,
using the empirical relation between the optical luminosity
and
,
for Ton S 180 is
expected to be of the order of 100 lt.d.,
using the empirical relation between the optical luminosity
and
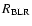 (Kaspi et al. 2000).
This radius corresponds to 0.085 pc
(Kaspi et al. 2000).
This radius corresponds to 0.085 pc
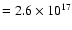 cm;
equivalently,
cm;
equivalently,
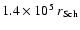 for
for
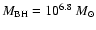 .
Thus, the broad-line region is likely located
between the inner radius of the torus
(
.
Thus, the broad-line region is likely located
between the inner radius of the torus
(
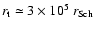 )
and the outer radius of the self-gravitating disc
(
)
and the outer radius of the self-gravitating disc
(
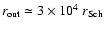 ).
However, the constraint on
).
However, the constraint on
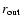 derived in Sect. 3.2 is rather weak.
If the outer massive disc extends at
derived in Sect. 3.2 is rather weak.
If the outer massive disc extends at
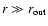 ,
the clouds in the broad-line region may not be in
Keplerian motion, which will lead to an uncertainty
for the
,
the clouds in the broad-line region may not be in
Keplerian motion, which will lead to an uncertainty
for the
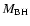 -estimation with H
-estimation with H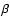 width (e.g., Krolik 2001).
width (e.g., Krolik 2001).
Since the main purpose of this paper is to report
the discovery of the spectral window for observing a
self-gravitating disc,
and to demonstrate a spectral fit to the observed spectrum
of a super-Eddington accreting AGN,
we did not treat the following two issues very accurately:
(i) the vertical self-gravity (the last term in the
right-hand-side of Eq. (12)) in the inner, non self-gravitating disc,
and (ii) the effect of realistic absorption opacity in deriving
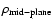 (Sect. 2.1).
Also, possible outflow from the disc is not taken into
account either in the inner slim part or in the outer self-gravitating
part.
Outflow/evaporation at the outer region may contribute to the
formation of BLR clouds or broad absorption line (BAL) clouds.
These issues will be examined in the future.
(Sect. 2.1).
Also, possible outflow from the disc is not taken into
account either in the inner slim part or in the outer self-gravitating
part.
Outflow/evaporation at the outer region may contribute to the
formation of BLR clouds or broad absorption line (BAL) clouds.
These issues will be examined in the future.
We have presented the
outermost radius of the non self-gravitating accretion disc (
 )
around a super-massive black hole (BH), i.e.
the inner edge of the self-gravitating disc,
as a function of the BH mass
)
around a super-massive black hole (BH), i.e.
the inner edge of the self-gravitating disc,
as a function of the BH mass
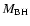 ,
accretion rate
,
accretion rate 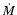 and
viscosity parameter
and
viscosity parameter 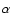 .
We then showed the
corresponding wavelength (
.
We then showed the
corresponding wavelength (
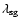 )
that is relevant to the
emission from
)
that is relevant to the
emission from
 .
.
When
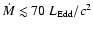 (for
(for
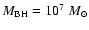 ),
),
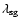 is roughly
proportional to
is roughly
proportional to
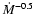 for fixed
for fixed
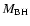 and
and 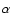 .
With a higher
.
With a higher 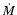 ,
,
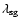 reaches and stays at
reaches and stays at 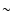
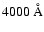 for
for
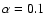 .
Interestingly,
.
Interestingly,
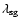 is as small as
is as small as 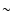
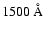 for
the lowest
for
the lowest 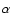 case in this study (i.e.
case in this study (i.e.
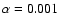 ).
Therefore, the continuum emission from
).
Therefore, the continuum emission from 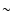
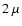 m to
m to
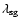 arises
from the self-gravitating part of the super-Eddington accreting disc.
Thus, we have discovered a spectral window for observing the
self-gravitating disc, which has only been studied by maser spots
at the parsec-scale for a few nearby objects.
arises
from the self-gravitating part of the super-Eddington accreting disc.
Thus, we have discovered a spectral window for observing the
self-gravitating disc, which has only been studied by maser spots
at the parsec-scale for a few nearby objects.
Next, we demonstrated that the mid-IR to X-ray spectrum
of a bright, well-studied Narrow-Line Seyfert 1 galaxy, Ton S 180,
is indeed well fitted by the spectrum arising from
the following three components: an inner slim disc (with a corona),
an outer, self-gravitating non-Keplerian disc
and a dusty torus.
Comparing the model spectra of the slim disc with the
observed UV-X-ray one, the following parameters are favored:
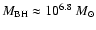 ,
,
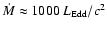 ,
and
,
and
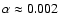 .
In the model for the outer, self-gravitating disc,
we allow the viscosity parameter
.
In the model for the outer, self-gravitating disc,
we allow the viscosity parameter 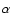 to increase
with radius, and
an outer radius of
to increase
with radius, and
an outer radius of
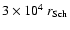 is inferred.
Various profiles for the surface density
is inferred.
Various profiles for the surface density 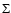 are
acceptable, e.g., from
are
acceptable, e.g., from
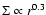 to
to
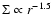 ,
depending on
,
depending on 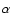 at the outermost radius
of the disc.
at the outermost radius
of the disc.
The accretion disc is quite massive, and the disc mass
can be
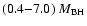 .
The total mass, BH mass plus the entire disc mass,
is found to be about
.
The total mass, BH mass plus the entire disc mass,
is found to be about
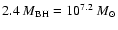 if
if
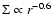 ,
which is consistent
with the central mass estimated by H
,
which is consistent
with the central mass estimated by H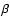 and [O III] line widths.
This indicates that
and [O III] line widths.
This indicates that
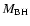 -estimations using line widths
systematically overestimate the BH mass.
Although the disc mass is quite high relative to the BH mass,
the Toomre Q parameter remains greater than one in the whole disc,
so that the disc is marginally stable.
-estimations using line widths
systematically overestimate the BH mass.
Although the disc mass is quite high relative to the BH mass,
the Toomre Q parameter remains greater than one in the whole disc,
so that the disc is marginally stable.
Moreover,
 can be less than the photon trapping radius
for
can be less than the photon trapping radius
for
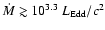 .
Thus, a self-gravitating,
optically-thick, advection-dominated accretion disc
is expected to appear
in the extremely high accretion rate regime.
.
Thus, a self-gravitating,
optically-thick, advection-dominated accretion disc
is expected to appear
in the extremely high accretion rate regime.
Acknowledgements
We thank
Suzy Collin,
Helene Sol,
Julien Woillez,
Catherine Boisson,
and Shin Mineshige for useful comments.
Detailed and productive comments from the
referee, Anuradha Koratkar, are also appreciated.
We are deeply grateful to Ryoji Matsumoto and Fumio Honma
who developed
the numerical code to solve the radial structure of
super-Eddington accretion discs.
This research has made use of the NASA/IPAC
Extragalactic Database (NED)
which is operated by the Jet Propulsion Laboratory,
California Institute of Technology, under contract with the National
Aeronautics and Space Administration.
T.K. is supported by the Japan
Society for the Promotion of Science (JSPS)
Postdoctoral Fellowships for Research Abroad (464).
- Abramowicz, M. A., Czerny, B.,
Lasota, J. P., & Szuszkiewicz, E. 1988, ApJ, 332, 646
In the text
NASA ADS
-
Adams, F. C., Ruden, S. P., & Shu, F. H. 1989, ApJ, 347, 959
NASA ADS
- Balluch, M. 1988, A&A, 200, 58
NASA ADS
- Begelman, M. C., &
Meier, D. L. 1982, ApJ, 253, 873
In the text
NASA ADS
- Brandt, N., & Boller,
T. 1998, Astron. Nachr., 319, 163
In the text
NASA ADS
- Collin, S., Boisson, C.,
Mouchet, M., et al.
2002, A&A, 388, 771
In the text
NASA ADS
- Clavel, J., Wamsteker, W., & Glass, I. S. 1989, ApJ, 337, 236
In the text
NASA ADS
- Czerny, B., & Elvis,
M. 1987, ApJ, 321, 305
In the text
NASA ADS
- Efstathiou, A., Hough, J. H., & Young, S. 1995,
MNRAS, 277, 1134
In the text
NASA ADS
- Frank, J., King, A., & Raine, D. 1992, Accretion Power in Astrophysics (Cambridge Univ. Press), second edition
- Glass, I. S. 1992, MNRAS, 256, 23
In the text
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 97
In the text
NASA ADS
- Grupe, D., Beuermann, K., Thomas, H.-C., Mannheim, K., &
Fink, H. H. 1998, A&A, 330, 25
In the text
NASA ADS
-
Honma, F., Matsumoto, R., & Kato, S. 1991a, PASJ, 43, 147
In the text
NASA ADS
-
Honma, F., Matsumoto, R., Kato, S., & Abramowicz, M. A. 1991b, PASJ, 43, 261
NASA ADS
-
Hoshi, R., & Inoue, H. 1988, PASJ, 40, 421
In the text
NASA ADS
- Huré, J.-M. 1998, A&A, 337, 625
In the text
NASA ADS
- Huré, J.-M. 2002,
A&A, 395, L21
In the text
NASA ADS
- Huré, J.-M. 2003, A&A, submitted
In the text
- Kaspi, S., Smith, P. S.,
Netzer, H., et al.
2000, ApJ, 533, 631
NASA ADS
- Kato, S.,
Fukue, J., & Mineshige, S. 1998, Black-hole accretion disks (Kyoto Univ. Press), Chap. 3
In the text
- Kawaguchi, T. 2003, ApJ, 593, 69
In the text
NASA ADS
- Kobayashi, Y., Sato,
S., Yamashita, T., Shiba, H., & Takami, H. 1993, ApJ, 404, 94
In the text
NASA ADS
- Koratkar, A., &
Blaes, O. 1999, PASP, 111, 1
In the text
NASA ADS
- Krolik, J. H. 2001, ApJ, 551, 72
In the text
NASA ADS
-
Lodato, G., & Bertin, G. 2001, A&A, 375, 455
In the text
NASA ADS
- Lodato, G., & Bertin, G. 2003, A&A, 398, 517
In the text
NASA ADS
- Lodato, G., & Rice, W. K. M. 2003, Proc. in
Plasmas in the laboratory and in the Universe: new insights and new
challenges [astro-ph/0309570]
- Madej, J. 1974, Acta
Astron., 24, 327
In the text
NASA ADS
- Mariotti, J.-M., Coude
Du Foresto, V., Perrin, G., Zhao, P., & Lena, P. 1996, A&AS, 116, 381
In the text
NASA ADS
-
Matsumoto, R., Kato, S., Fukue, J., & Okazaki, A. T. 1984, PASJ, 36, 71
In the text
NASA ADS
- Mineshige, S., Kawaguchi, T., Takeuchi, M., & Hayashida, K.
2000, PASJ, 52, 499
In the text
NASA ADS
- Miyoshi, M., Moran, J., Herrnstein, J., et al. 1995, Nature, 372, 127
In the text
- Mushotzky,
R. F., Done, C., & Pounds, K. A. 1993, ARA&A, 31, 717
In the text
NASA ADS
- Nakai, N., Inoue, M., & Miyoshi, M. 1993, Nature, 361, 45
In the text
NASA ADS
- Nelson, B. O. 1996, ApJ, 465, L87
In the text
NASA ADS
- Neugebauer, G., Green, R. F., Matthews, K., et al. 1987,
ApJS, 63, 615
In the text
NASA ADS
- Pier, E. A., & Krolik,
J. H. 1993, ApJ, 418, 673
In the text
NASA ADS
- Perrin, G., Lai, O., Lena, P. J., & Coude du Foresto, V.
2000, in
Interferometry in Optical Astronomy, ed. P. J. Lena, & A. Quirrenbach,
Proc. SPIE, 4006, 708
In the text
- Polletta, M., & Courvoisier, T. J.-L. 1999, A&A, 350, 765
In the text
NASA ADS
-
Pringle, J. E. 1981, ARA&A, 19, 137
In the text
NASA ADS
-
Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in
Astrophysics (New York: John Willey & Sons)
In the text
-
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337
In the text
NASA ADS
- Shimura, T., & Manmoto, T. 2003, MNRAS, 338, 1013
In the text
NASA ADS
- Shore, S. N., & White, R. L. 1982, ApJ, 256, 390
In the text
NASA ADS
- Thatte, N., Quirrenbach, A., Genzel, R.,
Maiolino, R., & Tecza, M. 1997, ApJ, 490, 238
In the text
NASA ADS
- Telesco, C. M., Becklin, E. E., Wynn-Williams, C. G.,
& Harper, D. A. 1984, ApJ, 282, 427
In the text
NASA ADS
-
Turner, T. J., Romano, P., Kraemer, S. B., et al. 2002, ApJ, 568, 120
In the text
NASA ADS
-
Vaughan, S., Boller, T., Fabian, A. C., et al.
2002, MNRAS, 337, 247
In the text
NASA ADS
-
Wandel, A., & Petrosian, V. 1988, ApJ, 329, L11
In the text
NASA ADS
- Wandel,
A., Peterson, B. M., & Malkan, M. A. 1999, ApJ, 526, 579
In the text
NASA ADS
- Wang, T., & Lu, Y. 2001,
A&A, 377, 52
In the text
NASA ADS
- Wang, J.-M., & Netzer, H. 2003, A&A, 398, 927
In the text
NASA ADS
- Wisotzki, L., Dreizler, S., Engels, D., Fink, H.-H., &
Heber, U. 1995, A&A, 297, L55
In the text
NASA ADS
Copyright ESO 2004
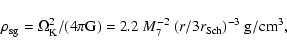
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3925f2.eps}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg59.gif)
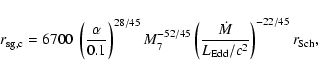
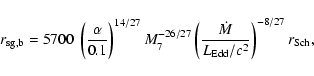
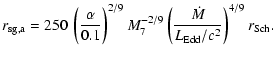
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm,clip]{MS3925f3.epsi}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg76.gif)
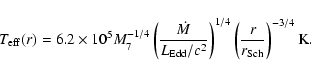
![\begin{displaymath}
{\lambda_{\rm sg}}= \frac{h c}{4 k {T_{\rm eff}}({r_{\rm sg...
...frac{{T_{\rm eff}}({r_{\rm sg}})}{\rm K}\right]^{-1} {\rm cm}.
\end{displaymath}](/articles/aa/full/2004/07/aa3925/img80.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=12.9cm,clip]{MS3925f4.eps}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg86.gif)
![$\displaystyle \Delta\log_{10}{\lambda_{\rm sg}}
\simeq \frac{1}{8}
\log_{10}\le...
...m sg}})}
{\kappa_{\rm abs}({r_{\rm sg}})+\kappa_{\rm es}({r_{\rm sg}})}\right],$](/articles/aa/full/2004/07/aa3925/img92.gif)
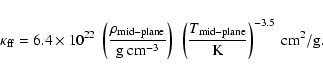
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{MS3925f5.eps}
\end{figure}](/articles/aa/full/2004/07/aa3925/Timg132.gif)