A&A 414, 895-903 (2004)
DOI: 10.1051/0004-6361:20031683
H. Falcke1,2,3 - E. Körding3 - S.
Markoff4,![]()
1 - ASTRON, PO Box 2, 7990 AA Dwingeloo, The Netherlands
2 -
Adjunct Professor, Astronomy Department, University of Nijmegen, Postbus 9010, 6500 GL Nijmegen,
The Netherlands
3 -
Max-Planck-Institut für Radioastronomie, Auf dem Hügel
69, 53121 Bonn,
Germany
4 -
Massachusetts Institute of Technology, Center for Space Research,
77 Massachusetts Ave., Rm. NE80-6035, Cambridge, MA 02139, USA
Received 20 May 2003 / Accepted 30 October 2003
Abstract
We explore the evolution in power of black holes of all
masses, and their associated jets, within the scheme of an accretion
rate-dependent state transition. Below a critical value of the
accretion rate all systems are assumed to undergo a transition to a
state where the dominant accretion mode is optically thin and
radiatively inefficient. In these significantly sub-Eddington
systems, the spectral energy distribution is predicted to be
dominated by non-thermal emission from a relativistic jet whereas
near-Eddington black holes will be dominated instead by emission
from the accretion disk. Reasonable candidates for such a
sub-Eddington state include X-ray binaries in the hard and quiescent
states, the Galactic Center (Sgr A*), LINERs, FR I radio galaxies,
and a large fraction of BL Lac objects. Standard jet physics
predicts non-linear scaling between the optically thick (radio) and
optically thin (optical or X-ray) emission of these systems, which
has been confirmed recently in X-ray binaries. We show that this
scaling relation is also a function of black hole mass and only
slightly of the relativistic Doppler factor. Taking the scaling into
account we show that indeed hard and quiescent state X-ray binaries,
LINERs, FR I radio galaxies, and BL Lacs can be unified and fall on
a common radio/X-ray correlation. This suggests that jet domination
is an important stage in the luminosity evolution of accreting black
hole systems.
Key words: X-rays: binaries - radiation mechanisms: non-thermal - stars: winds, outflows - black hole physics - accretion, accretion disks
The most important parameters of accreting black holes are probably the mass and the accretion rate, both of which can vary over many orders of magnitude. Additional parameters which likely impact the observable characteristics of black holes are the spin and the inclination angle of their spin axes. Inclination-based unified schemes of AGN merge apparently different objects based on the angle between the spin axis and the line of sight (see e.g., Antonucci 1993; Urry & Padovani 1995). The success of this scheme supports the evidence for angle-dependent obscuration and relativistic beaming.
However, the exact effect that changes in the accretion rate have on the appearance of their associated black hole systems is a matter of ongoing debate. A good understanding of this is crucial for modeling the cosmic evolution of black holes and for disentangling the different source classes.
A number of recent results suggests that the transition from a
high-accretion-rate black hole to a low-accretion-rate one is not smooth,
but rather accompanied by a "phase transition''. In the low-power
phase, the optically thick disk emission is either dominated by emission from
an optically thin corona, completely reduced to a radiatively
inefficient inflow, or is truncated and an optically thin inner
radiatively inefficient flow exists closer to the compact object (see
Poutanen 1998 for a review of the various models). For XRBs
Esin et al. (1997) estimate that this transition occurs
once the accretion rate for a black hole of mass ![]() drops to
less than a critical value (
drops to
less than a critical value (![]() 10% of the Eddington accretion
rate,
10% of the Eddington accretion
rate,
![]() for
for
![]() ). More recent work suggests that this transition could
already occur around 2%
). More recent work suggests that this transition could
already occur around 2%
![]() (Maccarone 2003), and
that there is a hysteresis in the critical accretion rate value
depending on which direction the transition is going along
(Maccarone & Coppi 2003). Regardless of the exact details, a crucial
point for this paper is a phase-transition as a function of black hole
mass and accretion power.
(Maccarone 2003), and
that there is a hysteresis in the critical accretion rate value
depending on which direction the transition is going along
(Maccarone & Coppi 2003). Regardless of the exact details, a crucial
point for this paper is a phase-transition as a function of black hole
mass and accretion power.
We have previously suggested that the contribution of jets and
outflows to the spectral energy distribution (SED) of black holes can
be significant in supermassive as well as stellar-mass black holes
(Falcke & Markoff 2000; Yuan et al. 2002; Markoff et al. 2001; Fender 2001) and that the jet contribution may
dominate the disk emission in a JDAF - a jet-dominated accretion
flow. Jets are inherently broad-band, since they remain
self-similar over many orders of magnitude in spatial scale and
produce non-thermal particle distributions ranging over many orders
of magnitude in energy. For this reason they should always be
considered as potential contributors at every wavelength. This
concept of jet domination has now been empirically demonstrated for
XRBs, where below
![]() the kinetic energy
output through radiatively inefficient jets (assumed to radiate only
radio-through-IR) dominates the radiative output of the optically
thin or thick disk (assumed to solely account for the X-ray
emission; Fender et al. 2003). If the jet contributes
to the X-rays as well, the jet domination may hold at even higher
absolute luminosities.
the kinetic energy
output through radiatively inefficient jets (assumed to radiate only
radio-through-IR) dominates the radiative output of the optically
thin or thick disk (assumed to solely account for the X-ray
emission; Fender et al. 2003). If the jet contributes
to the X-rays as well, the jet domination may hold at even higher
absolute luminosities.
The importance of jets to the emission of low-power accreting black holes may hold the key to understanding the relationship between stellar and galactic sized systems. In the next section (Sect. 2) we suggest how this concept can be used to provide a unified picture for AGN as a function of mass and power for a range of sources that may be operating at sub-Eddington accretion rates. This directly leads to a prediction of radio/optical/X-ray scaling which we test on data from several sources in Sect. 3.
Our proposed scheme is based on three assumptions:
I) The accretion flow and disk form a coupled jet-disk system, with jet and disk always present in some form ("jet-disk symbiosis'', see Falcke & Biermann 1995).
II) Below a certain critical accretion rate,
![]() (
(
![]() ), the inner part of the
accretion flow becomes radiatively inefficient
(e.g., Esin et al. 1997).
), the inner part of the
accretion flow becomes radiatively inefficient
(e.g., Esin et al. 1997).
III) Below
![]() ,
or for face-on orientation
(relativistic beaming), the jet emission dominates the emission from
the accretion flow (e.g., Yuan et al. 2002).
,
or for face-on orientation
(relativistic beaming), the jet emission dominates the emission from
the accretion flow (e.g., Yuan et al. 2002).
In short, the postulate is that near-Eddington black holes are disk-dominated and distinctly sub-Eddington black holes are jet-dominated.
Can we classify many of the various accreting systems we know of in terms of this scheme, based on observational evidence? Let us first consider X-ray binaries where time scales are short enough that individual sources can appear in a number of different states. The two most pronounced states are the high (soft) state, with a soft power-law spectrum dominated by a thermal "bump'', and the low (hard) state characterized by a dominant hard power-law and weak-to-absent thermal spectrum (e.g., Nowak 1995). The former is commonly interpreted as multi-color blackbody emission from a standard thin disk, while the latter is commonly attributed to an optically thin accretion flow or corona. However, Markoff et al. (2001) have suggested that the hard power law could also be attributed to synchrotron emission from the jet in these systems. This is strengthened by the finding of a tight non-linear correlation between radio and X-ray luminosity in GX 339-4 (Corbel et al. 2003) and other X-ray binaries in the low state (Gallo et al. 2003), which exactly fits the non-linear predictions of the jet model (e.g., Markoff et al. 2003, for GX 339-4). This correlation extends down into the quiescent state, which is therefore now interpreted as an extremely low luminosity hard state. It has also been argued that some of the ultra-luminous X-ray sources in nearby galaxies could be the beamed equivalents of the well-known Galactic XRBs ("microblazars''; Körding et al. 2002; Mirabel & Rodríguez 1999).
For AGN, the situation is more complicated since a large number of source classes exists. When considering higher luminosity sources with strong disk signatures, the supermassive black hole equivalents to soft-state XRBs are FR II radio galaxies, radio-loud quasars, and blazars (with emission lines) among the radio loud objects. Within the standard "unified scheme'' these are mainly related through different inclination angles. On the radio quiet side, Seyfert galaxies, radio-quiet quasars, and perhaps radio-intermediate quasars (Falcke et al. 1996; Miller et al. 1993) are the other analogs for high state XRBs. All of these AGN varieties show direct or indirect evidence for a soft ultraviolet bump that can be readily understood as emission from a standard accretion disk (Sun & Malkan 1989). This emission also provides ample photons to produce the strong emission line regions seen in the optical spectra.
On the other hand, several low-power AGN classes seem to lack
evidence of a blue bump and strong emission lines, and are therefore
candidates for equivalents to the hard-state XRBs. These are FR I
radio galaxies, BL Lacs and LINERs. The Galactic Center (Sgr A*; see
Melia & Falcke 2001) could also be in this category, but with its
faint and soft spectrum it is not clear what state in XRBs it would
correspond to. However, the almost-daily flares in Sgr A*
(Baganoff et al. 2001) have a hard spectrum, so it may
occasionally achieve a state analogous to the hard state in XRBs.
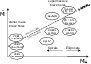 |
Figure 1: A proposed unification scheme for accreting black holes in the mass and accretion rate plane. Above a few percent of the Eddington accretion rate, the systems are proposed to be dominated by disk emission, while below they are inherently dominated by jet emission (RG = radio galaxy). Standard inclination-based unified schemes (Antonucci 1993; Urry & Padovani 1995) are still assumed to be valid but are not explicitly shown here. Given a correlation between bulge mass and black hole mass, the AGN with the most massive black holes are supposed to reside in elliptical galaxies, while less massive black holes are predominantly in spirals. This is, of course, not applicable to XRBs. |
| Open with DEXTER | |
In terms of radio power, FR I radio galaxies form a smooth continuum with FR II radio galaxies, but are comparatively underluminous in emission lines and lack a big blue bump (Falcke et al. 1995; Zirbel & Baum 1995). While FR I sources do seem to have optical cores, their fluxes scale tightly with their radio flux (Chiaberge et al. 1999). This has been used to argue for a synchrotron nature of these optical cores rather than a thermal origin in the accretion disk. Interestingly, within the standard unified scheme FR I radio galaxies are coupled to BL Lac objects which are thought to be their relativistically beamed versions. BL Lacs - by definition - lack emission lines and there is no population intermediate in inclination angle between FR I and BL Lacs which does show a blue bump or evidence for a standard optically thick accretion disk.
Similarly, for low-luminosity AGN and LINERs, Ho (1999) argues that their SED precludes the presence of a blue bump and of a standard accretion disk. On the other hand, radio observations of LINERs show a strong jet presence (Nagar et al. 2001; Falcke et al. 2000), and fits to individual objects indicate that the higher wavelengths may also be dominated by jet emission (Yuan et al. 2002). Some of these LINERs are in big elliptical galaxies and may be the lower-luminosity continuation of FR I radio galaxies, while others sit in spiral galaxies and may be somewhere in between Seyferts and our own Galactic Center in terms of power.
Hence BL Lacs, FR Is, and LINERs are good candidates for sub-Eddington and jet-dominated AGN. Although this conclusion is already widely accepted for BL Lacs because of beaming arguments, and the case for FR Is is strengthening, the proposal for LINERs remains highly debated.
A sketch of the proposed scheme is shown in Fig. 1. Note that this is naturally very rough. In a number of cases the dividing lines between individual classes may be blurred. Also, in jet-dominated sources there may still be a sizeable disk contribution and vice versa. In addition, as is commonly known, inclination effects play an important role in unified schemes. For radio-loud quasars, for example, a small inclination to the line of sight (i.e., in a blazar) can lead to a significant jet contribution despite the fact that here we classify these sources as intrinsically disk-dominated. This is in contrast to BL Lacs objects, which we consider as intrinsically jet-dominated in addition to being beamed (with FR I radio galaxies as the parent population). This may have some analogy for XRBs, where some ultra-luminous X-ray sources might be affected by beaming as well (Körding et al. 2002). In general the selection of BL Lacs requires significant care (Landt et al. 2002; Marcha et al. 1996) and the application of the scheme is not always straightforward without good understanding of source properties and selection effects.
With such a scheme at hand, one wonders what the consequences are and how they can be tested. First of all, if indeed black hole engines make a qualitative transition with accretion power, a number of AGN diagnostics has to be considered with even greater care. One example is the ratio between radio and optical flux that is commonly used as a radio-loudness parameter (Kellermann et al. 1989; Falcke et al. 1996). In most interpretations it is supposed to represent the relative prominence of jet and disk in a source. This has been particularly useful for quasars, where one can well assume that the optical flux represents disk emission. If, however, in sub-Eddington AGN both wavelengths are coming from the jet, this parameter is physically no longer meaningful as a jet-strength parameter and other factors have to be taken into account.
This issue is particularly difficult when considering large samples of AGN. Within each luminosity bin one can expect a range of black hole masses to contribute and hence Eddington and sub-Eddington black holes may be mixed if there are no well-sampled SEDs and spectra in radio, optical, and X-rays. Moreover, mass itself can become a crucial factor. This can in principle enhance scatter and spoil any possible correlations or dichotomies. On the other hand, if the SED of black holes is jet-dominated, it may be possible to describe their evolution with accretion power in a unified way. In the following we will concentrate on the expected scaling of radio, optical, and X-ray emission from a jet-only model and compare it to data from samples of sub-Eddington black holes.
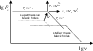 |
Figure 2:
A schematic jet spectrum and its theoretically expected scaling with mass and accretion rate.
The spectrum has a flat-to-inverted, optically thick part below a turn-over
frequency
|
| Open with DEXTER | |
Here we want to concentrate on the AGN core itself, leaving out the
extended emission. In the simplest picture
(Blandford & Königl 1979; Falcke & Biermann 1995), the jet spectrum can be
naturally described by a flat-to-inverted radio spectrum up to a
turn-over frequency
![]() ,
which reveals an optically thin
power-law (see Fig. 2). The flat spectrum is the sum of
self-absorbed components along the jet, where higher frequencies
correspond to smaller regions closer to the black hole. The power law
results from optically thin emission from a power-law distribution of
electrons at the smallest scale in the jet where particle acceleration
exists. One can then roughly approximate the jet spetrum by a broken
power law normalized to a monochromatic luminosity (energy per time
and frequency)
,
which reveals an optically thin
power-law (see Fig. 2). The flat spectrum is the sum of
self-absorbed components along the jet, where higher frequencies
correspond to smaller regions closer to the black hole. The power law
results from optically thin emission from a power-law distribution of
electrons at the smallest scale in the jet where particle acceleration
exists. One can then roughly approximate the jet spetrum by a broken
power law normalized to a monochromatic luminosity (energy per time
and frequency) ![]() at
at
![]() ,
,
Scaling laws for this type of jet spectrum as a function of jet power ![]() and mass have been described by Falcke & Biermann (1995)
and Markoff et al. (2003). The main assumptions are that the
jet expands freely (conical shape), maintains an (arbitrary but fixed)
equipartition factor, and the distance of the first particle
acceleration zone,
and mass have been described by Falcke & Biermann (1995)
and Markoff et al. (2003). The main assumptions are that the
jet expands freely (conical shape), maintains an (arbitrary but fixed)
equipartition factor, and the distance of the first particle
acceleration zone,
![]() ,
scales linearly with mass, e.g., is
always around some hundred to thousand
,
scales linearly with mass, e.g., is
always around some hundred to thousand ![]() .
.
![]() is the gravitational radius of the black hole.
is the gravitational radius of the black hole.
As described in Falcke & Biermann (1995) and
Markoff et al. (2003), it follows from simple analytic theory
that
![]() and
and
![]() and hence
and hence
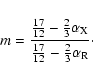 |
(6) |
For relativistic steady jets, there will also be a dependency on the
Doppler factor
![]() (Lind & Blandford 1985).
However, since as a first-order approximation the monochromatic
luminosity at both frequencies is beamed by the same amount, the
correlation between
(Lind & Blandford 1985).
However, since as a first-order approximation the monochromatic
luminosity at both frequencies is beamed by the same amount, the
correlation between
![]() and
and
![]() will only go as
will only go as
![]() ,
i.e. less than linear for typical values. If there is a
significant velocity gradient along the jet, radio and X-rays could be
beamed by different amounts and the effect would become stronger.
,
i.e. less than linear for typical values. If there is a
significant velocity gradient along the jet, radio and X-rays could be
beamed by different amounts and the effect would become stronger.
Further parameters may affect the correlation. For example,
source-to-source variations in the equipartition factors or the
turn-over frequency
![]() caused by different locations of the
first acceleration zone
caused by different locations of the
first acceleration zone
![]() can lead to different
X-ray/radio ratios. However, since we have no good theoretical
understanding of such plasma parameters we have to accept this
uncertainty as a major source of scatter.
can lead to different
X-ray/radio ratios. However, since we have no good theoretical
understanding of such plasma parameters we have to accept this
uncertainty as a major source of scatter.
The scaling also only holds as long as a non-thermal power law is
produced in the optically thin regime and
![]() remains
roughly constant. This may not always be the case for sources that
approach quiescence, such as the Galactic Center in its non-flaring
state.
remains
roughly constant. This may not always be the case for sources that
approach quiescence, such as the Galactic Center in its non-flaring
state.
At least for an individual X-ray binary, Markoff et al. (2003) showed that this scaling with accretion rate can exactly reproduce the tight non-linear radio/X-ray scaling of the X-ray binary GX 339-4. Such a scaling has now been found to be fairly representative for low-luminosity XRBs (Gallo et al. 2003). In the case of GX 339-4, the mass term and Doppler factor were not included in the formula, since only one source was considered. This is fine for XRBs, where the jet power and accretion rate in one object changes over many orders of magnitude within months and years. For AGN such changes take too long to be discovered in individual objects and hence statistical samples have to be used to cover a large range in instantaneous jet powers and accretion rates. In this case the mass becomes an important factor for the thermal and non-thermal spectrum.
An important additional point concerns which wavelength to use in such
comparative studies of different source types and black hole masses. In
the scaling law, we have been mainly comparing the optically thick
flux (mainly radio) to the optically thin flux (mainly X-rays). However
it is important to know which wavelength belongs to which branch of
the jet SED in a certain type of source. In essentially all sources
the compact radio emission is safely on the optically thick
branch of the jet core spectrum; however, since the turnover frequency
scales inversely with mass, the useful wavelength range over which one
can probe the optically thin branch of the SED may vary from one type
of source to another. We know, for example, that in BL Lacs at least
the optical part of the SED belongs to the synchrotron branch. In some
cases this extends all the way into the X-rays; in other cases,
however, X-rays may already be affected by the inverse Compton
components of the SED. Hence, for BL Lacs (and FR I radio galaxies for that matter) optical flux measurements are a much
safer region to
probe the optically thin part of the SED (which we still parameterize by
![]() and
and ![]() ). In contrast, X-ray binaries may
have a very high turn-over frequency, so that the optical flux may
still be on the optically thick branch (as discussed in
Markoff et al. 2001). Here, X-ray fluxes are
the better choice, even though here inverse Compton might also
contribute. Whatever one chooses, a proper comparison requires one to
normalize the optically thin and optically thick fluxes to common
reference frequencies. This is done in
Eq. (7). Since we here use an X-ray frequency as
the common reference frequency for the normalized optically thin flux,
we continue using the term radio/X-ray correlation in the following, even
though it could for a number of sources equally well be a
radio/optical correlation.
). In contrast, X-ray binaries may
have a very high turn-over frequency, so that the optical flux may
still be on the optically thick branch (as discussed in
Markoff et al. 2001). Here, X-ray fluxes are
the better choice, even though here inverse Compton might also
contribute. Whatever one chooses, a proper comparison requires one to
normalize the optically thin and optically thick fluxes to common
reference frequencies. This is done in
Eq. (7). Since we here use an X-ray frequency as
the common reference frequency for the normalized optically thin flux,
we continue using the term radio/X-ray correlation in the following, even
though it could for a number of sources equally well be a
radio/optical correlation.
To test finally our hypothesis that the radio/X-ray correlation can be traced from XRBs through LINERs, FR Is, to BL Lac objects, we use a number of different samples from the literature where mass estimates, radio and X-ray or optical fluxes have been published. For certain types of sources (e.g. LLAGN) we are naturally limited by the small number of well-defined samples that have been observed with the new generation of X-ray telescopes.
For the XRBs we include the above mentioned multiple epochs of
GX 339-4 (Corbel et al. 2003). We scaled the 8.6 GHz radio flux
to 5 GHz, assuming
![]() .
Hynes et al. (2003) give a mass for GX 339-4 around
.
Hynes et al. (2003) give a mass for GX 339-4 around
![]() .
A distance of 4 kpc has been used to derive the luminosity
(Zdziarski et al. 1998). We note that other methods may give
somewhat different distances (e.g., Maccarone 2003) and that
the mass is a strict lower limit. Nevertheless, the correlation for
GX 339-4 seems to be representative for a large number of XRBs in
the hard state (Gallo et al. 2003).
.
A distance of 4 kpc has been used to derive the luminosity
(Zdziarski et al. 1998). We note that other methods may give
somewhat different distances (e.g., Maccarone 2003) and that
the mass is a strict lower limit. Nevertheless, the correlation for
GX 339-4 seems to be representative for a large number of XRBs in
the hard state (Gallo et al. 2003).
As the lowest-luminosity supermassive black hole, we included Sgr A*. The 5 GHz radio flux was taken from the average spectrum in
Melia & Falcke (2001). The X-ray luminosity in the quiet and the flaring
state were taken from (Baganoff et al. 2001), which we
scaled with the given photon indices to a 3-9 keV luminosity. The
black hole mass is taken to be
![]() (Schödel et al. 2002) and the distance of 8 kpc has been used.
(Schödel et al. 2002) and the distance of 8 kpc has been used.
For the LINERS we included the Chandra sample of
Terashima & Wilson (2003). They selected 14 objects with radio
cores from the Low-Luminosity AGN (LLAGN) sample of
Nagar et al. (2000), with a flat or inverted radio core
![]() .
Nagar et al. (2000) selected
their sources from the Ho et al. (1995) sample (a
magnitude-limited sample) according to preliminary spectral
classification as LINER or as transitional object. To compare the
X-ray luminosity with GX 339-4, we scaled the 2-10 keV X-ray
luminosity to a 3-9 keV luminosity assuming a power-law index of
.
Nagar et al. (2000) selected
their sources from the Ho et al. (1995) sample (a
magnitude-limited sample) according to preliminary spectral
classification as LINER or as transitional object. To compare the
X-ray luminosity with GX 339-4, we scaled the 2-10 keV X-ray
luminosity to a 3-9 keV luminosity assuming a power-law index of
![]() for all objects.
for all objects.
For the FR Is, we took the radio and HST data given in
Chiaberge et al. (1999) who selected their sample from the 3CR catalogue (Spinrad et al. 1985) which have been
morphologically identified as FR I radio sources. The 33 sources form
a complete, flux-limited sample. The optical cores have been
extrapolated to a corresponding X-ray luminosity using
Eq. (4) under the assumption that the synchrotron power
law has a spectral index of
![]() .
We did not use
actual X-ray data, as the HST observations had higher resolution, and
within the jet model for FR I and BL Lacs some of these high-mass
sources could have their synchrotron cut-off already below the X-ray
band, such that X-rays could be dominated by synchrotron self-Compton.
.
We did not use
actual X-ray data, as the HST observations had higher resolution, and
within the jet model for FR I and BL Lacs some of these high-mass
sources could have their synchrotron cut-off already below the X-ray
band, such that X-rays could be dominated by synchrotron self-Compton.
For the BL Lacs we took X-ray (XBLs) and radio selected (RBLs) BL Lacs
from Sambruna et al. (1996). These originate from two
complete samples: the Einstein Observatory Extended Medium-Sensitivity
Survey (EMSS) XBL sample (Morris et al. 1991) and the 1 Jy RBL
sample (Stickel et al. 1991). Similar to FR Is we calculate
the corresponding monochromatic X-ray luminosity from the optical data
assuming
![]() .
Since BL Lacs are thought to be
strongly affected by beaming, we corrected the radio and the
equivalent X-ray luminosity for Doppler boosting, assuming an average
Doppler factor of
.
Since BL Lacs are thought to be
strongly affected by beaming, we corrected the radio and the
equivalent X-ray luminosity for Doppler boosting, assuming an average
Doppler factor of
![]() (Ghisellini et al. 1993).
As mentioned above, for the X-ray/radio correlation the Doppler factor
largely cancels out and enters less than linearly. Of course, the
position along the correlation will be affected more strongly.
For all source populations other than the BL Lacs, we assume a Doppler
factor around unity.
(Ghisellini et al. 1993).
As mentioned above, for the X-ray/radio correlation the Doppler factor
largely cancels out and enters less than linearly. Of course, the
position along the correlation will be affected more strongly.
For all source populations other than the BL Lacs, we assume a Doppler
factor around unity.
For all sources we calculated the radio luminosity from the 5 GHz flux density. The distances of the sources were derived from the redshift with H0 = 75 km s-1 Mpc. We selected from these samples all sources, for which we found black hole mass estimates either in the literature or by using the bulge velocity and the bulge/black hole mass relation from Merritt & Ferrarese (2001). Central velocity dispersion values were taken from Prugniel et al. (1998) and its update in the "Hypercat'' database or from Woo & Urry (2002). The black hole masses and fluxes are tabulated in Table 1.
Table 1: Sources used in this paper. Column 1 lists the names of the sources and Col. 2 gives the distance used to derive the luminosities from the fluxes. The black hole mass was calculated from the velocity dispersion relation Merritt & Ferrarese (2001). Columns 4 and 5 give the measured radio and X-ray fluxes. For the LLAGN sample we only list the radio luminosity as directly taken from the original paper. The last two columns give the radio luminosity and the equivalent X-ray luminosity as described in Eq. (7). This luminosity has also been corrected for the different observed energy bands assuming a photon index of 1.6.
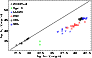 |
Figure 3: Radio/X-ray correlation for XRBs with our AGN sample. We only extrapolate the optical measurements of some AGN (FR I radio galaxies) to a corresponding monochromatic X-ray luminosity without a mass correction. For Sgr A* we show the quiescent and the flare spectrum. The solid line is the analytically predicted non-linear radio/X-ray correlation from the jet model, normalized for GX 339-4. The supermassive black holes fall below the extrapolation from the X-ray binaries. |
| Open with DEXTER | |
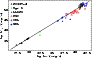 |
Figure 4:
The same as Fig. 3 but for an equivalent X-ray
luminosity,
|
| Open with DEXTER | |
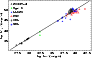 |
Figure 5: The same as Fig. 4 but the radio and X-ray luminosities of BL Lac objects have been corrected for Doppler boosting. As discussed in the text, this mainly moves BL Lacs along the correlation and they now occupy the same region as FR Is - their parent population within the inclination-based unified scheme. |
| Open with DEXTER | |
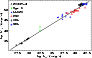 |
Figure 6:
Radio/X-ray correlation for XRBs and AGN, where the X-ray flux of all
AGN has been increased by a constant value of 107, corresponding to
an average AGN mass of
|
| Open with DEXTER | |
In Figs. 3 to 6 we show the radio and X-ray luminosities of the sources discussed above with various correction factors applied. Figure 3 shows the uncorrected data, with only optical luminosities extrapolated to corresponding X-ray luminosities. Clearly, the AGN fall well below the extrapolation of the radio/X-ray correlation of X-ray binaries. In other terms: by simply increasing the accretion rate in an X-ray binary one will never obtain the SED of an AGN.
In Fig. 4 we have included in the correlation the analytically predicted mass scaling (Eq. (7)) but not yet the correction of the Doppler factor for BL Lacs. Surprisingly, with this simple scaling, all the source populations seem to be scaled by just the right amount to fall more or less on the predicted scaling with power from the XRBs with a relatively low scatter. This means that in the parameter space of X-ray luminosity, radio luminosity, and black hole mass, sub-Eddington black holes form a fundamental plane. It also suggests that the theoretically motivated and predicted scaling seems to hold for stellar mass as well as for supermassive black holes. We point out that two of the outliers (NGC 6500 and NGC 1275) are known from high-resolution VLBI observations to have radio cores that are significantly affected by extended emission (Walker et al. 2000; Falcke et al. 2000) and hence appear too bright in the radio. The same may be true to some degree for FR Is in general, but should be negligible for BL Lacs.
Figure 5 demonstrates the effect of a Doppler factor correction. As discussed in the previous section, the X-ray/radio-ratio is rather insensitive to the Doppler factor and sources will mainly move along the correlation. In our case the BL Lacs are pushed from the upper end of the correlation into the regime where FR I radio galaxies lie. Given that BL Lacs are supposed to be the beamed population of FR I radio galaxies within the inclination-based unified scheme, this seems to be an appropriate correction and provides further support for that scheme.
Finally, in Fig. 6 we show the radio and X-ray
luminosities, where the X-ray flux has been corrected by a constant
factor 107, thus ignoring the individual mass estimates. With this
factor the radio/X-ray correlation can also be continued to
AGN. Scaling by 107 is identical to assuming a constant black hole
mass of ![]()
![]() for all objects. The black hole
mass of FR I Radio Galaxies and BL Lac objects scatter around this
value. LLAGN have an average mass of somewhat less than
for all objects. The black hole
mass of FR I Radio Galaxies and BL Lac objects scatter around this
value. LLAGN have an average mass of somewhat less than
![]() ,
thus in comparison with Fig. 5,
the LLAGN have higher X-ray fluxes. The Galactic black hole (Sgr A*) has a mass of only
,
thus in comparison with Fig. 5,
the LLAGN have higher X-ray fluxes. The Galactic black hole (Sgr A*) has a mass of only
![]() so the X-ray flux is
increased too much and the X-ray flare state - which may in fact
contain the here crucial non-thermal power law - lies above the
extrapolation.
so the X-ray flux is
increased too much and the X-ray flare state - which may in fact
contain the here crucial non-thermal power law - lies above the
extrapolation.
A better distinction of the mass effects might be possible with the inclusion of more low-mass AGN. Another conclusion is that, for example, a linear dependency of the X-ray/radio-ratio with mass would not be appropriate, and over-correct the data.
We have suggested that black holes operating at sub-Eddington accretion rates make a transition to a radiative inefficient state, where most of the emission is dominated by the non-thermal emission of a jet ("JDAFs''). In this picture the radiative output of sub-Eddington black holes is non-thermally dominated, while near-Eddington black holes are thermally dominated. This scheme allows one to unify the radiative properties of black holes over a large range of accretion powers. At sub-Eddington accretion rates, the scaling between radio and optical or X-ray cores is then predicted to follow the scaling laws outlined in Falcke & Biermann (1995) and Markoff et al. (2003). This requires taking the black hole mass into account.
Near-Eddington black holes are presumably found in quasars, luminous Seyfert galaxies, and soft-state X-ray binaries which are considered to be in the high state. As pointed out elsewhere (Maccarone et al. 2003; Pounds et al. 1995) Narrow-Line Seyfert 1s may also be related to the very high state of X-Ray binaries.
On the other hand, candidates for sub-Eddington black holes are XRBs in the low-hard state, Sgr A*, LINERs, FR I radio galaxies, and BL Lac objects. In terms of beaming and inclination-based unified schemes, which we do not explicitly discuss but consider valid, it may be worth pointing out that ultra-luminous X-ray sources might be low-mass analogs to BL Lacs and blazars (Körding et al. 2002).
Using various samples of sub-Eddington black holes, we are able to show that all these different types of sources seem to fall near the predicted radio/X-ray correlation, if the scaling with black hole mass is taken into account.
The crucial underlying assumption is that all these sources are intrinsically jet-dominated and have essentially the same SED in common: a flat, optically thick radio spectrum and an optically thin power law beyond a turn-over frequency. Shape and scaling of the SED needed to explain the radio/X-ray correlation is just what one expects in a pure jet model and supports the notion of jet-dominated accretion flows ("JDAF''). On the other hand, some form of radiative inefficient accretion flows/corona is also clearly needed for this picture to work, since there is always a need for a power and matter source for the outflow. It may be possible to adapt the scheme fo a situation where the X-ray emission is dominated by emission from optically thin accretion flows, if their X-ray flux follows a similar non-linear scaling as predicted in the jet case.
An interesting corollary for jets is that, in order to obtain the
scaling with mass, one has to assume that the region of the onset of
particle acceleration in the jet - producing the optically thin power
law - is always around a fixed location in mass-scaled units (![]()
![]() ).
).
With the large range of black hole powers and masses discovered the proposed picture may warrant further investigation and detailed tests. If solidified and further evolved it may help to predict the luminosity evolution of black holes at various wavebands over many orders of magnitude. Interestingly, two other papers have recently appeared that come to very similar conclusion in terms of the expected scaling (Heinz & Sunyaev 2003) and its application to black holes of different masses (Merloni et al. 2003).
Acknowledgements
We are thankful to Tom Maccarone, Rob Fender, and an anonymous referee for helpful comments that improved the masnucript. S.M. is supported by an NSF Astronomy and Astrophysics Postdoctoral Fellowship, under award AST-0201597.