A&A 414, 1105-1108 (2004)
DOI: 10.1051/0004-6361:20034297
D. Reimers 1 - S. Jordan 2 - N. Christlieb 1
1 - Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
2 - Institut für Astronomie und Astrophysik, Eberhard-Karls-Universität Tübingen, Sand 1,
72076 Tübingen, Germany
Received 10 Septembre 2003 / Accepted 3 November 2003
Abstract
In the course of the Hamburg/ESO survey we have discovered a
white dwarf whose spectrum
exhibits many similarities with the prototype of magnetic white
dwarfs Grw+70![]() 8247. In particular several stationary line components
indicative for magnetic fields between about 150 and 400 MG are found
in both objects. However, the features between 5000 and 5500 Å in the spectrum of HE0241-0155
cannot be explained by stationary line components and demand a relatively
homogeneous magnetic field with clustering around 200 MG. For this reason
a pure dipole model failed to reproduce this spectral region. An
offset-dipole configuration led to some improvement in the fit but a
good agreement was only possible for a geometry - described by an
expansion into spherical harmonics - where most of the surface is
covered with magnetic field strengths strongly clustered around
200 MG. This may indicate the presence of a large
magnetic spot whose presence could be tested with time resolved
spectro-polarimetry.
8247. In particular several stationary line components
indicative for magnetic fields between about 150 and 400 MG are found
in both objects. However, the features between 5000 and 5500 Å in the spectrum of HE0241-0155
cannot be explained by stationary line components and demand a relatively
homogeneous magnetic field with clustering around 200 MG. For this reason
a pure dipole model failed to reproduce this spectral region. An
offset-dipole configuration led to some improvement in the fit but a
good agreement was only possible for a geometry - described by an
expansion into spherical harmonics - where most of the surface is
covered with magnetic field strengths strongly clustered around
200 MG. This may indicate the presence of a large
magnetic spot whose presence could be tested with time resolved
spectro-polarimetry.
Key words: stars: white dwarfs - stars: magnetic fields - radiative transfer - magnetic fields
Table 1: Journal of observations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA20030297_fig1a.eps}\par\...
...ce{-1.6mm}
\includegraphics[width=8.8cm,clip]{AA20030297_fig1b.eps}
\end{figure}](/articles/aa/full/2004/06/aa0297/Timg4.gif) |
Figure 1: Observed spectra of HE0241-0155 compared to the position of the hydrogen line components. The upper spectrum (obtained 28/11/98) with a resolution of 5 Å has been smoothed (second curve) in order to match the 15 Å resolution of the lower spectrum (13/9/98). The main features arise from magnetic field strengths of about 200 MG (marked with circles) and are not in all cases due to stationary line components. In order to identify the telluric features a spectrum of HD7041 by Stevenson (1994) observed at an airmass 1.7 is shown. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA20030297_fig2.eps}
\end{figure}](/articles/aa/full/2004/06/aa0297/Timg5.gif) |
Figure 2: Best fit for a magnetic field geometry described by an expansion into spherical harmonics up to l=4 with m=0 (convolved with a 5 Å Gaussian and plotted over the low resolution spectrum, second curve from below), a pure dipole field (lower curve), and a dipole with an offset along the magnetic field axis (second curve from above). For comparison the upper curves show the high resolution spectrum together with the best fit model convolved with a Gaussian of 5 Å. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{AA20030297_fig3.eps}
\end{figure}](/articles/aa/full/2004/06/aa0297/Timg6.gif) |
Figure 3: Distribution of the absolute values of the magnetic field strength over the observed hemisphere predicted by the three best fit models: the dipole model (thick line), the off-set dipole model (medium), and expansion into spherical harmonics (thin) up to l=4 (m=0). |
| Open with DEXTER | |
Prominent broad absorption lines are seen at 4060, 4170, 4280, 4435, 4690, 5093, 5220, 5390,
and
5830 Å . Further lines in the red are at 6780, 7310 and 8300 Å (Fig. 1).
Note, however, that the features in the red are partly contaminatedby telluric features,
which can be identified by the comparison spectrum of HD7041 taken by Stevenson (1994)
at high airmass, also shown in Fig. 1.
A comparison with known magnetic white dwarfs shows its obvious similarity with Grw+70![]() 8247
which is a DA with a 320 MG dipole field according to Wickramasinghe & Ferrario (1988)
and Jordan (1989).
8247
which is a DA with a 320 MG dipole field according to Wickramasinghe & Ferrario (1988)
and Jordan (1989).
If a pure magnetic dipole is assumed, the best fit (Fig. 2)
to the observed data was obtained
for a polar field strength of 398 MG, with the dipole axis oriented almost
(
![]() )
perpendicular to the observer, and an effective temperature of
12 000 K. However, this model fails to account for the
features at 5093, 5218, and 5287 Å. These features do not correspond to any
stationary line component in any reasonable range of magnetic field
strengths; the closest agreement would have the 4f
)
perpendicular to the observer, and an effective temperature of
12 000 K. However, this model fails to account for the
features at 5093, 5218, and 5287 Å. These features do not correspond to any
stationary line component in any reasonable range of magnetic field
strengths; the closest agreement would have the 4f
![]() 2s0 components with a maximum at 5119 Å and 61 MG.
The wavelengths of stationary line components go through maxima or minima as functions of
the magnetic field strength; they are visible in the
spectra of magnetic white dwarfs despite a considerable variation of the field
strengths as in the case of a pure magnetic dipole (where the field strength is a factor
of two higher at the pole than at the equator, and the distribution of the magnetic field strengths
over the visible stellar surface is relatively flat (see Fig. 3).
2s0 components with a maximum at 5119 Å and 61 MG.
The wavelengths of stationary line components go through maxima or minima as functions of
the magnetic field strength; they are visible in the
spectra of magnetic white dwarfs despite a considerable variation of the field
strengths as in the case of a pure magnetic dipole (where the field strength is a factor
of two higher at the pole than at the equator, and the distribution of the magnetic field strengths
over the visible stellar surface is relatively flat (see Fig. 3).
As indicated by the circles in Fig 1, the features missing in the fit could be due to a relatively homogeneous field of about 200 MG. One possibility to describe a field distribution where the majority of the surface is covered by a magnetic field close to 200 MG is a dipole field with a large offset of the dipole relative to the center of the star. Although the total variation of field strengths is larger in this case, more magnetic field strengths cluster around one relatively homogeneous magnetic field on one pole.
The best fit for an offset dipole (only offsets along the magnetic axis are
considered) is obtained for the same polar field strength (399 MG) and
the same orientation (
![]() ), but for an offset of 0.16 stellar radii
away from the observer.
The histogram Fig. 3 shows the effect: the magnetic field strengths
are now even more strongly peaked at 200 MG and the vast majority of surface elements has
a magnetic field between 200 and 250 MG. The resulting fit (upper curve of Fig. 2)
has improved considerably, and particularly the missing three line features are
now visible - although still somewhat too shallow - in the theoretical model.
), but for an offset of 0.16 stellar radii
away from the observer.
The histogram Fig. 3 shows the effect: the magnetic field strengths
are now even more strongly peaked at 200 MG and the vast majority of surface elements has
a magnetic field between 200 and 250 MG. The resulting fit (upper curve of Fig. 2)
has improved considerably, and particularly the missing three line features are
now visible - although still somewhat too shallow - in the theoretical model.
Finally, a more general approach, an expansion of the magnetic field into spherical harmonics,
assuming that the source of the magnetic field lie entirely within the star
(Jacobs 1987):
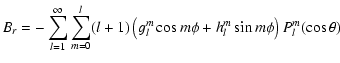 |
|||
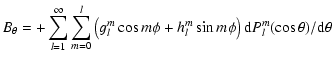 |
|||
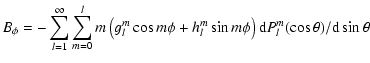 |
Figure 2 shows now that the overall agreement between observation and theoretical fit is almost perfect. The corresponding histogram is now even stronger peaked around 200 MG.
It is clear that the limitation to spectra without polarization data cannot lead to a unique solution. All distributions that cluster around 200 MG should lead to similar results. Such a strong clustering could be a hint for a magnetic spot with a relative homogeneous magnetic field covering a large portion of the visible hemisphere, as discussed for the magnetic white dwarfs PG 1031+234 (Latter et al. 1987) and RE 0317-853 (Vennes et al. 2003). The origin of such a spot-like feature, is however unclear although star spots have been found on the possible progenitors of magnetic white dwarfs, the Ap stars, where the spots are connected to abundance anomalies and can be detected via Doppler imaging (Khokhlova et al. 1986; Rice & Wehlau 1994).
An extremely homogeneous field was also found in phase-resolved low-state spectra
of the polar MR Ser. Schwope et al. (1993) revealed a strongly decentered
dipolar (
![]() stellar radii).
stellar radii).
However, it must be pointed out that in Ap stars, which also have fossil magnetic fields, low order multipole expansions describe statistical aspects of overall field geometry, but do not provide a realistic representation of the actual distribution of field vectors over the surface; the latter would be more constrained by observations of circular polarization. Therefore, our solution only means that the field modulus is quite uniform and large over the visible hemisphere of the star. The relatively small region with a higher field modulus does not strongly contribute to the strength of the line features.
In the framework of multipole exansions Muslimov et al. (1995) have shown that a weak quadrupole (or octupole,
etc.) component on the surface magnetic field of a white dwarf may survive the
dipole component und specific initial conditions: particularly the evolution of
the quadrupole mode is very sensitive (via Hall effect) to the presence of
internal toroidal field. For a 0.6 ![]() white dwarf with a toroidal fossil
magnetic field of strength <109 G the dipole component declines by a factor
of three in 109 yr, while the quadrupole component is practically
unaffected. Without an internal toroidal field the dipole component still
declines by a factor of three but the quadrupole component is a factor of six
smaller after 10 Gyr. This is much longer than the cooling age of
a 12 000 K white dwarf, which well under 1 Gyr for 0.6
white dwarf with a toroidal fossil
magnetic field of strength <109 G the dipole component declines by a factor
of three in 109 yr, while the quadrupole component is practically
unaffected. Without an internal toroidal field the dipole component still
declines by a factor of three but the quadrupole component is a factor of six
smaller after 10 Gyr. This is much longer than the cooling age of
a 12 000 K white dwarf, which well under 1 Gyr for 0.6 ![]() and
larger than 3 Gyr only for masses larger than 1.2
and
larger than 3 Gyr only for masses larger than 1.2 ![]() .
.
Whether spot-like structures could also survive for the long cooling time of white dwarfs has to be investigated theoretically.
If a magnetic spot is indeed present a strong temporal variation of
the spectrum and particularly the polarization is expected, if the star
is rotating. However, no significant differences could be found between the spectra
taken in September, 1998 and November, 1998, respectively. This may be an indication
for only slow rotation as known in the case of Grw+70![]() 8247 where a rotational
period of decades or centuries is possible (Schmidt & Norsworthy 1991; Friedrich &
Jordan 2001).
Therefore, a more detailed analysis and a decision whether a spot is present has to wait
until time resolved spectro-polarimetry of this object becomes available.
8247 where a rotational
period of decades or centuries is possible (Schmidt & Norsworthy 1991; Friedrich &
Jordan 2001).
Therefore, a more detailed analysis and a decision whether a spot is present has to wait
until time resolved spectro-polarimetry of this object becomes available.
Acknowledgements
We thank the referee John Landstreet for his very valuable comments particularly on the situation in Ap stars. Work on magnetic white dwarfs in Tübingen is supported by the DLR grant 50 OR 0201.