A&A 414, 1081-1090 (2004)
DOI: 10.1051/0004-6361:20034037
A. Moya 1 - R. Garrido 1 - M. A. Dupret 1,2,![]()
1 - Instituto de Astrofísica de Andalucía-CSIC, Granada,
Spain
2 -
Institut d'Astrophysique et de Géophysique de l'Université de Liège,
Belgium
Received 2 July 2003 / Accepted 28 October 2003
Abstract
Phase differences and amplitude ratios at different colour
photometric bands are currently being used to discriminate pulsation modes
to facilitate mode identification
of ![]() -driven non-radial pulsating stars. In addition to physical inputs
(e.g., mass,
-driven non-radial pulsating stars. In addition to physical inputs
(e.g., mass,
![]() ,
etc.), these quantities depend on the non-adiabatic
treatment of the atmosphere. This paper presents theoretical results concerning
,
etc.), these quantities depend on the non-adiabatic
treatment of the atmosphere. This paper presents theoretical results concerning
![]() Scuti pulsating stars. The envelope of each of these stellar
structures possesses a convection zone whose development is determined
by various factors. An interacting pulsation-atmosphere physical treatment
is introduced which supplies two basic non-adiabatic physical quantities:
the relative effective temperature variation and
the phase lag
Scuti pulsating stars. The envelope of each of these stellar
structures possesses a convection zone whose development is determined
by various factors. An interacting pulsation-atmosphere physical treatment
is introduced which supplies two basic non-adiabatic physical quantities:
the relative effective temperature variation and
the phase lag
![]() ,
defined as the angle between effective temperature
variation and radial displacement. These quantities can be used to derive
the phase differences and amplitude ratios. Numerical
values for these quantities depend critically on the
,
defined as the angle between effective temperature
variation and radial displacement. These quantities can be used to derive
the phase differences and amplitude ratios. Numerical
values for these quantities depend critically on the ![]() MLT parameter
used to calculate the convection in the envelope. The dependence on
MLT parameter
used to calculate the convection in the envelope. The dependence on ![]() was analyzed and it was found that the use of colour observations may be of
considerable importance in testing the MLT.
Finally, examples are given of how
was analyzed and it was found that the use of colour observations may be of
considerable importance in testing the MLT.
Finally, examples are given of how ![]() introduces uncertainties
in the theoretical predictions regarding phases and amplitudes of photometric
variations in
introduces uncertainties
in the theoretical predictions regarding phases and amplitudes of photometric
variations in ![]() Scuti pulsating stars.
Scuti pulsating stars.
Key words: stars: variables: ![]() Scuti - stars: atmosphere - stars: oscillations
Scuti - stars: atmosphere - stars: oscillations
Asteroseismology is presently being developed as an efficient instrument in the
study of stellar interiors and evolution. Pulsational periods are the most
important asteroseismological observational inputs. However,
for non-solar like oscillations, such as those characterizing ![]() Scuti stars, the information contained in these periods is not sufficient to
adequately constrain theoretical predictions. Without additional
observational data, mode identification is, therefore, not feasible in
non-solar like contexts. The primary obstacles
are that the pulsation modes of
Scuti stars, the information contained in these periods is not sufficient to
adequately constrain theoretical predictions. Without additional
observational data, mode identification is, therefore, not feasible in
non-solar like contexts. The primary obstacles
are that the pulsation modes of ![]() Scuti stars: 1) do not lie within the
asymptotic regime and 2) may be affected by the "avoided crossing''
phenomenon. Furthermore, rotation and eventual coupling also destroy
any possible regular pattern.
Scuti stars: 1) do not lie within the
asymptotic regime and 2) may be affected by the "avoided crossing''
phenomenon. Furthermore, rotation and eventual coupling also destroy
any possible regular pattern.
One way to obtain more information on the basis of photometric observations is to study the multicolor flux variations. The linear approximation to non-radial flux variations of a pulsating star was first derived by Dziembowski (1977b), and later reformulated by Balona & Stobie (1979a, 1979b) and by Watson (1988). In Garrido et al. (1990), the linear approximation was successfully used to discriminate the spherical orders l of these pulsating star modes. Several attempts to fit observations have shown that the method can be applied, at least to low rotational velocities (e.g., FG Vir in Breger et al. 1999; BI CMi in Breger et al. 2002; 4 CVn in Breger et al. 1999; V1162 in Arentoft et al. 2001 and some other stars in Garrido 2000; for fast rotators, see Daszynska et al. 2002).
Most theoretical and numerical pulsation models have been developed using the adiabatic approximation (Christensen-Dalsgaard 1982; Tran & Leon 1995). However, pulsation is highly non-adiabatic in stellar surface layers, in which thermal relaxation time is either of the same order or even lower than the pulsation period. The accurate determination of the eigenfunctions in these layers will therefore require the use of a non-adiabatic description which includes the entire atmosphere. This procedure then makes it possible to relate multicolor photometric observables with such eigenfunctions.
A number of authors (e.g., Dziembowski 1977a; Saio & Cox 1980; Pesnell 1990; Townsend 2002) have developed non-adiabatic codes and performed stellar pulsation calculations. However, these works have been carried out without a complete description of pulsation-atmosphere interaction.
In this paper two approaches are compared. The first follows Unno et al. (1989) for the equations and the numerical method used to solve them. Outer boundary conditions are imposed at the level of the photosphere. This approximation will be referred to below as "without atmosphere''. The second applies a non-adiabatic pulsational treatment to the atmosphere derived by Dupret et al. (2002). This treatment has made it possible to obtain photometric observable values that are more realistic when compared with those generated by the "without'' atmosphere approximation (referred to below as "with atmosphere''). The latter approach allows theoretical predictions to be more directly connected with photometric observations than they previously had been by using only period comparisons.
Theoretical and observed amplitude ratios and phase differences
can be compared as observed in different color photometric bands.
Garrido et al. (1990) showed that the wavelength dependence of the
limb darkening integrals is very weak for low l values. Thus,
at least three color combinations, distributed in the widest possible
range of wavelengths, give consistent values for phase lag
![]() and R. The latter parameter was defined by Watson (1988) and
designed to measure departures from adiabatic conditions. Comparisons
between non-adiabatic predictions and multicolor photometric observations have
been made by Cugier et al. (1994) for
and R. The latter parameter was defined by Watson (1988) and
designed to measure departures from adiabatic conditions. Comparisons
between non-adiabatic predictions and multicolor photometric observations have
been made by Cugier et al. (1994) for ![]() Cephei stars,
Balona & Evers (1999) for
Cephei stars,
Balona & Evers (1999) for ![]() Scuti stars and Townsend
(2002) for Slowly Pulsating B stars. However, such comparisons
were made without carrying out a detailed non-adiabatic pulsation
treatment for the atmosphere. Photometric magnitude variations have been
reformulated by Dupret et al. (2003), thus making it possible to obtain
theoretical non-adiabatic quantities which explicitly include the atmosphere
(Dupret et al. 2002). This reformulation has been
employed in the study of
Scuti stars and Townsend
(2002) for Slowly Pulsating B stars. However, such comparisons
were made without carrying out a detailed non-adiabatic pulsation
treatment for the atmosphere. Photometric magnitude variations have been
reformulated by Dupret et al. (2003), thus making it possible to obtain
theoretical non-adiabatic quantities which explicitly include the atmosphere
(Dupret et al. 2002). This reformulation has been
employed in the study of ![]() Cephei and Slowly Pulsating B stars.
Cephei and Slowly Pulsating B stars.
In the present paper the approach of Dupret et al. (2002, 2003)
is applied to ![]() Scuti stars. Non-adiabatic theoretical
models "with'' and "without'' atmosphere, as well as their resolution
algorithms, are presented. Solutions are compared in order to show the
improvement introduced by including the pulsation-atmosphere interaction. One
possible procedure for mode identifications using multicolor
photometric diagrams is also suggested. For
Scuti stars. Non-adiabatic theoretical
models "with'' and "without'' atmosphere, as well as their resolution
algorithms, are presented. Solutions are compared in order to show the
improvement introduced by including the pulsation-atmosphere interaction. One
possible procedure for mode identifications using multicolor
photometric diagrams is also suggested. For ![]() Scuti
stars, the non-adiabatic observables with which we are working can be
directly related with the characteristics of their thin convective envelopes.
These envelopes are described by the Mixing Length Theory (MLT) and
parametrized by
Scuti
stars, the non-adiabatic observables with which we are working can be
directly related with the characteristics of their thin convective envelopes.
These envelopes are described by the Mixing Length Theory (MLT) and
parametrized by ![]() ,
which is defined as the proportionality constant
relating the mean path of a convective element with local pressure scale
height. The
,
which is defined as the proportionality constant
relating the mean path of a convective element with local pressure scale
height. The ![]() parameter can be constrained by searching for the best fit
between theoretical and observed photometric amplitude ratios and phase
differences in color photometric bands. Such observables also depend on the
opacity variation in the HeII, HeI and HI ionization zones.
parameter can be constrained by searching for the best fit
between theoretical and observed photometric amplitude ratios and phase
differences in color photometric bands. Such observables also depend on the
opacity variation in the HeII, HeI and HI ionization zones.
Equilibrium stellar models have been computed using the CESAM code (Morel 1997). In this code, the stellar atmosphere is described: 1) as a single layer (i.e., the photosphere) calculated in the Eddington approximation, or 2) using the Kurucz equilibrium atmospheric models (Kurucz 1993) to reconstruct the atmosphere from a specific Rosseland optical depth until reaching the last edge of the star. Table 1 shows the global characteristics of the equilibrium models. In the convective core of these models, overshooting has been set to 0.2 times the local pressure scale height.
The pulsational code begins by computing the adiabatic solution for fixed
values of n and l, and this computation is used as trial input
for the non-adiabatic computations "with'' or "without'' atmosphere.
These calculations then make it possible to derive
![]() ,
,
![]() and
and
![]() ,
which
are directly related to the photometric color variations.
,
which
are directly related to the photometric color variations.
Here the adiabatic and non-adiabatic equations have been derived following
Unno et al. (1989). However, two variables regarding the stellar
interior have been modified in order to directly link the interior and
atmosphere pulsation equations. These variables are
| y1 | = | 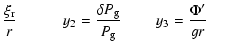 |
|
| y4 | = | 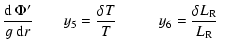 |
(1) |
Table 1: Global characteristics of the equilibrium models.
The linear non-adiabatic pulsation equations corresponding to these variables
are described in Appendix A (Eqs. (A.1) to (A.6)), and
are obtained by neglecting the effects of rotation and the magnetic field.
The "frozen'' convection flux approximation,
![]() and
and
![]() ,
has been chosen by following Unno et al.
(1989). Boundary conditions are also taken from the same source.
Internal conditions are described by Eqs. (A.9) to (A.11) in
Appendix A. Surface conditions are given here because they are particularly
relevant to the comparison of the "with atmosphere''
(Sect. 2.2) and "without atmosphere'' treatment results:
,
has been chosen by following Unno et al.
(1989). Boundary conditions are also taken from the same source.
Internal conditions are described by Eqs. (A.9) to (A.11) in
Appendix A. Surface conditions are given here because they are particularly
relevant to the comparison of the "with atmosphere''
(Sect. 2.2) and "without atmosphere'' treatment results:
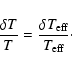 |
(5) |
Equations (A.1)-(A.6) are also used to describe the pulsation inside
the star, whereas Eqs. (A.9)-(A.11) describe the internal boundary
conditions. However, the complete atmosphere pulsation equations
are solved following Dupret et al. (2002). The latter equations
have been derived by taking into account that: 1) the radiation field is not
isotropic in the atmosphere and the diffusion approximation is therefore not
valid in this case; and 2) the radiation stress tensor cannot be represented by
a diagonal matrix with a constant element:
![]() .
.
For these reasons, new approximations have been used with respect to those
solved for the interior in order to obtain an improved description of the
atmosphere. This new approach is based on the fact that the atmosperic thermal
relaxation time is very short as compared to pulsation periods. Consequently,
it can be assumed that during each pulsation period, the atmosphere remains in
thermal equilibrium. Rewriting the equations given in Dupret et al.
(2002), those corresponding to the atmosphere are:
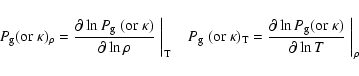 |
(12) |
In comparison to those used for the "without'' atmosphere treatment, the boundary conditions for these equations are:
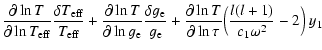 |
|||
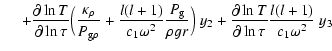 |
|||
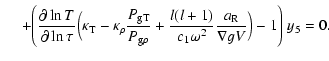 |
(16) |
One of the uncertainties of the "with'' atmosphere global algorithm is the
location of the optical depth in which this connecting layer is defined,
being that, despite the above-mentioned constraints, a small set of possible
locations still exists. Figure 1 shows the non-adiabatic
results for two
![]() stellar models at different evolutionary stages,
locating the connecting layer at
stellar models at different evolutionary stages,
locating the connecting layer at
![]() and 1.3. Note that these
results are not significantly affected by this choice. The connecting layer is
selected at
and 1.3. Note that these
results are not significantly affected by this choice. The connecting layer is
selected at ![]() .
.
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{0037f1a.eps} }\vspace*{4mm}
{\includegraphics[width=8.8cm,clip]{0037f1b.eps} }
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg78.gif) |
Figure 1:
Non-adiabatic quantities
|
| Open with DEXTER | |
The two additional variables
![]() and
and
![]() can be derived
from:
can be derived
from:
An important application of our non-adiabatic code is that its theoretical
predictions can be tested against multicolor photometric observations. The
non-adiabatic quantities
![]() ,
,
![]() and
and
![]() can be related to the photometric observables: amplitude ratios and
phase differences between filters. In a one-layer linear approximation, the
monochromatic magnitude variation of a non-radially pulsating star is given by:
can be related to the photometric observables: amplitude ratios and
phase differences between filters. In a one-layer linear approximation, the
monochromatic magnitude variation of a non-radially pulsating star is given by:
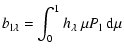 |
(20) | ||
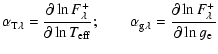 |
(21) | ||
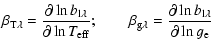 |
(22) | ||
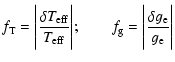 |
(23) |
One appropriate way to test multicolor theoretical predictions is to construct
phase-amplitude diagrams corresponding to well-chosen combinations of
photometric bands. In these diagrams the theoretical results corresponding to
modes of different spherical degrees ![]() occupy well differentiated regions.
This enables the identification of
occupy well differentiated regions.
This enables the identification of ![]() by searching for the best fit
between theory and observations. As is shown in Sect. 4, the
non-adiabatic quantities
by searching for the best fit
between theory and observations. As is shown in Sect. 4, the
non-adiabatic quantities ![]() ,
,
![]() and
and
![]() ,
which play a
major role in Eq. (19), are highly sensitive to
the characteristics of the convective envelope. The confrontation between the
theoretical and observed amplitude ratios and phase differences can thus
be used to constrain the physical conditions of this convection zone.
,
which play a
major role in Eq. (19), are highly sensitive to
the characteristics of the convective envelope. The confrontation between the
theoretical and observed amplitude ratios and phase differences can thus
be used to constrain the physical conditions of this convection zone.
As a prerequisite to the presentation of the "with'' atmosphere treatment
results, of particular interest is that the differences be analized between the
non-adiabatic observables appearing as a consequence of "with'' and
"without'' atmosphere descriptions. In Fig. 2
these differences are displayed for a
![]() model in the middle of the
evolutionary phase (
model in the middle of the
evolutionary phase (
![]() )
towards the exhaustion hydrogen in the core.
For the relative amplitude of the local effective temperature
variation, the effect of introducing the atmospheric treatment is slight,
though significant, especially around the overstable modes (between Q=0.02and Q=0.012 days in this model). However, the phase lag
)
towards the exhaustion hydrogen in the core.
For the relative amplitude of the local effective temperature
variation, the effect of introducing the atmospheric treatment is slight,
though significant, especially around the overstable modes (between Q=0.02and Q=0.012 days in this model). However, the phase lag
![]() is
more sensitive to this treatment for all frequencies and displays a mean
difference of
is
more sensitive to this treatment for all frequencies and displays a mean
difference of
![]() for the overstable modes. As of the latter modes,
these quantities increase with the frequency. It should be noted that the
differences in
for the overstable modes. As of the latter modes,
these quantities increase with the frequency. It should be noted that the
differences in
![]() between the "with'' and "without''
atmosphere models are negligible. Furthermore, it should be stressed that the
frequencies obtained using both treatments are almost identical, i.e., the only
difference between the two treatments appears in the outermost layers, and this
has no effect on the frequency results. In Fig. 2 it can be seen
that the non-adiabatic results for a fixed model are independent of the
spherical degree l for p-modes.
between the "with'' and "without''
atmosphere models are negligible. Furthermore, it should be stressed that the
frequencies obtained using both treatments are almost identical, i.e., the only
difference between the two treatments appears in the outermost layers, and this
has no effect on the frequency results. In Fig. 2 it can be seen
that the non-adiabatic results for a fixed model are independent of the
spherical degree l for p-modes.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f...
...sizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f2b.eps}}
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg100.gif) |
Figure 2:
Non-adiabatic quantities
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f...
...sizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f3b.eps}}
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg101.gif) |
Figure 3:
Non-adiabatic quantities
|
| Open with DEXTER | |
Only pulsation models "with'' atmosphere will be considered in what follows.
In Fig. 3 non-adiabatic results are compared as obtained for
models of
![]() and
and
![]() ,
and with different values for the MLT
parameter (
,
and with different values for the MLT
parameter (
![]() ). The non-adiabatic
quantities
). The non-adiabatic
quantities
![]() and
and
![]() are significantly affected by the value of
are significantly affected by the value of ![]() ,
especially the
phase lag. A more detailed description of the sensitivity of the non-adiabatic
results to
,
especially the
phase lag. A more detailed description of the sensitivity of the non-adiabatic
results to ![]() is given in Fig. 4. This figure displays
the ratio between radiative and total luminosity (top), the convective
efficiency (middle) and the luminosity phase lag
is given in Fig. 4. This figure displays
the ratio between radiative and total luminosity (top), the convective
efficiency (middle) and the luminosity phase lag
![]() (bottom
panel), all three as a function of the logarithm of temperature. Note that
(bottom
panel), all three as a function of the logarithm of temperature. Note that
![]() closely follows
closely follows
![]() at the photosphere throughout Eq.
(17).
at the photosphere throughout Eq.
(17).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f...
...sizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f4b.eps}}
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg104.gif) |
Figure 4:
Radiative luminosity over total luminosity ( top panel),
convective efficiency ( middle panel) and the luminosity phase lag
|
| Open with DEXTER | |
The bottom panel of Fig. 4 shows that along the
radius of the star there are two zones in which a phase lag is introduced: the
first located in the partial ionization zone of HeII and the second,
in the surface convection zone (partial HI and HeI ionization).
In this panel it can also be seen that the the phase lag sensitivity to
![]() appears in the surface convection zone.
appears in the surface convection zone.
The convective efficiency in MLT, defined as
As is shown in Fig. 1, the non-adiabatic results are highly
sensitive to the evolutionary phase of the star. As the star evolves in the HR
diagram, changes in these quantities are larger for the relative variations of
the effective temperature than for the phase lags. Changes in the evolution
phase do not qualitatively affect the non-adiabatic results in the same manner
as do changes in ![]() .
In the latter case, only the characteristics of the
convective zone are influenced. In contrast, changes in the evolution phase
have an effect on both the characteristics of the superficial convective zone
and the position of the HeII partial ionization zone.
.
In the latter case, only the characteristics of the
convective zone are influenced. In contrast, changes in the evolution phase
have an effect on both the characteristics of the superficial convective zone
and the position of the HeII partial ionization zone.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f...
...sizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f5b.eps}}
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg110.gif) |
Figure 5:
Non-adiabatic quantities
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[width=8.7cm,clip]{0037f...
...sizebox{8.8cm}{!}{\includegraphics[width=8.8cm,clip]{0037f6b.eps}}
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg111.gif) |
Figure 6:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.7cm,clip]{0037f7.eps} }
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg112.gif) |
Figure 7:
|
| Open with DEXTER | |
Figure 5 is obtained by plotting the phase lag and
![]() versus
versus
![]() for the fundamental radial mode of two complete
tracks of 2.0
for the fundamental radial mode of two complete
tracks of 2.0 ![]() and 1.8
and 1.8 ![]() stars. Three values of
the MLT parameter
stars. Three values of
the MLT parameter ![]() (1.5, 1.0 and 0.5) have been used. When stellar
temperatures are high enough to originate a negligible external
convective zone, the values are independent of
(1.5, 1.0 and 0.5) have been used. When stellar
temperatures are high enough to originate a negligible external
convective zone, the values are independent of ![]() ;
this only occurs for
the 2.0
;
this only occurs for
the 2.0 ![]() models presented. For cooler models, however, convection
becomes more efficient, thus producing different phase lags and relative
effective temperature variations for similar effective temperatures (Balona &
Evers 1999).
models presented. For cooler models, however, convection
becomes more efficient, thus producing different phase lags and relative
effective temperature variations for similar effective temperatures (Balona &
Evers 1999).
Figure 4 refers to the behaviour of these phase lags. Each step
in the figure makes it possible to view the phase lag,
![]() ,
as
the sum of two phases (
,
as
the sum of two phases (
![]() ). The latter can be
referred to as the
). The latter can be
referred to as the ![]() -phase (
-phase (
![]() phase difference
between
phase difference
between
![]() and
and
![]() (at
(at
![]() )) and the
convective-phase (
)) and the
convective-phase (
![]() phase difference between
phase difference between
![]() (at
(at
![]() )
and
)
and
![]() (at
(at
![]() )). Figure 6 is obtained by plotting both versus
)). Figure 6 is obtained by plotting both versus
![]() .
.
The ![]() -phase lag
-phase lag
![]() displays a behaviour which is directly
related to the position of the model in the HR diagram and which is independent
of the
displays a behaviour which is directly
related to the position of the model in the HR diagram and which is independent
of the ![]() parameter. Therefore,
parameter. Therefore,
![]() shows the contribution of
only one of the phase sources, the opacity variation, since convection is
not efficient in this part of the star.
shows the contribution of
only one of the phase sources, the opacity variation, since convection is
not efficient in this part of the star.
The contribution to the convection zone phase, in this case
![]() ,
is
in turn a sum of two phase sources. For hot models the
,
is
in turn a sum of two phase sources. For hot models the ![]() driving
mechanism is not yet efficient enough to introduce a phase lag, and the
behaviour of
driving
mechanism is not yet efficient enough to introduce a phase lag, and the
behaviour of
![]() depends mainly on the convection treatment. When the
convective layers are not efficient, models with different values of
depends mainly on the convection treatment. When the
convective layers are not efficient, models with different values of ![]() produce the same values of
produce the same values of
![]() .
At
.
At
![]() the
convective layers become sufficiently efficient to distinguish between models
using different values of
the
convective layers become sufficiently efficient to distinguish between models
using different values of ![]() ,
independently of the mass. From
,
independently of the mass. From
![]() to cooler models, an increase is observed in the value of
this phase lag, again displaying different behaviours for different masses and
values of
to cooler models, an increase is observed in the value of
this phase lag, again displaying different behaviours for different masses and
values of ![]() .
This is accounted for by the fact that, within this range
of temperature, the
.
This is accounted for by the fact that, within this range
of temperature, the ![]() driving mechanism in the HI and HeI ionization
zone becomes efficient enough to make a significant contribution to
driving mechanism in the HI and HeI ionization
zone becomes efficient enough to make a significant contribution to
![]() .
.
Figure 7 is obtained by displaying
![]() versus the
integral of the convective efficiency, as defined in Eq. (24) for all
models. The behaviour of these quantities can be distinguished
independently of the mass of the model, which in this case is exclusively a
function of the evolution phase and
versus the
integral of the convective efficiency, as defined in Eq. (24) for all
models. The behaviour of these quantities can be distinguished
independently of the mass of the model, which in this case is exclusively a
function of the evolution phase and ![]() .
.
All of the above-mentioned calculations have a direct influence on the phase
difference - amplitude ratio diagrams. Now phase lags, as well as relative
variations in
![]() and
and
![]() can be used to overcome the uncertainties in previous
phase-ratio color diagrams. In Garrido (2000) these discrimination diagrams
were made using parametrized values for departures from adiabaticity and phase
lags. The only remaining degree of freedom is now the choice of the MLT
can be used to overcome the uncertainties in previous
phase-ratio color diagrams. In Garrido (2000) these discrimination diagrams
were made using parametrized values for departures from adiabaticity and phase
lags. The only remaining degree of freedom is now the choice of the MLT
![]() parameter in order to describe the convection. Therefore,
discrimination diagrams depend only on this parameter, as is
shown in Fig. 8 where theoretical predictions are plotted for two
specific Strömgren photometric bands ((b-y) and y) with a given
theoretical model using three different MLT
parameter in order to describe the convection. Therefore,
discrimination diagrams depend only on this parameter, as is
shown in Fig. 8 where theoretical predictions are plotted for two
specific Strömgren photometric bands ((b-y) and y) with a given
theoretical model using three different MLT ![]() parameters in the
fundamental radial mode regime (pulsation constant near 0.033 days) and in the
3rd overtone regime (near 0.017 days).
parameters in the
fundamental radial mode regime (pulsation constant near 0.033 days) and in the
3rd overtone regime (near 0.017 days).
A clear separation between the l-values exists for periods around the
fundamental radial. Similar behaviour is found for other modes in the proximity
of the 3rd radial overtone, although for these shorter periods some
overlappings start to appear at the lowest l-values. They also show the same
trend as in the fundamental radial mode: high amplitude ratios for low MLT
![]() and the spherical harmonic l=3. A more detailed description of these
diagrams using different models and photometric bands will be given in a
forthcoming paper.
and the spherical harmonic l=3. A more detailed description of these
diagrams using different models and photometric bands will be given in a
forthcoming paper.
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm,clip]{0037f8.eps}
\end{figure}](/articles/aa/full/2004/06/aa0037/Timg121.gif) |
Figure 8:
The top panel shows theoretical predictions for two specific
Strömgren photometric bands ((b-y) and y) for a given theoretical model
using three MLT |
| Open with DEXTER | |
This paper uses the CESAM package to generate equilibrium models. A new
non-adiabatic pulsation code has been developed and applied to the study of
![]() Scuti stars. This code takes into account the stellar atmosphere
in two ways: 1) as the boundary layer of the star
("without'' atmosphere); in this case photospheric observables
such as amplitudes and phases of both
Scuti stars. This code takes into account the stellar atmosphere
in two ways: 1) as the boundary layer of the star
("without'' atmosphere); in this case photospheric observables
such as amplitudes and phases of both
![]() and gravity, reflect the
boundary conditions we impose; and 2) particular consideration is given to
pulsation treatment ("with'' atmosphere), thus extending the star beyond the
photosphere. As a consequence of applying the "with'' atmosphere treatment,
photospheric observables become determinable as a solution to a set of
differential equations. These equations have been described by Dupret et al.
(2002).
and gravity, reflect the
boundary conditions we impose; and 2) particular consideration is given to
pulsation treatment ("with'' atmosphere), thus extending the star beyond the
photosphere. As a consequence of applying the "with'' atmosphere treatment,
photospheric observables become determinable as a solution to a set of
differential equations. These equations have been described by Dupret et al.
(2002).
The non-adiabatic code presented in this paper enables the determination of the
photometric observables
![]() ,
,
![]() and
and
![]() .
The results of the "without'' atmosphere approach strongly depend on
the choice of external boundary conditions. In contrast, the "with''
atmosphere approach only implies those uncertainties brought about by the
physical assumptions imposed in order to obtain the differential equations.
.
The results of the "without'' atmosphere approach strongly depend on
the choice of external boundary conditions. In contrast, the "with''
atmosphere approach only implies those uncertainties brought about by the
physical assumptions imposed in order to obtain the differential equations.
The comparison of the results generated by both treatments shows that the
values for
![]() are relatively similar in most of the
spectrum. However, differences become notable for shorter periods, in which
"without'' atmosphere solutions are larger than those of the "with''
atmosphere treatment. Differences in
are relatively similar in most of the
spectrum. However, differences become notable for shorter periods, in which
"without'' atmosphere solutions are larger than those of the "with''
atmosphere treatment. Differences in
![]() are significant and have a mean
value of approximately
are significant and have a mean
value of approximately
![]() within the range of the periods
studied. The non-adiabatic results presented here are highly sensitive to the
characteristics of the superficial convective zone, parametrized by using
the mixing length parameter
within the range of the periods
studied. The non-adiabatic results presented here are highly sensitive to the
characteristics of the superficial convective zone, parametrized by using
the mixing length parameter ![]() .
In particular, we have shown that
there are two regions in which the phase lag originates. A first phase lag
takes place in the partial ionization zone of HeII, where the
.
In particular, we have shown that
there are two regions in which the phase lag originates. A first phase lag
takes place in the partial ionization zone of HeII, where the ![]() mechanism drives the oscillations. This phase lag is very
sensitive to the evolution phase. A second one occurs in the
convective envelope (partial ionization zone of HI and HeI) and is
sensitive mainly to
mechanism drives the oscillations. This phase lag is very
sensitive to the evolution phase. A second one occurs in the
convective envelope (partial ionization zone of HI and HeI) and is
sensitive mainly to ![]() .
Though to a lesser extent, this phase lag is
also sensitive to the evolutionary phase because of the
.
Though to a lesser extent, this phase lag is
also sensitive to the evolutionary phase because of the ![]() driving
mechanism and the size of the convection zone change.
driving
mechanism and the size of the convection zone change.
In this paper it is shown that theoretical photometric amplitude ratios and
phase differences are very sensitive to non-adiabatic calculations.
The treatment and location of the outer boundary conditions, here
referred to as "with'' and "without'' atmosphere, have been shown
to give significantly different theoretical predictions. Consequently, our
improved non-adiabatic treatment of the atmosphere will
probably enable more accurate photometric mode identifications. Our
results confirm the recent theoretical results of Daszynska-Daszkiewicz
et al. (2003) which show
that phases and amplitudes in different colours are affected by the
choice of the ![]() parameter, although the authors calculated the model
atmospheres in the Eddington approximation.
By determining the best fit between theory and observations, it may thus be
possible to constrain the MLT parameter
parameter, although the authors calculated the model
atmospheres in the Eddington approximation.
By determining the best fit between theory and observations, it may thus be
possible to constrain the MLT parameter ![]() .
.
Acknowledgements
This work was partialy financed by program ESP 2001-4528-PE. The authors are also grateful to Marco Bettini for thorough editing of the original English manuscript.
These equations have been developed following Unno et al.
(1989). Eigenfunctions
![]() and
and
![]() have been replaced by
have been replaced by
![]() and
and
![]() to adapt the equations to the atmospheric ones. This was done to make the
transition in the connecting layer as smooth as possible. Having introduced
these modifications, the nonadiabatic nondimensional equations for the
stellar interior are
to adapt the equations to the atmospheric ones. This was done to make the
transition in the connecting layer as smooth as possible. Having introduced
these modifications, the nonadiabatic nondimensional equations for the
stellar interior are
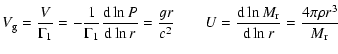 |
|||
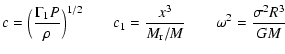 |
(A.7) |
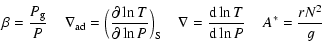 |
|||
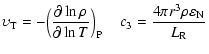 |
|||
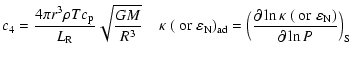 |
|||
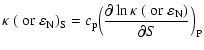 |
(A.8) |
The interior boundary conditions are common to both pulsational treatments, given that the stellar interior is solved using the same equations. In our formalism, these conditions are: