A&A 414, 445-451 (2004)
DOI: 10.1051/0004-6361:20034155

The origin of H I-deficiency in galaxies on the outskirts of the Virgo cluster

I. How far can galaxies bounce out of clusters?

G. A. Mamon 1,2 - T. Sanchis 3 - E. Salvador-Solé3,4 - J. M. Solanes3,4


1 - Institut d'Astrophysique de Paris (CNRS UMR 7095), 98bis Bld Arago, 75014 Paris, France
2 - GEPI (CNRS UMR 8111), Observatoire de Paris, 92195 Meudon Cedex, France
3 - Departament d'Astronomia i Meteorologia, Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain
4 - CER on Astrophysics, Particle Physics, and Cosmology, Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain

Received 1 August 2003 / Accepted 21 October 2003

Abstract
Spiral galaxies that are deficient in neutral hydrogen are observed on the outskirts of the Virgo cluster. If their orbits have crossed the inner parts of the cluster, their interstellar gas may have been lost through ram pressure stripping by the hot X-ray emitting gas of the cluster. We estimate the maximum radius out to which galaxies can bounce out of a virialized system using analytical arguments and cosmological N-body simulations. In particular, we derive an expression for the turnaround radius in a flat cosmology with a cosmological constant that is simpler than previously derived expressions. We find that the maximum radius reached by infalling galaxies as they bounce out of their cluster is roughly between 1 and 2.5 virial radii. Comparing to the virial radius of the Virgo cluster, which we estimate from X-ray observations, these H  I-deficient galaxies appear to lie significantly further away from the cluster center. Therefore, if their distances to the cluster core are correct, the H  I-deficient spiral galaxies found outside of the Virgo cluster cannot have lost their gas by ram pressure from the hot intracluster gas.

Key words: galaxies: evolution - methods: analytical - methods: N-body simulations

   
1 Introduction

Radio observations at 21cm have revealed that spiral galaxies within clusters are deficient in neutral hydrogen (e.g. Chamaraux et al. 1980), and their H  I-deficiency, normalized to their optical diameter and morphological type, is largest for the spirals near the cluster center (Solanes et al. 2001; Haynes & Giovanelli 1986; Cayatte et al. 1990). Chamaraux et al. (1980) suggested that the H  I-deficiency of cluster spirals was caused by the ram pressure stripping of their interstellar Hydrogen by the hot intracluster gas that emits in X-rays. Galaxies falling face-on into a cluster experience a ram pressure that scales as $\rho_{\rm cl}~v^2$ (Gunn & Gott 1972), where $\rho_{\rm cl}$ is the cluster gas density and v is the relative velocity of the spiral galaxy in its cluster. Therefore, ram pressure stripping requires the large infall velocities present in rich clusters.

Solanes et al. (2002) recently discovered deficient spirals in the periphery of the Virgo cluster, with several ones typically over 5 Mpc in front or behind the cluster core. In an ensuing study, Sanchis et al. (2002) could not discard the possibility that some of these galaxies could have passed through the cluster core and in the process had their interstellar gas swept out by the ram pressure caused by the intracluster hot diffuse gas.

The idea of galaxies beyond the virial radius having passed through the main body of a cluster in the past has been addressed by Balogh et al. (2000) in the context of the discovery of reduced star formation rates on the outskirts of clusters in comparison with the field (Balogh et al. 1997). Using cosmological simulations, Balogh et al. analyzed 6 clusters within a sphere of 2 times their final virial radius and found that $54\pm20$% of the particles between r200 and 2 r200 (where r200 is the radius where the mean density of the cluster is 200 times the critical density) have actually been inside the virial radius of the main cluster progenitor at some earlier time. Unfortunately, Balogh et al. do not provide any precision on the maximum distances that such particles that were once within a cluster progenitor can move out to. Furthermore, one needs to check if 2 r200 represents a sufficient distance for particles bouncing out of virialised structures to explain the H  I-deficient galaxies on the outskirts of the Virgo cluster.

In this paper, we ask whether the H  I-deficient galaxies on the outskirts of the Virgo cluster have previously passed through the core of the cluster, using both analytical arguments and the output of cosmological N-body simulations. In Sect. 2, we describe the N-body simulations analyzed in this paper. Next, in Sect. 3, we study the structure in radial phase space of dark matter halos of the simulations. In Sect. 4, we compute the maximum rebound radius, both analytically, making use of the turnaround radius of cosmological structures, which we compute in an appendix, and by studying the structure of our simulated halos in radial phase space, as well as analyzing the orbital evolution of particles in the cosmological simulations of Fukushige & Makino (2001). In Sect. 5, we estimate the virial radius and other virial parameters of the Virgo cluster to permit the estimation of the Virgo rebound radius in physical units. We discuss our results in Sect. 6.

In a companion paper (Sanchis et al. 2004), we discuss in more detail the origin of the H  I-deficiency in galaxies on the outskirts of the Virgo cluster, by analyzing 2D slices of the 4D phase space (right ascension, declination, distance and radial velocity) and comparing them with the cosmological N-body simulations used here.

   
2 N-body simulations

The N-body simulations used here to find N-body replica of the Virgo cluster were carried out by Ninin (1999, see Hatton et al. 2003) in the context of the GALICS (Hatton et al.) hybrid N-body/semi-analytic model of hierarchical galaxy formation. Here we are basically interested in the density and velocity fields directly traced by dark matter particles. The N-body simulation contains 2563 particles of mass $8.3 \times 10^9\ M_{\odot}$ in a box of 150 Mpc size and it is run with a softening length amounting to a spatial resolution of 29 kpc. The simulation was run for a flat universe with cosmological parameters $\Omega_{0} = 0.333, \lambda_{0} = 0.667$, $H_{0}=66.7~\rm km~s^{-1}~Mpc^{-1}$, and $\sigma_8 = 0.88$. Once the simulation is run, halos of dark matter are detected with a "Friends-of-Friends'' (FoF) algorithm (Davis et al. 1985), with a variable linking length such that the minimum mass of the FoF groups is $1.65 \times 10^{11} M_{\odot}$ (20 particles) at any time step. With this method, over $2 \times 10^{4}$ halos are detected at the final timestep, corresponding to the present-day (z=0) Universe. The GALICS halo finder does not allow halos within halos, so that a cluster, to which is assigned a massive halo, cannot contain smaller halos within it.

   
3 Halo structure in radial phase space


  \begin{figure} \par {\includegraphics[width=17.cm,clip]{0155_f1.ps} } \end{figure} Figure 1: 3D radial phase space plots (radial velocity versus radial distance, both relative to the halo center and normalized to the virial circular velocity and radius, respectively) of dark matter particles in a $\Lambda $CDM cosmological N-body simulation for the four most massive halos at redshift z=0. The virial radius, mass and circular velocity at virial radius are listed on the right corner of each plot. The open and small closed circles are the identified halos in the cosmological simulation respectively without and with galaxies within them.
Open with DEXTER

Figure 1 shows the radial phase space diagrams, i.e. radial velocity vs. radial distance, both relative to the halo center, for 4 massive halos. We have studied the final output of the simulation at z=0. The centers of the isolated halos shown in Fig. 1 are provided by the simulation output and correspond to the barycenter of the FoF groups of particles. Radial distances are normalized to the virial radius $r_{\rm 100}$, corresponding to the radius where the mean density is 100 times the critical density of the Universe. We use r100 instead of r200 because the former represents better the virial radius in universes with non zero cosmological constant (Kitayama & Suto 1996). Velocities are normalized to the respective circular velocities at r100.

Most of the massive halos in the simulation have a phase space diagram similar to those for the 4 halos shown in Fig. 1, once scaled to the virial radius and circular velocity at the virial radius. In particular, all plots show a virialized region for radii smaller than the r100(although this virialization is not perfect, for example see the excess of positive velocity particles in the lower left plot, presumably caused by a large group that is bouncing out of the cluster), and an infalling region with velocity increasing with radius and asymptotically reaching the (linear) Hubble flow. One clearly notices groups or small clusters of particles in the outer regions (e.g. at r = 3 r100 in the upper right plot), which display Fingers of God patterns in phase space. The material within 1 or 2 r100 that bounces out of the cluster should form a pattern symmetric to the infalling pattern relative to the zero velocity line. It is smeared out by numerical two-body relaxation (S. Colombi informed us that the rebounding region is seen more sharply when simulations are run with increased potential softening lengths that reduce the numerical relaxation). The global aspect of these phase space plots is similar to those shown by Fukushige & Makino (2001, Fig. 21), at various epochs of their cosmological simulations (run with a standard - $\Omega_0 = 1$, $\lambda_0 = 0$ - CDM cosmology).

   
4 Maximum rebound radius

An inspection of Fig. 1 shows that dark matter particles beyond the virialized core and outside the infalling/expanding zone of phase space can reach 2 or 2.5 times the virial radius, but not any further, and moreover come in groups of particles which appear to be tidally shredded in phase space. In other words, particles that cross through the core of a cluster cannot bounce out beyond 2.5 virial radii.

Now galaxies are not just particles, but arise within particle condensations known as dark matter halos, which should arise as vertically-elongated (Fingers of God) particle condensations in phase space, and therefore ought to avoid the fairly sparse regions of phase space where the outermost outgoing particles are seen. The open circles in Fig. 1 indicate the halos without galaxies within them in GALICS. The absence of galaxies within halos is a feature of GALICS for halos that cross a larger one (its galaxies become part of the larger halo). Empty halos can also occur in GALICS for isolated halos in which galaxies have not yet had time to form. The empty halos outside the infalling/expanding region do not extend beyond 1.7 r100 (upper left and lower right panels, with the former possibly a member of the group at 1.9 r100). In contrast, the normal halos (filled circles in Fig. 1) outside the infalling/expanding region do not extend as far from the main halo. The positions of the empty circles in Fig. 1 therefore suggests that halos crossing the main halo do not bounce out further than 1.7 r100.

This maximum rebound radius is consistent with a close inspection of the right panel of Fig. 20 from Fukushige & Makino (2001), which shows that the largest rebound radii in one of their cosmological simulations, i.e. the largest radii of a particle that has experienced at least one pericenter, is 2 Mpc, occurring at the present epoch, for a cluster whose present-day virial radius (r200) is at 1.7 Mpc (see their Table 2). Hence for that particular shell, the rebound radius is only 1.2 times r200 and an even smaller factor times r178 (the canonical radius for the cosmology used). Given the $\Omega_0 = 1$ cosmology used, for which the spherical infall model yields scale-free growth, the rebound radius should be proportional to the turnaround radius, which itself should be proportional to the virial radius, with a time growth of $r \sim t^{8/9}$ (Gott 1975). We checked that the other rebound radii occurring earlier were even smaller than the scaled expectation of a 2 Mpc radius today.

One can confirm this result through simple analytical arguments. First, if one identifies the virial radius to the radius where infalling shells meet the rebounding shells, this will be very close to the rebound radius itself, defined as the radius where a shell reaches its second apocenter (see Fig. 1 of Mamon 1992), so that the rebound radius will be very close to r100.

Moreover, one can estimate the rebound radius for a flat cosmology in the following manner. To begin, assume that the rebound radius is $\tilde r$times smaller than the turnaround radius (the first apocenter of the shell), and occurs at a time equal to $\tilde t$ times the epoch of turnaround. The mass within a shell that has reached its second apocenter will be close to but greater than the mass M within the same shell at turnaround, since some additional matter will be infalling for the first time. We write this as

 \begin{displaymath}\rho_{\rm reb} (t_0) \ga {\tilde r}^3~\rho_{\rm ta} (T_{\rm ta}) \ , \end{displaymath} (1)

where the rebound density is for the present epoch, while the turnaround density is for the epoch of a shell's first apocenter given that its second apocenter is today. Given that the mass within the shell at turnaround is
                        M = $\displaystyle {4\pi\over3} (1+\delta_i)~\rho_i~r_i^3$  
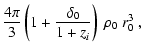  = $\displaystyle {4\pi\over3} \left (1+{\delta_0\over 1+z_i}\right)~\rho_0 ~r_0^3 \ ,$ (2)

where we used Eqs. (A.10) and (A.17), we obtain a mean density within the turnaround radius that satisfies

 \begin{displaymath}{\rho_{\rm ta} \over \rho_0} = \left (1+{\delta_0\over 1+z_i}\right)~{1\over y_{\rm ta}^3} \simeq {1\over y_{\rm ta}^3} \cdot \end{displaymath} (3)

Equations (1) and (3) lead to

 \begin{displaymath}\rho_{\rm reb} \ga \left ({\tilde r \over y_{\rm ta}} \right )^3~\Omega_0~\rho_{\rm c,0} \ , \end{displaymath} (4)

where $\rho_{\rm c,0}$ is the present day critical density. Inverting mean density into mass, assuming ${\rm d}\ln\rho/{\rm d}\ln r = -\alpha$, leads to

 \begin{displaymath}{r_{\rm reb} \over r_{\rm vir}} \la \left ({\Omega_0\over \De... ...}~\left ({\tilde r \over y_{\rm ta}} \right )^{-3/\alpha} \ , \end{displaymath} (5)

where the virial radius $r_{\rm vir}$ is defined such that the mean density within it is $\Delta$ times the critical density. For Navarro et al. (1995, hereafter NFW) density profiles, with concentration parameters $c \simeq 6$, as found by Bullock et al. (2001) in recent $\Lambda $CDM cosmological simulations, using $\Delta \simeq 100$, we obtain a slope $\alpha = 2.4$ at the virial radius.

There are two ways one can reach a large rebound radius today: either with a large ratio of rebound to turnaround radius for a given shell (i.e. $\tilde r$ as small as possible, but it cannot be smaller than unity), or with a turnaround as late as possible (i.e. $\tilde t$ as small as possible), which implies a lower turnaround density, hence a lower rebound density (for given $\tilde r$).

In the first case, the rebound radius could be equal to the initial turnaround radius, i.e. $\tilde r = 1$. One then expects that a shell that is presently at its second apocenter, should have reached turnaround at epoch t0/3, i.e. $\tilde t = 3$. We make use of the reasonably simple expression for the turnaround radius versus time obtained in the Appendix. Solving Eq. (A.21) for $\delta_0$, using Eqs. (A.18) and (A.19) for $y_{\rm ta}$ and $(\Omega_0=0.3,\lambda_0=0.7)$, yields $\delta_0 = 2.69$ and $y_{\rm ta}=0.229$. Eq. (5) and $\alpha = 2.4$ then lead to $r_{\rm reb} \la 1.8~r_{\rm 100}$.

Second, in the spirit of the shell rapidly virializing through violent relaxation at full collapse, one can assume that the shell reaches its second apocenter right after its first pericenter (full collapse), i.e. $\tilde t \ga 2$, with a radius near half its turnaround radius ( $\tilde r = 2$). This yields (not surprisingly) $r_{\rm reb} = 1.03~r_{100}$. The very best case requires $\tilde r = 1$ and $\tilde t = 2$, and leads to $r_{\rm reb} = 2.46~r_{100}$. Table 1 summarizes these estimates of the rebound radius, where $\delta_0$ and $y_{\rm ta}$ come from Eqs. (A.18), (A.19) and (A.21) and $r_{\rm reb}/r_{100}$ from Eq. (5). The last four lines are for the four particle orbits from the simulations of Fukushige & Makino (2001) that rebound within the last 7 Gyr, and for these $\delta_0$ is computed so that the epoch of the second apocenter is the present time, hence the epoch of turnaround is $t_0/(t_{\rm reb}/t_{\rm ta})$.

Table 1: Rebound radius in different scenarios.

Although, the uncertain effects of relaxation as the shell crosses through the virialized region lead to uncertain values of the ratios of rebound to turnaround radius ($\tilde r$) and time ($\tilde t$ ), in the most favorable spherical infall model, the rebound radius cannot be greater than 2.5 times the virial radius. The cosmological simulations of Fukushige & Makino suggest rebound radii of order of r100, but recall that they are for a different cosmology ( $\Omega_0 = 1, \lambda_0 = 0$). The use of real simulations has the added advantage of incorporating the effects of two-body encounters that can push material beyond the theoretical rebound radius. However, it is not always easy to distinguish in a given snapshot of phase space (e.g. Fig. 1) the material that is bouncing out of a structure with material that is infalling for the first time (except that the former particles are in halos without galaxies), and the analysis of particle histories, done for the simulations of Fukushige & Makino, is beyond the scope of this paper for the GALICS simulations.

   
5 Virial radius, mass and velocity of the Virgo cluster

For the application of results of Sect. 4 to the Virgo cluster, we require an estimate of the virial radius of the cluster. We estimate r100 through the large-scale X-ray observations of the Virgo cluster obtained with the ROSAT All-Sky Survey by Schindler et al. (1999). The peak of the X-ray emission in Virgo coincides with the position of the giant elliptical M 87, and we use the integrated mass profile around M 87 obtained by Schindler et al. to derive the virial radius. With their isothermal approximation for the total mass profile (their Fig. 11a), M(r)/r is independent of radius for $r \gg r_{\rm c}$ and also of the assumed distance to Virgo, yielding

 \begin{displaymath}{G~M(r)\over r} = 3~\beta~{kT\over \mu m_{\rm p}} , \end{displaymath} (6)

where $\beta = 0.47$ is the shape parameter of the X-ray gas density profile, $kT = 2.7~\rm keV$ and $\mu m_{\rm p}$ is the mean particle mass, generally assumed for a hot plasma to be roughly $0.6~m_{\rm p}$, where $m_{\rm p}$ is the proton mass. The virial radius, r100, is then obtained through

 \begin{displaymath}\overline \rho = {3 M_{100} \over 4 \pi r_{100}^3} = \Delta~{3~H_0^2\over 8~\pi~G} \ , \end{displaymath} (7)

where $\Delta = 100$ is the spherical overdensity at the virial radius. Solving Eqs. (6) and (7), one obtains
   
                                       $\displaystyle r_{100} = {1\over H_0}~\sqrt{2 \over \Delta}~\sqrt{3~\beta~ kT \over\mu m_{\rm p}} = 1.65~h_{2/3}^{-1}~\rm Mpc \ ,$ (8)
    $\displaystyle M_{100} = {1\over G~H_0}~\sqrt{2~\over \Delta}~\left ({3~\beta~kT\over \mu m_{\rm p}}\right )^{3/2}$  
    $\displaystyle \qquad \ = 2.30 \times 10^{14}~h_{2/3}^{-1}~{M}_{\odot} \ ,$ (9)
    $\displaystyle v_{100} = \sqrt{G~M_{100}\over r_{100}} = \sqrt{3~\beta~kT\over \mu m_{\rm p}} = 780 ~ \rm km ~ s^{-1} \ ,$ (10)

where v100 is the circular velocity at r100 and $h_{2/3} = H_0 / (66.7 ~ \rm km ~ s^{-1} ~Mpc^{-1})$.

The Virgo cluster is believed to have a complex structure, as it may be composed of several subclusters (Binggeli et al. 1987) around the elliptical galaxies M 87 (NGC 4486), M 86 (NGC 4406), and M 49 (NGC 4472). The virial radius of  $1.65~h_{2/3}^{-1}~\rm Mpc$ is such that the important substructure surrounding M 86 is well within it, at a distance of 0.22 (projected) and 0.42 (3D) times r100 of M 87. Similarly, the important substructure around M 49 lies just within the virial radius, at a distance of 0.78 (projected) and 0.84 (3D) times the virial radius of M 87. Among the other Messier elliptical galaxies in Virgo, which all have fairly secure distances, M 60 is well within the virial radius, M 89 lies just at the virial radius, while M 59 is outside.

Analyzing the X-ray emission of the intra-cluster gas, Schindler et al. (1999) found that the M 49 subcluster is 2.4 times less massive than the M 87 subcluster. The ratio of masses between the M 87 and the M 86 subclusters is even larger (Böhringer et al. 1994). It therefore appears that the structure surrounding M 87 is by far the most massive component in the Virgo cluster, and it is not a bad approximation to choose a single halo to represent the cluster, so we can apply the results of Sect. 4.

   
6 Discussion

The analysis of Sect. 4 indicates that the maximum rebound radius is between 1 and 2.5 times the virial radius. Given the virial radius of 1.65 Mpc for the Virgo cluster, which we derived in Sect. 5, and the maximum rebound radius derived in Sect. 4, galaxies passing through the Virgo cluster core in the past cannot lie further than $(1{-}2.5) \times 1.65 = 1.7{-}4.1$ Mpc from the cluster center.

Balogh et al. (2000) found that a very significant fraction of particles at a distance between 1 and 2 r200 from the centres of cosmologically simulated clusters have passed through the main body ( r < r200) of a cluster progenitor at some earlier epoch. Note that although the analysis of Balogh et al. was performed in terms of r200, they would have very probably gotten similar results had they scaled their clusters and progenitors with r100 instead. As mentioned in Sect. 1, it is not clear from their analysis if particles can escape beyond 2 r200 or even beyond, say, only 1.5 r200. Also, it is easier to displace out to large distances particles rather than large groups of particles representing a galaxy (or subhalo). In any event, the result of Balogh et al. is consistent with our analysis of Sect. 4.

An examination of Fig. 2 of Solanes et al. (2002) indicates $3~\sigma$H  I-deficient galaxies lying between 9 and 30 Mpc from the Local Group, and in particular galaxies at 10 and 28 Mpc from the Local Group, whose distance error bars do not reach the wide range of distances to the Virgo cluster found in the literature (14 Mpc by Ciardullo et al. 1998 to 21 Mpc by Ekholm et al. 2000). Therefore, it appears very difficult to explain such H  I-deficient galaxies over 5 Mpc in front or behind the cluster center as having crossed through the center of the cluster and bounced out if their distance estimates are accurate. This would suggest that the H  I-deficient galaxies on the outskirts of the Virgo cluster have not had their interstellar gas ram pressure stripped by the intracluster diffuse hot gas.

An alternative explanation to the presence on the outskirts of clusters of H  I-deficient spirals, as well as to the decreased star formation rates and redder colours of galaxies in these regions, relative to field galaxies, is that the three effects of H  I removal, decreased star formation and redder colours, all intimately linked, may be caused by a significant enhancement of massive groups of galaxies at the outskirts of clusters, as expected from the statistics of the primordial density field (Kaiser 1984) applied to small groups versus rich clusters (Mamon 1995). If this is the case, we would then expect a correlation between H  I-deficiency and X-ray emission from the intragroup gas. However, while tidal effects, which to first order depend on mean density, regardless of orbit eccentricity (Mamon 2000), are similar between less massive groups and more massive clusters, ram pressure stripping effects, which also depend on the squared velocity dispersion of the environment, will be much reduced in groups relative to clusters (e.g. Abadi et al. 1999).

In the companion paper (Sanchis et al. 2004), we consider different explanations to the origin of the H  I-deficiency of these outlying galaxies: 1) incorrect distances, so these objects would in fact lie close enough to the cluster core to be within the rebound radius and their gas could have been removed by ram pressure stripping, 2) incorrect estimation of the H  I-deficiencies and 3) tidal perturbations (stripping or heating) by nearby companions or within groups.

Acknowledgements

We wish to thank Stéphane Colombi, Yehuda Hoffman, and Ewa \Lokas for useful discussions, François Bouchet, Bruno Guiderdoni and coworkers for kindly providing us with their N-body simulations, and Jeremy Blaizot for answering our technical questions about the design and access to the simulations. We also thank an anonymous referee for helpful comments. TS acknowledges hospitality of the Institut d'Astrophysique de Paris where most of this work was done, and she and GAM acknowledge Ewa \Lokas for hosting them at the CAMK in Warsaw, where part of this work was also done. TS was supported by a fellowship of the Ministerio de Eduación, Cultura y Deporte of Spain.

   
Appendix A: Radius, time and density of turnaround in a flat $\Lambda $CDM cosmology

In this appendix, we compute the parameters of shells at turnaround, i.e. reaching their first apocenter, in a $\Lambda $CDM Universe without quintessence (wQ=-1).

In a non-quintessential Universe with a cosmological constant, the equation of motion of a shell of matter is

 \begin{displaymath}{{\rm d}^2 R\over {\rm d}t^2} = - {G M(R,t) \over R^2} + {\Lambda \over 3}~R \ , \end{displaymath} (A.1)

where the first term on the right hand side is the gravitational force and the second term is the repulsive effect of the cosmological constant $\Lambda $. A given shell of matter that first expands with the Universe and then turns around and collapses will begin to cross shells that have already settled in a structure only slightly before its own collapse. Therefore, during the expansion phase, there is no shell crossing and hence $M(R,t) = \hbox{cst}$.

The equation of motion can then be easily integrated to yield the energy equation

 \begin{displaymath}E = {1\over 2}~{\dot r}^2 - {GM\over r} - {1\over 6}~\Lambda... ... 2}~{\dot r_i}^2 - {GM\over r_i} - {1\over 6}~\Lambda~r_i^2 ~, \end{displaymath} (A.2)

where E is the energy per unit mass of the shell, and where the i subscript refers to a very early time ti, corresponding to redshift $z_i \gg 1$ (e.g. zi=1000). It is convenient to use the quantities

 \begin{displaymath}\Omega \equiv {8\pi G\rho \over 3~H^2} \ , \qquad \hbox{and}\qquad \lambda \equiv {\Lambda \over 3~H^2} \ , \end{displaymath} (A.3)

which represent the dimensionless mass density and dark energy of the Universe at any epoch, and we will use subscripts "0'' to denote the present epoch (z=0). In the case of a flat Universe ( $\Omega_0 + \lambda_0 = 1$), as confirmed with the WMAP CMB experiment by Spergel et al. (2003), mass and energy conservation applied to the Universe lead to (e.g. Richstone et al. 1992)

 \begin{displaymath}H_i^2 = H_0^2~\left [\Omega_0~(1+z_i)^3 + \lambda_0\right] . \end{displaymath} (A.4)

At time ti, the mass enclosed within radius ri is

 \begin{displaymath}M = {4~\pi\over 3}~\left (1+\delta_i \right) ~\Omega_i~\rho_{... ...\left (1+\delta_i \right) ~\Omega_i ~H_i^2 ~{r_i^3 \over G}\ , \end{displaymath} (A.5)

where $\delta_i$ is the relative overdensity within radius ri at time ti(normalized to the density of the Universe at that epoch), and where we made use of the critical density of the Universe at ti:

 \begin{displaymath}\rho_{\rm c,i} = {3~H_i^2\over 8~\pi~G} \cdot \end{displaymath} (A.6)

With a dimensionless radial growth factor u(r,t) = r/ri, the first energy equation can be expressed as

 \begin{displaymath}\dot u = H_i~\sqrt{{2~E \over H_i^2 r_i^2} + {(1+\delta_i)~\Omega_i\over u} + \lambda_i~u^2} \ , \end{displaymath} (A.7)

where we made use of Eqs. (A.2)-(A.5). The energy E of the shell is obtained by expressing Eq. (A.7) for the epoch ti, yielding

 \begin{displaymath}{2~E \over H_i^2 r_i^2} = {{\dot {u_i}}^2 \over H_i^2} - \left [(1+\delta_i)~\Omega_i + \lambda_i \right ] \ . \end{displaymath} (A.8)

The second equality of Eq. (A.3) yields
 
                              $\displaystyle \lambda_i$ = $\displaystyle \left ({H_0\over H_i}\right)^2~\lambda_0 = \left ({\Omega_0\over \lambda_0}~(1+z_i)^3+1 \right)^{-1}$  
  = $\displaystyle O \left((1+z_i)^{-3}\right) \ll 1 \ .$ (A.9)

Mass conservation amounts to a mean density of the Universe that varies as

 \begin{displaymath}\rho_i \equiv \rho(z_i) = \rho_0~(1+z_i)^3 \ , \end{displaymath} (A.10)

where $\rho_0$ is the present-day mass density of the Universe. This then yields
 
                            $\displaystyle \Omega_i$ = $\displaystyle \Omega_0~(1+z_i)^3~\left ({H_0\over H_i}\right)^2$  
  = $\displaystyle \left [1+{\lambda_0\over\Omega_0}~(1+z_i)^{-3} \right ]^{-1} = 1 - \lambda_i.$ (A.11)

Inserting Eqs. (A.8), (A.9) and (A.11) into Eq. (A.7) yields

 \begin{displaymath}\dot u = H_i ~\sqrt{{{\dot{u_i}}^2\over H_i^2} + {1+\delta_i-\lambda_i\over u} + \lambda_i~u^2 - (1+\delta_i)} \ , \end{displaymath} (A.12)

where we discarded terms in $o(\lambda_i)$. Now, as pointed out by Chodorowski (1988), Bartelmann et al. (1993) and Padmanabhan (1993), one should not assume that the initial flow is a pure Hubble flow ( $\dot u_i = H_i$), but incorporate the peculiar motion acquired before zi. Using the Zeldovich (1970) approximation, Chodorowski and Bartelmann et al. show that

 \begin{displaymath}\dot u_i = H_i~\left (1-{\delta_i \over 3} \right ) \cdot \end{displaymath} (A.13)

Inserting Eq. (A.13) into Eq. (A.12) and discarding high order terms in (1+zi)-1 and $\lambda_i$ - writing $\delta_i = O(1/(1+z_i)) = \delta_0/(1+z_i)$ - yields

 \begin{displaymath}\dot u = H_i~\sqrt{-{5\over 3}~\delta_i + {1\over u} + \lambda_i~u^2} \ . \end{displaymath} (A.14)

The turnaround radius is obtained by solving for $\dot u = 0$, i.e. solving

 \begin{displaymath}\lambda_i~u_{\rm ta}^3 - {5\over 3}~\delta_i~u_{\rm ta} + 1 = 0 \ \end{displaymath} (A.15)

for $u_{\rm ta}$. okas & Hoffman (2001) found the same solution without the 5/3 term, as their $\delta_i$refers to the total initial density, whereas our $\delta_i$ refers to the growing mode only. We can go further than okas & Hoffman by expressing and solving a cubic equation in terms of present-day quantities. With Eq. (A.9), Eq. (A.15) reduces to solving

 \begin{displaymath}{1-\Omega_0\over \Omega_0}~y_{\rm ta}^3 - {5\over 3}~\delta_0~y_{\rm ta} + 1 = 0 \end{displaymath} (A.16)

for $y_{\rm ta} = u_{\rm ta}/(1+z_i) = r_{\rm ta} / r_0 < 1$, where

 
r0 = ri (1+zi) (A.17)

is the comoving radius of the initial perturbation. The smallest real positive solution of the cubic Eq. (A.16) is
  
    $\displaystyle y_{\rm ta} = {2~\sqrt{5}\over 3}~ \sqrt{\delta_0~\Omega_0\over 1-\Omega_0}~\cos \left ({\phi+\pi\over3} \right ),$ (A.18)
    $\displaystyle \phi = \cos^{-1} \sqrt{{729\over 500}~\left [{\left(1-\Omega_0\right)/\Omega_0 \over \delta_0^3} \right ]},$ (A.19)

for $\delta_0 \geq 2^{1/3}~9/10 ~\left[\left(1-\Omega_0\right)/\Omega_0\right]^{1/3}$.

The time of turnaround is then obtained by integrating equation (A.14) and writing u = (1+zi) y, yielding

 \begin{displaymath}{H_i~T_{\rm ta} \over \left (1+z_i\right)^{3/2}} = \int_0^{y_... ...left [\left (1-\Omega_0\right)/ \Omega_0 \right ]~y^3}} \cdot \end{displaymath} (A.20)

The starting point of the integration is taken at 0 instead of 1/(1+zi), which corresponds to adding the negligible time between the t=0 and ti. With Eq. (A.4), Eq. (A.20) becomes

 \begin{displaymath}H_0~T_{\rm ta} = \int_0^{y_{\rm ta}} {\sqrt{y}\ {\rm d}y \ove... ...}~\delta_0~\Omega_0~y + \left (1-\Omega_0\right) ~y^3}} \cdot \end{displaymath} (A.21)

For $\Omega_0 = 1$, $\lambda_0 = 0$, we get $y_{\rm ta} = 3/(5~\delta_0)$, $H_0~T_{\rm ta} = (\pi/2)~[3/(5\delta_0)]^{3/2}$, so that a shell that collapses today, hence turns around at $H_0~T_{\rm ta} = H_0~t_0/2 = 1/3$, requires a linearly extrapolated density contrast of $\delta_0 = (3/5)~(3~\pi/2)^{2/3} = 1.686$, as expected.

References


Copyright ESO 2004