A&A 414, 223-233 (2004)
DOI: 10.1051/0004-6361:20034015
On the light echo in V838 Mon
R. Tylenda
N. Copernicus Astronomical Center, Department for Astrophysics,
Rabianska 8, 87-100 Torun, Poland
Received 26 June 2003 / Accepted 30 September 2003
Abstract
We present a theoretical outline of the light echo phenomenon and
results of simple numerical simulations and we study the available images of
the light echo in V838 Mon obtained with HST. An investigation of the observed
expansion of the light echo leads us to conclude that the distance to V838 Mon is
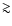 5 kpc. From an analysis of the inner bright echo rim we
estimate the distance to be
5 kpc. From an analysis of the inner bright echo rim we
estimate the distance to be
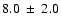 kpc.
We also investigate the structure of the dust distribution
in the vicinity of the object. We find no obvious signs of spherical symmetry
in the resultant distribution. Near the central object there is a strongly
asymmetric dust-free region which we interpret as produced by a fast wind
from the V838 Mon system. The asymmetry would imply that V838 Mon is
moving relative to the dusty medium. From these results we conclude
that the dust illuminated by the light echo is of interstellar origin rather
than produced by mass loss from V838 Mon in the past.
kpc.
We also investigate the structure of the dust distribution
in the vicinity of the object. We find no obvious signs of spherical symmetry
in the resultant distribution. Near the central object there is a strongly
asymmetric dust-free region which we interpret as produced by a fast wind
from the V838 Mon system. The asymmetry would imply that V838 Mon is
moving relative to the dusty medium. From these results we conclude
that the dust illuminated by the light echo is of interstellar origin rather
than produced by mass loss from V838 Mon in the past.
Key words: stars: individual: V838 Mon - stars: distances -
stars: circumstellar matter - ISM: reflection nebulae
V838 Mon was discovered in eruption in the beginning of
January 2002 (Brown 2002).
The main outburst, however, started at the beginning of
February 2002 and, in the optical, lasted for about two months (e.g. Munari
et al. 2002a). The nature of the eruption is enigmatic (e.g. Munari
et al. 2002a; Kimeswenger et al. 2002). It cannot be
accounted for by known thermonuclear events (classical nova, late He-shell
flash) and therefore new, as yet unexplored, mechanisms have been searched for
(Soker & Tylenda 2003; Retter & Marom 2003).
V838 Mon has recently received significant publicity, even in non-scientific
media, due to its light echo. This event was discovered shortly
after the main eruption in February 2002 (Henden et al. 2002).
However, the most spectacular images of the V838 Mon light echo
were provided later by HST (Bond et al. 2003).
The light echo is a rare event and can be observed when a light outburst
illuminates circumstellar or interstellar dust. So far it has primarily been
observed for extragalactic supernovae
(e.g. Crotts 1988; Xu et al. 1995; Schmidt et al. 1994;
Cappellaro et al. 2001; Sugerman & Crotts 2002). In our Galaxy this
phenomenon has been observed in Nova Persei 1901
(e.g. Couderc 1939).
Analyses of light echoes can be used while investigating supernova light curves
(e.g. Chevalier 1986). Observed evolution of the light echo arround
SN 1987A in LMC has enabled one to study the dust distribution
in front of the
supernova up to a distance of  1 kpc from the supernova
(see e.g. Xu et al. 1995).
Supernova light echoes can also be used to measure distances to galaxies
(Sparks 1994).
1 kpc from the supernova
(see e.g. Xu et al. 1995).
Supernova light echoes can also be used to measure distances to galaxies
(Sparks 1994).
Munari et al. (2002a) and Kimeswenger et al. (2002)
have attempted to use the observed expansion of the light echo arround
V838 Mon to measure the distance. Their calculations were based
on a naive interpretation of the light echo expansion (i.e. that it
expands at the velocity of light) and the derived values
of 0.6-0.8 kpc are in fact significant underestimates of the distance. A more
realistic analysis in Bond et al. (2003) gave a lower limit to the
distance of  6 kpc.
6 kpc.
In this paper we present an analysis of the available data on the light echo
in V838 Mon. After presenting theoretical considerations
and results of
simple simulations of light echoes (Sect. 2) we attempt to use the
observational data to constrain the distance to V838 Mon
(Sects. 3 and 4.2)
and to study the
dust distribution near the object (Sect. 4). The results are
summarized and discussed in Sect. 5.
2 Basic considerations and numerical simulations
Couderc (1939) was probably the first to give a correct explanation for the
light echo arcs observed arround Nova Persei 1901. More recently,
theoretical considerations on the light echo can be found in
papers devoted to supernova light echoes (e.g. Chevalier
1986; Sparks 1994).
The subject is however relatively unknown in the field of
stellar astrophysics. This is probably the reason why
in some papers oversimplified or even incorrect
interpretations of the V838 Mon light echo can be found. Therefore
we summarize
basic formulae describing the structure and evolution of the light echo.
We define a rectangular (x,y,z) coordinate system with
its origin being in the light source. The z axis is along the line of sight
toward the observer. The (x,y) plane is perpendicular to the z axis,
i.e. is a tangent to the sky sphere in the source. Let the source emits
short light flash at time t = 0. We assume the so-called single
scattering approximation, i.e. that photons are scattered only once in the
dusty medium surrounding the source.
Suppose that the scattered echo is seen
by the observer at a time t. Then the illuminated dust lies on a surface
defined by
where c is the velocity of light, d is the distance between the source and
the observer,
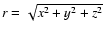 is the distance of the
scattering dust from the source, and
is the distance of the
scattering dust from the source, and
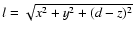 is the distance of the dust from the observer. Equation (1) is an
ellipsoid having foci in the source and the observer.
is the distance of the dust from the observer. Equation (1) is an
ellipsoid having foci in the source and the observer.
The considerations can be simplified when x and y are much smaller than d, i.e. when the observed angular dimensions of the echo are small.
Setting l = d - z Eq. (1) becomes
or equivalently
|
x2 + y2 = (ct)2 + 2zct.
|
(3) |
This is a paraboloid symmetric around the z axis (line of sight) and
having its focus in the source. In the
case of V838 Mon the echo has dimensions of order of
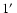 so
in this case the relative accuracy of Eqs. (2) and (3)
is better than 10-3.
so
in this case the relative accuracy of Eqs. (2) and (3)
is better than 10-3.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{parab.eps}
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg13.gif) |
Figure 1:
The light echo paraboloid (Eq. (3)) shown in the xz plane
for ct = 1 and ct = 2. The axes are in units of ct. The dot marks the
source position at
x = 0, z = 0. The observer is at
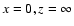 . . |
| Open with DEXTER |
Figure 1 shows Eq. (3) in the xz plane for ct = 1and ct = 2 (axes in the figure are in units of ct).
Several important conclusions can be drawn from Fig. 1.
If the source (at
x = 0, z = 0) produced a short flash of light at t = 0then at t = 1/c and t = 2/c the observer would see dust illuminated on
paraboloids ct = 1 and ct = 2, respectively. However, if the flash
started at t = 0 and lasted up to t = 1/c then at t = 1/c all dust
within the paraboloid ct = 1 would be illuminated for the observer.
At t = 2/c the illuminated dust would be between the paraboloids ct =1 and
ct = 2. Thus
contrary to naive considerations the echo does not expand
spherically starting from the source. It starts from the line of sight, i.e.
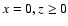 ,
and most effectively penetrates regions situated
in front of the source. Behind the source the penetration is slowest.
,
and most effectively penetrates regions situated
in front of the source. Behind the source the penetration is slowest.
The observed echo is in the (x,y) plane and its structure and evolution
depends on the dust distribution around the source.
An important conclusion drawn from Fig. 1 is that
if the observed echo has a well defined outer edge (as observed in the case of
V838 Mon) the dusty medium around the source has to have a rather well
defined outer boundary in front of the source.
In order to illustrate
dependence of the light echo structure and evolution on the dust
distribution let us consider two simple dust geometries,
i.e. a plane-parallel slab and a spherical shell centred on the source.
2.1 Plane-parallel dust slab
Let us assume that a thin plane-parallel slab of dust intersects the line of sight
at z0 and that the normal to the slab is inclined to the z axis
at an angle 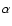 .
Let us also assume, for simplicity, that the normal lies in
the (x,z) plane. The slab is then described by
.
Let us also assume, for simplicity, that the normal lies in
the (x,z) plane. The slab is then described by
where
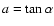 .
Equation (4), when used to eliminate z from
Eq. (3), gives the echo shape as follows
.
Equation (4), when used to eliminate z from
Eq. (3), gives the echo shape as follows
|
x2 + y2 = (ct)2 + 2z0ct - 2axct.
|
(5) |
Thus the echo is in the shape of a ring whose radius, 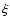 ,
is
given by
,
is
given by
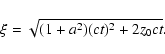 |
(6) |
The ring is centred at
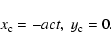 |
(7) |
The velocity of expansion of the echo ring, v, is
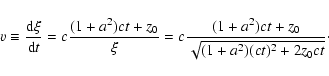 |
(8) |
An analysis of
Eqs. (6)-(8) leads to the following
conclusions.
The echo ring is centred on the
source only if the dust slab is perpendicular to the line of sight.
In almost all the cases the echo expansion is superluminal.
Only if z0 = 0 and a = 0 the echo expands at c.
For z0 > 0 (the slab in front of the source) the echo appears at the same
time as the
source flash, i.e. at t = 0. It starts expanding from the source position,
i.e. from
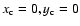 .
For z0 < 0 (the slab behind the source)
the echo appears with a time delay relative to the source flash,
i.e. it starts at
t = (-2z0)/((1+a2)c). In this case it begins expanding
from the position
.
For z0 < 0 (the slab behind the source)
the echo appears with a time delay relative to the source flash,
i.e. it starts at
t = (-2z0)/((1+a2)c). In this case it begins expanding
from the position
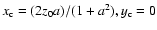 .
In both cases the expansion velocity is
.
In both cases the expansion velocity is 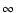 at the moment of the echo
appearance, i.e. at t = 0 if z0 > 0 and at
t = (-2z0)/((1+a2)c)if z0 < 0. It decreases asymptotically to
at the moment of the echo
appearance, i.e. at t = 0 if z0 > 0 and at
t = (-2z0)/((1+a2)c)if z0 < 0. It decreases asymptotically to
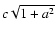 when
when
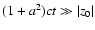 .
For slabs non-perpendicular to the line of sight,
i.e. when
.
For slabs non-perpendicular to the line of sight,
i.e. when 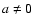 ,
the echo centre moves away from the source at a constant
velocity of |a|c. The direction of this movement is opposite to the
direction of the slab normal projected on the sky surface.
,
the echo centre moves away from the source at a constant
velocity of |a|c. The direction of this movement is opposite to the
direction of the slab normal projected on the sky surface.
2.2 Spherical dust shell
Let us assume that a thin spherically symmetric shell of dust having
a radius, r0, is centred on the source, so it is described by
This when used to eliminate z from Eq. (3) gives
|
x2 + y2 = 2r0ct - (ct)2.
|
(10) |
Thus the echo is in the shape of a ring with the radius, 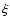 ,
given by
,
given by
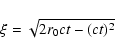 |
(11) |
and centred on the source (
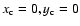 ).
The echo expansion velocity, v, is
).
The echo expansion velocity, v, is
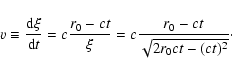 |
(12) |
As can be seen from Eq. (11), the echo radius
starts from zero at t = 0, reaches a maximum equal to r0at t = r0/c, and collapses to zero at
t = 2r0/c.
Note that in a coordinate system (
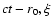 )
Eq. (11) describes a circle centred on the origin and having
the radius equal to r0.
The expansion velocity of the echo ring starts from
)
Eq. (11) describes a circle centred on the origin and having
the radius equal to r0.
The expansion velocity of the echo ring starts from 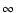 at
t = 0, decreases and reaches zero at t = r0/c, and continues decreasing to
at
t = 0, decreases and reaches zero at t = r0/c, and continues decreasing to
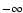 at
t = 2r0/c.
at
t = 2r0/c.
To illustrate the evolution of the echo in different geometries of
the dust distribution we have performed simple numerical simulations based
on the theoretical considerations outlined above. The
structure of the light echo has been determined in the paraboloid
approximation, i.e. using Eq. (3), and adopting the single
scattering approximation.
If the
central source radiates at a luminosity, 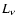 ,
the intensity,
,
the intensity, 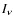 ,
of
the radiation scattered at a point (x,y,z)
can be calculated from
,
of
the radiation scattered at a point (x,y,z)
can be calculated from
 |
(13) |
where
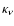 is the scattering coefficient which is usually
written in the form (e.g. Chevalier 1986)
is the scattering coefficient which is usually
written in the form (e.g. Chevalier 1986)
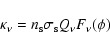 |
(14) |
where 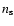 is the number density of scattering particles,
is the number density of scattering particles,
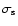 is the
particle cross section,
is the
particle cross section, 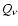 is the scattering efficiency (albedo),
is the scattering efficiency (albedo),
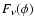 is the scattering phase function for the scattering angle
is the scattering phase function for the scattering angle 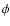 defined as
defined as
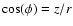 .
Integrating Eq. (13)
along the z axis over the dusty medium
gives the echo surface brightness, in units of flux per unit solid angle,
at any given time.
.
Integrating Eq. (13)
along the z axis over the dusty medium
gives the echo surface brightness, in units of flux per unit solid angle,
at any given time.
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{sheet50.eps} \includegrap...
....5cm]{sheet400.eps} \includegraphics[width=5.5cm]{sheet500.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg42.gif) |
Figure 2:
The evolution of the echo structure produced by four dust slabs
perpendicular to the line of sight at the z positions of
-0.10, 0.00, 0.30, and 1.00 pc. The source (not shown in the
figure but lying in the centre of each image) has experienced a
50 days long flash of constant luminosity. All the slabs have the same
thickness of 0.02 pc and the same value (constant within the
slabs) of the scattering coefficient
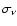 .
The object is
assumed to be observed from a distance of 5 kpc. The images are
ordered from upper-left to lower-right and correspond to the time
epochs of 50, 150, 250, 300, 400, and 500 days after the beginning
of the source flash. The axes of the images are in arcsec.
The grey scale is logarithmic and is normalized to the
brightest region in the figure.
The brightest centre of the first image and the faintest
outer ring in the last images span .
The object is
assumed to be observed from a distance of 5 kpc. The images are
ordered from upper-left to lower-right and correspond to the time
epochs of 50, 150, 250, 300, 400, and 500 days after the beginning
of the source flash. The axes of the images are in arcsec.
The grey scale is logarithmic and is normalized to the
brightest region in the figure.
The brightest centre of the first image and the faintest
outer ring in the last images span  4 orders of magnitude in
the surface brightness. 4 orders of magnitude in
the surface brightness. |
| Open with DEXTER |
The simulations have been done for two simple
geometries of the dust distribution, i.e. plane-parallel slabs and
concentring shells. In all cases it has been assumed that dust is uniformly
distributed, i.e.
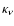 = const., in slabs or shells and that
scattering is isotropic, i.e.
= const., in slabs or shells and that
scattering is isotropic, i.e.
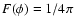 .
Note that the simulations
adopt very simple scenarios and have not been meant to mimic the situation
observed in V838 Mon, although parameters like times and distances are of
the order of those seen or expected in this particular case.
.
Note that the simulations
adopt very simple scenarios and have not been meant to mimic the situation
observed in V838 Mon, although parameters like times and distances are of
the order of those seen or expected in this particular case.
Figure 2 presents the simulated evolution of the echo structure
from a model in which dust is distributed in four
plane-parallel slabs perpendicular to the z axis. The z0 positions of the
slabs are -0.10, 0.00, 0.30, and 1.00 pc. The slab thickness,
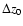 ,
is the
same in all cases and is equal to 0.02 pc.
,
is the
same in all cases and is equal to 0.02 pc. 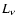 has been adopted to
be constant during the source flash which lasted
has been adopted to
be constant during the source flash which lasted
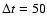 days
(otherwise
days
(otherwise 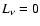 ).
Figure 2 shows the echo structure as observed from a
distance of 5 kpc at 50, 150, 250, 300, 400, and 500 days
after the beginning of the flash. The grey scale is logarithmic and it has
been normalized to the maximum surface brightness in the images. Between the
brightest centre of the first image and the faintest outer ring in the last
image there is a span of 4 orders of magnitude in the surface brightness.
).
Figure 2 shows the echo structure as observed from a
distance of 5 kpc at 50, 150, 250, 300, 400, and 500 days
after the beginning of the flash. The grey scale is logarithmic and it has
been normalized to the maximum surface brightness in the images. Between the
brightest centre of the first image and the faintest outer ring in the last
image there is a span of 4 orders of magnitude in the surface brightness.
The first image in Fig. 2 shows the echo just at the end of the
source flash. According to the discussion of Fig. 1 all dust
being within the paraboloid defined by the time elapsed since the beginning
of the flash, is illuminated. Thus the echo is composed of three filled
circles produced by three slabs having
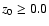 (the fourth slab at
z0 = -0.1 pc is not seen as it has not yet been reached by the light
paraboloid). Later on the illuminated dust is situated between
two paraboloids,
i.e. the first one corresponding to the begining of the flash
and the second one defined by the epoch of the flash end.
Thus in the second image, taken 100 days after the end of the flash, the echo
consists of three rings. The slab at
z0 = -0.10 pc
is reached by the first paraboloid at
(the fourth slab at
z0 = -0.1 pc is not seen as it has not yet been reached by the light
paraboloid). Later on the illuminated dust is situated between
two paraboloids,
i.e. the first one corresponding to the begining of the flash
and the second one defined by the epoch of the flash end.
Thus in the second image, taken 100 days after the end of the flash, the echo
consists of three rings. The slab at
z0 = -0.10 pc
is reached by the first paraboloid at
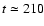 days, whereas the
second paraboloid starts leaving it at
days, whereas the
second paraboloid starts leaving it at
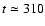 days. Therefore this
slab is seen in the form of a central disc in the third and fourth image.
Later on it produces the innermost ring in the image.
days. Therefore this
slab is seen in the form of a central disc in the third and fourth image.
Later on it produces the innermost ring in the image.
As can be
seen from Fig. 2 the surface brightness of the rings decreases
with time but the rate of fading depends on z0.
The reason for the fading is, of course, the increasing geometric dilution.
For a thin slab
the surface brightness of the scattered radiation,
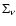 ,
is just
,
is just
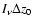 .
Thus, in general case, using Eqs. (13),
(2) and (4) one finds
.
Thus, in general case, using Eqs. (13),
(2) and (4) one finds
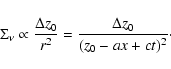 |
(15) |
Consequently, in our simulations the
surface brightness in the ring corresponding to z0 = 0.0 decreases by
factor  500 between the first image and the last one in
Fig. 2, while the same drop in the case of the outermost ring
(
z0 = 1.00 pc) is only factor
500 between the first image and the last one in
Fig. 2, while the same drop in the case of the outermost ring
(
z0 = 1.00 pc) is only factor  2. With time the echo rings would
continue expanding with the velocity aproaching c according to
Eq. (8) and the surface brightness decreasing as
described by Eq. (15).
2. With time the echo rings would
continue expanding with the velocity aproaching c according to
Eq. (8) and the surface brightness decreasing as
described by Eq. (15).
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{spher50.eps} \includegrap...
...5cm]{spher600.eps} \includegraphics[width=5.5cm]{spher750.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg53.gif) |
Figure 3:
The same as Fig. 2 but for three spherical shell of
dust centred on the source. The shells have the same thickness
of 0.02 pc and radii of 0.10, 0.30, and 1.00 pc. The images shows
the echo as observed 50, 150, 250, 400, 600, and
750 days after the beginning of the source flash.
The brightest and the faintest regions in the figure span
 2.5 orders of magnitude in the surface brightness. 2.5 orders of magnitude in the surface brightness. |
| Open with DEXTER |
Figure 3 shows the evolution of the echo structure produced by
three spherically symmetric dust shells centred on the source. The radii of
the shells, r0, are 0.10, 0.30, and 1.00 pc. All shells have the same
thickness
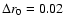 pc.
As in the previous case the source flash has lasted
pc.
As in the previous case the source flash has lasted
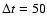 days and the object is observed from a distance of 5 kpc. The
consecutive images correspond to the epochs of 50, 150, 250, 400, 600, and
750 days after the beginning of the source flash.
days and the object is observed from a distance of 5 kpc. The
consecutive images correspond to the epochs of 50, 150, 250, 400, 600, and
750 days after the beginning of the source flash.
As in Fig. 2 the first image in Fig. 3 corresponds to
the end of the source flash and all the dust within the light paraboloid
produced by the beginning of the flash is illuminated. The echo is thus
composed of three filled circles produced by illuminated sections of the
corresponding shells. The echo components initially expand superluminally.
However, as discussed in Sect. 2.2, the expansion rate of an echo
produced by a shell slows down to 0 when reaching the maximum radius equal to
the value of r0. For
the shells in our simulations, i.e. having r0 = 0.1, 0.3, and 1.0 pc,
it happens at
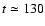 ,
370, and 1200 days, respectively.
After this, the echo ring starts shrinking and finally disappears as a
fast collapsing disc. In our simulations the echoes due to the shells
having r0 = 0.1, 0.3, and 1.0 pc disappear at t = 310, 790, and
2450 days, respectively. The echo from the innermost shell is
close to its maximum radius in the second image of Fig. 3
whereas in the third image it is collapsing.
The echo from the shell having r0 = 0.3 pc is
near its maximum radius in the fourth image whereas its collapse is
observed in the last two images.
,
370, and 1200 days, respectively.
After this, the echo ring starts shrinking and finally disappears as a
fast collapsing disc. In our simulations the echoes due to the shells
having r0 = 0.1, 0.3, and 1.0 pc disappear at t = 310, 790, and
2450 days, respectively. The echo from the innermost shell is
close to its maximum radius in the second image of Fig. 3
whereas in the third image it is collapsing.
The echo from the shell having r0 = 0.3 pc is
near its maximum radius in the fourth image whereas its collapse is
observed in the last two images.
The echo rings in our simulations
reach maximum surface brightness at the maximum radius, i.e. at
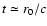 .
At this time
.
At this time
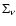 is about twice as high as in the begining of the echo
evolution, i.e. at
is about twice as high as in the begining of the echo
evolution, i.e. at
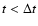 .
In general case, however, the evolution
of
.
In general case, however, the evolution
of
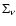 depends on the ratio of
depends on the ratio of
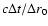 .
To show this let us consider a short flash, i.e.
.
To show this let us consider a short flash, i.e.
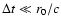 ,
illuminating a thin shell,
i.e.
,
illuminating a thin shell,
i.e.
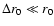 .
It is quite straightforward to show from simple geometric considerations
and Eq. (2) that the light echo
illuminates a constant part of the shell
equal to
.
It is quite straightforward to show from simple geometric considerations
and Eq. (2) that the light echo
illuminates a constant part of the shell
equal to
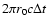 .
Thus the total flux scattered by the shell
is also constant with time and proportional to
.
Thus the total flux scattered by the shell
is also constant with time and proportional to
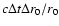 .
From Eq. (11) one can calculate the echo radii corresponding
to possible combinations of t and
.
From Eq. (11) one can calculate the echo radii corresponding
to possible combinations of t and
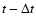 with
with
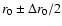 .
Taking extreme radii as the boundaries of the echo ring
and retaining only linear terms of
.
Taking extreme radii as the boundaries of the echo ring
and retaining only linear terms of
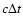 and
and
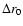 one gets that the surface of the echo ring is equal to
one gets that the surface of the echo ring is equal to
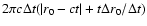 .
Consequently the surface brightness of the echo varies as
.
Consequently the surface brightness of the echo varies as
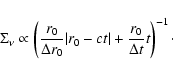 |
(16) |
As can be seen from Eq. (16), in the begining of the echo evolution,
i.e. at t = 0,
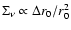 .
Near the maximum echo radius, i.e. at t = r0/c,
.
Near the maximum echo radius, i.e. at t = r0/c,
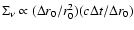 .
At the end, i.e. at
t = 2r0/c,
.
At the end, i.e. at
t = 2r0/c,
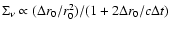 .
Between these extreme time moments the surface brightness evolves
monotonically. For
.
Between these extreme time moments the surface brightness evolves
monotonically. For
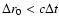 the maximum surface brightness
occurs at the maximum radius, i.e. at t = r0/c. This is the case of our
simulations where
the maximum surface brightness
occurs at the maximum radius, i.e. at t = r0/c. This is the case of our
simulations where
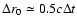 .
If, however,
.
If, however,
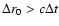 the maximum surface brightness takes
place at t = 0. The surface brightness is lowest at the end of
the echo, i.e. at
t = 2r0/c.
the maximum surface brightness takes
place at t = 0. The surface brightness is lowest at the end of
the echo, i.e. at
t = 2r0/c.
The above considerations, although done for simplified cases,
demonstrate that long term observations of the evolution of the echo
structure can provide information on the dust distribution and thus,
indirectly, also on the origin of the dust producing the echo. If dust
results from a past mass loss from the central object it would tend to
show certain symmetries in its distribution around the source. Usually mass loss is
not continuous at a constant rate but it takes place in the form of more or less
periodic fluctuations of the mass loss rate, e.g. during the AGB phase,
or discrete events of strong mass loss separated by longer periods of
quiescence, e.g. in nova-like outbursts. Then the dust distribution would show
a succession of shell-like structures or be in the form of a more or less defined
envelope. The evolution of the light echo in such circumstances would follow
the general patterns discussed in Sect. 2.2 and Fig. 3.
The initially fast expansion, slowing down when reaching maximum sizes corresponding
to outer edges of the dust shells or envelope, would be followed by an accelerated
collapse.
If, however, dust is not related to the source and is rather of
interstellar nature, no obvious symmetry with respect to the light source is
expected. Instead dust would rather be confined in
extended sheets, zones or filaments and our considerations of
plane-parallel slab
geometries in Sect. 2.1 and Fig. 2 would be more
appropriate. The echo would expand more and more with slowly decreasing
brightness as more and more distant regions are illuminated.
Note that for studying the general character of the dust distribution around
the source the echo has to be observed for a long enough time.
The initial evolution of the echo produced by spherical dust shells is
similar to that due to slabs. The light paraboloid is close to the line
of sight so the echo does not feel differences in the general shape of the
dust distribution. This can be seen from Eqs. (6) and
(11) which reduce to the same form if
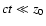 and
and
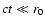 ,
respectively.
Therefore the first image in Fig. 3 is
not much different from that in Fig. 2 (the reason why the
innermost (brightest) disc in Fig. 2 is significantly smaller
than the corresponding one in Fig. 3 is that in the former case it
is produced by the slab at z0 = 0.0 whereas in the latter case the shell
has r0 = 0.1 pc). Later on, when ct is not any more negligible with
respect to z0 and r0, the two geometries can be better disentangled
from the echo evolution.
,
respectively.
Therefore the first image in Fig. 3 is
not much different from that in Fig. 2 (the reason why the
innermost (brightest) disc in Fig. 2 is significantly smaller
than the corresponding one in Fig. 3 is that in the former case it
is produced by the slab at z0 = 0.0 whereas in the latter case the shell
has r0 = 0.1 pc). Later on, when ct is not any more negligible with
respect to z0 and r0, the two geometries can be better disentangled
from the echo evolution.
3 Distance to V838 Mon constrained from the echo expansion
An analysis of the light echo evolution can be used to estimate the
distance to the object. An attempt to derive the distance to V838 Mon has
been done by Bond et al. (2003), who measured expansion rates in
ring-like structures in the echo from two consecutive images and found
that the distance is greater than 2 kpc. Note, however, that this estimate
assumed that the ring-like structures were produced by concentric shells
which is not justified, as discussed below.
The same authors have also applied the observed
polarization structure of the echo, as
proposed by Sparks (1994), which led them to conclude that the lower
limit to the distance is  6 kpc.
6 kpc.
We have attempted to put constraints on the distance to V838 Mon by
measuring the outer echo edge expansion. As it is clear from the
considerations in Sect. 2 the outer edge of the echo is produced
by the beginning of the light flash reflected at the outermost edge of the dust
distribution in front of the source.
For the plane slab geometry
Eq. (6) when combined with Eq. (7) can be rewritten as
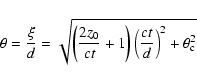 |
(17) |
where d is the distance to
the object, 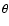 is the angular radius of the echo, and
is the angular radius of the echo, and
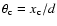 is the
angular distance of the echo centre from the source.
At early epochs, i.e. when
is the
angular distance of the echo centre from the source.
At early epochs, i.e. when
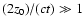 ,
Eq. (17) allows to determine only the value of z0/d2.
Thus unless z0 is known the distance cannot be determined. However, in
later epochs, when
,
Eq. (17) allows to determine only the value of z0/d2.
Thus unless z0 is known the distance cannot be determined. However, in
later epochs, when
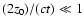 ,
Eq. (17) can be
used to derive d from the observed values of
,
Eq. (17) can be
used to derive d from the observed values of 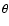 and
and
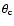 .
.
In the case of the spherical symmetry Eq. (11) can be rewritten as
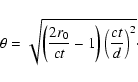 |
(18) |
Thus, not only in early phases (fast initial expansion) but also in late
phases (final collapse) the distance cannot be determined unless the value
of r0 is known. Only near the maximum size of the echo, i.e. when
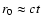 ,
Eq. (18) can give a direct estimate of
the distance.
,
Eq. (18) can give a direct estimate of
the distance.
In a real case, such as the one of V838 Mon,
we do not know a priori what is the
distance of the outer edge of dust from the source nor
what is the geometry of this edge. The distance of the scattering dust
could, in principle, be constrained from an analysis of the echo surface
brightness as the amount of the radiation scattered depends on the distance
squared (Eq. (13)). This, however, requires
calibrated data which are not available to the author.
Thus the only way is to look at the observed evolution of the echo radius
and try to fit it with Eq. (17)
or Eq. (18).
For this purpose we have measured the positions of the outer edge of the
light echo of V838 Mon in five images obtained by H.E. Bond and available
on the HST web site (http://hubblesite.org/newscenter/archive/2003/10/, see also Bond et al. 2003). They have been taken on April 30,
May 20, September 2, October 28, and
December 17, 2002. In each image the positions of
typically 60-70 points at the outer edge of the echo
(more or less equally spaced in the azimuthal angle) have been measured.
In most cases the outer echo edge is quite well defined and can be rather
easily measured. However,
in some instances, mostly in south-eastern directions,
the edge is broken or composed of incomplete arcs. This introduces certain
ambiguity in measurements and uncertainties in the results.
Note that all the measurements (also those reported in the next section)
have been done on negatives of the published images as the emission
edges and other details in the light echo are then more easily seen.
The positions have been determined in the coordinate system centred on
V838 Mon with the x and y axes pointing to west and north, respectively.
Then a circle has been fitted to the measured positions in each image using
the 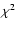 minimum method.
The results are presented in Table 1. First column
shows the time of observations,
minimum method.
The results are presented in Table 1. First column
shows the time of observations,
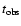 ,
given in days since January 1, 2002.
The radius of the echo,
,
given in days since January 1, 2002.
The radius of the echo, 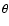 ,
and its uncertainty
are given in the next column. The last
two columns show the position of the centre of the fitted circle relative
to the central star. All the results are in arcsec.
,
and its uncertainty
are given in the next column. The last
two columns show the position of the centre of the fitted circle relative
to the central star. All the results are in arcsec.
Table 1:
Results of fitting a circle to the outer edge of the light echo of
V838 Mon. Time of observations,
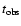 ,
is in days since January 1, 2002. Results are in arcsec.
,
is in days since January 1, 2002. Results are in arcsec.
In order to make a quantitative analysis of the results in
Table 1, it is necessary to determine
the time moment of the zero age of the echo t0.
The echo has been discovered in mid-February 2002 (Henden et al.
2002) and it has been suggested that it results from
the main outburst, which started at the beginning of February 2002
(Munari et al. 2002a; Bond et al. 2003).
This is supported by the fact that in the HST images the outer echo rim is blue and
it was at the beginning of the main outburst when the star was bluest (see
e.g. Bond et al. 2003). The main outburst started on February 1 and
the maximum was reached on February 5-6 (Munari et al. 2002a;
Bond et al. 2003). Thus we adopt February 3 as the date of the zero age
of the echo, i.e. t0 = 34 days (since Jan. 1, 2002).
As can be seen from Table 1, the centre of the echo migrates
from the central star. The migration keeps more or less the same direction
and the distance between the echo centre and the star
increases roughly linearly with time since the zero age.
This is what is expected from the plane geometry of the dust
distribution (see Eq. (7)). It cannot be reconciled with a
spherically symmetric distribution. Thus
the shape of the outer edge of dust in front of the star can be approximated
by a plane inclined to the line of sight rather then a sphere centred on the star.
A linear fit to the observed evolution of the distance of the echo centre
from the star as given in Table 1 results in a relation
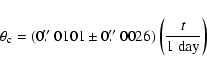 |
(19) |
where
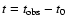 is the time since the zero age of the echo.
This with Eq. (7) allows to derive the inclination of
the dust surface to the line of sight, i.e.
is the time since the zero age of the echo.
This with Eq. (7) allows to derive the inclination of
the dust surface to the line of sight, i.e.
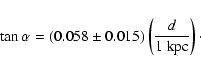 |
(20) |
Unfortunately the distance cannot be determined with a satisfactory accuracy
(see below). Adopting d = 5 kpc one obtaines
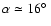 whereas for d = 10 kpc Eq. (20) gives
whereas for d = 10 kpc Eq. (20) gives
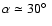 .
Note that the azimuthal angle of the normal to the dust surface is opposite
(i.e.
.
Note that the azimuthal angle of the normal to the dust surface is opposite
(i.e.
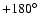 )
to that of the echo centre.
)
to that of the echo centre.
A least square fit of Eq. (17) to the observed values of
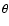 in Table 1 gives the best fit for
in Table 1 gives the best fit for
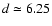 kpc
and
kpc
and
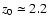 pc. However the
pc. However the 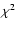 minimum is rather shallow and
extended along a
minimum is rather shallow and
extended along a
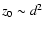 relation.
From a 90% confidence level on the (d,z0) plane we can only state that
the lower limit to the distance is
relation.
From a 90% confidence level on the (d,z0) plane we can only state that
the lower limit to the distance is  2.9 kpc.
2.9 kpc.
Clearly we are well before the phase when the distance can be unambigiously
determined, i.e. when
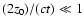 .
The large
uncertainty in our distance estimate is also due to uncertainties
in the observed values of the echo radius, as given in Table 1.
They are simply due to the fact that the echo edge is not ideally
reproduced by a circle. Evidently the outer edge of the dust distribution in
front of V838 Mon is not a perfect plane.
.
The large
uncertainty in our distance estimate is also due to uncertainties
in the observed values of the echo radius, as given in Table 1.
They are simply due to the fact that the echo edge is not ideally
reproduced by a circle. Evidently the outer edge of the dust distribution in
front of V838 Mon is not a perfect plane.
Table 2:
Results of fitting a circle centred on the star to the north-west
quadrant (x>0, y>0) of the outer edge of the light echo of
V838 Mon. Time of observations,
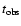 ,
is in days since January 1, 2002. Results are in arcsec.
,
is in days since January 1, 2002. Results are in arcsec.
We have found, however, that in the north-west quadrant, i.e. for x > 0 and
y > 0, the echo edge is quite well defined and its shape can be well
reproduced by a circle centred on the star. This, following the discussion
in Sect. 2, implies that the dust edge
is here either perpendicular to the line of sight or forms a partial sphere
centred on the star. As we shall see below in this paper
the former possibility is more consistent with the data.
The results of a least square
fit of a circle centred on the star to the observed echo rim in the
north-west quadrant are given in Table 2. As can be seen from
Table 2 the fit is significantly better
than that in Table 1.
A least square fit of Eq. (17) to the data
in Table 2 gives the best fit for
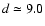 kpc
and
kpc
and
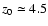 pc.
Although the 90% confidence region is now more confined
than in the previous case, the uncertainty in the distance is still
large. All what can be said is that the distance to V838 Mon is greater
than
pc.
Although the 90% confidence region is now more confined
than in the previous case, the uncertainty in the distance is still
large. All what can be said is that the distance to V838 Mon is greater
than  4.8 kpc.
4.8 kpc.
An attempt to fit a sphere, i.e. Eq. (18), to the data in
Table 2 has given less consistent results.
The 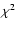 test was unable to find a
minimum. It gives acceptable fits starting from
test was unable to find a
minimum. It gives acceptable fits starting from
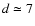 kpc but
finds better and better fits for increasing distances, well beyond
reasonable limits. Clearly the test "prefers'' the situation in which the
sphere section illuminated by the echo is closer and closer to a plane. This
suggests that the constant z model better approximates the outer edge of
dust in the north-west quadrant of the V838 Mon echo than the spherical
model.
kpc but
finds better and better fits for increasing distances, well beyond
reasonable limits. Clearly the test "prefers'' the situation in which the
sphere section illuminated by the echo is closer and closer to a plane. This
suggests that the constant z model better approximates the outer edge of
dust in the north-west quadrant of the V838 Mon echo than the spherical
model.
4 Structure of the dust region near V838 Mon
The structure of the light echo observed in V838 Mon is rather complex
especially in the last three images. This obviously reflects the complex
distribution of the circumstellar dust. We have attempted to study
this distribution from an analysis of the available images. Of course only
dust illuminated by the light echo can be studied which limits
the analysis mainly to the regions lying in front of V838 Mon.
The results referring to the global dust distribution are presented in
Sect. 4.1; Sect. 4.2 analyses the structure of the
dust-free region arround the central object.
4.1 Dust distribution
In the available echo images, apart from the outer edge, one can also
distinguish emission edges inside the echo. These edges are usually
either blue or red in colour. From the light curve of V838 Mon it is clear
that the object was bluest at the beginning of the outburst (beginning of
February 2002) while during the fading (mid-April 2002) it was extremely
red (Munari et al. 2002a; Bond et al. 2003).
Suppose that the paraboloids ct = 2 and ct = 1 in Fig. 1
correspond to the blue beginning and the red end of the light flash,
respectively. Suppose also that, say, between z = 5 and z = 10 there is
a dust layer. Then the observer would see an echo ring whose outer edge
would be blue and would correspond to the intersection of z = 10 with
ct = 2, while the inner edge would be red and would correspond to
the intersection of z = 5 with ct = 1. Thus measurements of the positions
of the blue and red edges in the light echo of V838 Mon can be used to estimate
positions of the boundaries of dust layers producing bright regions in the
echo.
We have measured, apart from the outer edge discussed in
Sect. 3, positions of blue and red edges inside the echo
images. This concerns primarily the images taken on Sep. 2, Oct. 28 and
Dec. 17 showing several well defined details in the echo structure. In the
image from May 20 only the inner red edge has been measured (apart from the
outer blue edge). On Apr. 30 only a B image was taken so no (inner) red edge
can be identified. Following the above considerations we assume that the blue
edges are produced by the beginning of the outburst so, as discussed in
Sect. 3, they correspond to the light paraboloid with t0 = 34 days.
From the I curve in Bond et al. (2003) it can be found that near
Apr. 17 V838 Mon declined by factor 2 from its last peak. Therefore we
assume that the red edges in the light echo correspond to the paraboloid with
t0 = 107 days.
Knowing x and y from measurements of an edge in
the echo observed at a given time, t,
one can calculate the z coordinate of the dust edge from
Eq. (3). Obviously we measure only the angular values of x and y so in order to have their absolute values we have to assume the distance.
Following
the analysis done later on in Sect. 4.2
we assume that V838 Mon is at a distance of 8 kpc.
![\begin{figure}
\par\mbox{\includegraphics[width=4.9cm,clip]{d_str_a.eps}\hspace*...
...}\hspace*{5mm}
\includegraphics[width=4.9cm,clip]{d_str_c.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg118.gif) |
Figure 4:
Structure of the dust distribution illuminated by the lihgt echo
of V838 Mon. In all the images the
ordinate is the z axis. The abscissa, x', is inclined to the x
(east-west) axis at an angle, 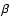 ,
(clockwise in respect to the x axis)
given in the bottom-left corner of each image. Only the points having the
position angle within ,
(clockwise in respect to the x axis)
given in the bottom-left corner of each image. Only the points having the
position angle within
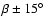 are shown in each image. Open and full
symbols correspond to upper and lower (in the z coordinate) boundaries of
the dusty regions, respectively. Thin curves show the echo paraboloids
(with t0 = 34 days) on Apr. 30 and Dec. 17.
The position of the central star is shown by an asterisk.
are shown in each image. Open and full
symbols correspond to upper and lower (in the z coordinate) boundaries of
the dusty regions, respectively. Thin curves show the echo paraboloids
(with t0 = 34 days) on Apr. 30 and Dec. 17.
The position of the central star is shown by an asterisk. |
| Open with DEXTER |
The results on the dust structure are
presented in Fig. 4. It shows three cuts across the three
dimensional distribution of the dust boundaries inferred from the measurements of
the blue (open points) and red (full points) edges in the light echo.
The
plane of each panel of Fig. 4 goes through the z axis and is
inclined to the x (east-west) axis at an angle, 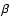 ,
(counted clockwise
from the x axis) given in the bottom-left corner of each part of the
figure. Only the points having an
azimuthal angle within
,
(counted clockwise
from the x axis) given in the bottom-left corner of each part of the
figure. Only the points having an
azimuthal angle within
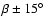 are shown.
The scale of the axes is in parsecs.
Thin curves show the echo blue paraboloids
(with t0 = 34 days) on Apr. 30 and Dec. 17. Thus, in principle, we can study
only the dust distribution between these two paraboloids. The exception is the
inner red edge on May 20 whose (red) paraboloid lies within the (blue)
paraboloid on Apr. 30. Dust is present above the full and below the open symbols
(it is absent above the open and below the full points).
are shown.
The scale of the axes is in parsecs.
Thin curves show the echo blue paraboloids
(with t0 = 34 days) on Apr. 30 and Dec. 17. Thus, in principle, we can study
only the dust distribution between these two paraboloids. The exception is the
inner red edge on May 20 whose (red) paraboloid lies within the (blue)
paraboloid on Apr. 30. Dust is present above the full and below the open symbols
(it is absent above the open and below the full points).
The cuts shown in Fig. 4 have been chosen so as to show the
global distribution of dust. They are more or less equally spaced in the
azimuthal angle 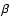 but they also avoid too detailed structures which
would make the discussion too complicated and less clear. We recommend
consulting the original echo images
(e.g. at http://hubblesite.org/newscenter/archive/2003/10/) for an easier
understanding of the discussion below.
but they also avoid too detailed structures which
would make the discussion too complicated and less clear. We recommend
consulting the original echo images
(e.g. at http://hubblesite.org/newscenter/archive/2003/10/) for an easier
understanding of the discussion below.
Figure 4a shows the cut done close to
the south-north direction. It goes more or less across the major axis
of the central hole in the echo images. In the southern part
(x' < 0 in Fig. 4a) dust
extends from the inner boundary which lies very close to ( 0.15 pc from)
the central object up to
0.15 pc from)
the central object up to  3 pc in z. In the northern part (x' > 0)
the inner dust boundary is much futher away, i.e
3 pc in z. In the northern part (x' > 0)
the inner dust boundary is much futher away, i.e  1.5 pc, from the
central object. Then dust goes up to
1.5 pc, from the
central object. Then dust goes up to  3.5 pc.
3.5 pc.
The section in Fig. 4b goes close to
the east-west direction. In the eastern part (x' < 0) dust starts rather
close to the central star
(similarily as for x' < 0 in Fig. 4a)
but extends only up to  1.5 pc. Then above there is an empty
region. Only at
1.5 pc. Then above there is an empty
region. Only at  4.5 pc there is a thin dust layer. On the western side
of the section (x' > 0) there is a thin dust layer at
4.5 pc there is a thin dust layer. On the western side
of the section (x' > 0) there is a thin dust layer at  0.7 pc.
Then the main dust layer extends between
0.7 pc.
Then the main dust layer extends between  1.5 and
1.5 and  3.5 pc.
3.5 pc.
The last section presented in Fig. 4c has been made along the
north-east - south-west direction. In the north-eastern part (x' < 0) the
dust structure is rather complex. There are two thin dust layers seen at
 0.7 pc and
0.7 pc and  3.7 pc. Between them there is
a much thicker dust region which extends from
3.7 pc. Between them there is
a much thicker dust region which extends from  1.0 pc to
1.0 pc to
 2.5 pc. Note however that this region has its own complex structure as
can be best inferred from the echo image taken on Dec. 17.
In the south-western
part an extended dust region begins at
2.5 pc. Note however that this region has its own complex structure as
can be best inferred from the echo image taken on Dec. 17.
In the south-western
part an extended dust region begins at  0.15 pc from the star and goes
up to
0.15 pc from the star and goes
up to  3.3 pc.
3.3 pc.
The general picture that emerges from our analysis is as follows. Near the
central object there is a dust-free region (which is separately discussed in
the following subsection).
Above it there is the main dust region whose outer boundary to the
north, west and south lies at  3.0-3.5 pc. In all eastern
directions the boundary is closer to the star and near the east axis it is as
close as
3.0-3.5 pc. In all eastern
directions the boundary is closer to the star and near the east axis it is as
close as  1.5 pc. Finally, in the eastern directions there is a thin dust
layer at a distance of
1.5 pc. Finally, in the eastern directions there is a thin dust
layer at a distance of  4 pc.
4 pc.
Note that the obtained positions of
the dust regions depend on the assumed distance to V838 Mon. The most
sensitive is the z coordinate which depends
on the square of the distance. Fortunatelly, the relative picture of the dust
distribution presented in Fig. 4 would be little affected if
other values of the distance were adopted.
In Sect. 3 we have
interpreted the outer edge of the observed echo in the north-west quadrant as
produced by a flat surface perpendicular to the line of sight. From the
results in the present section it results that it was a reasonable
assumption. The z values of the outer rim points from this quadrant
(i.e. having x > 0, y > 0) are scattered by less
than 3% (standard deviation) around its mean value of 3.50 pc.
4.2 Central dust-free region
As mentioned above our analysis of the echo images of V838 Mon leads to
the conclusion
that there is a quite well defined dust-free region around the central
object. This statement obviously results from the fact that all the echo
images analysed in the present study show a clear central hole. All the
images have been taken after the outburst of V838 Mon. The light echo has
then been well separated from the line of sight in front of the star. Thus,
as can be seen from Fig. 1 or Fig. 4,
the central parts of the echo tells
us about the dust distribution behind the star and in the directions from
the star more or less perpendicular to the line of sight.
The principal characteristic of the central hole in the light echo observed
around V838 Mon is that it expands strongly asymmetrically. This immediately
implies that the dust-free region around the central object is strongly
asymmetric. The hole expands most rapidly in the north and north-west
directions. In the east, south-east and south directions it expands
very little or even not at all.
Another important characteristic is that the inner echo edge is
well defined, in the sense that it is usually marked by bright emission regions or
bright rims. In particular, clear rim-like structures are seen in the east,
south-east and south directions. They are most pronounced on Sep. 2 but
can be easily identified more or less in the same distance from
the central star in all the images.
On Oct. 28 an emission appears in the south-east quadrant between
the rim and the central star.
On Dec. 17 this central emission becomes extended to the north-east.
Evidently on Oct. 28 we started seeing dust behind the central object.
The bright rim, relatively stable and seen for  8 months implies that
to the south, south-east and east of the central star there is
a sort of a dust layer more or less parallel to the line of sight.
We suggest that this is a compressed edge of a cavity more or
less centred on the star, whose illuminated parts are roughly
tangent to the line of sight. This interpretation is supported by the
appearance of the emission from
behind the star on Oct. 28 and its futher growth on Dec. 17, as discussed above.
8 months implies that
to the south, south-east and east of the central star there is
a sort of a dust layer more or less parallel to the line of sight.
We suggest that this is a compressed edge of a cavity more or
less centred on the star, whose illuminated parts are roughly
tangent to the line of sight. This interpretation is supported by the
appearance of the emission from
behind the star on Oct. 28 and its futher growth on Dec. 17, as discussed above.
The dense edge of the cavity with a geometry as suggested above offers
a possibility to
estimate the distance to V838 Mon. At a certain time moment the light echo
would illuminate parts of the edge which lie at z = 0. The distance of
these parts from the central star would be equal to ct at this moment
(cf. Eq. (6)). The main problem is to identify the
right moment. Bond et al. (2003) have attempted to explore this
possibility following considerations of Sparks (1994).
They have detected that on Sep. 2 the light from the discussed rim was
strongly polarized indicating that it was scattered at an angle
close to
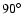 .
From this they conclude that the distance is at least
6 kpc, suggesting that the
.
From this they conclude that the distance is at least
6 kpc, suggesting that the
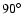 scattering in the rim had not yet
occured.
Our measurements on the images from Sep. 2, Oct. 28 and Dec. 17 give
that the inner bright rim in the south-east quadrant is
practically at the same distance of
scattering in the rim had not yet
occured.
Our measurements on the images from Sep. 2, Oct. 28 and Dec. 17 give
that the inner bright rim in the south-east quadrant is
practically at the same distance of
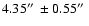 from the central star. (Note that the uncertainity mainly
results from the fact that the rim is not perfectly circular.)
On May 20 the same rim
was at
from the central star. (Note that the uncertainity mainly
results from the fact that the rim is not perfectly circular.)
On May 20 the same rim
was at
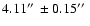 .
Apparently on May 20 the rim
resulted from illumination of the regions in front of the star, i.e. at
z>0. On Oct. 28 and particularly on Dec. 17 the light echo was already
partly illuminating dust behind the star, i.e. at z<0. Thus it seems
reasonable to adopt that the maximum illumination of the rim at z=0 occured
between Sep. 2 and Oct. 28. Taking that this has happened at
.
Apparently on May 20 the rim
resulted from illumination of the regions in front of the star, i.e. at
z>0. On Oct. 28 and particularly on Dec. 17 the light echo was already
partly illuminating dust behind the star, i.e. at z<0. Thus it seems
reasonable to adopt that the maximum illumination of the rim at z=0 occured
between Sep. 2 and Oct. 28. Taking that this has happened at
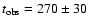 days and that the zero age of the echo is
days and that the zero age of the echo is
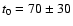 days (middle of the main outburst and half duration of the
outburst) one obtains the distance to V838 Mon of
days (middle of the main outburst and half duration of the
outburst) one obtains the distance to V838 Mon of 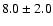 kpc.
kpc.
In order to study more quantitatively the structure of the central dust-free
region we have remeasured the positions of the inner echo edge on the images
taken on May 20, Sep. 2, Oct. 28 and Dec. 17. Contrary to the previous
measurements reported above, which referred to regions where the emission
became almost invisible, we have measured the positions where, going
from the central star, the echo emission becomes significant. In particular
when the edge is marked by a bright rim the position of the maximum emission
in the rim has been determined. In addition, on the images from Oct. 28 and
Dec. 17, we have also measured the positions of the emission
appearing in the south-east quadrant between the inner rim and the star.
![\begin{figure}
\par\mbox{ \includegraphics[width=6.1cm,clip]{hole_a.eps}\hspace*...
...s}\hspace*{3mm}
\includegraphics[width=6.1cm,clip]{hole_d.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg125.gif) |
Figure 5:
Structure of the dust-free region near
V838 Mon. The axes and the definition of
the azimuthal angle, 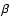 ,
given in the bottom-left corner of each part,
are the same as in Fig. 4. Full symbols show
the positions of the inner edge of dust (within ,
given in the bottom-left corner of each part,
are the same as in Fig. 4. Full symbols show
the positions of the inner edge of dust (within
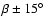 ).
Comet-like tails emerging radially from the symbols
indicate directions in which dust extends.
Thin curves show the echo paraboloids corresponding to t0 = 70 days
on May 20 (inner) and Dec. 17 (outer). ).
Comet-like tails emerging radially from the symbols
indicate directions in which dust extends.
Thin curves show the echo paraboloids corresponding to t0 = 70 days
on May 20 (inner) and Dec. 17 (outer). |
| Open with DEXTER |
We do not know when, i.e. in which part of the outburst, the light
illuminating the measured regions was emitted. Therefore when calculating
the z coordinates of these regions from Eq. (3) we have
assumed t0=70 days, which is the time of the middle of the main outburst.
Following the above estimate, the 8 kpc distance to V838 Mon has been
assumed.
The resulting structure of the inner edge of the dusty region
surrounding V838 Mon is shown in Fig. 5. The axes
and the azimuthal angle of
the abscissa, 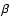 ,
given in the bottom-left corner of each section,
are defined in the same way as in Fig. 4. Full symbols show
the positions of the inner edge of dust. Comet-like tails of the symbols
have been drawn to indicate directions in which dust extends. Inside, i.e.
between the full points and the central star, there is no (observable) dust.
,
given in the bottom-left corner of each section,
are defined in the same way as in Fig. 4. Full symbols show
the positions of the inner edge of dust. Comet-like tails of the symbols
have been drawn to indicate directions in which dust extends. Inside, i.e.
between the full points and the central star, there is no (observable) dust.
The plane of Fig. 5a is
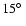 inclined to the west from the south-north axis in the echo images.
The dust-free region is here most asymmetric. For x' < 0 and
inclined to the west from the south-north axis in the echo images.
The dust-free region is here most asymmetric. For x' < 0 and 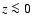 the
dust edge is as close as 0.10-0.15 pc from the star. In front of the star
(z > 0) the dust edge increases its distance from the star with the
increasing x' up to
the
dust edge is as close as 0.10-0.15 pc from the star. In front of the star
(z > 0) the dust edge increases its distance from the star with the
increasing x' up to  1.5 pc. We do not have information about the
dust distribution beyond the outer paraboloid in Fig. 5 but the
dust-free region certainly extends beyond this paraboloid in
Fig. 5a for x' > 0 and
1.5 pc. We do not have information about the
dust distribution beyond the outer paraboloid in Fig. 5 but the
dust-free region certainly extends beyond this paraboloid in
Fig. 5a for x' > 0 and 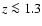 pc.
pc.
The distribution of the points in
Fig. 5c, whose plane is perpendicular to that of
Fig. 5a, is fairly symmetric in relation to the x' = 0 line.
The planes fo Figs. 5b and d are inclined
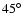 and
and
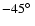 to the plane of Fig. 5a.
The distribution of the points
in Fig. 5b is almost a mirror image
of that in Fig. 5b.
Therefore it can be concluded that the dust-free region shows a
noticable symmetry with respect to the plane of Fig. 5a.
Note, however, that the
symmetry is not perfect. In Fig. 5d we see almost a complete
shape of the dust edge around the central object. In Fig. 5b,
however, the dust-free region extends beyond the outer paraboloid for
x' > 0 and
to the plane of Fig. 5a.
The distribution of the points
in Fig. 5b is almost a mirror image
of that in Fig. 5b.
Therefore it can be concluded that the dust-free region shows a
noticable symmetry with respect to the plane of Fig. 5a.
Note, however, that the
symmetry is not perfect. In Fig. 5d we see almost a complete
shape of the dust edge around the central object. In Fig. 5b,
however, the dust-free region extends beyond the outer paraboloid for
x' > 0 and 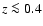 pc.
pc.
The (compressed) dust edge
producing the bright inner echo rim
discussed above (and which have been used to estimate the
distance to V838 Mon) is clearly seen as a concentration of points
near the central star at x' < 0 in Figs. 5a and b and at x' > 0 in Fig. 5d.
5 Discussion and conclusions
For all astrophysical objects it is important to know their distances. In
the case of V838 Mon this is particularly important.
The outburst of V838 Mon
does not fit any known class of outbursting stars so the determination of
its luminosity is crucial for discussing possible mechanisms of the
event. The early estimates of 0.6-0.8 kpc based on a naive interpretation
of the light echo expansion (Munari et al. 2002a;
Kimeswenger et al. 2002) led to the maximum luminosity of

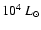 which is typical for nova or nova-like
outbursts. Our analysis presented in Sect. 3, similar to that of
Bond et al. (2003), clearly shows that the
distance and thus also the luminosity are much larger. The observed
expansion of the outer echo edge led us to conclude that the distance to
V838 Mon is
which is typical for nova or nova-like
outbursts. Our analysis presented in Sect. 3, similar to that of
Bond et al. (2003), clearly shows that the
distance and thus also the luminosity are much larger. The observed
expansion of the outer echo edge led us to conclude that the distance to
V838 Mon is 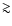 5 kpc. From an analysis of the inner rim of the echo done
in Sect. 4.2 we
have estimated the distance to be
5 kpc. From an analysis of the inner rim of the echo done
in Sect. 4.2 we
have estimated the distance to be 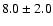 kpc.
This distance estimate is in
agreement with that of Bond et al. (2003), as well as with that of
Munari et al. (2002b). Even our lower limit of
kpc.
This distance estimate is in
agreement with that of Bond et al. (2003), as well as with that of
Munari et al. (2002b). Even our lower limit of
 5 kpc makes the maximum luminosity
5 kpc makes the maximum luminosity 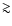
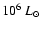 which places the outburst of V838 Mon among the most luminous
events in our Galaxy.
which places the outburst of V838 Mon among the most luminous
events in our Galaxy.
As it has been shown in Sect. 4 the evolution of the light echo can be
used as a very useful tool for studying the dust distribution near the light
source. Although the absolute characteristics of the obtained distribution
depend on the distance, which is uncertain in the case of V838 Mon,
the relative structure is fairly insensitive to this parameter.
What we have done it is a rather simple analysis. A much more detailed study
could be done on calibrated images of the echo which were not
available to the author. Certainly further observations would be very
valuable. When the light paraboloid becomes larger and larger, newer and
newer regions of dust are illuminated and more and more complete images of
the dust distribution in the vicinity of the star can be obtained. As it can be
seen from Fig. 4, only a small part of the volume around
V838 Mon could be studied so far. But even from this interesting
conclusions can be drawn.
We have found no signs of spherical symmetry in
the dust distribution which would have been expected if the observed dust had
resulted from mass loss activities of V838 Mon in the past.
Thus the results of our study contradict the
assumption made in Bond et al. (2003) that the V838 Mon light echo
has been produced by "a series of nested spherical dust shells centered on
the star''. In fact, even a simple qualitative analysis of the echo images
leads to the conclusion that the assumption of Bond et al. is doubtful.
Numerous
ring-like structures seen on the images of Apr. 30 and May 20 might be
considered as justifying the assumption of spherical symmetry. However, one
has to keep in mind that the echo image is determined by two, to some
extent competing, factors:
dust distribution and shape of the light echo paraboloid. The latter is
symmetric relatively to the line of sight so in the echo image
it will always tend to give features symmetric relative to the central
star. At early epochs when the
opening angle of the echo paraboloid is small the shape of the echo is
dominant in structuring the echo image. Thus it is not surprising that
the images of Apr. 30 and May 20 show so many symmetric or ring-like
features. But it also
implies that they say little about the dust distribution. At later
epochs, when the echo paraboloid becomes more and more open, details in
the dust distribution become more and more important in producing
the resulting echo image.
Thus the fact that numerous ring-like structures seen on Apr. 30 and May 20
become less and less evident in later images and that the light echo
develops more and more asymmetric features implies that the dust
distribution is asymmetric.
The outer edge of the dust distribution in front of V838 Mon, studied in
Sect. 3, if tentatively fitted by a simple geometry gives
a plane inclined to the
line of sight at 
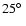 (for d = 8 kpc).
The detailed study of the dust distribution done in Sect. 4.1 shows
that the main dust region in the western part has the
outer boundary relatively flat and almost perpendicular to the line
of sight. Near the south-north line it bends toward
the central star or rather splits into a thin outer layer and a
thicker zone closer to the central star.
(for d = 8 kpc).
The detailed study of the dust distribution done in Sect. 4.1 shows
that the main dust region in the western part has the
outer boundary relatively flat and almost perpendicular to the line
of sight. Near the south-north line it bends toward
the central star or rather splits into a thin outer layer and a
thicker zone closer to the central star.
Near the central object there is a
dust-free region. Our detailed analysis of the central hole in the echo
images done in Sect. 4.2 has shown that this dust-free region
is strongly asymmetric. Its boundary is
quite close to the star in the southern directions but in the northern
directions it is at least 10 times further away.
Holes near central stars
of e.g. planetary nebulae or HII regions, are often observed. They are
produced by fast winds from the stars which sweep out the
nebular matter. V838 Mon has a B3V companion (Munari et al. 2002b).
It is also plausible that V838 Mon itself was also of similar spectral type
before the outburst (Tylenda, in preparation).
According to the standard calibration (Drilling &
Landolt 2000) B3V stars have
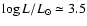 which,
using the mean relation of Howarth & Prinja (1989), turns into
a mass loss rate of
which,
using the mean relation of Howarth & Prinja (1989), turns into
a mass loss rate of 
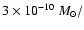 yr.
Thus, it is quite probable that the fast wind from the V838 Mon system has
created the central hole in the dusty medium. The fact that
the hole is strongly asymmetric would imply that V838 Mon is moving
relative to the dusty medium. The bright inner echo rim to the east, south-east
and south discussed in Sect. 4.2 and
the shape of the inner edge of dust in these directions displayed in
Fig. 5 fit almost perfectly the idea that these are
regions compressed by the wind ahead of the moving star. The structure of
the dust-free region shown in Fig. 5suggests that the direction of the
V838 Mon movement relative to the dusty medium lies close to the plane of
Fig. 5a and that the star moves in the south-south-east
direction. The
angle between this direction and the line of sight is uncertain as we cannot
see the other side of the dust-free region in Fig. 5a. It seems,
however, to be almost certainly lower than
yr.
Thus, it is quite probable that the fast wind from the V838 Mon system has
created the central hole in the dusty medium. The fact that
the hole is strongly asymmetric would imply that V838 Mon is moving
relative to the dusty medium. The bright inner echo rim to the east, south-east
and south discussed in Sect. 4.2 and
the shape of the inner edge of dust in these directions displayed in
Fig. 5 fit almost perfectly the idea that these are
regions compressed by the wind ahead of the moving star. The structure of
the dust-free region shown in Fig. 5suggests that the direction of the
V838 Mon movement relative to the dusty medium lies close to the plane of
Fig. 5a and that the star moves in the south-south-east
direction. The
angle between this direction and the line of sight is uncertain as we cannot
see the other side of the dust-free region in Fig. 5a. It seems,
however, to be almost certainly lower than
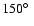 and probably greater
than
and probably greater
than
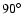 .
.
The above conclusion that V838 Mon is moving relative to the dusty medium
would be difficult to understand if the
medium were produced by mass loss from V838 Mon in the past. It is
however quite natural if the dust is of interstellar origin.
We therefore conclude that dust illuminated
by the light echo of V838 Mon is most probably of interstellar
origin. This is also supported by the general lack of spherical
symmetries in the dust distribution, as discussed above.
Thus the presence of circumstellar dust seen in the light echo is not
evidence that V838 Mon
had several outbursts in the recent past as claimed by Bond et al.
(2003).
Consequently their criticism of the merger scenario proposed by
Soker & Tylenda (2003) is not relevant. Note, however, that in
view of the distance to V838 Mon being much larger than 1 kpc, the
scenario of Soker & Tylenda should be revised (which will be done in a
separate paper).
Finally, as it is evident from the analysis and discussion
made in the present paper, future
observations of the V838 Mon light echo would be of particular
importance and interest.
Acknowledgements
The author is very grateful to Noam Soker for his comments on the initial
version of the paper and to the referee (F. Patat) whose thorough
remarks were very helpful while improving the final version of the
paper.
-
Bond, H. E., Henden, A., Levay, Z. G., et al. 2003, Nature, 422, 405
In the text
NASA ADS
-
Brown, N. J. 2002, IAU Circ., 7785
In the text
-
Cappellaro, E., Patat, F., Mazzali, P. A., et al. 2001, ApJ, 549, L215
In the text
NASA ADS
-
Chevalier, R. A. 1986, ApJ, 308, 225
In the text
NASA ADS
-
Couderc, P. 1939, Ann. Astrophys. 2, 271
In the text
NASA ADS
-
Crotts, A. P. S. 1988, ApJ, 333, L51
In the text
NASA ADS
-
Drilling, J. S., & Landoldt, A. U. 2000, in Allen's Astrophysical Quantities,
the 4th edition, ed. A. N. Cox (New York: Springer-Verlag), 381
In the text
-
Henden, A., Munari, U., & Schwartz, M. B. 2002, IAU Circ., 7859
In the text
-
Howarth, I. D., & Prinja, R. K. 1989, ApJS, 69, 527
In the text
NASA ADS
-
Kimeswenger, S., Lederle, C., Schmeja, S., & Armsdorfer, B. 2002,
MNRAS, 336, L43
In the text
NASA ADS
-
Munari, U., Henden, A., Kiyota, S., et al. 2002a, A&A, 389, L51
In the text
NASA ADS
-
Munari, U., Desidera, S., & Henden, A. 2002b, IAU Circ., 8005
In the text
-
Retter, A., & Marom, A. 2003, MNRAS, 345, L25
In the text
NASA ADS
-
Schmidt, B. P., Kirshner, R. P., Leibundgut, B., et al. 1994, ApJ, 434, L19
In the text
NASA ADS
-
Soker, N., & Tylenda, R. 2003, ApJ, 582, L105
In the text
NASA ADS
-
Sparks, W. 1994, ApJ, 433, 19
In the text
NASA ADS
-
Sugerman, B. E. K., & Crotts, A. P. S. 2002, ApJ, 581, L97
In the text
NASA ADS
-
Xu, J., Crotts, A. P. S., & Kunkel, W. E. 1995, ApJ, 451, 806
In the text
NASA ADS
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{parab.eps}
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg13.gif)
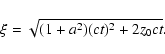
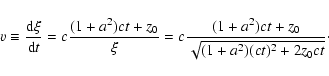
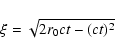
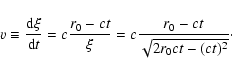

![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{sheet50.eps} \includegrap...
....5cm]{sheet400.eps} \includegraphics[width=5.5cm]{sheet500.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg42.gif)
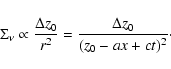
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{spher50.eps} \includegrap...
...5cm]{spher600.eps} \includegraphics[width=5.5cm]{spher750.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg53.gif)
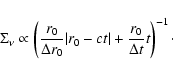
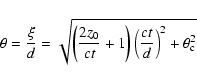
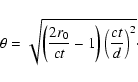
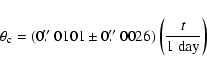
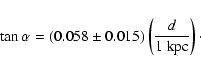
![\begin{figure}
\par\mbox{\includegraphics[width=4.9cm,clip]{d_str_a.eps}\hspace*...
...}\hspace*{5mm}
\includegraphics[width=4.9cm,clip]{d_str_c.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg118.gif)
![\begin{figure}
\par\mbox{ \includegraphics[width=6.1cm,clip]{hole_a.eps}\hspace*...
...s}\hspace*{3mm}
\includegraphics[width=6.1cm,clip]{hole_d.eps} }
\end{figure}](/articles/aa/full/2004/04/aa0015/Timg125.gif)