A&A 413, 1143-1151 (2004)
DOI: 10.1051/0004-6361:20031569
E. Forgács-Dajka
Eötvös University, Department of Astronomy, Budapest, Pf. 32, 1518 Hungary Konkoly Observatory, Budapest, Pf. 67, 1525 Hungary
Received 14 November 2002 / Accepted 1 October 2003
Abstract
We present detailed numerical calculations of the fast solar tachocline based on
the assumption that the dynamo field dominates over
the dynamics of the tachocline. In the present paper of the series,
we focus on three shortfalls of the earlier models. First, instead of
the simple oscillating dipole poloidal field we study the more general magnetic
field structures reminiscent of the butterfly diagram.
The migrating field is prescribed as the observed axisymmetric radial magnetic field
(Stenflo 1994, 1988). Our results are in good agreement with our analytical estimate
and our previous works in Forgács-Dajka & Petrovay (2001, 2002), but the polar "dip'' in isorotational surfaces is
strongly reduced in this case.
On the other hand, a more realistic model should have a magnetic diffusivity decreasing significantly inside
the radiative interior, so we also explore the effect of diffusivity and magnetic Prandtl number
varying with depth. We found that the downwards decreasing magnetic diffusivity and Prandtl number
have no significant effect on the solution, although the temporal variation of the tachocline thickness
has decreased.
Key words: Sun: interior - MHD - Sun: rotation
Helioseismic data allow us to study the structure and rotation
rate of the solar interior. The tachocline is a thin
transitional layer below the solar convective zone. In this layer
the surface-like rotation of the convection zone changes to
near-uniform rotation in the radiative interior. The existence
and properties of this layer have been known from helioseismic
studies, recently reviewed by Corbard et al. (2001). The
tachocline is known to be extremely thin; the central radius of
the tachocline appears to lie within the range
![]() ,
and its thickness is estimated to be
<
,
and its thickness is estimated to be
<
![]() (Charbonneau et al. 1999; Corbard et al. 1999; Schou et al. 1998; Kosovichev 1996).
(Charbonneau et al. 1999; Corbard et al. 1999; Schou et al. 1998; Kosovichev 1996).
Precise values for the parameters of the solar tachocline as such
mean position, thickness, latitudinal and temporal
variations, depend on the inversion techniques used for
helioseismic data. Elliott & Gough (1999) suggest that there
exists a difference in the sound speed profile between the observations and the
Standard Solar Models. By including an additional mixing layer below
the convection zone, they calibrate the thickness of the tachocline and
they find that the mean tachocline thickness is
![]() with a formal
standard error of about 5%. The observed light-element
abundances at the surface also suggest that the mixing process in the solar tachocline
is confined to a shallow layer (Brun et al. 1999, 2002).
with a formal
standard error of about 5%. The observed light-element
abundances at the surface also suggest that the mixing process in the solar tachocline
is confined to a shallow layer (Brun et al. 1999, 2002).
Making use of the most recent helioseismic results one can investigate the temporal variation
and the latitudinal structure of the tachocline. Basu & Antia (2001) found that
the tachocline is prolate, with the difference between the tachocline position at ![]() and that at
and that at ![]() latitude being about
latitude being about
![]() .
This is in
agreement with results obtained by Charbonneau et al. (1999). Basu & Antia (2001)
also report an increase in thickness of the tachocline with latitude, but this
increase is less significant, though still at the
.
This is in
agreement with results obtained by Charbonneau et al. (1999). Basu & Antia (2001)
also report an increase in thickness of the tachocline with latitude, but this
increase is less significant, though still at the ![]() level. Regarding the
dynamical aspect, one would expect temporal variations associated with the solar cycle
to appear in the tachocline (Basu & Antia 2001; Corbard et al. 2001; Howe et al. 2000).
Howe et al. (2000) report that a large-scale oscillation may be
taking place in this layer with a period about 1.3 yr. It is not clear
whether this period is associated with solar-cycle-related variations, and
Basu & Antia (2001) did not find any periodic or systematic changes in
rotation rate in the tachocline region.
This fact may be the consequence of the insufficiency of the helioseismic
data.
level. Regarding the
dynamical aspect, one would expect temporal variations associated with the solar cycle
to appear in the tachocline (Basu & Antia 2001; Corbard et al. 2001; Howe et al. 2000).
Howe et al. (2000) report that a large-scale oscillation may be
taking place in this layer with a period about 1.3 yr. It is not clear
whether this period is associated with solar-cycle-related variations, and
Basu & Antia (2001) did not find any periodic or systematic changes in
rotation rate in the tachocline region.
This fact may be the consequence of the insufficiency of the helioseismic
data.
The extreme thinness of the tachocline implies a strongly anisotropic
transport of angular momentum (Spiegel & Zahn 1992). Several different
mechanisms have been proposed for this transport, but it is now widely believed
that the magnetic field is instrumental in its origin.
It is known that an oscillating magnetic field cannot propagate far into
the radiative zone. The extent of the penetration of this magnetic field is the skin depth
![]() ,
where
,
where ![]() is the magnetic diffusivity and
is the magnetic diffusivity and
![]() is the frequency of the cycle. On the one hand, for
is the frequency of the cycle. On the one hand, for
![]() cm2/s
the dynamo field cannot penetrate the tachocline, and we can expect the
tachocline to be pervaded by the internal primordial field. On the other hand,
for
cm2/s
the dynamo field cannot penetrate the tachocline, and we can expect the
tachocline to be pervaded by the internal primordial field. On the other hand,
for
![]() cm2/s the tachocline dynamics should be governed by the dynamo field.
As the associated diffusive and Lorentz timescales are also very different,
these two cases basically correspond to the case of "slow'' and "fast'' tachocline,
discussed in the literature (see esp. Table 1 in Gilman 2000).
cm2/s the tachocline dynamics should be governed by the dynamo field.
As the associated diffusive and Lorentz timescales are also very different,
these two cases basically correspond to the case of "slow'' and "fast'' tachocline,
discussed in the literature (see esp. Table 1 in Gilman 2000).
In recent years the case of a slow tachocline has been investigated extensively by a number of authors. Rüdiger & Kitchatinov (1997) and MacGregor & Charbonneau (1999) studied the interaction between a large-scale field with fixed poloidal component and differential rotation without taking into consideration the meridional circulation. They found that the internal poloidal field of 10-3 G is sufficient to confine the tachocline to its observed thickness if the internal field is fully contained within the radiative zone. Gough & McIntyre (1998) presented a model for the solar tachocline which allows the nonlinear interaction between the meridional flows and a large-scale magnetic field in self-consistent way. Garaud (2001) performed calculations taking into account the meridional flow and the self-consistent evolution of the poloidal field.
In the first paper of these series (Forgács-Dajka & Petrovay 2002, hereafter Paper I),
we studied the alternative case of a fast,
turbulent tachocline with a turbulent diffusivity
of about
![]() cm2/s and we presented detailed
numerical calculations allowing for the self-consistent evolution of
the dipolar poloidal field. It was found that a sufficiently
strong oscillatory poloidal field with dipolar latitude dependence at
the tachocline-convective zone boundary is able to confine the tachocline to its observed
thickness. This is in good agreement with our analitical estimate in Forgács-Dajka & Petrovay (2001).
cm2/s and we presented detailed
numerical calculations allowing for the self-consistent evolution of
the dipolar poloidal field. It was found that a sufficiently
strong oscillatory poloidal field with dipolar latitude dependence at
the tachocline-convective zone boundary is able to confine the tachocline to its observed
thickness. This is in good agreement with our analitical estimate in Forgács-Dajka & Petrovay (2001).
In this paper, instead of a dipolar field we consider the more realistic case of a migrating field, studying its effect on the dynamics of the solar tachocline. After formulating the mathematical problem in Sect. 2, results of our model containing a migrating magnetic field will be presented in Sect. 3. We also explore the effect of the meridional flow and the impact of varying the diffusivity with radius. Finally, Sect. 4 summarizes the main results.
In order to describe the differential rotation and the evolution of the large-scale magnetic field in the solar interior it is useful to write the equation of motion and the hydromagnetic induction equation in a frame rotating with the fixed internal rotation rate. These equations can be found in the first paper of these series (Paper I, Sect. 2.1).
The flow field was treated in the same manner as in Paper I, nevertheless,
some additional remarks are taken here.
As we mentioned in Paper I, Sect. 3.4, the total flow field can be written as
the sum of the differential rotation and meridional circulation.
While we compute the evolution of the angular velocity with time,
the meridional circulation is prescribed in our region, because
in this case we focus on the effect of any meridional circulation in the
tachocline, not on the complex problem of meridional circulation
in the convective zone. Recent
helioseismic inversions have shown that the outer convective
envelope is pervaded by a ![]()
![]() poleward
meridional flow. Such inversions currently do not provide accurate
meridional flow information at greater depth, thus we turn for
guidance to the numerical simulations of thermally driven turbulent
convection recently carried out by Miesch et al. (2000),
Küker & Stix (2001) and Kitchatinov & Rüdiger (1995).
These simulations generate a mean meridional
circulation and in these the meridional flow penetrates into the stable interior.
In an attempt to incorporate at least qualitatively these observational
and computational results, we used a model similar to that described in
Paper I.
poleward
meridional flow. Such inversions currently do not provide accurate
meridional flow information at greater depth, thus we turn for
guidance to the numerical simulations of thermally driven turbulent
convection recently carried out by Miesch et al. (2000),
Küker & Stix (2001) and Kitchatinov & Rüdiger (1995).
These simulations generate a mean meridional
circulation and in these the meridional flow penetrates into the stable interior.
In an attempt to incorporate at least qualitatively these observational
and computational results, we used a model similar to that described in
Paper I.
The strong subadiabatic stratification of the solar interior sets
an upper limit to the meridional flow. An elementary estimate discussed
in Paper I yields
![]() .
On the other hand Miesch et al. (2000) found that depending on assumed values of some of the input
parameters this pattern is a persistent equatorward or poleward
circulation in the overshoot region.
Accordingly, the flow parameters used in our calculations were chosen to produce simple
smooth one- and two-celled flow patterns obeying the amplitude constraint
as before mentioned, while reproducing the observed flow speed near the surface.
For the density, we used the following expression:
.
On the other hand Miesch et al. (2000) found that depending on assumed values of some of the input
parameters this pattern is a persistent equatorward or poleward
circulation in the overshoot region.
Accordingly, the flow parameters used in our calculations were chosen to produce simple
smooth one- and two-celled flow patterns obeying the amplitude constraint
as before mentioned, while reproducing the observed flow speed near the surface.
For the density, we used the following expression:
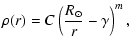 |
(1) |
It is well known that sunspot activity occurs in the form of waves with periods
![]() 11 yr, which propagate from middle latitudes towards the solar equator. In the extended
butterfly diagram (Makarov & Sivaraman 1989), one can see the poleward migration of
the magnetic fields indicated by the migration pattern of a number of tracers such as
quiescent prominences or the coronal green line.
11 yr, which propagate from middle latitudes towards the solar equator. In the extended
butterfly diagram (Makarov & Sivaraman 1989), one can see the poleward migration of
the magnetic fields indicated by the migration pattern of a number of tracers such as
quiescent prominences or the coronal green line.
Stenflo (1994, 1988) analyzed
33 yr of synoptic observations of the Sun's magnetic field carried out daily at the Mount Wilson
and Kitt Peak observatories over all solar latitudes and longitudes. The observed longitudinal
magnetic field has been converted to a radial magnetic field assuming that the field
direction is on average radial in the layers where the field is measured.
This provides an opportunity to analyse the global modes of the Sun.
Stenflo (1994, 1988) expanded the radial
magnetic field in spherical harmonics and he found that the zonal magnetic field pattern can be
represented as a superposition of N discrete modes with purely sinusoidal time variations
with frequency
![]() yr-1. Consequently, the evolutionary pattern of
the axisymmetric radial magnetic field can be written
in the following form:
yr-1. Consequently, the evolutionary pattern of
the axisymmetric radial magnetic field can be written
in the following form:
![$\displaystyle B_r(t,x)=\sum_{l=1}^N \vert a_l\vert\cos\left[\omega_{\mbox{\scriptsize cyc}}\left(t-t_l\right)\right]P_l(x),$](/articles/aa/full/2004/03/aah4110/img30.gif) |
(2) |
| (3) |
Petrovay & Szakály (1999) found that the
latitudinal distribution of the field at the surface reflects the conditions at
the bottom of the convective zone, i.e. in this regard the convective
zone behaves as a "steamy window''.
Thus, if we assume that the above formula describes the time-evolution of the radial magnetic field
at the base of the convective zone, then the development of the vector potential is given by:
Thus, the development of the vector potential is represented as a superposition of the sinusoidal,
22 yr variations for the 7 odd modes with
![]() ,
as
,
as
![$\displaystyle A(\theta,t)=A_0\sum_{k=0}^6 V_{1+2k}(\theta)\vert a_{1+2k}\vert\cos\left[\omega_{\mbox{\scriptsize cyc}}\left(t-t_{1+2k}\right)\right]$](/articles/aa/full/2004/03/aah4110/img36.gif) |
|||
| (5) |
| |
Figure 1: Illustration of the evolution of the vector potential. Solid lines represent positive A and dashed lines denote negative A. |
| Open with DEXTER | |
Based on Paper I, Sect. 2.1, the azimuthal components
of Eqs. (1) and (2), including the effects of
diffusion, Coriolis force, meridional circulation, toroidal field production by
shear, and Lorentz force, read
Our model does not include the convection zone, so
the computational domain for the present calculations consists of just an annular
meridional cut in the northern hemisphere
![]() in
the upper part of the radiative interior, between radii
in
the upper part of the radiative interior, between radii
![]() and
and
![]() ,
where
,
where
![]() is the radius of the bottom of the convection zone. For the
solution of Eqs. (6)-(8)
we use the following boundary conditions.
is the radius of the bottom of the convection zone. For the
solution of Eqs. (6)-(8)
we use the following boundary conditions.
Assuming the deep radiative core to be a rigidly rotating perfect conductor, we set both B and A to zero at the lower boundary. Both these quantities are also set to zero along the symmetry axis and they are antisymmetric about the equator. Furthermore, our upper boundary condition on the poloidal field is the solution of Eq. (4). For the upper boundary condition chosen for the toroidal field we assume that the toroidal field is negligible in the convective zone compared to its value in the tachocline. Such a hypothetical situation is in line with current thinking in dynamo theory, and it may be a natural consequence of buoyancy-driven instabilities effectively removing any toroidal flux from the convective zone.
For ![]() we require axial and equatorial symmetry, and
at the bottom of the convection zone we suppose that
the rotation rate can be described with the same
expression as in the upper part of the convection zone.
Since the observations
indicate that the differential rotation varies little within the convection
zone and in the deep radiative interior, we can take
we require axial and equatorial symmetry, and
at the bottom of the convection zone we suppose that
the rotation rate can be described with the same
expression as in the upper part of the convection zone.
Since the observations
indicate that the differential rotation varies little within the convection
zone and in the deep radiative interior, we can take
![]() at the bottom
of the computational domain, so
the lower boundary condition for
at the bottom
of the computational domain, so
the lower boundary condition for ![]() is different than in
Forgács-Dajka & Petrovay (2001, 2002) where
is different than in
Forgács-Dajka & Petrovay (2001, 2002) where ![]() at the bottom of our box.
Finally, we summarize and formulate these conditions in this way:
at the bottom of our box.
Finally, we summarize and formulate these conditions in this way:
![\begin{figure}
\par\includegraphics[width=13cm,clip]{H4110F2.ps}
\end{figure}](/articles/aa/full/2004/03/aah4110/Timg78.gif) |
Figure 2:
Spreading of the differential rotation into the radiative
interior for
|
| Open with DEXTER | |
In accordance with the
observations of the GONG network, the expression used for
![]() is
is
| (10) |
The Navier-Stokes, the induction equations and the equation for
the poloidal magnetic field are coupled, nonseparable partial differential
equations. We solve them as an initial-boundary value problem.
We use a time relaxation method with a finite difference scheme first order
accurate in time to solve the equations. A uniformly spaced grid is set up
with 128 grid points in the r direction and 64 grid points in the ![]() direction.
direction.
The initial conditions chosen for all calculations are
As stated above, we examine the influence of a migrating field on the radial spreading of the differential rotation into the radiative interior. Prescribing a migrating magnetic field at the top we define the form of the vector potential from the observed radial magnetic field. Besides the effect of the field strength, we study the consequences of the varying the diffusivity and the magnetic Prandtl number with radius, and the influence of the meridional circulation.
In the first calculations, only the field strength varies from case to case.
The values of the viscosity and magnetic diffusivity chosen for these
simulations are identical,
![]() ,
i.e. the magnetic Prandtl number is one
,
i.e. the magnetic Prandtl number is one
![]() and
the meridional circulation is neglected. Several calculations were run with
different field strengths and we chose the most suitable case for us,
where the sufficiently strong
magnetic field is able to interfere the spreading of the
differential rotation into the radiative interior and to reproduce the observed
thickness of the tachocline. This case is shown in Fig. 2
after relaxation
and
the meridional circulation is neglected. Several calculations were run with
different field strengths and we chose the most suitable case for us,
where the sufficiently strong
magnetic field is able to interfere the spreading of the
differential rotation into the radiative interior and to reproduce the observed
thickness of the tachocline. This case is shown in Fig. 2
after relaxation![]() .
.
In the left-hand panel
we plotted the contours of the time-average of the rotation rate, which
is defined as
| |
= | (12) | |
| = | 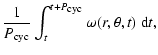 |
(13) |
In the right-hand panel we plotted the rotation rate at different latitudes as
a function of radius.
We note that in Paper I we plotted the differential rotation amplitude
![]() in right-hand panels, where
in right-hand panels, where ![]() was weighted with latitude
and
was weighted with latitude
and
![]() was normalized (see Eq. (23) in Paper I).
However, in this paper we retained
the values of the frequency, so in this case the results can be compared easier
with helioseismic observations and even the more insignificant
variations of the rotation rate are more conspicouos.
Based on the helioseismic observations we expect that the
differential rotation changes to the rigid rotation in a thin transition region.
It is well visible that the prescribed differential rotation at the base of the
convection zone changes to the near-uniform rotation in a thin layer.
was normalized (see Eq. (23) in Paper I).
However, in this paper we retained
the values of the frequency, so in this case the results can be compared easier
with helioseismic observations and even the more insignificant
variations of the rotation rate are more conspicouos.
Based on the helioseismic observations we expect that the
differential rotation changes to the rigid rotation in a thin transition region.
It is well visible that the prescribed differential rotation at the base of the
convection zone changes to the near-uniform rotation in a thin layer.
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{H4110F3.ps}
\end{figure}](/articles/aa/full/2004/03/aah4110/Timg89.gif) |
Figure 3: Latitudinal variation of the tachocline thickness for the case in Fig. 2. The solid line represents the thickness from the model and the dashed and dashed-dot lines show w from MDI and GONG data respectively (Basu & Antia 2001). The grey and the hatched areas show the error estimates on these. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{H4110F4.ps}
\end{figure}](/articles/aa/full/2004/03/aah4110/Timg90.gif) |
Figure 4:
Latitudinal variation of the radial jump in |
| Open with DEXTER | |
We also study in detail the dynamics of the tachocline and compare to the observations.
Accordingly, the thickness of the tachocline and the change in the rotation rate across
the tachocline are defined as in Basu (1997).
Thus, the jump in the rotation rate across the tachocline
![]() is the
difference between the rotation rate at the base of the convection zone and the
rotation rate in the interior. The thickness of the tachocline w is defined as
the rotation rate increases from the factor 1/(1+e) of its maximum value to
the factor 1-1/(1+e) of its maximum value in the range
is the
difference between the rotation rate at the base of the convection zone and the
rotation rate in the interior. The thickness of the tachocline w is defined as
the rotation rate increases from the factor 1/(1+e) of its maximum value to
the factor 1-1/(1+e) of its maximum value in the range
![]() to
to
![]() .
.
The fast tachocline shows a quite marked latitude-dependence
in our results, as illustrated in Figs. 3 and 4.
In both figures we also plot the results of the helioseismic measurements
from MDI and GONG (Basu & Antia 2001). It should be noted that, according to the
helioseismic results, the latitudinal variation in position of tachocline is
significant, while the variation in width is not clear, but the results tend
to suggest that the thickness increases with latitude. Since
the top of the computational domain is fixed at
![]() in our model,
therefore the position of the tachocline cannot be directly compared with
the observations.
Notice that the thickness of the tachocline is close to zero at around the colatitude of
in our model,
therefore the position of the tachocline cannot be directly compared with
the observations.
Notice that the thickness of the tachocline is close to zero at around the colatitude of ![]() ,
because at this colatitude the rotation rate is equal to
the rigid rotation velocity. This region is the so-called corotation zone (Fig. 3).
In addition to latitudinal variations, we also investigate the temporal variations
in the properties of the tachocline, and we find that the thickness of the tachocline
depends on cycle phase (Fig. 5).
This variation is not confirmed by the observations, but the helioseismic data set is
relatively short.
The development of the toroidal magnetic field
and the radial magnetic field shown in Fig. 6 correspond to
the observed evolutionary pattern of the magnetic field, i.e. the butterfly diagram.
,
because at this colatitude the rotation rate is equal to
the rigid rotation velocity. This region is the so-called corotation zone (Fig. 3).
In addition to latitudinal variations, we also investigate the temporal variations
in the properties of the tachocline, and we find that the thickness of the tachocline
depends on cycle phase (Fig. 5).
This variation is not confirmed by the observations, but the helioseismic data set is
relatively short.
The development of the toroidal magnetic field
and the radial magnetic field shown in Fig. 6 correspond to
the observed evolutionary pattern of the magnetic field, i.e. the butterfly diagram.
In the second case, we study the influence of the meridional circulation.
As we mentioned, the strong subadiabatic stratification sets an upper limit to
the amplitude of the meridional circulation (
![]() ).
).
We use the flow patterns shown in Paper I, Figs. 9 and 10, where the speed of the
horizontal flow is weak.
In these cases, we considered the
effect of the meridional flow on the magnetic field
(M2, M3 in Eqs. (7) and (8)).
The results with the meridional circulation included can be seen in
Fig. 7. The poloidal field amplitude used
here was the same as in the previous case.
Notice that the effect of the weak meridional flow of ![]()
![]() on the magnetic field is not dramatic.
on the magnetic field is not dramatic.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{H4110F5.ps}
\end{figure}](/articles/aa/full/2004/03/aah4110/Timg95.gif) |
Figure 5: The thickness of the tachocline at different latitudes as a function of time for the case in Fig. 2. |
| Open with DEXTER | |
In Fig. 7 it can be seen
that the rigid rotation rate is shifted compared to the first case in
accordance with the direction of flow. An equatorward flow in the tachocline region
increases the near-uniform rotation rate, while a poleward flow reduces it.
We remark that the lower boundary condition for ![]() is different than in
Forgács-Dajka & Petrovay (2001, 2002) where
is different than in
Forgács-Dajka & Petrovay (2001, 2002) where ![]() at the bottom of our box.
In these cases
at the bottom of our box.
In these cases
![]() at the bottom
of the computational domain, so the effect of the meridional circulation
on the rotation is perceptible in the radiative interior. It is apparent that the
deep meridional flow changes the rigid rotation rate.
If we raised the amplitude of the meridional circulation at the upper part of the
radiative interior (
at the bottom
of the computational domain, so the effect of the meridional circulation
on the rotation is perceptible in the radiative interior. It is apparent that the
deep meridional flow changes the rigid rotation rate.
If we raised the amplitude of the meridional circulation at the upper part of the
radiative interior (
![]() ), but we reduced the penetration
of the meridional circulation - the meridional motion is in the overshoot region -,
the shift is not dramatic. This result could play an important role in
the model for the solar dynamo models wherein a meridional flow penetrates
into the stable layers below the tachocline (Nandy & Choudhuri 2002).
), but we reduced the penetration
of the meridional circulation - the meridional motion is in the overshoot region -,
the shift is not dramatic. This result could play an important role in
the model for the solar dynamo models wherein a meridional flow penetrates
into the stable layers below the tachocline (Nandy & Choudhuri 2002).
In Fig. 8 the differences between the three results are apparent.
Note that the rotation rate in the interior is changed in these cases and we used it to define
the thickness of the tachocline.
It is well visible that the effect of the weak circulation is not dramatic and
chiefly limited to the pole. In this paper the toroidal field strength is higher as in
the earlier paper and on the other hand the upper boundary condition
on the poloidal field is controlling the influence of the meridional motion.
In case of equatorward circulation it can be seen that the tachocline thickness at the pole
extended and in the corotation zone the peak is apparent. Both are due to the transport by
the equatorward motion. If we assume that in the tachocline region the circulation is
toward the pole then the thickness at the high latitudes is reducible. It must be noted
of course that the solar dynamo theories favour the counterclockwise circulation.
On the other hand in our model we have not emphasized the role of the circulation, but
the role of the Maxwell stresses which are capable to limit the shear layer to its
observed thickness. We studied it for the sake of completeness.
| |
Figure 6: Time-latitude diagram for the toroidal field ( shaded region) and the radial field ( contours) at the base of the convection zone. Equidistant contour levels of the radial field are separated by intervals of 30 G. |
| Open with DEXTER | |
In this section the diffusivity is allowed to vary with radius. In
Paper I we only investigated cases where the
diffusivities are constant throughout the computational domain.
The question may arise that the high viscosity in the deep
radiative zone could be a disfigurement to our results? In order to
answer, we change the magnetic diffusivity and the viscosity with radius as
Thus, in this case we set these parameters
as follows:
![]() ,
,
![]() and
and
![]() ,
and the magnetic Prandtl number is one
,
and the magnetic Prandtl number is one
![]() .
The magnetic diffusivity is varied with depth between approx. 105 and 1010.
This variation of the diffusivity,
while quantitatively much milder than expected physically, provides an opportunity for us
to consider the effects of a variable diffusivity without the necessity of impossibly
long integration times.
.
The magnetic diffusivity is varied with depth between approx. 105 and 1010.
This variation of the diffusivity,
while quantitatively much milder than expected physically, provides an opportunity for us
to consider the effects of a variable diffusivity without the necessity of impossibly
long integration times.
In left-hand panel of Fig. 9 it is clearly visible that the
influence of the downwards decreasing diffusivity on the solution is small.
However it is noticeable that in the polar region the differential rotation
penetrates into deeper layers of the radiative interior. On the other hand
the amplitude of the temporal variation of the thickness is smaller than in
the case of Fig. 5.
| |
Figure 7: Same as in Fig. 2, but including the meridional circulation. In left-hand panel the circulation is counterclockwise, while in right-hand panel it is clockwise. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{H4110F8.ps}
\end{figure}](/articles/aa/full/2004/03/aah4110/Timg107.gif) |
Figure 8: Latitudinal variation of the tachocline thickness. The solid line represents the case shown in Fig. 2 and the dashed and dashed-dot lines respectively denote the thickness including the meridional circulation. |
| Open with DEXTER | |
| |
Figure 9: Same as in Fig. 2. Left-hand panel: the diffusivity is varied with radius. Right-hand panel: the magnetic Prandtl number is varied with depth. |
| Open with DEXTER | |
Under realistic conditions, the turbulent magnetic diffusivity in the tachocline should be reduced to the microscopic magnetic diffusivity in the radiative core and the turbulent viscosity to molecular and radiative viscosity. However the magnetic diffusivity is greater than the viscosity and it is less reduced than the viscosity (see esp. Fig. 1 in Rüdiger & Kitchatinov 1997), so the magnetic Prandtl number is varied with depth.
As argued earlier, the low diffusivities often make the numerical simulations
problematic, therefore we tried to give a qualitative test instead of a
quantitative analysis. Accordingly,
we used the above formula (14) to define the variation of
![]() and
and ![]() with radius and
the required parameters are following:
with radius and
the required parameters are following:
![]() ,
,
![]() ,
,
![]() for
for ![]() and
and
![]() ,
,
![]() ,
,
![]() for
for ![]() ,
so the magnetic Prandtl number
is varied between 0.024 and 0.1.
,
so the magnetic Prandtl number
is varied between 0.024 and 0.1.
Our result is illustrated in right-hand panel of Fig. 9. In this case
the poloidal field strength is
![]() G and the maximum value of the
toroidal field is
G and the maximum value of the
toroidal field is
![]() G. It is well visible that
the penetration of the differential rotation into the radiative interior is strongly reduced
in the polar region and the temporal variation of the thickness
is also decreased (see Fig. 10).
G. It is well visible that
the penetration of the differential rotation into the radiative interior is strongly reduced
in the polar region and the temporal variation of the thickness
is also decreased (see Fig. 10).
The models discussed in this paper show that the dynamo field dominates over
the dynamics of the fast solar tachocline provided that the turbulent diffusivity
in the tachocline region exceeds
![]() cm2/s.
cm2/s.
In our first work (Forgács-Dajka & Petrovay 2001) we presented an analytical estimate for
the strength of an oscillatory poloidal field, which is able to confine
the tachocline to its observed thickness for
![]() cm2/s.
Based on the estimate we showed a simple numerical calculation.
A crucial assumption in this calculation is that the oscillatory poloidal
magnetic field does penetrate below the convective zone to depths comparable to
the tachocline thickness and the penetration is prescribed a priori.
cm2/s.
Based on the estimate we showed a simple numerical calculation.
A crucial assumption in this calculation is that the oscillatory poloidal
magnetic field does penetrate below the convective zone to depths comparable to
the tachocline thickness and the penetration is prescribed a priori.
In our forthcoming model (Paper I), instead of the a priori prescribed oscillatory poloidal magnetic field we included the evolution equation for the poloidal field, but the poloidal field was a simple oscillating dipole, which was not very realistic. In that work we also explored the parameter space a bit more widely by varying the magnetic Prandtl number and the diffusivity, but we did not investigate the effects of the variations of these parameters with depth. We found that the confining field strength increased with increasing viscosity and magnetic Prandtl number.
In the present work we focus on three shortfalls of the earlier models. First, instead of the simple oscillating dipole poloidal field we study the more general magnetic field structures reminiscent of the butterfly diagram. On the other hand, a more realistic model should have a magnetic diffusivity decreasing significantly inside the radiative interior.
For the more general magnetic field structures, we use the results of
Stenflo (1994, 1988), where
the evolutionary pattern of the axisymmetric magnetic field can be written
as a superposition of the sinusoidal, 22 yr variations for the 7 odd
modes spherical harmonic components. Based on our previous works we studied
the field strength and we found that a sufficiently
strong migrating magnetic field is able to reproduce the observed thickness
of the tachocline. This agrees with the results in Forgács-Dajka & Petrovay (2001, 2002),
apart from the fact that the time-latitude diagram for the toroidal field
(Fig. 6) is now similar to the butterfly diagram.
The lower boundary condition for ![]() is different than in
Forgács-Dajka & Petrovay (2001, 2002), giving us a possibility to
study the effect of the dynamics of the upper layers on the inside layers.
In Fig. 2 it can be seen that because of the high diffusivity
there is a little deviation in the rotation rate compared to the fixed internal
rotation rate
is different than in
Forgács-Dajka & Petrovay (2001, 2002), giving us a possibility to
study the effect of the dynamics of the upper layers on the inside layers.
In Fig. 2 it can be seen that because of the high diffusivity
there is a little deviation in the rotation rate compared to the fixed internal
rotation rate ![]() at different latitudes. Furthermore an equatorward
meridional circulation in the tachocline region
increases the near-uniform rotation rate, while a poleward flow reduces it.
Note that this phenomenon is sensitive to the penetration depth of the flow into
the upper radiative interior. We found that the internal rotation rate is not
shifted extremly in spite of the increasing amplitude of circulation if the
circulation is dominated in the upper part of the tachocline.
The downwards decreasing diffusivity or rather the magnetic Prandtl number does not
appreciably affect the solution. Evidently, this model is simplified treatment of the
turbulence in the tachocline, nevertheless it gave us an opportunity to consider
these effects. The varying magnetic diffusivity and Prandtl number with depth
give rise to a change of the temporal variation of the tachocline thickness.
It is shown in Fig. 10
that the downwards decreasing magnetic Prandtl number tends to reduce the
spatiotemporal variation.
at different latitudes. Furthermore an equatorward
meridional circulation in the tachocline region
increases the near-uniform rotation rate, while a poleward flow reduces it.
Note that this phenomenon is sensitive to the penetration depth of the flow into
the upper radiative interior. We found that the internal rotation rate is not
shifted extremly in spite of the increasing amplitude of circulation if the
circulation is dominated in the upper part of the tachocline.
The downwards decreasing diffusivity or rather the magnetic Prandtl number does not
appreciably affect the solution. Evidently, this model is simplified treatment of the
turbulence in the tachocline, nevertheless it gave us an opportunity to consider
these effects. The varying magnetic diffusivity and Prandtl number with depth
give rise to a change of the temporal variation of the tachocline thickness.
It is shown in Fig. 10
that the downwards decreasing magnetic Prandtl number tends to reduce the
spatiotemporal variation.
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{H4110F10.ps}
\end{figure}](/articles/aa/full/2004/03/aah4110/Timg117.gif) |
Figure 10: The thickness of the tachocline at different latitudes as a function of time for the case in right-hand panel of Fig. 9 (varying the magnetic Prandtl number with depth). |
| Open with DEXTER | |
The main results of present and earlier models is that the dynamo field
in the turbulent tachocline by Maxwell stresses is capable to limit the
shear layer to its observed thickness. The next step of this analysis consists in
comparing the numerical results in the present work and the model in
Paper I with the helioseismic results. In Paper I
the thickness of the tachocline showed the "pit'' at the pole, which is not confirmed
by the available helioseismic information, which may be in consequence of
the latitudinal limit of observations.
In Paper I the poloidal field was a simple oscillating dipole,
and the reality of this pit needs to be verified with other poloidal field geometries and
other parameters. In this paper we found that in case of the more general magnetic field
structure the polar pit is reduced to its half and in case of varying the magnetic
Prandtl number with depth the pit is almost disappeared (Fig. 11).
If we use the more
general field geometry reminiscent of the butterfly diagram, the penetration depth of
the differential rotation into the radiative interior in the polar region is decreased
owing to the fact that at higher latitudes the stonger magnetic fields stay up.
In case of the decreasing magnetic Prandtl number the influence of the Maxwell stresses
are in the ascendant compared with the viscous stresses,
so the permeation of the differential rotation below the convective
zone at the pole reduces further.
On the other hand regarding the dynamical aspect, we studied the temporal variations of
tachocline. Due to the relatively short helioseismic data set, the temporal variations
associated with the solar cycle to appear in the tachocline is not clear. In both models,
the vector potential of the magnetic field is prescribed with a period of 22 years at the
top of the computational domain, so we found that the thickness of the tachocline depends
on cycle phase. However the amplitude of the temporal variations can be reduced if the impact of
Maxwell stresses is enhanced compared with the viscous stresses - for example the
magnetic Prandtl number is less than one (cf. Fig. 10).
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{H4110F11.ps}
\end{figure}](/articles/aa/full/2004/03/aah4110/Timg118.gif) |
Figure 11: Latitudinal variation of the tachocline thickness. The solid line represents the case shown in Fig. 6 of Paper I, while the dashed and dashed-dot lines denote the results obtained by the present models. |
| Open with DEXTER | |
As stated earlier, an important shortfall of these models
is obviously the extremely simplified treatment of the turbulent transport.
If the turbulence arises from the instabilities in the tachocline,
then the diffusivities should clearly be some, possibly very complex,
functionals of the velocity field and of the magnetic field. The next step to
model this would be to use a Smagorinsky-type formula or
![]() model
for the diffusivities.
model
for the diffusivities.
Other important points what we should consider in the future are the boundary conditions on the magnetic field and the complete dynamo-generated poloidal field, because the conditions in the present treatment poorly represent the dynamical interaction between the flow and the magnetic field in the tachocline and the convection zone (Petrovay 2000). Many theoretical models suggest that the toroidal magnetic field is up to 105 G in the tachocline, required to produce sunspots in low latitudes (Petrovay & Moreno-Insertis 1997). In our model the peak toroidal field is above about 104 G, but this may change if different boundary conditions are used or the dynamo-generated field is included. Dikpati & Gilman (2001), Gilman & Dikpati (2002) suggest that the dynamo-generated toroidal field should play an important role in the global instability of tachocline differential rotation. In future work we plan to develop our model along the lines described above.
Acknowledgements
I would like to thank J. O. Stenflo for providing the parameters of the evolutionary pattern of the axisymmetric radial magnetic field, K. Petrovay for helpful discussions on the manuscript and my colleagues (T. Borkovits and V. Könyves) for their help. This work was supported in part by the OTKA under grant No. T043741.