A&A 413, 1163-1175 (2004)
DOI: 10.1051/0004-6361:20031564
Properties of the nuclei of Centaurs Chiron and Chariklo
O. Groussin - P. Lamy - L. Jorda
Laboratoire d'Astronomie Spatiale,
BP 8, 13376 Marseille Cedex 12, France
Received 12 February 2003 / Accepted 30 September 2003
Abstract
We analyze visible, infrared, radio and spectroscopic
observations of 2060 Chiron in a synthetic way to determine the
physical properties of its nucleus. From visible observations
performed from 1969 to 2001, we determine an absolute V magnitude
for the nucleus of
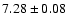 with an amplitude of
with an amplitude of
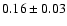 ,
implying a nearly spherical nucleus with a ratio of semi-axes
,
implying a nearly spherical nucleus with a ratio of semi-axes
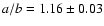 .
Infrared observations at 25, 60, 100 and 160
.
Infrared observations at 25, 60, 100 and 160  m (i.e., covering the broad maximum of the spectral energy
distribution) obtained with the Infrared Space Observatory Photometer
(ISOPHOT) in June 1996 when Chiron was near its perihelion are
analyzed with a thermal model which considers an intimate mixture of
water ice and refractory materials and includes heat conduction into
the interior of the nucleus. We find a very low thermal inertia of
3+5-3 J K-1 m-2 s-1/2 and a radius of
m (i.e., covering the broad maximum of the spectral energy
distribution) obtained with the Infrared Space Observatory Photometer
(ISOPHOT) in June 1996 when Chiron was near its perihelion are
analyzed with a thermal model which considers an intimate mixture of
water ice and refractory materials and includes heat conduction into
the interior of the nucleus. We find a very low thermal inertia of
3+5-3 J K-1 m-2 s-1/2 and a radius of
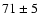 km. Combining the visible and infrared observations, we
derive a geometric albedo of
km. Combining the visible and infrared observations, we
derive a geometric albedo of
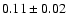 .
We find that the observed
spectra of Chiron can be fitted by a mixture of water ice (
.
We find that the observed
spectra of Chiron can be fitted by a mixture of water ice (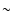 30%) and refractory (
30%) and refractory (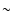 70%) grains, and that this surface model
has a geometric albedo consistent with the above value. We also
analyze the visible, infrared and radio observations of Chariklo (1997
CU26) and derive a radius of
70%) grains, and that this surface model
has a geometric albedo consistent with the above value. We also
analyze the visible, infrared and radio observations of Chariklo (1997
CU26) and derive a radius of 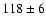 km, a geometric albedo of
km, a geometric albedo of
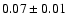 and a thermal inertia of 0
+2-0 J K-1 m-2 s-1/2. A mixture of water ice (
and a thermal inertia of 0
+2-0 J K-1 m-2 s-1/2. A mixture of water ice (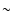 20%)
and refractory (
20%)
and refractory (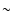 80%) grains is compatible with the
near-infrared spectrum and the above albedo.
80%) grains is compatible with the
near-infrared spectrum and the above albedo.
Key words: minor planets, asteroids
2060 Chiron (hereafter Chiron) is a transition object between the
Kuiper belt objects and the Jupiter family comets (Kowall
1996). Its semimajor axis a=13.620 AU classifies it
in the Centaur family, with an orbit between Jupiter (a=5 AU) and
Neptune (a=30 AU). Chiron is actually one of the few Centaurs
which displays activity (Tholen et al. 1988) together with,
for example, P/Oterma, P/Schwassmann-Wachmann 1 and C/NEAT (2001 T4)
(Bauer et al. 2003). It has therefore attracted
considerable interest, in particular during its perihelion passage (15
Feb. 1996, at q=8.45 AU), because it was anticipated that its
activity would increase. From the numerous observations carried out
so far and which will be later discussed in detail, it emerges the
picture of a body having the following properties. The radius
determinations vary from 74 to 104 km. The synodic rotation period
is well determined and was equal to 5.917813 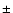 0.000007 h on
January 1991 (Marcialis & Buratti 1993). The short
period lightcurve patterns detected by Marcialis & Buratti
(1993) "probably are due to an irregular or
faceted body, and they offer evidence that Chiron currently presents
an approximately equatorial aspect to the Earth''. Moreover, the
amplitude of the lightcurve indicates a quasi-spherical body. The
geometric albedo of the nucleus is
0.14-0.03+0.06 (Campins et al. 1994) which is larger than the range of
0.04
0.000007 h on
January 1991 (Marcialis & Buratti 1993). The short
period lightcurve patterns detected by Marcialis & Buratti
(1993) "probably are due to an irregular or
faceted body, and they offer evidence that Chiron currently presents
an approximately equatorial aspect to the Earth''. Moreover, the
amplitude of the lightcurve indicates a quasi-spherical body. The
geometric albedo of the nucleus is
0.14-0.03+0.06 (Campins et al. 1994) which is larger than the range of
0.04 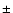 0.02 found for other cometary nuclei (Lamy et al.
2004). The spectrum of Chiron is featureless and quite
flat in the 0.5-0.9
0.02 found for other cometary nuclei (Lamy et al.
2004). The spectrum of Chiron is featureless and quite
flat in the 0.5-0.9  m range, although variations of a few
percents in the slope of the spectral reflectivity can occur (Lazzaro
et al. 1997). Recent publications by Foster et al.
(1999) and Luu et al. (2000) reported the
detection of water ice on the basis of absorption features near 2.0
m range, although variations of a few
percents in the slope of the spectral reflectivity can occur (Lazzaro
et al. 1997). Recent publications by Foster et al.
(1999) and Luu et al. (2000) reported the
detection of water ice on the basis of absorption features near 2.0  m. A similar result already obtained on
Pholus and
Chariklo(1997 CU26) suggests that water ice is probably ubiquitous on the
surface of Centaurs (Brown 2000). During the 1987 to 1990 interval,
when Chiron was beyond 11 AU from the Sun, a large brightening was
observed which is not yet very well understood. At such a
heliocentric distance, the activity is believed to be dominated by the
sublimation of CO (Capria et al. 1996).
m. A similar result already obtained on
Pholus and
Chariklo(1997 CU26) suggests that water ice is probably ubiquitous on the
surface of Centaurs (Brown 2000). During the 1987 to 1990 interval,
when Chiron was beyond 11 AU from the Sun, a large brightening was
observed which is not yet very well understood. At such a
heliocentric distance, the activity is believed to be dominated by the
sublimation of CO (Capria et al. 1996).
In this paper, we analyze visible, infrared, radio and spectroscopic
observations of 2060 Chiron in a synthetic way to determined the
physical properties of its nucleus. In Sect. 2, we first summarize
observations of Chiron at visible, infrared (including unique ISOPHOT
observations at 25, 60, 100 and 160  m) and radio wavelengths
and by stellar occultation, discussing the results of each approach
and their limitations. In Sect. 3, we explain in detail our thermal
model used to interpret the infrared observations, which includes
dust, water ice and heat conduction into the interior of the nucleus.
In Sect. 4, we discuss the results: thermal inertia, radius,
geometric albedo, reflectance of the nucleus, composition of the
surface, contribution of the coma to the visible and infrared fluxes,
and comparison of our model with previous infrared observations. In
Sect. 5, we extend our analysis to the Centaur Chariklo (1997 CU26).
m) and radio wavelengths
and by stellar occultation, discussing the results of each approach
and their limitations. In Sect. 3, we explain in detail our thermal
model used to interpret the infrared observations, which includes
dust, water ice and heat conduction into the interior of the nucleus.
In Sect. 4, we discuss the results: thermal inertia, radius,
geometric albedo, reflectance of the nucleus, composition of the
surface, contribution of the coma to the visible and infrared fluxes,
and comparison of our model with previous infrared observations. In
Sect. 5, we extend our analysis to the Centaur Chariklo (1997 CU26).
Figure 1 summarizes measurements of the magnitude of
Chiron performed between September 1969 and August 2001. We favored
the V magnitudes when available, otherwise we converted the Rmagnitudes using V-R=0.37 (Hartmann et al. 1990).
This quasi-solar color correction is justified by the neutral spectrum
of Chiron obtained in June 1996 by Lazzaro et al.
(1997). Our observation was performed with the Danish
1.54 m telescope at ESO, La Silla, in support of the ISOPHOT
observations performed 10 days before. Several images were acquired
through the R filter on 1996 June 25.02 UT, when the comet was at
a helicentric distance of 8.468 AU and a geocentric distance of
8.326 AU. Standard stars from the Landolt field PG1323-086
(Landholt 1992) were used to perform an absolute
calibration of the images. We obtained a magnitude
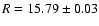 which we converted to
which we converted to
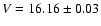 with the above color index.
with the above color index.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f1.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg20.gif) |
Figure 1:
Absolute magnitudes Hv of Chiron as a function of heliocentric distance and time. |
| Open with DEXTER |
The derivation of the absolute magnitude
Hv=V(1,1,0) requires
a correction for the phase effect. From their observations of
December 1986 which covered a very small range of phase angles
(1.05 to 1.62
to 1.62 )
and using the (H,G) formalism,
Bus et al. (1989) derived a value G=0.7. But later in
1996, when Chiron was at a comparable level of activity, Lazzaro et al. (1997) determined a very different value, G=0.42.
We do concur with Lazzaro et al. (1996) that the
correction for the phase effect poses a problem because of the
activity of Chiron resulting in a variable coma and that the (H,G)formalism may not be appropriate in this case. In view of this
situation, we decided to adopt the simple linear phase function with a
coefficient
)
and using the (H,G) formalism,
Bus et al. (1989) derived a value G=0.7. But later in
1996, when Chiron was at a comparable level of activity, Lazzaro et al. (1997) determined a very different value, G=0.42.
We do concur with Lazzaro et al. (1996) that the
correction for the phase effect poses a problem because of the
activity of Chiron resulting in a variable coma and that the (H,G)formalism may not be appropriate in this case. In view of this
situation, we decided to adopt the simple linear phase function with a
coefficient
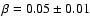 mag deg-1, typical of
cometary nuclei and also consistent with the data of Bus et al.
(1989). We applied this phase correction to the whole set
of observations plotted in Fig. 1. In this present
study, the above problem is alleviated by the fact that we focus our
attention to the faintest magnitudes of Chiron, hopefully reflecting a
situation where the coma was negligibly faint. Moreover, the
difference between Hv calculated with G=0.7 or
mag deg-1, typical of
cometary nuclei and also consistent with the data of Bus et al.
(1989). We applied this phase correction to the whole set
of observations plotted in Fig. 1. In this present
study, the above problem is alleviated by the fact that we focus our
attention to the faintest magnitudes of Chiron, hopefully reflecting a
situation where the coma was negligibly faint. Moreover, the
difference between Hv calculated with G=0.7 or
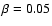 mag/deg is lower than 2% for Chiron as the phase
angle is always
mag/deg is lower than 2% for Chiron as the phase
angle is always
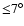 .
.
As illustrated by the variations of Hv with heliocentric
distance (Fig. 1), Chiron underwent considerable
variations of its activity, with a general trend totally uncorrelated
with its heliocentric distance. A long phase of activity took place
before 1978, fully documented by Bus et al. (2001).
Beginning at some unknown time prior to the earliest observations in
1969, the brightness of Chiron reached a peak by late 1972, about two
years after aphelion and was then 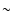 0.4 mag brighter than at
the second outburst of 1989. Following the 1972 peak, the activity
gradually decreased so that a minimum was reached between 14 and 16 AU. It then resumed quite rapidly to reach a maximum at 12.5 AU in
September 1988 and then progressively decayed. Chiron was still
active at perihelion (8.45 AU). Post-perihelion, the decrease of
activity continued and Chiron reached what appears to be its absolute
minimum of activity in June 1997 with
Hv=7.28, i.e. 0.5
magnitude lower than the minimum of 6.8 reached at 14-16 AU
pre-perihelion. This therefore yields the best estimate of the
magnitude of the nucleus. Next, the activity increased again very
rapidly and the magnitude reached 5.75 on April 2001. The whole set
of data displays conspicuous "short-term'' variations of the activity
which can reach 0.3-0.4 mag over a few months.
0.4 mag brighter than at
the second outburst of 1989. Following the 1972 peak, the activity
gradually decreased so that a minimum was reached between 14 and 16 AU. It then resumed quite rapidly to reach a maximum at 12.5 AU in
September 1988 and then progressively decayed. Chiron was still
active at perihelion (8.45 AU). Post-perihelion, the decrease of
activity continued and Chiron reached what appears to be its absolute
minimum of activity in June 1997 with
Hv=7.28, i.e. 0.5
magnitude lower than the minimum of 6.8 reached at 14-16 AU
pre-perihelion. This therefore yields the best estimate of the
magnitude of the nucleus. Next, the activity increased again very
rapidly and the magnitude reached 5.75 on April 2001. The whole set
of data displays conspicuous "short-term'' variations of the activity
which can reach 0.3-0.4 mag over a few months.
The large outbursts which culminated at 12.5 AU pre-perihelion and
10.5 AU post-perihelion as well as the aphelion outburst are not
well understood. Water ice does not sublimate beyond 6 AU and CO
and/or CO2 must probably be invoked to explain such an activity
at large heliocentric distances (Capria et al. 1996).
CO has indeed been marginally detected in June 1995 when Chiron was at
8.50 AU from the Sun by Womack & Stern (1997) who
derived a production rate of
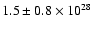 s-1.
Rauer et al. (1997) derived an upper limit of
s-1.
Rauer et al. (1997) derived an upper limit of
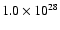 s-1 for the CO production rate near
perihelion. Different mechanisms have been proposed: a heat wave
reaching the CO sublimation front (Schmitt et al.
1991), shape and/or albedo effects on the surface of the
nucleus and mantle disruption (Johnson 1991). The most
comprehensive work to explain the activity variations of Chiron was
performed by Duffard et al. (2002): using a model for
the coma developed by Meech & Belton (1990) and assuming
a long lifetime of 1400 days for the particules in the coma, they
could fit all the photometric data over 30 yr. According to this
model, outbursts could be produced by the gas outflow of CO, CO2,
or another element of similar volatility from an active region.
s-1 for the CO production rate near
perihelion. Different mechanisms have been proposed: a heat wave
reaching the CO sublimation front (Schmitt et al.
1991), shape and/or albedo effects on the surface of the
nucleus and mantle disruption (Johnson 1991). The most
comprehensive work to explain the activity variations of Chiron was
performed by Duffard et al. (2002): using a model for
the coma developed by Meech & Belton (1990) and assuming
a long lifetime of 1400 days for the particules in the coma, they
could fit all the photometric data over 30 yr. According to this
model, outbursts could be produced by the gas outflow of CO, CO2,
or another element of similar volatility from an active region.
The question of the detection of the nucleus of Chiron can also be
approached by considering its rotational lightcurve, as its variation
with a period of 5.92 h is correctly attributed to a spinning,
non-spherical solid body. Since the direction of the spin axis is not
expected to change, the long-term change in the amplitude
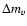 of the lightcurve of Chiron (nucleus+coma) can be
unambiguously attributed to the varying level of the coma. This can
be verified by the excellent anti-correlation between
of the lightcurve of Chiron (nucleus+coma) can be
unambiguously attributed to the varying level of the coma. This can
be verified by the excellent anti-correlation between
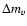 and Hv as summarized in Table 1, with the
exceptions of the 29 February 1988 and 20 February 1993 observations.
The first observation (19 January 1985) gave a lower limit as it
missed the extrema of the lightcurve. The formal method to analyze
and Hv as summarized in Table 1, with the
exceptions of the 29 February 1988 and 20 February 1993 observations.
The first observation (19 January 1985) gave a lower limit as it
missed the extrema of the lightcurve. The formal method to analyze
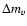 was presented by Luu & Jewitt (1990)
who derived a formula relating
was presented by Luu & Jewitt (1990)
who derived a formula relating
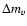 ,
Hv, the
absolute magnitude H0 of the nucleus and the amplitude of its
lightcurve
,
Hv, the
absolute magnitude H0 of the nucleus and the amplitude of its
lightcurve
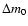 :
:
![\begin{displaymath}
\Delta m_{v} = H_0-H_{v} -2.5 \log\Big[10^{0.4(H_0-H_{v})}+10^{-0.4\Delta m_0} -1\Big].
\end{displaymath}](/articles/aa/full/2004/03/aa3595/img28.gif) |
(1) |
The analysis of the observations reported in Table 1
(with the exceptions noted above) is performed using the
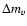 -Hv diagram (Fig. 2) where
-Hv diagram (Fig. 2) where
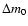 and H0 are the two free parameters.
and H0 are the two free parameters.
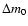 can be
estimated from the largest amplitude
can be
estimated from the largest amplitude
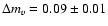 reported by Bus et al. (1989). The corresponding
Hv=6.62 indicates that a coma was still present so that we must
choose a larger value for the nucleus. Adopting the faintest measured
magnitude (Fig. 1) for the magnitude of the nucleus,
i.e.,
reported by Bus et al. (1989). The corresponding
Hv=6.62 indicates that a coma was still present so that we must
choose a larger value for the nucleus. Adopting the faintest measured
magnitude (Fig. 1) for the magnitude of the nucleus,
i.e.,
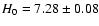 ,
we found that
,
we found that
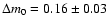 is the
best value that fits all the observations of Fig. 2,
using a
is the
best value that fits all the observations of Fig. 2,
using a 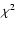 test. The errors bar of 0.03 on
test. The errors bar of 0.03 on
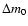 is
calculated in order to fit all the measurements at the 1
is
calculated in order to fit all the measurements at the 1 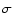 level. Our value
level. Our value
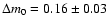 together with the
consideration of Marcialis & Buratti (1993) that
"Chiron currently presents an approximately equatorial aspect to
the Earth'', indicates a nearly spherical nucleus with a ratio of
semi-axes
together with the
consideration of Marcialis & Buratti (1993) that
"Chiron currently presents an approximately equatorial aspect to
the Earth'', indicates a nearly spherical nucleus with a ratio of
semi-axes
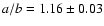 ,
assuming a uniform albedo distribution.
Moreover, as the inclination of Chiron is low (6.9
,
assuming a uniform albedo distribution.
Moreover, as the inclination of Chiron is low (6.9 )
and as
it was observed far from the Earth by Marcialis & Buratti
(
)
and as
it was observed far from the Earth by Marcialis & Buratti
(
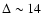 AU), we conclude that its pole is approximately
perpendicular to its orbital plane.
AU), we conclude that its pole is approximately
perpendicular to its orbital plane.
Table 1:
Absolute magnitudes Hv and magnitude variations
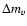 of the lightcurve of Chiron.
of the lightcurve of Chiron.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f2.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg34.gif) |
Figure 2:
The amplitude of the lightcurve
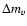 of Chiron as a function of the absolute magnitude Hv. The data points are the observations reported in Table 1 (except those of 29 February 1988 and 20 February 1993).
of Chiron as a function of the absolute magnitude Hv. The data points are the observations reported in Table 1 (except those of 29 February 1988 and 20 February 1993). |
| Open with DEXTER |
Table 2:
Infrared and radio observations of Chiron
Table 2 summarizes the infrared and radio observations of Chiron. The results are separated in three different wavelength intervals: 10-25  m for the mid-infrared, 25-160
m for the mid-infrared, 25-160  m for the far-infrared and 800-1200
m for the far-infrared and 800-1200  m for the radio (submillimetric and millimetric) domains. There is no observations between 160 and 800
m for the radio (submillimetric and millimetric) domains. There is no observations between 160 and 800  m.
m.
The first interval 10-25  m is in the Wien region of the spectral energy distribution (SED) for an expected color temperature of 120 K (Campins et al. 1994).
Observations in this range were first performed by Lebofsky et al. (1984) at 22.5
m is in the Wien region of the spectral energy distribution (SED) for an expected color temperature of 120 K (Campins et al. 1994).
Observations in this range were first performed by Lebofsky et al. (1984) at 22.5  m, later by Campins et al. (1994) between 10.6 and 20.0
m, later by Campins et al. (1994) between 10.6 and 20.0  m, and recently by Fernandez et al. (2002) at 12.5 and 17.9
m, and recently by Fernandez et al. (2002) at 12.5 and 17.9  m. Altogether, these observations lead to a large range of radius values, between 70 and 104 km (Table 3).
m. Altogether, these observations lead to a large range of radius values, between 70 and 104 km (Table 3).
The second interval 25-160  m contains the maximum of the SED. The IRAS observations performed in 1983 at 25 and 60
m contains the maximum of the SED. The IRAS observations performed in 1983 at 25 and 60  m (Sykes & Walker 1991) did not detect Chiron but allow to set an upper limit for the radius of 186 km.
Chiron was later unambigously detected thanks to observations performed with the ISOPHOT photometer aboard the ISO satellite from 8 to 15 June 1996 (Peschke 1997). Chiron was then near perihelion at a heliocentric distance of 8.46 AU, thus maximizing its thermal emission. Four filters centered at 25, 60, 100 and 160
m (Sykes & Walker 1991) did not detect Chiron but allow to set an upper limit for the radius of 186 km.
Chiron was later unambigously detected thanks to observations performed with the ISOPHOT photometer aboard the ISO satellite from 8 to 15 June 1996 (Peschke 1997). Chiron was then near perihelion at a heliocentric distance of 8.46 AU, thus maximizing its thermal emission. Four filters centered at 25, 60, 100 and 160  m were used. We calculated the average of the infrared fluxes over the three nights of observation, weighted by the error on the flux for each wavelength and normalized to
m were used. We calculated the average of the infrared fluxes over the three nights of observation, weighted by the error on the flux for each wavelength and normalized to
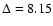 AU (the difference on
AU (the difference on 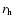 and
and 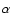 is marginal), and we obtained
is marginal), and we obtained 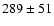 mJy,
mJy, 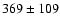 mJy,
mJy, 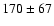 mJy and
mJy and 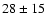 mJy at 25
mJy at 25  m, 60
m, 60  m, 100
m, 100  m and 160
m and 160  m respectively. The error-bars reflect the statistical errors derived with the ISOPHOT Interactive Analysis software (PIA) and the current absolute calibration accuracy of 30% of the detectors.
The fluxes at 160
m respectively. The error-bars reflect the statistical errors derived with the ISOPHOT Interactive Analysis software (PIA) and the current absolute calibration accuracy of 30% of the detectors.
The fluxes at 160  m must be considered with caution. Measurements of faint point sources with ISOPHOT at this wavelength were exceedingly difficult because of the sky confusion noise (Kiss et al. 2001). The real uncertainty on those measurements is therefore larger than the formal values given in Table 2. The ISOPHOT observations at 25, 60 and 100
m must be considered with caution. Measurements of faint point sources with ISOPHOT at this wavelength were exceedingly difficult because of the sky confusion noise (Kiss et al. 2001). The real uncertainty on those measurements is therefore larger than the formal values given in Table 2. The ISOPHOT observations at 25, 60 and 100  m are particulary well suited to determine the radius of Chiron, as they cover the maximum of the SED. The interpretation of these ISOPHOT observations, which has not yet been done, is presented in Sect. 4.
m are particulary well suited to determine the radius of Chiron, as they cover the maximum of the SED. The interpretation of these ISOPHOT observations, which has not yet been done, is presented in Sect. 4.
The last wavelength interval 800-1200  m corresponds to the Rayleigh-Jeans regime where the flux is proportional to
m corresponds to the Rayleigh-Jeans regime where the flux is proportional to
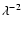 .
The observations are very difficult to perform, because the expected signal is very low. The main advantage of these measurements resides in their low sensitivity to the color temperature of the body, that is to the thermal model. Jewitt & Luu (1992) could not detect Chiron at 800
.
The observations are very difficult to perform, because the expected signal is very low. The main advantage of these measurements resides in their low sensitivity to the color temperature of the body, that is to the thermal model. Jewitt & Luu (1992) could not detect Chiron at 800  m, and they gave a
m, and they gave a 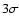 upper limit of 150 km for the radius. The successful detection of Chiron later performed by Altenhoff & Stumpff (1995) at 1200
upper limit of 150 km for the radius. The successful detection of Chiron later performed by Altenhoff & Stumpff (1995) at 1200  m led to a radius of 84 km.
m led to a radius of 84 km.
Table 3:
Radius and geometric albedo determination of Chiron.
The past infrared and radio observations were interpreted using either a standard thermal model (STM) which assumes no thermal inertia, or an isothermal-latitude model (ILM) which assumes an infinite thermal inertia (Lebofsky & Spencer 1989), or a modified STM which includes thermal inertia (Jewitt & Luu 1992).
The strong influence of the thermal inertia I is highlighted in Fig. 3 where the surface temperature at the equator is plotted as a function of longitude.
When I increases, the profile becomes smoother as more energy is transfered by conduction from the day side into the nucleus to heat the night side. In other words, when I increases, the temperature decreases on the day side and increases on the night side. In the extreme case of an infinite thermal inertia, the temperature is constant across the nucleus for a given latitude.
Note that Chiron was always observed with a phase angle
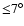 .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f3.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg46.gif) |
Figure 3:
Equatorial temperature profiles over the nucleus surface for thermal inertia I=0, 10, 100 J K-1 m-2 s-1/2 and  at r=8.5 AU.
at r=8.5 AU. |
| Open with DEXTER |
When using the infrared or radio observations alone, the size of the nucleus is determined assuming a geometric albedo. Adding visible observations allows to independently determine the size and the geometric albedo. This method, extensively used on asteroids, can give excellent results as recently demonstrated for 433 Eros: the combination of the visible and infrared ground-based observations performed in 1974/75 by Morrison (1976) led to a radius of 22 km and a geometric albedo of 0.18, a result in very good agreement with the recent in-situ observations performed by the NEAR spacecraft which led to a
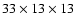 km nucleus and a geometric albedo of 0.16.
Table 3 summarizes the radius and geometric albedo determinations obtained by different authors for Chiron. Depending upon the observation and the model, the values vary from 71 km to 104 km with a mean value of
km nucleus and a geometric albedo of 0.16.
Table 3 summarizes the radius and geometric albedo determinations obtained by different authors for Chiron. Depending upon the observation and the model, the values vary from 71 km to 104 km with a mean value of  88 km. Values of the geometric albedo range from 0.10 to 0.17, with a mean value of
88 km. Values of the geometric albedo range from 0.10 to 0.17, with a mean value of  0.14.
0.14.
The determination of the radius and the geometric albedo of the nucleus of Chiron faces two kinds of difficulties. First, it is model-dependent as a thermal model is required to interpret the infrared and radio observations. It is important to assess this dependence and, in particular, the impact of the thermal inertia. Second, the nucleus is often active and its coma, even too faint to be detected, may affect the results.
The occultation of a star by a solid body is in principle a powerful method to determine its size. Such an event took place for Chiron in November 1993 and observations were attempted from five different sites in California. Only one site was successful in recording a useful lightcurve, although a second site had a marginal detection of the extinction of the starlight, and a preliminary value of the size of Chiron was reported by Buie et al. (1993). There are many problems involved in the analysis of an occulation, amplified in this case by the very small apparent size of Chiron ( 0.03 arcsec) and by the presence of a coma. Moreover the sampling of the lightcurve is somewhat sparse, only eight points, and its interpretation is not unique, especially if a coma is introduced. The detailed analysis performed by Bus et al. (1996) led to two slightly different values (Table 3) depending upon whether the marginal detection is considered. Their analysis convincingly shows that the star track was nearly diametral and that a dust coma was indeed present (and possibly jets) consistent with an absolute magnitude
Hv=6.41 at the time of the occultation. Taking into account the marginal detection, they determined a radius of 89.6
0.03 arcsec) and by the presence of a coma. Moreover the sampling of the lightcurve is somewhat sparse, only eight points, and its interpretation is not unique, especially if a coma is introduced. The detailed analysis performed by Bus et al. (1996) led to two slightly different values (Table 3) depending upon whether the marginal detection is considered. Their analysis convincingly shows that the star track was nearly diametral and that a dust coma was indeed present (and possibly jets) consistent with an absolute magnitude
Hv=6.41 at the time of the occultation. Taking into account the marginal detection, they determined a radius of 89.6 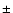 6.8 km.
6.8 km.
In order to interpret the ISOPHOT observations as well as all other thermal observations in a coherent way, we considered a thermal model as well as appropriate assumptions. We assumed a spherical nucleus rotating with a period of 5.92 h with its spin axis perpendicular to the comet orbital plane, in good agreement with the observations discussed in the previous section.
The parameter 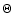 introduced by Spencer et al. (1989) is useful to estimate the influence of the heat conduction and to choose the appropriate thermal model. It is defined as:
introduced by Spencer et al. (1989) is useful to estimate the influence of the heat conduction and to choose the appropriate thermal model. It is defined as:
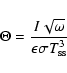 |
(2) |
where I is the thermal inertia, 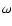 is the rotational frequency,
is the rotational frequency, 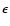 is the infrared emissivity,
is the infrared emissivity, 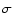 is the Stefan Boltmann's constant and
is the Stefan Boltmann's constant and
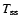 is the subsolar equilibrium temperature.
is the subsolar equilibrium temperature.
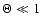 implies a slow-rotator and
implies a slow-rotator and
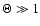 ,
a fast-rotator. For Chiron, with a nucleus spin period
,
a fast-rotator. For Chiron, with a nucleus spin period
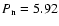 h and a maximum surface temperature
h and a maximum surface temperature
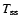 of 150 K (Fig. 3), we obtained
of 150 K (Fig. 3), we obtained
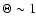 for a thermal inertia I=10 MKS (where 1 MKS unit = 1 J K-1 m-2 s-1/2) and
for a thermal inertia I=10 MKS (where 1 MKS unit = 1 J K-1 m-2 s-1/2) and
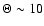 for I=100 MKS. Chiron is therefore intermediate between the slow and the fast-rotators and the heat conduction into the nucleus must be introduced.
We consider a mixed model of refractory dust and water ice grains in an attempt to take into account the detection of water ice on the surface of Chiron (Foster et al. 1999; Luu et al. 2000). Our model does not take into account the sublimation of CO as we assumed that CO is located deep below the surface so that its effects on the surface temperature are negligible.
for I=100 MKS. Chiron is therefore intermediate between the slow and the fast-rotators and the heat conduction into the nucleus must be introduced.
We consider a mixed model of refractory dust and water ice grains in an attempt to take into account the detection of water ice on the surface of Chiron (Foster et al. 1999; Luu et al. 2000). Our model does not take into account the sublimation of CO as we assumed that CO is located deep below the surface so that its effects on the surface temperature are negligible.
The mixed model (MM) has already been introduced by Lamy et al. (2002) to interpret the infrared observations of the nucleus of 22P/Kopff. It assumes an intimate, microscopic mixture of dust and water ice grains, so that the thermal coupling between the grains is perfect and there is only one temperature for the mixture. As the ice is "dirty'', the geometric albedo can be low (Clark & Lucey 1984) and this is further discussed in Sect. 4.2 below. As explained by Jewitt & Luu (1992), the sublimation of water ice can be neglected for Chiron, and in this case, our MM is equivalent to their thermal model: a STM with heat conduction.
Thermal balance on the surface between the solar flux received by the nucleus on the one hand, the reradiated flux and the heat conduction on the other hand is expressed as:
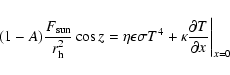 |
(3) |
where A=pvq is the product of the geometric albedo pv with the phase integral q,
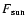 [Wm-2] is the solar constant,
[Wm-2] is the solar constant, 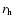 [AU] is the heliocentric distance, z is the zenithal angle,
[AU] is the heliocentric distance, z is the zenithal angle, 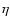 is the beaming factor introduced by Lebofsky & Spencer (1989), T [K] is the surface temperature,
is the beaming factor introduced by Lebofsky & Spencer (1989), T [K] is the surface temperature, 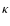 [Wm-1K-1] is the thermal conductivity and x measures the depth. Numerical values for the parameters will be discussed in Sect. 3.4.
Although the sublimation of water ice is neglected, its presence on the surface will appear through the Bond albedo A.
[Wm-1K-1] is the thermal conductivity and x measures the depth. Numerical values for the parameters will be discussed in Sect. 3.4.
Although the sublimation of water ice is neglected, its presence on the surface will appear through the Bond albedo A.
We considered the one-dimensional time-dependent equation for the heat conduction:
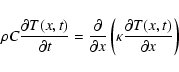 |
(4) |
where 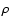 [kg/m3] is the mass density and C [J/kg/K] is the specific heat capacity of the nucleus. We solved this equation using a method similar to that described by Spencer et al. (1989). We changed x to
[kg/m3] is the mass density and C [J/kg/K] is the specific heat capacity of the nucleus. We solved this equation using a method similar to that described by Spencer et al. (1989). We changed x to 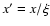 ,
where
,
where
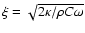 [m] is the characteristic length of the heat wave which propagates into the subsurface. Then,
Eq. (4) becomes Eq. (5) and
Eq. (3) becomes Eq. (6):
[m] is the characteristic length of the heat wave which propagates into the subsurface. Then,
Eq. (4) becomes Eq. (5) and
Eq. (3) becomes Eq. (6):
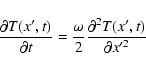 |
(5) |
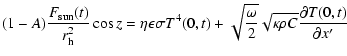 |
|
|
(6) |
where
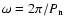 is the rotational frequency.
is the rotational frequency.
The boundary conditions are given by Eq. (6) at the surface, and by Eq. (7) at a depth d:
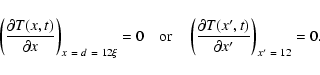 |
(7) |
This last condition assumes that the temperature remains constant below a (thick enough) layer of thickness d. The choice of this constant temperature is explained in detail by Spencer et al. (1989). We took 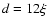 ,
which ensures a good convergence; a higher d does not change the surface temperature.
,
which ensures a good convergence; a higher d does not change the surface temperature.
In Eq. (6), all thermal parameters of the nucleus are regrouped into a single quantity, the thermal inertia
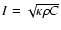 [J K-1 m-2 s-1/2]. This is now the only parameter that we will consider when solving the system of Eqs. (5)+(6)+(7). Table 4 gives estimates of the thermal inertia for different bodies of the Solar System.
[J K-1 m-2 s-1/2]. This is now the only parameter that we will consider when solving the system of Eqs. (5)+(6)+(7). Table 4 gives estimates of the thermal inertia for different bodies of the Solar System.
The nucleus is divided in several layers of thickness dx' where dx'=0.25 is enough for Chiron to ensure a good convergence. The longitude is represented by the time parameter t. As t increases, the nucleus rotates and the longitude, reckoned from the sub-solar point, changes. We took a step d
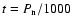 ,
which correponds to
,
which correponds to 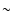 21 s for a period
21 s for a period
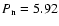 h and which is enough to reach the convergence. Tests were performed with lower values of dx' and dt and led to marginal differences.
h and which is enough to reach the convergence. Tests were performed with lower values of dx' and dt and led to marginal differences.
We calculated the temperature T at each point
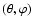 of the surface to obtain a temperature map
of the surface to obtain a temperature map
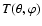 ,
where
,
where 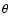 is the latitude and
is the latitude and 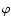 is the longitude. For illustration, the temperature profile along the equator (
is the longitude. For illustration, the temperature profile along the equator (
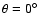 )
is displayed in Fig. 3 for different thermal inertia.
)
is displayed in Fig. 3 for different thermal inertia.
Table 4:
Estimated thermal inertia I for different bodies of the Solar System.
The thermal flux
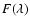 of an unresolved nucleus measured by an observer located at geocentric distance
of an unresolved nucleus measured by an observer located at geocentric distance 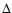 is the integral over the nucleus of
is the integral over the nucleus of
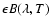 where
where
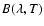 is the Planck function and
is the Planck function and
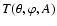 is given by the MM:
is given by the MM:
![\begin{displaymath}
F(\lambda) = \epsilon
\int \int {B}\left[\lambda,T(\theta,\varphi,A)\right] \Omega {\rm d}S.
\end{displaymath}](/articles/aa/full/2004/03/aa3595/img84.gif) |
(8) |
The solid angle 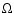 is given by:
is given by:
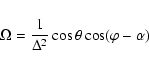 |
(9) |
and the element of surface by:
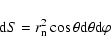 |
(10) |
where 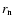 is the radius of the nucleus,
is the radius of the nucleus, 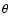 is the latitude,
is the latitude, 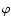 is the longitude measured from the sub-solar point and
is the longitude measured from the sub-solar point and 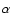 is the phase angle.
is the phase angle. 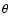 and
and 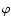 are linked to the zenithal angle z by
are linked to the zenithal angle z by
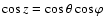 .
We calculated the thermal flux by performing a double integration over the hemisphere of the nucleus which is visible from Earth i.e., satifying
.
We calculated the thermal flux by performing a double integration over the hemisphere of the nucleus which is visible from Earth i.e., satifying
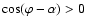 .
.
The various parameters involved in the thermal models are not known for cometary nuclei. We discuss below how we selected their respective values.
The infrared emissivity 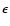 is taken equal to 0.95, the middle point of the interval 0.9-1.0 always quoted in the literature. As the interval is very small and the value near 1.0, this uncertainty has a negligible influence on the calculated thermal flux.
is taken equal to 0.95, the middle point of the interval 0.9-1.0 always quoted in the literature. As the interval is very small and the value near 1.0, this uncertainty has a negligible influence on the calculated thermal flux.
The beaming factor 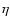 reflects the influence of surface roughness which produces an anisotropic thermal emission, and theorically ranges from 0 to 1. For physical reasons,
reflects the influence of surface roughness which produces an anisotropic thermal emission, and theorically ranges from 0 to 1. For physical reasons, 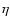 is higher than 0.7, otherwise it implies a very high, unrealistic, roughness, with a rms slope higher than 1 (Lagerros 1998). We adopted the value of
is higher than 0.7, otherwise it implies a very high, unrealistic, roughness, with a rms slope higher than 1 (Lagerros 1998). We adopted the value of
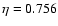 ,
derived from observations of 1 Ceres and 2 Pallas by Lebofsky et al. (1986), as those objects have a geometric albedo (0.10 and 0.14 respectively) similar to that of Chiron. Note that, on the basis of the work of Lagerros (1998), Lamy et al. (2002) used a slightly larger value
,
derived from observations of 1 Ceres and 2 Pallas by Lebofsky et al. (1986), as those objects have a geometric albedo (0.10 and 0.14 respectively) similar to that of Chiron. Note that, on the basis of the work of Lagerros (1998), Lamy et al. (2002) used a slightly larger value 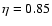 for the nucleus of 22P/Kopff as this body has a lower geometric albedo
pv=0.04. As the temperature varies as
for the nucleus of 22P/Kopff as this body has a lower geometric albedo
pv=0.04. As the temperature varies as
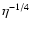 ,
the beaming factor may have an important effect on thermal flux and, in turn, on the radius determination of the nucleus.
,
the beaming factor may have an important effect on thermal flux and, in turn, on the radius determination of the nucleus.
The Bond albedo A requires a knowledge of the phase integral q, which measures the angular dependence of the scattered radiation.
We choose q=0.4, the value found for 2 Pallas (Lebofsky et al. 1986) since its geometric albedo
pv=0.14 is comparable to that of Chiron. We note that this value of q is significantly different from the value q=0.28 chosen for 22P/Kopff (Lamy et al. 2002) since those two objects have quite difference surface properties. However q has little influence and the above values yielded similar results.
For the geometric albedo, we took
pv=0.11, which is the value derived from the ISOPHOT observations and which will be discussed in the next section. It will then be shown that the results are almost independent of the geometric albedo in the range 0.01-0.15.
The determination of the thermal inertia I and the radius 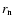 of the nucleus is performed by minimizing the
of the nucleus is performed by minimizing the 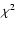 expression defined as:
expression defined as:
![\begin{displaymath}\chi^2(I,r_{\rm n})=\sum_{i=1}^{n}\Bigg[\frac{F_i-F(\lambda_i,I,r_{\rm n})}{\sigma_i}\Bigg]^2
\end{displaymath}](/articles/aa/full/2004/03/aa3595/img93.gif) |
(11) |
where Fi is the measured flux at the wavelength 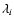 and
and 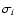 the corresponding error bar. We took into account the average ISOPHOT fluxes from the three nights of observation presented in Sect. 2.2 (Table 2), at 25, 60 and 100
the corresponding error bar. We took into account the average ISOPHOT fluxes from the three nights of observation presented in Sect. 2.2 (Table 2), at 25, 60 and 100  m. We did not take into account the observation at 160
m. We did not take into account the observation at 160  m in our discussion for reasons explained in Sect. 2.2. Figure 4 presents the value of
m in our discussion for reasons explained in Sect. 2.2. Figure 4 presents the value of 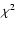 as a function of I and
as a function of I and 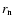 .
Its lower value is obtained, at the 1
.
Its lower value is obtained, at the 1 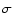 level (
level (
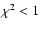 ), for a radius
), for a radius
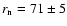 km and a thermal inertia
I=3+5-3 MKS.
km and a thermal inertia
I=3+5-3 MKS.
Figure 5 displays the SED of Chiron from 10  m to 200
m to 200  m for the mixed model (MM), for the above values and the 1
m for the mixed model (MM), for the above values and the 1 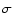 uncertainty. The fit to the data points is excellent, except at 160
uncertainty. The fit to the data points is excellent, except at 160  m for reasons already discussed.
m for reasons already discussed.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3595_f4.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg97.gif) |
Figure 4:
Value of the 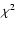 expression as a function of the radius
expression as a function of the radius 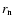 and the thermal inertia I. The cross represents best estimate of
and the thermal inertia I. The cross represents best estimate of 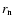 and I, i.e. where
and I, i.e. where 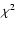 is minimum.
is minimum. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f5.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg98.gif) |
Figure 5:
The SED of the nucleus of Chiron for the mixed model (MM) with a radius
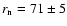 km and a thermal inertia
I=3+5-3 MKS. The squares are the ISOPHOT data at 25, 60, 100 and 160 km and a thermal inertia
I=3+5-3 MKS. The squares are the ISOPHOT data at 25, 60, 100 and 160  m with their m with their 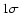 error bars.
error bars. |
| Open with DEXTER |
The value of 71 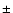 5 km for the radius is lower than the bulk of
the previous estimates (Table 3), but in excellent
agreement with the recent determination of 74
5 km for the radius is lower than the bulk of
the previous estimates (Table 3), but in excellent
agreement with the recent determination of 74 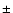 4 km by Fernandez
et al. (2002). The value of
3+5-3 MKS for
the thermal inertia is very low, but coherent with our present
understanding of primitive bodies. Indeed, Fernandez et al.
(2002) determined a thermal inertia <10.5 MKS for
Asbolus, and Spencer et al. (1989) suggested a thermal
inertia <15 MKS for asteroids Ceres and Pallas, lower than that
of the Moon (50 MKS). The low thermal inertia of Chiron indicates
a low thermal conductivity for the surface material, and probably a
porous surface as supposed for the majority of cometary nuclei (e.g.
Klinger et al. 1996; Skorov et al. 1999).
4 km by Fernandez
et al. (2002). The value of
3+5-3 MKS for
the thermal inertia is very low, but coherent with our present
understanding of primitive bodies. Indeed, Fernandez et al.
(2002) determined a thermal inertia <10.5 MKS for
Asbolus, and Spencer et al. (1989) suggested a thermal
inertia <15 MKS for asteroids Ceres and Pallas, lower than that
of the Moon (50 MKS). The low thermal inertia of Chiron indicates
a low thermal conductivity for the surface material, and probably a
porous surface as supposed for the majority of cometary nuclei (e.g.
Klinger et al. 1996; Skorov et al. 1999).
As pointed out above, the only parameter on which the thermal model
and consequently the results are sensitive is the beaming factor
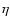 ,
which ranges from 0.7-1.0 (see Sect. 3.4). For
,
which ranges from 0.7-1.0 (see Sect. 3.4). For
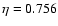 ,
as justified in Sect. 3.4, we obtained the best fit
with a radius
,
as justified in Sect. 3.4, we obtained the best fit
with a radius
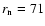 km and a thermal inertia I=3 MKS.
For the extreme, unrealistic value of
km and a thermal inertia I=3 MKS.
For the extreme, unrealistic value of 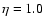 ,
the best fit is
obtained with
,
the best fit is
obtained with
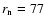 km and I=0 MKS, and for
km and I=0 MKS, and for
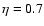 with
with
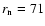 km and I=5 MKS. For
km and I=5 MKS. For
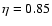 ,
the value used for 22P/Kopff (Lamy et al.
2002), we obtained
,
the value used for 22P/Kopff (Lamy et al.
2002), we obtained
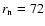 km and I=0 MKS.
Consequently, the choice of
km and I=0 MKS.
Consequently, the choice of 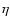 ,
in the range 0.7-0.85, has
practically no influence on the determination of the radius and the
thermal inertia.
,
in the range 0.7-0.85, has
practically no influence on the determination of the radius and the
thermal inertia.
In order to determine the size and the geometric albedo of Chiron
without any assumptions, we need two independent relationships. The
first one is given by the visible observations and we used the value
discussed in Sect. 2.1,
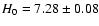 ,
for the absolute Vmagnitude of the nucleus. The nucleus radius
,
for the absolute Vmagnitude of the nucleus. The nucleus radius 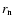 and the
geometric albedo pv are linked to H0 using the
relationship of Bowell et al. (1989):
and the
geometric albedo pv are linked to H0 using the
relationship of Bowell et al. (1989):
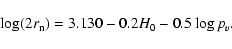 |
(12) |
The second relationship between 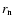 and pv is given by the thermal flux via
Eq. (8) where the surface temperature T depends on
pv through A=pvq. We used I=3 MKS, as
determined previously, and the ISOPHOT fluxes at 25, 60 and 100
and pv is given by the thermal flux via
Eq. (8) where the surface temperature T depends on
pv through A=pvq. We used I=3 MKS, as
determined previously, and the ISOPHOT fluxes at 25, 60 and 100  m. We graphically combined the visible and the infrared
constraints, as illustrated in Fig. 6. The
curves represents the infrared and visible constraints which cross
themselves nearly orthogonally; this minimizes the error on the
determination of
m. We graphically combined the visible and the infrared
constraints, as illustrated in Fig. 6. The
curves represents the infrared and visible constraints which cross
themselves nearly orthogonally; this minimizes the error on the
determination of 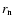 and pv. Moreover, the infrared
constraint is almost independent of the geometric albedo in the range
0.01-0.15, yielding a quasi constant value for the radius in this
range (variation <3%). The geometric albedo is only constrained by
the absolute magnitude of the nucleus H0.
and pv. Moreover, the infrared
constraint is almost independent of the geometric albedo in the range
0.01-0.15, yielding a quasi constant value for the radius in this
range (variation <3%). The geometric albedo is only constrained by
the absolute magnitude of the nucleus H0.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{3595_f6.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg105.gif) |
Figure 6:
The albedo-radius diagram for Chiron. The infrared constraints come from the ISOPHOT observations with the models presented in Fig. 3. The visible constraint is given by the visible absolute magnitude of the nucleus of Chiron
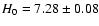 . . |
| Open with DEXTER |
For our solution, a MM with a thermal inertia of 3 MKS and a radius
of 71 km, we obtained a geometric albedo of 0.11 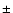 0.02, the
uncertainty coming from the error affecting H0. This value is in
excellent agreement with the determination of Campins et al.
(1994). Fernandez et al. (2002)
obtained a higher geometric albedo of 0.17
0.02, the
uncertainty coming from the error affecting H0. This value is in
excellent agreement with the determination of Campins et al.
(1994). Fernandez et al. (2002)
obtained a higher geometric albedo of 0.17 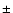 0.02 assuming
H0=6.96. Using H0=7.28 instead yields 0.13
0.02 assuming
H0=6.96. Using H0=7.28 instead yields 0.13 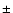 0.02, in
excellent agreeement with our determination. The geometric albedo
cannot be used to constrain the thermal inertia. This shows the
importance of combining infrared AND visible observations to estimate
altogether pv,
0.02, in
excellent agreeement with our determination. The geometric albedo
cannot be used to constrain the thermal inertia. This shows the
importance of combining infrared AND visible observations to estimate
altogether pv, 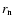 and I.
and I.
The geometric albedo of 0.11 is higher than the typical range
0.02-0.06 found for the nucleus of short period comets (Lamy et al.
2004) and this probably results from the presence of water
ice at the surface of Chiron, a question discussed in the following
section.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f7.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg106.gif) |
Figure 7:
Observed spectra of Chiron compared to laboratory experiments
with mixtures of charcoal and water ice. |
| Open with DEXTER |
We now consider the spectrum of Chiron to characterize its surface.
We assembled a composite spectrum by combining the results of Lebofsky
et al. (1984), Foster et al. (1999) and
Luu et al. (2000) in Figs. 7-10. We normalized the spectrum of Foster et al.
and Luu et al. at 2.2  m, and we applied a scaling factor of
0.95 to the spectrum of Lebofsky et al. (originally normalized at
0.55
m, and we applied a scaling factor of
0.95 to the spectrum of Lebofsky et al. (originally normalized at
0.55  m) in order to insure continuity at 1
m) in order to insure continuity at 1  m. Each
spectrum was sampled and then interpolated using cubic splines.
There are obvious problems with the infrared spectra, in particular
with that of Luu et al. (2000): the 1.5
m. Each
spectrum was sampled and then interpolated using cubic splines.
There are obvious problems with the infrared spectra, in particular
with that of Luu et al. (2000): the 1.5  m band
appears misplaced and the apparent absorption longward of 2.2
m band
appears misplaced and the apparent absorption longward of 2.2  m is probably spurious. However, the composite spectrum exhibit
well-defined features, an almost flat part extending from 0.5 to
1.1
m is probably spurious. However, the composite spectrum exhibit
well-defined features, an almost flat part extending from 0.5 to
1.1  m and the two aborption band of water ice at 1.5 and
2.0
m and the two aborption band of water ice at 1.5 and
2.0  m. These features, and particulary the contrast of the
bands, can be used to set limits on the fractional coverage of ice.
m. These features, and particulary the contrast of the
bands, can be used to set limits on the fractional coverage of ice.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f8.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg107.gif) |
Figure 8:
Observed spectra of Chiron compared to two mixtures
of astronomical silicate and water ice grains in different proportions.
The grain size is 10  m. m. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f9.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg108.gif) |
Figure 9:
Observed spectra of Chiron compared to two mixtures
of astronomical silicate and water ice grains, with grain sizes of 1 and
100  m. m. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f10.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg109.gif) |
Figure 10:
Observed spectra of Chiron compared to three different mixtures of 30% of water ice +70% of refractory grains (silicate, glassy carbon or kerogen). The grain size is 10  m. m. |
| Open with DEXTER |
We start by comparing the spectrum of Chiron with laboratory results
on different samples which are intimate, microscopic mixtures of
different grains. The main advantage of using spectra obtained
with laboratory experiments is that they are far more realistic than
computed spectrum, which further involve many unknown parameters.
Figure 7 diplays the reflectance of two
mixtures of water ice and charcoal measured by Clark & Lucey
(1984) using the experiment chamber of Clark
(1981). Mixture A (50% charcoal +50% water ice)
exhibits a 2.0  m band approximately similar to the observed
one but unfortunately a steep gradient in the visible. Mixture B
(70% charcoal +30% water ice) alleviates this problem at the
expense of producing too low a reflectance in the visible and too low
a contrast of the 2.0
m band approximately similar to the observed
one but unfortunately a steep gradient in the visible. Mixture B
(70% charcoal +30% water ice) alleviates this problem at the
expense of producing too low a reflectance in the visible and too low
a contrast of the 2.0  m band. None of the two mixtures
exhibits the 1.5
m band. None of the two mixtures
exhibits the 1.5  m aborption band. It is tempting to use a
linear combination of the A and B spectra to better reproduce the
observations. Figure 7 displays the solution
"0.25 A + 0.75 B'' which indeed offers a better fit to the
observations than any of the two individual mixtures. Applying the
above linear scaling, this solution contains approximately 65% of
charcoal and 35% of water ice. The fit is not perfect but gives
a rough idea of the amount of water ice on the surface of Chiron,
m aborption band. It is tempting to use a
linear combination of the A and B spectra to better reproduce the
observations. Figure 7 displays the solution
"0.25 A + 0.75 B'' which indeed offers a better fit to the
observations than any of the two individual mixtures. Applying the
above linear scaling, this solution contains approximately 65% of
charcoal and 35% of water ice. The fit is not perfect but gives
a rough idea of the amount of water ice on the surface of Chiron,
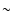 35%. Unfortunately, the geometric albedo of a body having
a surface composed of such a mixture is not known but is probably low
owing to the large percentage of refractory material, a result
justified in the next section.
35%. Unfortunately, the geometric albedo of a body having
a surface composed of such a mixture is not known but is probably low
owing to the large percentage of refractory material, a result
justified in the next section.
We now calculate the reflectance of simple areal mixtures of water ice
and other refractory materials. The advantage of this approach
is twofold, first the parameters may be varied at will, and second the
reflectance and the geometric albedo of a body covered with the
considered mixture can be simultaneously calculated. The drawback of
this approach is the large number of (unknown) parameters such as the
optical properties of the materials and the distribution function of
the grain size, and the solutions are no means unique. The model
considers macroscopic mixtures so that there is no interaction
between the components, and the resulting reflectance spectrum is a
linear combination of the individual spectra according to the selected
fractional coverage of each component. It has already been
applied to Chiron: Foster et al. (1999) combined 20%
of water ice with 80% of a spectrally neutral material while Luu et
al. (2000) combined water ice and olivine in unspecified
proportion to interpret their observations.
For the present study, we used the numerical code of Roush
(1994), based on the Hapke formalism (Hapke
1993) and considered mixtures of water ice with three
different refractory materials. First, a silicate, known as
"astronomical silicate'' in the literature; its optical constants
come from Draine & Lee (1984). Second, glassy carbon,
an amorphous form of carbon; its optical constants come from Edoh
(1983). Third, a kerogen, a highly processed organic
residue; its optical constants come from Khare et al.
(1990). The optical constants of water ice come from
Warren (1984).
Figure 8 displays our results obtained for
a mixture of water ice + silicate with a unique grain size
of 10  m. The percentage of water ice was tuned to produce the
observed contrast of the 2.0
m. The percentage of water ice was tuned to produce the
observed contrast of the 2.0  m band. It amounts to 15%
to match the spectrum of Foster et al. (1999) and to
30% to match that of Luu et al. (2000). The fits are
quite satisfactory in the interval 1.4 to 2.1
m band. It amounts to 15%
to match the spectrum of Foster et al. (1999) and to
30% to match that of Luu et al. (2000). The fits are
quite satisfactory in the interval 1.4 to 2.1  m in spite of a
slight mismatch of the 1.5
m in spite of a
slight mismatch of the 1.5  m band, but this may comes
from the spectrum of Luu et al. (2000) as discussed above.
However, the amount of water ice strongly depends upon the grain size.
Figure 9 displays the same fit but, for
two different grain sizes, 1
m band, but this may comes
from the spectrum of Luu et al. (2000) as discussed above.
However, the amount of water ice strongly depends upon the grain size.
Figure 9 displays the same fit but, for
two different grain sizes, 1  m and 100
m and 100  m. In order to
match the observed spectrum and especially the contrast of the 2.0
m. In order to
match the observed spectrum and especially the contrast of the 2.0  m band, the amount of water ice must be less than 3% for a grain
size of 100
m band, the amount of water ice must be less than 3% for a grain
size of 100  m, and larger than 80% for a grain size of 1
m, and larger than 80% for a grain size of 1  m.
m.
In order to test whether the above mixtures are compatible with
the albedo of 0.11 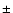 0.02 determined in Sect. 4.2, we used a
numerical code written by Roush (1994) to calculate the
geometric albedo of a spherical body in the framework of the Hapke
formalism. The results for the four mixtures water ice + astronomical
silicate considered in Figs. 8 and 9 are represented in Table 5. We obtained similar results for the
other refractory materials, glassy carbon and kerogen. The solution
which best matches both the observed reflectance and albedo of Chiron
corresponds to a mixture of 30% of water ice +70% of refractory
material and a common grain size of
0.02 determined in Sect. 4.2, we used a
numerical code written by Roush (1994) to calculate the
geometric albedo of a spherical body in the framework of the Hapke
formalism. The results for the four mixtures water ice + astronomical
silicate considered in Figs. 8 and 9 are represented in Table 5. We obtained similar results for the
other refractory materials, glassy carbon and kerogen. The solution
which best matches both the observed reflectance and albedo of Chiron
corresponds to a mixture of 30% of water ice +70% of refractory
material and a common grain size of  10
10  m. The resulting
spectra are displayed in Fig. 10. Smaller grain
sizes would require larger water ice fractions resulting in very large
albedos while larger grain sizes result in the opposite situation.
None of the mixture exhibits the observed visible spectrum of Chiron
althougth the discrepancies are not that large and much reduced
compared to the previous solution (Fig. 7).
One cannot reasonably hope that any of the selected material precisely
corresponds to the refractory component of Chiron. For the three
cases of surface composition introduced above (Fig.
10), we found geometric albedos of respectively
0.11 (silicate), 0.13 (glassy carbon) and 0.10 (kerogen), all in
excellent agreement with our result of 0.11
m. The resulting
spectra are displayed in Fig. 10. Smaller grain
sizes would require larger water ice fractions resulting in very large
albedos while larger grain sizes result in the opposite situation.
None of the mixture exhibits the observed visible spectrum of Chiron
althougth the discrepancies are not that large and much reduced
compared to the previous solution (Fig. 7).
One cannot reasonably hope that any of the selected material precisely
corresponds to the refractory component of Chiron. For the three
cases of surface composition introduced above (Fig.
10), we found geometric albedos of respectively
0.11 (silicate), 0.13 (glassy carbon) and 0.10 (kerogen), all in
excellent agreement with our result of 0.11  0.02.
0.02.
Table 5:
Calculated geometric albedos for different mixtures of water
ice + astronomical silicates and different grain sizes.
In summary, the spectrum of the nucleus of Chiron and its relatively
high geometric albedo are both consistent with a surface approximately
composed of 30% of water ice and 70% of a refractory material.
We now systematically apply our thermal model, i.e., the mixed model
with the parameters given in Sect. 3.4, a geometric albedo of 0.11
and a thermal inertia of 3 MKS, to all past infrared and radio
observations. This is the first time that this set of observations is
homogeneously analyzed with the same model, thus allowing a meaningful
comparison of the resulting sizes of the nucleus of Chiron. Table 6 summarizes the different radius determinations
which may differ from those found by the authors (cf. Table 3) since they used different thermal models and/or different
parameters. Figure 11 displays the radius
determination versus wavelength for all observations listed in
Table 6. Our result
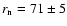 km
given by our mixed model is in excellent agreement with all
observations above 20
km
given by our mixed model is in excellent agreement with all
observations above 20  m, including the submillimetric
observations of Altenhoff & Stumpff (1995) at
1200
m, including the submillimetric
observations of Altenhoff & Stumpff (1995) at
1200  m. Our result is also consistent with the observations
of Fernandez et al. (2002) at 17.9
m. Our result is also consistent with the observations
of Fernandez et al. (2002) at 17.9  m and one
observation of Campins et al. (1994) at 19
m and one
observation of Campins et al. (1994) at 19  m.
The other observations of Campins et al. (1994) tend to
suggest a larger radius. This trend is more pronounced at
m.
The other observations of Campins et al. (1994) tend to
suggest a larger radius. This trend is more pronounced at  10
10  m, and the observations of Campins et al. (1994)
and Fernandez et al. (2002) yield a radius of
87-112 km. A radius of
m, and the observations of Campins et al. (1994)
and Fernandez et al. (2002) yield a radius of
87-112 km. A radius of 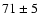 km is not compatible with the
occultation performed by Bus et al. (1996), unless taking
into account their error bars at the 3
km is not compatible with the
occultation performed by Bus et al. (1996), unless taking
into account their error bars at the 3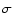 level. The question of
reconciling thermal infrared observations with results from
occultations has already been addressed by Fernandez et al.
(2002).
level. The question of
reconciling thermal infrared observations with results from
occultations has already been addressed by Fernandez et al.
(2002).
Table 6:
Nucleus radius from IR and radio observations of Chiron.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f11.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg112.gif) |
Figure 11:
Determination of the radius of Chiron from the infrared and radio observations of Table 2, using a mixed model (MM) with a geometric albedo of 0.11 and a thermal inertia of 3 MKS. The solid bold line and the hatched band represent our determination of 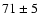 km. km. |
| Open with DEXTER |
We address the question of a possible contamination of the ISOPHOT observations by the coma by noting that our visible observation performed 10 days later (25 June 1996) yielded
Hv=6.57.
Assuming an absolute V magnitude of the nucleus of 7.28, we derived a coma contribution of 48% using:
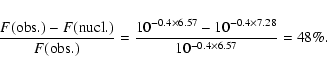 |
(13) |
But, since we derived a radius of 71 km, lower than previous determinations, it is very unlikely that there was any significant contribution of the coma to the infrared fluxes (if present at all, a faint coma contribution would be hidden by the large uncertainty of 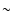 30% affecting the measurements). This has already been pointed out by Campins et al. (1994), two years before the ISOPHOT observations, when Chiron was even more active, and by West (1991), who argued that the blue color of the coma is most likely due to scattering by submicron dust grains.
30% affecting the measurements). This has already been pointed out by Campins et al. (1994), two years before the ISOPHOT observations, when Chiron was even more active, and by West (1991), who argued that the blue color of the coma is most likely due to scattering by submicron dust grains.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f12.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg114.gif) |
Figure 12:
Determination of the radius of Chariklo from the 20.3  m infrared and 1.2 mm radio observations of Table 7. Differents symbols are used for I=0, 10 and 100 MKS. The symbols at 1.2 mm have been deliberately offset left-right for clarity. The solid bold line and the hatched band represent our determination of m infrared and 1.2 mm radio observations of Table 7. Differents symbols are used for I=0, 10 and 100 MKS. The symbols at 1.2 mm have been deliberately offset left-right for clarity. The solid bold line and the hatched band represent our determination of 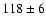 km. km. |
| Open with DEXTER |
Chariklo (1997 CU26) was discovered in 1997 with the Spacewatch
telescope (Scotti 1997). It has a perihelion of 13.07 AU, an aphelion of 18.35 AU, an excentricity of 0.31 and an
inclination of 30.1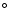 ,
which classifies it in the Centaur
family. Several observations were attempted in order to characterize
its physical properties. The visible observations of Davies et al.
(1998) gave an absolute V magnitude
,
which classifies it in the Centaur
family. Several observations were attempted in order to characterize
its physical properties. The visible observations of Davies et al.
(1998) gave an absolute V magnitude
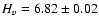 ,
using a linear phase function with
,
using a linear phase function with
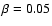 mag deg-1. Combining this result with the infrared flux
obtained at 20.3
mag deg-1. Combining this result with the infrared flux
obtained at 20.3  m, Jewitt & Kalas (1998)
derived a radius of 151 km and a geometric albedo of 0.045.
Altenhoff et al. (2001) performed radio observations
at 1.2 mm and determined a radius of 137 km and a geometric
albedo of 0.055. The infrared and radio observations are presented in
Table 7. The recent observations of
Peixinho et al. (2001) present evidences for
variations of the absolute magnitude of Chariklo over a few months.
Using these data with a linear phase function correction
(
m, Jewitt & Kalas (1998)
derived a radius of 151 km and a geometric albedo of 0.045.
Altenhoff et al. (2001) performed radio observations
at 1.2 mm and determined a radius of 137 km and a geometric
albedo of 0.055. The infrared and radio observations are presented in
Table 7. The recent observations of
Peixinho et al. (2001) present evidences for
variations of the absolute magnitude of Chariklo over a few months.
Using these data with a linear phase function correction
(
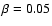 mag deg-1), we determined a range for Hv from 6.52 to 6.90, well within the error bars. We applied our
model used for Chiron to those visible, infrared and radio
observations, in order to determine altogether the radius, the
geometric albedo and the thermal inertia of Chariklo. We adopted a
rotation period of 24 h (Davies et al. 1998).
mag deg-1), we determined a range for Hv from 6.52 to 6.90, well within the error bars. We applied our
model used for Chiron to those visible, infrared and radio
observations, in order to determine altogether the radius, the
geometric albedo and the thermal inertia of Chariklo. We adopted a
rotation period of 24 h (Davies et al. 1998).
Table 7:
Infrared and radio observations of Chariklo.
As done for Chiron, we minimized the 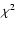 expression, using the infrared (Jewitt & Kalas 1998) and radio (Altenhoff et al. 2001) constraints, and we derived a radius of 118
expression, using the infrared (Jewitt & Kalas 1998) and radio (Altenhoff et al. 2001) constraints, and we derived a radius of 118 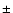 6 km and a thermal inertia of 0
+2-0 MKS. As noted previously, this results depend on
6 km and a thermal inertia of 0
+2-0 MKS. As noted previously, this results depend on 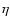 .
For
.
For 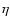 in the range 0.7-1.0, the
in the range 0.7-1.0, the 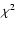 expression is minimum for a radius in the range 115-126 km and a thermal inertia of 0 MKS. Consequently, the influence of
expression is minimum for a radius in the range 115-126 km and a thermal inertia of 0 MKS. Consequently, the influence of 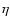 is null on the thermal inertia and <10% on the radius. For Chariklo, I must be less than 2 MKS, otherwise the infrared and radio observations are not compatible. This is illustrated in Fig. 12, where we represented the radius determination for different thermal inertia in the range 0-100 MKS, as a function of wavelength. The infrared observations lead to a range of radius of 124 to 266 km, while the radio observations lead to a much narrower range of 116 to 128 km, thus giving a stringent constraint on the nucleus. This large difference of range between the two spectral domains has already been addressed (Sect. 2.2). Using Eq. (12) with the values of
is null on the thermal inertia and <10% on the radius. For Chariklo, I must be less than 2 MKS, otherwise the infrared and radio observations are not compatible. This is illustrated in Fig. 12, where we represented the radius determination for different thermal inertia in the range 0-100 MKS, as a function of wavelength. The infrared observations lead to a range of radius of 124 to 266 km, while the radio observations lead to a much narrower range of 116 to 128 km, thus giving a stringent constraint on the nucleus. This large difference of range between the two spectral domains has already been addressed (Sect. 2.2). Using Eq. (12) with the values of
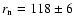 km and
km and
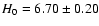 ,
we derived a geometric albedo of 0.07
,
we derived a geometric albedo of 0.07 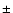 0.01.
0.01.
In order to complete the analysis of Chariklo, we considered its
reflectance using the spectrum obtained by Brown et al.
(1998), which we normalized at 2.2  m. We favored
this spectrum over that obtained more recently by Brown
(2000) as this latter is of lower quality. Likewise that
of Chiron, it exhibits the water ice absorption bands at 1.5 and
2.0
m. We favored
this spectrum over that obtained more recently by Brown
(2000) as this latter is of lower quality. Likewise that
of Chiron, it exhibits the water ice absorption bands at 1.5 and
2.0  m with approximatively the same contrast (compare Figs. 13 and 10). We
know from Sect. 5.1 that the geometric albedo of Chariklo
(
m with approximatively the same contrast (compare Figs. 13 and 10). We
know from Sect. 5.1 that the geometric albedo of Chariklo
(
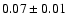 )
is slightly lower than that of Chiron (
)
is slightly lower than that of Chiron (
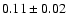 ),
and this requires that the fractional coverage of ice be reduced
in comparison to that of Chiron. In view of the previous discussion
in Sect. 4.3.2, we adopted a grain size of 10
),
and this requires that the fractional coverage of ice be reduced
in comparison to that of Chiron. In view of the previous discussion
in Sect. 4.3.2, we adopted a grain size of 10  m and found
that the solution which best matches the observed spectrum is composed
of 20% of water ice +80% of refractory materials (either kerogen,
silicate or glassy carbon). As illustrated in Fig. 13, these mixtures give excellent fits to the
spectrum of Chariklo. The corresponding geometric albedos are 0.07
(silicate), 0.09 (glassy carbon) and 0.07 (kerogen), in good agreement
with the above determination of
m and found
that the solution which best matches the observed spectrum is composed
of 20% of water ice +80% of refractory materials (either kerogen,
silicate or glassy carbon). As illustrated in Fig. 13, these mixtures give excellent fits to the
spectrum of Chariklo. The corresponding geometric albedos are 0.07
(silicate), 0.09 (glassy carbon) and 0.07 (kerogen), in good agreement
with the above determination of
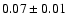 .
.
In summary, the spectrum of the nucleus of Chariklo and its
geometric albedo of 0.07  0.01 are both consistent with a surface
approximately composed of 20% of water ice and 80% of a refractory
material.
0.01 are both consistent with a surface
approximately composed of 20% of water ice and 80% of a refractory
material.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f13.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg119.gif) |
Figure 13:
The observed spectrum of Chariklo compared to four different mixtures of water ice and refractory grains (silicate, glassy carbon or kerogen). The grain size is 10  m. m. |
| Open with DEXTER |
We have analyzed visible, infrared, radio and spectroscopic observations of 2060 Chiron and 1997 CU26 Chariklo in a synthetic way to determine the physical properties of its nucleus. Our main results are summarized below:
- 1.
- The analysis of the visible observations performed from September 1969 to August 2001 leads to an absolute V magnitude for the nucleus of Chiron
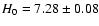 with a lightcurve amplitude of 0.16
with a lightcurve amplitude of 0.16 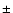 0.03 mag, implying a nearly spherical nucleus with a ratio of semi-axes
0.03 mag, implying a nearly spherical nucleus with a ratio of semi-axes
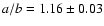 .
.
- 2.
- The analysis of the infrared ISOPHOT observations of Chiron, which covers the maximum of the SED (25, 60 and 100
 m), with a thermal model which includes heat conduction leads to a thermal inertia of
3+5-3 J K-1 m-2 s-1/2 and a radius of 71
m), with a thermal model which includes heat conduction leads to a thermal inertia of
3+5-3 J K-1 m-2 s-1/2 and a radius of 71 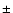 5 km. Combining the visible and infrared observations, we found a geometric albedo of
5 km. Combining the visible and infrared observations, we found a geometric albedo of
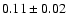 .
This solution is remarkably consistent with observations ranging from 17.9
.
This solution is remarkably consistent with observations ranging from 17.9  m (Fernandez et al. 2002) to 1200
m (Fernandez et al. 2002) to 1200  m (Altenhoff et al. 1995).
m (Altenhoff et al. 1995).
- 3.
- This very low value of the thermal inertia, the lowest ever determined for a body of the Solar System, is supported by other evidences and is coherent with our present understanding of primitive bodies. It implies a low thermal conductivity and probably a porous structure as often assumed for cometary nuclei.
- 4.
- The spectrum of the nucleus of Chiron and its relatively high geometric albedo are both consistent with a surface composed of a mixture of water ice (
 30%) and refractory (
30%) and refractory ( 70%) grains.
70%) grains.
- 5.
- The same analysis for the visible, infrared and radio observations of Chariklo (1997 CU26), yields a radius of
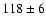 km, a geometric albedo of
km, a geometric albedo of
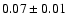 and a thermal inertia of 0
+2-0 J K-1 m-2 s-1/2, making Chariklo the largest Centaur detected so far. A surface composed of a mixture of water ice (
and a thermal inertia of 0
+2-0 J K-1 m-2 s-1/2, making Chariklo the largest Centaur detected so far. A surface composed of a mixture of water ice ( 20%) and refractory (
20%) and refractory (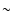 80%) grains is compatible with its near-infrared spectrum and the above albedo.
80%) grains is compatible with its near-infrared spectrum and the above albedo.
The wide diversity in the optical and near-infrared reflection spectra of Centaurs is now well established and can be interpreted in terms of different histories leading to mantles of different nature (Jewitt & Fernandez 2001). This is reinforced by the differences in albedo as illustrated by the two cases considered here, Chiron and Chariklo, which can be related to different properties (composition, porosity) of the uppermost layers of the two nuclei. Our results further suggest different thermal inertia for Chiron and Chariklo. It is tempting to relate this possible difference to the presence (Chiron) or absence (Chariklo) of activity, the larger heat conduction in Chiron implying that more energy reach the CO layer inside the nucleus thus producing its sublimation. This question is beyong the scope of the present study but would be worth exploring.
As Centaurs will eventually become ecliptic comets, it is quite interesting to compare the properties of these two families. A major difference is that water ice has been detected at the surface of several Centaurs on the basis of the 1.5 and 2.0  m absorption bands, while it has never been detected on any ecliptic comet nucleus. From the few determinations presently available and clearly on the basis on the above results, several Centaurs have a geometric albedo distinctly larger than that of short period comets. Our calculation suggests that the large fraction of water ice present on the surface of these Centaurs also explain these large albedo values. This would indicate that sublimation is quite effective in weathering the cometary surfaces and decreasing their albedo.
m absorption bands, while it has never been detected on any ecliptic comet nucleus. From the few determinations presently available and clearly on the basis on the above results, several Centaurs have a geometric albedo distinctly larger than that of short period comets. Our calculation suggests that the large fraction of water ice present on the surface of these Centaurs also explain these large albedo values. This would indicate that sublimation is quite effective in weathering the cometary surfaces and decreasing their albedo.
Acknowledgements
We express our gratitude to T.L. Roush, who kindly made his program to calculate the reflectance and the geometric albedo available to us and for his helpful comments. We thank the referee, D.P. Cruikshank, for many helpful comments.
- Altenhoff, W. J., & Stumpff, P. 1995,
A&A, 293, L41
In the text
NASA ADS
- Altenhoff, W. J., Menten, K. M., & Bertoli, F. 2001,
A&A, 366, L9
In the text
NASA ADS
- Bauer, J. M., Meech, K. J., Fernández, Y. R., et al. 2003,
Icarus, in press
In the text
- Bowell, E., Hapke, B., Domingue, D., et al. 1989,
Asteroids II
In the text
- Brown, R. H., Cruikshank, D. P., Pendleton, Y., & Veeder, G. J. 1998,
Science, 280, 1430
In the text
NASA ADS
- Brown, M. E. 2000,
AJ, 119, 977
In the text
NASA ADS
- Buie, M. W., Olkin, C., McDonald, S., et al. 1993,
IAU Circ., 5898
In the text
- Bus, S. J., & Bowell, E. 1988,
IAU Circ., 4684
- Bus, S. J., Bowell, E., Harris, A. W., & Hewitt, A. V. 1989,
Icarus, 77, 223
In the text
NASA ADS
- Bus, S. J., Buie, M. W., Schleicher, D. G., et al. 1996,
Icarus, 123, 478
In the text
NASA ADS
- Bus, S. J., A'Hearn, M. F., Bowell, E., & Stern, S. A. 2001,
Icarus, 150, 90
In the text
- Campins, H., Telesco, C. M., Osip, D. J., et al. 1994,
AJ, 108, 2318
In the text
NASA ADS
- Capria, M. T., Capaccioni, F., Coraldini, A., et al. 1996,
Planet. Space Sci., 44, 987
In the text
NASA ADS
- Clark, R. N. 1981,
JGR, 86, 3074
In the text
NASA ADS
- Clark, R. N., & Lucey, P. G. 1984,
JGR, 89, 6341
In the text
NASA ADS
- Davies, J. K., McBride, N., Ellison, S. L.,
Green, S. F., & Ballantyne, D. R. 1998,
Icarus, 134, 213
In the text
NASA ADS
- Draine, B. T., & Lee, H. M. 1984,
ApJ, 285, 89
In the text
NASA ADS
- Duffard, R.,
Lazzaro, D., Pinto, S., et al. 2002,
Icarus, 160, 44
In the text
NASA ADS
- Edoh, O. 1983,
Ph.D. Thesis, Univ. of Arizona
In the text
- Fernández,
Y. R., Jewitt, D. C., & Sheppard, S. S. 2002,
AJ, 123, 1050
In the text
NASA ADS
- Foster, M. J., Green, S. F., & McBride, N. 1999,
Icarus, 141, 408
In the text
NASA ADS
- Froidevaux, L., Matthews, K., & Neugebauer, G. 1981,
Icarus, 46, 18
NASA ADS
- Hapke, B. 1993,
Theory of reflectance and emittance spectroscopy (Cambridge University Press)
In the text
- Hartmann, W. K., Tholen, D. J., Meech, K. J., & Cruikshank, D. P. 1990,
Icarus, 83, 1
In the text
NASA ADS
- Jewitt, D., & Luu, J. 1992,
AJ, 104, 398
In the text
NASA ADS
- Jewitt, D., & Kalas, P. 1998,
ApJ, 499, L103
In the text
NASA ADS
- Jewitt, D., & Fernandez, Y. 2001,
Physical properties of Planet-Crossing Objects,
261, 143
In the text
- Johnson, R. 1991,
JGR, 96, 17553
In the text
- Julian, W. H.,
Samarasinha, N. H., & Belton, M. J. S. 2000,
Icarus, 144, 160
NASA ADS
- Khare, B. N., Thompson, W. R., Sagan, C., et al. 1990,
Lunar and Planetary Institute Conference Abstracts, 21, 627
In the text
- Kieffer, H., Martin, T., Peterfreund, A., et al. 1977,
JGR, 82, 4249
NASA ADS
- Kiss, C., Ábrahám, P., Klaas, U., Juvela, M., & Lemke, D. 2001,
A&A, 379, 1161
In the text
NASA ADS
- Klinger, J., Levasseur-Regourd, A. C., Bouziani, N., & Enzian, A.
1996,
Planet. Space Sci., 44, 637
In the text
NASA ADS
- Kowal, C. T. 1996,
Asteroids: their nature and utilization (2d ed. New York: Wiley)
In the text
- Lagerros, J. S. V. 1998,
A&A, 332, 1123
In the text
NASA ADS
- Lamy, P. L., Toth, I.,
Jorda, L., et al. 2002,
Icarus, 156, 442
In the text
NASA ADS
- Lamy, P. L., Toth, I., Fernandez, Y., & Weaver, H. A. 2004, COMETS II, ed. M. Festou, H. U. Keller, & H. A. Weaver (University of Arizona Press), in press
In the text
- Landholt, A. U. 1992,
AJ, 104, 340
In the text
NASA ADS
- Lazzaro, D., Florczak, M. A., Betzler, A. S., et al. 1996,
Planet. Space Sci., 44, 1547
In the text
NASA ADS
- Lazzaro, D., Florczak, M. A., Angeli, C. A., et al. 1997,
Planet. Space Sci., 45, 1607
In the text
NASA ADS
- Lebofsky, L. A., Tholen, D. J., Rieke, G. H., & Lebofsky, M. J. 1984,
Icarus, 60, 532
In the text
NASA ADS
- Lebofsky, L. A., Sykes, M. V., Tedesco, E. F., et al. 1986,
Icarus, 68, 239
In the text
NASA ADS
- Lebofsky, L. A., & Spencer, J. R. 1989,
Radiometry and thermal modeling of asteroids.
Asteroids II
In the text
- Lunine, J., Neugebauer, G., & Jakosky, B. 1982,
JGR, 87, 10297
- Luu, X. J., & Jewitt, D. C. 1990,
AJ, 100, 913
In the text
NASA ADS
- Luu, X. J. 1993,
Icarus, 104, 138
NASA ADS
- Luu, X. J., Jewitt, D. C., & Trujillo, C. 2000,
ApJ, 531, L151
In the text
NASA ADS
- Marcialis, R. L., & Buratti, B. J. 1993,
Icarus, 104, 234
In the text
NASA ADS
- Meech, K. J., & Belton, J. S. 1990,
AJ, 100, 1323
In the text
NASA ADS
- Meech, K. J., Buie, M. W., Samarashina, N. H., Mueller, B. E. A., & Belton, M. J. S. 1997,
AJ, 113, 844
NASA ADS
- Morrison, D., Cruikshank, D. P., Murphy, R. E., et al. 1971,
ApJ, 167, L107
NASA ADS
- Morrison, D. 1976,
Icarus, 28, 125
In the text
NASA ADS
- Peixinho, N., Lacerda, P., Ortiz, J. L., et al. 2001,
A&A, 371, 753
In the text
NASA ADS
- Peschke, S. 1997,
Ph.D. Thesis, University of Heidelberg
In the text
- Rauer, H., Biver, N., Crovisier, J., et al. 1997,
Planet. Space Sci., 45, 799
In the text
NASA ADS
- Roush, T. L. 1994,
Icarus, 108, 243
In the text
NASA ADS
- Schmitt, B., Epinasse, S., & Klinger, J. 1991,
in 19th luunar and planetary science conference, ed. A. W. Harris, & E. Bowell (Houston: Lunar and Planetary Insitute)
In the text
- Scotti, J. V. 1997,
Minor Planet Circular 1997-D11
In the text
- Silva, A. M., & Cellone, S. A. 2001,
Planet. Space Sci., 49, 1325
NASA ADS
- Skorov, Yu. V., Kömle, N. I., Markiewicz W. J., & Keller, H. U. 1999,
Icarus, 140, 173
In the text
NASA ADS
- Spencer, J. R., Lebofsky, L. A., & Sykes, M. V. 1989,
Icarus, 78, 337
In the text
NASA ADS
- Sykes, M. V., & Walker, R. G. 1991,
Science, 251, 777
In the text
NASA ADS
- Tholen, D. J., Hartmann, W., & Cruikshank, D. P. 1988,
IAU Circ., 4554
In the text
- Warren, S. G. 1984,
Appl. Opt., 23, 1206
In the text
NASA ADS
- West, R. M. 1991,
A&A, 241, 635
In the text
NASA ADS
- Winter, D., & Saari, J. 1969,
ApJ, 156, 1135
NASA ADS
- Womack, M., & Stern, S. A. 1997,
Proc. Lunar Planet. Sci. Conf. XXVIII, 1575
In the text
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f1.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg20.gif)
![\begin{displaymath}
\Delta m_{v} = H_0-H_{v} -2.5 \log\Big[10^{0.4(H_0-H_{v})}+10^{-0.4\Delta m_0} -1\Big].
\end{displaymath}](/articles/aa/full/2004/03/aa3595/img28.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f2.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f3.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg46.gif)
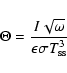
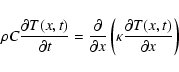
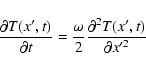
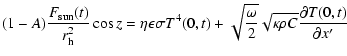
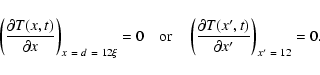
![\begin{displaymath}
F(\lambda) = \epsilon
\int \int {B}\left[\lambda,T(\theta,\varphi,A)\right] \Omega {\rm d}S.
\end{displaymath}](/articles/aa/full/2004/03/aa3595/img84.gif)
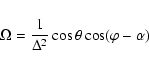
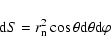
![\begin{displaymath}\chi^2(I,r_{\rm n})=\sum_{i=1}^{n}\Bigg[\frac{F_i-F(\lambda_i,I,r_{\rm n})}{\sigma_i}\Bigg]^2
\end{displaymath}](/articles/aa/full/2004/03/aa3595/img93.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3595_f4.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f5.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg98.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{3595_f6.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg105.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f7.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f8.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg107.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f9.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg108.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f10.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg109.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f11.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg112.gif)
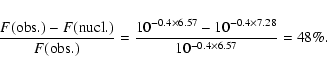
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{3595_f12.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg114.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3595_f13.ps}\end{figure}](/articles/aa/full/2004/03/aa3595/Timg119.gif)