IRIS data (the low degree
A&A 413, 1135-1142 (2004)
DOI: 10.1051/0004-6361:20031541
D. Salabert1,2 - E. Fossat1 - B. Gelly1 - S. Kholikov3,4 - G. Grec5 - M. Lazrek5,6 - F. X. Schmider1
1 - Laboratoire Universitaire d'Astrophysique de Nice, Université de Nice-Sophia Antipolis, 06108 Nice Cedex 2, France
2 - School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
3 - Astronomical Institute of the Uzbek Academy of Sciences, 33, Astronomicheskaya, Tashkent 700052, Uzbekistan
4 - National Solar Observatory, 950 North Cherry Avenue, Tucson, AZ 85719, USA
5 - Observatoire de la Côte d'Azur, Lab. Cassini CNRS UMR 6529, 06304 Nice Cedex 4, France
6 - Laboratoire d'Astronomie du CNCPRST, BP 1346, Rabat, Morocco
Received 20 January 2003 / Accepted 3 September 2003
Abstract
IRIS data (the low degree
![]() helioseismology network) have been analysed for the study of p-mode parameters variability over the falling phase of the solar activity cycle 22 and the rising phase of the solar activity cycle 23. The IRIS duty cycle has been improved by the so-called "repetitive music method'', a method of partial gap filling. We present in this paper an analysis of the dependence of p-mode frequencies and linewidths with frequency and with solar magnetic activity. We confirm also the periodicity of about 70
helioseismology network) have been analysed for the study of p-mode parameters variability over the falling phase of the solar activity cycle 22 and the rising phase of the solar activity cycle 23. The IRIS duty cycle has been improved by the so-called "repetitive music method'', a method of partial gap filling. We present in this paper an analysis of the dependence of p-mode frequencies and linewidths with frequency and with solar magnetic activity. We confirm also the periodicity of about 70 ![]() Hz of the high-frequency pseudo modes, with a much reduced visibility during the phase of higher activity.
Hz of the high-frequency pseudo modes, with a much reduced visibility during the phase of higher activity.
Key words: Sun: helioseismology - Sun: activity
As early as in 1984, different authors have noticed that during the
maximum of solar activity, the low-degree p-mode solar frequencies
have higher values than during the minimum of activity, implying sensitivity of solar p modes to the solar magnetic
activity. Woodard & Noyes (1985) and Fossat et al. (1987) first, and more
recently Chaplin et al. (1998), Howe et al. (1999), Salabert et al. (2002) and
Gelly et al. (2002) report using several databases of low-degree and
intermediate-degree p modes, from both ground and space observations,
that these frequency shifts increase with frequency, following the
inverse mode-mass law. As shown by Goldreich et al. (1991), these
frequency shifts are mostly explained by a change in the position of
the upper turning point, that is decreasing with magnetic activity,
while the main effect of the sound speed change would be
opposite. Measurements of shifts for high (![]() )
and intermediate degrees (
)
and intermediate degrees (
![]() )
have shown values significantly higher than for low degrees (
)
have shown values significantly higher than for low degrees (
![]() ). High-
). High-![]() and intermediate-
and intermediate-![]() modes propagate closer to the Sun's surface, whereas low-
modes propagate closer to the Sun's surface, whereas low-![]() p modes go deeper into the Sun. This degree dependence tends to confirm the idea that the frequency shifts are mostly controlled by very near surface phenomena, and depend little on the deeper solar structure. Above 3.7-3.9 mHz, a downturn is observed and the frequency shifts start to decrease with even a reversal in sign. Anguera Gubau et al. (1992) and Jiménez-Reyes et al. (2001) report an oscillatory behaviour for low degrees (the shift oscillating between positive and negative values beyond 4 mHz or so), but the observations of this downturn are very scarse (Chaplin et al. 1998; Gelly et al. 2002; Salabert et al. 2002), and there is almost no observation of frequency shifts above the cut-off frequency for low-degree p modes. Observations with intermediate degrees
p modes go deeper into the Sun. This degree dependence tends to confirm the idea that the frequency shifts are mostly controlled by very near surface phenomena, and depend little on the deeper solar structure. Above 3.7-3.9 mHz, a downturn is observed and the frequency shifts start to decrease with even a reversal in sign. Anguera Gubau et al. (1992) and Jiménez-Reyes et al. (2001) report an oscillatory behaviour for low degrees (the shift oscillating between positive and negative values beyond 4 mHz or so), but the observations of this downturn are very scarse (Chaplin et al. 1998; Gelly et al. 2002; Salabert et al. 2002), and there is almost no observation of frequency shifts above the cut-off frequency for low-degree p modes. Observations with intermediate degrees
![]() (Jefferies 1998; Ronan et al. 1994) show clearly this downturn with a change of sign of frequency shifts, followed by an upturn above the 5.5 mHz cut-off frequency.
(Jefferies 1998; Ronan et al. 1994) show clearly this downturn with a change of sign of frequency shifts, followed by an upturn above the 5.5 mHz cut-off frequency.
Although the frequency shifts are the most studied of the p-mode parameters, the linewidths and the amplitudes are also sensitive to solar activity. First, Pallé et al. (1990a,b) and Anguera Gubau et al. (1992) have reported that the power (i.e. ![]() amplitude
amplitude ![]() linewidth) contained in the low-
linewidth) contained in the low-![]() modes increases as the solar activity cycle approaches its minimum. Today, the duration and quality of helioseismic data have become sufficient for a detailed analysis along all the phases of the solar activity of these amplitude and energy parameters, as well as linewidth and energy generation rate. Recently, Jiménez et al. (2002) with the VIRGO/SPM photometer on board SOHO and Salabert et al. (2003) with data from the IRIS++ ground-based observations have shown clear evidence for the variations of these parameters along the solar cycle, with an increase of the linewidth with the solar activity, and a decrease of the amplitude and the velocity power at the same time. As for the energy supply rate, no dependence with the solar activity is found.
modes increases as the solar activity cycle approaches its minimum. Today, the duration and quality of helioseismic data have become sufficient for a detailed analysis along all the phases of the solar activity of these amplitude and energy parameters, as well as linewidth and energy generation rate. Recently, Jiménez et al. (2002) with the VIRGO/SPM photometer on board SOHO and Salabert et al. (2003) with data from the IRIS++ ground-based observations have shown clear evidence for the variations of these parameters along the solar cycle, with an increase of the linewidth with the solar activity, and a decrease of the amplitude and the velocity power at the same time. As for the energy supply rate, no dependence with the solar activity is found.
In this paper, we have analyzed 10 years of data from the IRIS network, from July 1989 to August 1999, spanning the falling phase of solar cycle 22 and the rising phase of solar cycle 23. p-mode parameters have been extracted (frequencies and frequency shifts, linewidths), the duty cycle of the timeseries being improved by the so-called "repetitive music'' method, a method of partial gap filling and we present their dependence over frequency and time (i.e. solar activity).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3485f1.eps}\end{figure}](/articles/aa/full/2004/03/aa3485/Timg22.gif) |
Figure 1: 4-month summer 1991 IRIS power spectra (up: with no gap filling / down: with repetitive music method). |
| Open with DEXTER | |
The IRIS (International Research of Interior of the Sun) network for full-disk helioseismology has been operated since July 1st, 1989. The observations consist of daily measurements of the solar radial velocity obtained
with a resonant sodium (589.6 nm) cell spectrophotometer. The full-disk integration gives access to low-degree p modes with ![]() .
This dataset has been used to constrain the solar internal structure and rotation of the deep solar interior through the precise measurement of low-degree frequencies (Gelly el al. 1997; Fossat et al. 2003; Serebryanskiy et al. 2001) and frequency splittings (Lazrek et al. 1996; Fossat et al. 2003; Gizon et al. 1997; Loudagh et al. 1993) or an accurate measurement of the solar acoustic cut-off frequency (Fossat et al. 1992). The IRIS network has never succeeded in doing better than a 50% duty cycle in a complete year. The effects of the temporal window that damage the power spectrum can be reduced by means of various kinds of deconvolution of this window function. However, for improving the duty cycle, a method of partial gap filling, called repetitive music (Fossat et al. 1999) is used, which considerably reduced the temporal window convolution effects. The sidelobes are reduced and the S/N is increased (Fig. 1). Fossat et al. (1999) have noticed that the full-disk signal has a very high level of coherence after slightly more than 4 hours. It is above 70% and this is significantly more than its coherence after just one period of 5 min. This means that the original signal is almost periodic in time, with a quasi periodicity of a little more than 4 hours. So a gap is replaced by the signal collected 4 hours earlier or/and 4 hours later. This temporal shift noted
.
This dataset has been used to constrain the solar internal structure and rotation of the deep solar interior through the precise measurement of low-degree frequencies (Gelly el al. 1997; Fossat et al. 2003; Serebryanskiy et al. 2001) and frequency splittings (Lazrek et al. 1996; Fossat et al. 2003; Gizon et al. 1997; Loudagh et al. 1993) or an accurate measurement of the solar acoustic cut-off frequency (Fossat et al. 1992). The IRIS network has never succeeded in doing better than a 50% duty cycle in a complete year. The effects of the temporal window that damage the power spectrum can be reduced by means of various kinds of deconvolution of this window function. However, for improving the duty cycle, a method of partial gap filling, called repetitive music (Fossat et al. 1999) is used, which considerably reduced the temporal window convolution effects. The sidelobes are reduced and the S/N is increased (Fig. 1). Fossat et al. (1999) have noticed that the full-disk signal has a very high level of coherence after slightly more than 4 hours. It is above 70% and this is significantly more than its coherence after just one period of 5 min. This means that the original signal is almost periodic in time, with a quasi periodicity of a little more than 4 hours. So a gap is replaced by the signal collected 4 hours earlier or/and 4 hours later. This temporal shift noted ![]() can be defined as
can be defined as
![]() ,
where n is the number of points between the missing points and the points used to fill the gaps, and
,
where n is the number of points between the missing points and the points used to fill the gaps, and ![]() ,
the temporal sampling (in the case of the IRIS observations,
,
the temporal sampling (in the case of the IRIS observations,
![]() s). It must be noticed that the background noise becomes modulated with a periodicity around 67.5
s). It must be noticed that the background noise becomes modulated with a periodicity around 67.5 ![]() Hz, which is the inverse of this pseudo-periodic translated signal. The fine adjustement of the partial gap-filling method consists of placing the maxima of this modulation on the p-mode frequencies: if a mode frequency was located near one minimum of modulation, its visibility would be nearly cancelled by the fact that the translated signal will have an opposite phase. For the frequency range 1.7 mHz
Hz, which is the inverse of this pseudo-periodic translated signal. The fine adjustement of the partial gap-filling method consists of placing the maxima of this modulation on the p-mode frequencies: if a mode frequency was located near one minimum of modulation, its visibility would be nearly cancelled by the fact that the translated signal will have an opposite phase. For the frequency range 1.7 mHz
![]() 3.7 mHz, the modulation introduced is
3.7 mHz, the modulation introduced is ![]() = 330
= 330 ![]() 45 s (
45 s (
![]() hours). Above
hours). Above ![]() = 3.7 mHz, the modulation is
= 3.7 mHz, the modulation is ![]() = 324
= 324 ![]() 45 s. With this method, we obtain annual duty cycles up to 75% and even between 75% and 90% during the best summer 4-month periods (Table 1).
45 s. With this method, we obtain annual duty cycles up to 75% and even between 75% and 90% during the best summer 4-month periods (Table 1).
Two types of spectra are computed depending on the frequency range observed:
Table 1: IRIS duty cycles (%). (a) annual IRIS; (b) annual partial gap filled IRIS; (c) 4-month summer IRIS ; (d) 4-month summer partial gap filled IRIS. (NB: (1) Values for 1989 start the 1st July. For the 4-month duty cycle values, only July, August and September are used / (2) Values for 1999 ending 30 August. For the 4-month duty cycle values, only June, July and August are used.).
A p mode is regarded as a one dimensional damped and randomly excited oscillator. This assumes that the peaks in the Fourier power spectrum (Fig. 1) are asymptotically described by Lorentz profiles:
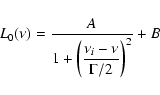 |
(1) |
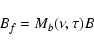 |
(2) |
The case of the modes is quite different in the sense that they are coherent in time, on timescales significantly (but not indefinitely) longer than ![]() (of course, this is exactly why the gap-filling method is efficient). The main effect of the convolution by the window function is to spread part of the peak power (this fractional part being equal to the missing fraction of the duty cycle), generally mostly in sidelobes proportional to (one-day)-1 when the window contains the 24-hour periodicity, which is still the case in a network timeseries. This means that after gap filling, the peak is enhanced, by recovering a fraction of its power that was spread around.
(of course, this is exactly why the gap-filling method is efficient). The main effect of the convolution by the window function is to spread part of the peak power (this fractional part being equal to the missing fraction of the duty cycle), generally mostly in sidelobes proportional to (one-day)-1 when the window contains the 24-hour periodicity, which is still the case in a network timeseries. This means that after gap filling, the peak is enhanced, by recovering a fraction of its power that was spread around.
The mode profile to be fitted for parameter estimation includes then two different "modulation functions'', Mb for the noise and ![]() for the line profile, such as:
for the line profile, such as:
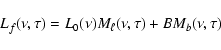 |
(3) |
The frequency errorbars are computed using the formula proposed by Toutain & Appourchaux (1994):
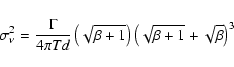 |
(4) |
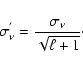 |
(5) |
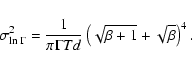 |
(6) |
Up to 3.7 mHz, all individual modes are fitted, taking into account a fixed value of the rotational splitting. Above 3.7 mHz, the ![]() triplet is given up as it becomes a negligible contribution to the total linewidth, but the
triplet is given up as it becomes a negligible contribution to the total linewidth, but the ![]() and
and ![]() modes are still both included in the fit. That works until 4.2 mHz, beyond which their separation becomes unresolved. In the
modes are still both included in the fit. That works until 4.2 mHz, beyond which their separation becomes unresolved. In the ![]() ,
,
![]() pair, the
pair, the ![]() profile becomes lost in the wing of the
profile becomes lost in the wing of the ![]() ,
and only one mode is fitted beyond 3.7 mHz. It is then slightly overestimated in linewidth and left biased in frequency (keep in mind that we study here the time variability, not the accurately estimated p-mode parameters). The uncertainties on the frequencies and the linewidths have been estimated using Eqs. (5) and (6) respectively. They are slightly optimistic since the duty cycle values taken into account ignore the fact that the filled parts are only correlated at a level of about 80% with the unknown reality.
,
and only one mode is fitted beyond 3.7 mHz. It is then slightly overestimated in linewidth and left biased in frequency (keep in mind that we study here the time variability, not the accurately estimated p-mode parameters). The uncertainties on the frequencies and the linewidths have been estimated using Eqs. (5) and (6) respectively. They are slightly optimistic since the duty cycle values taken into account ignore the fact that the filled parts are only correlated at a level of about 80% with the unknown reality.
One power spectrum per year is then computed by means of the "repetitive music'' partial gap-filling method, followed by the modified fitting method of Fierry-Fraillon & Appourchaux (2001), so that the frequencies are obtained without any bias due to the gap-filling spectrum modulation.
Two different methods are then used to follow the drifts of p-mode frequencies from year to year along the solar cycle. The first one is quite straightforward. It makes direct use of the line fitting process using Eq. (3), in which frequency, linewidth, amplitude and background noise are the four free parameters (the splitting is fixed, and the two components of the ![]() = 1 doublet are forced to be identical, as well as the three components of the
= 1 doublet are forced to be identical, as well as the three components of the ![]() = 2 triplet). The fits on the group of modes 0-2 and on the group of modes 1-3 are computed separately. The average frequencies of 1995 and 1996 are taken as reference frequencies, these two years being well centered around the latest solar minimum. The frequency shift is simply obtained by a comparison of a mode frequency with its reference. However, this method was only used up to 3.8 mHz: beyond this frequency, because of both the reduced lifetime of the modes and the reduced S/N, the uncertainties on the extracted p-mode parameters by fitting a Lorentzian profile are more important.
= 2 triplet). The fits on the group of modes 0-2 and on the group of modes 1-3 are computed separately. The average frequencies of 1995 and 1996 are taken as reference frequencies, these two years being well centered around the latest solar minimum. The frequency shift is simply obtained by a comparison of a mode frequency with its reference. However, this method was only used up to 3.8 mHz: beyond this frequency, because of both the reduced lifetime of the modes and the reduced S/N, the uncertainties on the extracted p-mode parameters by fitting a Lorentzian profile are more important.
The second method computes the cross-correlation between a given annual spectrum and the reference spectrum, again taken as the average of 1995 and 1996. The cross-correlation is computed over each group of modes separately. The position of the maximum of correlation gives the frequency shift. It is measured by means of the least square fit of a second order polynomial on the logarithmic correlation, inside an interval ![]()
![]() (where
(where ![]() is the second order moment) around this peak. More details about this method can be found in Pallé et al. (1989), or Jiménez-Reyes et al. (1998). This method presents the advantage of not requiring any line fitting, and then no assumption on the shape of the line profiles. It is free of the need for modeling the p-mode excitation and damping mechanisms. Such a cross-correlation method is more efficient at higher frequency with a decreasing S/N.
is the second order moment) around this peak. More details about this method can be found in Pallé et al. (1989), or Jiménez-Reyes et al. (1998). This method presents the advantage of not requiring any line fitting, and then no assumption on the shape of the line profiles. It is free of the need for modeling the p-mode excitation and damping mechanisms. Such a cross-correlation method is more efficient at higher frequency with a decreasing S/N.
Beyond 4.5 mHz, where the damping time of p modes becomes shorter than one day, we have simply used individual days
of data, with the original sampling of 15 s. Each daily timeseries (selected for being at least 9 hours long) is split in three
independent series, each one with a 45 s sampling time. They are
then resampled on the same time frame, so that 3 different cross
spectra can be computed and averaged instead of one single power
spectrum, thus reducing very significantly the contribution of the
photon statistic noise. Many such daily average cross spectra are
then averaged, across the periods of solar maximum and solar
minimum. Then the same cross-correlation method is applied to these
two averaged spectra, on bandwidths of 136 ![]() Hz. The fit of the
peak of correlation is now Gaussian, since the 9-hour
resolution is unable to show the Lorentz profile and the convolution
of the cross-correlation makes the final profile quite close to a
Gaussian one. The frequency shifts obtained by this method can cover
the whole p-mode frequency range, up to the acoustic cut-off
frequency. They are shown as black diamonds in Fig. 2. It is not easy to estimate the uncertainty on
these numbers, it is rather displayed by the scatter of individual
values around the mean tendency. Only this kind of cross-correlation on daily files is totally free of any window function pollution, and still provides enough frequency resolution in the highest part of the p-mode range. It is the only one used beyond 4.5 mHz, where the pairs of even or odd degree can no longer be efficiently separated. At lower frequencies, all three methods provide consistent results, as shown by the comparable point by point scatters.
Hz. The fit of the
peak of correlation is now Gaussian, since the 9-hour
resolution is unable to show the Lorentz profile and the convolution
of the cross-correlation makes the final profile quite close to a
Gaussian one. The frequency shifts obtained by this method can cover
the whole p-mode frequency range, up to the acoustic cut-off
frequency. They are shown as black diamonds in Fig. 2. It is not easy to estimate the uncertainty on
these numbers, it is rather displayed by the scatter of individual
values around the mean tendency. Only this kind of cross-correlation on daily files is totally free of any window function pollution, and still provides enough frequency resolution in the highest part of the p-mode range. It is the only one used beyond 4.5 mHz, where the pairs of even or odd degree can no longer be efficiently separated. At lower frequencies, all three methods provide consistent results, as shown by the comparable point by point scatters.
Figure 2, showing the frequency shifts obtained by these different methods between maximum (from mid 1989 to mid 1992) and minimum of activity, can be separated in three different parts.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS3485f2.eps}\end{figure}](/articles/aa/full/2004/03/aa3485/Timg47.gif) |
Figure 2:
IRIS frequency shifts in the frequency range from 1.8 mHz to the acoustic cut-off frequency. (1) from the Lorentzian profile fitting
|
| Open with DEXTER | |
The p-mode frequencies have been estimated with an assumed known and imposed splitting. The other parameters are estimated by means of the next step of an iterative process, in which the frequencies are themselves fixed, the linewidths, the amplitudes and the background level being kept as free parameters of the fit.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS3485f3.eps}\end{figure}](/articles/aa/full/2004/03/aa3485/Timg48.gif) |
Figure 3:
Solar p-mode linewidths |
| Open with DEXTER | |
As already shown (Komm et al. 2000; Gelly et al. 2002; Chaplin et al. 1997), the linewidths ![]() increase with frequencies, with a plateau of value about 1
increase with frequencies, with a plateau of value about 1 ![]() Hz between 2.3 and 3.2 mHz. This plateau becomes even a slight dip during the time of low activity, centered near 3 mHz. Above 3.2 mHz, the linewidths increase and the profiles become quickly very broad. It is visible that the quality of the resonating p modes increases when the Sun is not spotted (Fig. 3). Another piece of evidence is that the mode amplitudes are changing in opposite phase, being smaller when the Sun is more spotted.
Hz between 2.3 and 3.2 mHz. This plateau becomes even a slight dip during the time of low activity, centered near 3 mHz. Above 3.2 mHz, the linewidths increase and the profiles become quickly very broad. It is visible that the quality of the resonating p modes increases when the Sun is not spotted (Fig. 3). Another piece of evidence is that the mode amplitudes are changing in opposite phase, being smaller when the Sun is more spotted.
A subtle change of slope of the linewidth increase is visible near 3.8 mHz. This has already been seen by other authors (Komm et al. 2000; Gelly et al. 2002). Possibly a different or additional damping mechanism becomes active at higher frequencies. It also happens that 3.8 mHz is the frequency above which the frequency drifts abruptly change their behaviour.
Our results are consistent with those of Boumier et al. (2002) and Gelly et al. (2002), who have shown that in the GOLF data, the linewidths change by about 20% at 3.5 mHz, and also with the results of Komm et al. (2000) who reported the same kind of linewidth increase with activity in the intermediate and high degree range of the GONG data.
As mentioned earlier, each individual p-mode frequency is estimated on an annual basis by means of the described fitting process. It is then compared to the average reference of the maximum activity period. Then, all the frequency shifts are averaged between 2.6 and 3.7 mHz to produce our first index
![]() .
Between 3.7 and 4.5 mHz, the annual comparison is made by means of the cross-correlation technique, and produces our second index
.
Between 3.7 and 4.5 mHz, the annual comparison is made by means of the cross-correlation technique, and produces our second index
![]() .
Figure 4 shows these two indexes, with a solar activity proxy (here, the International Sunspot Number
.
Figure 4 shows these two indexes, with a solar activity proxy (here, the International Sunspot Number ![]() ), with an adjusted scale for comparison. The very good correlation between solar activity and our first index is clearly visible, while the higher frequency shifts, although not so precisely defined (the error bars are significantly larger), tend to show an opposite correlation with activity that confirms that the frequency shifts shown in
Fig. 2 change sign somewhere around 4 mHz. The amplitudes of frequency shifts between the maximum of solar activity cycle 22 and the minimum of solar activity cycle 22 are
), with an adjusted scale for comparison. The very good correlation between solar activity and our first index is clearly visible, while the higher frequency shifts, although not so precisely defined (the error bars are significantly larger), tend to show an opposite correlation with activity that confirms that the frequency shifts shown in
Fig. 2 change sign somewhere around 4 mHz. The amplitudes of frequency shifts between the maximum of solar activity cycle 22 and the minimum of solar activity cycle 22 are
![]()
![]() Hz in the intermediate-frequency range and
Hz in the intermediate-frequency range and
![]()
![]() Hz in the high-frequency range.
Hz in the high-frequency range.
Figure 5 shows the same comparison with the same index of activity for the p-mode linewidths, averaged in the same frequency range of 2.6-3.7 mHz. Again, the correlation is clearly visible, the p modes being definitely more strongly damped with higher magnetic activity. The relative amount of change for the averaged linewidths between a period covering the minimum of activity and one covering the maximum of activity is about -26%, which is consistent with Sect. 3.2.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS3485f4.eps}\end{figure}](/articles/aa/full/2004/03/aa3485/Timg51.gif) |
Figure 4:
p-mode frequency shifts (solid line:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS3485f5.eps}\end{figure}](/articles/aa/full/2004/03/aa3485/Timg52.gif) |
Figure 5:
Linewidths |
| Open with DEXTER | |
The presence of "fringes'' in the power spectra above the acoustic cut-off frequency (about 5.5 mHz, see Fossat et al. 1992) has been reported several times in the case of medium- and high-degree helioseismic data (Jefferies et al. 1988; Duvall et al. 1991; Ronan & Labonte 1993; Libbrecht 1988). It has also been reported more recently in the case of low-degree full-disk data from GOLF (García et al. 1998; Gelly et al. 2002) and BiSON (Chaplin et al. 2001) observations. Kumar & Lu (1991) have described a model in which the spectrum at high frequency is a continuous acoustic spectrum
(because these
waves are not confined in a cavity) in which high-frequency
interference peaks (HIPs) appear due to constructive interference
between vertically travelling waves, one wave train coming directly from the acoustic source located somewhere beneath the solar surface, and another wave train having first travelled down before being refracted until it moves up again. The period of the HIPs is an indicator of the depth of the acoustic source within the photosphere. In the GOLF signal, García et al. (1998) and Gelly et al. (2002) have found a constant period at
![]() 70
70 ![]() Hz between 5.8 mHz
Hz between 5.8 mHz
![]() 7.5 mHz. Gelly et al. (2002) observe also a very important change in the amplitudes of the HIPs between the first period of GOLF (from April 1996 up to 1998, before the temporary loss of SoHO) on the blue wing of the Na lines and the second period of GOLF (from 1998 up to December 2001) on the red wing of the Na lines. They conclude that HIPs visibility in the spectra should be sensitive to the wavelength, or rather to the level in the photosphere to which they are observed. The stability of the period
7.5 mHz. Gelly et al. (2002) observe also a very important change in the amplitudes of the HIPs between the first period of GOLF (from April 1996 up to 1998, before the temporary loss of SoHO) on the blue wing of the Na lines and the second period of GOLF (from 1998 up to December 2001) on the red wing of the Na lines. They conclude that HIPs visibility in the spectra should be sensitive to the wavelength, or rather to the level in the photosphere to which they are observed. The stability of the period
![]() indicates that the position of the acoustic source remains the same in the precision level. On the other hand, Balmforth & Gough (1990) explain the "mode-like'' structure at high frequencies by wave reflection which takes place near discontinuities in the density gradient. Wave reflection from the chromosphere-corona transition region results in an "extended'' acoustic cavity. Time-distance measurements of the high-frequency waves (Jefferies et al. 1997) suggest that a small amount of wave reflection (
indicates that the position of the acoustic source remains the same in the precision level. On the other hand, Balmforth & Gough (1990) explain the "mode-like'' structure at high frequencies by wave reflection which takes place near discontinuities in the density gradient. Wave reflection from the chromosphere-corona transition region results in an "extended'' acoustic cavity. Time-distance measurements of the high-frequency waves (Jefferies et al. 1997) suggest that a small amount of wave reflection (![]() 6%) may be occuring in the Sun's chromosphere.
6%) may be occuring in the Sun's chromosphere.
For the visibility of these fringes, the requirement on the data analysis forbids the use of our "repetitive music'' gap-filling method, for the very simple reason that this method exactly creates the appearance of such fringes in the power spectra. An important requirement is the need for a low high-frequency noise level. A severe selection of individual days has been made on this unique criterium (i.e. the integral of the noise above the cut-off frequency in the daily power spectra). Then, it must be noted that the fringe separation is of the order of 70 ![]() Hz, so that a time of integration at about 8 hours is theoretically sufficient for resolving them. It has then been decided to use only the average of daily power spectra, with a second selection criterium: only days with at least 9 hours of data without gaps have been selected.
Hz, so that a time of integration at about 8 hours is theoretically sufficient for resolving them. It has then been decided to use only the average of daily power spectra, with a second selection criterium: only days with at least 9 hours of data without gaps have been selected.
![\begin{figure}
\par\includegraphics[angle=0,width=8.8cm,clip]{MS3485f6.eps}\end{figure}](/articles/aa/full/2004/03/aa3485/Timg55.gif) |
Figure 6: Daily averaged IRIS power spectrum. |
| Open with DEXTER | |
To reduce by one more step the background noise, the same method described in Sect. 3.1 to follow p-mode frequencies beyond 4.5 mHz is applied on the original timeseries. Then, each daily spectrum is in fact the average of three cross spectra between independent series. Figure 6 shows the average of several hundred such daily spectra, with a frequency resolution of the order of (10-hour)-1 or about 27 ![]() Hz.
Hz.
The next step of this analysis is to select a given bandwidth in the high-frequency range where the visibility of these pseudo modes will be investigated. Figure 7 shows the power spectrum of the relative fluctuation of the continuum spectrum in Fig. 6 in the frequency range extending from 5.8 to 7.5 mHz. The prominent peak in Fig. 7 indicates the existence of a periodicity of 70.8 ![]() Hz in this pseudo-mode range, in good agreement with the results obtained by García et al. (1998) and Gelly et al. (2002) with the GOLF data.
Hz in this pseudo-mode range, in good agreement with the results obtained by García et al. (1998) and Gelly et al. (2002) with the GOLF data.
A further step has been attempted by separating all the individual days of data into two sequences, one around the maximum of activity and one near the minimum, in order to track the continuation of Fig. 2 on the extreme-right side. However, the smaller amplitude of the pseudo modes during the high activity period (which was also reported by Gelly et al. (2002) with GOLF observations), together with the reduced statistics with only half the number of individual days, results in a worse visibility and a much larger uncertainty in the periodicity estimation, so that no measurement of the frequency shift with activity in the pseudo-mode range can be claimed with the IRIS data.
Nevertheless, while the GOLF data did not use the same spectral window along the sodium lines at minimum and during the rising activity phase, this is not the case with the IRIS data. The decreased visibility, in this case, cannot be explained by a difference of altitude in the solar atmosphere. Presumably then, both effects must be present: a reduced amplitude at a given altitude with more activity, and also a reduced amplitude at higher altitude independent of magnetic activity.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3485f7.eps}\end{figure}](/articles/aa/full/2004/03/aa3485/Timg56.gif) |
Figure 7:
Power spectrum of the continuum part in Fig. 6 over the frequency range from 5.8 to 7.5 mHz. The prominent peak corresponds to a periodicity of 70.8 |
| Open with DEXTER | |
The adapted line-fitting method for the so-called "repetitive music'' process used to analyze the helioseismic IRIS data provides adequate measurements of the low-![]() p-mode parameters and of their evolution with solar activity, along the falling phase of the solar cycle 22 and the rising phase of the solar cycle 23. Also applicable and useful for stellar seismic observations, this gap-filling method was recently used by Bouchy & Carrier (2002) in the analysis of the acoustic spectrum of
p-mode parameters and of their evolution with solar activity, along the falling phase of the solar cycle 22 and the rising phase of the solar cycle 23. Also applicable and useful for stellar seismic observations, this gap-filling method was recently used by Bouchy & Carrier (2002) in the analysis of the acoustic spectrum of ![]() Cen A.
Cen A.
In the present paper, the solar p-mode frequencies have been followed over a large frequency range, up to the acoustic cut-off frequency at ![]() 5.5 mHz. The well known increase of frequency shifts
5.5 mHz. The well known increase of frequency shifts ![]() in the frequency range 2.0-3.7 mHz, following the inverse mode-mass law is reported. Above 3.7 mHz, a downturn of the frequency shifts is observed, which becomes clearly negative above 4.5 mHz with a rapid decrease up to the 5.5 mHz cut-off frequency reaching a significant value of
in the frequency range 2.0-3.7 mHz, following the inverse mode-mass law is reported. Above 3.7 mHz, a downturn of the frequency shifts is observed, which becomes clearly negative above 4.5 mHz with a rapid decrease up to the 5.5 mHz cut-off frequency reaching a significant value of ![]() -5
-5 ![]() Hz. This drop was only observed to-date for the intermediate degrees (Jefferies 1998; Ronan et al. 1994) and recently in low-
Hz. This drop was only observed to-date for the intermediate degrees (Jefferies 1998; Ronan et al. 1994) and recently in low-![]() modes by Gelly et al. (2002) in GOLF on-board SoHO experiment. Our value of
modes by Gelly et al. (2002) in GOLF on-board SoHO experiment. Our value of ![]() -5
-5 ![]() Hz at about the acoustic cut-off frequency is consistent with those found by these authors. Above the cut-off frequency, Jefferies (1998) and Ronan et al. (1994) have even observed an upturn for intermediate-
Hz at about the acoustic cut-off frequency is consistent with those found by these authors. Above the cut-off frequency, Jefferies (1998) and Ronan et al. (1994) have even observed an upturn for intermediate-![]() ,
creating such a dip around 5.5 mHz.
,
creating such a dip around 5.5 mHz.
The strong increase in the frequency shifts with frequency up to 3.7 mHz reflects changes in and just below the photosphere with solar activity. The abrupt decline above 3.7 mHz may be the effect of changes in the chromosphere, which acts as a cavity in which p modes are trapped (Goldreich et al. 1991). For Jain & Roberts (1996), the observed frequency shifts are to be understood as a consequence of both magnetic and thermal changes, the rise phase being a consequence of an increase in the mean photospheric magnetic field with the observed abrupt decline coming from a combination of an increase in mean chromospheric magnetic field strength and an increase in chromospheric temperature. Although these simultaneous effects can qualitatively explain the observed frequency shifts, the required temperature changes seem quite large.
We confirm the linewidths ![]() increase with solar activity and show the good
and positive correlation between the oscillation
damping and solar activity: during the maximum of solar activity cycle, oscillation damping is larger than during the minimum of solar activity. The averaged frequency shifts
increase with solar activity and show the good
and positive correlation between the oscillation
damping and solar activity: during the maximum of solar activity cycle, oscillation damping is larger than during the minimum of solar activity. The averaged frequency shifts
![]() computed for each year over the increasing phase of the frequency shifts are well correlated with solar activity. On the other hand,
computed for each year over the increasing phase of the frequency shifts are well correlated with solar activity. On the other hand,
![]() measured beyond the downturn observed at about 3.7 mHz shows a negative correlation with solar activity.
measured beyond the downturn observed at about 3.7 mHz shows a negative correlation with solar activity.
Above the acoustic cut-off frequency, Libbrecht (1988) first observed a regularly spaced peaked structure in the so-called pseudo-mode range. As no p-mode visibility is expected beyond the cut-off frequency, these fringes are generally interpreted as real fringes of interference between travelling acoustic waves. The IRIS data confirm the HIPs periodicity of about 70 ![]() Hz, and also the much reduced visibility during the phase of higher activity. Unfortunately, this reduced amplitude does not permit us to confirm the stability of the HIPs structure along the solar cycle with the IRIS data alone.
Hz, and also the much reduced visibility during the phase of higher activity. Unfortunately, this reduced amplitude does not permit us to confirm the stability of the HIPs structure along the solar cycle with the IRIS data alone.
Acknowledgements
Data from the IRIS network depends on the coordinated efforts of many people from several nations. The authors wish to thank those who have conceived the instrument: E. Fossat and G. Grec; those who have contributed to build and maintain all instruments on site: B. Gelly, J.F. Manigault, G. Rouget, J. Demarcq, G. Galou, A. Escobar, J.M. Robillot; those who have operated the observing sites: M. Baijumamov, S. Ehgamberdiev, S. Ilyasov, S. Kholikov, I. Khamitov, G. Menshikov, S. Raubaev, T. Hoeksema, Z. Benkhaldoun, M. Lazrek, S. Kadiri, H. Touma, M. Anguera, A. Jiménez, P.L. Pallé, A. Pimienta, C. Régulo, T. Roca Cortés, L. Sanchez, F.X. Schmider; R. Luckhurst, those who have developed the analysis software: S. Ehgamberdiev, S. Kholikov, E. Fossat, B. Gelly, M. Lazrek, P.L. Pallé, L. Sanchez, E. Gavryuseva, V. Gavryusev; and those who have contributed to the success of the IRIS project in other critical ways: P. Delache, D. Gough, I. Roxburgh, F. Hill, T. Roca-Cortés, G. Zatsepin, T. Yuldashbaev, L. Woltjer, H. Van der Laan, D. Hofstadt, J. Kennewell, D. Cole, P.H. Scherrer, F. Sanchez, J.P. Veziant.
The Uzbek contribution has been supported by the Intas 97-31198 and SCOPES 7UZPJ065728.01/1 grants. The authors acknowledge also J. Provost for providing mode-mass values and wish to thank P. Boumier from IAS, Université Paris Sud, for many constructive remarks and helpful suggestions in the final writing of this paper.