A&A 413, L11-L14 (2004)
DOI: 10.1051/0004-6361:20034636

Constraints on the heliospheric magnetic field variation during the Maunder Minimum from cosmic ray modulation modelling

K. Scherer 1 - H. Fichtner 2


1 - Institut für Astrophysik und Extraterrestrische Forschung der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2 - Institut für Theoretische Physik IV: Weltraum- und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany

Received 6 October 2003 / Accepted 24 November 2003

Abstract
Using a dynamic multifluid model of the global heliosphere (Bonn model) we found, that the variation of the heliospheric interface and the corresponding cosmic ray modulation can not be made responsible for the increase of the mean cosmic ray flux during the Maunder Minimum. This is because the diffusion coefficients of cosmic rays required to simulate their flux increase need an "intrinsic'' time variation, i.e. one that can be attributed to the solar or heliospheric magnetic field, thus, to the solar dynamo. Our study of the diffusion coefficients constrains the decrease in the strength of the solar magnetic field during the Maunder Minimum to about a factor of 4.

Key words: cosmogenic isotopes - cosmic ray modulation - Maunder Minimum - heliospheric magnetic field - solar dynamo

1 Motivation

For theories of the solar dynamo it is very important to have knowledge about the heliospheric magnetic field and its variation on various time scales in order to obtain contraints on the solar magnetic field (Lockwood et al. 1999; Solanki et al. 2000; Wang & Sheeley 2003). It is of particular interest not only to understand the variations on the short time scales of the Schwabe- and the Hale cycle, i.e. $\sim$11and $\sim$22 years, respectively, but also for the so-called grand minima of solar activity like the Maunder Minimum lasting from about 1645 to 1715 (Eddy 1983). Although poorly documented by observations of physical parameters, the Maunder Minimum is most interesting in this context, because of its proximity to the present and its long duration.

The heliospheric magnetic field and its turbulence levels are responsible for the modulation of cosmic rays. In contrast to measurements of the heliospheric magnetic field the cosmic ray flux can be indirectly traced back into the distant past significantly earlier than the Maunder Minimum. This is possible because the production rate of cosmogenic isotopes in the atmosphere of Earth depends on the flux of cosmic rays (e.g. Masarik & Beer 1999; Beer 2000).

Thus, long-term records of cosmogenic isotopes, in particular of 10Be, are a proxy for the long-term variation of the cosmic ray flux at Earth. The observed 10Be concentration presented in Fig. 1 shows a strong increase during the Maunder Minimum, which in the line of the arguments given above is caused by an increasing cosmic ray flux. Excluding external variations (see, e.g., Shaviv 2003) on the time scales of interest here, the cosmic ray flux can most effectively be influenced by the heliospheric magnetic field strength and turbulence levels both of which are most likely anticorrelated to the cosmic ray flux. Because of the direct relation between the heliospheric magnetic field and the solar magnetic field, one can conclude that during the Maunder Minimum also the solar magnetic field was weak as might indeed be indicated by the almost complete absence of sunspots during this period.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{Fj062_fig1.ps} \end{figure} Figure 1: The observed concentration of 10Be form 1500-2000. Also shown is the observed sunspot number from 1600-2000. The figure is taken from McCracken & McDonald (2001) who applied an averaging procedure to the original data published by Beer et al. (1990).
Open with DEXTER

While it is clear that the cosmic ray flux is anticorrelated to the solar activity, it is less clear whether there is a direct or an indirect connection in the case of grand minima, like the Maunder Minimum. The former is provided by the solar/heliospheric magnetic field variation, while an example for the latter is given by the dynamics of the heliosphere in response to the solar activity.

Due to the variation of the solar wind ram pressure with solar activity the so-called heliospheric interface, i.e. the layer of subsonic plasma between the supersonic solar and interstellar wind, is changing in time. Depending on its dynamically changing structure the heliospheric interface might act as diffusion barrier to galactic cosmic rays. Thus, it can provide a modulation of the cosmic ray flux, which is indirectly related to the solar activity.

Both alternatives have been discussed as causes for the cosmic ray flux increase during the Maunder Minimum. Wang & Sheeley (2003) considered the direct effect of a solar/heliospheric magnetic field decrease, while McCracken & McDonald (2001) proposed the indirect effect of modulation within the heliospheric interface (see also Bonino et al. 1997; Usoskin et al. 2001; Webber & Higbie 2003).

In order to study the relative importance of both effects, we applied the so-called Bonn Model (Fahr et al. 2000; Scherer & Fahr 2003a,b), a dynamic multifluid model of the global heliosphere, to the cosmic ray modulation during the Maunder Minimum. To the best of our knowledge, this is the first study of cosmic ray modulation during the Maunder Minimum with a sophisticated model of heliospheric dynamics including selfconsistently the cosmic ray modulation.

We find that the dynamics of the heliospheric interface and the corresponding cosmic ray modulation can not explain the cosmic ray flux increase during the Maunder Minimum.

We further show that the most plausible maximum variation of the solar wind speed during the Maunder Minimum and the corresponding heliospheric magnetic field changes are also not consistent with the observed flux increases. This is because the diffusion coefficients required to simulate the cosmic ray flux variations need an additional "intrinsic'' time variation, that can be attributed to the solar magnetic field and, thus, to the solar dynamo.

Therefore, studying the diffusion coefficients of cosmic rays provides constraints to the time variation and strength of the magnetic field in the heliosphere and on the Sun.

2 Modelling the cosmic ray modulation with the Bonn model

The Bonn model describes the interaction of the solar wind with the interstellar medium. The resulting dynamics of the heliosphere is treated selfconsistently on the basis of the mutual interactions of protons, hydrogen atoms, pickup ions, anomalous and galactic cosmic rays. The Bonn model is discussed in detail in Fahr et al. (2000) and especially its dynamics in Scherer & Fahr (2003a,b). Therefore, we restrict ourselves to explain only the modelling of the long-term variation of the solar wind parameters simulating a grand minimum as proxy for the Maunder Minimum. In addition, we describe the time variation of the cosmic ray diffusion used for the simulations.

2.1 The simulated Maunder Minimum

The explicit time dependence in the Bonn model was first studied by Scherer & Fahr (2003a,b). Here we will describe the additional modifications which are necessary to model a long-term variation of the solar wind speed and density keeping the solar wind flux constant (McComas et al. 2000). We use the form of the solar cycle variation derived from observations as described in Fahr et al. (1987), see also Scherer & Fahr (2003b):

\begin{displaymath}f_i(t) = a_i + b_i~ \cos(\omega_i~t - \phi_i) ~ \exp\left[c_i~\cos(\omega_i~t - \phi_i)\right] \end{displaymath} (1)

such that $0\le f_i(t) \le 1$. The constants $\phi_i$ can be used to avoid a discontinuity introduced when switching on the time dependence and to shift the variation patterns in time. This form is used for both the short- and long-term variations by adjusting the constants  ai, bi, ci, which are not independent:

\begin{displaymath}b_i = d_i [\exp(c_i) + \exp(-c_i)]^{-1}\ \ ; \quad a_i = b_i \exp(-c_i). \end{displaymath} (2)

For the 11-year cycle we used c1 = 1, d1 = 1 and $\omega_1 = 2 \pi/({\rm 11[years]})$, while for the Maunder Minimum we chose $c_2 = 6, d_2=0.5, \omega_2 = 2\pi/({\rm 280[years]})$. The period of 280 years is arbitrary, but guarantees a sufficiently large separation of grand minima. The amplitude of the 11-year variation of the solar wind speed during the Maunder Minimum is controlled by the parameter d2=0.5, which corresponds to a 50% reduction of the solar wind speed.

The motivation for using the same functional form fi(t) is the assumption, that grand minima simply occur with a longer period, but that otherwise their physical characteristics are identical.

Then the speed dependence is given by:

\begin{displaymath}v(t) = v_{\rm max} -(v_{\rm max} - v_{\rm min})~f_1(t)~(1 - f_2(t)) \end{displaymath} (3)

with $v_{\rm max} = 800$ km s-1 and $v_{\rm min} = 300$ km s-1. This is displayed in the upper panel of Fig. 2. The simulated Maunder Minimum is the extended period of, on average, higher solar wind speed.

While even during a solar minimum the wind speed near the ecliptic never reaches an average value of 800 km s-1, it is near this value throughout most of the heliosphere (McComas et al. 2000). Observations show that the region of slower wind is limited to heliographic latitudes between $\sim$$\pm$$30^\circ$ (see also Srivastava & Schwenn 2000). The remaining $60^\circ$ per hemisphere, i.e. about 75%, are filled with a high-speed wind. Given that the Bonn model is 2-D, and, thus, has to be considered as an averaging model regarding heliographic latitude, the average will be a high-speed value rather than a low-speed one.

Furthermore, the chosen value of 800 km s-1 must be understood as an upper limit for the effect of a solar activity persisting throughout the Maunder Minimum, resulting in a larger excursion of the heliospheric interface than for simulations with smaller values (see Scherer & Fahr 2003b).

  \begin{figure} \par\includegraphics[width=7.9cm,angle=0,clip]{Fj062_fig2.ps} \end{figure} Figure 2: In the upper panel the solar wind speed variation for a Maunder like grand minimum is shown, see Eq. (3). In the lower panel the corresponding variation for the diffusion coefficient is shown, see Eq. (5). Note, that the increase during the simulated Maunder Minimum is not a velocity effect, but has to be attributed to a change of the solar magnetic field. The origin of time (in years) is arbitrary.
Open with DEXTER

2.2 The diffusion model

In the two-dimensional Bonn model the diffusion of cosmic rays is described with a tensor of the form

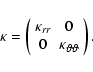\begin{displaymath}\kappa = \left( \begin{array}{cc} \kappa_{rr} & 0 \\ 0 & \kappa_{\vartheta\vartheta}\\ \end{array}\right). \end{displaymath} (4)

In the ecliptic plane, $\kappa_{rr}$can be interpreted as the coefficient  $\kappa_{\perp}$ describing diffusion perpendicular to the heliospheric magnetic field, while $\kappa_{\vartheta\vartheta} = \kappa_{\Vert}$ corresponds to the parallel diffusion. Besides using the well-established relation  $\kappa_{\perp} = \eta\kappa_{\Vert}$(Giacalone & Jokipii 1999) with $\eta = 0.03$ we employ the representation:

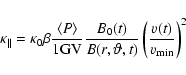\begin{displaymath}\kappa_{\Vert} = \kappa_0 \beta \frac{\langle P \rangle}{1 {\... ...)}{B(r,\vartheta,t)} \left(\frac{v(t)}{v_{\rm min}}\right)^2 \end{displaymath} (5)

where $\beta$ is the particle speed normalized to the speed of light, $\langle P\rangle = 13~{\rm GV}$ is the mean rigidity required in the fluid approach (Fahr et al. 2000) and it corresponds to the energy range of those cosmic rays producing most of the cosmogenic isotopes. The time-varying solar wind speed v(t) is described above, $B(r,\vartheta,t)$ is the Parker field, and  $\kappa_{0} = 10^{22}$ cm2 s-1 at Earth.

We incorporated a time variation of $\kappa_{\Vert}$ which is based on fits to observations, see Ferreira (2002) and Ferreira & Potgieter (2003), where we use a slightly different parametrization in Eq. (5) than these authors.

As is demonstrated below, the increase of the diffusion coefficient due to the on-average higher solar wind speed during the Maunder Minimum is not sufficient to explain the mean flux increase of galactic cosmic rays indicated by the 10Be data. It is rather necessary to introduce an "intrinsic'' time variation of the heliospheric magnetic field (i.e. also the solar magnetic field) given by

B0(t) = B00  [1 + 3 f3(t)]-1 (6)

where the constants in f3(t) are $c_3=15, d_3=1, \omega_3 = \omega_2$. B00, which cancels out in Eq. (5), is giving the strength of the Parker field at 1 AU at the beginning of the simulation where we used standard solar wind values (see Scherer & Fahr 2003b).

As nothing is known about this time variation, there is no preferred choice for f3. For simplicity, we have chosen a form similar to f1 and f2. Note, because we study only the long-term trend, details of the time variation of f3 do not influence our findings described below.

3 Discussion of the simulations


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{Fj062_fig3.ps} \end{figure} Figure 3: The simulated cosmic ray variation during and around the Maunder Minimum in a dynamical heliosphere. The dashed line indicates the flux level for f3(t)=0, see Eq. (6).
Open with DEXTER

We have simulated the dynamics of the outer heliosphere without using the additional variation of the diffusion coefficient during the Maunder Mininum, i.e. f3(t) = 0. In that case, the variation of the diffusion coefficient is entirely determined by the velocity profile shown in the upper panel of Fig. 2. The finding is a cosmic ray flux during the Maunder Minimum that never exceeds the maximum of periods other than that of a grand minimum, as indicated by the dashed line in Fig. 3. This means that the motion of the heliospheric interface, particularly that of the termination shock and the heliopause, does not affect the cosmic ray flux at 1 AU. This is to be expected, because on a time-scale of about fifty years of quiet solar wind the cosmic ray flux is independent of the dynamics of the outer heliospheric, due to a characteristic diffusion time that is much shorter than the relaxation time of the heliospheric interface. So far, our modelling does not indicate an influence of the diffusion coefficient in the interface region on this result. While only a negligible effect is expected for the 1 AU flux, a more detailed investigation appears interesting in the light of recent results by Florinski et al. (2003), because it might give insight into the structure of the heliosheath possibly observed by the Voyager spacecraft in the near future (Krimigis et al. 2003; McDonald et al. 2003).

The only way to further increase the mean cosmic ray flux during the Maunder Minimum is to increase the diffusion coefficient appropriately. As argued above this cannot be a velocity effect, and therefore the function f3(t) in Eq. (6) should not be zero. This corresponds to a variation of the solar/heliospheric magnetic field as modelled by Wang & Sheeley (2003) resulting in the time profile of the diffusion coefficient displayed in the lower panel of Fig. 2. The resulting galactic cosmic flux in the inner heliosphere is depicted in Fig. 3. Obviously, an additional increase by a factor of 4 (see Eq. (6)) during the Maunder Minimum is evidently reflected in a mean cosmic ray flux increase. Note, that this factor is much smaller than that needed for the variation during a normal Schwabe- or Hale cycle. The latter can, depending on the cosmic ray energy, be as high as 50 (Ferreira 2002).

The cosmic ray flux increase during the Maunder Minimum amounts to 20% of its value at the beginning of this grand minimum. According to Masarik & Beer (1999), who performed extended computations of the cosmogenic nuclide production due to cosmic rays in the Earth atmosphere, such increase results in a $\sim$60% increase of the 10Be production rate. As can be seen in Fig. 1 this is indeed observed during the Maunder Minimum. Evidently, our simulations reproduce the correct increases of the cosmic ray flux.

4 Conclusion

We have found, that an increase of the mean cosmic ray flux of 20% - required to explain the observed 10Be increase during the Maunder Minimum - can only be obtained with a decreasing solar and heliospheric magnetic field. Variations of the heliospheric interface in response to solar activity are not sufficiently strong to enhance the cosmic ray flux in the inner heliosphere. Therefore, the on-average increased concentration of cosmogenic isotopes during the Maunder Minimum is most likely correlated to a changing solar dynamo. With our modelling we can constrain the decrease of the solar magnetic field to about a factor of 4.

Acknowledgements
We are very grateful for discussions with S.E.S. Ferreira, H. Moraal, and M.S. Potgieter as well as for their hospitality during our visit at the Potchefstroom University. K.S. benefitted from financial support granted by the Deutsche Forschungsgemeinschaft in the frame of the project Heliotrigger (Fa 97/28-1). We thank an anonymous referee for help in improving the paper.

References


Copyright ESO 2003