A&A 413, 779-787 (2004)
DOI: 10.1051/0004-6361:20034356
S. N. Nahar
Department of Astronomy, The Ohio State University, Columbus, OH 43210, USA
Received 19 September 2003 / Accepted 4 October 2003
Abstract
An extensive set of oscillator strengths (f), line strengths (S)
and radiative decay rates (A) for dipole allowed, intercombination
and forbidden transitions in Fe XX is presented. Results
include 1792 bound fine structure levels of total angular momenta
J=1/2-19/2 of even and odd parities, with 2 ![]() 10, 0
10, 0
![]() 14, orbital angular momenta, 0
14, orbital angular momenta, 0 ![]() 14, and total
spin multiplicities 2S+1 = 2,4,6, yielding to about
14, and total
spin multiplicities 2S+1 = 2,4,6, yielding to about
![]() allowed and 13,874 forbidden transitions in Fe XX. These results
far exceed the available data in literature. The existing
data compiled by the National Institute for Standards and Technology
(NIST) are available for little over one hundred transitions, and the
previously calculated data under the Opacity Project includes 75 590
LS multiplets. The present ab initio calculations are carried out in
the close coupling approximation using the relativistic Breit-Pauli
R-matrix method for allowed and intercombination E1 transitions.
The wavefunction expansion includes 20 fine structure levels of
configurations 2s22p2, 2s2p3, and 2p4 of the core ion Fe XXI.
Computed energy levels are identified spectroscopically using a newly
developed procedure based on quantum defects and channel contributions.
All 55 observed levels have been identified and are in agreement to
much less than 1% with most of the calculated values. Coefficients
for radiative decays for the forbidden E2, E3, M1 transitions are
obtained through atomic structure calculations including relativistic
terms in the Breit-Pauli approximation using the code SUPERSTRUCTURE.
The theoretical transition probabilities are compared with available
values, with varying degree of agreement.
allowed and 13,874 forbidden transitions in Fe XX. These results
far exceed the available data in literature. The existing
data compiled by the National Institute for Standards and Technology
(NIST) are available for little over one hundred transitions, and the
previously calculated data under the Opacity Project includes 75 590
LS multiplets. The present ab initio calculations are carried out in
the close coupling approximation using the relativistic Breit-Pauli
R-matrix method for allowed and intercombination E1 transitions.
The wavefunction expansion includes 20 fine structure levels of
configurations 2s22p2, 2s2p3, and 2p4 of the core ion Fe XXI.
Computed energy levels are identified spectroscopically using a newly
developed procedure based on quantum defects and channel contributions.
All 55 observed levels have been identified and are in agreement to
much less than 1% with most of the calculated values. Coefficients
for radiative decays for the forbidden E2, E3, M1 transitions are
obtained through atomic structure calculations including relativistic
terms in the Breit-Pauli approximation using the code SUPERSTRUCTURE.
The theoretical transition probabilities are compared with available
values, with varying degree of agreement.
Key words: atomic data
Highly charged ions of iron are observed in a variety of high-temperature astrophysical sources, ranging from the UV to the X-ray. Spectral analysis and modeling of these spectra require accurate radiative data. However, currently available data is inadequate and incomplete for these purposes. While laboratory work has been carried out for some transitions, such measurements are generally very limited in scope and usually entail only the low-lying transitions. Systematic calculations with high precision have not yet been done for most of the iron ions. On the other hand, recent observations from space based UV and X-ray observatories, such as the HST, FUSE, Chandra and XMM-Newton, show a plethora of high excitation/high ionization lines of most ionization stages of iron. In order to address the great and growing need, work has been initiated to compute radiative data for Fe ions under the Iron Project (Hummer et al. 1993).
In this report large scale datasets for oscillator strengths (f-values), line strengths (S), and transition probabilities (A-values) for E1 (dipole allowed and intercombination), and forbidden electric quadrupole (E2) and octupole (E3), and magnetic dipole (M1) fine structure transitions in nitrogen-like Fe XX are presented. Calculations are carried out using the relativistic Breit-Pauli R-matrix method developed under the Iron Project for the E1 transitions, and configuration interaction atomic structure calculations using the code SUPERSTRUCTURE (Eissner et al. 1974; Nahar et al. 2003) for the forbidden E2, E3, and M1 transitions. All together these data should comprise a reasonably complete set of transitions for all practical applications involving Fe XX.
Currently, a limited number of 124 transitions in Fe XX are found in the evaluated compilation of results, obtained by various investigators using different methods, from the web based database of the National Institute for Standards and Technology (NIST). The most extensive previous calculations for oscillator strengths for Fe XX were carried out by VM Burke and DJ Lennon, under the Opacity Project (OP 1995, 1996), that are now accessible through the OP database, TOPbase (Cunto et al. 1993). However, the OP f-values were obtained for 75 590 dipole allowed multiplets in LS coupling; neglect of fine structure in the OP work was not crucial in the calculation of mean stellar opacities. But fine structure is of paramount importance in spectral line diagnostics of highly charged ions. The present work reports both the allowed and the forbidden transitions for Fe XX including fine structure, of potential importance not only for more accurate plasma opacities, but also in the synthesis of spectral models and in experimental or observational spectral analysis.
The Breit-Pauli R-matrix (BPRM) method, developed under the Iron Project
(IP, Hummer et al. 1993; Berrington et al. 1987, 1995) includes
relativistic effects in the Breit-Pauli approximation (Scott & Burke
1980; Scott & Taylor 1982). It enables calculation of both the dipole
allowed (
![]() )
and the intercombination (
)
and the intercombination (
![]() )
E1
transition probabilities in intermediate coupling, in contrast to the
OP work in LS coupling where only dipole allowed multiplet transitions
could be considered. Also, incorporation of the relativistic effects
in the close coupling R-matrix method yields a large number of fine
structure transition probabilities with higher accuracy.
)
E1
transition probabilities in intermediate coupling, in contrast to the
OP work in LS coupling where only dipole allowed multiplet transitions
could be considered. Also, incorporation of the relativistic effects
in the close coupling R-matrix method yields a large number of fine
structure transition probabilities with higher accuracy.
Many relevant theoretical details of the relativistic BPRM method are discussed in previous works, such as in the first large scale relativistic BPRM calculations for bound-bound transitions in Fe XXIV and Fe XXV (Nahar & Pradhan 1999) and for other ions (Nahar & Pradhan 2000 for Fe V, Nahar et al. 2000 for Fe V, Nahar 2002a for C II and C II, Nahar 2002b for Fe XXI and Ar XIII, Nahar et al. 2003 for Fe XVII). A detailed description of atomic structure calculations for the forbidden transitions, involving the various terms in the Breit-Pauli Hamiltonian, are presented in Nahar et al. (2003). Below, we outline the salient features of these calculations.
In the CC approximation the wavefunction expansion, ![]() ,
for a
(N+1) electron system with total spin and orbital angular momenta
symmetry
,
for a
(N+1) electron system with total spin and orbital angular momenta
symmetry ![]() or total angular momentun symmetry
or total angular momentun symmetry ![]() ,
is
described in terms of the target ion states as:
,
is
described in terms of the target ion states as:
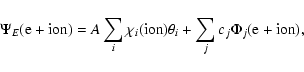 |
(1) |
The relativistic (N+1)-electron Hamiltonian for the N-electron target
ion and a free electron in the Breit-Pauli approximation, as adopted in
the IP BPRM codes, is
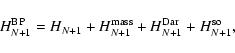 |
(2) |
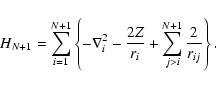 |
(3) |
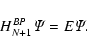 |
(4) |
The primary quantity expressing radiative excitation or de-excitation
in a weak field is the line strength
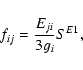 |
(6) |
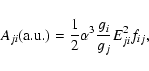 |
(7) |
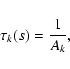 |
(11) |
The CC calculations using the BPRM method proceed in several stages. Below we describe these as they pertain to Fe XX.
The most important initial step is to construct an accurate representation
of the target or core ion eigenstates. The wavefunction expansion for
the Fe XX
![]() (e + Fe XXI) system consists of 20 fine strucuture
levels (Table 1) of the target ion Fe XXI from configurations 2s22p2,
2s2p3, 2p4. The target wavefuctions were obtained from atomic
structure calculations using SUPERSTRUCTURE (Eissner et al. 1974). Table 1
lists the set of spectroscopic and correlation configurations, and
the values of Thomas-Fermi scaling parameters for individual orbitals
(e + Fe XXI) system consists of 20 fine strucuture
levels (Table 1) of the target ion Fe XXI from configurations 2s22p2,
2s2p3, 2p4. The target wavefuctions were obtained from atomic
structure calculations using SUPERSTRUCTURE (Eissner et al. 1974). Table 1
lists the set of spectroscopic and correlation configurations, and
the values of Thomas-Fermi scaling parameters for individual orbitals
![]() employed in the atomic structure calculations.
All orbitals up to the 3d were treated as spectroscopic, i.e. included
in the total Fe XX wavefunction expansion. The relative energies given
in Table 1 are the measured values in the NIST database that are
used in the BPRM calculations for radiative data.
employed in the atomic structure calculations.
All orbitals up to the 3d were treated as spectroscopic, i.e. included
in the total Fe XX wavefunction expansion. The relative energies given
in Table 1 are the measured values in the NIST database that are
used in the BPRM calculations for radiative data.
Table 1:
Fine structure levels and the relative energies
of the target (core) ion Fe XXI in wavefunction expansion of Fe XX. The
atomic structure calculations for the wavefunction employs
spectroscopic set of configurations:
2s22p2, 2s2p3, 2p4, 2s22p3s, 2s22p3p, 2s22p3d,
2s2p23s, 2s2p23p, 2s2p23d, 2p33s, and correlation
configurations: 2p33p, 2p33d, 2p34s, 2p34p, 2p34d,
2s22p4s, 2s22p4p, 2s22p4d, 2s2p24s, 2s2p24p, 2s2p24d,
and the Thomas-Fermi scaling parameters for the orbitals:
![]() (1s), 1.25(2s), 1.15(2p), 1.25(3s), 1.15(3p), 1.17(3d), -1.20(4s),
-1.20(4p), -1.2(4d).
(1s), 1.25(2s), 1.15(2p), 1.25(3s), 1.15(3p), 1.17(3d), -1.20(4s),
-1.20(4p), -1.2(4d).
The bound-channel term of the wavefunction, the second term in Eq. (1), includes all possible (N+1)-configurations from vacant orbitals to maximum occupancies 2s2, 2p6, 3s2, 3p2, and 3d2.
As mentioned, the BPRM calculations involve several stages and
begin with the wavefunctions of the target or the core eigenstates.
The one-electron orbitals from SUPERSTRUCTURE are used as the input for
the BPRM codes to compute the one- and two-electron radial integrals, in
STG1. The (e + ion) algebraic and angular coefficients are computed in
STG2. The intermediate coupling calculations are enabled on recoupling
the LS symmetries in a pair-coupling representation in stage RECUPD.
The (e + core) Hamiltonian matrix is diagonalized for each resulting
![]() in STGH.
in STGH.
Calculations for Fe XX transitions included all possible bound
levels for 1/2
![]() 19/2 of even and odd parities, with
19/2 of even and odd parities, with
![]() ,
,
![]() 14, and (2S+1)=2, 4, 6.
The fine structure bound levels are obtained on scanning through the
poles in the (e + ion) Hamiltonian with a fine mesh of effective
quantum number
14, and (2S+1)=2, 4, 6.
The fine structure bound levels are obtained on scanning through the
poles in the (e + ion) Hamiltonian with a fine mesh of effective
quantum number ![]() ,
at
,
at
![]() = 0.001 or less. The mesh is
orders of magnitude finer than the typical
= 0.001 or less. The mesh is
orders of magnitude finer than the typical ![]() = 0.01 generally
employed in the OP work to obtain the LS energy terms. This is one of
the main reasons that the BPRM calculations require orders of magnitude
more CPU time and memory than LS coupling. Since the fine structure
components lie in smaller energy gaps, a very fine mesh is essential to
avoid any missing levels and to obtain accurate energies for high-lying
levels.
= 0.01 generally
employed in the OP work to obtain the LS energy terms. This is one of
the main reasons that the BPRM calculations require orders of magnitude
more CPU time and memory than LS coupling. Since the fine structure
components lie in smaller energy gaps, a very fine mesh is essential to
avoid any missing levels and to obtain accurate energies for high-lying
levels.
The large number of theoretically computed fine structure energy levels
are identified using a newly developed spectroscopic identification
procedure encoded in the code PRCBPID (Nahar & Pradhan 2000). The levels
obtained from the BPRM calculations occur at eigenvalues of the
BP Hamiltonian, labeled only by the total angular momentum and parity,
i.e. by ![]() ,
which is insufficient for unique identification.
The computed energies however yield quantum defects relative to the
parent target level SiLiJi to which a given Rydberg series of
bound levels (
,
which is insufficient for unique identification.
The computed energies however yield quantum defects relative to the
parent target level SiLiJi to which a given Rydberg series of
bound levels (
![]() belongs. The identification procedure
coded in PRCBPID employs quantum defect analysis of levels computed up
to effective quantum number
belongs. The identification procedure
coded in PRCBPID employs quantum defect analysis of levels computed up
to effective quantum number
![]() ,
together with an analysis
of the wavefunction components of all coupled channels. However, often
a level can be assiged to a multiple spectroscopic identification.
The spectroscopic identification of low lying levels are reconfirmed by
comparing with those of available levels, especially those found in
the NIST database. The remaining energy levels, following Hund's rule,
are assigned notation such that a level with higher angular orbital
momentum L and/or higher spin multiplicity lies below the lower L
and/or lower spin multiplicity. The final designation assignment
is given as
,
together with an analysis
of the wavefunction components of all coupled channels. However, often
a level can be assiged to a multiple spectroscopic identification.
The spectroscopic identification of low lying levels are reconfirmed by
comparing with those of available levels, especially those found in
the NIST database. The remaining energy levels, following Hund's rule,
are assigned notation such that a level with higher angular orbital
momentum L and/or higher spin multiplicity lies below the lower L
and/or lower spin multiplicity. The final designation assignment
is given as
![]() ,
where
,
where ![]() ,
,
![]() ,
,
![]() are the configuration, LS term and parity, and total angular
momentum of the target, nl are the principal and orbital quantum
numbers of the outer or the valence electron, and J and
are the configuration, LS term and parity, and total angular
momentum of the target, nl are the principal and orbital quantum
numbers of the outer or the valence electron, and J and ![]() are
the total angular momentum, LS term and parity of the (N+1)-electron
system. In addition the level identification procedure establishes
a unique correspondence between the fine structure levels and their
LS terms such that exact number of fine structure levels are accounted
for each LS term.
are
the total angular momentum, LS term and parity of the (N+1)-electron
system. In addition the level identification procedure establishes
a unique correspondence between the fine structure levels and their
LS terms such that exact number of fine structure levels are accounted
for each LS term.
Forbidden transition are considered through configuration interaction
atomic structure calculations using the code SUPERSTUCTURE (Eissner et al.
1974). The code has been updated to consider electric octupole (E3)
and magnetic quadrupole (M2) transitions in addition to electric dipole
(E1) and quadrupole (E2) and magnetic dipole (M1) in Breit-Pauli
approximation (Nahar et al. 2003). First reported results on higher multipole
transitions are on Fe XVII (Nahar et al. 2003).
![]() ,
,
![]() ,
and
,
and
![]() are obtained for almost 14 000 forbidden transitions among
the first 215 levels of Fe XX.
are obtained for almost 14 000 forbidden transitions among
the first 215 levels of Fe XX.
Computed data are presented and discussed separately for energy levels, oscillator strengths for E1 transitions, and forbidden transitions.
1792 fine structure levels are found theoretically. Oscillator strengths,
line strengths, and transition probabilities for the bound-bound allowed
and forbidden transitions among these levels in Fe XX are computed.
The energy levels correspond to total angular momenta 1/2
![]() 19/2 of even and odd parities, and levels up to
19/2 of even and odd parities, and levels up to ![]() 10 and 0
10 and 0
![]() 14, with total orbital angular momenta 0
14, with total orbital angular momenta 0
![]() 14 and spin multiplicities 2S + 1 = 2, 4, 6.
14 and spin multiplicities 2S + 1 = 2, 4, 6.
A total of 63 levels (55 from energy table and 8 from the transition
table) are available from the NIST compilation. Each of them has been
identified in the theoretical dataset. Table 2 presents comparison
between calculated BPRM energies and the measured values. Most
of the calculated levels are well within 1% of the measured energies,
with the largest discrepancy being 3.4% for the level
2s22p2(3P)4d(4P5/2). The measured value for this component,
4P5/2, is relatively larger compared to the other two components
4P3/2 and 4P1/2, where the differences are less than 1%.
The level index, IJ, in the table, is the position of the calculated
level in the given ![]() symmetry. This establishes the correspondence
between the calculated and the observed levels, useful in applications.
symmetry. This establishes the correspondence
between the calculated and the observed levels, useful in applications.
Table 2:
Comparison of calculated BPRM absolute energies,
![]() ,
with the observed ones,
,
with the observed ones, ![]() ,
for Fe XX. IJ is the level
index for calculated energy position in symmetry
,
for Fe XX. IJ is the level
index for calculated energy position in symmetry ![]() .
The asterisk
next to a J-value indicates that the term has incomplete set of
observed fine structure levels.
.
The asterisk
next to a J-value indicates that the term has incomplete set of
observed fine structure levels.
The complete set of calculated energy levels of Fe XX is availabe
eletronically. Following previous works, (e.g. Nahar et al. 2000) the
energies are presented in two formats, (i) where levels are ordered as
components of a LS term showing spectroscopic completeness of the set,
and (ii) in ascending energy order for each ![]() symmetry for
practical applications.
symmetry for
practical applications.
In the LS term format the fine structure components LSJ are
grouped together according to the same configuration CLSJ, useful for
spectroscopic diagnostics. It also provides the check for completeness
of sets of energy levels that should belong to the corresponding LS
term, and detects any missing level. Table 3a presents a sample set of
Fe XX levels in this format. The columns provide the core information,
![]() ,
the configuration of the outer electron, nl, total
angular momentun, J, energy in Rydbergs, the effective quantum number
of the valence electron,
,
the configuration of the outer electron, nl, total
angular momentun, J, energy in Rydbergs, the effective quantum number
of the valence electron, ![]() (
(
![]() ,
where
,
where ![]() is the
next immediate target threshold energy), and possible LS term
designations of the level. No effective quantum number is assigned for an
equivalent electron state. The top line of each set provides the expected
number of fine structure levels (Nlv) for the
is the
next immediate target threshold energy), and possible LS term
designations of the level. No effective quantum number is assigned for an
equivalent electron state. The top line of each set provides the expected
number of fine structure levels (Nlv) for the
![]() terms,
where spin multiplicity (2S+1) and parity
terms,
where spin multiplicity (2S+1) and parity ![]() are defined. Values
of L and of total angular momentum J associated with each
L are specified within parentheses next to L. The line is followed
by set of BPRM energy levels of same configurations. Nlv(c) at the end
of the set specifies total number of calculated J-levels obtained.
If
Nlv = Nlv(c) for a given term, the calculated energy set is complete.
The correspondence of coupled channel wavefunctions and completeness
of levels is obtained by the program PRCBPID, which also detects the
missing levels. Each level is further identified by all possible LS
terms in the last column. In case of multiple assignment of LS terms,
spectroscopic identification of the level can be reduced to the most
probable but approximate one by application of Hund's rule mentioned
above. It may be noted that levels in the table are grouped consistently,
in closely spaced energy ranges and in effective quantum numbers,
confirming further the proper designation of the LS terms on the whole.
are defined. Values
of L and of total angular momentum J associated with each
L are specified within parentheses next to L. The line is followed
by set of BPRM energy levels of same configurations. Nlv(c) at the end
of the set specifies total number of calculated J-levels obtained.
If
Nlv = Nlv(c) for a given term, the calculated energy set is complete.
The correspondence of coupled channel wavefunctions and completeness
of levels is obtained by the program PRCBPID, which also detects the
missing levels. Each level is further identified by all possible LS
terms in the last column. In case of multiple assignment of LS terms,
spectroscopic identification of the level can be reduced to the most
probable but approximate one by application of Hund's rule mentioned
above. It may be noted that levels in the table are grouped consistently,
in closely spaced energy ranges and in effective quantum numbers,
confirming further the proper designation of the LS terms on the whole.
Table 3a:
Sample table of fine structure energy levels of Fe
XX as sets of LS term components. ![]() is the core configuration,
is the core configuration,
![]() is the effective quantum number.
is the effective quantum number.
Table 3b:
Sample table for calculated fine structure energy
levels of Fe XX in ![]() energy order. Nlv is the total number of
levels of the symmetry.
energy order. Nlv is the total number of
levels of the symmetry.
In this format the fine structure levels are presented as sets,
ordered in descending energies, belonging to various ![]() symmetries.
A sample is shown in Table 3b. The format is convenient for
easy implementation in astrophysical models requiring large number of
energy levels and corresponding transitions. At the top of each
set the total number of energy levels Nlv and the symmetry
symmetries.
A sample is shown in Table 3b. The format is convenient for
easy implementation in astrophysical models requiring large number of
energy levels and corresponding transitions. At the top of each
set the total number of energy levels Nlv and the symmetry ![]() are specified. For example, the table shows that there are 127 fine
structure levels of Fe XX with
are specified. For example, the table shows that there are 127 fine
structure levels of Fe XX with
![]() .
The levels are
identified by the configuration and LS term designation of the parent
core, the outer electron quantum numbers (nl), absolute energy in
Rydberg, the effective quantum number (
.
The levels are
identified by the configuration and LS term designation of the parent
core, the outer electron quantum numbers (nl), absolute energy in
Rydberg, the effective quantum number (![]() ), and the final LSterm designation. A level may be assigned to one or more LS terms in
the last column. If the number of possible terms is more than one, all
are specified. However, the assigned term may be determined from a
variation of Hund's rule as a guideline, as mentioned before,:
the term with higher angular momentum lies lower in energy. One reason
for specifying all possible terms is that the order of calculated
energy levels may not match exactly with that of the measured ones.
The other reason is that Hund's rule often does not apply to all cases
in complex ions, especially the low lying ones; nonetheless,
we find it is useful to establish completeness and order.
), and the final LSterm designation. A level may be assigned to one or more LS terms in
the last column. If the number of possible terms is more than one, all
are specified. However, the assigned term may be determined from a
variation of Hund's rule as a guideline, as mentioned before,:
the term with higher angular momentum lies lower in energy. One reason
for specifying all possible terms is that the order of calculated
energy levels may not match exactly with that of the measured ones.
The other reason is that Hund's rule often does not apply to all cases
in complex ions, especially the low lying ones; nonetheless,
we find it is useful to establish completeness and order.
The allowed E1 (
![]() )
transitions are treated with
the BPRM method. The 1792 fine structure levels of Fe XX yield
approximately
)
transitions are treated with
the BPRM method. The 1792 fine structure levels of Fe XX yield
approximately
![]() allowed E1 (dipole allowed and
intercombination)
transitions. The table of oscillator strengths of complete set of fine
structure transitions is available electronically. The table contains
calculated transition probabilities, oscillator strengths, and line
strengths alongwith the level energies. Although A, the f, and the
S are related, all three are listed since different applications
require one or the other quantity.
allowed E1 (dipole allowed and
intercombination)
transitions. The table of oscillator strengths of complete set of fine
structure transitions is available electronically. The table contains
calculated transition probabilities, oscillator strengths, and line
strengths alongwith the level energies. Although A, the f, and the
S are related, all three are listed since different applications
require one or the other quantity.
A sample set of transitions in Fe XX is presented in Table 4. The top
of the table specifies the nuclear charge (Z=26) and number of
electrons in the ion (
![]() = 7). Then sets of oscillator
strengths belonging to various pairs of symmetries
= 7). Then sets of oscillator
strengths belonging to various pairs of symmetries
![]() are given. The transition symmetries are expressed in the form of 2Ji,
are given. The transition symmetries are expressed in the form of 2Ji,
![]() (
(![]() for even and
for even and ![]() for odd parity), 2Jk and
for odd parity), 2Jk and ![]() to make whole numbers, at the top of the set. Hence Table 4 presents
partial transitions of symmetries
to make whole numbers, at the top of the set. Hence Table 4 presents
partial transitions of symmetries
![]() .
The next line gives
the number of bound levels belonging to each symmetry, NJi
and NJk. The line is followed by the number of transitions,
.
The next line gives
the number of bound levels belonging to each symmetry, NJi
and NJk. The line is followed by the number of transitions,
![]() .
The first two columns are level indices Ii
and Ik whose identification can be found from the energy table, the
third and the fourth columns provide the energies Ei and Ek in
Rydbergs. The fifth column is gfL, where fL is the oscillator
strength in length formulation and g=2J+1 is the statistical weight
factor of the initial or the lower level. The sign of gf indicates the
upper and lower levels such that a negative value
means that i is the lower level, while a positive value means k
is the lower level. Column six is line strength S, and the last column
is transition probability
.
The first two columns are level indices Ii
and Ik whose identification can be found from the energy table, the
third and the fourth columns provide the energies Ei and Ek in
Rydbergs. The fifth column is gfL, where fL is the oscillator
strength in length formulation and g=2J+1 is the statistical weight
factor of the initial or the lower level. The sign of gf indicates the
upper and lower levels such that a negative value
means that i is the lower level, while a positive value means k
is the lower level. Column six is line strength S, and the last column
is transition probability
![]() .
Spectroscopic notation of
the transition can be obtained from Table 3b by referrring to the values
of
.
Spectroscopic notation of
the transition can be obtained from Table 3b by referrring to the values
of ![]() ,
Ii,
,
Ii, ![]() ,
and Ik.
,
and Ik.
Table 4:
Sample set of f-, S and A-values for allowed
E1 transitions in Fe XX in ![]() order.
order. ![]() means
means
![]() .
.
A subset of BPRM transition probabilities for Fe XX has been reprocessed using observed energy differences rather than the calculated ones to obtain the f- and A-values from the line strengths (S). The S-values are energy independent quantities. As the observed energies have lower uncertainties than the calculated ones, use those instead of the calculated energies improves the accuracy of the f- and A-values for the relevant transitions. (This is a common procedure and is used in the NIST compilation.) The astrophysical models also attempt to use observed transition energies to compute f- and A-values. For any comparison with experimental measurement, observation or spectral diagnostics therefore, values from these sets should be used if given.
The reprocessing of f- and A-values has been carried out for all
the allowed transitions (
![]() )
among observed levels.
This subset consists of 289 transitions of Fe XX (also
available electronically).
The reprocessed transitions are further ordered in terms of their
configurations and LS terms. This enables one to obtain the
f-values for LS multiplets and check the completeness of the
set of fine structure components belonging to a given multiplet. However,
the completeness depends also on the observed set of fine structure
levels since the transitions correspond only to the observed levels.
The LS multiplets are useful for various comparisons with other
calculations and experiments where fine structure transitions can not
be resolved. A partial set of these transitions is presented in Table
5. The level index, Ii, for each energy level in the tables is given
next to the J-value for easy access to the complete f-file.
)
among observed levels.
This subset consists of 289 transitions of Fe XX (also
available electronically).
The reprocessed transitions are further ordered in terms of their
configurations and LS terms. This enables one to obtain the
f-values for LS multiplets and check the completeness of the
set of fine structure components belonging to a given multiplet. However,
the completeness depends also on the observed set of fine structure
levels since the transitions correspond only to the observed levels.
The LS multiplets are useful for various comparisons with other
calculations and experiments where fine structure transitions can not
be resolved. A partial set of these transitions is presented in Table
5. The level index, Ii, for each energy level in the tables is given
next to the J-value for easy access to the complete f-file.
The BPRM A-values for Fe XX are compared with other calculations in
Table 6 (adopted from the compiled table by NIST). The alphabetic
notation next to A-values in NIST column are accuracy estimation (Ac)
by the NIST. Cheng et al. (1979) employed multiconfiguration Dirac-Fock
(MCDF) method for the
![]() and
and
![]() transitions in Fe XX, where they
included the Breit interaction and the Lamb shift. However, in the early
stage of their code development they carried out single configuration
calculations for Fe XX and most of the correlation was omitted.
Mason & Bhatia (1983) employed a scaled Thomas-Fermi approach with
configuration interactions and relativistic effects for
transitions in Fe XX, where they
included the Breit interaction and the Lamb shift. However, in the early
stage of their code development they carried out single configuration
calculations for Fe XX and most of the correlation was omitted.
Mason & Bhatia (1983) employed a scaled Thomas-Fermi approach with
configuration interactions and relativistic effects for
![]() and
and
![]() transitions using an earlier version of
SUPERSTRUCTURE. Their calculations also omitted much of the correlation
as they included only three configurations (a relatively large
calculation at that time). The NIST compilation lists 124 transitions,
mainly from these two publications. Table 6 compares transitions of
the type
2J-2J'=4-6, 4-4, and 4-2. A wide range of scatter
can be noticed between the present BPRM and previous A-coefficients for
spontaneous radiative decays. Among the
2J-2J' = 4-6 transitions, BPRM
A-values show good agreement with Cheng et al. (1979) for transitions
such as
transitions using an earlier version of
SUPERSTRUCTURE. Their calculations also omitted much of the correlation
as they included only three configurations (a relatively large
calculation at that time). The NIST compilation lists 124 transitions,
mainly from these two publications. Table 6 compares transitions of
the type
2J-2J'=4-6, 4-4, and 4-2. A wide range of scatter
can be noticed between the present BPRM and previous A-coefficients for
spontaneous radiative decays. Among the
2J-2J' = 4-6 transitions, BPRM
A-values show good agreement with Cheng et al. (1979) for transitions
such as
![]() -
-
![]() ,
but shows a large difference
for the
,
but shows a large difference
for the
![]() transition.
transition.
The forbidden transitions of higher order electric (E2, E3) and magnetic (M1) transitions are treated through atomic structure calculations using SUPERSTRUCTURE. Forbidden transition probabilities are computed for 13 874 transitions among the lowest 215 fine structure levels of 9 configurations of Fe XX, as given in Table 7. Both this table and the transition table were processed from SUPERSTRUCTURE output to standard spectroscopic notation. The energies in Table 7 agree with the observed values within 1%. The set of levels and corresponding forbidden transitions data are available electronically. The transitions among levels listed in the observed table have been reprocessed with observed energy difference as in Table 5. Table 8 presents a sample table of forbidden transitions in Fe XX.
Table 5:
Dipole allowed and intercombination transitions in
Fe XX, corrected with the observed energies. The notation a(b) means
![]() .
.
Present A-coefficients for forbidden transitions are compared with previous works in Table 6. In contrast to E1 transitions, present results for E2 and M1 transitions, agree well in general with those by Cheng et al. (1979).
Table 6:
Comparison of present A-coefficients (in units os 108
![]() for Fe XX with those in NIST compilation. Notation a+b means
for Fe XX with those in NIST compilation. Notation a+b means
![]() .
.
Table 7:
Sample set of fine strucuture levels of Fe XX and their
relative energies for which forbidden transitions are considered. The
configuration indices (Cf) correspond to
![]() (1),
(1),
![]() (2),
(2),
![]() (3),
(3),
![]() (4),
(4),
![]() (5),
(5),
![]() (6),
(6),
![]() (7),
(7),
![]() (8),
(8),
![]() (9).
(9).
Accurate and large-scale calculations have been carried out for allowed and forbidden transitions in Fe XX corresponding to 1792 calculated fine structure energy levels upto n=10. All levels have been spectroscopically identified and checked for completenss. The set of results far exceeds the currently available experimental and theoretical data.
The results are obtained in intermediate coupling, including relativistic effects using the Breit Pauli R-matrix method (BPRM) in the close coupling approximation for allowed E1 transitions and configuration interaction atomic structure calculations using SUPERSTRUCTURE for forbidden electric quadrupole (E2), and octupole (E3), and magnetic quadrupole (M1) transitions. The energies show very good agreement, within 1%, with most of the measured values compiled by the NIST. However, present transition probabilities show varying degree of agreement, especially for E1 transitions, with the previous calculations obtained using lower configurations interactions. The results from the present work should be particularly useful in the analysis of X-ray and Extreme Ultraviolet spectra from astrophysical and laboratory sources where non-local thermodynamic equilibrium (NLTE) atomic models with many excited levels are needed.
All data are available electronically. A subset of f-values has been reprocessed using available observed energies for better accuracy.
Table 8:
Line strength (S) and A-coefficients for the forbidden
electric quadrupole (E2) and octupole (E3), and magnetic dipole (M1)
transitions in Fe XX. The level numbers (i, j) and configurations
indices (Ci and Cj) correspond to those in Table 7, such as
![]() (1),
(1),
![]() (2),
(2), ![]() (3),
(3),
![]() (4),
(4),
![]() (5), etc.
(5), etc.
Acknowledgements
This work was partially supported by US National Science Foundation (AST-9870089) and the NASA ADP program. The computational work was carried out on the Cray SV1 at the Ohio Supercomputer Center in Columbus, Ohio.