A&A 413, 681-691 (2004)
DOI: 10.1051/0004-6361:20034326
The spatial structure of the  Pictoris gas disk
Pictoris gas disk![[*]](/icons/foot_motif.gif)
A. Brandeker1 -
R. Liseau1 -
G. Olofsson1 -
M. Fridlund2
1 - Stockholm Observatory, AlbaNova University Centre,
106 91 Stockholm, Sweden
2 -
ESA/ESTEC, PO Box 299, 2200 AG Noordwijk, The Netherlands
Received 17 September 2003 / Accepted 7 October 2003
Abstract
We have used VLT/UVES to spatially resolve the gas disk of
 Pictoris. 88 extended emission lines are observed, with the
brightest coming from Fe I, Na I and Ca II. The extent of the gas
disk is much larger than previously anticipated; we trace Na I radially
from 13 AU
out to 323 AU and Ca II to heights of 77 AU above the disk plane,
both to the limits of our observations. The degree of flaring is
significantly larger for the gas disk than the dust disk. A strong
NE/SW brightness
asymmetry is observed, with the SW emission being abruptly truncated at
150-200 AU. The inner gas disk is tilted about 5
Pictoris. 88 extended emission lines are observed, with the
brightest coming from Fe I, Na I and Ca II. The extent of the gas
disk is much larger than previously anticipated; we trace Na I radially
from 13 AU
out to 323 AU and Ca II to heights of 77 AU above the disk plane,
both to the limits of our observations. The degree of flaring is
significantly larger for the gas disk than the dust disk. A strong
NE/SW brightness
asymmetry is observed, with the SW emission being abruptly truncated at
150-200 AU. The inner gas disk is tilted about 5 with respect to the outer disk, similar to the appearance of the disk
in light scattered from dust. We show that most, perhaps all, of the
Na I column density seen in the "stable'' component of absorption,
comes from the extended disk. Finally, we discuss the effects of
radiation pressure in the extended gas disk and show that the assumption of
hydrogen, in whatever form, as a braking agent is inconsistent with observations.
with respect to the outer disk, similar to the appearance of the disk
in light scattered from dust. We show that most, perhaps all, of the
Na I column density seen in the "stable'' component of absorption,
comes from the extended disk. Finally, we discuss the effects of
radiation pressure in the extended gas disk and show that the assumption of
hydrogen, in whatever form, as a braking agent is inconsistent with observations.
Key words: stars: individual:  Pictoris -
stars: circumstellar matter - stars: planetary systems: formation -
stars: planetary systems: protoplanetary disks
Pictoris -
stars: circumstellar matter - stars: planetary systems: formation -
stars: planetary systems: protoplanetary disks
The young, near-by main-sequence star  Pictoris has been
the subject of intense studies ever since it was discovered to
harbour circumstellar cold dust (Aumann 1985), distributed along a
linear shape (Smith & Terrile 1984), interpreted as a "debris disk''
(Backman & Paresce 1993). These studies have been largely motivated by the
possibility of observing an analogue to the solar system in its
early stages, in the hope of finding clues to the mechanisms of
planet formation. Asymmetries found in the disk from light
scattered by the dust (Heap et al. 2000; Kalas & Jewitt 1995)
have indeed been suggested to be the signature of perturbing
planet(s) (Augereau et al. 2001; Moulliet et al. 1997), but so far no direct detection of
a planet around
Pictoris has been
the subject of intense studies ever since it was discovered to
harbour circumstellar cold dust (Aumann 1985), distributed along a
linear shape (Smith & Terrile 1984), interpreted as a "debris disk''
(Backman & Paresce 1993). These studies have been largely motivated by the
possibility of observing an analogue to the solar system in its
early stages, in the hope of finding clues to the mechanisms of
planet formation. Asymmetries found in the disk from light
scattered by the dust (Heap et al. 2000; Kalas & Jewitt 1995)
have indeed been suggested to be the signature of perturbing
planet(s) (Augereau et al. 2001; Moulliet et al. 1997), but so far no direct detection of
a planet around  Pic has been made.
Asymmetries have also been detected in thermal emission
from the dust (Liseau et al. 2003; Weinberger et al. 2003 with references
therein). Recent papers reviewing the
Pic has been made.
Asymmetries have also been detected in thermal emission
from the dust (Liseau et al. 2003; Weinberger et al. 2003 with references
therein). Recent papers reviewing the  Pic disk are those
by Artymowicz (2000), Lagrange et al. (2000) and Zuckerman (2001).
Pic disk are those
by Artymowicz (2000), Lagrange et al. (2000) and Zuckerman (2001).
Circumstellar gas, seen in absorption against
the star, was also found early on (Hobbs et al. 1985), thanks to the
favourable edge-on orientation of the disk. Finding and characterising
the gas content is important for understanding its relation to the
dust and the general evolution of the disk (Artymowicz 2000). Gas
is also useful as a probe of physical conditions in the disk,
where density, composition, temperature and bulk velocities
under favourable conditions can be directly estimated.
The gas found at relative rest to  Pic, consisting
of metals, raised the problem why it is not blown away from the
system by the high radiation pressure.
Lagrange et al. (1998) made some detailed calculations and found that the
gas drag from a dense enough H I ring
(
Pic, consisting
of metals, raised the problem why it is not blown away from the
system by the high radiation pressure.
Lagrange et al. (1998) made some detailed calculations and found that the
gas drag from a dense enough H I ring
(
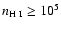 cm-3) close to the star
(
cm-3) close to the star
( 0.5 AU) could brake migrating particles sufficiently,
provided they started out inside the ring.
The picture was complicated by the announcement of H2detected in emission by the Infrared Space Observatory (Thi et al. 2001),
implying large quantities (
0.5 AU) could brake migrating particles sufficiently,
provided they started out inside the ring.
The picture was complicated by the announcement of H2detected in emission by the Infrared Space Observatory (Thi et al. 2001),
implying large quantities ( 50
50
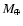 )
of molecular
hydrogen, and the sub-sequent report of sensitive upper limits
(
)
of molecular
hydrogen, and the sub-sequent report of sensitive upper limits
(
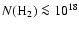 cm-2) of H2 from
FUV absorption lines using
cm-2) of H2 from
FUV absorption lines using  Pic as a
background source (Lecavelier des Etangs et al. 2001). In addition,
Olofsson et al. (2001, hereafter Paper I) found spatially resolved widespread
gas emission from Na I in the disk, stretching out to at least 140 AU.
Pic as a
background source (Lecavelier des Etangs et al. 2001). In addition,
Olofsson et al. (2001, hereafter Paper I) found spatially resolved widespread
gas emission from Na I in the disk, stretching out to at least 140 AU.
Here we present observations improved by a factor of two in both spatial
and spectral resolution, as well as a greatly increased spectral coverage,
compared to Paper I.
We put emphasis on the observed spatial structure of the gas disk,
derive an empirical density profile of Na I atoms and use a
photoionisation code to construct disk models consistent with our
observations. We discuss implications of the radiation pressure under
various conditions derived from these models. Results from a detailed
study of the observed chemical abundances will be discussed in a
forthcoming paper.
Table 1:
VLT/UVES observation log.
The star  Pictoris was observed with the echelle spectrograph
UVES on the 8.2 m Kueyen telescope at the Very Large Telescope of ESO,
Paranal, Chile. The observations were made in service mode to take advantage
of the excellent seeing conditions occasionally provided by the site.
Service mode means that the observers prepare observation blocks that
are executed by the local telescope operators provided certain
conditions (like air mass and seeing) are met. A total of 12
observation blocks during 2001-2002 (see Table 1) lasting about an
hour each were successfully executed. The air mass and seeing at zenith
were always below 1.5 and 0
Pictoris was observed with the echelle spectrograph
UVES on the 8.2 m Kueyen telescope at the Very Large Telescope of ESO,
Paranal, Chile. The observations were made in service mode to take advantage
of the excellent seeing conditions occasionally provided by the site.
Service mode means that the observers prepare observation blocks that
are executed by the local telescope operators provided certain
conditions (like air mass and seeing) are met. A total of 12
observation blocks during 2001-2002 (see Table 1) lasting about an
hour each were successfully executed. The air mass and seeing at zenith
were always below 1.5 and 0
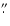 6, respectively. The UVES spectrograph
was used in standard dichroic modes, meaning that a dichroic mirror was used
to split the light into two wavelength ranges, each using its own
echelle grating and CCD detectors. Two types of gratings were used for
each arm, together covering the wavelengths 3300 Å to
10 400 Å with a spectral resolution ranging from
6, respectively. The UVES spectrograph
was used in standard dichroic modes, meaning that a dichroic mirror was used
to split the light into two wavelength ranges, each using its own
echelle grating and CCD detectors. Two types of gratings were used for
each arm, together covering the wavelengths 3300 Å to
10 400 Å with a spectral resolution ranging from
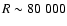 in the blue
to
in the blue
to
 in the red. The blue arm was equipped with a single CCD of
type EEV 44-82 and size
in the red. The blue arm was equipped with a single CCD of
type EEV 44-82 and size
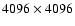 pixels, while the red arm had
a mosaic of two CCDs of sizes
pixels, while the red arm had
a mosaic of two CCDs of sizes
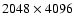 each, of the types
EEV 44-82 and MIT-LL CCID-20. The spectroscopic slits were 0
each, of the types
EEV 44-82 and MIT-LL CCID-20. The spectroscopic slits were 0
 4 and
0
4 and
0
 3 wide in the blue and red arm, respectively. To adequately separate
the echelle orders, slits were restricted to
lengths between 8
3 wide in the blue and red arm, respectively. To adequately separate
the echelle orders, slits were restricted to
lengths between 8
 and 12
and 12
 ,
depending on setting
(see Table 1). Slits were positioned at 4 overlapping locations along
the
,
depending on setting
(see Table 1). Slits were positioned at 4 overlapping locations along
the  Pic dust disk, and at 4 locations orthogonal to the
disk, reaching a distance of 17
Pic dust disk, and at 4 locations orthogonal to the
disk, reaching a distance of 17
 from the star in the disk plane, and
a height of 6
from the star in the disk plane, and
a height of 6
 above the plane (see Fig. 1). From the data,
we determined the positioning of the slits, with respect to
above the plane (see Fig. 1). From the data,
we determined the positioning of the slits, with respect to  Pic, to
be better than
Pic, to
be better than  0
0
 2. Calibration data (flat-fields, bias frames,
Th-Ar lamp wavelength calibration spectra, flux standard stars, etc.) were
provided by the UVES calibration plan.
2. Calibration data (flat-fields, bias frames,
Th-Ar lamp wavelength calibration spectra, flux standard stars, etc.) were
provided by the UVES calibration plan.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{b0326_f1.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg23.gif) |
Figure 1:
Orientations and positions of the 8 different slit settings used. The background
image shows observations of the dust as obtained by HST/STIS (Heap et al. 2000). |
| Open with DEXTER |
The data were reduced using a modified version of the UVES pipeline 1.2,
that runs in the ESO MIDAS environment. The pipeline
automatically generates the appropriate calibration sets from the
calibration data obtained as a part of the UVES calibration plan,
and apply them to the science frames. The raw frames are bias
subtracted, flat-fielded, background subtracted, order extracted,
and wavelength calibrated. An error was corrected in the pipeline
version 1.2, that associated a wavelength calibration to the wrong
order when 2D extraction was selected without merging the orders.
The orders of the echelle grating are slightly inclined on the CCD
with respect to pixel columns. Since the observations with the
star on slit were performed under excellent seeing (the seeing
measured in the spectra was  0
0
 7), this
resulted in a very high flux gradient between the pixels on and
off the star. By default, the orders are resampled linearly,
but this caused the spectrum to show a periodic "spiky'' pattern
in the flux. We found that linear interpolation does not work
properly due to the strong
non-linear shape of the point spread function (PSF) at the pixel
resolution. By modifying the order extracting routine to use a third
order Catmull-Rom spline interpolation instead of linear, we found
the spikes to be greatly reduced (though not completely eliminated).
7), this
resulted in a very high flux gradient between the pixels on and
off the star. By default, the orders are resampled linearly,
but this caused the spectrum to show a periodic "spiky'' pattern
in the flux. We found that linear interpolation does not work
properly due to the strong
non-linear shape of the point spread function (PSF) at the pixel
resolution. By modifying the order extracting routine to use a third
order Catmull-Rom spline interpolation instead of linear, we found
the spikes to be greatly reduced (though not completely eliminated).
The reduction procedure was complicated by the sheer load of
data. With about 600 spectra, each
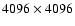 pixels,
plus calibration frames etc., the raw data were close to 50 GB.
pixels,
plus calibration frames etc., the raw data were close to 50 GB.
The end product of the pipeline reduction consisted of
individual orders separated into individual files with
the spatial information along the slit preserved, and a
wavelength calibration guaranteed to be better than
0.5 km s-1.
To trace the circumstellar gas emission as close as possible to
the star, we had to subtract the scattered light from the star,
in the cases where the star was in the slit. To do this, we
estimated the stellar spectrum S by centering a small aperture
on the star. To allow for slow gradients, we took advantage of the
fact that the gas emission lines are narrow (a few pixels) and
produced a median filtered version M of the stellar spectrum S, using a window of 30-60 pixels. We also obtained the median
filtered spectrum mi at each spatial position i, using the
same median filter window. The stellar PSF subtracted spectrum was
then estimated as
si = ri - mi S/M,
where ri is the spectrum at position i. For the observations
where the star was off the slit, we just subtracted the median filtered
background scattered light (scattered both locally by the dust
disk and in the atmosphere / telescope),
si = ri - mi.
To flux-calibrate the data, we made use of the master response curves
provided by the UVES team. The master response curves are generated
from long-time monitoring of the sensitivity trends of the instrument,
and are provided for various standard settings and periods in time.
The claimed absolute flux calibration is 10%, but comparing with
standard flux stars observed (with an open slit) the same nights as  Pic we found the derived fluxes to deviate by as much as 40% from
tabulated values for these stars. We thus used the master response
curves to correct only for the over-all sensitivity dependence on wavelength,
and used the standard star spectra obtained in connection with the
Pic we found the derived fluxes to deviate by as much as 40% from
tabulated values for these stars. We thus used the master response
curves to correct only for the over-all sensitivity dependence on wavelength,
and used the standard star spectra obtained in connection with the  Pic observations to correct the absolute flux calibration. By
looking at the variations of the derived absolute fluxes of disk emission
lines observed several times, we estimate that the error on the absolute
flux is about 5-10%. Since we use a narrow slit (0
Pic observations to correct the absolute flux calibration. By
looking at the variations of the derived absolute fluxes of disk emission
lines observed several times, we estimate that the error on the absolute
flux is about 5-10%. Since we use a narrow slit (0
 3-0
3-0
 4),
the slit losses from a point source like
4),
the slit losses from a point source like  Pic are substantial and
very seeing dependent. The error of the absolute flux from the star is
therefore expected to be substantially higher. Our main concern, however,
is the flux of the disk emission, which, due to its spatial extension, is
much more stable with regard to seeing variations.
Pic are substantial and
very seeing dependent. The error of the absolute flux from the star is
therefore expected to be substantially higher. Our main concern, however,
is the flux of the disk emission, which, due to its spatial extension, is
much more stable with regard to seeing variations.
The wavelength calibration obtained from the UVES pipeline does not
correct for the velocity of the instrument relative to the centre of
the Sun. To transform the observed spectrum to a heliocentric frame,
we made use of the software program RV written by P. T. Wallace and
C. A. Clayton![[*]](/icons/foot_motif.gif) .
The obtained accuracy in the transformation is better
than 0.01 km s-1, fully adequate for our purposes.
.
The obtained accuracy in the transformation is better
than 0.01 km s-1, fully adequate for our purposes.
3.5 Line flux measurements
From the reduced, PSF subtracted and wavelength calibrated spectra,
the disk emission lines were measured in several steps. First the
lines were identified by correlating their measured wavelengths with
the atomic line database provided by NIST![[*]](/icons/foot_motif.gif) .
This procedure
was greatly simplified by the high accuracy of the wavelength calibration,
better than 0.5 km s-1, corresponding to 0.01 Å at 6000 Å. A
median systematic velocity was then calculated for the brightest and most
accurately measured emission lines, assuming all shared the same systematic
radial velocity. For the brightest lines, the measured flux as a function
of apertures centred on the systematic velocity was evaluated. A large
aperture samples more signal, but also more noise. We were therefore
interested in finding the best balance, in order to achieve the highest
signal to noise (S/N). The apertures used to measure emission lines were
consequently chosen as a function of line strength and background noise,
with smaller apertures for fainter lines. We assumed that all lines from
a particular ion share the same spatio-spectral profile, and scaled the flux
measured in small apertures of fainter lines with the ratio between equally
sized and maximum sized apertures placed on the sum of several bright lines.
In this way we estimated the signal from a faint line without integrating up
too much noise. The method is analogous to methods used in aperture
photometry to measure star fluxes in, e.g., a CCD image.
.
This procedure
was greatly simplified by the high accuracy of the wavelength calibration,
better than 0.5 km s-1, corresponding to 0.01 Å at 6000 Å. A
median systematic velocity was then calculated for the brightest and most
accurately measured emission lines, assuming all shared the same systematic
radial velocity. For the brightest lines, the measured flux as a function
of apertures centred on the systematic velocity was evaluated. A large
aperture samples more signal, but also more noise. We were therefore
interested in finding the best balance, in order to achieve the highest
signal to noise (S/N). The apertures used to measure emission lines were
consequently chosen as a function of line strength and background noise,
with smaller apertures for fainter lines. We assumed that all lines from
a particular ion share the same spatio-spectral profile, and scaled the flux
measured in small apertures of fainter lines with the ratio between equally
sized and maximum sized apertures placed on the sum of several bright lines.
In this way we estimated the signal from a faint line without integrating up
too much noise. The method is analogous to methods used in aperture
photometry to measure star fluxes in, e.g., a CCD image.
For the slits placed orthogonally to the disk, we summed up all flux in the
spatial direction, i.e. along the height of the disk (Table 2).
The quantity thus derived has the unit of flux per arcsecond.
We detected 88 spatially extended emission lines from
the  Pic gas disk, identified as emission from
Fe I, Na I, Ca II, Ni I, Ni II, Ti I, Ti II, Cr I and
Cr II. Table 2 shows a selection of the brightest lines.
Following the brightest emission lines
(
Pic gas disk, identified as emission from
Fe I, Na I, Ca II, Ni I, Ni II, Ti I, Ti II, Cr I and
Cr II. Table 2 shows a selection of the brightest lines.
Following the brightest emission lines
(
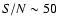 )
from Na I and Fe I radially (Figs. 2 and 3), we
observe a strong asymmetry between the north-east (NE) and the south-west (SW) parts of the disk, similar to the brightness asymmetry in the dust
emission (Kalas & Jewitt 1995),
but asymmetric to a much higher degree. The NE gas emission extends
smoothly to the limits of our observations (17
)
from Na I and Fe I radially (Figs. 2 and 3), we
observe a strong asymmetry between the north-east (NE) and the south-west (SW) parts of the disk, similar to the brightness asymmetry in the dust
emission (Kalas & Jewitt 1995),
but asymmetric to a much higher degree. The NE gas emission extends
smoothly to the limits of our observations (17
 ,
corresponding to
330 AU at the distance of
,
corresponding to
330 AU at the distance of  Pic), whereas the SW emission is
abruptly truncated at 150-200 AU. In the inner
regions, the SW emission dominates over the NE part, in agreement with
Fig. 2 of Paper I.
Pic), whereas the SW emission is
abruptly truncated at 150-200 AU. In the inner
regions, the SW emission dominates over the NE part, in agreement with
Fig. 2 of Paper I.
Table 2:
Selected gas emission lines, 3
 SW in disk.
SW in disk.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{b0326_f2.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg29.gif) |
Figure 2:
Na D2 (
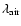 = 5889.951 Å) emission from the
= 5889.951 Å) emission from the
 Pic disk, as seen through
four slits parallel to the disk (see Fig. 1). The vertical
axis is along the spatial direction, with positive offsets
north-east of the star, while the spectral dispersion is along the
horizontal axis, centred on the Pic disk, as seen through
four slits parallel to the disk (see Fig. 1). The vertical
axis is along the spatial direction, with positive offsets
north-east of the star, while the spectral dispersion is along the
horizontal axis, centred on the  Pic rest frame of the
Na D2 line. The inner 11 AU, showing mostly residual noise from the
PSF subtraction, have been masked out. The velocity shift of the NE and
SW side is due to Keplerian rotation of the disk, with the SW rotating
towards us (Paper I). The grey scale
has been scaled non-linearly with the intensity, in order to bring out
the bright disk structure close to the star as well as the faint features
at greater distances. The emission in the NE can be traced out to the
limits of our observations at 323 AU, while the emission in the SW ends
abruptly at 150-200 AU (see also Fig. 3).
Close to -25 km s-1, telluric Na D2 emission is seen covering
the slit. The relative velocity of the sky emission to Pic rest frame of the
Na D2 line. The inner 11 AU, showing mostly residual noise from the
PSF subtraction, have been masked out. The velocity shift of the NE and
SW side is due to Keplerian rotation of the disk, with the SW rotating
towards us (Paper I). The grey scale
has been scaled non-linearly with the intensity, in order to bring out
the bright disk structure close to the star as well as the faint features
at greater distances. The emission in the NE can be traced out to the
limits of our observations at 323 AU, while the emission in the SW ends
abruptly at 150-200 AU (see also Fig. 3).
Close to -25 km s-1, telluric Na D2 emission is seen covering
the slit. The relative velocity of the sky emission to  Pic varies
slightly between the mosaiced observations due to the orbital motion of
the Earth between the epochs. Pic varies
slightly between the mosaiced observations due to the orbital motion of
the Earth between the epochs. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.7cm,clip]{b0326_f3.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg30.gif) |
Figure 3:
Determined surface intensity as a function of radial distance in NE and SW for
Na D1,2 and Fe I 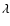 3859.911, 3859.911, 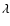 3820.425. The fit of
Sect. 5.1 is shown for Na I D2 as a an unbroken line.
Note the sharp decrease in flux in the SW at 150 AU-200 AU. 3820.425. The fit of
Sect. 5.1 is shown for Na I D2 as a an unbroken line.
Note the sharp decrease in flux in the SW at 150 AU-200 AU. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{b0326_f4.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg31.gif) |
Figure 4:
Measured positions of the Na I and Fe I gas emission
relative to the plane at position angle 30$.^$75. The bars correspond
to derived scale heights, obtained by deconvolving the observed height
profiles with a Gaussian of 0
 7 FWHM simulating the seeing. The
inclined dash-dotted lines show the empirical opening angle of the gas
disk, corresponding to H/r=0.28 (see Sect. 5.1).
The error in positioning of the slits is on the order of 0 7 FWHM simulating the seeing. The
inclined dash-dotted lines show the empirical opening angle of the gas
disk, corresponding to H/r=0.28 (see Sect. 5.1).
The error in positioning of the slits is on the order of 0
 1. 1. |
| Open with DEXTER |
Determining the centre of emission from the orthogonal profiles,
it becomes apparent that the inner part of the disk is slightly
tilted with respect to the outer parts, in particular on the
NE side (Fig. 4). We estimate this
tilt to be
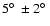 (1
(1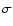 ), similar to the
4
), similar to the
4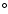 -5
-5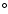 tilt observed by HST/STIS in the inner dust
disk (Heap et al. 2000).
tilt observed by HST/STIS in the inner dust
disk (Heap et al. 2000).
The scale height (FWHM) of the gas disk, estimated on observations deconvolved
with a Gaussian of 0
 7 to simulate the seeing, is
7 to simulate the seeing, is  20 AU at 3
20 AU at 3
 (58 AU),
similar to the dust disk scale height (Heap et al. 2000). At 6
(58 AU),
similar to the dust disk scale height (Heap et al. 2000). At 6
 (116 AU), however,
the gas disk is significantly thicker,
(116 AU), however,
the gas disk is significantly thicker, 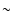 30 AU compared to
30 AU compared to 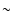 15 AU
for the dust (see Fig. 5).
15 AU
for the dust (see Fig. 5).
A very complex height profile is shown by the Ca II H & K lines
(Figs. 5 and 6). Especially at 6
 distance from the star, the emission from the disk midplane is much
fainter than the emission away from the midplane. In particular,
the detected Ca II emission, at 6
distance from the star, the emission from the disk midplane is much
fainter than the emission away from the midplane. In particular,
the detected Ca II emission, at 6
 SW of the star, keeps
increasing to the limits of the spectroscopic slit 4
SW of the star, keeps
increasing to the limits of the spectroscopic slit 4
 above
the disk midplane, meaning that there is a significant number of
Ca II ions at 77 AU height above the midplane at 116 AU distance
from the star. From Fig. 6 it is evident that the
radial velocities of these Ca II ions are small - on the order
of a few km s-1. Implications of this fact are discussed
in Sect. 5.2.
above
the disk midplane, meaning that there is a significant number of
Ca II ions at 77 AU height above the midplane at 116 AU distance
from the star. From Fig. 6 it is evident that the
radial velocities of these Ca II ions are small - on the order
of a few km s-1. Implications of this fact are discussed
in Sect. 5.2.
In order to determine the heliocentric velocity of  Pic
accurately, we averaged the heliocentric gas velocities as
observed on each side at the distances 3
Pic
accurately, we averaged the heliocentric gas velocities as
observed on each side at the distances 3
 and 6
and 6
 from the star. In this way, we can assess the system velocity
independently from the lines observed in absorption, which are
sensitive to possible radial velocities of the absorbers
(caused by, e.g., radiation pressure). We determined the
heliocentric radial velocity of
from the star. In this way, we can assess the system velocity
independently from the lines observed in absorption, which are
sensitive to possible radial velocities of the absorbers
(caused by, e.g., radiation pressure). We determined the
heliocentric radial velocity of  Pic to be
Pic to be
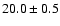 km s-1, with the error mainly due to the
uncertainty in wavelength calibration.
km s-1, with the error mainly due to the
uncertainty in wavelength calibration.
In the spectrum of the star, we measured the absorption profiles
corresponding to observed ground state emission lines. Most lines
were found to be at, or close to, the system velocity of
 Pic (Table 3).
Pic (Table 3).
Table 3:
Radial velocities relative  Pic of ions measured in absorption.
Pic of ions measured in absorption.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{b0326_f5.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg37.gif) |
Figure 5:
The flux calibrated vertical profile of
the disk gas emission at 3
 and 6
and 6
 NE and SW of the
star for a few selected lines of Na I, Fe I and Ca II.
Zero spatial offset refers to the dust disk midplane defined
by the position angle 30$.^$75 relative to the star, with
the positive spatial direction to the north-west (NW). The
centre and FWHM for Gaussian fits to the profiles are printed
in the panels of Gaussian shaped profiles. The SW
side dominates the emission at 3
NE and SW of the
star for a few selected lines of Na I, Fe I and Ca II.
Zero spatial offset refers to the dust disk midplane defined
by the position angle 30$.^$75 relative to the star, with
the positive spatial direction to the north-west (NW). The
centre and FWHM for Gaussian fits to the profiles are printed
in the panels of Gaussian shaped profiles. The SW
side dominates the emission at 3
 ,
while the NE side
slightly dominates at 6 ,
while the NE side
slightly dominates at 6
 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{b0326_f6.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg39.gif) |
Figure 6:
The velocity distribution of the gas
emission as observed by slits orthogonal to the disk at 3
 and 6
and 6
 NE and SW of the star for Ca II, Fe I and Na I.
To improve the signal to noise, the H & K lines of Ca II,
10 of the brightest Fe I lines, and D1 and D2 of Na I
were added for each species. The profiles were then normalised so
that each level increases one tenth of the peak. The noise in the
Fe I and Na I plots is below the lowest level curve, while the
lowest level curve for Ca II still shows some noise.
Velocities are referred to the
system velocity 20.0 km s-1 of
NE and SW of the star for Ca II, Fe I and Na I.
To improve the signal to noise, the H & K lines of Ca II,
10 of the brightest Fe I lines, and D1 and D2 of Na I
were added for each species. The profiles were then normalised so
that each level increases one tenth of the peak. The noise in the
Fe I and Na I plots is below the lowest level curve, while the
lowest level curve for Ca II still shows some noise.
Velocities are referred to the
system velocity 20.0 km s-1 of  Pic, with the positive
direction being away from us. Positive offsets in the spatial direction
are directed to the north-west (NW). The dash-dotted vertical lines
correspond to the system velocity of Pic, with the positive
direction being away from us. Positive offsets in the spatial direction
are directed to the north-west (NW). The dash-dotted vertical lines
correspond to the system velocity of  Pic, the dotted lines
to the Kepler velocity at the projected distance from Pic, the dotted lines
to the Kepler velocity at the projected distance from  Pic
(assuming a stellar mass of Pic
(assuming a stellar mass of
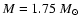 ),
while the dashed ellipse in each graph shows the spectral and
spatial resolution attained. Note the complexity of
the Ca II profile, and how the emission at 6 ),
while the dashed ellipse in each graph shows the spectral and
spatial resolution attained. Note the complexity of
the Ca II profile, and how the emission at 6
 SW
(right-most panels) can be traced to the limit of the
observations. The detected emission profiles from Ni I, Ni II,
Ti I, Ti II, Cr I and Cr II are of much lower S/N, but similar to
the profiles of Na I and Fe I.
SW
(right-most panels) can be traced to the limit of the
observations. The detected emission profiles from Ni I, Ni II,
Ti I, Ti II, Cr I and Cr II are of much lower S/N, but similar to
the profiles of Na I and Fe I. |
| Open with DEXTER |
We proceed by inverting the observations of the projected disk
to a radial density law for Na I, and then extend the result
by calculating the ionisation structure to find an estimate on
the total Na density. By making assumptions of the abundances
we construct two models with distinct H densities,
test how well the models compare with observations of H I and H2, and examine how the kinematics of ions in these models are
affected by radiation pressure.
5.1 Sodium gas density profile
From the spatial emission profiles we estimate the density distribution
of the observed gas by making the following assumptions:
- 1.
- The disk is axisymmetric and the density of the emitting medium
is well described by
![\begin{displaymath}
n(r,h) = n_0 \left[
\left( \frac{r}{r_0} \right)^{2a} +
\lef...
...
\exp \left[ - \left( \frac{h}{\alpha r} \right) ^2 \right],
\end{displaymath}](/articles/aa/full/2004/02/aa0326/img40.gif) |
(1) |
where r and h are the cylindrical coordinates describing the
midplane distance and height over the midplane, respectively, n0is a normalising density, r0 is the broken power-law break
distance, a and b are power-law exponents of the inner and
outer regions respectively, and 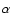 is related to the scale
height H of the disk at midplane
distance r as
is related to the scale
height H of the disk at midplane
distance r as
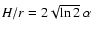 .
.
- 2.
- The inclination of the disk is close to zero, i.e. we
see it edge-on.
- 3.
- The emission is optically thin and isotropic.
- 4.
- The emitting gas traces the full gas population of that ion.
The observed disk is, of course, not axisymmetric but quite
asymmetric in appearance
(Figs. 2, 3 and 6). The
difference between the NE and SW parts of the inner disk
is not that dramatic, though, less than a factor of two
in the region where most gas is located (30-120 AU). Thus
the assumption of axisymmetry is probably not too bad.
We chose the Na I D1,2 lines for the inversion because (A) the S/N is high (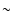 50), (B) the line ratio
between D2 and D1 is close to 2, implying that the emission
is optically thin, and (C) we expect nearly all Na I atoms
to be in their ground state (see Sect. 5.3), meaning
the resonance D1,2 lines trace all of the Na I population.
The parameters of Eq. (1) were fitted by constructing
a numerical model, simulating observed spatial profiles as
a function of the parameters and
50), (B) the line ratio
between D2 and D1 is close to 2, implying that the emission
is optically thin, and (C) we expect nearly all Na I atoms
to be in their ground state (see Sect. 5.3), meaning
the resonance D1,2 lines trace all of the Na I population.
The parameters of Eq. (1) were fitted by constructing
a numerical model, simulating observed spatial profiles as
a function of the parameters and 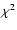 -minimising the
difference between the model and the observations. In more
detail, the model was initiated on a three dimensional grid
of height
-minimising the
difference between the model and the observations. In more
detail, the model was initiated on a three dimensional grid
of height  width
width  depth dimensions
40 AU
depth dimensions
40 AU  800 AU
800 AU  2000 AU at 1 AU resolution.
The central star was assumed to emit
2000 AU at 1 AU resolution.
The central star was assumed to emit
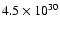 erg s-1 Å-1 at wavelengths
close to the Na I D2 line, and
erg s-1 Å-1 at wavelengths
close to the Na I D2 line, and
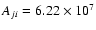 s-1 was
used as the D2 transition Einstein coefficient for
spontaneous emission, in calculating the scattering
cross-section. For each cell, a specific line luminosity
was calculated, summed up along the line of sight and
geometrically diluted to the distance of the observer at 19.3 pc. This "ideal'' image of the disk was then convolved
with a Gaussian of
s-1 was
used as the D2 transition Einstein coefficient for
spontaneous emission, in calculating the scattering
cross-section. For each cell, a specific line luminosity
was calculated, summed up along the line of sight and
geometrically diluted to the distance of the observer at 19.3 pc. This "ideal'' image of the disk was then convolved
with a Gaussian of
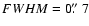 ,
simulating the atmospheric
seeing, and sampled along the various spectroscopic
slit settings of Fig. 1 to fit the observations.
In the fit we used the midplane
radial emission distribution from 13 AU out to 323 AU of
the NE, and the orthogonal profiles at 3
,
simulating the atmospheric
seeing, and sampled along the various spectroscopic
slit settings of Fig. 1 to fit the observations.
In the fit we used the midplane
radial emission distribution from 13 AU out to 323 AU of
the NE, and the orthogonal profiles at 3
 and 6
and 6
 NE of the star. The derived parameters of Eq. (1) for
Na I are:
NE of the star. The derived parameters of Eq. (1) for
Na I are:
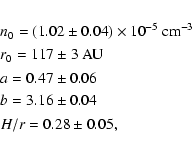
where the quoted errors are 1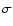 formal fitting errors
obtained by making an additional number of fits
to artificial data generated by adding random noise, at the
estimated noise level, to the observed profile. We
have over plotted the Na I fit into Fig. 3.
formal fitting errors
obtained by making an additional number of fits
to artificial data generated by adding random noise, at the
estimated noise level, to the observed profile. We
have over plotted the Na I fit into Fig. 3.
We can use Eq. (1) with the above parameters to
estimate the midplane column density of Na I, to compare
with column densities estimated from Na I absorption in
the stellar spectrum seen through the disk. If we
integrate only over the radii where we are sensitive to Na I emission, that is, from 13 AU out to 323 AU, we
obtain a column density of
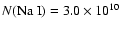 cm-2.
Extrapolating Eq. (1) to all radii, that is,
from zero radius out to infinity, we increase the Na I column density by 40% to
cm-2.
Extrapolating Eq. (1) to all radii, that is,
from zero radius out to infinity, we increase the Na I column density by 40% to
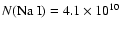 cm-2. This can be compared to
our observed column density
cm-2. This can be compared to
our observed column density
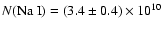 cm-2. We conclude that
most, perhaps all, of the Na I gas seen in absorption
is situated in the extended gas disk seen in emission.
We have no reason to doubt that originators of other
"stable'' gas absorption components also belong to this
extended disk.
cm-2. We conclude that
most, perhaps all, of the Na I gas seen in absorption
is situated in the extended gas disk seen in emission.
We have no reason to doubt that originators of other
"stable'' gas absorption components also belong to this
extended disk.
5.2 Radiation pressure
Ions in the  Pic gas disk are subject to appreciable
radiation pressure. To evaluate the significance, it is common
to define the ratio between the forces of gravitation and radiation,
Pic gas disk are subject to appreciable
radiation pressure. To evaluate the significance, it is common
to define the ratio between the forces of gravitation and radiation,
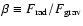 .
Since both the radiation and gravitational fields are inversely
proportional to the square of the distance to the source,
.
Since both the radiation and gravitational fields are inversely
proportional to the square of the distance to the source,  is constant throughout the
is constant throughout the  Pic disk. For the observed
atoms Na I and Fe I,
Pic disk. For the observed
atoms Na I and Fe I,
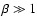 ,
meaning that if left alone,
gravity would be largely irrelevant and these atoms would rapidly
accelerate out of the system at high velocities. This is not observed
(Table 3 and Fig. 6). To investigate
what the effects of a braking medium are, we solve the
equation of motion for a gas particle,
,
meaning that if left alone,
gravity would be largely irrelevant and these atoms would rapidly
accelerate out of the system at high velocities. This is not observed
(Table 3 and Fig. 6). To investigate
what the effects of a braking medium are, we solve the
equation of motion for a gas particle,
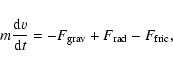 |
(2) |
where
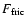 is the frictional force. Assuming
is the frictional force. Assuming
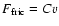 ,
where C is the friction coefficient
(proportional to the density of the braking medium), and that
the distance an atom travels before reaching the terminal velocity
is much shorter than the size of the disk, Eq. (2)
may be solved to yield the terminal velocity (as
,
where C is the friction coefficient
(proportional to the density of the braking medium), and that
the distance an atom travels before reaching the terminal velocity
is much shorter than the size of the disk, Eq. (2)
may be solved to yield the terminal velocity (as
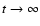 )
)
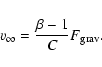 |
(3) |
Equation (2) ignores magnetic forces, which
should be of little importance for neutral atoms. If appreciable
magnetic fields are present, however, ions with net charges may
be significantly affected. We ignore this complication for the
moment and assume that the magnetic fields are small enough to
play a negligible role for the kinematics of the observed gas
particles in the disk.
For  Pic we estimate
Pic we estimate
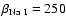 and
and
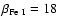 ,
while C depends on the detailed
density and temperature structure. We calculated terminal velocities as a function
of radius for the two models of
Sects. 5.3.1 and 5.3.2. Details of the
solution to Eq. (2), with estimates of C and
,
while C depends on the detailed
density and temperature structure. We calculated terminal velocities as a function
of radius for the two models of
Sects. 5.3.1 and 5.3.2. Details of the
solution to Eq. (2), with estimates of C and  for several ions, are found in Liseau (2003).
for several ions, are found in Liseau (2003).
5.3 Ionisation structure
To estimate the gas density of all Na atoms in the disk, and also
get an idea of the total gas density, we need to address the
ionisation structure of the disk. We employed the one-dimensional
photoionisation/PDR code Cloudy (Ferland et al. 1998) for the task.
Cloudy consistently maintains the ionization and thermal balance,
and solves the radiative transfer by making use of the Sobolev
approximation. For a detailed description of the code we used,
see Liseau et al. (1999).
Several assumptions have to be made in order to
compute the ionisation structure, perhaps the most important
being that of the chemical abundances of the atomic gas.
Since we have no detailed information, we confine ourselves
to study two cases of chemical abundances: solar composition
and a strongly metal depleted model. At first we also considered
a case with typical interstellar medium abundances, but
dismissed it due to the very high degree of Ca depletion
compared to solar values, in contradiction with observations.
We have no a priori reason to expect any of these assumed
abundances to reflect reality, but we believe they still serve
as valuable reference cases.
Another important assumption is that of the stellar spectral
energy distribution (SED). We assume the atmosphere of
 Pic to be well represented by an ATLAS 9 model (Kurucz 1992)
with
Pic to be well represented by an ATLAS 9 model (Kurucz 1992)
with
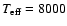 K,
K,
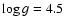 (in cm s-2)
and
(in cm s-2)
and
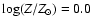 ,
and the effective radius to be
,
and the effective radius to be
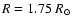 ,
implying the luminosity
,
implying the luminosity
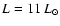 .
Recent VLTI observations of
.
Recent VLTI observations of  Pic estimate the stellar
radius to be
Pic estimate the stellar
radius to be
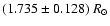 (Di Folco et al. 2003), and
comparing the ATLAS 9 SED of
(Di Folco et al. 2003), and
comparing the ATLAS 9 SED of  Pic with observed data
from the HST and FUSE archives, we find the agreement to be
generally excellent (see Liseau 2003). Some deviations are found in
the far-ultraviolet, where
Pic with observed data
from the HST and FUSE archives, we find the agreement to be
generally excellent (see Liseau 2003). Some deviations are found in
the far-ultraviolet, where  Pic seems to be a slightly
atypical A5V star with possible chromospheric activity
(Bouret et al. 2002).
Pic seems to be a slightly
atypical A5V star with possible chromospheric activity
(Bouret et al. 2002).
5.3.1 Solar composition disk
Assuming solar abundances throughout the disk, we
can fit the radial Na I density of Sect. 5.1
to within 1% by setting the radial density profile
of hydrogen nucleii to
![\begin{displaymath}
n({\rm H})=2.25\times10^3 \left[ \left( \frac{r}{r_0} \right...
...rac{r}{r_0} \right)^{5.3} \right]^{-\frac{1}{2}}{\rm cm}^{-3},
\end{displaymath}](/articles/aa/full/2004/02/aa0326/img66.gif) |
(4) |
where r0 is the same as in Sect. 5.1. The average
fraction of neutral Na in the model is 10-3, while hydrogen is
entirely neutral. The hydrogen column densities are
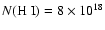 cm-2 and
cm-2 and
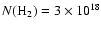 cm-2, consistent with the observational
upper limits of
cm-2, consistent with the observational
upper limits of
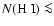 a few
a few
 cm-2 (Freudling et al. 1995)
and
cm-2 (Freudling et al. 1995)
and
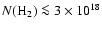 cm-2
(
cm-2
(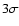 ,
Lecavelier des Etangs et al. 2001). The
gas temperature of the model disk is low,
,
Lecavelier des Etangs et al. 2001). The
gas temperature of the model disk is low,
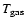 (100 AU) = 13 K, while
the dust is significantly warmer,
(100 AU) = 13 K, while
the dust is significantly warmer,
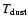 (100 AU) = 50 K.
With a radial density as in Eq. (4) and a vertical profile similar
to the Na I gas, the total gas disk mass out to 1000 AU becomes
(100 AU) = 50 K.
With a radial density as in Eq. (4) and a vertical profile similar
to the Na I gas, the total gas disk mass out to 1000 AU becomes
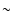 0.1
0.1
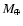 .
.
Using the equations of motion of Sect. 5.2 to
calculate the terminal velocity of elements subject to the
gas drag of the hydrogen density law of Eq. (4) and
temperature structure from Cloudy, we find that both Fe and Na,
both with
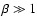 ,
would reach
radial velocities on the order of hundreds to thousands km s-1.
That is in clear contradiction with the observed radial velocities
reported in
Table 3. The purported explanation of
Paper I, that Na is ionised most of the time and therefore is
subject to a small average radiation pressure, does not apply to Fe;
indeed, both Fe I and Fe II experience a radiation pressure with
,
would reach
radial velocities on the order of hundreds to thousands km s-1.
That is in clear contradiction with the observed radial velocities
reported in
Table 3. The purported explanation of
Paper I, that Na is ionised most of the time and therefore is
subject to a small average radiation pressure, does not apply to Fe;
indeed, both Fe I and Fe II experience a radiation pressure with
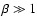 .
We know of only one remaining plausible explanation:
there is a braking agent keeping the gas from reaching high
velocities.
.
We know of only one remaining plausible explanation:
there is a braking agent keeping the gas from reaching high
velocities.
5.3.2 Metal depleted disk
To investigate the possibility of a more massive disk than implicated
by solar abundances of Na I, we impose a radial density profile for
hydrogen nucleii,
![\begin{displaymath}
n({\rm H})=10^6 \left[ \left( \frac{r}{r_0} \right)^{2.4} +
...
...rac{r}{r_0} \right)^{5.4} \right]^{-\frac{1}{2}}{\rm cm}^{-3},
\end{displaymath}](/articles/aa/full/2004/02/aa0326/img75.gif) |
(5) |
and tune the metal depletion to reproduce the Na I density
profile. We found that an overall depletion factor of 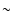 10-3(more precisely
10-3(more precisely
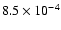 )
of the metals with respect to solar composition was required. Due
to higher dust-gas interaction, the temperatures of the gas and
the dust are similar over the disk, with
)
of the metals with respect to solar composition was required. Due
to higher dust-gas interaction, the temperatures of the gas and
the dust are similar over the disk, with
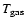 (100 AU) = 36 K and
(100 AU) = 36 K and
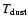 (100 AU) = 51 K.
The column densities of hydrogen are
(100 AU) = 51 K.
The column densities of hydrogen are
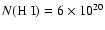 cm-2 and
cm-2 and
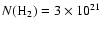 cm-2, significantly higher than the
observed upper limits reported by Freudling et al. (1995) and Lecavelier des Etangs et al. (2001).
With a radial density as in
Eq. (5) and a vertical profile similar to the Na I
gas, the total gas disk mass out to 1 000 AU becomes
cm-2, significantly higher than the
observed upper limits reported by Freudling et al. (1995) and Lecavelier des Etangs et al. (2001).
With a radial density as in
Eq. (5) and a vertical profile similar to the Na I
gas, the total gas disk mass out to 1 000 AU becomes
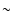 40
40
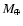 ,
similar to the mass recently inferred
from possible emission in the pure rotational transitions of H2,
,
similar to the mass recently inferred
from possible emission in the pure rotational transitions of H2,
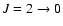 (28
(28 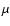 m) and J=3
m) and J=3
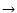 1(17
1(17 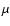 m), detected from
m), detected from  Pic in ISO/SWS data
(Thi et al. 2001). Due to the low gas temperatures of our model,
however, the predicted fluxes in the 17
Pic in ISO/SWS data
(Thi et al. 2001). Due to the low gas temperatures of our model,
however, the predicted fluxes in the 17 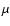 m
and 28
m
and 28 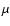 m lines are only
m lines are only
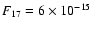 erg s-1 cm-2 and
erg s-1 cm-2 and
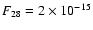 erg s-1 cm-2, respectively,
for ortho/para in thermal equilibrium.
This is more than an order of magnitude lower than the fluxes
erg s-1 cm-2, respectively,
for ortho/para in thermal equilibrium.
This is more than an order of magnitude lower than the fluxes
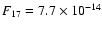 erg s-1 cm-2 and
erg s-1 cm-2 and
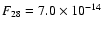 erg s-1 cm-2reported by Thi et al. (2001), and can be traced to their higher
assumed gas temperature of 100 K.
erg s-1 cm-2reported by Thi et al. (2001), and can be traced to their higher
assumed gas temperature of 100 K.
Calculating the terminal velocities of the radiation pressure
sensitive elements Fe and Na, we produce Fig. 7,
where the terminal velocity is plotted against the radial distance.
We find that the derived terminal velocities are consistent with
observed radial velocities reported in Table 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{b0326_f7.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg86.gif) |
Figure 7:
The terminal velocities for Na I and Fe I in
a metal depleted disk with the radial density of
Eq. (5), as a function of radius. The horizontal
dashed lines show the measured radial velocities,
as determined from absorption lines (Table 3),
with the estimated error shown by the vertical bar. The error
is dominated by the wavelength calibration uncertainty of
0.5 km s-1. |
| Open with DEXTER |
We have found that in our thin disk, constructed by
fitting a solar composition gas to the Na I observations,
the predicted H I and H2 column densities are consistent
with the observed limits. With these low densities, however, the
radiation pressure is predicted to accelerate, e.g., Na I to
radial velocities inconsistent with observations.
On the other hand, in our thick disk, constructed by fixing
the H density to be consistent as the braking agent for the
metals, the predicted column densities of H I and H2 are
both above the observed upper limits, although the predicted H2 emission is still far below the claimed detection.
The situation is puzzling, but a possible solution may be found
if a main braking agent different from hydrogen is in action.
If, e.g., the observed gas is replenished from dust collisions rather than
being primordial, as seems suggested by the close spatial correlation
between gas and dust, then a more natural candidate might be
oxygen or oxygen bearing species (P. Artymowicz, private communication).
More detailed models are in preparation, but hopefully the upcoming Space
InfraRed Telescope Facility will solve the issue unambiguously by better
observational constraints.
Our main observational results are:
- 1.
- We have observed 88 spatially resolved emission lines coming from
Fe I, Na I, Ca II, Ni I, Ni II, Ti I, Ti II, Cr I and
Cr II in the
 Pictoris gas disk.
Pictoris gas disk.
- 2.
- We trace the gas emission to the limits of our observations, from 0
 7
(13 AU) out to 17
7
(13 AU) out to 17
 (323 AU) radially to the NE in Na I, and 4
(323 AU) radially to the NE in Na I, and 4
 (77 AU) above the disk
plane at radius 6
(77 AU) above the disk
plane at radius 6
 (116 AU) in Ca II.
(116 AU) in Ca II.
- 3.
- The scale height of the gas at 6
 from the star is twice as high as
the equivalent dust scale height.
from the star is twice as high as
the equivalent dust scale height.
- 4.
- There is a brightness NE/SW asymmetry in the gas emission reminiscent
of the dust asymmetry, although much stronger.
- 5.
- The inner gas disk is tilted by
 5
5 ,
similarly to the dust disk.
,
similarly to the dust disk.
- 6.
- The heliocentric radial velocity of
 Pic is
Pic is
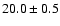 km s-1.
km s-1.
- 7.
- The radial velocities of ions observed in absorption are close to or
at the system velocity of
 Pic (to a few km s-1).
Pic (to a few km s-1).
- 8.
- The estimated radial density from Na I in emission predicts a column
density similar to the one observed in absorption, meaning that most, perhaps
all, Na I is distributed in the observed disk. We have no reason to doubt
that originators of other "stable'' gas absorption components also
belong to this extended disk.
- 9.
- Our disk models show that assuming hydrogen to be the braking agent
for metals pushed out by radiation pressure in the
 Pic disk
leads to contradictions with observations.
Pic disk
leads to contradictions with observations.
A more detailed study of the chemical composition of the
 Pic disk will be presented in a forthcoming paper.
Pic disk will be presented in a forthcoming paper.
Acknowledgements
We would like to thank the staff at the VLT and UVES for their outstanding
contributions in performing these demanding service observations, in particular
Fernando Comerón for kindly rescheduling an erroneous observation block, and
Andrea Modigliani for addressing errors in the UVES pipeline. We acknowledge
the interesting discussions we have had with Pawel Artymowicz, Doug Lin, and Philippe
Thébault. We thank the referee Alain Lecavelier des Etangs for a rapid and
detailed report.
This research has made use of NASA's Astrophysics Data System Bibliographic Services,
atomic line lists compiled by the National Institute for Standards and Technology,
and the SIMBAD database.
- Artymowicz, P. 2000, Space Sci. Rev., 92, 69
In the text
NASA ADS
- Augereau, J. C., Nelson, R. P., Lagrange, A. M.,
Papaloizou, J. C. B., & Mouillet, D. 2001, A&A, 370, 447
In the text
NASA ADS
- Aumann, H. H. 1985, PASP, 97, 885
In the text
NASA ADS
- Backman, D. E., & Paresce, F. 1993,
in Protostars and Planets III, ed. E. H. Levy, & J. I. Lunine
(Tucson: Univ. Arizona Press), 1253
In the text
- Bouret, J.-C., Deleuil, M.,
Lanz, T., et al. 2002, A&A, 390, 1049
In the text
NASA ADS
- Di Folco, E., Kervella, P., Thévenin, F.,
et al. 2003, poster at IAU Symp., 221, Sydney, Australia
In the text
- Ferland, G. J., Korista, K. T., &
Verner, D. A. 1998, PASP, 110, 761
In the text
NASA ADS
- Freudling, W., Lagrange, A. M.,
Vidal-Madjar, A., Ferlet, R., & Forveille, T. 1995, A&A, 301, 231
In the text
NASA ADS
- Heap, S. R., Lindler, D. J., Lanz, T. M., et al. 2000,
ApJ, 539, 435
In the text
NASA ADS
- Hobbs, L. M., Vidal-Madjar, A., Ferlet, R.,
Albert, C. E., & Gry, C. 1985, ApJ, 293, L29
In the text
NASA ADS
- Holland, W. S., Greaves, J. S.,
Zuckerman, B., et al. 1998, Nature, 392, 788
NASA ADS
- Kalas, P., & Jewitt, D. 1995, AJ, 110, 794
In the text
NASA ADS
- Kurucz, R. L. 1992, in
The Stellar Populations of Galaxies, ed.
B. Barbuy, & A. Renzini (Dordrecht: Kluwer), IAU Symp., 149, 225
In the text
- Lagrange, A. M.,
Backman, D. E., & Artymowicz, P. 2000, in Protostars and Planets IV,
ed. V. Mannings, A. P. Boss, & S. S. Russell
(Tucson: Univ. Arizona Press), 639
In the text
- Lagrange, A.-M., Beust, H.,
Mouillet, D., et al. 1998, A&A, 330, 1091
In the text
NASA ADS
- Lecavelier des Etangs, A.,
Vidal-Madjar, A., Roberge, A., et al. 2001, Nature, 412, 706
In the text
NASA ADS
- Liseau, R. 2003, ESA Special Publication SP-539, in press
In the text
- Liseau, R., Brandeker, A., Fridlund, M.,
et al. 2003, A&A, 402, 183
In the text
NASA ADS
- Liseau, R., White, G. J., Larsson, B., et al. 1999,
A&A, 344, 342
In the text
NASA ADS
- Mouillet, D., Larwood, J. D., Papaloizou, J. C. B.,
& Lagrange, A. M. 1997, MNRAS, 292, 896
In the text
NASA ADS
- Olofsson, G., Liseau, R.,
& Brandeker, A. 2001, ApJ, 563, L77 (Paper I)
In the text
NASA ADS
- Smith, B. A., & Terrile, R. J. 1984,
Science, 226, 1421
In the text
NASA ADS
- Thi, W. F., Blake, G. A.,
van Dishoeck, E. F., et al. 2001, Nature, 409, 60
In the text
NASA ADS
- Weinberger, A. J.,
Becklin, E. E., & Zuckerman, B. 2003, ApJ, 584, L33
In the text
NASA ADS
- Zuckerman, B. 2001, ARA&A, 39, 549
In the text
NASA ADS
Copyright ESO 2003
![]() Pictoris. 88 extended emission lines are observed, with the
brightest coming from Fe I, Na I and Ca II. The extent of the gas
disk is much larger than previously anticipated; we trace Na I radially
from 13 AU
out to 323 AU and Ca II to heights of 77 AU above the disk plane,
both to the limits of our observations. The degree of flaring is
significantly larger for the gas disk than the dust disk. A strong
NE/SW brightness
asymmetry is observed, with the SW emission being abruptly truncated at
150-200 AU. The inner gas disk is tilted about 5
Pictoris. 88 extended emission lines are observed, with the
brightest coming from Fe I, Na I and Ca II. The extent of the gas
disk is much larger than previously anticipated; we trace Na I radially
from 13 AU
out to 323 AU and Ca II to heights of 77 AU above the disk plane,
both to the limits of our observations. The degree of flaring is
significantly larger for the gas disk than the dust disk. A strong
NE/SW brightness
asymmetry is observed, with the SW emission being abruptly truncated at
150-200 AU. The inner gas disk is tilted about 5![]() with respect to the outer disk, similar to the appearance of the disk
in light scattered from dust. We show that most, perhaps all, of the
Na I column density seen in the "stable'' component of absorption,
comes from the extended disk. Finally, we discuss the effects of
radiation pressure in the extended gas disk and show that the assumption of
hydrogen, in whatever form, as a braking agent is inconsistent with observations.
with respect to the outer disk, similar to the appearance of the disk
in light scattered from dust. We show that most, perhaps all, of the
Na I column density seen in the "stable'' component of absorption,
comes from the extended disk. Finally, we discuss the effects of
radiation pressure in the extended gas disk and show that the assumption of
hydrogen, in whatever form, as a braking agent is inconsistent with observations.
![]() Pictoris -
stars: circumstellar matter - stars: planetary systems: formation -
stars: planetary systems: protoplanetary disks
Pictoris -
stars: circumstellar matter - stars: planetary systems: formation -
stars: planetary systems: protoplanetary disks
![]() Pic, consisting
of metals, raised the problem why it is not blown away from the
system by the high radiation pressure.
Lagrange et al. (1998) made some detailed calculations and found that the
gas drag from a dense enough H I ring
(
Pic, consisting
of metals, raised the problem why it is not blown away from the
system by the high radiation pressure.
Lagrange et al. (1998) made some detailed calculations and found that the
gas drag from a dense enough H I ring
(
![]() cm-3) close to the star
(
cm-3) close to the star
(![]() 0.5 AU) could brake migrating particles sufficiently,
provided they started out inside the ring.
The picture was complicated by the announcement of H2detected in emission by the Infrared Space Observatory (Thi et al. 2001),
implying large quantities (
0.5 AU) could brake migrating particles sufficiently,
provided they started out inside the ring.
The picture was complicated by the announcement of H2detected in emission by the Infrared Space Observatory (Thi et al. 2001),
implying large quantities (![]() 50
50
![]() )
of molecular
hydrogen, and the sub-sequent report of sensitive upper limits
(
)
of molecular
hydrogen, and the sub-sequent report of sensitive upper limits
(
![]() cm-2) of H2 from
FUV absorption lines using
cm-2) of H2 from
FUV absorption lines using ![]() Pic as a
background source (Lecavelier des Etangs et al. 2001). In addition,
Olofsson et al. (2001, hereafter Paper I) found spatially resolved widespread
gas emission from Na I in the disk, stretching out to at least 140 AU.
Pic as a
background source (Lecavelier des Etangs et al. 2001). In addition,
Olofsson et al. (2001, hereafter Paper I) found spatially resolved widespread
gas emission from Na I in the disk, stretching out to at least 140 AU.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{b0326_f1.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg23.gif)
![]() 0
0
![]() 7), this
resulted in a very high flux gradient between the pixels on and
off the star. By default, the orders are resampled linearly,
but this caused the spectrum to show a periodic "spiky'' pattern
in the flux. We found that linear interpolation does not work
properly due to the strong
non-linear shape of the point spread function (PSF) at the pixel
resolution. By modifying the order extracting routine to use a third
order Catmull-Rom spline interpolation instead of linear, we found
the spikes to be greatly reduced (though not completely eliminated).
7), this
resulted in a very high flux gradient between the pixels on and
off the star. By default, the orders are resampled linearly,
but this caused the spectrum to show a periodic "spiky'' pattern
in the flux. We found that linear interpolation does not work
properly due to the strong
non-linear shape of the point spread function (PSF) at the pixel
resolution. By modifying the order extracting routine to use a third
order Catmull-Rom spline interpolation instead of linear, we found
the spikes to be greatly reduced (though not completely eliminated).
![]() pixels,
plus calibration frames etc., the raw data were close to 50 GB.
pixels,
plus calibration frames etc., the raw data were close to 50 GB.
![]() SW in disk.
SW in disk.![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{b0326_f2.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=17.7cm,clip]{b0326_f3.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg30.gif)
![]() (1
(1![]() ), similar to the
4
), similar to the
4![]() -5
-5![]() tilt observed by HST/STIS in the inner dust
disk (Heap et al. 2000).
tilt observed by HST/STIS in the inner dust
disk (Heap et al. 2000).
![]() 7 to simulate the seeing, is
7 to simulate the seeing, is ![]() 20 AU at 3
20 AU at 3
![]() (58 AU),
similar to the dust disk scale height (Heap et al. 2000). At 6
(58 AU),
similar to the dust disk scale height (Heap et al. 2000). At 6
![]() (116 AU), however,
the gas disk is significantly thicker,
(116 AU), however,
the gas disk is significantly thicker, ![]() 30 AU compared to
30 AU compared to ![]() 15 AU
for the dust (see Fig. 5).
15 AU
for the dust (see Fig. 5).
![]() distance from the star, the emission from the disk midplane is much
fainter than the emission away from the midplane. In particular,
the detected Ca II emission, at 6
distance from the star, the emission from the disk midplane is much
fainter than the emission away from the midplane. In particular,
the detected Ca II emission, at 6
![]() SW of the star, keeps
increasing to the limits of the spectroscopic slit 4
SW of the star, keeps
increasing to the limits of the spectroscopic slit 4
![]() above
the disk midplane, meaning that there is a significant number of
Ca II ions at 77 AU height above the midplane at 116 AU distance
from the star. From Fig. 6 it is evident that the
radial velocities of these Ca II ions are small - on the order
of a few km s-1. Implications of this fact are discussed
in Sect. 5.2.
above
the disk midplane, meaning that there is a significant number of
Ca II ions at 77 AU height above the midplane at 116 AU distance
from the star. From Fig. 6 it is evident that the
radial velocities of these Ca II ions are small - on the order
of a few km s-1. Implications of this fact are discussed
in Sect. 5.2.
![]() Pic
accurately, we averaged the heliocentric gas velocities as
observed on each side at the distances 3
Pic
accurately, we averaged the heliocentric gas velocities as
observed on each side at the distances 3
![]() and 6
and 6
![]() from the star. In this way, we can assess the system velocity
independently from the lines observed in absorption, which are
sensitive to possible radial velocities of the absorbers
(caused by, e.g., radiation pressure). We determined the
heliocentric radial velocity of
from the star. In this way, we can assess the system velocity
independently from the lines observed in absorption, which are
sensitive to possible radial velocities of the absorbers
(caused by, e.g., radiation pressure). We determined the
heliocentric radial velocity of ![]() Pic to be
Pic to be
![]() km s-1, with the error mainly due to the
uncertainty in wavelength calibration.
km s-1, with the error mainly due to the
uncertainty in wavelength calibration.
![]() Pic (Table 3).
Pic (Table 3).
![]() Pic of ions measured in absorption.
Pic of ions measured in absorption.![\begin{figure}
\par\includegraphics[width=15cm,clip]{b0326_f5.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg37.gif)
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{b0326_f6.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg39.gif)
![]() 50), (B) the line ratio
between D2 and D1 is close to 2, implying that the emission
is optically thin, and (C) we expect nearly all Na I atoms
to be in their ground state (see Sect. 5.3), meaning
the resonance D1,2 lines trace all of the Na I population.
The parameters of Eq. (1) were fitted by constructing
a numerical model, simulating observed spatial profiles as
a function of the parameters and
50), (B) the line ratio
between D2 and D1 is close to 2, implying that the emission
is optically thin, and (C) we expect nearly all Na I atoms
to be in their ground state (see Sect. 5.3), meaning
the resonance D1,2 lines trace all of the Na I population.
The parameters of Eq. (1) were fitted by constructing
a numerical model, simulating observed spatial profiles as
a function of the parameters and ![]() -minimising the
difference between the model and the observations. In more
detail, the model was initiated on a three dimensional grid
of height
-minimising the
difference between the model and the observations. In more
detail, the model was initiated on a three dimensional grid
of height ![]() width
width ![]() depth dimensions
40 AU
depth dimensions
40 AU ![]() 800 AU
800 AU ![]() 2000 AU at 1 AU resolution.
The central star was assumed to emit
2000 AU at 1 AU resolution.
The central star was assumed to emit
![]() erg s-1 Å-1 at wavelengths
close to the Na I D2 line, and
erg s-1 Å-1 at wavelengths
close to the Na I D2 line, and
![]() s-1 was
used as the D2 transition Einstein coefficient for
spontaneous emission, in calculating the scattering
cross-section. For each cell, a specific line luminosity
was calculated, summed up along the line of sight and
geometrically diluted to the distance of the observer at 19.3 pc. This "ideal'' image of the disk was then convolved
with a Gaussian of
s-1 was
used as the D2 transition Einstein coefficient for
spontaneous emission, in calculating the scattering
cross-section. For each cell, a specific line luminosity
was calculated, summed up along the line of sight and
geometrically diluted to the distance of the observer at 19.3 pc. This "ideal'' image of the disk was then convolved
with a Gaussian of
![]() ,
simulating the atmospheric
seeing, and sampled along the various spectroscopic
slit settings of Fig. 1 to fit the observations.
In the fit we used the midplane
radial emission distribution from 13 AU out to 323 AU of
the NE, and the orthogonal profiles at 3
,
simulating the atmospheric
seeing, and sampled along the various spectroscopic
slit settings of Fig. 1 to fit the observations.
In the fit we used the midplane
radial emission distribution from 13 AU out to 323 AU of
the NE, and the orthogonal profiles at 3
![]() and 6
and 6
![]() NE of the star. The derived parameters of Eq. (1) for
Na I are:
NE of the star. The derived parameters of Eq. (1) for
Na I are:
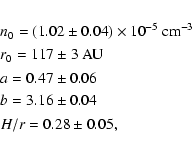
![]() cm-2.
Extrapolating Eq. (1) to all radii, that is,
from zero radius out to infinity, we increase the Na I column density by 40% to
cm-2.
Extrapolating Eq. (1) to all radii, that is,
from zero radius out to infinity, we increase the Na I column density by 40% to
![]() cm-2. This can be compared to
our observed column density
cm-2. This can be compared to
our observed column density
![]() cm-2. We conclude that
most, perhaps all, of the Na I gas seen in absorption
is situated in the extended gas disk seen in emission.
We have no reason to doubt that originators of other
"stable'' gas absorption components also belong to this
extended disk.
cm-2. We conclude that
most, perhaps all, of the Na I gas seen in absorption
is situated in the extended gas disk seen in emission.
We have no reason to doubt that originators of other
"stable'' gas absorption components also belong to this
extended disk.
![]() Pic we estimate
Pic we estimate
![]() and
and
![]() ,
while C depends on the detailed
density and temperature structure. We calculated terminal velocities as a function
of radius for the two models of
Sects. 5.3.1 and 5.3.2. Details of the
solution to Eq. (2), with estimates of C and
,
while C depends on the detailed
density and temperature structure. We calculated terminal velocities as a function
of radius for the two models of
Sects. 5.3.1 and 5.3.2. Details of the
solution to Eq. (2), with estimates of C and ![]() for several ions, are found in Liseau (2003).
for several ions, are found in Liseau (2003).
![]() Pic to be well represented by an ATLAS 9 model (Kurucz 1992)
with
Pic to be well represented by an ATLAS 9 model (Kurucz 1992)
with
![]() K,
K,
![]() (in cm s-2)
and
(in cm s-2)
and
![]() ,
and the effective radius to be
,
and the effective radius to be
![]() ,
implying the luminosity
,
implying the luminosity
![]() .
Recent VLTI observations of
.
Recent VLTI observations of ![]() Pic estimate the stellar
radius to be
Pic estimate the stellar
radius to be
![]() (Di Folco et al. 2003), and
comparing the ATLAS 9 SED of
(Di Folco et al. 2003), and
comparing the ATLAS 9 SED of ![]() Pic with observed data
from the HST and FUSE archives, we find the agreement to be
generally excellent (see Liseau 2003). Some deviations are found in
the far-ultraviolet, where
Pic with observed data
from the HST and FUSE archives, we find the agreement to be
generally excellent (see Liseau 2003). Some deviations are found in
the far-ultraviolet, where ![]() Pic seems to be a slightly
atypical A5V star with possible chromospheric activity
(Bouret et al. 2002).
Pic seems to be a slightly
atypical A5V star with possible chromospheric activity
(Bouret et al. 2002).
![]() ,
would reach
radial velocities on the order of hundreds to thousands km s-1.
That is in clear contradiction with the observed radial velocities
reported in
Table 3. The purported explanation of
Paper I, that Na is ionised most of the time and therefore is
subject to a small average radiation pressure, does not apply to Fe;
indeed, both Fe I and Fe II experience a radiation pressure with
,
would reach
radial velocities on the order of hundreds to thousands km s-1.
That is in clear contradiction with the observed radial velocities
reported in
Table 3. The purported explanation of
Paper I, that Na is ionised most of the time and therefore is
subject to a small average radiation pressure, does not apply to Fe;
indeed, both Fe I and Fe II experience a radiation pressure with
![]() .
We know of only one remaining plausible explanation:
there is a braking agent keeping the gas from reaching high
velocities.
.
We know of only one remaining plausible explanation:
there is a braking agent keeping the gas from reaching high
velocities.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{b0326_f7.eps}
\end{figure}](/articles/aa/full/2004/02/aa0326/Timg86.gif)