A&A 413, 465-476 (2004)
DOI: 10.1051/0004-6361:20034172

Analysis of two-point statistics of cosmic shear

II. Optimizing the survey geometry

M. Kilbinger1 - P. Schneider1,2


1 - Institut f. Astrophysik u. Extr. Forschung, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2 - Max-Planck-Institut f. Astrophysik, Postfach 1317, 85741 Garching, Germany

Received 8 August 2003 / Accepted 30 September 2003

Abstract
We present simulations of a cosmic shear survey and show how the survey geometry influences the accuracy of determination of cosmological parameters. We numerically calculate the full covariance matrices $\mbox{Cov}$ of two-point statistics of cosmic shear, based on the expressions derived in the first paper of this series. The individual terms are compared for two survey geometries with large and small cosmic variance. We use analyses based on maximum likelihood of $\mbox{Cov}$ and the Fisher information matrix in order to derive expected constraints on cosmological parameters. As an illustrative example, we simulate various survey geometries consisting of 300 individual fields of $13^\prime \times 13^\prime $ size, placed (semi-)randomly into patches which are assumed to be widely separated on the sky and therefore uncorrelated. Using the aperture mass statistics $\left\langle M_{\rm ap}^2 \right\rangle$, the optimum survey consists of 10 patches with 30 images in each patch. If $\Omega_{\rm m}, \sigma_8$ and $\Gamma$ are supposed to be extracted from the data, the minimum variance bounds on these three parameters are 0.17, 0.25 and 0.04 respectively. These variances increase slightly when the initial power spectrum index $n_{\rm s}$ is also to be determined from the data. The cosmological constant is only poorly constrained.

Key words: cosmology: observations - gravitational lensing - cosmology: large-scale structure of Universe

1 Introduction

Weak gravitational lensing by the large-scale matter distribution in the Universe, called cosmic shear, has become a valuable tool for cosmology since its first detection in 2000 (Bacon et al. 2000; Wittman et al. 2000; Kaiser et al. 2000; van Waerbeke et al. 2000). Constraints on cosmological parameters, in particular the (dark+luminous) matter density parameter $\Omega _{\rm m}$and the power spectrum normalization ${\sigma _8}$, have been obtained from cosmic shear with survey areas of up to several dozen square degrees (e.g. van Waerbeke et al. 2001; Gladders et al. 2002; Réfrégier et al. 2002; van Waerbeke et al. 2002; Jarvis et al. 2003; Maoli et al. 2001).

Cosmic shear probes the statistical properties of the total matter distribution projected along the line-of-sight between the observer and distant galaxies which are typically at redshifts between 0.5 and 2. It is independent of any possible bias between dark and luminous matter - e.g. no assumptions about how galaxies trace the dark matter have to be made.

Cosmic shear is sensitive to a large number of cosmological parameters, most notably on $\Omega_{\rm m}, \sigma_8$ and the shape parameter $\Gamma$, but also to the source galaxy redshift distribution. The dependancy on these parameters is partially degenerate. Some of these near-degeneracies can be broken when weak lensing is combined with other cosmological measurements like CMB anisotropy experiments, the statistics of the Lyman-$\alpha$ forest or galaxy redshift surveys. The parameter dependencies are very different for the individual methods, for example the $\Omega _{\rm m}$-${\sigma _8}$-degeneracy is nearly orthogonal between cosmic shear and CMB (van Waerbeke et al. 2002). Even the most precise measurement of cosmological parameters up to now, which comes from the first data release of WMAP (Spergel et al. 2003; Bennett et al. 2003), can be improved substantially when weak lensing data is added (Hu & Tegmark 1999; Contaldi et al. 2003).

In the first paper of this series (Schneider et al. 2002, hereafter Paper I), we reviewed the properties and relations of various two-point statistics of cosmic shear. We defined unbiased estimators and calculated their covariances. In Sect. 5 of Paper I, an explicit expression for the covariance of the two-point correlation function was given. Using that, we calculated expected constraints on various cosmological parameters for a cosmic shear survey.

However, this ansatz is an approximation which is only valid for a large and connected survey area. Any real cosmic shear survey will most likely consist of single unconnected fields-of-view and have a complicated geometry. In this paper, we present a method which allows one to calculate the covariance of the two-point functions of cosmic shear for an arbitrary survey geometry.

The measurement of cosmic shear with a sufficient high precision to constrain cosmological parameters requires many independent lines-of-sight, lowering the sampling variance ("cosmic variance''). On the other hand, it is important to measure the shear on a large range of angular scales. Even with modern wide-field imaging cameras, separations of more than a few degrees cannot be accessed by individual fields-of-view - one has to observe some fields near to each other and measure galaxy shape correlations across individual fields. In a recent work (Jarvis et al. 2003), cosmic shear has been measured from 1 to 100 arcmin, and constraints on $\Omega _{\rm m}$ and ${\sigma _8}$ have been obtained.

Kaiser (1998) remarked that for a survey of 9 square degrees, consisting of a single $3^\circ \times 3^\circ$-field, the noise due to the intrinsic ellipticity dispersion can be neglected on large scales, because of the huge number of galaxy pairs. He also noted that cosmic variance is dominant, and that "sparse sampling'', meaning the distribution of smaller fields on a larger region of the sky, reduces the cosmic variance dramatically.

A cosmic shear survey has to cover a large area containing hundreds of thousands of galaxies, whose shapes can be determined. Because telescope time is limited, one has to carefully choose the locations of the pointings, in other words, the geometry of the survey. In this work, cosmic shear surveys with different geometrical configurations are simulated. They are compared with respect to their ability to constrain cosmological parameters, using two-point statistics.

The individual fields-of-view of the simulated surveys are placed in patches on the sky in order to measure the shear correlation on large angular scales. Several patches, distributed randomly on the sky in order to reduce cosmic variance, build up the survey.

The comparison of the geometries is done with a likelihood analysis using the covariances of two-point statistics of cosmic shear. These were derived in Paper I, Sects. 4 and 6. In this paper, the covariance matrices are calculated via a Monte-Carlo-like method using the simulated galaxy positions of the surveys.

The different survey geometries considered here are presented in Sect. 2. In Sect. 3, we review the two-point statistics of cosmic shear relevant for this work, as well as their estimators and covariances, as derived in Paper I. The method for the numerical calculation of the covariances is given in Sect. 4. Results for some patch geometries are presented in Sect. 4.3. A likelihood analysis is performed in Sect. 5, where the expected constraints on pairs of cosmological parameters is considered and compared for various cosmic shear survey geometries. Finally, in Sect. 6, the Fisher information matrix is used to compare constraints on three and four parameters simultanously.

This work is intended to be a preparation for a cosmic shear survey with the wide-field camera VIMOS on the 8.2 m ESO-VLT telescope UT3 (Melipal). The numerical codes used for this paper are publically available[*].

   
2 Survey geometries

The different survey geometries considered in this work consist of circular patches, in which individual images are distributed randomly, but non-overlapping. We define "image'' as one single field-of-view. It is assumed that the shear correlation functions can be measured across image boundaries, thus the cosmic shear can be determined in principle on scales up to the patch diameter. Because there are always bright stars or foreground galaxies which have to be avoided, we cannot specify in much more detail the image positions, thus a random distribution of the images in a patch is assumed.

The patches are assumed to be separated by at least several degrees. On these scales, the correlation functions are virually zero, so different patches can be considered as uncorrelated; they probe statistically independent parts of the large-scale structure.

In our simulations, the individual images are $13^\prime \times 13^\prime $-fields, corresponding roughly to the field-of-view of VIMOS. A survey consists of P patches of radius R, each patch containing N images. The total number of images, $n = P \cdot N$ is kept fixed for all geometries. The larger the number of patches P, the smaller is the cosmic variance. On the other hand, the larger the number of images N per patch, the larger is the number of galaxy pairs for which the correlation is measured, thus the lower is the shot noise. One of the goals of this work is to find a configuration which is optimal in the sense that the two-point correlation function can be measured most accurately; we characterize this "accuracy'' by considering constraints on pairs of cosmological parameters from the measurement of the correlation function.

We use a total image number of n=300, corresponding to 14 square degrees for the whole survey. For N, being a factor of n, the values 10, 20, 30, 50, and 60 are considered, corresponding to geometries with P= 30, 15, 10, 6 and 5 patches, respectively. An illustration of some patches is given in Fig. 1.


  \begin{figure} \par\resizebox{4.2cm}{!}{\includegraphics[clip]{4535.f1a.ps}}\hsp... ...ce*{0.3mm} \resizebox{4.2cm}{!}{\includegraphics[clip]{4535.f1d.ps}}\end{figure} Figure 1: Realisations of patches; the squares represent the individual images. Nis the number of images per patch, R the patch radius. Each image has a size of 13 arcmin.
Open with DEXTER

The patch geometries are compared to a configuration which consists of 300 single uncorrelated images, where "uncorrelated'' again means separated by at least several degrees. This configuration has the smallest possible cosmic variance, but the shear correlation can be only measured up to $\sqrt{2} \times 13$ arcmin.

   
3 Two-point statistics of cosmic shear, their estimators and covariances

We follow here the notation of Bartelmann & Schneider (2001). See Paper I for a more detailed presentation of the formulae reviewed in this Section. Two points $\vec \vartheta$and $\vec \vartheta+ \vec \theta$ define in a natural way a direction given by the connecting vector $\vec \theta$, with respect to which the tangential and cross-component of the shear,

 \begin{displaymath}\gamma_{\rm t} \equiv - ~ \Re \left( \gamma {\rm e}^{-2 {\rm ... ...quiv - ~ \Im \left( \gamma {\rm e}^{-2 {\rm i}\varphi} \right) \end{displaymath} (1)

are defined, where $\varphi$ is the polar angle of the connecting vector. The two independent shear correlation functions $\xi_\pm(\vartheta)$ are related to the power spectrum of the projected matter density $P_\kappa$,
  
                                    $\displaystyle \xi_{\pm}(\theta)$ $\textstyle \equiv$ $\displaystyle \left\langle \gamma_{\rm t}( {\boldmath\hbox{$\vartheta$ }\unbold... ...theta$ }\unboldmath } + {\boldmath\hbox{$\theta$ }\unboldmath } ) \right\rangle$ (2)
  = $\displaystyle \frac{1}{2 \pi} \int\limits_0^\infty {\rm d}\ell ~ \ell ~ P_\kappa(\ell) {\it J}_{0,4}(\ell \theta),$ (3)

where the first-kind Bessel function ${\it J}_0$ (${\it J}_4$) corresponds to the "+'' ("-'') correlation function, see e.g. Kaiser (1992). Another second-order statistics of cosmic shear is the dispersion of the weighted tangential shear in a circular aperture B of radius $\theta$ (Schneider 1996),

 \begin{displaymath}{M_{\rm ap}}(\theta) = \int\limits_{B(\theta)} {\rm d}^2 \vartheta~ Q(\vartheta) \gamma_{\rm t}(\vartheta). \end{displaymath} (4)

With the weight function $Q(\vartheta) = {2}/{\vartheta^2} \int_0^\vartheta{\rm d}\rho ~ \rho ~ U(\rho) - U(\vartheta)$, where U is a compensated filter function, i.e. $\int_0^\theta {\rm d}\vartheta~ \vartheta~ U(\vartheta) = 0$ (Schneider et al. 1998), its dispersion is related to the power spectrum by

 \begin{displaymath}\left\langle M_{\rm ap}^2(\theta) \right\rangle = \frac{1}{2\... ...4 ~ {\it J}_4(\ell \theta)}{( \ell \theta )^2} \right)^2 \cdot \end{displaymath} (5)

This aperture mass measures the gradient component or E-mode of the shear. Analogously to (4), one can also define the weighted cross-component of the shear in an aperture, $\left\langle M_\perp \right\rangle$, which is a measure of the curl component or B-mode only.

The two aperture mass statistics can be expressed in terms of the two-point correlation functions,

 
$\displaystyle \left\langle M_{{\rm ap}, \perp}^2(\theta) \right\rangle = \frac{... ...pm \xi_-(\theta^\prime) T_-\left( \frac{\theta^\prime}{\theta} \right) \right],$     (6)

where T+ and T- are given explicitly in Schneider et al. (2002).

The shear due to the tidal gravitational field of the large-scale structure is a pure gradient field[*] (Kaiser 1995), therefore, no B-modes should be present. However, there are other effects which can produce B-modes; these are mainly systematic measurement errors and intrinsic galaxy orientation correlations. The contribution from the latter can be reduced if the survey is deep, or if photometric redshift information of the source galaxies is taken into account (Heymans & Heavens 2003; King & Schneider 2002). Minor contributions to B-modes are source clustering (Schneider et al. 2002) and higher-order lensing effects (Jain et al. 2000).

The separate measurement of E- and B-modes allows one to quantify contaminations to the gravitational shear signal. In recent cosmic shear surveys, a non-zero B-mode signal has been measured (Hoekstra et al. 2002; Jarvis et al. 2003; van Waerbeke et al. 2002), using the statistics (6). However, a recent re-analysis of the VIRMOS-DESCART data shows no significant B-mode signal any more; the previously found B-modes were obviously due to insufficient PSF corrections[*].

   
3.1 Shear estimators

The shear estimators used here are similar to those introduced in Paper I. For simplicity, all weight factors which account for differences in the precision of ellipticity measurement of individual galaxies are set to unity. Further, we assume that the correlation function is to be estimated in logarithmic bins; therefore, the following function is defined,

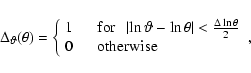\begin{displaymath}\Delta_\vartheta(\theta) = \left\{ \begin{array}{ll} 1 \;\;\;... ...heta}{2} \\ 0 \;\;\;\; & \mbox{otherwise} \end{array}\right., \end{displaymath} (7)

which selects bins with logarithmic bin width $\Delta \ln \theta$around $\vartheta $. Then, if the ith galaxy is located at angular position $\vec \theta_i$ with the observed ellipticity $\varepsilon_i$,

 \begin{displaymath}\hat \xi_{\pm}(\vartheta) = \frac{1}{N_{\rm p}(\vartheta)} \s... ...} _i - {\boldmath\hbox{$\theta$ }\unboldmath } _j\vert\right), \end{displaymath} (8)

are unbiased estimators of the correlation functions (2). Here, $N_{\rm p}(\vartheta)$ is the number of galaxy pairs in the bin corresponding to $\vartheta $. The double sum is performed over all galaxy pairs.

Unbiased estimators for the aperture mass dispersions  $\left\langle M_{\rm ap}^2 \right\rangle$and $\left\langle M_\perp^2 \right\rangle$ are

 
$\displaystyle {\cal M}_\pm(\theta) = \frac{1}{2 \theta^2} \sum_{i=1}^{I} \Delta... ...m \hat \xi_-(\vartheta_i) T_-\left( \frac{\vartheta_i}{\theta} \right) \right],$     (9)

where an index has been attached to the bin width $\Delta \vartheta_i$ to account for variable (e.g. logarithmic) bin widths. The limit I of the sum must be chosen such that $\theta$ is half the upper limit of the Ith bin.

   
3.2 Covariances

In Paper I we calculated the covariance matrices of the estimators defined in the last section. These consist of several terms which we call shot noise or diagonal term (D), mixed term (M) and pure cosmic variance term (V). We perform the following decomposition:

 
$\displaystyle \mbox{Cov}\left(\hat \xi_+, \vartheta_1 ; \hat \xi_+, \vartheta_2\right)$ = D   +   M++   +   V++  
$\displaystyle \mbox{Cov}\left(\hat \xi_-, \vartheta_1 ; \hat \xi_-, \vartheta_2\right)$ = D   +   M-   +   V- (10)
$\displaystyle \mbox{Cov}\left(\hat \xi_+, \vartheta_1 ; \hat \xi_-, \vartheta_2\right)$ = M+-   +   V+-,  

where the individual terms are
 
                                           $\displaystyle D \equiv \frac{\sigma_\varepsilon^4}{F} \bar \delta(\vartheta_1 - \vartheta_2) N_{\rm p}(\vartheta_1)$  
    $\displaystyle M_{++} \equiv \frac {2 \sigma_\varepsilon^2} F ~ \sum_{ijk} \Delta_{\vartheta_1}^{i j} \Delta_{\vartheta_2}^{i k} \xi_+(j k)$  
    $\displaystyle V_{++} \equiv \frac 1 F \sum_{ijkl} \Delta_{\vartheta_1}^{i j} \Delta_{\vartheta_2}^{k l} \Big( \xi_+(i l) \xi_+(j k)$  
    $\displaystyle + \cos 4 (\vp_{il} - \vp_{jk}) \xi_-(i l) \xi_-(j k) \Big)$  
    $\displaystyle M_{--} \equiv \frac{2 \sigma_\varepsilon^2} F ~ \sum_{ijk} \Delta... ...a_1}^{i j} \Delta_{\vartheta_2}^{i k} \cos 4 ( \vp_{ik} - \vp_{ij} ) \xi_+(j k)$ (11)
    $\displaystyle V_{--} \equiv \frac 1 F \sum_{ijkl} \Delta_{\vartheta_1}^{i j} \Delta_{\vartheta_2}^{k l} \Big( \cos 4 (\vp_{ij} - \vp_{il} - \vp_{jk} + \vp_{kl} )$  
    $\displaystyle {}~ \times \xi_-(i l) \xi_-(j k) + \cos 4 ( \vp_{ij} - \vp_{kl} ) \xi_+(i l) \xi_+(j k) \Big)$  
    $\displaystyle M_{+-} \equiv \frac{2\sigma_\varepsilon^2} F ~ \sum_{ijk} \Delta_... ...a_1}^{i j} \Delta_{\vartheta_2}^{i k} \cos 4 ( \vp_{ik} - \vp_{jk} ) \xi_-(j k)$  
    $\displaystyle V_{+-} \equiv \frac 2 F \sum_{ijkl} \Delta_{\vartheta_1}^{i j} \Delta_{\vartheta_2}^{k l} \cos 4 ( \vp_{il} - \vp_{kl} ) \xi_-(i l) \xi_+(j k),$  

with $F \equiv {N_{\rm p}(\vartheta_1)N_{\rm p}(\vartheta_2)}$, $\Delta_\vartheta^{ij} \equiv \Delta_\vartheta(\left\vert \vec \theta_i - \vec \theta_j \right\vert)$ and $\xi_\pm(ij) \equiv \xi_\pm(\left\vert \vec \theta_i - \vec \theta_j\right\vert)$for brevity. $\bar \delta(\vartheta_1 - \vartheta_2)$ is unity if $\vartheta _1$ and $\vartheta _2$ are in the same bin and zero otherwise. $\sigma_\varepsilon$ is the ellipticity dispersion of the galaxies in the absence of shear.

The covariances of the aperture mass dispersions are

 
             $\displaystyle \mbox{Cov}({\cal M}_\pm; \theta_1, \theta_2)$ = $\displaystyle \frac{1}{4 ~ \theta_1^2 \theta_2^2} \sum_{i=1}^{I_1} \sum_{j=1}^{I_2} \Delta \vartheta_i \Delta \vartheta_j \vartheta_i \vartheta_j$  
    $\displaystyle \times \Bigg[ T_+ \left( \frac{\vartheta_i}{\theta_1} \right) T_+... ...\right) \mbox{Cov}\left(\hat \xi_+, \vartheta_i; \hat \xi_+, \vartheta_j\right)$  
    $\displaystyle + T_- \left( \frac{\vartheta_i}{\theta_1} \right) T_- \left( \fra... ...\right) \mbox{Cov}\left(\hat \xi_-, \vartheta_i; \hat \xi_-, \vartheta_j\right)$  
    $\displaystyle \pm T_+ \left( \frac{\vartheta_i}{\theta_1} \right) T_- \left( \f... ...\right) \mbox{Cov}\left(\hat \xi_+, \vartheta_i; \hat \xi_-, \vartheta_j\right)$  
    $\displaystyle \pm T_+ \left( \frac{\vartheta_j}{\theta_2} \right) T_- \left( \f... ...\mbox{Cov}\left(\hat \xi_+, \vartheta_j; \hat \xi_-, \vartheta_i\right) \Bigg].$ (12)

The upper limits $I_k, \; k=1,2,$ must be chosen such that $\theta_k$ is half the upper limit of the Ikth bin. For brevity, the notions $\mbox{Cov}_{++} \equiv \mbox{Cov}(\hat \xi_+, .; \hat \xi_+, .), \mbox{Cov}_{--} \equiv \mbox{Cov}(\hat \xi_-, .; \hat \xi_-, .)$ and $\mbox{Cov}_{+-} \equiv \mbox{Cov}(\hat \xi_+, .; \hat \xi_-, .)$ are used from now on.

We note here that the expressions for the cosmic variance terms Vof the covariances are only valid if the shear field is Gaussian. On scales below $\sim$10 arcmin, the non-Gaussianity of the shear field gets important, e.g. Fig. 4 of van Waerbeke et al. (2002), see also Scoccimarro et al. (1999). On scales below 1 arcmin, the shot noise term D dominates over V, see Fig. 4 of this paper and Fig. 3 of Paper I, thus with the Gaussian assumption we expect to slightly underestimate the covariances in this transition regime between 1 and 10 arcmin.

  \begin{figure} \par\includegraphics[width=8cm,clip]{0172f2.eps}\end{figure} Figure 2: Number of galaxy pairs per angular bin $N_{\rm p}$ against the bin centre $\vartheta $, for a single $13^{\prime} \times 13^{\prime}~$-field. The points are the pair numbers obtained from the subrandom distribution, the dashed line is the approximation $N(\vartheta ) = 2 \pi A n^2 \vartheta \Delta \vartheta $ (Paper I), where A is the survey area and n the galaxy number density, which was taken to be 30 per square arcmin. The dotted curve is from King & Schneider (2003).
Open with DEXTER

   
4 Numerical calculation of the covariance matrices

Given a model for the shear correlation functions or, equivalently, the power spectrum $P_\kappa$, the covariance matrices (10) only depend on the positions of the observed galaxies, in other words, on the survey geometry. For a given data set with known positions of observed galaxies, it is straightforward to calculate the covariances. An a priori estimate of the covariances is made using simulated galaxy positions for the summations in (11). Note that only the positions of the galaxies have to be simulated, not their ellipticities. In order not to introduce artificial Poisson noise, the galaxies are not distributed randomly but subrandomly onto the fields, see Chapter 7 of Press et al. (1992).

Throughout, 20 logarithmic bins in angular separation are used, the smallest bin being centred around 10 arcsec. The largest separation considered is either $\sqrt {2} \times 13^\prime $for the uncorrelated images, or equal to the patch radius R in the case of a patch geometry. Thus, the bin widths differ for geometries with different patch radii.

  \begin{figure} \includegraphics[width=12.2cm,clip]{0172f3.eps}\end{figure} Figure 3: Contour plots of the covariance matrices of the correlation functions (11) and the aperture mass dispersions (12) $\left\langle M_{\rm ap}^2 \right\rangle$ ("E-mode'') and $\left\langle M_\perp^2 \right\rangle$ ("B-mode''), for a single $13^{\prime} \times 13^{\prime}~$-image. Logarithmic contours are used, ranging from $2 \times 10^{-13}$ to 10-8, with 4 spacings per decade. Negative values are plotted as dotted contours. The "boxiness'' of some contour lines is due to the coarse resolution; the matrices are calculated on a logarithmic $20 \times 20 ~ $-grid for  $\vartheta _1$ and  $\vartheta _2$. The axes show  $\vartheta _1$and $\vartheta _2$ in arcmin. Note that the aperture mass covariances can only be calculated up to half the largest scale where the covariances of the correlation functions are known.
Open with DEXTER

The number of galaxy pairs per bin is shown in Fig. 2 for a single $13^{\prime} \times 13^{\prime}~$-field. For intermediate angles, $N_{\rm p}(\vartheta) \propto \vartheta^2$, as follows from Eq. (26) of Paper I, with $\Delta \vartheta \propto \vartheta$ for logarithmic bins. Deviations show up for large scales, which are due to boundary effects and for very small scales, because of the subrandom galaxy distribution. The curve agrees well with the theoretical expectation (King & Schneider 2003).

Throughout, we set the intrinsic ellipticity dispersion to $\sigma_\varepsilon= 0.3$. The number of galaxies per square arcmin, for which a shape mesurement is feasible, is set to 30. To obtain this number density, a limiting R-band magnitude of about 25.5 is needed.

Because the number of operations for the calculation of the covariances increases with the number of galaxies to the fourth power, it is not feasible, except for a very small survey area, to sum over all galaxy positions. Instead, a random subsample of galaxies is used.

The summations over galaxy positions can be written as sums over pairs of galaxies, which have a fixed separation for each matrix element $(\vartheta_1, \vartheta_2)$, as determined by the $\Delta$-functions. Thus it is convenient to store galaxy pairs for each angular bin. The mixed terms M (11) can then be split up into a sum over all those $\vartheta _1$- and $\vartheta _2$-pairs which have a galaxy in common. This can be done efficiently if the pairs for each bin are sorted by galaxy number. The cosmic variance terms V are simply double sums over all $\vartheta _1$- and $\vartheta _2$-pairs.

In order to decrease the computing time to a feasible value, we use random subsamples of all galaxy pairs for the summations, which consists of 300 000pairs per bin for the triple sums and 1000 pairs per bin for the quadruple sums.

The calculation of the individual addends in the covariances is straightforward. The correlation functions are obtained by linear interpolation between grid points calculated beforehand, using (3). The cosine of the sum of angles is expanded into a sum over products of cosines, and by using the relation $\cos 4 \varphi= 2 [ 2 x^2/(x^2+y^2)^2 - 1]^2 - 1$, where $\varphi$ is the polar angle of the vector (x,y), no single time-consuming trigonometric function actually has to be evaluated.

   
4.1 Cosmological model

For the power spectrum of the matter fluctuations, we assume an initial power spectrum $P_{\rm i} \propto k^{n_{\rm s}}$, the transfer function for Cold Dark Matter from Bardeen et al. (1986) and the fitting formula for the non-linear evolution of Peacock & Dodds (1996). The redshift distribution of the source galaxies is (Smail et al. 1995).

 \begin{displaymath}p(z) {\rm d}z = \frac{\beta}{z_0 \Gamma\left(3/\beta\right)} ... ..._0} \right)^2 {\rm e}^{- \left( z/z_0 \right)^\beta} {\rm d}z, \end{displaymath} (13)

where $\Gamma$ denotes the Eulerian gamma function. Our reference cosmology is a flat $\Lambda$CDM model with $\Omega_{\rm m}= 0.3$, $\Omega _\Lambda =0.7$, the shape parameter $\Gamma=0.21$, $n_{\rm s} = 1$ and the normalisation $\sigma_8=1$. The parameters of the redshift distribution are z0=1 and $\beta=1.5$, which corresponds to a mean source redshift of $\approx $1.5.
  \begin{figure} \includegraphics[width=18cm,clip]{0172f4.eps}\end{figure} Figure 4: The diagonal elements of the covariance matrices (10), split up into the individual terms D, M and V (11). Upper row: 300 single uncorrelated images, where the largest scale is $\sqrt {2} \times 13^\prime $ (thick lines) and a patch geometry with N=60 and $R=80^\prime $ (thin lines). Lower row: N=10, $R=100^\prime $ (thick lines) and N=60, $R=100^\prime $ (thin lines). The left and middle panels are logarithmic plots, the y-axis of the right panel is linear. Note that the bin widths are different for the different geometries which affects D. Because logarithmic bins are used, the differences in the bin widths are small, however.
Open with DEXTER

   
4.2 The covariance matrices

In Fig. 3, contour plots of the three covariance matrices are shown for a single $13^{\prime} \times 13^{\prime}~$-field. The diagonal of $\mbox{Cov}_{++}$ is enhanced above the non-diagonal elements only for small angular separations, which is mainly due to the (1/Np)-dependence of the shot noise term D. The $\mbox{Cov}_{--}$-matrix shows a more contrasted diagonal, with a rapid falloff away from the diagonal. This stems from the fact that $\xi_-$filters the convergence power spectrum more locally than $\xi_+$, resulting in smaller intercorrelations of different angular scales. The asymmetric matrix $\mbox{Cov}_{+-}$ has also negative diagonal elements, meaning anticorrelation. For $\vartheta_2 \approx 1.4 ~ \vartheta_1$, $\mbox{Cov}_{+-}$ is zero.

The covariance matrices of the two aperture mass statistics are quite similar to each other, indicating that the third and fourth terms in (12) are small in comparison to the first two terms. Moreover, they also resemble $\mbox{Cov}_{--}$, which is due to the resembling functional behaviour of $\xi_-$ and $\left\langle M_{\rm ap}^2 \right\rangle$; the filter functions for both statistics (J4(x) and [J4(x)/x]2respectively) are strongly peaked and thus filter the power spectrum very locally.

   
4.3 Comparison of various geometries

In Fig. 4, the individual terms (11) contributing to the diagonal ( $\vartheta_1 = \vartheta_2$) of the covariance matrices (10), calculated for four survey geometries, are compared. One sees the $(1/N_{\rm p})$-dependence of D; it decreases as the number of pairs increases towards larger separations. Only for scales comparable to the image or patch boundary, the number of pairs decreases. This leads to an increase of D (see also Fig. 2). For $~ \mbox{Cov}_{++}$, the cosmic variance V dominates on scales larger than about one arcmin. $\mbox{Cov}_{--}$ is dominated by D. The $\mbox{Cov}_{+-}$-elements are very small compared to those of the two symmetric matrices.

In the upper row of Fig. 4, all terms for the two extreme geometries regarding cosmic variance are shown: the 300 uncorrelated images, and the configurations with only five patches with a radius of 80 arcmin. The difference is about a factor of two in the cosmic variance term V++ The other terms are quite similar for the two geometries, except on scales comparable to the image size. V- is much smaller; at this level, the differences between the geometries are presumably mainly due to numerical noise, as well as the negative value at about 0.6 arcmin for the patch geometry. Thus, $\xi_+$ is much more affected by cosmic variance than $\xi_-$.

Obviously, the covariances corresponding to the patch geometry extend to larger angular scales than those for the uncorrelated images. One important question which is adressed in this paper is whether the additional information of the shear on large scales can compensate for the larger cosmic variance on smaller scales.

The lower row of panels of Fig. 4 compares the covariance terms of patch geometries with the same radius, but with a low (N=10) and a high (N=60) image density in the patches. In the first case, there is quite a sharp transition at a scale where the image boundary is exceeded, all terms increase at about 10 arcmin. The case N=60 shows a less drastic change; because of the higher image density, a large number of pairs at this separation on different images is found, thus the transition is smoother.

   
4.4 Comparison with the approximation of Paper I

We compare the single terms of the covariance matrix $\mbox{Cov}_{++}$ (10) obtained by the summation of simulated galaxy positions presented in this paper with the integration method from Paper I, Sect. 5, for a large connected field. We found deviations at large separations, where the assumption validating the approximation for the integration method breaks down. Further, for small separations, the diagonal elements of the mixed term M++ term are enhanced in the summation method. This is due to the discreteness of the galaxies: for $\vartheta_1 = \vartheta_2$, there are $N_{\rm p}(\vartheta_1)$ summands where j=k. This gives a contribution of $N_{\rm p}(\vartheta_1) ~ \xi_+(0)$which is not present for the off-diagonal elements. A similar but smaller contribution adds to V++. These effects do not enter the integration method, where a smooth galaxy distribution is assumed.

Further differences between the two methods were found for the cosine-part of the V++-term which is due to fact that $\xi_-$decreases very slowly for large separations and thus the $\varphi$-integration in Eq. (34) of Paper I obtains a considerable contribution from separations which are larger than the field boundary.

Altogether, the deviations are quite small. In particular, the resulting likelihood contour plots (see next section) are very similar, which confirms the consistency of the two methods.

   
5 Likelihood analysis


  \begin{figure} \includegraphics[width=11.6cm,clip]{4535.f5.eps}\end{figure} Figure 5: 1-$\sigma $, 2-$\sigma $ and 3-$\sigma $ confidence contours of the figure-of-merit (14). Solid lines correspond to $\chi ^2_{\rm tot}$, dotted lines to $\chi ^2_+$ and dashed lines to $\chi ^2_-$. The left panels show the results for the 300 uncorrelated images, the right panels are for a $(N=60, R=80^\prime )$-patch geometry. The parameter $\Sigma _8 \propto \sigma _8$ is defined in (17).
Open with DEXTER

By using the covariance matrices, we construct an à priori estimate on cosmological parameter constraints from a cosmic shear survey. This allows us to compare different survey geometries. As in Paper I, we use the following figure-of-merit:

 \begin{displaymath}\chi^2(p) \equiv \sum_{ij} \left( \xi_i(p) - \xi^{\rm t}_i \r... ... \mbox{Cov}_{ij}^{-1} \left( \xi_j(p) - \xi^{\rm t}_j \right), \end{displaymath} (14)

where the superscript $^{\rm t}$ denotes the fiducial model and p is a set of cosmological parameters which is tested against the fiducial model, as specified in Sect. 4.1. The summation indices label the angular bins of the correlation functions. As noted in Paper I, either $\xi_+$ or $\xi_-$ can be inserted for $\xi$ in (14), in which case the corresponding covariance matrices $\mbox{Cov}_{++}$ or $\mbox{Cov}_{--}$, respectively, have to be used for $\mbox{Cov}$. The resulting function is called $\chi ^2_+$ or $\chi ^2_-$ respectively. The figure-of-merit $\chi ^2_{\rm tot}$ combining all information is obtained using the vector $\xi = \left( \xi_{+1}, \xi_{+2}, \ldots, \xi_{+N}, ~ ~ \xi_{-1}, \ldots, \xi_{-N} \right)$ together with the block matrix

 \begin{displaymath}{\rm Cov} = \left(\begin{array}{ll} {\rm Cov}_{++} & {\rm Cov... ...m] {\rm Cov}_{+-}^{\rm T} & {\rm Cov}_{--}\end{array}\right) . \end{displaymath} (15)

Analogously to (14), a figure-of-merit using the $\left\langle M_{\rm ap}^2 \right\rangle$-statistics can be defined,

 \begin{displaymath}\chi^2_{\rm E}(p) \equiv \sum_{ij} \left( \left\langle M_{{\r... ...langle M_{{\rm ap}}^2(\theta_j) \right\rangle^{\rm t} \right), \end{displaymath} (16)

which is a likelihood measure using only the E-modes. Unfortunately, $\chi_B^2$, using $M_\perp$ and thus testing the B-modes, cannot properly be defined in this way. In the model used throughout in this work, no B-modes are present, thus $\left\langle M_\perp^2 \right\rangle = 0$. The correlation functions (3) only depend on the E-mode power spectrum; up to now, no models for the B-mode power spectrum have been obtained. Predictions of the amplitude of intrinsic galaxy alignment differ by orders of magnitudes and although some observational results have been presented, stringent constraints have not yet been obtained (see Brown et al. 2002, and references therein).

Two of the four parameters $\Omega_{\rm m}, \sigma_8, \Gamma$ and z0 are varied in a few combinations, while all others are kept fixed, with the exception that a flat universe is assumed throughout. In Figs. 5 and 6, the expected likelihood contours for the two extreme geometrical configurations regarding cosmic variance are plotted: the uncorrelated images and the $(N=60, R=80^\prime )$-patch geometry.


  \begin{figure} \includegraphics[width=11.3cm,clip]{4535.f6.eps}\end{figure} Figure 6: Confidence levels of the figure-of-merit (14). As in Fig. 5, 1-$\sigma $, 2-$\sigma $ and 3-$\sigma $ contours are plotted; the solid lines display $\chi ^2_{\rm tot}$, the dotted and dashed lines correspond to $\chi ^2_+$ and $\chi ^2_-$, respectively. The left panels show the results for the 300 uncorrelated images, the right panels are for a $(N=60, R=80^\prime )$-patch geometry.
Open with DEXTER

5.1 ${\Omega _{m}}$ and ${\sigma _8}$

The strongest degeneracy between two parameters exists for  $\Omega _{\rm m}$ and ${\sigma _8}$, which is also expected from simulations and cosmic shear measurements (e.g. van Waerbeke et al. 2002). In order to compensate for the high elongation of the contours, we use the combined parameter

 \begin{displaymath}\Sigma_8 \equiv \sigma_8 \left[ 0.41 + 0.59 \left( \frac{\Omega_{\rm m}}{0.3} \right)^{-0.68} \right]^{-1} \end{displaymath} (17)

which has been obtained in Paper I by fitting the minimum "valley'' in the ( $\Omega _{\rm m}$-${\sigma _8}$)-plot. Clearly, the $\chi ^2_-$-contours are more extended in the case of the uncorrelated images than for the patch geometry. This is because $\xi_-$ contains much information on large scales which is absent in the case of the uncorrelated images. In contrast, the $\chi ^2_+$-contours are tighter in this case than for the patch geometry.

Furthermore, in both cases, the difference between $\chi ^2_+$ and  $\chi ^2_{\rm tot}$ are small. Thus, most of the information concerning cosmology is contained in $\xi_+$; the additional information coming from $\xi_-$ is relatively small.

5.2 Other combinations

There is also a strong degeneracy between other combinations of parameters, as seen in Figs. 5 and 6. In all cases, the $\chi ^2_{\rm tot}$- and $\chi ^2_+$-contours are tighter for the uncorrelated images, whereas the opposite is true for $\chi ^2_-$. The patch survey geometry yields constraints from $\xi_-$ compatible to those from $\xi_+$, in particular when z0 is one of the parameters; for the combination ${\sigma _8}$-z0, the $\chi_-$-contours are even tighter than the $\chi_+$-contours.

   
5.3 Quadrupole moments

For a more detailed analysis, a quantitative description of the $\chi^2$-contour plots presented in the last section is needed. The quadrupole moments of the underlying probability function can be used as a measure of the surface of the contours. These are defined as

 \begin{displaymath}Q_{ij} \equiv \frac{\int {\rm d}^2 p ~ L(p_1, p_2) \left(p_i ... ...left(p_j - p_j^{\rm t}\right)}{\int {\rm d}^2 p ~ L(p_1, p_2)} \end{displaymath} (18)

for i,j = 1,2. The integration variables p1, p2 are the parameters which are plotted on the axis in Figs. 5 and 6. $p_i^{\rm t}$ denotes the value of the parameter of the fiducial set, $L \propto \exp(-\chi^2/2)$ is the likelihood function.

The determinant of the quadrupole moment is then a measure of the surface enclosed by the likelihood contours,

 \begin{displaymath}q \equiv \sqrt{\det Q_{ij}} = \sqrt{ Q_{11} Q_{22} - Q^2_{12}}. \end{displaymath} (19)

If the $\chi^2$-function was quadratic, the likelihood L would be a bivariate Gaussian. If in addition the two parameters p1 and p2 were uncorrelated, $q \propto \Delta p_1 \cdot \Delta p_2$, where $\Delta p_i$ is the variance of pi. In general, the smaller the value of q, the tighter are the likelihood contours, and the better the cosmological parameters can be constrained. For the likelihood function L in (18), or equivalently, for $\chi^2$, the three functions $\chi^2_+, \chi^2_-$ and $\chi ^2_{\rm tot}$ can be inserted. The resulting q's will be refered to as q+, q-and  $q_{\rm tot}$ respectively. When (16) is used as the figure-of-merit, the inferred contour surface measure is $q_{\rm E}$.

Values of q for different geometries are given in Fig. 7. The likelihood contours of all three combinations of parameters considered here show the same behaviour. Note that the values of q only have a sensible meaning when compared to each other for the same combination of cosmological parameters.


  \begin{figure} \includegraphics[width=8.8cm,clip]{0172f7.eps}\end{figure} Figure 7: The parameter q (19) for the $\Omega _{\rm m}$-$\Sigma _8$-contours. On the x-axes, the patch radius Rin arcmin is plotted, thus each point represents a patch geometry with N images in patches of radius R. The horizontal line in the upper panels indicates the value for the 300 uncorrelated images (omitted for q- and $q_{\rm E}$, see also Table 1).
Open with DEXTER

As expected, the tightest constraints are obtained for $q_{\rm tot}$, as it combines the information of all measurements. $q_{\rm tot}$ is almost monotonically decreasing with increasing patch radius R, and with decreasing number of images per patch N. This indicates that cosmic variance is the most crucial source of errors: therefore, large patches and most notably a large number of directions on the sky should be observed.

q+ behaves similarly to $q_{\rm tot}$, but gives less tight constraints on the parameters, as was already seen in the contour plots. The q--behaviour is opposite to $q_{\rm tot}$ and q+. The fact that q- increases towards small image numbers Nper patch is due to the weak dependence on cosmic variance for $\mbox{Cov}_{--}$. Further, small patches give better constraints, indicating that dense sampling on medium scales is more important than large-scale information.

The quadrupole moment measure $q_{\rm E}$ of the $\left\langle M_{\rm ap}^2 \right\rangle$-statistics shows a behaviour similar to q-. This is because of the similarity between $\xi_-$ and $\left\langle M_{\rm ap}^2 \right\rangle$. However, while the R-dependence of $q_{\rm E}$ is quite monotonic, this is not the case for N. For most patch radii R, the tightest constraints are archieved for N=30.

Table 1: Quantitative measures of the $\Omega_{\rm m}~$-${\sigma _8}$ likelihood contours for the 300 uncorrelated $13^\prime \times 13^\prime $ images. Table entries are in units of 10-4.

For the uncorrelated images, values of q are given in Table 1; $q_{\rm tot}$ is smaller than for every patch geometry. As expected, q- is larger than for any patch geometry, because $\xi_-$ is important on medium scales which are not sampled by the uncorrelated images.

In Sect. 6.2, we take into account the simultaneous determination of three and four cosmological parameters.

   
6 Fisher matrix analysis

The Fisher information matrix is defined as

 \begin{displaymath}F_{ij} = \left\langle \frac{\partial^2 [-\ln L]}{\partial p_i... ...ac{\partial^2 \chi^2}{\partial p_i \partial p_j} \right\rangle \end{displaymath} (20)

where L is the likelihood function and $\chi^2$ is the figure-of-merit (14) which depends on the parameters pi(see e.g.Tegmark et al. 1997; Kendall & Stuart 1969). The inverse of the Fisher matrix is a local measure of the curvature at the minimum of $\chi^2$. Its eigenvalues and (pairwise orthogonal) eigenvectors can be interpreted as the axes of an ellipsoid which determines how fast the log-likelihood falls off the maximum in different directions. According to the Cramér-Rao inequality, the smallest possible variance for any unbiased estimator of a parameter pi, if all parameters are to be estimated from the data, is

 \begin{displaymath}\sigma(p_i) = \sqrt{(F^{-1})_{ii}}, \end{displaymath} (21)

thus defining a minimum variance bound.

Because we will later use the $\left\langle M_{\rm ap}^2 \right\rangle$-statistics, we insert (16) into (20) and evaluate the equation at the minimum of $\chi^2$ to get

 \begin{displaymath}F_{ij} = \sum_{kl} \left[\mbox{Cov}^{-1}\left({\cal M}_+\righ... ...l\left\langle M_{\rm ap}^2 \right\rangle_l}{\partial p_j}\cdot \end{displaymath} (22)

Given the covariance matrices, we can easily calculate the minimum variance for the cosmological parameters used in this analysis.

6.1 Comparison with the likelihood

First, we compare the minimum variance bound (21) with the likelihood contours from Sect. 5, using $\chi ^2_{\rm tot}$. In this case, the Fisher information matrix reduces to a $2\times2$ matrix. This comparison is shown in Fig. 8. As expected from the Cramér-Rao inequality, the likelihood contours are larger than the 1-$\sigma $-ellipse from the Fisher matrix. The orientation of the Fisher error ellipse coincides with the likelihood shapes, i.e. the direction of the minimal and maximal degeneracy of parameters is recovered. The larger the degeneracy between two parameters, the larger is the deviation between the local approximation by the Fisher matrix and the likelihood function. For the case where the curvature is fixed (flat Universe, $\Omega_{\rm m}+ \Omega_\Lambda = 1$), the degeneracy is much larger than for a fixed cosmological constant $\Omega _\Lambda =0.7$.


  \begin{figure} \includegraphics[width=8.8cm,clip]{0172f8.eps}\end{figure} Figure 8: 1-$\sigma $-likelihood contours (solid lines) using $\chi ^2_{\rm tot}$(14) compared with the 1-$\sigma $-error ellipse from the Fisher matrix (22): the dashed ellipse is for a flat Universe (as it is the case for the likelihood contours), the dotted one is for $\Omega _\Lambda =0.7$. a/b is the axis ratio of the ellipses (the case $\Omega _\Lambda =0.7$ is in parentheses). The configuration is a survey of 300 uncorrelated images.
Open with DEXTER

   
6.2 More parameters

Next, we calculate the minimum variance bound of three and more parameters out of ( $\Omega_{\rm m}, \sigma_8, \Gamma, \Omega_\Lambda, n_{\rm s}$) simultaneously, corresponding to a full marginalization over these parameters. As seen in Fig. 7, the aperture mass clearly gives less tight constraints than the combined two-point correlation functions. However, this difference gets smaller the more parameters are included, in some cases (for $\Gamma$ and $n_{\rm s}$), the minimum variance bound is even smaller for $\left\langle M_{\rm ap}^2 \right\rangle$. Another advantage of the aperture mass is its ability to separate E- from B-modes (see Sect. 3). Therefore, we will focus on this statistics from now on. However, we must note that because of the local filtering of the power spectrum, very large scales are not well sampled by  $\left\langle M_{\rm ap}^2 \right\rangle$.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{4535.f9.eps}}\end{figure} Figure 9: The minimum variance for the parameters $\Omega _{\rm m}, \Gamma $ and ${\sigma _8}$ using (21) and (22), for the $\left\langle M_{\rm ap}^2 \right\rangle$-statistics. $\Omega _{\rm m}, \Gamma $ and ${\sigma _8}$ are assumed to be determined from the data, all other parameters are kept fixed and a flat Universe is assumed. Each point in the plot represents a patch geometry with N images in patches of radius R. The minimum variance bound for the uncorrelated images is given in Table 2.
Open with DEXTER

Table 2: The minimum variance for several combinations of parameters, for the 300 uncorrelated image configuration. In each row, those parameters which have an entry are assumed to be determined from the data, the other parameters are fixed. The counterpart of the three rows for the patch geometries are the Figs. 9-11.

Figures 9-11 show the minimum variance for a different number of free cosmological parameters for the individual patch geometries. The fixed parameters are set to the values given in Sect. 4.1. In the cases where $\Omega _\Lambda $ is not a free parameter, the prior is a flat Universe ( $\Omega_\Lambda = 1 - \Omega_{\rm m}$).

When taking into account three or more parameters, the uncorrelated image configuration give very poor constraints on these parameters. The minimum variance bound is in most cases more than double the value of the least optimal patch geometry. The reason is that the lack of large-scale information highly raises the degeneracy between parameters. This cannot be compensated by the small cosmic variance.

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{4535.f10.eps}}\end{figure} Figure 10: The minimum variance for the parameters $\Omega _{\rm m}, \Gamma , \sigma _8$ and $\Omega _\Lambda $ using the $\left\langle M_{\rm ap}^2 \right\rangle$-statistics. See Fig. 9 for more details. The minimum variance bound for the uncorrelated images is given in Table 2.
Open with DEXTER


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[clip]{4535.f11.eps}}\end{figure} Figure 11: The minimum variance for the parameters $\Omega _{\rm m}, \Gamma , \sigma _8$ and $n_{\rm s}$ using the $\left\langle M_{\rm ap}^2 \right\rangle$-statistics. See Fig. 9 for more details. The minimum variance bound for the uncorrelated images is given in Table 2.
Open with DEXTER

When adding $\Omega _\Lambda $ as a free parameter (compare Fig. 9 with Fig. 10), the variance of the shape parameter increases by more than a factor of two, whereas the variances of $\Omega _{\rm m}$ and ${\sigma _8}$ are only slightly enhanced. For large patches, the variances of the three parameters are just rescaled, whereas for small patches, the change is more complicated. The constraint on the cosmological constant is very poor, confirming a statement made by Bernardeau et al. (1997).

When the spectral index $n_{\rm s}$ is added (Fig. 11), the minimum variance bound of $\Omega _{\rm m}$ and ${\sigma _8}$ again increase in the same way as when adding $\Omega _\Lambda $, although by a greater amount. The variance on $\Gamma$ changes completely, taking a similar functional form on R and N as the variance on $n_{\rm s}$. The reason for this is, that both parameters determine more or less the shape of the power spectrum, whereas $\Omega _{\rm m}$ and ${\sigma _8}$influence mainly its amplitude.

For each data point in Figs. 9-11, corresponding to a survey with N images in P = 300/N patches, only one realization of the random image positions for each of the P patches was used. We produced some more realizations for two of the patch geometries and found that the scattering of the minimum variance bound is about one percent.

From Fig. 9, the best geometry is a survey with five (N=60, $R=120^\prime$)-patches. Considering Fig. 11, a configuration with N=30 and small R yields the best minimum variance bounds. For both cases, a survey with 30 images and a patch radius of around 100 arcmin seems to be a good choice. However, the patch radius only has a small influence on the minimum variance bound, more important are the number of images per patch and therefore the number of patches.

The difference in the minimum variance bound between individual patch geometries can make up to 25 percent.

   
7 Conclusions

We calculated numerically the covariance matrices (11-12) for the second-order estimators of cosmic shear $\xi_\pm$ and $\left\langle M_{\rm ap}^2 \right\rangle$, which were derived in Paper I, via a Monte-Carlo-like technique. Galaxy positions were simulated for various cosmic shear survey geometries of 14 square degree area. These surveys consisted of a total of 300 images of size $13^\prime \times 13^\prime $ which were randomly distributed in patches on the sky. A number of (semi-)random patch configurations were compared to a survey consisting of 300 completely uncorrelated images. We performed several analyses based on maximum likelihood and the Fisher information matrix, enabling us to estimate the expected constraints on several combinations of cosmological parameters. First, we assumed that only two cosmological parameters are to be determined from the data, fixing all the other parameters. In this case, using both two-point shear correlation functions $\xi_+$ and $\xi_-$ in combination, the tightest constraints were obtained for the uncorrelated image configuration. Further, patch geometries with small cosmic variance gave also good results. For the aperture mass statistics $\left\langle M_{\rm ap}^2 \right\rangle$, the best results came from a patch geometry with N=30 images in 10 patches of radius $R=60^\prime$. The uncorrelated images could not compete with any patch geometry.

We then took into account three and four cosmological parameters out of ( $\Omega_{\rm m}, \sigma_8, \Gamma, \Omega_\Lambda, n_{\rm s}$). The more parameters are assumed to be determined from the data, the more important becomes large-scale information in order to resolve the near parameter degeneracies. Using the combined $\xi_+$ and $\xi_-$, some of the patch geometries yield tighter constraints than the uncorrelated image configuration. The aperture mass is best applied to patches with N=30 images, the results are nearly independent of the patch radius in most cases.

In most cases, the constraints obtained from the combined $\xi_+$ and $\xi_-$ were tighter than those from $\left\langle M_{\rm ap}^2 \right\rangle$. However, the differences became smaller the more cosmological parameters were included.

The differences between the individual patch geometries made up to 25 percent for the minimum variance bound on several parameters. Thus, a 25 percent improvement on the determination on cosmological parameters can be obtained solely by choosing an appropriate geometry for a future cosmic shear survey.

Acknowledgements
The authors want to thank Lindsay King, Ludovic van Waerbeke and Patrick Simon for useful discussions, and the anonymous referee for helpful suggestions.

References


Copyright ESO 2003