Table 3 and Appendix A are only available in electronic form at http://www.edpsciences.org

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Note that some of the APED lines are defined in the j-j coupling formalism, while CHIANTI always uses the L-S coupling expression.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ones

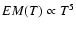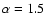Note that there is no mean of obtaining $EM(T) \propto T^{5}$ by summing up emission measure distributions whose ascending slope is $\alpha =1.5$ .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... widths

Note that they made single-Gaussian fits to line profiles also in cases, such as the Fe XXI line, where the profile is flat-topped and decidedly non-Gaussian.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... work

The formation temperature of the O V 1371 Å line is outside the range of temperatures where the EM(T) has been reconstructed.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... reconstruction

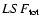This is the reason why we chose the Lorentzian function as the line profile. We have also tried to perform the fitting to the $LSF_{\rm tot}$ with Gaussians and beta-functions: in the first case, the observed line profile is poorly matched both in the core and in the line wings; in the case of beta-functions, we found an even better approximation of the core, with respect to the case of the lorenzian; yet, since these functions fall off very rapidly away from the maximum, their integrals were systematically lower than that of the ${\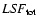it LSF}_{\rm tot}$ by $\sim$ $20\%$ (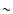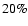or more). So, using the beta-function as the line profile would have required corrections for all measurements and would have implied errors larger than those we have obtained using the Lorentzian.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.